MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
OpenCL: ネィティブから、より洞察力のあるプログラミングへ

OpenCL: ネィティブから、より洞察力のあるプログラミングへ

MetaTrader 5 — 例 | 28 10月 2015, 16:12
5 067 0
Sceptic Philozoff
Sceptic Philozoff

はじめに

最初の記事 "OpenCL: The Bridge to Parallel Worlds（OpenCL：平行世界への架け橋）" は、OpenCLのトピックへのイントロダクションです。OpenCL(カーネルとも呼ばれます)のプログラムとMQL5の外部（ホスト）プログラムの連携における基本的な問題について焦点を当てています。いくつかの言語のパフォーマンス能力（例えば、ベクトルデータ型の使用など）は、pi = 3.14159265...の計算によって例示されます。

プログラムのパフォーマンスの最適化は、相当なものです。しかしながら、すべての最適化は、計算を実行するために使用されるハードウェアの特性を考慮に入れていないため、ネィティブのものとなっています。これらの特性に関する知識は、多くの場合、CPUの能力を超える速度の向上につながります。

これらの最適化を紹介するために、著者は、OpenCLの文献にて研究された例に頼る必要がありました。それは二つの大きい行列の掛け算です。

まずは主要なものから始めましょう - 実際のハードウェアアーキテクチャでの実装の特徴と、OpenCLのメモリーモデルについてです。


1. モダンなコンピューティング機器におけるメモリーヒエラルキー

1.1. OpenCLメモリモデル

一般的に、メモリシステムは、コンピューターのプラットフォームによって、それぞれ大きく異なっています。例えば、現代のCPUは、自動的なデータの取得をサポートしており、反対にGPUはサポートしていません。

コードの汎用性を保証するために、抽象的なメモリモデルがOpenClに適用されており、このモデルを実際のハードウェアに実装する必要のあるベンダーやプログラマは、違いを考える必要がありません。OpenCLで定義されているメモリは、以下の図にて示されています。

OpenCLメモリモデル

図1. OpenCLメモリモデル

データがホストからデバイスに移されれば、グローバルデバイスメモリに格納されます。反対の方向に移されるデータは、グローバルメモリに格納されます（しかし、今回は、グローバルホストメモリです。）キーワードである__global(アンダースコア二つです!)は、特定のポインターに関連するデーターは、グローバルメモリに格納されることを示す修飾子です。  

__kernel void foo( __global float *A ) { /// kernel code }

グローバルメモリはホストのRAMのようなデバイス内のユニットにアクセス可能です。

コンスタントメモリは、名前に対して、必ずしも読み込み専用のデータを格納しません。この種類のメモリは、それぞれの要素が同時にすべてのワークユニットからアクセスされるデータのために設計されています。定数の変数は、このカテゴリーに当てはまります。OpenCLモデルのコンスタントメモリは、グローバルメモリの一部であり、グローバルオブジェクトに移されたメモリオブジェクトは、__constantとして明記されます。

ローカルメモリは、アドレス部分がそれぞれのデバイスで異なるメモ帳メモリです。ハードウェアにて、オンチップメモリの形ですが、OpenCLにおけるものと同じものである要求はありません。

ローカルメモリはすべてのワークグループからアクセス可能であり、つまり、そのグループ内のすべてのワークユニットにて共有され、その他のワークグループからアクセスできません。

この種類のメモリへのアクセスは、より少ない待ち時間であり、そのメモリの帯域幅は、グローバルメモリのものよりも大きいです。カーネルのパフォーマンス最適化のための待ち時間を利用します。

OpenCLの明記では、ローカルメモリの変数は、カーネルヘッダーの両方にて宣言されていると述べられています。

__kernel void foo( __local float *sharedData ) { }
ボディ部分；
__kernel void foo( __global float *A )
{
   __local float sharedData[ 64 ];   
}
動的な配列は、カーネルボディでは宣言されないことに注意してください。サイズを常に明記してください。


二つの大きい行列の掛け算のためのカーネルの最適化にて、ローカルデータを扱う方法や、MetaTrader5での実装の特徴を紹介します。

プライベートメモリはそれぞれのワークユニットにて固有のものです。そのユニットからしかアクセスできず、その他のワークユニットとは共有されていません。

ローカル変数とポインターを含まないカーネルの引数は標準としてプライベートです。（もし__local修飾なしで明記され場合)これらの変数は、レジスター内に位置しています。また逆もしかりで、プライベートの配列や こぼれたレジスターは、普通、オフチップメモリに格納されており、高いレイテンシメモリです。Wikipediaから関連する情報を引用します：

多くのプログラミング言語では、プログラマは、多くの変数を恣意的に配置する錯覚を持っています。しかしながら、コンパイル中、コンパイラはこれらの変数を小さい限られたレジスター内に配置する方法を決定しなければなりません。すべての変数が、同時に使用されず、いくつかのレジスターが一つ異常の変数を割り当てられる場合もあります。しかし、使用される二つの変数は、同時に同じレジスターに値を破壊せず割り当てられません。

いくつかのレジスターに配置できない変数は、RAMの中で保存され、すべての読み書き時にロードされます。RAMへのアクセスは、レジスターへのアクセスよりもかなり遅く、コンパイルされたプログラムの実行速度を落とします。なので、最適化するコンパイラーは、できる限り多くの変数をレジスターに割り当てようとします。レジスタープレッシャーは、最適な数よりも少ないハードウェアレジスタしかない場合に使用されます；高いプレッシャーは、普通、より多くのあふれやリロードが必要であることを意味します。

限られたチップエリアでの多いコア数のため、たくさんのレジスターを持つことができず、レジスタープレッシャーは、GPUのプログラミングの現実です。


紹介されたOpenCLメモリモデルは、GPUのモダンな構造にとても似ています。以下の図は、OpenCLメモリとGPUAMD Radeon HD 6970メモリモデル間の関係を示します。

図2. Radeon HD 6970メモリすとらくちゃ　と、抽象的OpenCLメモリモデルの関係

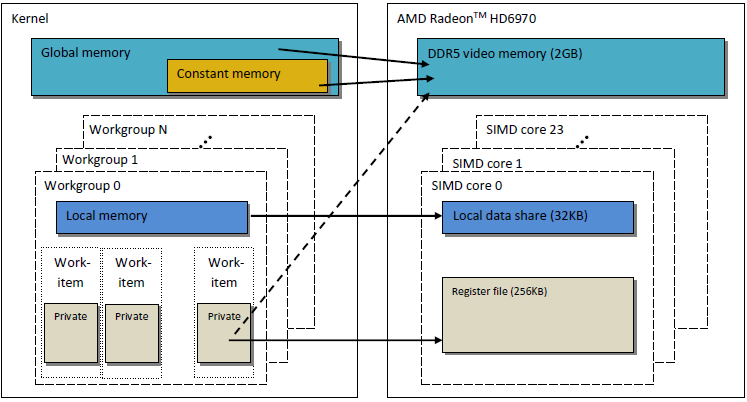
図2. Radeon HD 6970メモリすとらくちゃ　と、抽象的OpenCLメモリモデルの関係

特定のGPUメモリに関連する問題について詳しく見ていきましょう。


1.2. モダンな離散GPUのメモリ

1.2.1. 癒合するメモリ要求

この情報は、カーネルの実行の最適化において重要で、主なゴールは、高いメモリ帯域幅を獲得することです。

以下の図をよく見て、メモリのアドレス指定プロセスを理解しましょう。

図3. グローバルデバイスメモリのデータへのアドレス指定のスキーム

図3. グローバルデバイスメモリのデータへのアドレス指定のスキーム

intの変数の配列へのポインターが、Х = 0x00001232というアドレスであると想定します。すべてのintが４バイトのメモリを取ります。スレッド (カーネルコードを実行するワークユニットのソフトウェア類似物です）は、X[ 0 ]にデータのアドレス指定すると考えます: 

int tmp = X[ 0 ];

メモリのバス幅は、32バイト (256ビットであるとします。. このバス幅は、Radeon HD 5870などの強力なGPUsには典型的なものです。いくつかのGPUでは、データのバス幅は異なり、例えば、NVidiaモデルでは384ビットや、512になります。

メモリバスのアドレス指定は、そのストラクチャーに一致する必要があります。つまり、メモリのデータは、32バイト（256ビット）のブロックに格納されます。0x00001220から0x0000123Fの範囲内でのアドレス指定に関係なく、 (この範囲には正確に32バイトあります)0x00001220を読み込みの開始地点として取得できます。

0x00001232へのアクセスは、 0x00001220から0x0000123Fの範囲内のアドレスの全データを返します。それゆえ、28バイト（７ユニット数）が役に立たない一方、４倍との使用可能なデータが残ります。

図4. メモリから必要なデータを取得するスキーム

以前明記したアドレス0x00001232に位置する数字は、スキーム内にて囲まれています。

バスの使用を最大化するためには、GPUは、異なるスレッドからのメモリアクセスを、一つのメモリ要求に統合しようとします。より少ないメモリアクセスであればあるほど、良いです。その理由は、グローバルデバイスメモリへのアクセスは、時間がかかり、大いにそのプログラムにスピードを要させるためです。カーネルのコードの以下の行を考えてみてください：

int tmp = X[ get_global_id( 0 ) ];

私たちのX配列は、上記の例の配列であると想定してください。それから、最初の16のスレッド（カーネル）は、 0x00001232から0x00001272のアドレスにアクセスします（この範囲では16の数字、64バイトがあります。）もしすべての要求が、一つのメモリ要求に統合されずにカーネルにより個別に送られれば、それぞれの16の要求は、役に立つ4バイトと役に立たない28のバイトを含み、64の使用済み、448の使用されていないバイト数を作成します。

この計算は、同じ32のバイトメモリブロックに位置するアドレスへのすべてのアクセスは、同一のデータを返すということに基づいています。これは重要な点です。複数の要求をひとつの一貫した要求に統合し、使用しない要求に保存することがより正しいです。この処理は、統合要求と呼ばれ、コヒーレントと呼ばれます。


図5. ３つのメモリ要求は、必要なデータを取得するために必要です。

上記の図の各セルは４バイトです。例では、３つの要求で十分です。もしその配列の最初が、各32バイトのメモリブロックの最初のアドレスに沿っていれば、２つのリクエストのみでも十分です。

AMD GPU 64では、スレッドは、波先 の一部であり、それゆえ、SIMDの実行内と同様の指示を実行する必要があります。get_global_id(0)によって調整された16スレッドは、波先の丁度4分の１であり、効率的なバスの使用のためにコーヒレント要求に統合されます。

以下は、「自発的な」要求と比較されるコーヒレントリクエストに必要なメモリ帯域幅の図示です。Radeon HD 5870を含みます。類似の結果は、NVdiaカードのために監視されます。

図6. コーヒレントと非コーヒレント要求のために必要なメモリ帯域幅の比較分析

コーヒレントメモリ要求は、ひとつの注文のによりメモリ帯域幅を拡大することができることがわかると思います。


1.2.2. メモリバンク

メモリは、データが格納されるバンクからなります。モダンGPUでは、32ビットの単語があります。シリアルデータは、隣接するメモリバンクに格納されています。シリアル要素にアクセスするスレッドのグループは、バンクコンフリクトを生みません。

最大のバンクコンフリクトによる悪影響はローカルのGPUメモリにて監視されます。そのため、隣接するスレッドからのローカルデータへのアクセスは異なるメモリバンクをターゲットとすることが望ましいです。

AMDハードウェア上では、バンクコンフリクトを生成する波先は、ローカルメモリの処理が完了するまで停止します。これが、 シリアライゼーション につながり、並列化にて実行されるコードが順番に実行されます。カーネルのパフォーマンスに悪影響を与えます。

図7. バンクコンフリクトなしのメモリアクセスのスキーム

その図は、バンクコンフリクトなしのメモリアクセスのスキームを示し、すべてのスレッドは異なるデータへアクセスしています。

それでは、バンクコンフリクトのメモリアクセスを紹介します。


図8. バンクコンフリクトのあるメモリアクセス

その状況には、例外があります：もしすべてのアクセスが同じアドレスに対してであれば、そのバンクは遅延を避けるためにブロドキャストを実行します。

図9. すべてのスレッドは、同じアドレスにアクセスします。

類似したイベントは、グローバルメモリへアクセス時に発生しますが、そのようなコンフリクトの影響は、とても低いです。

1.2.3. GPUメモリ：結論
  • GPUメモリはCPUメモリとは異なります。プログラムのパフォーマンスのOpenCLを使用した最適化の目的は、CPU上のようにレイテンシーを下げるかわりに、最大の帯域幅を保証することです。
  • メモリアクセスの性質は、バスの使用の効果への影響を持っています。低いバスの使用の効果は、低い稼働スピードを意味します。
  • コードのパフォーマンスを向上するために、メモリアクセスはコーヒレントである必要があります。さらに、バンクコンフリクトを避けることが望ましいです。
  • ハードウェアの明記（バス幅、メモリバンクの数、シングルコーヒレントアクセスのために統合されるスレッド数）は、ベンダーに提供されるドキュメントで見つけることができます。

Random 5xxxシリーズビデオカードの明記は、以下の例のように定められています。

図10. ミドルとハイエンドのRadeon HD 58xxビデオカードの技術的詳細

それでは、プログラミンングに進みます。

2. 二乗の行列の掛け算：シリアルCPUコードから、並列GPUコードまで

2.1. MQL5コード

以前の記事"OpenCL: The Bridge to Parallel Worlds「OpenCL: 並列世界への架け橋」"でのタスクは、標準、つまり、二つの行列の掛け算です。主題についての情報は、異なるソースにて見つけることができるという事実のせいで、選ばれます。多くは、多かれ少なかれ調整されたソリューションを提供しています。これは、ステップごとのモデルストラクチャーの意味の分類を提供し、下方向へ向かう道ですが、一方実際のハードウェアに取り組むことを覚えておきましょう。

コンピューターの計算のために修正された線形幾何学の行列の掛け算の公式が以下です。最初のインデックスは、行列の列数、二番目のインデックスは、カラム数です。行列のすべての要素は、最初と二番目の行列内のそれぞれの要素を合計に追加することで、計算されます。最終的に、この合計は、計算されたアウトプット行列の要素です：

図11. 行列掛け算の公式

以下のように示されます。

図12. 模式的に示されている掛け算アルゴリズム（行列の要素の計算により例示されています）

図12. 模式的に示されている掛け算アルゴリズム（行列の要素の計算により例示されています）

両方の行列はNと同じ次元、足し算と掛け算の数を持っていることは、関数O(N^3)によって推定されます：すべての行列の要素を計算するには、最初の行列の列のスカラと、二番目の行列のカラムのスカラを得る必要があります。およそ2:Nの足し算と掛け算を必要とします。必要なステイは、行列N^2の数をかけることがで取得できます。従って、そのコードの稼働時間はNの３乗に依存しています。

行列の列とカラムの数は、都合により2000に設定されます。任意ですが、大きすぎてはいけません。

MQL5のコードはそこまで複雑ではありません：

//+------------------------------------------------------------------+
//|                                                matr_mul_2dim.mq5 |
//+------------------------------------------------------------------+
#define ROWS1           1000        // rows in the first matrix
#define COLSROWS        1000        // columns in the first matrix = rows in the second matrix 
#define COLS2           1000        // columns in the second matrix

float first[ ROWS1  ][ COLSROWS ];  // first matrix
float second[ COLSROWS ][ COLS2 ];  // second matrix
float third[ ROWS1 ][ COLS2 ];      // product
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   MathSrand(GetTickCount());

   Print("=======================================");
   Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2));

   genMatrices();
   ArrayInitialize(third,0.0f);

//--- execution on the CPU
   uint st1=GetTickCount();
   mul();
   double time1=(double)(GetTickCount()-st1)/1000.;
   Print("CPU: time = "+DoubleToString(time1,3)+" s.");

   return;
  }
//+------------------------------------------------------------------+
//| i2s                                                              |
//+------------------------------------------------------------------+
string i2s(int arg) { return IntegerToString(arg); }
//+------------------------------------------------------------------+
//| genMatrices                                                      |
//| generate initial matrices; this generation is not reflected      |
//| in the final runtime calculation                                 |
//+------------------------------------------------------------------+
void genMatrices()
  {
   for(int r=0; r<ROWS1; r++)
      for(int c=0; c<COLSROWS; c++)
         first[r][c]=genVal();

   for(int r=0; r<COLSROWS; r++)
      for(int c=0; c<COLS2; c++)
         second[r][c]=genVal();

   return;
  }
//+------------------------------------------------------------------+
//| genVal                                                           |
//| generate one value of the matrix element:                        |
//| uniformly distributed value lying in the range [-0.5; 0.5]       |
//+------------------------------------------------------------------+
float genVal()
  {
   return(float)(( MathRand()-16383.5)/32767.);
  }
//+------------------------------------------------------------------+
//| mul                                                              |
//| Main matrix multiplication function                              |
//+------------------------------------------------------------------+
void mul()
  {
// r-cr-c: 10.530 s 
   for(int r=0; r<ROWS1; r++)
      for(int cr=0; cr<COLSROWS; cr++)
         for(int c=0; c<COLS2; c++)
            third[r][c]+=first[r][cr]*second[cr][c];

   return;
  }

リスト1. ホストの初期のシーケンシャルなプログラム

異なるパラメーターを使用したパフォーマンス

2012.05.19 09:39:11    matr_mul_2dim (EURUSD,H1)    CPU: time = 10.530 s.
2012.05.19 09:39:00    matr_mul_2dim (EURUSD,H1)    ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000
2012.05.19 09:39:00    matr_mul_2dim (EURUSD,H1)    =======================================

2012.05.19 09:41:04    matr_mul_2dim (EURUSD,H1)    CPU: time = 83.663 s.
2012.05.19 09:39:40    matr_mul_2dim (EURUSD,H1)    ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.19 09:39:40    matr_mul_2dim (EURUSD,H1)    =======================================


ご覧の通り、稼働時間の線形行列サイズの依存は、真実であるようです：二重の行列の規模での拡大は、稼働時間の８重の増加につながりました。

そのアルゴリズムについて：ループの順番は、mul()関数ににて任意で変更できます。それは稼働時間に影響を与えます：最も遅いものと早い稼働時間の対比は、1.73に近くなります。

この記事は、最も早いものを紹介しています：残りのテスト版はこの記事の最後に貼り付けられたコードにあります（matr_mul_2dim.mq5）OpenCL Programming Guide (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) は以下のように言っています。512):

[これらの順序]は、メモリアクセスを変更するためにあり、３つの行列の中身がCPUで流されている通り、きゃあしゅからデータの再使用を変更します。

実装できる初期の「非並列」コードの最適化のすべてはありません。いくつかは、((S)SSEx instructions) ハードウェアに関連しており、その他はアルゴリズムに関連するものですStrassen アルゴリズム, Coppersmith–Winograd アルゴリズムなどです。古典的なアルゴリズムの速度の向上につながるStrassenアルゴリズムのための掛け算された行列のサイズは、小さく、64x64ほどです。この記事では、5000までの線のサイズである行列の掛け算をできるようにします。


2.2. OpenClのアルゴリズムの最初の実装

このアルゴリズムをOpenCLに移植し、ROWS1 * COLS2スレッドを作成しましょう。つまり、カーネルから外部のループを削除します。各スレッドは、COLSROWS反復を実行し、内部のループがカーネルの一部に残るようにします。

OpenCLカーネルのために３つの線形バッファーを作成しなければならないため、できるかぎりカーネルのアルゴリズムと類似するよう初期のアルゴリズムに再度取り組むことが合理的です。線形バッファのある「シングルコア CPU」の「非並列」プログラムのコードは、カーネルコードとともに提供されます。二次元配列のコードの最適性は、その類似物が線形バッファに最適になります：すべてのテストは繰り返される必要があります。それゆえ、線形幾何学の行列の掛け算の標準ロジックに一致する初期のバリアントとしてc-r-crを選択します。

混乱を生みだすような可能な行列/バッファー要素を避けるために、主な質問に答えてください：もし行列Matr(NカラムのM行)はが線形バッファーとしてグローバルGPUメモリに設計されるのであれば、Matr[ row ][ column ]の要素の線形シグとをどのように計算できるのでしょうか？

その問題のロジックのみによって決定されるため、GPUメモリに行列を設計する固定された順序はありません。例えば、両方の行列の要素は、バッファーとは異なった形で設計されます。というのも、行列掛け算アルゴリズムに関する限り、行列は非対称であり、最初の列は、二番目の行列のカラムによって掛け算されるためです。そのような再調整は、行列要素のグローバルCPメモリからのカーネルの反復におけるシーケンシャルな読み取りにおける計算のパフォーマンスに影響を与えます。

そのアルゴリズムの最初の実装は、同様の方法、主要な順番で設計された行列を特色とします。最初の行の要素はに番目の列などの要素によって続くバッファに格納されます。線形メモリでのMatr[ M (rows) ][ N (columns) ]の行列の二次元での表現を平坦化する公式は以下のようになります；

Matr[ row ][ column ] = buff[ row * N (Total_columns) + column ]


図13. GPUバッファに行列を設計するために、二次元インデックススペースを転換するアルゴリズム

図13. GPUバッファに行列を設計するために、二次元インデックススペースを転換するアルゴリズム

その図は、二次元の行列の表現は、カラムの順番で線形メモリに平坦化される方法の例を示しています。
以下は、OpenCLデバイスにて実行されたプログラムの実装のコードをわずかに減らします。

//+------------------------------------------------------------------+
//|                                                matr_mul_1dim.mq5 |
//+------------------------------------------------------------------+
#property script_show_inputs

#define ROWS1       2000      // rows in the first matrix
#define COLSROWS    2000      // columns in the first matrix = rows in the second matrix 
#define COLS2       2000      // columns in the second matrix
#define REALTYPE    float

REALTYPE first[];           // first linear buffer (matrix)     rows1 * colsrows
REALTYPE second[];          // second buffer                    colsrows * cols2
REALTYPE thirdGPU[ ];       // product - also a buffer          rows1 * cols2
REALTYPE thirdCPU[ ];       // product - also a buffer          rows1 * cols2

input int _device=1;           // here is the device; it can be changed (now 4870)

string d2s(double arg,int dig) { return DoubleToString(arg,dig); }
string i2s(long arg)           { return IntegerToString(arg); }

//+------------------------------------------------------------------+
const string clSrc=
                   "#define COLS2     "+i2s(COLS2)+"                                  \r\n"
                   "#define COLSROWS  "+i2s(COLSROWS)+"                               \r\n"
                   "#define REALTYPE  float                                             \r\n"
                   "                                                                    \r\n"
                   "__kernel void matricesMul( __global REALTYPE *in1,                  \r\n"
                   "                           __global REALTYPE *in2,                  \r\n"
                   "                           __global REALTYPE *out  )                \r\n"
                   "{                                                                   \r\n"
                   "  int r = get_global_id( 0 );                                       \r\n"
                   "  int c = get_global_id( 1 );                                       \r\n"
                   "  for( int cr = 0; cr < COLSROWS; cr ++ )                           \r\n"
                   "     out[ r * COLS2 + c ] +=                                        \r\n"
                   "              in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];     \r\n"
                   "}                                                                   \r\n";
//+------------------------------------------------------------------+
//| Main matrix multiplication function;                             |
//| Input matrices are already generated,                            |
//| the output matrix is initialized to zeros                        |
//+------------------------------------------------------------------+
void mulCPUOneCore()
  {
//--- c-r-cr: 11.544 s 
//st = GetTickCount( );
   for(int c=0; c<COLS2; c++)
      for(int r=0; r<ROWS1; r++)
         for(int cr=0; cr<COLSROWS; cr++)
            thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c];

   return;
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   initAllDataCPU();

//--- start working with non-parallel version ("bare" CPU, single core)
//--- calculate the output matrix on a single core CPU
   uint st=GetTickCount();
   mulCPUOneCore();

//--- output total calculation time
   double timeCPU=(GetTickCount()-st)/1000.;
   Print("CPUTime = "+d2s(timeCPU,3));

//--- start working with OCL
   int clCtx;             // context handle
   int clPrg;             // handle to the program on the device
   int clKrn;             // kernel handle
   int clMemIn1;          // first (input) buffer handle
   int clMemIn2;          // second (input) buffer handle
   int clMemOut;          // third (output) buffer handle

//--- start calculating the program runtime on GPU  
//st = GetTickCount( );  
   initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut);

//--- start calculating total OCL code runtime
   st=GetTickCount();

   executeGPU(clKrn);

//--- create a buffer for reading and read the result; we will need it later
   REALTYPE buf[];
   readOutBuf(clMemOut,buf);

//--- stop calculating the total program runtime 
//--- together with the time required for retrieval of data from GPU and transferring it back to RAM
   double timeGPUTotal=(GetTickCount()-st)/1000.;
   Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec.");

   destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut);

//--- calculate the time elapsed
   Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3));

//--- debugging: random checks. Multiplication accuracy is checked directly 
//--- on the initial and output matrices using a few dozen examples
   for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2);

   Print("________________________");
   return;
  }
//+------------------------------------------------------------------+
//| initAllDataCPU                                                   |
//+------------------------------------------------------------------+
void initAllDataCPU()
  {
//--- initialize random number generator
   MathSrand(( int) TimeLocal());
   Print("=======================================");
   Print("1st OCL martices mul:  device = "+i2s(_device)+";      ROWS1 = " +i2s(ROWS1)+
          "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2));

//--- set the required sizes of linear representations of the input and output matrices
   ArrayResize(first,ROWS1*COLSROWS);
   ArrayResize(second,COLSROWS*COLS2);
   ArrayResize(thirdGPU,ROWS1*COLS2);
   ArrayResize(thirdCPU,ROWS1*COLS2);

//--- generate both input matrices and initialize the output to zeros 
   genMatrices();
   ArrayInitialize( thirdCPU, 0.0 );
   ArrayInitialize( thirdGPU, 0.0 );

   return;
  }
//+------------------------------------------------------------------+
//| initAllDataCPU                                                   |
//| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]:     |
//| Matr[row][column] = buff[row * N(columns in the matrix) + column]| 
//| generate initial matrices; this generation is not reflected      |
//| in the final runtime calculation                                 |
//| buffers are filled in row-major order!                           |
//+------------------------------------------------------------------+  
void genMatrices()
  {
   for(int r=0; r<ROWS1; r++)
      for(int c=0; c<COLSROWS; c++)
         first[r*COLSROWS+c]=genVal();

   for(int r=0; r<COLSROWS; r++)
      for(int c=0; c<COLS2; c++)
         second[r*COLS2+c]=genVal();

   return;
  }
//+------------------------------------------------------------------+
//| genVal                                                           |
//| generate one value of the matrix element:                        |
//| uniformly distributed value lying in the range [-0.5; 0.5]       |
//+------------------------------------------------------------------+
REALTYPE genVal()
  {
   return(REALTYPE)((MathRand()-16383.5)/32767.);
  }
//+------------------------------------------------------------------+
//| initAllDataGPU                                                   |
//+------------------------------------------------------------------+
void initAllDataGPU(int &clCtx,       // context
                    int& clPrg,       // program on the device
                    int& clKrn,       // kernel
                    int& clMemIn1,    // first (input) buffer
                    int& clMemIn2,    // second (input) buffer
                    int& clMemOut)    // third (output) buffer
  {
//--- write the kernel code to a file
   WriteCLProgram();

//--- create context, program and kernel
   clCtx = CLContextCreate( _device );
   clPrg = CLProgramCreate( clCtx, clSrc );
   clKrn = CLKernelCreate( clPrg, "matricesMul" );

//--- create all three buffers for the three matrices
//--- first matrix - input
   clMemIn1=CLBufferCreate(clCtx,ROWS1   *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE);
//--- second matrix - input
   clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2   *sizeof(REALTYPE),CL_MEM_READ_WRITE);
//--- third matrix - output
   clMemOut=CLBufferCreate(clCtx,ROWS1   *COLS2   *sizeof(REALTYPE),CL_MEM_READ_WRITE);

//--- set arguments to the kernel
   CLSetKernelArgMem(clKrn,0,clMemIn1);
   CLSetKernelArgMem(clKrn,1,clMemIn2);
   CLSetKernelArgMem(clKrn,2,clMemOut);

//--- write the generated matrices to the device buffers
   CLBufferWrite(clMemIn1,first);
   CLBufferWrite(clMemIn2,second);
   CLBufferWrite(clMemOut,thirdGPU);   // 0.0 everywhere

   return;
  }
//+------------------------------------------------------------------+
//| WriteCLProgram                                                   |
//+------------------------------------------------------------------+
void WriteCLProgram()
  {
   int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI);
   FileWrite(h,clSrc);
   FileClose(h);
  }
//+------------------------------------------------------------------+
//| executeGPU                                                       |
//+------------------------------------------------------------------+
void executeGPU(int clKrn)
  {
//--- set the workspace parameters for the task and execute the OpenCL program
   uint offs[ 2 ]  = { 0, 0 };
   uint works[ 2 ] = { ROWS1,  COLS2 };
   bool ex=CLExecute(clKrn,2,offs,works);
   return;
  }
//+------------------------------------------------------------------+
//| readOutBuf                                                       |
//+------------------------------------------------------------------+
void readOutBuf(int clMemOut,REALTYPE &buf[])
  {
   ArrayResize(buf,COLS2*ROWS1);
//--- buf - a copy of what is written to the buffer thirdGPU[]
   uint read=CLBufferRead(clMemOut,buf);
   Print("read = "+i2s(read)+" elements");
   return;
  }
//+------------------------------------------------------------------+
//| destroyOpenCL                                                    |
//+------------------------------------------------------------------+
void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut)
  {
//--- destroy all that was created for calculations on the OpenCL device in reverse order
   CLBufferFree(clMemIn1);
   CLBufferFree(clMemIn2);
   CLBufferFree(clMemOut);
   CLKernelFree(clKrn);
   CLProgramFree(clPrg);
   CLContextFree(clCtx);
   return;
  }
//+------------------------------------------------------------------+
//| checkRandom                                                      |
//| random check of calculation accuracy                             |
//+------------------------------------------------------------------+
void checkRandom(REALTYPE &buf[],int rows,int cols)
  {
   int r0 = genRnd( rows );
   int c0 = genRnd( cols );

   REALTYPE sum=0.0;
   for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++)
      sum+=first[r0*COLSROWS+runningIdx]*
           second[runningIdx*COLS2+c0];
//--- element of the buffer m[]
   REALTYPE bufElement=buf[r0*COLS2+c0];
//--- element of the matrix not calculated in OpenCL
   REALTYPE CPUElement=thirdCPU[r0*COLS2+c0];
   Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+
         ";    thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+
         ";    buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8));
   return;
  }
//+------------------------------------------------------------------+
//| genRnd                                                           |
//+------------------------------------------------------------------+
int genRnd(int max)
  {
   return(int)(MathRand()/32767.*max);
  }

リスト2. OpenCLのプログラムの最初の実装 

最後二つの関数は、計算の正確性を確認するために役に立ちます。完成したコードは、この記事の最後に添付されたファイルで見つけることができます (matr_mul_1dim.mq5). 必ずしも行列の二乗に一致する必要はありjません。

さらなる変化は、カーネルコードに関連し、カーネル修正コードが以後設定されます。

REALTYPE型は、FloatからDouble型への正確な変更の利便性のために導入されています。REALTYPE型は、ホストプログラムだけではなく、カーネル内でも宣言されます。もし必要であれば、この種類に関する変化は、ホストプログラムの#defineと、カーネルコードの両方、二つの場所にて同時に実行されなければなりません。

そのコードのパフォーマンス結果（float型）：
CPU (OpenCL, _device = 0) :

2012.05.20 22:14:57    matr_mul_1dim (EURUSD,H1)    CPUTime / GPUTotalTime = 12.479
2012.05.20 22:14:57    matr_mul_1dim (EURUSD,H1)    OpenCL total: time = 9.266 sec.
2012.05.20 22:14:57    matr_mul_1dim (EURUSD,H1)    read = 4000000 elements
2012.05.20 22:14:48    matr_mul_1dim (EURUSD,H1)    CPUTime = 115.628
2012.05.20 22:12:52    matr_mul_1dim (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.20 22:12:52    matr_mul_1dim (EURUSD,H1)    =======================================

Radeon HD 4870 (_device = 1)にて実行された時:

2012.05.27 01:40:50    matr_mul_1dim (EURUSD,H1)    CPUTime / GPUTotalTime = 9.002
2012.05.27 01:40:50    matr_mul_1dim (EURUSD,H1)    OpenCL total: time = 12.729 sec.
2012.05.27 01:40:50    matr_mul_1dim (EURUSD,H1)    read = 4000000 elements
2012.05.27 01:40:37    matr_mul_1dim (EURUSD,H1)    CPUTime = 114.583
2012.05.27 01:38:42    matr_mul_1dim (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 01:38:42    matr_mul_1dim (EURUSD,H1)    =======================================

ご覧の通り、GPUのカーネルの実行はより遅いです。しかしGPUのための最適化に未だ取り組んでいません。

結論：

  • 二次元から線形への行列の表現の変更（デバイスで実行されたプログラムの表現に一致する）プログラムのシーケンシャル版の稼働時間に影響は与えません。
  • 線形幾何学での行列の掛け算の定義をマッチさせる最も直感的なアルゴリズムは、さらなる最適化のために初期のバリアントとして選択されました。最も速いものよりも遅いですが、GPUの将来の速度向上において、この要素は重要ではありません。
  • その稼働時間は、CLExecute() コマンドの後ではなく、むしろバッファをRAMに読み込んだのちに計算される必要があります。MetaDriver によって指摘されたその理由は、 以下のようです：
    MetaDriver: バッファから読み込む前に CLBufferRead() は、プログラムの終了を待ちます。CLExecute()は、実際は非同時性のキュー関数です。clコードの処理の終了前にその結果を即刻返します。
  • GPUのコンピューティングガイドは、普通、カーネルの稼働時間を計算しませんが、メモリ、アルゴリズムなど様々なオブジェクトに関連する スループットは計算します。後ほど同様のことを行います。

2000のサイズの行列の計算は、2*2000の足し算/掛け算を必要とします。行列の要素数によって（2000*2000）掛け算を行い、float型のデーターの処理合計数は160億になります。CPUでの実行は、115.628秒を取得します。それは、データストリーミングスピードに一致します。

throughput_arithmetic_CPU_no_OCL = 16 000000000 / 115.628 ~ 138 MFlops.


一方で、2000のサイズの行列での「シングルコアCPU」の最速の計算は、83.663秒必要とします（OpenCLの最初のコードをご覧ください。）結果

throughput_arithmetic_CPU_best_no_OCL = 16 000000000 / 83.663 ~ 191 MFlops.

この数字を最適化の最初の地点の参照として使用しましょう。

類似した、CPUでのOpenCLの使用により計算：
throughput_arithmetic_CPU_OCL =  16 000000000 / 9.266 ~ 1727 MFlops = 1.727 GFlops.


最後に、GPUでのスループットの計算：

throughput_arithmetic_GPU_OCL =  16 000000000 / 12.729 ~ 1257 MFlops = 1.257 GFlops.


2.3. 非コーヒレントデータアクセスの削除

カーネルコードを見ると、非最適化項目を簡単に見つけることができます。

カーネル内のループボディを見てみましょう：

for( int cr = 0; cr < COLSROWS; cr ++ )
   out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];

ループカウンター（cr++）が稼働している際、隣接するデータが 1[]の最初のバッファから取得されることが簡単にわかります。2[]の二番目のバッファからのデータはCOLS2と等しい「ギャップ」により取得されます。言い換えれば、二番目のバッファから取得されたデーターの大部分は、メモリ要求が非コーヒレントなので、役に立たなくなります。( 1.2.1. メモリリクエストの統合をみてください). この状況を修復するために、生成パターンとともに、2[]の配列のインデックスの計算の公式を変更することで、３つの場所にてコードを修復するだけで十分です。

- カーネルコード：
for( int cr = 0; cr < COLSROWS; cr ++ )
   out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];
ループカウンター（cr++）値が変化する際、両方の配列からのデータは、連続的に「ギャップ」なしで取得されます。

- genMatrices()でのバッファー内記述コード最初に使用された列中心注文の代わりのカラム中心注文にて記述されます：
   for( int r = 0; r < COLSROWS; r ++ )
      for( int c = 0; c < COLS2; c ++ )
         /// second[ r * COLS2 + c ] = genVal( );
         second[ r + c * COLSROWS ] = genVal( );
- chekRandom()関数での検証用コード
   for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++  )
      ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ];
      sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];
CPU上のパフォーマンス結果： 
2012.05.24 02:59:22    matr_mul_1dim_coalesced (EURUSD,H1)    CPUTime / GPUTotalTime = 16.207
2012.05.24 02:59:22    matr_mul_1dim_coalesced (EURUSD,H1)    OpenCL total: time = 5.756 sec.
2012.05.24 02:59:22    matr_mul_1dim_coalesced (EURUSD,H1)    read = 4000000 elements
2012.05.24 02:59:16    matr_mul_1dim_coalesced (EURUSD,H1)    CPUTime = 93.289
2012.05.24 02:57:43    matr_mul_1dim_coalesced (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.24 02:57:43    matr_mul_1dim_coalesced (EURUSD,H1)    =======================================
Radeon HD 4870: 
2012.05.27 01:50:43    matr_mul_1dim_coalesced (EURUSD,H1)    CPUTime / GPUTotalTime = 7.176
2012.05.27 01:50:43    matr_mul_1dim_coalesced (EURUSD,H1)    OpenCL total: time = 12.979 sec.
2012.05.27 01:50:43    matr_mul_1dim_coalesced (EURUSD,H1)    read = 4000000 elements
2012.05.27 01:50:30    matr_mul_1dim_coalesced (EURUSD,H1)    CPUTime = 93.133
2012.05.27 01:48:57    matr_mul_1dim_coalesced (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 01:48:57    matr_mul_1dim_coalesced (EURUSD,H1)    =======================================

ご覧の通り、データへのコーヒレントアクセスは、GPU上での稼働時間への影響はほとんどありません；しかし、CPU上の稼働時間を向上させました。後ほど最適化される要因に関連します、特に、すぐにでも取り除く必要のあるグローバル変数へのアクセスの待ち時間です。

throughput_arithmetic_CPU_OCL =  16 000000000 / 5.756 ~ 2.780 GFlops.
throughput_arithmetic_GPU_OCL =  16 000000000 / 12.979 ~ 1.233 GFlops.

新しいカーネルコードは、この記事の最後のmatr_mul_1dim_coalesced.mq5にて見つけることができます。

カーネルコードは、以下のように設定されます：

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  int c = get_global_id( 1 );                                                \r\n"
      "  for( int cr = 0; cr < COLSROWS; cr ++ )                                    \r\n"
      "     out[ r * COLS2 + c ] +=                                                 \r\n"
      "              in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];           \r\n"
      "}                                                                            \r\n";

リスト 3. 統合後のグローバルメモリのデータアクセス付きカーネル

さらなる最適化に進みましょう。


2.4. アウトプット行列からの「コストのかかる」グローバルGPUメモリアクセスの削除

グローバルGPUメモリアクセスのレイテンシはかなり高いです( 600から800サイクルほど). 例えば、二つの数字の追加を実行するレイテンシーは、おおよそ20サイクルです。GPU上での計算時の最適化の主な目的は、計算のスループットを向上させることで、レイテンシを隠すことです。以前開発されたカーネルのループ内で、時間のかかるグローバルメモリの要素に断続的にアクセスします。

カーネル内のローカル変数sumを紹介します。（ワークユニットレジスターに位置するカーネルのプライベート変数なので、何倍にも速くアクセスされます。）そして、ループ終了時に単独で取得されたsumの値をアウトプット配列に割り当てます。

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  int c = get_global_id( 1 );                                                \r\n"
      "  REALTYPE sum = 0.0;                                                        \r\n"
      "  for( int cr = 0; cr < COLSROWS; cr ++ )                                    \r\n"
      "     sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];             \r\n"
      "  out[ r * COLS2 + c ] = sum;                                                \r\n"
      "}                                                                            \r\n" ;

リスト 4. スカラ計算ループ内で累積する合計を計算するプライベート変数の紹介

完成したソースコードファイル、matr_mul_sum_local.mq5は、この記事の最後に添付されています。

CPU:

2012.05.24 03:28:17    matr_mul_sum_local (EURUSD,H1)    CPUTime / GPUTotalTime = 24.863
2012.05.24 03:28:16    matr_mul_sum_local (EURUSD,H1)    OpenCL total: time = 3.759 sec.
2012.05.24 03:28:16    matr_mul_sum_local (EURUSD,H1)    read = 4000000 elements
2012.05.24 03:28:12    matr_mul_sum_local (EURUSD,H1)    CPUTime = 93.460
2012.05.24 03:26:39    matr_mul_sum_local (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
GPU HD 4870:
2012.05.27 01:57:30    matr_mul_sum_local (EURUSD,H1)    CPUTime / GPUTotalTime = 69.541
2012.05.27 01:57:30    matr_mul_sum_local (EURUSD,H1)    OpenCL total: time = 1.326 sec.
2012.05.27 01:57:30    matr_mul_sum_local (EURUSD,H1)    read = 4000000 elements
2012.05.27 01:57:28    matr_mul_sum_local (EURUSD,H1)    CPUTime = 92.212
2012.05.27 01:55:56    matr_mul_sum_local (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 01:55:56    matr_mul_sum_local (EURUSD,H1)    =======================================
これが本当の生産性向上です！ 

throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops.
throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.

シーケンシャルな最適化において注意する主な規則は、以下です；まず、最も完全な方法でデータ構造を再調整する必要があります。その結果、特定の作業や根底のハードウェアにとって適切となり、それからやっと速い計算アルゴリズム、mad()やfma()などを用いた最適化に進みます。シーケンシャルな最適化は必ずしも向上したパフォーマンスに繋がりません。これは保証されません。

2.5. カーネルによって実行される処理の向上

並列プログラミングでは、並列処理の構成のオーバーヘッド（費やされる時間）を最小化するために計算を構成することが重要です。2000の規模の行列では、一つのアウトプット行列の要素を計算する一つのワークユニットは、合計の1 / 4000000の量に等しいタスクを実行します。

これはハードウェア上にて計算を実行する本当のユニット数からはかなりかけ離れています。それでは、カーネルの新しいバージョンにて、全体の行列の列を、一つの要素の代わりに計算していきます。

行列の一つの要素よりもむしろすべての列がカーネルの全タスクにて計算されるため、タスクスペースが２次元のものから、１次元のものに変更されているということが重要です。従って、タスクスペースは、行列の列数に変わります。

図14. アウトプット行列の全列の計算スキーム

カーネルコードはより複雑になります：

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE sum;                                                              \r\n"
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS; cr ++ )                                 \r\n"
      "        sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];          \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト5. アウトプット行列の全列の計算のためのカーネル

さらに、タスクの規模は、executeGPU( )関数にて変更されました。
void executeGPU( int clKrn )
{
   //--- set parameters of the task workspace and execute the OpenCL program
   uint offs[ 1 ]  = { 0 };
   uint works[ 1 ] = { ROWS1 };  
   bool ex = CLExecute( clKrn, 1, offs, works );
   return;
}

パフォーマンス結果(完全なソースコードは、matr_mul_row_calc.mq5にて観ることができます):

CPU:

2012.05.24 15:56:24    matr_mul_row_calc (EURUSD,H1)    CPUTime / GPUTotalTime = 17.385
2012.05.24 15:56:24    matr_mul_row_calc (EURUSD,H1)    OpenCL total: time = 5.366 sec.
2012.05.24 15:56:24    matr_mul_row_calc (EURUSD,H1)    read = 4000000 elements
2012.05.24 15:56:19    matr_mul_row_calc (EURUSD,H1)    CPUTime = 93.288
2012.05.24 15:54:45    matr_mul_row_calc (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.24 15:54:45    matr_mul_row_calc (EURUSD,H1)    =======================================

GPU 4870:

2012.05.27 02:24:10    matr_mul_row_calc (EURUSD,H1)    CPUTime / GPUTotalTime = 55.119
2012.05.27 02:24:10    matr_mul_row_calc (EURUSD,H1)    OpenCL total: time = 1.669 sec.
2012.05.27 02:24:10    matr_mul_row_calc (EURUSD,H1)    read = 4000000 elements
2012.05.27 02:24:08    matr_mul_row_calc (EURUSD,H1)    CPUTime = 91.994
2012.05.27 02:22:35    matr_mul_row_calc (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 02:22:35    matr_mul_row_calc (EURUSD,H1)    =======================================

CPUの稼働時間は、より悪くなり、GPUではそこまで悪くなっていません。ローカルレベルにて状況を一時的に悪化させる戦略的な変化は、劇的にパフォーマンスを向上させることになります。 

throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops.
throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
OpenCL APIを使用して最適化を行う際、ワークグループサイズ、すなわち、ワークグループ内のワークユニット数が外部にて設定されます。この可能性は、ターミナルの開発者によって開発された現在の実装においては提供されていません。ターミナルの今後のバージョンにて追加されることを願います。

2.6. プライベートメモリへの最初の配列の列を移動させる

行列の掛け算アルゴリズムの主な特徴は、結果の付随する蓄積との掛け算です。このアルゴリズムの適切な高品質の最適化は、データ遷移の最小化を意味します。しかし今の所、スカラの蓄積のループにおいての計算では、すべてのカーネルの修正がグローバルメモリ内の３つの行列のうち二つを格納しました。

これは、すべてのスカラにおいて、すべての入力データが（すべてのアウトプット行列の要素）断続的に、グローバルからプライベートへと、メモリーヒエラルキーを通して流されることを意味します。このトラフィックは、全ワークユニットがアウトプット行列内の全計算済み列における最初の行列の同じ列を再利用することを保証することで減少します。


図15. 最初の行列の列をワークユニットのプラベートメモリへの遷移

これについては、ホストのプログラムコードを変更しません。また、カーネル内の変更は最小のものです。中間１次元プライベート配列がカーネルによって生成されるという事実のため、GPUは、カーネルを実行するユニット内のプライベートメモリに配置しようとします。最初の行列の必要な列は、グローバルからプライベートメモリにコピーされます。このコピーでさえ比較的速く実行されています。そのトリックは、最も「コストのかかる」最初の配列の列要素のグローバルからプライベートメモリへのコピーは、コーヒレントで実行され、コピーにおけるオーバーヘッドは、アウトプット行列を計算するダブルループと一致します。

カーネルコード (メインループにてコメントアウトされているコードが以前のバージョンで記述されていたものです):

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE rowbuf[ COLSROWS ];                                               \r\n"
      "  for( int col = 0; col < COLSROWS; col ++ )                                 \r\n"
      "     rowbuf[ col ] = in1[ r * COLSROWS + col ];                              \r\n"
      "  REALTYPE sum;                                                              \r\n"
      "                                                                             \r\n"     
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS; cr ++ )                                 \r\n"
      "        ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];       \r\n"
      "        sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ];                      \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト 6. ワークユニットのプライベートメモリの最初の行列の列を特徴とするカーネル

CPU:
2012.05.27 00:51:46    matr_mul_row_in_private (EURUSD,H1)    CPUTime / GPUTotalTime = 18.587
2012.05.27 00:51:46    matr_mul_row_in_private (EURUSD,H1)    OpenCL total: time = 4.961 sec.
2012.05.27 00:51:46    matr_mul_row_in_private (EURUSD,H1)    read = 4000000 elements
2012.05.27 00:51:41    matr_mul_row_in_private (EURUSD,H1)    CPUTime = 92.212
2012.05.27 00:50:08    matr_mul_row_in_private (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 00:50:08    matr_mul_row_in_private (EURUSD,H1)    =======================================
GPU:
2012.05.27 02:28:49    matr_mul_row_in_private (EURUSD,H1)    CPUTime / GPUTotalTime = 69.242
2012.05.27 02:28:49    matr_mul_row_in_private (EURUSD,H1)    OpenCL total: time = 1.327 sec.
2012.05.27 02:28:49    matr_mul_row_in_private (EURUSD,H1)    read = 4000000 elements
2012.05.27 02:28:47    matr_mul_row_in_private (EURUSD,H1)    CPUTime = 91.884
2012.05.27 02:27:15    matr_mul_row_in_private (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 02:27:15    matr_mul_row_in_private (EURUSD,H1)    =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops.
throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.

CPUのスループットは、最後の時と同じレベルにて残り、一方、GPUのスループットは、新しい性能にて最高のレベルに戻りました。CPUのスループットは、まるでわずかに不安定にある一点で凍っているかのうようであり、GPUのスループットは、（常ではないが）かなりの幅で上昇を行います。

最初の行列のプライベートメモリへのコピーのため、より多くの処理が以前より実行されるため、実際の数学的スループットはより高いものである必要があることに注意しましょう。しかしながら、最終的な推定スループットに影響はほとんどありません。

そのソースコードは、 matr_mul_row_in_private.mq5にて見つけることができます。


2.7. 二番目の配列のカラムのローカルメモリへの移動

次のステップが何か推測するのは容易だと思います。すでにアウトプットと最初のインプット行列に関連するレイテンシを隠すステップはすでに取っています。二番目の行列が残っています。 

行列の掛け算にて使用されたスカラプロダクトのより詳細な研究がアウトプット行列の計算の中で、全てのワークユニットが二番目の掛け算された行列の同じカラムからのデータがデバイスを通して再び流されることを示しています。これは以下のスキームにて紹介されています：

図16. 二番目の行列のカラムをワークグループのLocal Data Shareへの移動

グローバルメモリからのデータの移動におけるオーバーヘッドは、もし行列の計算が始まる前にワークグループを作成するワークユニットが二番目の行列のカラムをワークグループメモリにコピーすれば、減少します。

これは、ホストプログラムに加えて、カーネル内での変更が必要です。最も重要な変化は、それぞれのカーネルにおいてローカルメモリの設定です。それは、動的なメモリ配置がOpenClではサポートされていないため外部にある必要があります。したがって、カーネル内にてさらに処理されるため、十分なサイズのメモリオブジェクトがホスト内にてまず配置される必要があります。

また、カーネルの実行時に、ワークユニットは、二番目の行列のカラムをローカルメモリのコピーを行います。これは、全てのワークグループのユニット内で、ループ反復の周期的配分を使用した配列にて実行されます。しかしながら、全てのコピーは、ワークユニットがその主な処理を始める前に完成される必要があります。

そのため、以下のコマンドがループ後に挿入されます。

barrier(CLK_LOCAL_MEM_FENCE);

これは、「ローカルメモリバリア」で、それぞれのワークユニットがその他のユニットと調和した状態にてローカルメモリが「見える」ことを保証します。全てのワークユニットは、カーネルの実行に進む前に、そのバリアまでのコマンドを実行しなければなりません。言い換えれば、そのバリアは特別なワークグループのユニット間の同期化の仕組みです。

ワークグループ間の同期化のメカニズムはOpenCLでは提供されていません。

バリアの詳細は以下になります。

図17. バリアの詳細

図17. バリアの詳細

実際は、ワークユニットは厳格に同時にコードを実行するように思えます。これは、OpenCLプログラミングモデルの抽象化です。

今の所、異なるワークユニットで実行されるカーネルコードは、処理の同期化を必要としておらず、カーネル内にて設定されるであろうユニット間の外部のコミュニケーションはありません。しかし、同期化はこのカーネルでは必要とされており、ローカル配列の記述のプロセスは、全ユニット間の並列にて配分されます。

言い換えれば、全てのワークユニットは、ローカルデータ共有内にその値を記述します。そのバリアは、あるワークユニットが必要になる前、つまり、ローカルの配列が完全に生成される前に、カーネルの実行に進むためにあります。

この最適化は、CPU上のパフォーマンスにて有益ではないことを理解する必要があります：IntelのOpenCL最適化ガイドでは、CPU上でカーネルを実行する際に、全てのOpenCLメモリオブジェクトはハードウェアによりキャッシュされます。ローカルメモリの使用による外部のキャッシングは、不必要なオーバーヘッドを生み出します。

この記事の著者に時間を取らせるのに値しない別の重要なポイントがあります。それは、ローカル変数がカーネル関数のヘッダー、すなわち、現在のターミナル開発者の実装でのコンパイルの段階にて、渡されることができないということに関連します。その理由は、メモリをカーネル関数の引数として、メモリオブジェクトに配置するために、外部にまずCPUメモリにそのようなオブジェクトをCLBufferCreate() 関数を使用し作成し、関数パラメーターとしてサイズを明記する必要があります。この関数は、唯一の場所であるグローバルCPUメモリにて格納されるメモリオブジェクトハンドルを返します。

しかし、ローカルメモリはグローバルとは異なるメモリであり、作成されたメモリオブジェクトは、ワークグループのローカルメモリには配置されません。

OpenCL APIは、外部の必要なサイズのメモリをポインターNULLにて、メモリオブジェクトを作成せずカーネルの引数を配置できるようにします。 (CLSetKernelArg()関数). しかし、完全な機能を持ったAPI関数のMQL5類似物であるCLSetKernelArgMem() 関数の構文では、メモリオブジェクトを作成せずに、その引数に配置されたメモリサイズを渡すことはできません。CLSetKernelArgMem()関数に渡すことができるものは、グローバルCPUメモリ内にてすでに生成された バッファハンドルのみで、グローバルGPUに遷移するよう意図されています。こちらがそのパラドックスです。

幸運にも、カーネル内にてローカルバッファを扱う同等の方法があります。カーネルのボディ内に、修飾子__local の付いたバッファを宣言します。そうすることで、ワークグループに配置されたローカルメモリは、コンパイル段階の代わりに、Runtime内に決定されます。

カーネルのバリアの後に来るコマンドは、（コード内のバリアは、赤色にマークされています。）以前の最適化の中と同様です。ホストプログラムコードは、同じ状態で残ります。 (そのソースコードは、matr_mul_col_local.mq5に見つけることができます。).

こちらが、新しいカーネルコードです：

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out )                          \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE rowbuf[ COLSROWS ];                                               \r\n"
      "  for( int col = 0; col < COLSROWS; col ++ )                                 \r\n"
      "     rowbuf[ col ] = in1[ r * COLSROWS + col ];                              \r\n"
      "                                                                             \r\n"
      "  int idlocal = get_local_id( 0 );                                           \r\n"     
      "  int nlocal = get_local_size( 0 );                                          \r\n"     
      "  __local  REALTYPE colbuf[ COLSROWS ] ;                                     \r\n"
      "                                                                             \r\n" 
      "  REALTYPE sum;                                                              \r\n"
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal )                \r\n"                 
      "        colbuf[ cr ] = in2[ cr + c * COLSROWS ];                             \r\n"                 
      "     barrier( CLK_LOCAL_MEM_FENCE );                                         \r\n"                 
      "                                                                             \r\n"                 
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS; cr ++ )                                 \r\n"
      "        sum += rowbuf[ cr ] * colbuf[ cr ];                                  \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト 7. ワークグループのローカルメモリに移された二番目の配列のカラム

CPU:
2012.05.27 06:31:46    matr_mul_col_local (EURUSD,H1)    CPUTime / GPUTotalTime = 17.630
2012.05.27 06:31:46    matr_mul_col_local (EURUSD,H1)    OpenCL total: time = 5.227 sec.
2012.05.27 06:31:46    matr_mul_col_local (EURUSD,H1)    read = 4000000 elements
2012.05.27 06:31:40    matr_mul_col_local (EURUSD,H1)    CPUTime = 92.150
2012.05.27 06:30:08    matr_mul_col_local (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 06:30:08    matr_mul_col_local (EURUSD,H1)    =======================================
GPU:
2012.05.27 06:21:36    matr_mul_col_local (EURUSD,H1)    CPUTime / GPUTotalTime = 58.069
2012.05.27 06:21:36    matr_mul_col_local (EURUSD,H1)    OpenCL total: time = 1.592 sec.
2012.05.27 06:21:36    matr_mul_col_local (EURUSD,H1)    read = 4000000 elements
2012.05.27 06:21:34    matr_mul_col_local (EURUSD,H1)    CPUTime = 92.446
2012.05.27 06:20:01    matr_mul_col_local (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 06:20:01    matr_mul_col_local (EURUSD,H1)    =======================================

両方のケースが、重要ではない、パフォーマンスの降下を示しています。そのパフォーマンスは、ワークグループのサイズを変えることにより、降下するよりもむしろ向上されます。その上記の例は、異なる目的を果たします - それはローカルメモリオブジェクトの使用方法を紹介することです。

ローカルメモリが使用された際、パフォーマンスが低下することを説明する仮設があります。 Comparing OpenCL with CUDA, GLSL and OpenMP（OpenCLとCUDA、GLSL、OpenMを比較する） というhabrahabr.ruが２年前に執筆した記事にて:

AMDカードは、物理レベルではローカルメモリをサポートしていません：代わりに、ローカルメモリの区域は、グローバルメモリにマッピングされます。
同じ記事の下方にて、著者は以下のようにコメントしています：
テストされたAMDカードは物理的にローカル音チップメモリを持っておらず、結果的にローカルメモリを必要とするアリゴリズムの速度が劇的に低下しました。

言い換えれば、2年前にリリースされたその製品のローカルメモリはグローバルメモリよりも速くないということでしょうか？上記が投稿された時期は、２年前、Radeon HD 58xx シリーズのビデオカードがすでにリリースされており、著者によれば、楽観的な状況ではありませんでした。AMDによるセンセーショナルなEvergreenシリーズに関してそれは特に信じ難いです。例えば、HD 69xxシリーズなど、よりモダンなカードを使用し、それをチェックすることは興味深いです。 

追加：GPU CAps Viewerを起動すると、OpenCLタブにて以下を見ることができます。

図18. HD 4870によりサポートされるOpenCLメインパラメーター

図18. HD 4870によりサポートされるOpenCLメインパラメーター

CL_DEVICE_LOCAL_MEM_TYPE: Global

Language Specificationにて提供されるこのパラメーターの説明 (図表 4.3, p. 41) は以下の通りです：

サポートされているローカルメモリの種類これは、CL_LOCALに設定され、SRAMやCL_GLOBALなどローカルメモリストレージを意味します。

従って、HD 4870 ローカルメモリは、本当にグローバルメモリの一部であり、このビデオカードでのローカルメモリの操作は、役に立たず、グローバルメモリより速くはなりません。こちらは、AMD専門家が、HD 4xxx シリーズについてこのポイントを明確化させるページのリンクです。あなたの持っているビデオカードにおいて、それは悪くなるということを意味しません：そのようなハードウェアに関する情報がどこで見つかるのか（この場合、GPU Caps Viewer内であるが）について示すためだけです。

throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops.
throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.

最後に、カーネルの外部でのベクトル化による最後の一仕上げを行いましょう。最初の配列のプライベートメモリ(matr_mul_row_in_private.mq5)への移動の段階にて派生したカーネルは、最速に見えるため、初期のカーネルとして機能します。


2.8. カーネルのベクトル化

この処理は、いくつかのステージに分解し、混乱を避ける必要があります。初期の修正では、カーネルの外部パラメーターのデータ型は変更せず、内部ループの計算をベクトル化します。

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "#define REALTYPE4 float4                                                     \r\n"     
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE rowbuf[ COLSROWS ];                                               \r\n"
      "  for( int col = 0; col < COLSROWS; col ++ )                                 \r\n"
      "  {                                                                          \r\n"
      "     rowbuf[ col ] =  in1[r * COLSROWS + col ];                              \r\n"
      "  }                                                                          \r\n"
      "                                                                             \r\n"     
      "  REALTYPE sum;                                                              \r\n"
      "                                                                             \r\n"     
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS; cr += 4 )                               \r\n"
      "        sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ],                            \r\n"
      "                                    rowbuf[ cr + 1 ],                        \r\n"     
      "                                    rowbuf[ cr + 2 ],                        \r\n"     
      "                                    rowbuf[ cr + 3 ] ),                      \r\n"     
      "                    ( REALTYPE4 ) ( in2[c * COLSROWS + cr     ],             \r\n"
      "                                    in2[c * COLSROWS + cr + 1 ],             \r\n"
      "                                    in2[c * COLSROWS + cr + 2 ],             \r\n"
      "                                    in2[c * COLSROWS + cr + 3 ] ) );         \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト8. float4(内部ループ)を使用したカーネルの部分的なベクトル化

完全なソースコードファイルは、matr_mul_vect.mq5です。もちろん、COLSWROWSパラメーターは４で割られる必要があります。

CPU:
2012.05.27 21:28:16    matr_mul_vect (EURUSD,H1)    CPUTime / GPUTotalTime = 18.657
2012.05.27 21:28:16    matr_mul_vect (EURUSD,H1)    OpenCL total: time = 4.945 sec.
2012.05.27 21:28:16    matr_mul_vect (EURUSD,H1)    read = 4000000 elements
2012.05.27 21:28:11    matr_mul_vect (EURUSD,H1)    CPUTime = 92.259
2012.05.27 21:26:38    matr_mul_vect (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 21:26:38    matr_mul_vect (EURUSD,H1)    =======================================

GPU:
2012.05.27 21:21:30    matr_mul_vect (EURUSD,H1)    CPUTime / GPUTotalTime = 78.079
2012.05.27 21:21:30    matr_mul_vect (EURUSD,H1)    OpenCL total: time = 1.186 sec.
2012.05.27 21:21:30    matr_mul_vect (EURUSD,H1)    read = 4000000 elements
2012.05.27 21:21:28    matr_mul_vect (EURUSD,H1)    CPUTime = 92.602
2012.05.27 21:19:55    matr_mul_vect (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 21:19:55    matr_mul_vect (EURUSD,H1)    =======================================

驚くべきことに、それぞれの原始的ベクトル化は、GPU上に良い結果をもたらしました。重要ではありませんが、その10%ほどの向上でした。

カーネル内でベクトル化を続ける：「コストのかかる」REALTYPE4ベクトル型変換処理と外部ベクトルコンポーネントの明記を、rowbuf[]プライベート変数を記述する補助的ループに移します。カーネル内にはまだ変化はありません。

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "#define REALTYPE4 float4                                                     \r\n"     
      "                                                                             \r\n"
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE4 rowbuf[ COLSROWS / 4 ];                                          \r\n"
      "  for( int col = 0; col < COLSROWS / 4; col ++ )                             \r\n"
      "  {                                                                          \r\n"
      "     rowbuf[ col ] =  ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ],          \r\n"
      "                                      in1[r * COLSROWS + 4 * col + 1 ],      \r\n"
      "                                      in1[r * COLSROWS + 4 * col + 2 ],      \r\n"
      "                                      in1[r * COLSROWS + 4 * col + 3 ] );    \r\n"
      "  }                                                                          \r\n"
      "                                                                             \r\n"     
      "  REALTYPE sum;                                                              \r\n"
      "                                                                             \r\n"     
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS / 4; cr ++ )                             \r\n"
      "        sum += dot(                 rowbuf[ cr ],                            \r\n"
      "                    ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr     ],         \r\n"
      "                                    in2[c * COLSROWS + 4 * cr + 1 ],         \r\n"
      "                                    in2[c * COLSROWS + 4 * cr + 2 ],         \r\n"
      "                                    in2[c * COLSROWS + 4 * cr + 3 ] ) );     \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト9. 「コストのかかる」型変換のカーネルのメインループ内での処理の除去

内部（補助的）ループカウンターの最大のカウント値は、最初の配列に必要な読み込み処理が、読み込みがベクトルの処理になる前に、４倍以下になったため、４倍低くなりました。

CPU: 
2012.05.27 22:41:43    matr_mul_vect_v2 (EURUSD,H1)    CPUTime / GPUTotalTime = 24.480
2012.05.27 22:41:43    matr_mul_vect_v2 (EURUSD,H1)    OpenCL total: time = 3.791 sec.
2012.05.27 22:41:43    matr_mul_vect_v2 (EURUSD,H1)    read = 4000000 elements
2012.05.27 22:41:39    matr_mul_vect_v2 (EURUSD,H1)    CPUTime = 92.805
2012.05.27 22:40:06    matr_mul_vect_v2 (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 22:40:06    matr_mul_vect_v2 (EURUSD,H1)    =======================================
GPU:
2012.05.27 22:35:28    matr_mul_vect_v2 (EURUSD,H1)    CPUTime / GPUTotalTime = 185.605
2012.05.27 22:35:28    matr_mul_vect_v2 (EURUSD,H1)    OpenCL total: time = 0.499 sec.
2012.05.27 22:35:28    matr_mul_vect_v2 (EURUSD,H1)    read = 4000000 elements
2012.05.27 22:35:27    matr_mul_vect_v2 (EURUSD,H1)    CPUTime = 92.617
2012.05.27 22:33:54    matr_mul_vect_v2 (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 22:33:54    matr_mul_vect_v2 (EURUSD,H1)    =======================================
算数的なスループット
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops.
throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.

ご覧の通り、CPUにおいてパフォーマンスの変化はかなりのものですが、一方GPUにおいては革命的です。ソースコードは、matr_mul_vect_v2.mq5にて見ることができます。

8の幅のベクトルのみを使用して、カーネルの最後のバリアントに関して同じ処理を実行しましょう。著者の決定は、GPUメモリの帯域幅は256ビットであり、すなわち32バイト、かfloat型の8の数であるという事実により説明できます：従って、float8の同時使用に等しい8Floatの同時の処理は、とても自然にように見えます。

COLSROWSの値は、８で割られなければなりません。これは、より良い最適化が特定の要件をデータに設定する自然な要求です。 

const string clSrc =
      "#define COLS2     "    + i2s( COLS2 )    +  "                            \r\n"
      "#define COLSROWS  "    + i2s( COLSROWS ) +  "                            \r\n"
      "#define REALTYPE  float                                                      \r\n"
      "#define REALTYPE4 float4                                                     \r\n"     
      "#define REALTYPE8 float8                                                     \r\n"     
      "                                                                             \r\n"
      "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b )                             \r\n"
      "{                                                                            \r\n"
      "  REALTYPE8  c = a * b;                                                      \r\n"      
      "  REALTYPE4  _1 = ( REALTYPE4 ) 1.;                                          \r\n"      
      "  return( dot( c.lo + c.hi, _1 ) );                                          \r\n"     
      "}                                                                            \r\n"           
      "                                                                             \r\n"           
      "__kernel void matricesMul( __global REALTYPE *in1,                           \r\n"
      "                           __global REALTYPE *in2,                           \r\n"
      "                           __global REALTYPE *out  )                         \r\n"
      "{                                                                            \r\n"
      "  int r = get_global_id( 0 );                                                \r\n"
      "  REALTYPE8 rowbuf[ COLSROWS / 8 ];                                          \r\n"
      "  for( int col = 0; col < COLSROWS / 8; col ++ )                             \r\n"
      "  {                                                                          \r\n"
      "     rowbuf[ col ] =  ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ],          \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 1 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 2 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 3 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 4 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 5 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 6 ],      \r\n"
      "                                      in1[r * COLSROWS + 8 * col + 7 ] );    \r\n"
      "  }                                                                          \r\n"
      "                                                                             \r\n"     
      "  REALTYPE sum;                                                              \r\n"
      "                                                                             \r\n"     
      "  for( int c = 0; c < COLS2; c ++ )                                          \r\n"
      "  {                                                                          \r\n"
      "     sum = 0.0;                                                              \r\n"
      "     for( int cr = 0; cr < COLSROWS / 8; cr ++ )                             \r\n"
      "        sum += dot8(                rowbuf[ cr ],                            \r\n"
      "                    ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr     ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 1 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 2 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 3 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 4 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 5 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 6 ],         \r\n"
      "                                    in2[c * COLSROWS + 8 * cr + 7 ] ) );     \r\n"
      "     out[ r * COLS2 + c ] = sum;                                             \r\n"
      "  }                                                                          \r\n"
      "}                                                                            \r\n" ;

リスト10. 8のベクトル幅を使用したカーネルのベクトル化

8の幅のベクトルにおけるスカラプロダクトの計算を可能にするインライン関数dot8()をカーネルコードを挿入しなければなりません。OpenCLでは、標準関数dot()が4の幅までのベクトルにおいて、スカラプロダクトを計算します。そのソースコードは、matr_mul_vect_v3.mq5で見ることができます。

CPU:
2012.05.27 23:11:47    matr_mul_vect_v3 (EURUSD,H1)    CPUTime / GPUTotalTime = 45.226
2012.05.27 23:11:47    matr_mul_vect_v3 (EURUSD,H1)    OpenCL total: time = 2.200 sec.
2012.05.27 23:11:47    matr_mul_vect_v3 (EURUSD,H1)    read = 4000000 elements
2012.05.27 23:11:45    matr_mul_vect_v3 (EURUSD,H1)    CPUTime = 99.497
2012.05.27 23:10:05    matr_mul_vect_v3 (EURUSD,H1)    1st OCL martices mul:  device = 0;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 23:10:05    matr_mul_vect_v3 (EURUSD,H1)    =======================================
GPU:
2012.05.27 23:20:05    matr_mul_vect_v3 (EURUSD,H1)    CPUTime / GPUTotalTime = 170.115
2012.05.27 23:20:05    matr_mul_vect_v3 (EURUSD,H1)    OpenCL total: time = 0.546 sec.
2012.05.27 23:20:05    matr_mul_vect_v3 (EURUSD,H1)    read = 4000000 elements
2012.05.27 23:20:04    matr_mul_vect_v3 (EURUSD,H1)    CPUTime = 92.883
2012.05.27 23:18:31    matr_mul_vect_v3 (EURUSD,H1)    1st OCL martices mul:  device = 1;      ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000
2012.05.27 23:18:31    matr_mul_vect_v3 (EURUSD,H1)    =======================================

その結果は期待されていたものとは異なりました：CPUの稼働時間は、以前より二倍少なく、一方でfloat8は、HD 4870 (に等しい256ビット)における十分なバス幅である二も関わらず、GPUにおいては増大していました。そして、こちらでGPU Caps Viewerを再度使用します。

説明は、図18のパラメーターリストの最後一つ前の行にて見ることができます。

CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4


OpenCL Specificationを使用すると、37ページにて図表4.3の最後のカラムにて、このパラメーターに関するテキストを見ることができます。:

ベクトル内に格納される内蔵スカラー型の望ましいネィテイブベクトル幅のサイズベクトル幅は、ベクトル内に保存されるスカラ要素の数として定義されます。

HD 4870に関して、ベクトルfloatNの望ましいベクトル幅は、float8ではなく、float4です。

カーネル最適化サイクルをここで終了しましょう。もうすこし先に進むこともできましたが、この記事の長さでは、そこまで深く進めることはできません。


結論

この記事は、カーネルにて実行される根底のハードウェアについて考察した際に開く最適化の可能性を紹介しました。

取得されたその数字は、最大値ではありませんが、わくわくさせるリソース（ターミナルの開発者によって実装されたOpen CL APIは、最適化のために重要なパラメーターを管理できません。ー 特に、ワークグループサイズは管理できません。）、ホストプログラム実行中のパフォーマンスは重要です。CPU上のシーケンシャルプログラムでのGPU上での実行で得られる利益は、およそ200 

有益なアドバイスや分散GPUを使用できる機会を提供してくれたMetaDriverに感謝いたします。


添付ファイルのコンテンツ：

  1. matr_mul_2dim.mq5 - ホスト上での二次元のデータ表現初期に関するシーケンシャルプログラム
  2. matr_mul_1dim.mq5 - MQL5 OpenCL APIにおける線形データ表現と関連するバインディング付きのカーネルの初期の実装
  3. matr_mul_1dim_coalesced - 統合グローバルメモリアクセスを特徴とするカーネル
  4. matr_mul_sum_local - グローバルメモリ内のアウトプット配列の計算されたせるへのアクセスの代わりのスカラプロダクトの計算に関して導入されたプライベート変数
  5. matr_mul_row_calc - カーネルのアウトプット行列の全列の計算
  6. matr_mul_row_in_private - プライベートメモリに移される最初の配列の列
  7. matr_mul_col_local.mq5 -ローカルメモリに移される二番目の配列のカラム
  8. matr_mul_vect.mq5 - カーネルの初期ベクトル化（メインループ内部のサブループ、float4のみを使用）
  9. matr_mul_vect_v2.mq5 - メインループでのデータ変換の「コストのかかる」処理の除去
  10. matr_mul_vect_v3.mq5 - 8のベクトル幅を用いたベクトル化


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/407

添付されたファイル |
ZIPをダウンロード
opencl_optimization_mql5.zip (35 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
OpenCL：パラレルワールドへの橋渡し OpenCL：パラレルワールドへの橋渡し
2012年1月下旬、MetaTrader 5の開発を支援するソフトウェア開発企業はMQL5でのOpenCLのネイティブサポートを発表しました。本稿では解説例を用いてMQL5 環境におけるOpenCL のプログラミング基礎を記述し、処理スピードを上げるプログラムのシンプルな最適化例を提供します。
MQL5.community - ユーザーメモ MQL5.community - ユーザーメモ
みなさんは登録したばかりで、おそらく「メッセージに写真を挿入する方法は？」、「MQL5 のソースコードをフォーマットする方法は？」、「個人のメッセージはどこに保存されるの？」などという疑問があることでしょう。またそのほかにも数多くの質問があるかもしれません。本稿では MQL5.communityに慣れていただくための実践的な情報を準備し、利用可能な機能を最大限に活用していただけるようにします。
MQL5 マーケットがトレーディング戦略およびテクニカルインディケータを販売するのにベストな場所である理由 MQL5 マーケットがトレーディング戦略およびテクニカルインディケータを販売するのにベストな場所である理由
MQL5.community マーケットは Expert Advisors 開発者に対してすでに何千人という潜在的購入者のいるできあがったマーケットを提供します。これは売買ロボットやテクニカルインディケータを販売するのにはベストな場所です。
MQL5 コード用自動作成ドキュメンテーション MQL5 コード用自動作成ドキュメンテーション
Java プログラマーの多くは JavaDocs により作成することのできる自動作成ドキュメンテーションを熟知されていることと思います。その考え方は、検索が簡単なヘルプファイルに抽出できる半構造法によりコードにコメントを追加するというものです。C++ 言語界にもまたドキュメンテーション自動作成機能があります。 Microsoft の SandCastle と Doxygen が代表的な2つです。本稿は MQL5 コードで構成済みコメントから HTML ヘルプファイルを作成するための Doxygen 使用について述べます。実験はひじょうにうまくいきましたから、Doxygen が MQL5 コードから作り出すヘルプのドキュメンテーションは大きな価値を加えると信じています。