誤信、パート１:資産管理は一番ではなく、あまり重要ではない

はじめに

この記事では、人をしばしば騙し得るとてもシンプルなもの、テストレポートのアカウントバランスのグラフについて議論します。初心者による戦略テストのレポートでは、時折テスト期間の終了までの数十億の結果や指数のバランス・資産グラフを見ることができます。そのような結果は普通、これらの指数が生まれるところを知る熟練のEA開発者による懐疑的なコメントを促し、固定ロットでの結果を示すことを推奨します。

固定0.1ロットでのテスト結果は、戦略の利点と欠点すべてを反映することが想定されます。この想定における議論は、かなり明確です：大半の通貨ペアにおいて、このグラフはある戦略が特定の期間でどれほどのポイントを作るかをしめしています。もし戦略が数ポイントの利益を出しているのであれば、その戦略は挑戦的であると考えられるという意見があります：しかし、もし数学的な予想結果がマイナスであれば、そのような戦略は利益を出しません。

もう一つ説得力のある主張：直線に近い「0.1ロット」のカーブは、指数グラフで見ることのできない戦略安定性の一種の暗示です。

しかしながら、すべての利点にもかかわらず、そのようなグラフは欠点があり、明確ではありません。これすべて理解するために、異なる資産管理システムでの戦略の結果を分析し、グラフを比較しましょう。

この記事で分析される資産管理種類EAの選択

それでは、オープンされたポジションの量が固定か、デポジットの増加関数である3種類のMMを分析します。以前のトレード結果を考慮に入れる効果的なMMの確率は、利益を生む/損失を出す確率は反対の結果のトレードが変化する確率よりも高い時のみ合理的に思えます。なので、この記事で記載されているMMはこちらです：

1. ロットは、デポジットの大きさに関係なく固定され、0.1に等しいです。この戦略を保守主義と呼びましょう。この記事では、"ロット0.1"か"0.1"ほどを意味します。
2. ロットは、デポジットに比例します。これは、攻撃的な資金管理です。それを「幾何学MM」と呼びます。
3. ロットはデポジットの平方根に比例して大きくなります穏健な戦略と呼びましょう。

エキスパートアドバイザーを分析しましょう"20_200 expertv4.2_AntS". この記事の範囲外であるため、パラメータによるEAの最適化は行いません；エキスパートアドバイザーの標準のパラメーターを用いましょう。2000/06/07から2008/03/15までのEURUSD H1での全ティックにてテストします。このテスト期間は、0.1ロットでのテストにてかなりよいバランスグラフを得るために意図的に選択されました。正確には、このEAはこの記事の主な供述を説明するために選択されています。このEAのソースコードは、 https://www.mql5.com/ja/code/7891 にあります。

エキスパートアドバイザーのより大きい部分はロットを選択する関数LotSize()で、1000行よりも少し大きく、(ソースファイルサイズ50Kのうち44K）、特異性を部分的に制約します。この関数は、ロットのバランスへの依存関数に近づくのであれば、0.1の必要なロットでのシンプルな行でのより短い形で実装することができます。少なくとも「nodes」でのソースコードの計算からの近似の差は、数千ものうちの１ノードから現れます。その戦略のパラメーターにほとんど影響を与えません。

ロットサイズを選択する正確なロジックを勉強しないことにし、コードを変更し、そのファイルをより小さくしました（最初は、EAコードはロット選択のこの関数に一致するアクティブなMMのみを持ちました。）非比例的なロットにつながっている部分もまたそのコードから除去され、EAからマーティンゲールの要素も排除されます。変更されたEAのコードはこの記事に添付されています。

以下は、EURUSDに適しているロットサイズ計算の関数です。

double LotSize() 
{
   double size;
   switch( _MM )
   {
      case 0:  size = 0.1;  
               break;
      case 1:  size = 0.1 * AccountBalance() / 1000; 
               break;
      case 2:  size = 0.1 * MathSqrt( AccountBalance() / 1000 ); 
               //size = 1. * MathSqrt( AccountBalance() / 10000 ); 
               break;
      default: size = 0.1;  break;
   }  
   if( size < 0.1 )          // is money enough for opening 0.1 lot?
      if( ( AccountFreeMarginCheck( Symbol(), OP_BUY,  0.1 ) < 10. ) || 
          ( AccountFreeMarginCheck( Symbol(), OP_SELL, 0.1 ) < 10. ) || 
          ( GetLastError() == 134 ) )
                  lot = 0.0; // not enough
      else        lot = 0.1; // enough; open 0.1
   else           lot = NormalizeDouble( size, 2 ); 
   
   return( lot ); 
}

この記事の想定

この記事の後半は、典型的な初心者の論理を追っていきます。

1. 初心者の方は、フォーラムを訪れ、 CodeBaseを入力し、このEAをみて、このEAがどういう傾向があるのかを理解しようとします。彼らはソースコードの詳細に興味があるのではなく、素早く結果を取得したいだけなのです。
2. 彼らは、履歴の可変性に関連するテスト結果の信頼性に対する疑問には興味がなく、EAが早く結果を出すように数年前から現在までのテスト期間のみを選択します。そのEAが８年間の間良い結果を出したのだから将来も同じように動くと信じきります。
3. 固定ロット0,1でのテスト結果を取得し、フォーラムにアクセスし、0.1でのテストが戦略の安定性において信頼できる結果を示したという熟練のフォーラム訪問者の典型的な答えを見て、バランスサイズに比例するサイズのポジションを開くという幾何学的な資産管理を導入することにします。コードを見ていないので、実際ストップロスが利食いよりもかなり大きいものであるとは考えません。そのバランスカーブがどのように変化するか知らないのです。
4. そして、最終的にMMを修正し、上記の３番目の種類のMMを発明しようとします。

テスト結果のいくつかのパラメーター、純利益やパーセントでの最大ドローダウン、回復要因などを監視し、取得した結果や初心者の行動を分析します。

テスト1: 固定ロット, "0.1"

こちらがテスト結果です：

ストラテジーテスターレポート 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

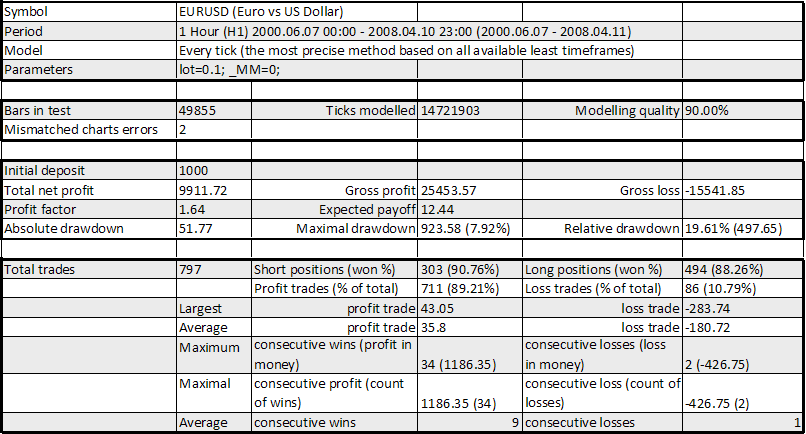
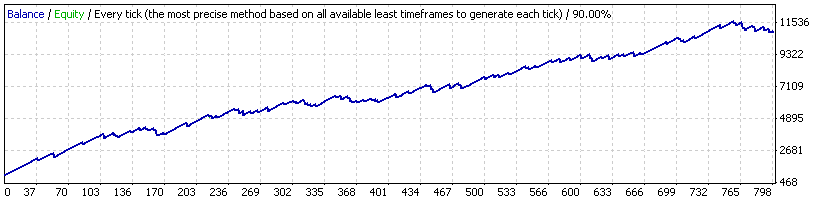
エキスパートアドバイザー 20_200 expert_v4.2_AntS, lot 0.1

もう一つパラメーターを加えます - 回復要因：

RF (Recovery Factor) = Total Net Profit / Maximal Drawdown = 9911.72 / 923.58 = 10.73

８年ほどの間ですが、そのカーブは悪くは見えず、RFもまたOKです。その図表のその他のすべてのパラメーターは、かなり良いです：数学的な予想は、12.44ポイント (より大きくはなりますがこれはそこまで悪くありません）、最大ドローダウンは、およそ20%です。平均トレード損失に対する平均トレード利益の比率は、35.80/180.72 = 0.198 = 1/5.05に等しいです; しかし、利益の出るトレードの数は、損失を出すトレードの数よりも多いです(89.21%/10.79%, 8.27で、5.05よりも大きいです). したがって、その戦略は役に立ちそうです。

これにより、初心者の彼らは自信を持ち、リスクをとることにします：固定ロットの代わりに、"デポジット 0.1/&1000"という穏健な比率に基づく幾何学的な資産管理を導入します。元のEAで提供されている比率（デポジット1/3ロットよりも少し多い）よりもリスクがありますが、気にせず、できる限りの資産を稼ぎ出そうとします。

テスト2, パート1: バランスに比例するロット «0.1/$1000»

レポートの中で興味深いいくつかの行を見てみましょう。

ストラテジーテスターレポート 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

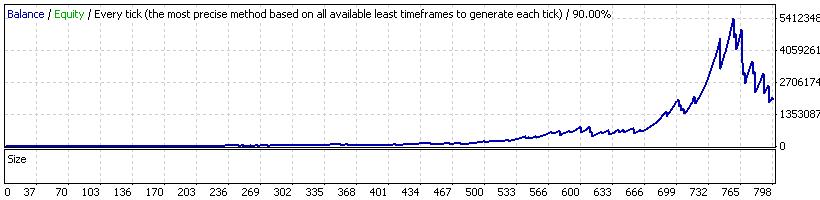
エキスパートアドバイザー 20_200 expert_v4.2_AntS, 幾何学的 MM

より見えやすいように、プロセスを追跡するのに役にたつビデオファイルを記録しました：幾何学的なMMの最終的な統計結果は、詳細が全て見えるので実際よりもより見えやすくなっています。そのビデオは、完全にその図にてあまり重要そうではない中間ドローダウンを示しています。これらのドローダウンはそこまで小さくなく、バランス最大値の50%にも時折達しています（実際、そのバランスが絶対的な最大値に達した後に受け取られる最後のドローダウンは重要ではありません）

幾何学的MM

あまり知らない変換機能のために、そのビデオは34秒まで見る必要があり；テストモードに関するメッセージが表示された後、その繰り返しのエンディングが表示されます。

状況はさらに悪くなっていることがわかると思います；そのグラフはあまり魅力的ではなく、興味を持っていたパラメーターもまた変化しています。バランスのピーク時にオープンされた取引の量が業者にとって本当のものであるかはここでは議論しません。純利益は大きく成長していますが、最大ドローダウンは70%以上で、その回復要因は

RF = 1989283.04 / 3883421.15 = 0.51 –

かなり大きく下がり、1以下になっています！もちろん、そのようなRFは最後のドローダウンの結果ですが、自己欺瞞には興味がなく、レポートからは排除しません。この状況は、有名な記事でフォーラムで最も引用されている "My First 'Grail'"にてすでに紹介されています。

これは、固定ロット0.1でのテストの結果を要求する熟練者の返信を受け取った初心者のための二重の教訓です。なので、"0.1"でのテストはあてにならないように見えます：ポジティブな数学的予想や0.1ロットでの戦略の安定性が示されているにもかかわらず、攻撃的なMMを追加することは一般的には十分ではなく、役に立つはずのポジティブな数学的予想に依存します。

カーブの特徴やそのパラメーターの鋭い変化の理由は明らかです："0.1"ロットでのテストの際、デポジットに関連するロットサイズが双曲線に基づき減少するため、そのデポジットの成長は、関連リスクの減少に従います。そして、幾何学的なMMの場合、そのリスクは低くならず、固定されたままです。これは、テスト期間の終了時の"dints"の拡大した深さを説明します。

もう一つ観測するものがあります：平均トレード損失と平均トレード利益の比率もまた悪くなっています。それは、20051.69/142644.96 = 0.141等しくなっており、 – 以前の”0.1”でのテストの35.80 / 180.72 = 0.198 という数値にはなっていません。なぜでしょうか？この答えは以下です：幾何学的なMMでの損失は、減少するバランス曲線の上部 、トレードのオープン時に一致するアカウントバランスでのロットサイズで計算されます。同時に利益の出るトレードの量は、バランス曲線の下部、オープン時のバランスにより、計算され、損失の出るトレードの量よりも少し少ないように見えます。

数学的な例：$5000に等しいバランスと幾何学的なMMで、 0.1*($5K/$1K) = 0.5ロットのトレードをオープンし、100ポイントの利益があると想定します。EURUSDにおける利益は、$500に等しくなります。100ポイントの損失をもたらすトレードをすぐにオープンすると想定します。損失はどうなるでしょうか？ロットは、0.1*($5K+$500)/$1K = 0.55に等しく、損失は利益よりも10%多い-$550になります。固定ロットではこれは起こりませんでした!

どのような結論を導くことができるでしょうか？

1. 攻撃的なMMを見れば、良いバランスカーブを得るために、0.1ロットでのテストの一致するカーブは"dints"なしで理想的なものである必要があることを理解しなければなりません。実際のトレーディングにて使用するMM変数はいずれも無視してはいけません。あなたのMMが違うものであれば、"0.1 testing"というもののみに先導されてはいけません。
2. 幾何学的なッMは、ドローダウンパーセンテージを向上させることを覚えておく必要があります。５年の期間での0.1ロットでのテストは、1000%のデポジットの成長を示しています（$1Kから$11K）それはかなり実際的な値です：60ヶ月間10000ポイントに一致し、一月167ポイントに値します。5年の期間の終わりまで、$11K にデポジットが等しい場合、5%の0.1ロットで少しのドローダウンがあり、その後、最後のトレードは利益を生むものであり、そのデポジットは今%11Kに等しくなっています。ドローダウンは、幾何学的なMMではどうなるでしょうか? デポジットの55%は – この"dint"前にどれほど上昇したかには関わりがありません。これの説明はさらに進む必要があります。
3. なので、オススメとしては、"golden mean"をあなたのMM戦略にて選択してください。0.1ロットを常に使う必要があるということではありませんが、百万に値するトレードでの幾何学的MMは、常にリスクの過小評価に伴う単なる夢でしかありません。
   

幾何学的なMMのドローダウンの主張の証拠:もし0.1でのテスト中にてその期間の終了までに（損失トレード前のバランスが$11Kの際）そのドローダウンは5%に等しく、 5%*$11K = $550, 550ポイントに等しくなります。それでは、幾何学的なMMにて同様のものを計算してみましょう。

もしこのドローダウンが一つのオープンされたポジションのみに由来するものであれば（例えば、ストップロスがない）これに対する推論はシンプルです："幾何学的なMM"でのこのドローダウン以前にそのバランスがX*$1Kに達したと想定します (このMMのせいで、Xは11以上になる可能性が高いですが、ここではあまり重要ではありません). そして、その X*0.1ロットのトレードがオープンされ、 lot*pipsvalue*pips = (X*0.1)*$10*550 = $550*Xで、これは100%*($550*X)/(X*$1K) = このドローダウン以前のデポジットの55%に等しい損失でクローズされます。

このドローダウンがいくつかの連続する負けトレードの結果である場合、より難しいですが、これらのトレードはおおよそ一つのトレードに組み込むことができ、このドローダウンは一つのトレードの結果であると考えられるようになります：しかし、複数の反対のトレードの蓄積の効果により、その結果は少し異なるようになります。

この推測は、論理的に幾何学的MMのテスト結果を説明しようとしている際のこの記事が描かれるプロセスの中で得たもので、この結果には以前驚いています。0.1ロットにて小さいドローダウンの魅力的な曲線を示す戦略に対して攻撃的なMMを追加することはできると信じていましたが、このドローダウンが"0.1 testing"にて示された結果と比較して不釣り合いに成長するとは考えませんでした。今では長く使用された幾何学的なMMについて懐疑的です。理由は、ドローダウンなしの戦略はないためです。

テスト2, パート2: Lucky EAと幾何学的MM

ドローダウンに関する議論を証明する驚くべき例を紹介します。これは、幾何学的なMMとともに使用しようとするEA 'Lucky'の開発者への教訓です（これは最初の考えです：ソースコードを以下からご覧ください https://www.mql5.com/ja/code/7464):

double GetLots()
{
   return (NormalizeDouble(AccountFreeMargin()/10000,1));
}

そのエキスパートアドバイザーは、0.1ロットのテストのためにわずかに修正され、1ポイント以上大きい利食いを行います（Prlimit=1という外部パラメーターを使用します）. さらに、ソースコードと異なり、EAでは１つの注文のみ一回でオープンされます（この場合、バランスカーブの特徴を大きく変化しません。）私たちは、EAが実際の証券業者で動作するか否かは興味はなく、それは目的ではありません。変更後のEAコードはこの記事に添付されています。

テストはパラメーター Shift=4, Limit=10, 固定ロット0.1、履歴2004.01.01から2008.04.04期間の Prlimit=1 (最初のデポジットは$1Kです)にて実行されます。こちらがそのバランスカーブです:

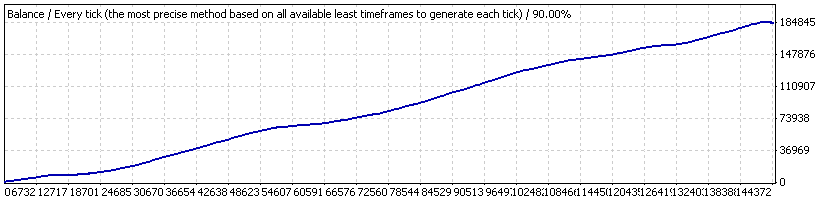
エキスパートアドバイザー Lucky, "0.1"

このカーブはテスターではみえますが、図では見えない小さい"dint"を保持しています；それは57890から58857までの注文番号における2004/12/31から2005/01/07までの期間です。この期間でのトータルのテスト期間を制限する"dint"を分析しましょう（ロットは以前固定され、0.1に等しいです；ポイントでのドローダウンに興味があるため、その初期のバランスは重要ではなく、$1000に等しいものです。）

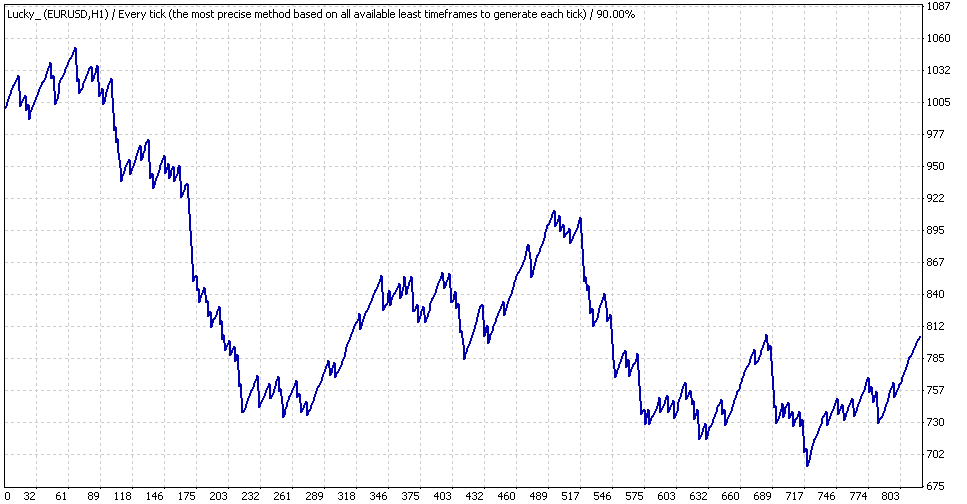
エキスパートアドバイザー Lucky, "0.1", "超小型" 実験

最大バランスはおおよそ$1050に等しく、最小は$690に等しいとわかります。0.1ロットのドローダウンは、$360に等しく、つまり、360ポイントになります。上記で記載されているものに類似したシンプルな計算を行い、幾何学的なMMにてこの値が36%のドローダウンに変化していることがわかります。幾何学的なMMにて同様の短期間のテストにより証明してみましょう(GetLots() は0.01, つまり、２になります):

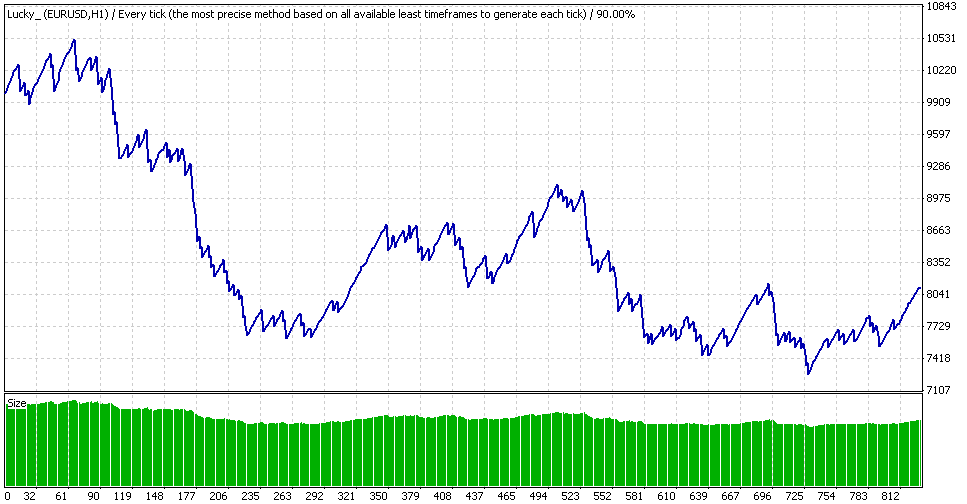
エキスパートアドバイザー Lucky, 同期間での幾何学的MM

実際のドローダウンは32%ですが（なぜなら、一つの注文に由来するものではないからです）、驚くべき結果になりました。（0.1ロットでのドローダウンは360/68000 ~ 0.5%に等しいです）チャートの中心のほとんど見えないdintは、60倍にまで成長しています。そして、これは"0.1"で0.89%ですが、1660ポイントのそのテスト期間の最後のドローダウンとは別で、このドローダウンはデポジットを実質失わせます 。

それでは、一見常識にそぐわないような人工的な例を作成します。

矛盾にした例. 表面的な調査

モジュールでは同じ結果である二つの連続するトレードが攻撃的なMMでは損失を生むという観測に基づき、0.1でテストし、幾何学的なMMでテストした際にその特徴を変え、安定した降下トレンド曲線に変わる!安定した成長を構築できます。エクセルで作成されたグラフが以下に表示されています。

その例は、私たちのトレードが結果（損失/利益）により変わるという考えに基づいており、100ポイントの利益のあるトレードがあり、そして、負けトレードに移行します。結果、幾何学的なMMで二つのトレードのトータルで損失があります。"0.1"のMMではトータルで利益があります。

最小ロットサイズと最小の増分に関する証券業者の制限は、考慮に入れられます(Alpari-IDCの条項によれば、0.1と0.01です). そのため、デポジットは最小サイズからの制限のために$1000よりも少なくなります。そして、そのような”境界効果”を避けるために、最初のデポジットは以前の$1000よりも10倍大きく取得されます

100ポイントの利益で、幾何学的MMがこの前に取得された利益に等しい損失を出す、利益100ポイントと損失値があるにも関わらず、その口座残高が特定の制限範囲の安定値内に入る損失トレード値があります。理由は未だにわかりません。以下で例をご覧になれます：初期のデポジットは常に$1000で、勝ちトレードは100ポイント、幾何学的MMの比率は、デポジット$1Kにつき0.1ロットです。

負けトレード - 91ポイント（勝ちトレードは、負けトレードよりも9ポイント大きいです。）

上の図は、異なるMMにおけるカーブ両方を示します。0.1ロットでの同じバランスカーブのノコギリ状の形を拡大しています。さらに、特徴が似ているためその２番目のグラフは表示されません。

91に等しい損失の数学的予想の値は、３重の負けトレードを示すために表示され、幾何学的なMMを用いた際に0.1MMの利益を生むシステムが利益や損失を生まないもに変わります。

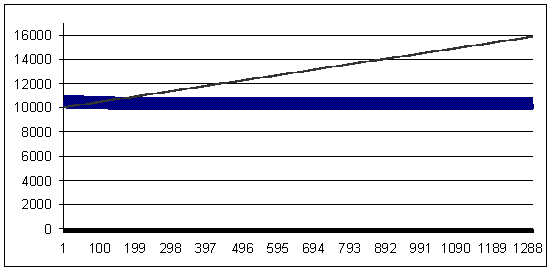
損失91、幾何学的な MM 0.1/$1000

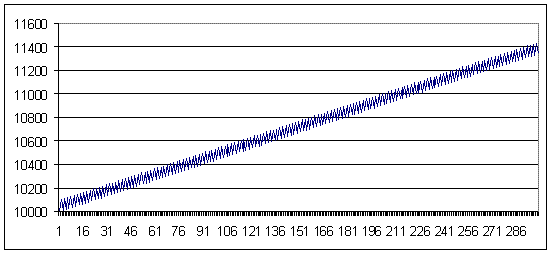
損失 91, lot = 0.1

負けトレード - 92ポイント (勝ちトレードは8ポイントも損失トレードより大きいです)

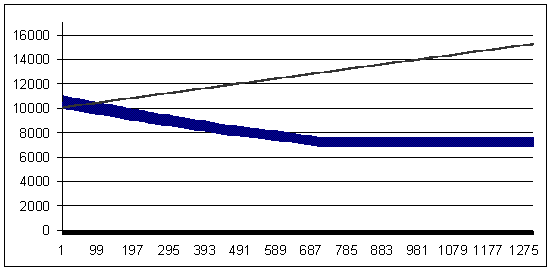
損失 92, 幾何学的 MM 0.1/$1000

負けトレード - 93ポイント (勝ちトレードは、負けトレードより7ポイント大きいです)

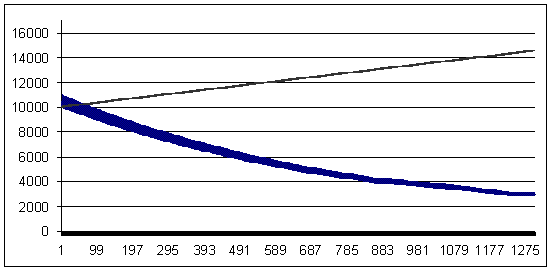
損失 93、幾何学的 MM 0.1/$1000

負けトレード - 94 ポイント (勝ちトレードは、負けトレードより6ポイント大きいです)

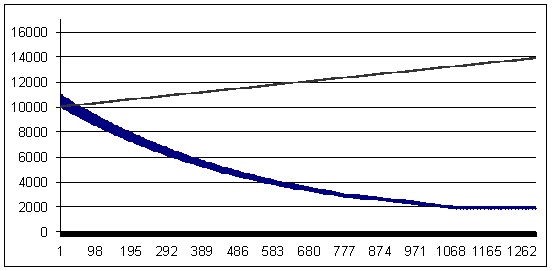
損失 94, 幾何学的MM 0.1/$1000

負けトレード - 96 ポイント (勝ちトレードは、負けトレードより4ポイント大きいです.)

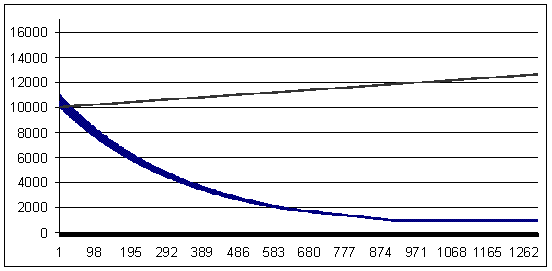
損失 96, 幾何学 ММ 0.1/$1000

その曲線は反対になっていることがわかります。もちろん、実際のシステムは「安定」とはなりませんが、もし”0.1”ロットのテストチャートを注意深く考えなければ怒るであろうことを示す例を含めました。

それでは、もし幾何学的MMをより攻撃的にすると何が怒るのかを見てみましょう（例えば、デポジット$1Kにつき0.2か0.33ロットです；フォーラムにてそのようなケースを見ることができます）さらに、負けトレードの境界値にのみ属するチャートを見ることができます（勝ちトレードは、依然100ポイントに等しいです）：もし負けトレードが境界値を越えれば、その幾何学的MMでのカーブはさらに悪くなります。

負けトレード - 84 ポイント (勝ちトレードは、負けトレードよりも16ポイント大きいです). MM - 幾何学的、0.2ロット/デポジットの$1K

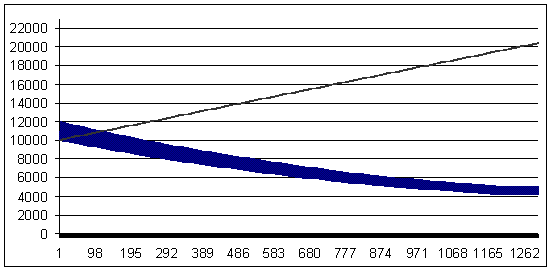
損失 84, 幾何学的 MM 0.2/$1000

負けトレード - 75 ポイント (勝ちトレードは、負けトレードよりも25ポイント大きいです). MM- 幾何学的, 0.33 ロット/デポジット $1K

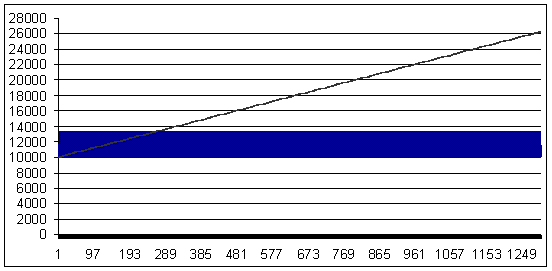
損失 75, 幾何学的 MMММ 0.33/$1000

結論: 勝ちトレードの変更されていない数学的予想の戦略での高い攻撃性は、その戦略に高い必要項目を設定します；ポイントにおけるトレードの数学的予想値は、増大されなければなりません。以下のパラメーターにて、負けトレードの初期値を定義する公式を決定できます。

- 勝ちトレードの利益 (profit),

-幾何学的MM (aggr)の攻撃性、つまり、デポジットの$10Kにつき、ポジションの量

- 安全な1ロットにおける１ポイントの値

その公式を証明するために、デポジット$10Kから始まる最初の二つのトレードのみをオープンする必要があり、この相関関係は取得されたデポジットに関係なく達成されます（Xパラメーターがキャンセルされたため少し早く証明されます）

1. その最初のトレードは利益を出します：デポジットは$10Kです。aggrロットに等しいい量のポジションをオープンしてください。 aggr * profit * pointval.に等しい利益を得ます。そのトレードをクローズします。
2. ２番目のトレードをオープンします。それは損失を出します。トレードのオープン時までに、そのデポジットは、$10000+ aggr*profit*pointval = $10K*(1+ aggr*profit*pointval/10000).に等しくなります。トレードの量は aggr*(1+ aggr*profit*pointval/10000)です。ドルでの望ましい負けトレードはaggr*(1+ aggr*profit*pointval/10000) * loss * pointval.です。
3. 二つの取得された式を同等化し、損失の公式を取得します；

loss = profit / (1+ aggr*profit*pointval /10000)

それでは、 EURUSD (pointval=$10)にて公式の正当性をチェックしましょう:

-もしprofit=100, aggr=1 であれば、loss = 100/(1+1*100*10/10000) = 100/1.1 ~ 90.91 pips.を得ます。以前見つけた通り、このケースでのその初期値は、91ポイントです;

-もしprofit=100, aggr=2 である場合、loss = 100/1.2 ~ 83.33.を取得します。その以前取得した初期値は、84ポイントに等しくなります。;

-もしprofit=100, aggr=3.33 であればloss = 100/1.33 ~ 75.19になります。その初期値は、75になります.

実験データとの合意は悪くありません。しかし、その実際の残高グラフはこのようにはなりません；利益と損失のトレードの比率は等しくありません。人工的な残高カーブの構築の原則は明確なので、より複雑なケースにこのモデルを適用しません。"moderate"と呼ばれる3種類目のMMのEAをテストし調査を終了しましょう。

テスト 3:ロットは、デポジットの平方根に比例します。

ストラテジーテスターレポート 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

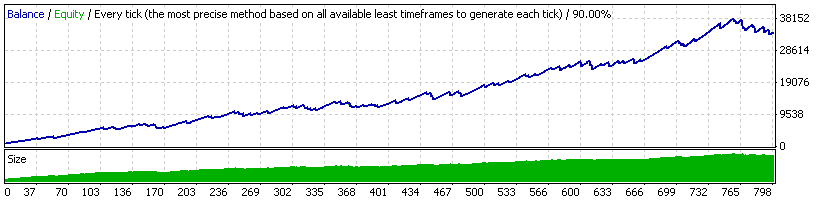
エキスパートアドバイザー 20_200 expert_v4.2_AntS, moderate MM

RF = 32764.09 / 5632.51 = 5.82

この場合、初期のデポジットは、 $1Kに等しくなり、初期のロットは - 0.1です。

このMMは、上記で分析された二つの中間のポジションを取ります。最大ドローダウンは、そこまで大きくありませんが、関連ドローダウンは依然大きいです。ただ、そのカーブはかなり魅力的で、２番目のもの（EA "20_200"）よりも断然良いです。さらに、２番目のものよりもずっと安定しています。

このバージョンの異なる型もあります。例えば、もし$10Kに等しい初期のデポジットを取得し、1.0に等しい初期ロットを設定すれば、(前のコードに記述):

case 2: size = 1. * MathSqrt( AccountBalance() / 10000 );

およそ8年の間、以前示された利益は10倍になりますが、関連ドローダウンは変わりません。

まとめ

結論の大半は、幾何学的なMMに対して捧げられた部分に記されています。著者は、いくつかの面白い戦略のトレード結果の分析に現れる統計的な規則性をカバーするために"Fallacies"の２番目の記事を執筆しています。数学的な記述レベルはこの記事よりも少し高いですが、そこまで理解できないものではありません。

そして、この記事の題名への最後のコメントがあります；ええ、資金管理は副次的なものです、なぜなら、それは0.1ロットで損失を生む戦略を控え、利益の出るものに変えないためです。しかしながら、「良いことは多すぎるということはない」ということわざを否定する２番目に記した内容は正しいです異なる種類の資金管理を可能にする戦略はたとえそれが利益を出す堅実なものでも、攻撃的なMMにかき消されてしまいます。