OpenCL: El puente hacia mundos paralelos
3 202
0
Introducción
Este artículo es el primero de una serie corta de publicaciones sobre programación en OpenCL o Open Computing Language. La plataforma de Meta Trader 5 en su versión actual, antes de proporcionar soporte para OpenCL, no lo permitía directamente, es decir, usar y disfrutar de forma nativa de las ventajas de los procesadores de múltiples núcleos para acelerar los cálculos.
Obviamente, los desarrolladores podían repetir sin parar que el terminal era multihilo y que "cada EA/script se ejecutaba en un hilo separado", aunque al código no se le daba una oportunidad para una relativamente fácil ejecución paralela del siguiente lazo simple (este es un código para calcular el valor de pi = 3.14159265...):
long num_steps = 1000000000; double step = 1.0 / num_steps; double x, pi, sum = 0.0; for (long i = 0; i<num_steps; i++) { x = (i + 0.5)*step; sum += 4.0/(1.0 + x*x); } pi = sum*step;
Sin embargo, hace tan solo 18 meses, un trabajo muy interesante llamado "Cálculos paralelos en MetaTrader 5" apareció en la sección artículos. Y aún...uno tiene la impresión de que a pesar de la ingenuidad del enfoque, es un tanto innatural, ya que toda una jerarquía del programa (el Expert Advisor y dos indicadores) escritos para acelerar los cálculos en el lazo anterior habrían sido demasiado buenos.
Ya sabemos que no hay planes para soportar OpenMP y somos conscientes del hecho de que añadir OMP requeriría una drástica reprogramación del compilador. Y mira por donde, no hay ninguna solución barata ni fácil para un programador si no es necesario pensar.
El anuncio de soporte nativo para OpenCL en МQL5 fueron noticias muy bien recibidas. Comenzando en la página 22 del mismo hilo de noticias, MetaDriver comenzó a publicar scripts que permitían evaluar la diferencia entre la implementación en CPU y GPU. OpenCL despertó un gran interés.
El autor de este artículo optó en primer lugar por salir del proceso: una configuración del PC muy pobre (Pentium G840/8 Gb DDR-III 1333/Sin tarjeta de video) no parece proporcionar un uso efectivo de OpenCL.
Sin embargo, tras la instalación de un software especializado desarrollado por AMD, el primer script propuesto por MetaDriver que ha estado ejecutándose por otros solo si había disponible una discreta tarjeta de video, se ejecutó con éxito en el PC del autor y demostró un incremento de la velocidad nada insignificante al compararlo con el tiempo de ejecución estándar de un script en un procesador de un núcleo, siendo aproximadamente 25 veces más rápido. Posteriormente, la mejora del tiempo de ejecución del mismo script fue de 75 veces, debido al tiempo de ejecución de OpenCL de Intel instalado con éxito con la ayuda del equipo de apoyo.
Habiendo estudiado detenidamente el foro y los materiales proporcionados por ixbt.com, el autor encontró que el procesador de gráficos integrados de Intel (IGP) soportaba OpenCL 1.1, solo empezando desde los procesadores Ivy Bridge en adelante. Por tanto, la aceleración alcanzada en el PC con la anterior configuración no tendría nada que ver con IGP y el código del programa OpenCL en este caso particular se ejecutó solo en una CPU con núcleo x86.
Cuando el autor mostró las cifras de aceleración a los expertos de ixbt, estos respondieron inmediatamente y todos a la vez que todo era el resultado de una falta de optimización sustancial del lenguaje fuente (MQL5). En la comunidad de profesionales de OpenCL, es un hecho conocido que una optimización correcta de un código fuente en C++ (por supuesto, sujeta al uso de procesadores de múltiples núcleos e instrucciones de vector SSEx) puede, en el mejor de los casos, dar una ganancia de varias docenas de puntos porcentuales en la emulación OpenCL. En el peor escenario, podemos perder, p.ej. debido al consumo extremadamente alto (de tiempo) al pasar los datos.
Por tanto, otra suposición: Las cifras "milagrosas" en Meta Trader 5 en la emulación pura de OpenCL deben tratarse adecuadamente sin atribuirlas a la "bondad" de OpenCL. Un ventaja verdaderamente importante de GPU sobre un programa en C++ bien optimizado, solo puede obtenerse utilizando una tarjeta gráfica muy potente, ya que sus capacidades de cálculo en algunos algoritmos son mucho mayores que las de cualquier CPU moderna.
Los desarrolladores del terminal afirman que aún no ha sido adecuadamente optimizado. También han dado un consejo sobre el grado de aceleración que será de varias veces tras la optimización. Todas las cifras de aceleración en OpenCL serán reducidas adecuadamente por las mismas "varias veces". Sin embargo, serán aún considerablemente mayores a la unidad.
Es una buena razón para aprender el lenguaje OpenCL (incluso si nuestra tarjeta gráfica no soporta OpenCL 1.1 o simplemente no disponemos de ella) del que vamos a tratar a continuación. Pero antes permítanme decir unas palabras sobre los fundamentos esenciales, el software que soporta OpenCL y el software adecuado.
1. Software y hardware esencial
1.1.AMD
AMD, Intel y NVidia producen el software adecuado, ya que son los miembros del consorcio de la industria sin fines de lucro, formando el Grupo Khronos que desarrolla diferentes especificaciones del lenguaje en relación con los cálculos en entornos heterogéneos.
Pueden encontrarse algunos materiales útiles en la web oficial del Grupo Khronos, p. ej.:
Estos documentos deberán usarse muy a menudo en el proceso de aprendizaje de OpenCL ya que el terminal no ofrece aún información de ayuda sobre Open CL (solo hay un resumen breve de la API de OpenCL). Las tres empresas (AMD, Intel y NVidia) son proveedores de hardware de video y cada una tiene su propia implementación del tiempo de ejecución de OpenCL y sus respectivos kits de desarrollo de software, SDK. Vamos a profundizar en las peculiaridades de elegir tarjetas gráficas, tomando los productos AMD como ejemplo.
Si nuestra tarjetas gráfica AMD no es muy antigua (primera versión en producción en los años 2009-2010 o posteriores) va a ser muy sencillo, ya que una actualización del driver de nuestra tarjeta gráfica debería ser suficiente para empezar a trabajar inmediatamente. Puede encontrarse una lista de tarjetas gráficas compatibles con OpenCL aquí. Por otro lado, incluso una tarjeta gráfica que sea muy buena para su época, como la Radeon HD 4850 (4870), no nos ahorrará el problema a la hora de tratar con OpenCL.
Si aún no tenemos una tarjeta gráfica pero queremos una, podemos echar un vistazo a sus especificaciones primero. Aquí podemos ver una muy amplia Tabla de especificaciones de tarjetas gráficas AMD actuales Lo más importante para nosotros es lo siguiente:
- La memoria instalada - la cantidad de memoria local. Cuanto más mejor. 1 GB sería normalmente suficiente.
- Velocidad de reloj del núcleo -frecuencia de operación del núcleo. También está claro: a mayor frecuencia de operación de los multiprocesadores GPU, mejor. 650-700 MHz no está nada mal..
- Tipo de memoria - tipo de memoria gráfica. La memoria debería ser idealmente rápida, es decir GDDR5. Pero GDDR3 también estaría bien aunque dos veces peor en términos de ancho de banda de memoria.
- Memoria de reloj (Ef.) - frecuencia de operación (efectiva) de la memoria gráfica. Técnicamente, este parámetro está muy relacionado con el previo. La frecuencia efectiva de operación GDDR5 es de media dos veces mayor que la frecuencia GDDR3. No tiene nada que ver con el hecho de que los tipos de memoria "superiores" funcionan a frecuencias mayores, sino que ello es así debido al número de canales de transferencia de datos utilizados por la memoria. En otras palabras, tiene que ver con el ancho de banda de memoria.
- Bus de memoria- ancho del bus de datos. Es aconsejable que sea al menos de 256 bit.
- MBW - ancho de banda de memoria. Este parámetro es actualmente una combinación de los tres parámetros de la memoria de video anteriores. Cuanto más mejor.
- Núcleo de configuración (SPU:TMU(TF):ROP) - configuración de las unidades de núcleo de GPU. Lo importante para nosotros, es decir, para los cálculos no gráficos, es el primer número. El dato 1024:64:32 significa que necesitamos el número 1024 (número de procesadores o shaders). Obviamente, cuanto más mejor.
- Potencia de procesado - rendimiento teórico en cálculos de coma flotante (FP32 (precisión única) / FP64 (precisión doble). Donde las tablas de especificación contienen un valor correspondiente a FP32 (todas las tarjetas gráficas pueden realizar cálculos de precisión única), este no es el caso de FP64 ya que la doble precisión no está soportada por todas las tarjetas gráficas. SI está seguro de que nunca necesitará doble precisión (tipo doble) en cálculos GPU, puede obviar el segundo parámetro. Pero sea cual sea el caso, cuanto mayor es este parámetro, mejor.
- TDP - Potencia de diseño térmica. Esta es, a grandes rasgos, la máxima potencia que disipa la tarjeta gráfica en los cálculos más difíciles. Si nuestro Expert Advisor va a acceder frecuentemente a GPU, la tarjeta gráfica no solo consumirá mucha potencia (lo que no es malo si da resultados) sino que también será muy ruidosa.
Ahora el segundo caso: no hay tarjeta gráfica o la que hay no soporta OpenCL 1.1 pero tenemos un procesador AMD. Aquí podemos descargar AMD APP SDK que, aparte del tiempo de ejecución, también contiene SDK, Kernel Analyzer y Profiler. Tras la instalación de AMD APP SDK, el procesador debería ser reconocido como un dispositivo OpenCL. Y podremos desarrollar las aplicaciones OpenCL en modo emulación en la CPU.
La característica principal de SDK, al contrario que AMD, es que también es compatible con los procesadores Intel (aunque al desarrollarlo en una CPU Intel, SDK es aún significativamente más eficiente ya que es capaz de soportar conjuntos de instrucciones SSE4.1, SSE4.2 y AVX que solo han estado disponibles actualmente en los procesadores AMD).
1.2. Intel
Antes de empezar el trabajo con los procesadores Intel, es aconsejable descargar Intel OpenCL SDK/Runtime.
Debemos indicar lo siguiente:
- Si intentamos desarrollar aplicaciones OpenCL usando solo CPU (modo de emulación OpenCL), debemos saber que el kernel de gráficos de la CPU de Intel no soporta OpenCL 1.1 para procesadores anteriores a Sandy Bridge, incluido. Esta compatibilidad solo está disponible con los procesadores Ivy Bridge pero no mostrará grandes diferencias incluso para la super poderosa unidad gráfica integrada Intel HD 4000. Para los procesadores más antiguos que Ivy Bridge, esto significa que la aceleración alcanzada en el entorno MQL5 solo es debida a las instrucciones de vector SS(S)Ex usadas. Incluso parece ser importante.
- Después de la instalación del SDL OpenCL de Intel, será necesario modificar la entrada del registro HKEY_LOCAL_MACHINE\SOFTWARE\Khronos\OpenCL\Vendors de la siguiente forma: sustituimos IntelOpenCL64.dll en la columna Nombre con intelocl.dll . Luego reiniciamos y ejecutamos Meta Trader 5. Ahora la CPU es reconocida como un dispositivo OpenCL 1.1.
Para ser honesto, la cuestión sobre la compatibilidad OpenCL de Intel no ha sido aún resuelta del todo, por lo que debemos esperar algunas aclaraciones de los desarrolladores del terminal en el futuro. Básicamente, la cuestión es que nadie va a estar vigilando los errores de código del kernel (el kernel de OpenCL es un programa ejecutado en GPU) por nosotros, no es el compilador MQL5. El compilador solo lo tomará en una sola línea del kernel e intentará ejecutarlo. Si, por ejemplo, no declaramos una variable interna x utilizada en el kernel, este será aún técnicamente ejecutado, aunque con errores.
Sin embargo, todos los errores que obtendremos en el terminal serán menos de una docena de los descritos en la ayuda en OpenCL API para las funciones CLKernelCreate() y CLProgramCreate(). La sintaxis del lenguaje es muy similar a la de C, mejorada con funciones vector y tipos de datos (de hecho este lenguaje es C99 que fue adoptado como estándar ANSI C en 1999).
Es el Intel OpenCL SDK Offline Compiler el que el autor de este artículo utiliza para depurar código para OpenCL. Es mucho más adecuado que buscar ciegamente los errores del kernel en MetaEditor. Por suerte, en el futuro la situación cambiará a mejor.
1.3. NVidia
Por desgracia, el autor no buscó información a este respecto. No obstante, las recomendaciones generales son las mismas. Los controladores para las tarjetas gráficas NVidia soportan automáticamente OpenCL.
Básicamente, el autor de este artículo no tiene nada en contra de las tarjetas gráficas NVidia, pero la conclusión obtenida en base al conocimiento adquirido a partir de la búsqueda de información y las conversaciones en los foros es la siguiente: para los cálculos no gráficos, las tarjetas gráficas AMD parecen ser más óptimas en términos de relación precio/rendimiento que las de NVidia.
Vamos ahora a ver la programación.
2. Primer programa MQL5 usando OpenCL
Para poder desarrollar nuestro primer y simple programa, necesitamos definir una tarea como tal. El uso del valor pi debe haberse hecho habitual en los cursos de programación paralela, que es aproximadamente igual a 3,14159265 como ejemplo.
Para este propósito, se usa la siguiente fórmula (el autor nunca se ha encontrado esta fórmula antes pero parece ser verdadera):
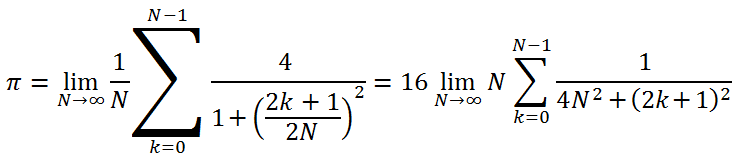
Queremos calcular el valor con una precisión de 12 decimales. Básicamente, tal precisión puede obtenerse con cerca de 1 millón de iteraciones, pero este número no nos permitirá evaluar las ventajas de los cálculos en OpenCL, ya que la duración de los cálculos en GPU se hace muy corta.
Los cursos de programación en GPGPU recomiendan elegir la cantidad de cálculos necesaria para que la duración de la tarea GPU sea al menos de 20 milisegundos. En nuestro caso, este límite debe establecerse a un valor mayor debido al gran error de la función GetTickCount() comparable a 100 milisegundos.
Este es el programa MQL5 donde se implementa el cálculo:
//+------------------------------------------------------------------+ //| pi.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" long _num_steps = 1000000000; long _divisor = 40000; double _step = 1.0 / _num_steps; long _intrnCnt = _num_steps / _divisor; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { uint start,stop; double x,pi,sum=0.0; start=GetTickCount(); //--- first option - direct calculation for(long i=0; i<_num_steps; i++) { x=(i+0.5)*_step; sum+=4.0/(1.+x*x); } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); //--- calculate using the second option start=GetTickCount(); sum=0.; long divisor=40000; long internalCnt=_num_steps/divisor; double partsum=0.; for(long i=0; i<divisor; i++) { partsum=0.; for(long j=i*internalCnt; j<(i+1)*internalCnt; j++) { x=(j+0.5)*_step; partsum+=4.0/(1.+x*x); } sum+=partsum; } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); Print("_______________________________________________"); return(0); } //+------------------------------------------------------------------+Una vez compilado y ejecutado obtenemos:
2012.05.03 02:02:23 pi (EURUSD,H1) The time to calculate PI was 8.783 seconds 2012.05.03 02:02:23 pi (EURUSD,H1) The value of PI is 3.141592653590 2012.05.03 02:02:15 pi (EURUSD,H1) The time to calculate PI was 7.940 seconds 2012.05.03 02:02:15 pi (EURUSD,H1) The value of PI is 3.141592653590
El valor de pi ~ 3.14159265 se calcula de dos formas ligeramente diferentes.
La primera puede considerarse casi un método clásico para mostrar las capacidades de las librerías multihilo como OpenMP, Intel TPP, Intel MKL y otras.
La segunda es el mismo cálculo en forma de un doble lazo. Todo el cálculo que comprende 1.000 millones de iteraciones se desglosa en dos grandes bloques del lazo exterior (hay 40.000 de estos ahí) donde cada bloque ejecuta 25.000 iteraciones "básicas" completando el bucle.
Podemos ver que este cálculo se ejecuta un poco más lento en un 10-15%. Pero es este cálculo en particular el que vamos a usar como base al convertir a OpenCL. La principal razón es la selección del kernel (la tarea de cálculo básica ejecutada en GPU) que realizará un equilibrio razonable entre el tiempo consumido en transferir los datos de un área de la memoria a otra y la ejecución de los cálculos en el kernel. De esta forma, en términos de la tarea actual, el kernel será, en general, el lazo interior del segundo algoritmo de cálculo.
Vamos ahora a calcular el valor utilizando OpenCL. A un código de programa completo le seguirán unos breves comentarios sobre las funciones, característico del lenguaje anfitrión (MQL5) obligatorio en OpenCL. Pero primero me gustaría destacar algunos puntos en relación a los "obstáculos" típicos que pueden interferir con la creación de código en OpenCL:
- El kernel no ve variables declaradas fuera del él. Por eso las variables globales _step y _intrnCnt debían ser declaradas de nuevo al principio del código del kernel (ver más abajo). Y sus respectivos valores tuvieron que ser transformados en strings para que pudieran leerse adecuadamente en el código del kernel. Sin embargo, esta peculiaridad de la programación en OpenCL ha mostrado luego ser muy útil, p. ej. al elaborar los tipos de datos vector que están nativamente ausentes en C.
- Intente dar tantos cálculos al kernel como sea posible manteniendo su número en una cifra razonable. Esto no es muy importante para este código ya que el kernel no es muy rápido aquí en el hardware existente. Pero este factor nos ayudará a acelerar los cálculos si se usa una tarjeta gráfica potente.
Este es el código script con el kernel OpenCL:
//+------------------------------------------------------------------+ //| OCL_pi_float.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs; input int _device=0; /// OpenCL device number (0, I have CPU) #define _num_steps 1000000000 #define _divisor 40000 #define _step 1.0 / _num_steps #define _intrnCnt _num_steps / _divisor string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(int arg) { return IntegerToString(arg); } const string clSrc= "#define _step "+d2s(_step,12)+" \r\n" "#define _intrnCnt "+i2s(_intrnCnt)+" \r\n" " \r\n" "__kernel void pi( __global float *out ) \r\n" // type float "{ \r\n" " int i = get_global_id( 0 ); \r\n" " float partsum = 0.0; \r\n" // type float " float x = 0.0; \r\n" // type float " long from = i * _intrnCnt; \r\n" " long to = from + _intrnCnt; \r\n" " for( long j = from; j < to; j ++ ) \r\n" " { \r\n" " x = ( j + 0.5 ) * _step; \r\n" " partsum += 4.0 / ( 1. + x * x ); \r\n" " } \r\n" " out[ i ] = partsum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt)); int clCtx=CLContextCreate(_device); int clPrg = CLProgramCreate( clCtx, clSrc ); int clKrn = CLKernelCreate( clPrg, "pi" ); uint st=GetTickCount(); int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float CLSetKernelArgMem(clKrn,0,clMem); const uint offs[ 1 ] = { 0 }; const uint works[ 1 ] = { _divisor }; bool ex=CLExecute(clKrn,1,offs,works); //--- Print( "CL program executed: " + ex ); float buf[]; // type float ArrayResize(buf,_divisor); uint read=CLBufferRead(clMem,buf); Print("read = "+i2s(read)+" elements"); float sum=0.0; // type float for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt]; float pi=float(sum*_step); // type float Print("pi = "+d2s(pi,12)); CLBufferFree(clMem); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); double gone=(GetTickCount()-st)/1000.; Print("OpenCl: gone = "+d2s(gone,3)+" sec."); Print("________________________"); return(0); } //+------------------------------------------------------------------+
Un poco más tarde se dará una explicación más detallada del código del script.
Mientras tanto, compilamos y ejecutamos el programa para obtener lo siguiente:
2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) ________________________ 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) OpenCl: gone = 5.538 sec. 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) pi = 3.141622066498 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) read = 40000 elements 2012.05.03 02:20:15 OCl_pi_float (EURUSD,H1) FLOAT: _step = 0.000000001000; _intrnCnt = 25000
Como puede verse, el tiempo de ejecución se ha reducido ligeramente. Pero esto no es suficiente para hacernos felices: el valor de pi ~ 3.14159265 obviamente solo es preciso hasta el tercer dígito después del separador decimal. Tal falta de precisión en los cálculos se debe al hecho de que en los cálculos reales el kernel utiliza números de tipo flotante cuya precisión está claramente por debajo de la requerida de 12 posiciones decimales.
De acuerdo a la Documentación MQL5, la precisión de un número en coma flotante solo es precisa en 7 cifras decimales. Mientras que la precisión de un número de tipo doble lo es en 15 cifras significativas.
Por tanto, necesitamos hacer que los datos reales sean "más precisos". En el código anterior, las líneas donde el tipo flotante debían reemplazarse con doble tipo se han marcado con el comentario ///type float. Tras la compilación utilizando los mismos datos de entrada obtenemos lo siguiente (nuevo archivo con el código fuente OCL_pi_double.mq5):
2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) OpenCl: gone = 12.480 sec. 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.03 03:25:23 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
El tiempo de ejecución se ha incrementado significativamente e incluso ha excedido el tiempo del código fuente sin OpenCL (8.783 seg.).
"Está claro que el tipo doble ralentiza los cálculos",- podríamos pensar. Vamos a experimentar y cambiar sustancialmente el parámetro de entrada _divisor de 40.000 a 40.000.000:
2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) OpenCl: gone = 5.070 sec. 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) read = 40000000 elements 2012.05.03 03:26:50 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25
No ha afectado a la precisión y el tiempo de ejecución ha sido incluso menor que en el caso del tipo flotante. Pero si solo cambiamos todos los tipos enteros de long a int y recuperamos el valor previo de _divisor = 40.000, el tiempo de ejecución del kernel disminuirá en torno a la mitad:
2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) OpenCl: gone = 2.262 sec. 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.16 00:22:44 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
Debemos siempre recordar que si hay un lazo muy "largo" pero "ligero" (es decir, un lazo con muchas iteraciones cada una de ellas sin mucha aritmética), un simple cambio en los tipos de datos de "pesados" (tipo largo - 8 bytes) a "ligeros" (int - 4 bytes) puede disminuir drásticamente el tiempo de ejecución del kernel.
Vamos ahora a dejar nuestros experimentos de programación durante un momento y nos centraremos en el significado de "vinculación" del código kernel para comprender los que estamos haciendo. Por "vinculación" del código del kernel queremos decir OpenCL API, es decir, un sistema de comandos que permiten que el kernel se comunique con el programa anfitrión (en este caso, con el programa MQL5).
3. Funciones API de OpenCL
3.1. Crear un contexto
Un comando de abajo crea el contexto, es decir, un entorno para la gestión de objetos y recursos de OpenCL.
int clCtx = CLContextCreate( _device );
Primero, una palabras sobre el modelo de plataforma.
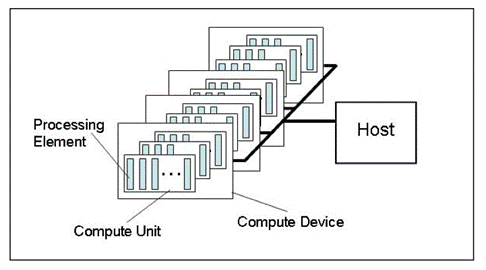
Fig. 1. Modelo abstracto de una plataforma de cálculo
La figura muestra un modelo abstracto de plataforma de cálculo. No es una representación muy detallada de la estructura del hardware con relación a las tarjetas gráficas pero está muy cerca de la realidad y da una buena idea general.
El anfitrión en la CPU principal que controla todo el proceso de ejecución del programa. Puede reconocer algunos dispositivos OpenCL (dispositivos de cálculo). En la mayoría de casos, cuando un operador tiene una tarjeta gráfica para los cálculos disponible en la unidad del sistema, a la tarjeta gráfica se la considera un dispositivo (¡una tarjeta gráfica de doble procesador será considerada como dos dispositivos!). Además de esto, el anfitrión en sí, es decir, la CPU es siempre considerada como un dispositivo OpenCL. Cada dispositivo tiene un único número en la plataforma.
Hay varias unidades de cómputo en cada dispositivo que, en caso de una CPU se corresponde con núcleos x86 (incluyendo los núcleos "virtuales" de la CPU de Intel, es decir "núcleos" creados mediante hiper-hilado). Para una tarjeta gráfica, estos serían motores SIMD, es decir, núcleos SIMD o mini procesadores en términos del artículo Computación GPU. Características de la arquitectura AMD/ATI Radeon. Las tarjetas gráficas potentes tienen normalmente cerca de 20 núcleos SIMD.
Cada núcleo SIMD contiene procesadores de flujo , p. ej. la tarjeta gráfica Radeon HD 5870 tiene 16 procesadores de flujo en cada motor SIMD.
Finalmente, cada procesador de flujo tiene 4 o 5 elementos de procesado, es decir, ALU en la misma tarjeta.
Debe señalarse que la terminología usada por todos los grandes proveedores de hardware es muy confusa, especialmente para los más iniciados. No siempre es obvio lo que quiere decir "bees" tan usado en un popular hilo de un foro sobre OpenCL. No obstante, el número de hilos, es decir, de hilos de cálculo simultáneos, en las tarjetas gráficas actuales es muy elevado. Por ejemplo, el número estimado de hilos en una tarjeta gráfica Radeon HD 5870 es de más de cinco mil.
La figura a continuación muestra las especificaciones técnicas estándar de esta tarjeta gráfica.
Fig. 2. Características de la GPU Radeon HD 5870
Todo lo especificado a continuación (recursos OpenCL) debe asociarse necesariamente con el contexto creado por la función CLContextCreate():
- dispositivos OpenCL, es decir, hardware utilizado en cálculos;
- Objetos de programa, es decir, código de programa ejecutando el kernel;
- Kernels, es decir, funciones ejecutadas en los dispositivos;
- Objetos de memoria, es decir, datos (p.ej. buffers, imágenes 2D y 3D) manipuladas por el dispositivo;
- Colas de comando (la implementación actual del lenguaje del terminal no proporciona la respectiva API).
El contexto creado puede ilustrarse como un campo vacío con dispositivos adjuntos a él debajo.
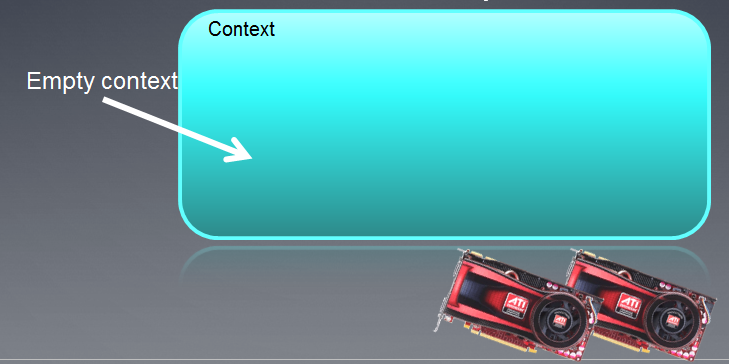
Fig. 3. Contexto OpenCL
Después de la ejecución de la función, el campo del contexto está vacío.
Debe señalarse que el contexto de OpenCL en MQL5 funciona solo con un dispositivo.
3.2. Crear un programa
int clPrg = CLProgramCreate( clCtx, clSrc );
La función CLProgramCreate() crea un recurso "programa OpenCL".
El objeto "Programa" es de hecho una colección de kernels OpenCL (que serán discutidos en el artículo siguiente) pero en la implementación de MetaQuotes solo puede haber, aparentemente, un kernel en el programa OpenCL. Para crear el "Programa" objeto, debemos asegurarnos de que el código fuente (aquí clSrc) se lee dentro de un string.
En nuestro caso no es necesario ya que el string clSrc ya ha sido declarado como variable global:
La figura a continuación muestra el programa como parte del contexto creado anteriormente.
Fig. 4. El Programa es parte del contexto
Si el programa no se puede compilar, el desarrollador iniciará de forma independiente un solicitud de datos a la salida del compilador. Una API OpenCL completa tiene la función API después de llamar en la que se devuelve un string a la salida del compilador.
La versión actual (b.642) no soporta esta función que podría merecer la pena que se incluyera en la API OpenCL para dar al desarrollador de OpenCL más información sobre la exactitud del código kernel.
Las "lengüetas" que proceden de los dispositivos (tarjetas gráficas) son colas de comando que parece que no serán soportadas en MQL5 a nivel API.
3.3. Crear un kernel
La función CLKernelCreate() crea un recurso de OpenCL "Kernel".
int clKrn = CLKernelCreate( clPrg, "pi" );
Kernel es una función declarada en el programa que se ejecuta en el dispositivo OpenCL.
En nuestro caso, es la función pi() con el nombre "pi". El objeto "kernel" es la función del kernel con sus respectivos argumentos. El segundo argumento en esta función es el nombre de la función que debe estar de acuerdo exactamente con el nombre de la función dentro del programa.
Fig. 5. Kernel
Los objetos "kernel" pueden usarse las veces que sean necesarias al establecer diferentes argumentos para uno y la misma función declarada como el kernel.
Pasemos ahora a las funciones CLSetKernelArg() y CLSetKernelArgMem() pero antes vamos a decir algunas palabras sobre los objetos almacenados en la memoria de los dispositivos.
3.4. Objetos de la memoria
En primer lugar, debemos entender que cualquier objeto "grande" procesado en GPU debe primero ser creado en la memoria de GPU o traído de la memoria anfitriona (RAM). Por objeto "grande" queremos decir un buffer (matriz de una dimensión) o una imagen que puede ser de dos o tres dimensiones (2D o 3D).
Un buffer es un gran área de la memoria que contiene elementos de buffer adyacentes separados. Estos pueden ser simples tipos de datos (carácter, doble, flotante, largo, etc.) o tipos de datos complejos (estructuras, uniones, etc.). Puede accederse directamente a los elementos separados de buffer, ser leídos y escritos.
No vamos a analizar imágenes por el momento ya que es un tipo de datos peculiar. El código proporcionado por los desarrolladores del terminal en la primera página del hilo sobre OpenCL sugiere que los desarrolladores no utilizan las imágenes.
En el código presentado, la función que crea el buffer parece ser de la siguiente forma:
int clMem = CLBufferCreate( clCtx, _divisor * sizeof( double ), CL_MEM_READ_WRITE );
El primer parámetro es un controlador de contexto con el que se asocia al buffer como recurso. El segundo parámetro es la memoria asignada para el buffer. El tercer parámetro muestra lo que puede hacerse con este objeto. El valor devuelto es un controlador al buffer OpenCL (si se crea on éxito) o -1 (si la creación ha fallado por un error).
En nuestro caso, el buffer se creó directamente en la memoria de GPU, es decir, el dispositivo OpenCL. Si se hubiera creado en la RAM sin utilizar esta función, se habría movido a la memoria del dispositivo OpenCL (GPU) como se muestra a continuación:
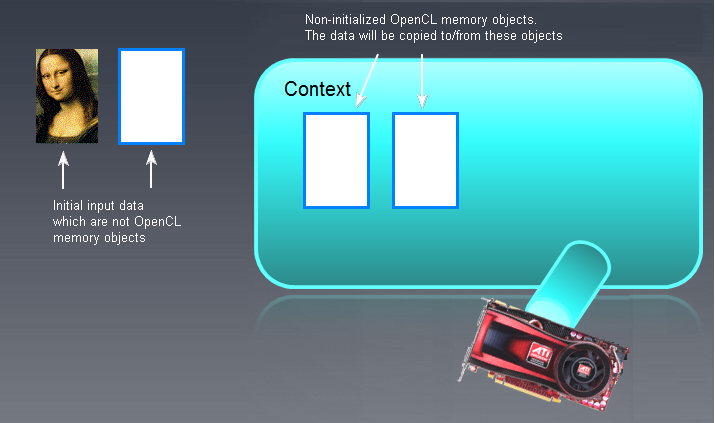
Fig. 6. Objetos de memoria OpenCL
Los buffers de entrada/salida (no necesariamente imágenes, ¡la Mona Lisa se muestra aquí solo con una finalidad ilustrativa!) que no son objetos de memoria de OpenCL se muestran a la izquierda. Los objetos OpenCL vacíos y no inicializados se muestran más a la derecho, en el campo de contexto principal. Los datos iniciales "la Mona Lisa" serán movidos consecuentemente al campo del contexto de OpenCLy cualquiera que sea el resultado del programa OpenCL requerirá moverse hacia atrás a la izquierda, es decir, a la RAM.
Los términos usados en OpenCL para copiar datos desde/en un dispositivo anfitrión/OpenCL son los siguientes:
- La copia de datos desde el anfitrión a la memoria del dispositivo se llama escritura (función CLBufferWrite());
- La copia de datos de la memoria del dispositivo a la memoria del anfitrión se llama lectura (función CLBufferRead(), ver más abajo).
El comando de escritura (anfitrión (host) -> dispositivo) inicializa un objeto de la memoria como dato y al mismo tiempo coloca el objeto en la memoria del dispositivo.
Debemos tener en cuenta que la validez de los objetos de memoria disponible en el dispositivo no está especificada en OpenCL ya que depende del proveedor de hardware correspondiente del dispositivo. Por tanto, debemos tener cuidado al crear objetos de memoria.
Una vez que los objetos de memoria han sido inicializados y escritos en los dispositivos, la situación parece ser algo como esto:
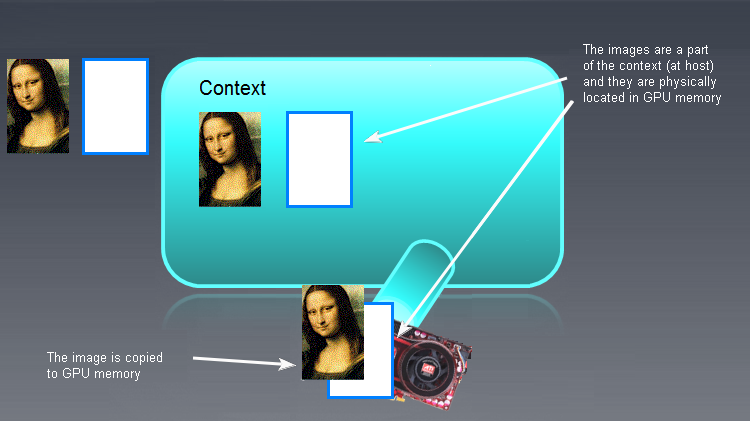
Fig. 7. Resultado de la inicialización de los objetos de memoria OpenCL
Ahora podemos pasar a las funciones que establecen parámetros del kernel.
3.5. Establecer los parámetros del kernel
CLSetKernelArgMem( clKrn, 0, clMem );
La función CLSetKernelArgMem() define el buffer creado antes como parámetro cero del kernel.
Si miramos ahora al mismo parámetro en el código del kernel, podemos ver que aparece de la siguiente forma:
__kernel void pi( __global float *out )
En el kernel, es la matriz out[] la que tiene el mismo tipo creado por la función API CLBufferCreate().
Hay una función similar para establecer los parámetros que no son de buffer:
bool CLSetKernelArg( int kernel, // handle to the kernel of the OpenCL program uint arg_index, // OpenCL function argument number void arg_value ); // function argument value
Si, por ejemplo, hemos decidido establecer algunos dobles x0 como segundo parámetro del kernel, sería necesario primero que fuese declarado e inicializado en el programa MQL5:
double x0 = -2;
y luego será necesario llamar a la función (también en el código MQL5):
CLSetKernelArg( cl_krn, 1, x0 );
Siguiendo la anterior instrumentalización, la situación sería así:
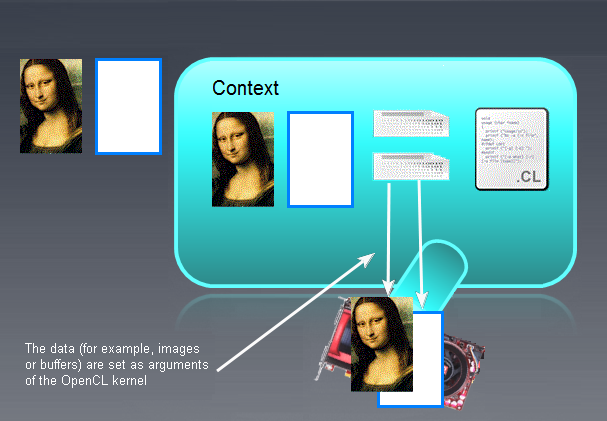
Fig. 8. Resultado de establecer los parámetros del kernel
3.6. Ejecución del programa
bool ex = CLExecute( clKrn, 1, offs, works );
El autor no encontró una analogía directa de esta función en la especificación OpenCL. La función ejecuta el kernel clKrn con los parámetros dados. El último parámetro "works" establece el número de tareas a ejecutar por cada cálculo de la tarea de procesado. La función muestra el principio SPMD (Datos múltiples de programa único): una llamada de la función crea instancias del kernel con sus propios parámetros en un número igual al valor del parámetro works. Estas instancias del kernel son, convencionalmente hablando, ejecutadas simultáneamente pero en distintos núcleos de flujo, en términos AMD.
La generalidad de OpenCL consiste en el hecho de que el lenguaje no está limitado a la infraestructura de hardware subyacente involucrada en la ejecución del código: el programador no tiene que conocer las especificaciones del hardware para ejecutar adecuadamente un programa OpenCL. Aún así será ejecutado. Es muy recomendable conocer estas especificaciones para mejorar la eficiencia del código (p.ej. la velocidad).
Por ejemplo, este código se ejecutó muy bien en el hardware del autor sin tener una tarjeta gráfica discreta. Dicho esto, el autor tiene una idea muy vaga de la estructura de la CPU misma donde tiene lugar toda la emulación.
Por tanto, el programa OpenCl ha sido ejecutado finalmente y podemos ahora utilizar sus resultados en el programa anfitrión.
3.7. Leyendo los datos de salida
A continuación se muestra un fragmento del programa anfitrión leyendo los datos del dispositivo:
float buf[ ]; ArrayResize( buf, _divisor ); uint read = CLBufferRead( clMem, buf );
Debemos recordar que la lectura de datos en OpenCL consiste en copiar los datos del dispositivo al anfitrión. Estas tres líneas muestran cómo se hace. Será suficiente declarar el buffer buf[] del mismo tipo que el buffer OpenCL leído en el programa principal y llamar a la función. El tipo de buffer creado en el programa anfitrión (aquí, en el lenguaje MQL5) puede ser diferente del tipo de buffer en el kernel pero sus tamaños deben coincidir exactamente.
Los datos han sido ahora copiados en la memoria del anfitrión y se encuentra completamente disponible en el programa principal, es decir, el programa en MQL5.
Después de todos los cálculos necesarios en el dispositivo OpenCL que hemos realizado, la memoria debe haberse liberado de todos los objetos.
3.8. Destrucción de todos los objetos OpenCL
Esto se hace utilizando los siguientes comandos:
CLBufferFree( clMem ); CLKernelFree( clKrn ); CLProgramFree( clPrg ); CLContextFree( clCtx );
La principal peculiaridad de estas funciones es que los objetos deben ser destruidos en orden inverso al de su creación.
Vamos a ver rápidamente al propio kernel.
3.9. Kernel
Como puede verse, todo el código del kernel es un único string largo con múltiples strings.
El encabezado del kernel parece una función estándar:
__kernel void pi( __global float *out )
Hay uno cuantos requisitos para el encabezado del kernel:
- El tipo de valor devuelto es siempre void;
- El especificador _kernel no tiene que incluir dos caracteres subrayados, también puede ser kernel;
- Si un argumento es una matriz (buffer), se pasa solo por referencia. El especificador de memoria _global (o global) significa que este buffer se almacena en una memoria global del dispositivo.
- Los argumentos de tipos de datos simples se pasan por valor.
El cuerpo del kernel no es de ningún modo distinto al código estándar de C.
Importante: el string:
int i = get_global_id( 0 );
significa que i es un número de una celda de cómputo en GPU que determina el resultado del cálculo en dicha celda. Este resultado se escribe además en la matriz de salida (en nuestro caso, out []) tras lo cual sus valores se añaden al programa anfitrión después de leer la matriz de la memoria de GPU en la memoria de la CPU.
Debe señalarse que puede haber más de una función en el código del programa OpenCL. Por ejemplo, una simple función inline situada fuera de la función pi() puede llamarse desde dentro de la función pi() del kernel "principal". Este caso será tratado más tarde.
Ahora que nos hemos familiarizado brevemente con la API de OpenCL en la implementación de MetaQuotes, podemos seguir experimentando. En este artículo, el autor no piensa profundizar en los detalles del hardware que permitirían optimizar el tiempo de ejecución al máximo. La principal tarea en este momento es proporcionar un punto de partida para programar en OpenCL como tal.
En otras palabras, el código es más bien ingenuo, ya que no tiene en cuenta las especificaciones del hardware. Al mismo tiempo, es bastante general, por lo que puede ejecutarse en cualquier hardware (CPU, IGP por AMD (GPU integrado en CPU)) o una tarjeta gráfica de AMD/NVidia.
Antes de considerar la optimización simple usando tipos de datos vector, tenemos primero que familiarizarnos con ellos.
4. Tipos de datos vectores
Los tipos de datos vectores son específicos de OpenCL, aparte de C99. Entre estos están cualquier tipo de (u)charN, (u)shortN, (u)intN, (u)longN, floatN, donde N = {2|3|4|8|16}.
Estos tipos se supone que son usados cuando sabemos (o asumimos) que el compilador integrado hará posible los cálculos en paralelo. Es necesario destacar aquí que este no es siempre el caso, incluso si los códigos de kernel solo difieren en el valor de N y son idénticos en lo demás (el autor pudo verlo por sí mismo).
Esta es la lista de tipos de datos incluidos:
Tabla 1. Tipos de datos incluidos en OpenCL
Estos tipos están soportados por cualquier dispositivo. Cada uno de estos tipos tiene el correspondiente tipo API para la comunicación entre el kernel y el programa anfitrión. Esto no está previsto en la implementación actual de MQL5 pero no es nada importante.
Hay también tipos adicionales pero estos deben especificarse explícitamente para ser usados ya que no están soportados por todos los dispositivos:
Tabla 2. Otros tipos de datos incluidos en OpenCL
Además, hay tipos de datos invertidos que son aún soportados en OpenCL. Hay una larga lista de ellos en la especificación del lenguaje.
Para declarar una constante o una variable de tipo vector, debemos seguir unas reglas simples e intuitivas:
A continuación se muestran algunos ejemplos:
float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f); uint4 u = ( uint4 ) ( 1 ); /// u is converted to a vector (1, 1, 1, 1). float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) ); float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f ); float4 f = ( float4 ) ( 1.0f, 2.0f ); /// error
Como puede verse, es suficiente hacer coincidir los tipos de datos a la derecha, juntarlos con el "ancho" de la variable declarada a la izquierda (aquí es igual a 4). La única excepción es la conversión de un escalar a un vector con los componentes iguales al escalar (línea 2).
Hay un mecanismo simple para tratar los componentes vector para cada tipo de datos vector. Por un lado, son vectores (matrices) mientras que por otro lado son estructuras. Luego, por ejemplo, el primer componente de vectores con ancho 2 (p.ej. float2 u) puede tratarse como u.x y el segundo como u.y.
Los tres componentes para un vector de tipo long3 u será:u.x, u.y y u.z.
Para un vector de tipo float4 u, serán, por consiguiente, .xyzw, es decir, u.x, u.y, u.z y u.w.
float2 pos; pos.x = 1.0f; // valid pos.z = 1.0f; // invalid because pos.z does not exist float3 pos; pos.z = 1.0f; // valid pos.w = 1.0f; // invalid because pos.w does not exist
Podemos seleccionar múltiples componentes de una vez e incluso intercambiarlos (notación de grupo):
float4 c; c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); c.z = 1.0f; c.xy = ( float2 ) ( 3.0f, 4.0f ); c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f ); float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 swiz= pos.wzyx; // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f ) float4 dup = pos.xxyy; // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )La notación de grupo del componente, es decir, la especificación de varios componentes, puede ocurrir a la izquierda de la declaración de asignación (es decir, I-value):
float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); pos.xw = ( float2 ) ( 5.0f, 6.0f ); // pos = ( 5.0f, 2.0f, 3.0f, 6.0f ) pos.wx = ( float2 ) ( 7.0f, 8.0f ); // pos = ( 8.0f, 2.0f, 3.0f, 7.0f ) pos.xyz = ( float3 ) ( 3.0f, 5.0f, 9.0f ); // pos = ( 3.0f, 5.0f, 9.0f, 4.0f ) pos.xx = ( float2 ) ( 3.0f, 4.0f ); // invalid as 'x' is used twice pos.xy = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // mismatch between float2 and float4 float4 a, b, c, d; float16 x; x = ( float16 ) ( a, b, c, d ); x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw ); x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz ); // invalid as the component a.xxxxxxx is not a valid vector type
Puede accederse a los componentes individuales usando otra notación, la letra s (o S) que se inserta antes de una dígito hexadecimal o varios dígitos en una notación de grupo:
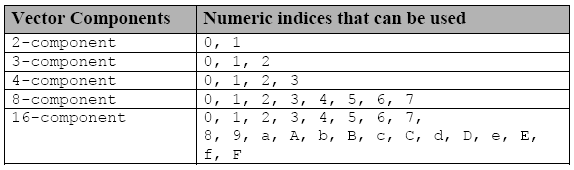
Tabla 3. Índices usados para acceder a los componentes individuales de los tipos de datos vectores
Si declaramos una variable vector f
float8 f;entonces f.s0 es el primer componente del vector y f.s7 es el octavo componente.
Igualmente, si declaramos un vector x de 16 dimensiones,
float16 x;entonces x.sa (o x.sA) es el onceavo componente del vector x y x.sf (o x.sF) se refiere al dieciséis del vector x.
Los índices numéricos (.s0123456789abcdef) y las notaciones en letras (.xyzw) no pueden entremezclarse en el mismo identificador con la notación de grupo del componente:
float4 f, a; a = f.x12w; // invalid as numeric indices are intermixed with the letter notations .xyzw a.xyzw = f.s0123; // valid
Y finalmente, hay aún otra forma de manipular componentes de tipo vector usando .lo, .hi, .even, .odd.
Estos sufijos se usan de la siguiente forma:
- .lo se refiere a la mitad inferior de un vector dado;
- .hi se refiere a la mitad superior de un vector dado;
- .even se refiere a todos los componentes pares de un vector dado;
- .odd se refiere a todos los componentes impares de un vector dado;
Por ejemplo:
float4 vf; float2 low = vf.lo; // vf.xy float2 high = vf.hi; // vf.zw float2 even = vf.even; // vf.xz float2 odd = vf.odd; // vf.yw
Esta notación puede usarse repetidamente hasta que aparezca un escalar (tipo de dato no vector):
float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f ); float2 s = u.lo.lo; // ( 1.0f, 2.0f ) float2 t = u.hi.lo; // ( 5.0f, 6.0f ) float2 q = u.even.lo; // ( 1.0f, 3.0f ) float r = u.odd.lo.hi; // 4.0f
La situación es ligeramente más complicada en un tipo vector de 3 componentes: técnicamente es un tipo de vector de 4 componentes con el valor del cuarto componente sin definir.
float3 vf = (float3) (1.0f, 2.0f, 3.0f); float2 low = vf.lo; // ( 1.0f, 2.0f ); float2 high = vf.hi; // ( 3.0f, undefined );
Breves reglas de aritmética (+, -, *, /).
Todas las operaciones aritméticas especificadas se definen por vectores de la misma dimensión y se hacen conocedores del componente.
float4 d = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 w = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f ); float4 _sum = d + w; // ( 6.0f, 10.0f, 13.0f, 3.0f ) float4 _mul = d * w; // ( 5.0f, 16.0f, 30.0f, -4.0f ) float4 _div = w / d; // ( 5.0f, 4.0f, 3.333333f, -0.25f )
La única excepción es cuando uno de los operandos es un escalar y el otro es un vector. En este caso, el tipo escalar es creado en el tipo de datos declarados en el vector mientras que el propio escalar se convierte en un vector con la misma dimensión que el operando del vector. A esto le sigue una operación aritmética. Lo mismo puede decirse de los operadores relacionales (<, >, <=, >=).
Derivados, los tipos de datos nativos C)) (p.ej. struct, union, arrays y otros) que pueden estar compuestos de los tipos de datos incluidos que se encuentran en la primera tabla de esta sección, también están soportados en el lenguaje OpenCL.
Y la última cosa: si queremos usar GPU para cálculos exactos, tendremos que usar inevitablemente el tipo de datos doble y por tanto doubleN.
Para este propósito, insertamos la línea:
#pragma OPENCL EXTENSION cl_khr_fp64 : enable
al principio del código del kernel.
Esta información debe ser ya suficiente para entender mucho de los que viene a continuación. Si tiene cualquier consulta, por favor, vea la especificación OpenCL 1.1.
5. Implementación del Kernel con los tipos de datos vector
Para ser honestos, el autor no ha podido escribir un código con tipos de datos vector con facilidad.
AL principio, el autor no prestó mucha atención leyendo la especificación del lenguaje pensando que todo funcionaría por sí mismo ya que el tipo de dato vector, por ejemplo duble8, es declarado dentro del kernel. Además, el intento del autor de declarar solo una matriz de salida como matriz de vectores double8 también fracasó.
Parece que darse cuenta de esto no es en absoluto suficiente para vectorizar eficazmente el kernel y alcanzar una aceleración real. El problema no se resolverá devolviendo resultados en la matriz del vector, ya que los datos no solo requieren ser introducidos y obtenidos rápidamente, sino también rápidamente calculados. La comprensión de este hecho aceleró el proceso e incrementó su eficiencia haciendo posible desarrollar finalmente un código mucho más rápido.
Pero hay más que eso. Mientras que el código del kernel que se describió antes pudo depurarse casi a ciegas, buscar los errores se ha convertido ahora en algo difícil debido al uso de datos del vector. ¿Qué información constructiva podemos obtener de este mensaje estándar:
ERR_OPENCL_INVALID_HANDLE - controlador no válido para el programa OpenCL
o este
ERR_OPENCL_KERNEL_CREATE - error interno al crear un objeto OpenCL
?
Por tanto, el autor tuvo que recurrir a SDK. En este caso, dada la configuración de hardware disponible para el autor, resultó ser al compilador Intel OpenCL SDF Offline (32 bit) suministrado en Intel OpenCL SDK (para CPU/GPU distintas a las de Intel, SDK debe contener también los correspondientes compiladores offline). Es recomendable porque permite depurar el código del kernel sin tener que vincular a la API del anfitrión.
Simplemente insertamos el código del kernel en la ventana del compilador, aunque no en la forma usada en el código de MQL5, sino en lugar de eso, sin los caracteres externos y "\r\n" (caracteres de retorno del carro) y pulsar el botón Construir con icono de una rueda de engranaje.
Al hacer esto, la ventana de registro de la construcción mostrará la información del proceso y su progreso:
Fig. 9. Compilación del programa en el compilador offline Intel OpenCL SDK
Para obtener el código del kernel sin los caracteres de comillas, sería útil escribir un simple programa en el lenguaje anfitrión (MQL5) que daría un código del kernel en un archivo - WriteCLProgram(). Ahora está incluido en el código del programa anfitrión.
Los mensajes del compilador no siempre son muy claros pero proporcionan más información de lo que MQL5 puede actualmente. Los errores pueden resolverse inmediatamente en la ventana del compilador una vez que nos aseguramos de que no hay más errores, los arreglos pueden transferirse al código del kernel en MetaEditor.
Y la última cosa. La idea inicial del autor era desarrollar un código vectorizado capaz de trabajar con vectores double4, duble8 y double16 mediante el establecimiento de un solo parámetro global "número de canales". Esto se consiguió al final, tras unos cuantos días pasando duros momentos con el operador ## que por alguna razón rechazaba funcionar dentro del kernel.
Durante este tiempo, el autor desarrolló con éxito un código del script con tres códigos del kernel, cada uno de los cuales es adecuado para su dimensión - 4, 8 o 16. Este código intermedio no se proporcionará en el artículo pero merecía la pena mencionarlo en caso de que quiera escribir el código de kernel sin tener muchos problemas. El código de la implementación de este script (OCL_pi_double_several_simple_kernels.mq5) se adjunta abajo al final del artículo.
Este es el código del kernel vectorizado:
"/// enable extensions with doubles \r\n" "#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _intrnCnt ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" "#define _CH " + i2s( _ch ) + " \r\n" "#define _DOUBLETYPE double" + i2s( _ch ) + " \r\n" " \r\n" "/// extensions for 4-, 8- and 16- scalar products \r\n" "#define dot4( a, b ) dot( a, b ) \r\n" " \r\n" "inline double dot8( double8 a, double8 b ) \r\n" "{ \r\n" " return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi ); \r\n" "} \r\n" " \r\n" "inline double dot16( double16 a, double16 b ) \r\n" "{ \r\n" " double16 c = a * b; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot4( c.lo.lo + c.lo.hi + c.hi.lo + c.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double16 v16 = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 ); \r\n" " double8 v8 = v16.lo; \r\n" " double4 v4 = v16.lo.lo; \r\n" " double2 v2 = v16.lo.lo.lo; \r\n" " \r\n" " /// all vector-related with the calculated type \r\n" " _DOUBLETYPE in; \r\n" " _DOUBLETYPE xVect; \r\n" " _DOUBLETYPE sumVect = ( _DOUBLETYPE ) ( 0.0 ); \r\n" " _DOUBLETYPE doubleOneVect = ( _DOUBLETYPE ) ( 1.0 ); \r\n" " _DOUBLETYPE doubleCHVect = ( _DOUBLETYPE ) ( _CH + 0. ); \r\n" " _DOUBLETYPE doubleSTEPVect = ( _DOUBLETYPE ) ( _STEP ); \r\n" " \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in = v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j ); \r\n" " xVect = ( in + 0.5 ) * doubleSTEPVect; \r\n" " sumVect += 4.0 / ( xVect * xVect + 1. ); \r\n" " } \r\n" " out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n" "} \r\n";
El programa anfitrión externo no ha cambiado mucho, excepto por la nueva constante global _ch que establece el número de "canales de vectorización" y la constante global _intrnCnt que es _ch veces menor. Por eso el autor decidió no mostrar el código del programa anfitrión aquí. Puede encontrarse en el archivo del script adjunto abajo al final del archivo (OCL_pi_double_parallel_straight.mq5).
Como puede verse, aparte de la función "principal" del kernel pi(), ahora tenemos dos funciones en línea que determinan el producto escalar de los vectores dotN(a,b) y una macro sustitución. Estas funciones están implicadas debido al hecho de que la función dot() en OpenCL es definida con relación a los vectores cuyas dimensiones no excedan de 4.
La macro dot4() que redefine la función dot() está ahí solo por la comodidad de llamar a la función dotN() con el nombre calculado:
" out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n"
Si hubiéramos usado la función dot() en su forma habitual, sin el índice 4, no habríamos sido capaces de llamarla tan fácilmente como se muestra aquí, cuando _ch = 4 (número de canales de vectorización igual a 4).
Esta línea ilustra otra característica útil de la forma del kernel específica basándose en el hecho de que el kernel como tal es tratado dentro del programa anfitrión como string: podemos usar los identificadores calculados en el kernel no solo para las funciones sino ¡también para los tipos de datos!
El código del programa anfitrión completo con este kernel se adjunta abajo (OCL_pi_double_parallel_straight.mq5).
Ejecutando el script con este "ancho" de vector siendo16 ( _ch = 16 ), obtenemos lo siguiente:
2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) ================================================== 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) CPUtime / GPUtime = 4.130 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The time to calculate PI was 8.830 seconds 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The value of PI is 3.141592653590 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The time to calculate PI was 8.002 seconds 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The value of PI is 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: gone = 2.138 sec. 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: pi = 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) read = 20000 elements 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) CLProgramCreate: unknown error. 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) ==================================================
Podemos ver que incluso la optimización utilizando los tipos de datos vector no hizo al kernel más rápido.
Pero si ejecutamos el mismo código en GPU, la ganancia de velocidad será mucho más considerable.
De acuerdo con la información proporcionada por MetaDriver (tarjeta gráfica HIS Radeon HD 6930, CPU - AMD Phenom II x6 1100T) el mismo código da los siguientes resultados:
2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) ================================================== 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) CPUtime / GPUtime = 84.983 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The time to calculate PI was 14.617 seconds 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The value of PI is 3.141592653590 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The time to calculate PI was 14.040 seconds 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The value of PI is 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: gone = 0.172 sec. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) read = 20000 elements 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) CLProgramCreate: unknown error. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) ==================================================
6. El toque final
Aquí hay otro kernel (puede encontrarse en el archivo OCL_pi_double_several_simple_kernels.mq5 adjunto más abajo que sin embargo no se ha demostrado aquí).
El script es una implementación de la idea de que tuvo el autor, cuando temporalmente ha abandonó el intento de escribir "un solo" kernel y pensó escribir cuatro kernels simples para diferentes dimensiones del vector (4, 8, 16, 32):
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _itInKern ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" " \r\n" "typedef struct \r\n" "{ \r\n" " double16 lo; \r\n" " double16 hi; \r\n" "} double32; \r\n" " \r\n" "inline double32 convert2double32( double a ) \r\n" "{ \r\n" " double32 b; \r\n" " b.lo = ( double16 )( a ); \r\n" " b.hi = ( double16 )( a ); \r\n" " return b; \r\n" "} \r\n" " \r\n" "inline double dot32( double32 a, double32 b ) \r\n" "{ \r\n" " double32 c; \r\n" " c.lo = a.lo * b.lo; \r\n" " c.hi = a.hi * b.hi; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo + c.lo.hi.hi + \r\n" " c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo + c.hi.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double32 _v32; \r\n" " _v32.lo = ( double16 ) ( 0., 1., 2., 3., 4., 5., 6., 7., \r\n" " 8., 9., 10., 11., 12., 13., 14., 15. ); \r\n" " _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23., \r\n" " 24., 25., 26., 27., 28., 29., 30., 31. ); \r\n" " \r\n" " /// all vector-related with undefined type \r\n" " double32 xVect; \r\n" " double32 sumVect = convert2double32( 0.0 ); \r\n" " double32 double1Vect = convert2double32( 1.0 ); \r\n" " \r\n" " double32 in; \r\n" " /// work only with 16-vectors in the loop! \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j ); \r\n" " in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j ); \r\n" " xVect.lo = ( in.lo + 0.5 ) * _STEP; \r\n" " xVect.hi = ( in.hi + 0.5 ) * _STEP; \r\n" " sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. ); \r\n" " sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. ); \r\n" " } \r\n" " out[ i ] = dot32( sumVect, double1Vect ); \r\n" "} \r\n";
Este kernel implementa la dimensión de vector 32. El nuevo tipo de vector y unas nuevas funciones en línea se definen fuera de la función principal del kernel. Además de eso (¡y esto es importante!) todos los cálculos en el lazo principal se han realizado intencionadamente con tipos de datos de vector estándar, lo tipos no estándar se gestionan fuera del lazo. Esto permite aumentar sustancialmente el tiempo de ejecución del código.
En nuestro cálculo, el kernel no parece ser más lento que cuando se usa para los vectores con un ancho de 16, ni tampoco es mucho más rápido.
De acuerdo con la información proporcionada por MetaDriver, el script con este kernel (_ch = 32)da los siguientes resultados:
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec. 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: unknown error or no error. 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; vectorization channels - 32 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================
Resumen y conclusiones
El autor comprende perfectamente bien que la tarea elegida para la demostración de los recursos de OpenCL no es muy típica de este lenguaje.
Habría sido mucho más fácil coger un libro de texto y elegir un ejemplo estándar de multiplicación de matrices grandes para publicarlo aquí. El ejemplo sería obviamente impresionante. Sin embargo, ¿hay muchos usuarios del foro de mql5.com que estén ocupados en cálculos financieros que requieran la multiplicación de grandes matrices? Lo dudo mucho. El autor ha querido elegir este ejemplo y salvar las dificultades encontradas por el camino por él mismo, mientras que al mismo tiempo ha intentado compartir esta experiencia con otros. Por supuesto, ustedes son los que van a juzgarlo, queridos usuarios del foro.
La ganancia en eficiencia en la emulación de OpenCL (en una CPU "desnuda") ha resultado ser muy pequeña comparada con la obtenida cientos e incluso miles de veces mayor usando los scripts de MetaDriver. Pero en una CPU adecuada, sería al menos un orden de magnitud mayor que en la emulación, incluso si ignoramos un tiempo de ejecución ligeramente mayor de la CPU con la CPU AMD. OpenCL merece la pena aprenderlo aún, ¡incluso si la ganancia en velocidad es solo de ese calibre!
El próximo artículo del autor pretende tratar las cuestiones relacionadas con las peculiaridades de los modelos abstractos de OpenCL en hardware real. El conocimiento de estas cosas a veces permite aumentar más la velocidad de los cálculos hasta un nivel considerable.
Al autor le gustaría dar especialmente las gracias a MetaDriver por los consejos de optimización de programación y funcionamiento de valor incalculable y al Equipo de Apoyo por la oportunidad de usar el Intel OpenCL SDK.
Contenido de los archivos adjuntos:
- pi.mq5 - un script en MQL5 puro con dos formas de calcular el valor de "pi";
- OCl_pi_float.mq5 - la primera implementación del script con el kernel de OpenCL usando cálculos reales con el tipo flotante;
- OCL_pi_double.mq5 - el mismo, solo incluyendo cálculos reales con el tipo doble;
- OCL_pi_double_several_simple_kernels.mq5 - un script con varios kernels específicos para varios "anchos" de vector (4, 8, 16, 32);
- OCL_pi_double_parallel_straight.mq5 - un script con un solo kernel para algunos anchos de vector (4, 8, 16).
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/405
OpenCL: De una programación simple a una más intuitiva
Por qué es el mercado de MQL5 el mejor lugar para vender estrategias de trading e indicadores técnicos
Programación basada en autómatas como nuevo enfoque en la creación de sistemas de trading automatizados
Oportunidades ilimitadas con Meta Trader 5 y MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso