OpenCL: Мост в параллельные миры
22 164
17
Введение
Настоящая статья открывает небольшой цикл публикаций, посвященных программированию на OpenCL, или Open Computing Language. Платформа MetaTrader 5 в ее текущем воплощении до подключения OpenCL не позволяла напрямую, т.е. нативно, использовать преимущества многоядерных процессоров для ускорения вычислений.
Разумеется, разработчики могли сколько угодно говорить о том, что терминал многопоточен, а "каждый эксперт/скрипт живет в отдельном потоке", но это не давало кодеру возможность относительно легко исполнить следующий простейший цикл параллельно (это код вычисления числа pi = 3.14159265...):
long num_steps = 1000000000; double step = 1.0 / num_steps; double x, pi, sum = 0.0; for (long i = 0; i<num_steps; i++) { x = (i + 0.5)*step; sum += 4.0/(1.0 + x*x); } pi = sum*step;
В разделе "Статьи", правда, еще полтора года назад написан очень любопытный опус Параллельные вычисления в MetaTrader 5 штатными средствами. И все же... создается впечатление, что при всей остроумности подхода он несколько неестественен: создавать целую программную иерархию (эксперт и два индикатора) ради ускорения вычисления в приведенном чуть ранее цикле - это, пожалуй, было бы слишком.
О том, что поддержка OpenMP не планируется, мы уже знаем, - так же как и о том, что добавление OMP является совершенно кардинальной переделкой компилятора. Увы, "дешево и сердито для кодера, когда ему думать не надо" - не получится.
Тем приятнее было увидеть анонс нативной поддержки OpenCL в МQL5. В той же ветке, начиная со страницы 22, MetaDriver начал выкладывать скрипты, позволяющие оценить разницу между исполнением на CPU и на GPU. Интерес к OpenCL резко вырос.
Автор этой статьи вначале чувствовал себя как бы в стороне от процесса: конфигурация персонального компьютера - вполне бюджетная (Pentium G840/8 Gb DDR-III 1333/No videocard), и она вроде бы не должна предполагать эффективного использования OpenCL.
Однако после инсталляции специального софта от AMD - AMD APP SDK - первый скрипт MetaDriver'a, который другие участники тестирования запускали только при наличии дискретной видеокарты, удалось запустить и на компьютере автора, и он продемонстрировал совсем не игрушечное ускорение в сравнении со стандартным его исполнением на одном ядре процессора - примерно в 25 раз. Позднее, с помощью Support Team удалось правильно подключить Intel OpenCL Runtime и достичь ускорения на этом же скрипте, равного примерно 75.
После штудирования форума и материалов ixbt.com удалось узнать, что встроенное видеоядро (IGP) процессоров от Intel подерживает OpenCL 1.1 только начиная с процессоров Ivy Bridge. Следовательно, ускорение, достигаемое на персональном компьютере с указанной выше конфигурацией, не имеет к IGP никакого отношения, и код программы OpenCL в данном частном случае исполняется только на х86-ядрах CPU.
Когда автор поделился с экспертами ixbt цифрами ускорения, они тут же в один голос заявили, что все это - следствие существенной недооптимизированности исходного языка (MQL5). В среде профессионалов, работающих с OpenCL, известно, что если правильно оптимизировать исходный код на С++ (конечно, с учетом многоядерности процессора и с подключением векторных инструкций SSEx), то выигрыш на эмуляции OpenCL будет в лучшем случае равен нескольким десяткам процентов, а в худшем мы можем даже проиграть - например, из-за чрезмерно дорогих расходов (времени) на пересылку данных.
Отсюда - второе предположение: к "чудесным" цифрам ускорения в MetaTrader 5 при чистой эмуляции OpenCL следует относиться с разумной осторожностью и не считать их "крутизной" самого OpenCL. Реально устойчивый выигрыш на GPU в сравнении с хорошо оптимизированной программой на С++ можно получить только при использовании достаточно мощной дискретной видеокарты, т.к. ее вычислительные возможности на некоторых алгоритмах несравненно выше возможностей любого современного CPU.
Разработчики терминала утверждают, что он еще не оптимизирован как следует. Намекнули разработчики и на порядок ускорения после оптимизации - в несколько раз. Соответственно, все цифры ускорений на OpenCL станут меньше в те же "несколько раз". Однако они все равно останутся значительно больше единицы.
Это хороший повод к освоению языка OpenCL (даже если ваша видеокарта не поддерживает OpenCL 1.1 или её просто нет), к чему мы сейчас и перейдем. Но вначале несколько слов о необходимом фундаменте - программном обеспечении, позволяющем работать на Open CL, и соответствующем "железе".
1. Необходимое программное обеспечение и hardware
1.1.AMD
Соответствующий софт выпускается компаниями AMD, Intel и NVidia, входящими в некоммерческий промышленный консорциум - группу Khronos, которая разрабатывает спецификации различных языков, связанных с вычислениями в гетерогенных средах.
На сайте этой группы размещены некоторые полезные нам материалы - например:
К этим документам при освоении OpenCL придется обращаться довольно часто, т.к. в терминале соответствующей справки по OpenCL еще нет (есть краткая справка только по OpenCL API). Все три компании (AMD, Intel и NVidia) являются поставщиками "видеожелеза", и каждая из них имеет свою реализацию OpenCL Runtime и соответствующих комплектов средств разработки - SDK. Остановимся на особенностях выбора видеокарт на примере компании-производителя AMD.
Если у вас стоит не самая древняя видеокарта от AMD (со сроком начала выпуска не ранее примерно 2009-2010 года), то все очень просто: достаточно обновить драйвер видеокарты, и этого должно быть достаточно, чтобы сразу приступать к работе. Здесь можно найти список видеокарт, совместимых с OpenCL. С другой стороны, если вы имеете даже очень неплохую в свое время видеокарту Radeon HD 4850 (4870), будьте готовы к проблемам при работе с OpenCL.
Если видеокарты от AMD у вас еще нет, но вы готовы ее приобрести, вначале посмотрите на ее характеристики. Здесь находится достаточно подробная таблица характеристик современных видеокарт AMD. Самыми главными для нас являются следующие характеристики:
- On-board Memory — объём локальной памяти. Чем ее больше, тем лучше. Обычно 1 GB вполне достаточно.
- Core Clock — частота работы ядра. Здесь тоже все ясно: чем выше частота работы мультипроцессоров GPU, тем лучше. 650-700 MHz - это уже неплохо.
- [Memory] Type — тип видеопамяти. Желательно, чтобы она была быстрой, т.е. GDDR5. Но если будет GDDR3 - тоже неплохо, хотя и значительно хуже по пропускной способности памяти (ПСП), примерно вдвое.
- [Memory] Clock (Eff.) - рабочая (effective, эффективная) частота видеопамяти. В принципе этот параметр тесно связан с предыдущим. В среднем эффективная частота работы GDDR5 примерно вдвое выше частоты для GDDR3. Это связано не с тем, что "более высокие" типы памяти работают на более высоких частотах, а с количеством каналов, по которым эта память передает данные. Другими словами, с ПСП.
- [Memory] Bus - ширина шины данных. Желательно, чтобы она была не ниже 256 бит.
- MBW (Memory BandWidth) — пропускная способность памяти (ПСП). Фактически этот параметр объединяет в себе все три приведенных выше параметра видеопамяти. Чем он выше - тем лучше.
- Config Core (SPU:TMU(TF):ROP) — конфигурация блоков графического процессора. Для нас, т.е. для неграфических вычислений, важна только первая цифра. Если указано 1024:64:32, то это означает, что нам интересно число 1024 (число универсальных потоковых процессоров, или шейдерных блоков). Разумеется, чем оно выше, тем лучше.
- Processing Power — теоретическая производительность на вычислениях с плавающей запятой (FP32 (Single Precision) — одинарная точность / FP64 (Double Precision) — двойная точность). Если напротив параметра FP32 в таблице всегда указана какая-нибудь цифра (все видеокарты умеют вычислять с одинарной точностью), то в случае с FP64 это далеко не так, т.е. далеко не каждая видеокарта поддерживает такие вычисления. Если вы уверены, что при вычислениях на GPU вам никогда не понадобится двойная точность (тип double), то на второй параметр можно не обращать внимание. Но, в любом случае, чем выше этот параметр - тем лучше.
- TDP (Thermal Design Power) — тепловой пакет. Это, грубо говоря, максимальная мощность, рассеиваемая видеокартой при самых тяжелых вычислениях. Если ваш советник часто будет обращаться к GPU, то видеокарта будет не только потреблять немало электрической энергии (это не очень страшно, если он себя окупает), но и будет серьезно шуметь.
Теперь - второй случай: видеокарты либо физически нет, либо она не поддерживает OpenCL 1.1, но установлен процессор от AMD. Здесь можно скачать AMD APP SDK, в котором помимо runtime имеются SDK, Kernel Analyzer и Profiler. После инсталляции AMD APP SDK процессор должен быть виден как устройство OpenCL (девайс). Вы сможете разрабатывать полноценные приложения для OpenCL в режиме эмуляции OpenCL на CPU.
Отличительная особенность SDK от AMD заключается в том, что он подходит и для процессоров Intel (хотя при разработке именно на Intel CPU "родной" SDK все же существенно эффективнее, т.к. способен поддерживать наборы векторных инструкций SSE4.1, SSE4.2 и AVX, которые только недавно появились у процессоров AMD).
1.2. Intel
Для работы на процессоре от Intel желательно скачать Intel OpenCL SDK/Runtime.
Следует отметить несколько обстоятельств:
- Если вы предполагаете разрабатывать OpenCL приложение с использованием только CPU (режим эмуляции OpenCL), то вам следует знать, что графическое ядро CPU от Intel для процессоров до Sandy Bridge включительно не поддерживает OpenCL 1.1. Эта поддержка включена только вместе с процессорами Ivy Bridge, но толку от нее вряд ли будет много, даже для самой мощной интегрированной графики Intel HD 4000. Для процессоров до Ivy Bridge это означает, что ускорение, достигаемое в среде MQL5, возникает только благодаря использованию векторных инструкций SS(S)Ex. Но и оно оказывается существенным.
- После инсталляции Intel OpenCL SDK необходимо отредактировать запись реестра HKEY_LOCAL_MACHINE\SOFTWARE\Khronos\OpenCL\Vendors следующим образом: вместо IntelOpenCL64.dll в колонке "Имя" нужно установить intelocl.dll. Затем перегружаемся и запускаем MetaTrader 5. Теперь CPU определяется как девайс OpenCL 1.1.
Откровенно говоря, вопрос поддержки OpenCL от Intel еще не до конца разрешен, так что в будущем наверняка появятся некоторые разъяснения от разработчиков терминала. Фактически дело обстоит так, что ошибки в коде кернела (OpenCL kernel - программа, выполняемая на GPU) никто за вас искать не будет: это не компилятор MQL5. Компилятор просто "проглотит" большую строку кернела целиком и попытается исполнить ее. Если, например, вы не объявили некую используемую в кернеле внутреннюю переменную х, кернел все равно будет формально исполняться, но с ошибками.
Однако все ошибки, которые вы получите в терминале, сводятся к менее чем десятку из числа тех, которые описаны в помощи к API OpenCL для функций CLKernelCreate() и CLProgramCreate(). Язык по синтаксису сильно похож на язык C, дополненный векторными функциями и типами данных (на самом деле это язык С99, который является стандартом ANSI С, утвержденным в 1999 году).
Автор этой статьи отлаживает код для OpenCL именно в Intel OpenCL SDK Offline Compiler, и это гораздо удобнее, чем почти вслепую искать ошибки в кернеле в редакторе MetaEditor. Будем надеяться, что в будущем ситуация изменится к лучшему.
1.3. NVidia
К сожалению, в этом направлении автор статьи "не копал". Но общие рекомендации остаются прежними. Драйверы новых видеокарт от NVidia автоматически поддерживают OpenCL.
Вообще говоря, автор статьи не имеет ничего против видеокарт NVidia, но по опыту поиска информации и общения на форумах приходится сделать вывод: для неграфических вычислений видеокарты AMD представляют собой более оптимальный выбор по соотношению "производительность/цена", нежели видеокарты от NVidia.
Теперь перейдем к программированию.
2. Первая программа на MQL5 с использованием OpenCL
Чтобы составить нашу первую очень простую программу, нужно определиться с самой задачей. В курсах по параллельному программированию, вероятно, стало уже традицией использовать для демонстрации вычисление числа "пи", которое примерно равно 3.14159265.
Для этого используется следующая формула (автор видит эту формулу впервые, но она, похоже, верна):
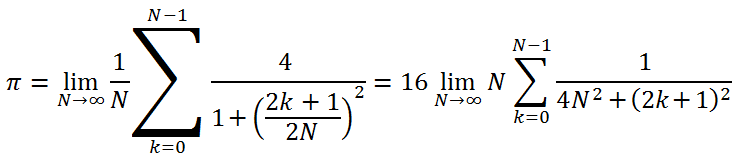
Мы хотим вычислить это число с точностью 12 знаков после запятой. В принципе для получения такой точности вполне достаточно примерно порядка 1 миллиона итераций, но это количество не даст нам возможность оценить "прибыль" от исполнения вычислений на OpenCL, т.к. продолжительность вычислений на GPU становится слишком малой.
В курсах по программированию на GPGPU рекомендуется выбирать объем вычислений так, чтобы продолжительность работы GPU была не меньше 20 миллисекунд. В нашем случае эту планку следует поднять еще выше - из-за значительной погрешности функции GetTickCount(), сравнимой со 100 мс.
Программа, реализующая это вычисление на MQL5, приведена ниже:
//+------------------------------------------------------------------+ //| pi.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" long _num_steps = 1000000000; long _divisor = 40000; double _step = 1.0 / _num_steps; long _intrnCnt = _num_steps / _divisor; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { uint start,stop; double x,pi,sum=0.0; start=GetTickCount(); //--- первый вариант, самый тупой for(long i=0; i<_num_steps; i++) { x=(i+0.5)*_step; sum+=4.0/(1.+x*x); } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); //--- считаем по второму варианту start=GetTickCount(); sum=0.; long divisor=40000; long internalCnt=_num_steps/divisor; double partsum=0.; for(long i=0; i<divisor; i++) { partsum=0.; for(long j=i*internalCnt; j<(i+1)*internalCnt; j++) { x=(j+0.5)*_step; partsum+=4.0/(1.+x*x); } sum+=partsum; } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); Print("_______________________________________________"); return(0); } //+------------------------------------------------------------------+Скомпилировав и запустив этот скрипт, получим:
2012.05.03 02:02:23 pi (EURUSD,H1) The time to calculate PI was 8.783 seconds 2012.05.03 02:02:23 pi (EURUSD,H1) The value of PI is 3.141592653590 2012.05.03 02:02:15 pi (EURUSD,H1) The time to calculate PI was 7.940 seconds 2012.05.03 02:02:15 pi (EURUSD,H1) The value of PI is 3.141592653590
Число pi ~ 3.14159265 вычисляется двумя немного разными способами.
Первый способ - почти "классика" для демонстрации возможностей многопоточных библиотек типа OpenMP, Intel TPP, Intel MKL и прочих.
Второй вариант - это такое же вычисление, но в виде двойного цикла. Все вычисление, состоящее из 1 миллиарда итераций, разбивается на крупные блоки внешнего цикла (здесь их 40000), а внутри каждого блока производится по 25000 "элементарных" итераций, составляющих внутренний цикл.
Видно, что это вычисление немного медленнее, на 10-15%. Но именно его мы будем использовать в качестве исходного при переносе на OpenCL. Главная причина - выбор кернела (элементарной расчетной задачи, исполняемой на GPU), реализующего разумный компромисс между расходами времени на пересылку данных из одной области памяти в другую - и собственно вычислениями, проводящимися в кернеле. Таким образом, в терминах этой задачи кернелом будет, грубо говоря, внутренний цикл второго алгоритма вычисления числа.
Теперь проведем вычисление при помощи OpenCL. Сначала будет приведен полный код программы, а далее мы потратим некоторое время на пояснение функций, специфических для "связки" OpenCL с языком хоста (MQL5). Но вначале хотелось бы высказать несколько общих наблюдений, связанных со стандартными "граблями" кодирования на OpenCL:
- Переменные, объявленные вне кернела, сам кернел не видит. Именно поэтому в начале кода кернела пришлось заново объявлять глобальные переменные _step и _intrnCnt (см. ниже). А чтобы они нормально читались в коде кернела, пришлось еще и преобразовывать числовые значения этих констант в строки. Тем не менее в дальнейшем эта особенность кодирования на OpenCL оказалась очень полезной - например, при создании векторных типов данных, отсутствующих в С "нативно".
- Старайтесь по возможности отдавать кернелу как можно больше вычислений, но "без фанатизма". Именно для данного кода это не слишком критично, т.к. в данном коде и на данном "железе" кернел не слишком быстр. Но если будете использовать мощную дискретную видеокарту, это обстоятельство может вам помочь в ускорении вычислений.
Итак, код скрипта с кернелом OpenCL:
//+------------------------------------------------------------------+ //| OCL_pi_float.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs; input int _device=0; /// номер девайса OpenCL (0 у меня CPU) #define _num_steps 1000000000 #define _divisor 40000 #define _step 1.0 / _num_steps #define _intrnCnt _num_steps / _divisor string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(int arg) { return IntegerToString(arg); } const string clSrc= "#define _step "+d2s(_step,12)+" \r\n" "#define _intrnCnt "+i2s(_intrnCnt)+" \r\n" " \r\n" "__kernel void pi( __global float *out ) \r\n" // type float "{ \r\n" " int i = get_global_id( 0 ); \r\n" " float partsum = 0.0; \r\n" // type float " float x = 0.0; \r\n" // type float " long from = i * _intrnCnt; \r\n" " long to = from + _intrnCnt; \r\n" " for( long j = from; j < to; j ++ ) \r\n" " { \r\n" " x = ( j + 0.5 ) * _step; \r\n" " partsum += 4.0 / ( 1. + x * x ); \r\n" " } \r\n" " out[ i ] = partsum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt)); int clCtx=CLContextCreate(_device); int clPrg = CLProgramCreate( clCtx, clSrc ); int clKrn = CLKernelCreate( clPrg, "pi" ); uint st=GetTickCount(); int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float CLSetKernelArgMem(clKrn,0,clMem); const uint offs[ 1 ] = { 0 }; const uint works[ 1 ] = { _divisor }; bool ex=CLExecute(clKrn,1,offs,works); //--- Print( "CL program executed: " + ex ); float buf[]; // type float ArrayResize(buf,_divisor); uint read=CLBufferRead(clMem,buf); Print("read = "+i2s(read)+" elements"); float sum=0.0; // type float for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt]; float pi=float(sum*_step); // type float Print("pi = "+d2s(pi,12)); CLBufferFree(clMem); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); double gone=(GetTickCount()-st)/1000.; Print("OpenCl: gone = "+d2s(gone,3)+" sec."); Print("________________________"); return(0); } //+------------------------------------------------------------------+
Более подробные пояснения по коду скрипта будут приведены немного позднее.
А пока компилируем и запускаем программу - и получаем следующее:
2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) ________________________ 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) OpenCl: gone = 5.538 sec. 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) pi = 3.141622066498 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) read = 40000 elements 2012.05.03 02:20:15 OCl_pi_float (EURUSD,H1) FLOAT: _step = 0.000000001000; _intrnCnt = 25000
Как видим, время исполнения немного уменьшилось. Но радости от этого мало: точность числа pi ~ 3.14159265 явно "хромает" уже в 4-м знаке после запятой. Причина такой грубости вычислений заключается в том, что для всех вещественных вычислений в кернеле используются числа типа float, точность которых явно ниже нужных нам 12+ знаков после запятой.
Согласно документации MQL5, точность числа float - всего 7 значащих цифр. В то же время точность числа типа double составляет 15 значимых цифр.
Следовательно, нужно сделать тип вещественных данных "более точным". В коде выше все строки, в которых теперь следует заменить тип с float на double, помечены комментарием ///type float. После компиляции на тех же входных данных получаем следующее (новый файл с исходным кодом - OCL_pi_double.mq5):
2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) OpenCl: gone = 12.480 sec. 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.03 03:25:23 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
Теперь время исполнения сильно выросло и даже превысило время для исходного кода без OpenCL (8.783 с).
"Конечно, все дело в типе double, с которым вычисления становятся медленнее",- подумаете вы. Но давайте все же поэкспериментируем и сильно изменим входной параметр _divisor c 40000 до 40000000:
2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) OpenCl: gone = 5.070 sec. 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) read = 40000000 elements 2012.05.03 03:26:50 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25
Точность не упала, а время исполнения стало даже немного меньше варианта с float. Но если просто изменить все целочисленные типы с long на int и вернуться к прежнему значению _divisor = 40000, время исполнения кернела уменьшится еще более чем вдвое:
2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) OpenCl: gone = 2.262 sec. 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.16 00:22:44 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
Об этом следует всегда помнить: если в кернеле есть достаточно "длинный", но "легкий" цикл (т.е. цикл, в котором много итераций, но в каждой из них - немного арифметических действий), то даже простое изменение типов переменных с "тяжелых" (тип long - это 8 байт) на "легкие" (int - 4 байта) может кардинально уменьшить время исполнения кернела.
Давайте теперь ненадолго остановимся с программистскими экспериментами и сосредоточимся на смысле всей "обвязки" кода кернела, чтобы хотя бы примерно понять, что мы делаем. "Обвязкой" кода кернела мы условно называем OpenCL API, т.е. систему команд, позволяющих кернелу общаться с хостовой программой (в данном случае - программой, написанной на языке MQL5).
3. Функции OpenCL API
3.1. Создание контекста
Команда, указанная ниже, создает контекст, т.е. некую среду для управления объектами и ресурсами OpenCL.
int clCtx = CLContextCreate( _device );
Вначале - несколько слов о модели платформы.
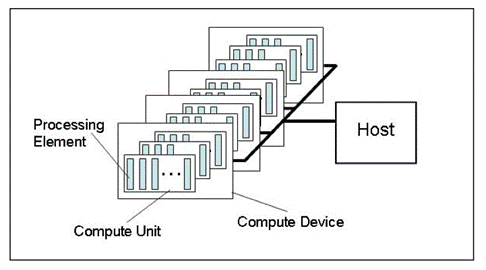
Рис. 1. Абстрактная модель вычислительной платформы
На рисунке изображена абстрактная модель вычислительной платформы. Этот рисунок не слишком детально описывает структуру "железа" для видеокарт, но весьма близок к ней и дает о ней хорошее представление.
Хост (Host) - это основной CPU, который управляет всем процессом исполнения программы. Он может "видеть" несколько OpenCL девайсов (Compute Device). В большинстве случаев, когда у трейдера в системном блоке стоит видеокарта для расчетов, каждый девайс - это видеокарта (если она двухпроцессорная, то это два девайса!). OpenCL-девайсом, кроме того, всегда является и сам хост, т.е. CPU. Каждый девайс имеет свой уникальный номер внутри платформы.
Каждый девайс имеет несколько Compute Units, которым в случае CPU соответствуют х86-ядра (в том числе, для CPU Intel, и "виртуальные", т.е. "ядра", включенные при поддержке технологии Hyperthreading), а в случае видеокарты это SIMD Engines, т.е. SIMD ядра, или минипроцессоры - по терминологии статьи Вычисления на GPU. Особенности архитектуры AMD/ATI Radeon. Типичное количество SIMD ядер в мощных видеокартах - порядка 20.
В каждом SIMD ядре имеются потоковые процессоры (Stream Cores). В случае видеокарты Radeon HD 5870 - по 16 в каждом SIMD Engine.
Наконец, каждый потоковый процессор имеет в той же карте по 4 или 5 вычислительных элементов (Processing Elements), т.е. ALU.
Следует отметить, что терминология всех основных вендоров графики, касающаяся "железа", весьма запутанна, особенно для новичков. Не всегда очевидно, что означает на уровне железа термин "пчелы", популярный в известной ветке об OpenCL. Тем не менее, укажем, что число нитей, т.е. одновременных потоков вычислений, в современных видеокартах весьма велико и, например, в видеокарте Radeon HD 5870 исчисляется более чем 5 тысячами.
На рисунке ниже показаны стандартные технические характеристики этой видеокарты.
Рис. 2. Технические характеристики видеокарты Radeon HD 5870
Всё перечисленное ниже далее (ресурсы OpenCL) обязательно должно ассоциироваться с контекстом, созданным функцией CLContextCreate():
- OpenCL девайсы, т.е. "железо", осуществляющее вычисления;
- Программные объекты, т.е. программный код, исполнящий кернел;
- Кернелы, т.е. функции, исполняемые на девайсах;
- Объекты памяти, т.е. данные (например, буферы, 2D- и 3D-рисунки), над которыми девайс выполняет некоторые действия;
- Командные очереди (в текущей реализации языка терминала соответствующий API не предусмотрен).
Созданный контекст на иллюстрации можно изобразить в виде пустого "поля", а внизу показаны девайсы, присоединенные к нему.
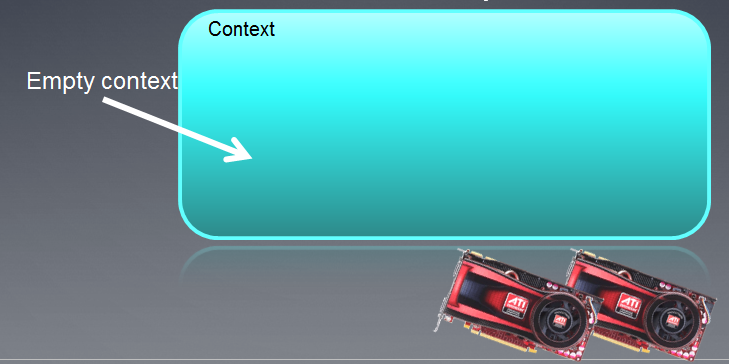
Рис. 3. Контекст OpenCL
В данный момент, после исполнения функции, контекст является пустым.
Следует отметить, что в MQL5 контекст OpenCL работает только с одним девайсом.
3.2. Создание программы
int clPrg = CLProgramCreate( clCtx, clSrc );
Функция CLProgramCreate() создает ресурс "Программа OpenCL".
Объект "Программа" на самом деле является коллекцией кернелов OpenCL (о которых речь в следующем пункте), но в реализации MetaQuotes кернел в программе OpenCL, судя по всему, может быть только один. Для создания объекта "Программа" необходимо обеспечить чтение исходного кода (здесь - clSrc) в строку.
В данном случае это необязательно, т.к. строка clSrc уже объявлена как глобальная переменная:
На рисунке ниже показана программа, являющаяся частью созданного ранее контекста.
Рис. 4. Программа - часть контекста
Если программа не скомпилировалась, разработчик должен самостоятельно запросить данные на выходе компилятора. В полноценном OpenCL API существует API функция clGetProgramBuildInfo(), после вызова которой возвращается строка на выходе компилятора.
В текущей версии (b.642) эта функция не поддерживается, но, вероятно, ее стоило бы включить в OpenCL API, дабы дать разработчику для OpenCL больше информации о корректности кода кернела.
"Язычки", исходящие из девайсов (видеокарт), - это командные очереди, поддержка которых в MQL5 на уровне API, по-видимому, не планируется.
3.3. Создание кернела
Функция CLKernelCreate() создает ресурс OpenCL "Кернел".
int clKrn = CLKernelCreate( clPrg, "pi" );
Кернел - это функция, объявленная в программе, исполняемой на девайсе OpenCL.
В нашем случае это функция pi(), имеющая имя "pi". Объект "кернел" - это функция кернела вместе с соответствующими аргументами. Второй аргумент в этой функции - это имя функции, которое должно полностью соответствовать ее имени внутри программы.
Рис. 5. Kernel
Объекты "кернел" могут быть использованы сколько угодно раз, если нужно устанавливать различные аргументы для одной и той же функции, объявленной как кернел.
Теперь мы должны переходить к функциям CLSetKernelArg() и CLSetKernelArgMem(), но вначале поговорим об объектах, хранящихся в памяти устройств.
3.4. Объекты памяти
Прежде всего нужно понимать, что любой "большой" объект, обрабатываемый на GPU, следует создать заранее в памяти самого GPU или переместить его из памяти хоста (RAM). Под "большим" объектом мы понимаем либо буферы (одномерные массивы), либо изображения (images), которые могут быть двух- или трехмерными (2D или 3D).
Буфер - это большая область памяти, в которой расположены отдельные смежные элементы буфера. Это могут быть или простые типы данных (char, double, float, long и т.п.), или сложные (структуры, объединения и т.п.). Доступ к отдельным элементам буфера - прямой, и их можно читать и записывать.
Об изображениях мы сейчас говорить не будем, это особый тип данных. Судя по коду, приведенному разработчиками терминала на первой странице ветки об OpenCL, разработчики не обращались к специфике работы с изображениями.
Функция, создающая буфер, выглядит в приведенном коде следующим образом:
int clMem = CLBufferCreate( clCtx, _divisor * sizeof( double ), CL_MEM_READ_WRITE );
Первый параметр - хендл контекста, с которым ассоциируется буфер OpenCL как ресурс, второй - выделяемая под буфер память, третий параметр указывает, что мы можем делать с этим объектом. Возвращаемое значение - хендл на буфер OpenCL (если создан успешно) или -1 (если он не создан из-за ошибки).
В данном случае буфер был создан непосредственно в памяти GPU, т.е. девайса OpenCL. Если же он был создан в памяти RAM без использования данной функции, его нужно обязательно переместить в память девайса OpenCL (GPU). Это проиллюстрировано рисунком ниже:
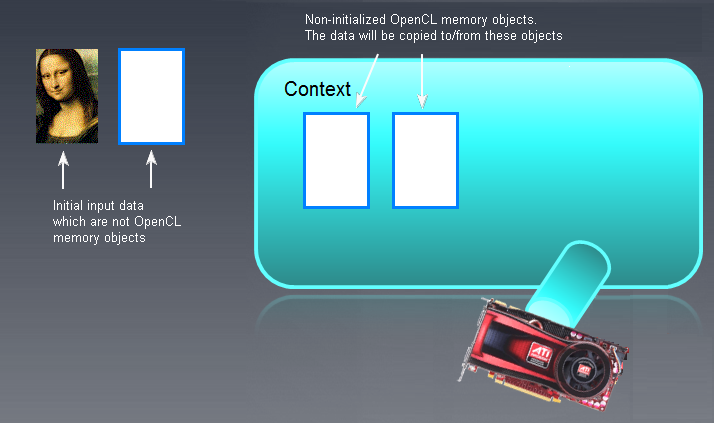
Рис. 6. Объекты памяти OpenCL
Слева изображены входные/выходные буферы (не обязательно изображения, Мона Лиза тут только для наглядности!), не являющиеся объектами памяти OpenCL. Правее в основном поле контекста, изображены пустые, неинициализированные объекты памяти OpenCL. Исходное данное "Мона Лиза" слева будет позднее перемещено в поле контекста OpenCL, а то, что будет на выходе программы OpenCL, нужно будет переместить обратно, влево, т.е. в память RAM.
Термины, принятые в OpenCL для копирования данных из/в хоста/девайс_OpenCL, таковы:
- Копирование данных из хоста в память девайса называется записью (функция CLBufferWrite());
- Копирование данных из памяти девайса в память хоста называется чтением (функция CLBufferRead(), см. чуть ниже).
Команда записи (хост -> девайс) одновременно инициализирует объект памяти данными и размещает объект в памяти девайса.
Следует помнить, что валидность (законность) объектов памяти, имеющихся на девайсе, внутри спецификации OpenCL не определена, т.к. зависит от вендора "железа", соответствующего девайсу. Поэтому при создании объектов памяти будьте внимательны.
После инициализации объектов памяти и записи их на девайсы картина становится примерно такой:
Рис. 7. Результат инициализации объектов памяти OpenCL
Теперь можно переходить к функциям, устанавливающим параметры кернела.
3.5. Установка параметров кернела
CLSetKernelArgMem( clKrn, 0, clMem );
Функция CLSetKernelArgMem() устанавливает в качестве нулевого параметра кернела буфер, созданный чуть раньше.
Если теперь посмотреть на этот же параметр в коде кернела, то он имеет следующий вид:
__kernel void pi( __global float *out )
В кернеле это массив out[ ], имеющий тот же тип, который создан функцией API CLBufferCreate().
Для установки небуферных параметров существует аналогичная функция:
bool CLSetKernelArg( int kernel, // хендл на кернел OpenCL программы uint arg_index, // номер аргумента OpenCL функции void arg_value ); // значение аргумента функции
Если бы мы, например, захотели установить в качестве второго параметра кернела некое double x0, то нам предварительно нужно было бы объявить и инициализировать его внутри программы MQL5:
double x0 = -2;
а затем вызвать функцию (тоже в коде MQL5):
CLSetKernelArg( cl_krn, 1, x0 );После всех перечисленных ранее манипуляций картинка станет такой:
Рис. 8. Результат установки параметров кернела
3.6. Выполнение программы
bool ex = CLExecute( clKrn, 1, offs, works );
Прямого аналога этой функции в спецификации OpenCL автор не обнаружил. Функция исполняет кернел clKrn с заданными параметрами. В последнем параметре works указано, сколько задач нужно выполнить по каждому из измерений расчетной задачи. Функция наглядно показывает принцип SPMD (Single Program Multiple Data): при одном вызове функции создается ровно works копий кернела со своими параметрами, которые, условно говоря, исполняются одновременно, но на разных "зернах" (Stream Cores, по терминологии AMD).
Универсальность OpenCL заключается в том, что язык "отвязан" от особенностей "железа", на котором исполняется код: кодеру для корректного исполнения программы OpenCL совсем не обязательно знать особенности "железа". Она все равно будет исполнена. Но для повышения эффективности выполнения кода (например, скорости) эти особенности знать крайне желательно.
Например, на "железе" автора статьи, в котором нет дискретной видеокарты, этот код исполняется без проблем. При этом автор имеет очень смутное представление о структуре самого CPU, на котором вся эмуляция и происходит.
ОК, программа OpenCL наконец выполнена, и мы теперь можем воспользоваться ее плодами - теперь в хостовой программе.
3.7. Чтение выходных данных
Ниже приведен фрагмент хостовой программы, читающий данные из девайса:
float buf[ ]; ArrayResize( buf, _divisor ); uint read = CLBufferRead( clMem, buf );
Напоминаем, что чтение данных в OpenCL - это копирование их из девайса на хост. Эти три строки показывают, как это сделать. Достаточно объявить в основной программе буфер buf[] такого же типа, который имеет считываемый буфер OpenCL, и вызвать функцию. Тип буфера, создаваемого в хостовой программе (здесь - на языке MQL5), может не совпадать с типом буфера в кернеле, но их размеры должны совпадать точно.
Теперь данные скопированы в память хоста, и они полностью доступны нам в рамках основной программы, т.е. программы на MQL5.
После того, как все нужные нам вычисления на девайсе OpenCL выполнены, нужно освободить память от всех объектов.
3.8. Уничтожение всех объектов OpenCL
Это выполняется перечисленными ниже командами:
CLBufferFree( clMem ); CLKernelFree( clKrn ); CLProgramFree( clPrg ); CLContextFree( clCtx );
Главная особенность этой серии функций заключается в том, что уничтожение объектов нужно выполнять в порядке, противоположном порядку их создания.
Теперь бросим краткий взгляд на сам код кернела.
3.9. Кернел
Как видим, весь код кернела - это одна большая строка, состоящая из множества строк.
Шапка кернела выглядит как обычная функция:
__kernel void pi( __global float *out )
К шапке кернела предъявляются следующие требования:
- Тип возвращаемого значения - всегда void;
- Спецификатор __kernel не обязан иметь два символа подчеркивания; это может быть и kernel;
- Если аргумент является массивом (буфером), он передается только по ссылке. Спецификатор памяти __global (или global) означает, что этот буфер хранится в глобальной памяти девайса.
- Аргументы простых типов данных передаются по значению.
Тело кернела в данном случае ничем особенным не отличается от обычного кода на языке С.
Важный момент: строка :
int i = get_global_id( 0 );
означает, что i является номером вычислительной ячейки внутри GPU, от которого зависит результат вычислений внутри этой ячейки. Этот результат в дальнейшем записывается в выходной массив (здесь out[]), после чего его значения суммируются уже в хостовой программе после чтения массива из памяти GPU в память CPU.
Следует отметить, что функция в коде программы OpenCL может быть не единственной. Например, внутри "основной" функции кернела pi() может вызываться простая inline функция, которая будет располагаться вне функции pi(). Этот случай будет рассмотрен дальше.
Теперь, когда мы вкратце познакомились с OpenCL API в реализации компании MetaQuotes, можно поэкспериментировать дальше. В этой статье автор не стремился слишком сильно углубляться в тонкости "железа", позволяющие максимально оптимизировать скорость исполнения. Сейчас главная задача - дать стартовую точку для кодирования на языке OpenCL как таковом.
Другими словами, код в меру "наивен", т.к. не учитывает особенности "железа". В то же время он достаточно общий, чтобы он мог исполняться на любом "железе" - CPU, IGP от AMD (GPU, интегрированный в CPU) или дискретной видеокарте от AMD / NVidia.
Перед рассмотрением последующих "наивных" оптимизаций с помощью векторных типов данных нам придется познакомиться с ними.
4. Векторные типы данных
Векторные типы данных - типы, специфичные для OpenCL и отличающие его от С99. К ним относятся любые типы (u)charN, (u)shortN, (u)intN, (u)longN, floatN при N = {2|3|4|8|16}.
Эти типы предполагается использовать тогда, когда мы знаем (или предполагаем), что встроенный компилятор сможет дополнительно распараллелить вычисления. Отметим сразу, что это происходит не всегда - даже если коды кернела отличаются только величиной N, а во всем остальном идентичны (автору пришлось убедиться в этом).
Ниже указаны встроенные типы данных:
Табл. 1. Встроенные векторные типы данных OpenCL
Эти типы поддерживаются любым девайсом. Каждому из этих типов сооветствует тип API для "общения" кернела с хостовой программой. В текущей реализации MQL5 это не предусмотрено, но ничего страшного в этом нет.
Существуют также и дополнительные типы, но для их использования это нужно указывать явно, т.к. не каждый девайс их поддерживает:
Табл. 2. Другие встроенные типы данных OpenCL
Кроме того, существуют также резервные типы данных, которые все еще не поддерживаются в OpenCL. Их список довольно длинный, загляните в Спецификацию языка.
Чтобы объявить константу или переменную векторного типа, достаточно следовать простым интуитивным правилам.
Ниже приведены несколько примеров:
float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f); uint4 u = ( uint4 ) ( 1 ); /// u конвертируется в вектор (1, 1, 1, 1). float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) ); float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f ); float4 f = ( float4 ) ( 1.0f, 2.0f ); /// ошибка
Как видим, достаточно, чтобы типы данных справа соответствовали в сумме "ширине" переменной, объявленной слева (здесь она равна 4). Единственное исключение - конвертация скаляра в вектор с компонентами, равными скаляру (строка 2).
Для каждого типа векторных данных существует простой механизм обращения к компонентам векторов. С одной стороны, это векторы (массивы), а с другой - это структуры. Так, например, для векторов с "шириной" 2 (например, float2 u) к первой компоненте можно обратиться как к u.x, а ко второй - u.y.
Для вектора типа long3 u все три компоненты по порядку будут выглядеть так: u.x, u.y, u.z.
Для вектора типа float4 u - соответственно .xyzw, т.е. u.x, u.y, u.z, u.w.
float2 pos; pos.x = 1.0f; // приемлемо pos.z = 1.0f; // неверно, т.к. pos.z не существует float3 pos; pos.z = 1.0f; // приемлемо pos.w = 1.0f; // неверно, т.к. pos.w не существует
Можно выбирать сразу несколько компонент и даже менять их местами (групповая нотация):
float4 c; c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); c.z = 1.0f; c.xy = ( float2 ) ( 3.0f, 4.0f ); c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f ); float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 swiz= pos.wzyx; // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f ) float4 dup = pos.xxyy; // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )Групповая нотация, т.е. указание нескольких компонент, может присутствовать в левой части оператора присваивания (т.е. является l-value):
float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); pos.xw = ( float2 ) ( 5.0f, 6.0f ); // pos = ( 5.0f, 2.0f, 3.0f, 6.0f ) pos.wx = ( float2 ) ( 7.0f, 8.0f ); // pos = ( 8.0f, 2.0f, 3.0f, 7.0f ) pos.xyz = ( float3 ) ( 3.0f, 5.0f, 9.0f ); // pos = ( 3.0f, 5.0f, 9.0f, 4.0f ) pos.xx = ( float2 ) ( 3.0f, 4.0f ); // недопустимо, т.к. 'x' использовано дважды pos.xy = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // недопустимо, т.к. выражению типа float2 присваивается выражение типа float4 float4 a, b, c, d; float16 x; x = ( float16 ) ( a, b, c, d ); x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw ); x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz ); // недопустимо, т.к. компонента a.xxxxxxx не является валидным векторным типом
Для доступа к отдельным компонентам можно использовать другую нотацию - с помощью символа s (или S), который вставляется перед шестнадцатиричной цифрой или несколькими цифрами при групповой нотации:
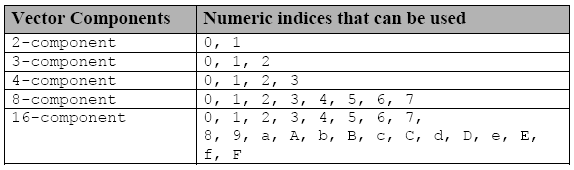
Табл. 3. Нотация индексов для доступа к отдельным компонентам векторных типов данных
Если объявить векторную переменную f
float8 f;то f.s0 - это 1-й компонент вектора element, а f.s7 - 8-й компонент.
В то же время, если мы объявим 16-мерный вектор x,
float16 x;то x.sa (или x.sA) - 11-й компонент вектора x, а x.sf (или x.sF) относится к 16-му компоненту вектора x.
Цифровые нотации (.s0123456789abcdef) и буквенные (.xyzw) нельзя использовать одновременно в одном идентификаторе с групповым указанием компонент:
float4 f, a; a = f.x12w; // неверно, т.к. цифровые индексы указаны вместе с буквенными .xyzw a.xyzw = f.s0123; // допустимо
И, наконец, еще одна возможность манипуляций с компонентами векторных типов - это .lo, .hi, .even, .odd.
Эти обозначения имеют следующий смысл:
- .lo указывает на "нижнюю половину" вектора;
- .hi обозначает "верхнюю половину" вектора;
- .even - это все компоненты вектора с четными индексами;
- .odd - все компоненты вектора с нечетными индексами.
Например:
float4 vf; float2 low = vf.lo; // vf.xy float2 high = vf.hi; // vf.zw float2 even = vf.even; // vf.xz float2 odd = vf.odd; // vf.yw
Эту нотацию можно использовать повторно - вплоть до тех пор, пока не получается скаляр (невекторный тип данных).
float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f ); float2 s = u.lo.lo; // ( 1.0f, 2.0f ) float2 t = u.hi.lo; // ( 5.0f, 6.0f ) float2 q = u.even.lo; // ( 1.0f, 3.0f ) float r = u.odd.lo.hi; // 4.0f
В векторах с размерностью 3 ситуация немного сложнее: формально это 4-вектор с неопределенной 4-й компонентой.
float3 vf = (float3) (1.0f, 2.0f, 3.0f); float2 low = vf.lo; // ( 1.0f, 2.0f ); float2 high = vf.hi; // ( 3.0f, не_определено );
Кратко - о правилах арифметических действий (+, -, *, /).
Все указанные действия определены для векторов одинаковой размерности и осуществляются покомпонентно.
float4 d = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 w = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f ); float4 _sum = d + w; // ( 6.0f, 10.0f, 13.0f, 3.0f ) float4 _mul = d * w; // ( 5.0f, 16.0f, 30.0f, -4.0f ) float4 _div = w / d; // ( 5.0f, 4.0f, 3.333333f, -0.25f )
Единственное исключение - когда один из векторов является скаляром, а второй - вектором. В этом случае тип данных скаляра приводится к типу данных, объявленных в векторе, а сам скаляр конвертируется в вектор с той же размерностью, что и вектор. После этого производится арифметическое действие. То же самое можно сказать и об операторах отношения (<, >, <=, >=).
Производные типы данных, нативные для языка С99 (например, struct, union, массивы и прочее), которые можно сконструировать из встроенных типов данных, указанных в первой таблице этого раздела, также поддерживаются в языке OpenCL.
И последнее: если вы хотите использовать GPU для точных вычислений, вам неминуемо придется воспользоваться типом данных double и соответственно doubleN.
Для этого достаточно вставить строку:
#pragma OPENCL EXTENSION cl_khr_fp64 : enable
в начало кода кернела.
Этого уже должно быть достаточно для понимания дальнейшего материала. Если у вас возникнут вопросы, загляните в Спецификацию языка OpenCL 1.1.
5. Реализация кернела с векторными типами данных
Откровенно говоря, автору не удалось "с наскока" написать работающий код с векторными типами данных.
Автор вначале не слишком внимательно читал спецификацию языка и решил, что все получится "само собой", как только удастся где-нибудь внутри кернела объявить векторный тип данных - например, double8. Более того, когда автор решил объявить один только выходной массив как массив векторов double8, тоже ничего не получилось.
Через некоторое время пришло осознание: для эффективной векторизации кернела и реального ускорения этого совершенно недостаточно. Организация вывода результатов в массив векторов не решает проблему, т.к. данные нужно не просто быстро вводить и выводить, но их нужно быстро вычислять. После осознания этого обстоятельства работа пошла быстрее и конструктивнее, и именно оно позволило, в конце концов, создать более быстрый код.
Но это еще не все. Если код кернела, написанный выше, удавалось отлаживать почти "вслепую", то теперь, при использовании векторных данных, искать ошибки стало довольно трудно. Ну какую конструктивную информацию может сообщить нам стандартное сообщение:
ERR_OPENCL_INVALID_HANDLE - невалидный хендл на program OpenCL
или
ERR_OPENCL_KERNEL_CREATE - внутренняя ошибка при создании объекта OpenCL
?
Поэтому пришлось использовать SDK. В данном случае, при использовании автрской конфигурации "железа", это оказался Intel OpenCL SDK Offline Compiler (32 bit), имеющийся в Intel OpenCL SDK (для пользователей процессоров/GPU компаний, отличных от Intel, в SDK тоже должны иметься офлайновые компиляторы). Он удобен тем, что позволяет отладить код кернела без какой-либо "обвязки" хостового API.
Достаточно просто вставить код кернела в окно компилятора - но не в том виде, как он используется внутри кода MQL5, а без символов внешних кавычек и "\r\n" (возврата каретки), и нажать на кнопку Build с рисунком шестеренки.
При этом внизу, в окне Build Log, отобразится информация о процессе Build и о его успешности:
Рис. 9. Компиляция программы в Intel OpenCL SDK Offline Compiler
Для получения кода кернела без кавычек полезно написать на хостовом языке (MQL5) несложную программу вывода кода кернела в файл - WriteCLProgram(). Она теперь включена в код хостовой программы.
Сообщения компилятора не всегда очень понятны, но информации все же намного больше, чем в текущее время может выдать MQL5. Можно исправлять ошибки сразу в окне компилятора, после чего, убедившись в отсутствии ошибок, перенести исправления в код кернела в MetaEditor.
И последнее. Первоначальной задумкой автора было написание "векторизованного" кода, способного работать с векторами double4, double8 и double16 путем задания единого глобального параметра "количества каналов". В конце концов, и это удалось сделать, но после нескольких дней мучений с макросом слияния токенов ##, который почему-то отказывался работать внутри кода кернела.
За это время удалось написать работающий код скрипта с тремя кодами кернелов, каждый из которых подходил для своей размерности - 4, 8 или 16. В тексте статьи этот промежуточный код не будет выложен, но это полезно знать, если вам захочется написать код кернела, не мучаясь слишком долго. Код этой реализации скрипта (OCL_pi_double_several_simple_kernels.mq5) приложен в конце статьи.
Ниже показан код "векторизованного" кернела:
"/// инэйблим икстеншен с даблами \r\n" "#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _intrnCnt ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" "#define _CH " + i2s( _ch ) + " \r\n" "#define _DOUBLETYPE double" + i2s( _ch ) + " \r\n" " \r\n" "/// расширения для 4-, 8- и 16- скалярных произведений \r\n" "#define dot4( a, b ) dot( a, b ) \r\n" " \r\n" "inline double dot8( double8 a, double8 b ) \r\n" "{ \r\n" " return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi ); \r\n" "} \r\n" " \r\n" "inline double dot16( double16 a, double16 b ) \r\n" "{ \r\n" " double16 c = a * b; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot4( c.lo.lo + c.lo.hi + c.hi.lo + c.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// определяем векторные константы \r\n" " double16 v16 = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 ); \r\n" " double8 v8 = v16.lo; \r\n" " double4 v4 = v16.lo.lo; \r\n" " double2 v2 = v16.lo.lo.lo; \r\n" " \r\n" " /// все векторное с вычисляемым типом \r\n" " _DOUBLETYPE in; \r\n" " _DOUBLETYPE xVect; \r\n" " _DOUBLETYPE sumVect = ( _DOUBLETYPE ) ( 0.0 ); \r\n" " _DOUBLETYPE doubleOneVect = ( _DOUBLETYPE ) ( 1.0 ); \r\n" " _DOUBLETYPE doubleCHVect = ( _DOUBLETYPE ) ( _CH + 0. ); \r\n" " _DOUBLETYPE doubleSTEPVect = ( _DOUBLETYPE ) ( _STEP ); \r\n" " \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in = v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j ); \r\n" " xVect = ( in + 0.5 ) * doubleSTEPVect; \r\n" " sumVect += 4.0 / ( xVect * xVect + 1. ); \r\n" " } \r\n" " out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n" "} \r\n";
Во внешней хостовой программе почти ничего не изменилось, не считая новой глобальной константы _ch, которая задает количество "каналов векторизации", и глобальной константы _intrnCnt, которая уменьшилась в _ch раз. Поэтому автор решил не показывать код хостовой программы. Он доступен в файле скрипта, приложенном в конце статьи (OCL_pi_double_parallel_straight.mq5).
Как видим, помимо "главной" функции кернела pi() у нас появились две inline функции, определяющие скалярное произведение векторов dotN( a, b ), и одна макроподстановка. Причина определения этих функций - в том, что в OpenCL функция dot() определена для размерности векторов, не превышающей 4.
Макрос dot4(), переопределяющий фунцию dot(), существует только для удобства вызова функции dotN() с вычисляемым именем:
" out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n"
Если бы мы сохранили функцию dot() в прежнем виде, без "индекса" 4, то при _ch = 4 (числе каналов векторизации, равном 4), нам не удалось бы вызвать ее так же просто, как это сделано здесь.
В этой строке продемонстрирована еще одна очень полезная особенность специфичной формы кернела, заключающейся в том, что сам кернел внутри хостовой программы воспринимается как строка: мы можем использовать в кернеле вычисляемые идентификаторы - не только для функций, но и для типов данных!
Код полной хостовой программы с данным кернелом приложен ниже (OCL_pi_double_parallel_straight.mq5).
Запуская скрипт при "ширине" вектора, равной 16 ( _ch = 16 ), получаем следующее:
2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) ================================================== 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) CPUtime / GPUtime = 4.130 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The time to calculate PI was 8.830 seconds 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The value of PI is 3.141592653590 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The time to calculate PI was 8.002 seconds 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The value of PI is 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: gone = 2.138 sec. 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: pi = 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) read = 20000 elements 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) CLProgramCreate: неопознанная ошибка. 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) ==================================================
Как видим, даже оптимизация с помощью векторных типов данных не помогла кернелу стать быстрее.
Но если запустить этот же код на GPU, выигрыш будет намного больше.
По данным MetaDriver'а (видеокарта - HIS Radeon HD 6930, CPU - AMD Phenom II x6 1100T), тот же код выдает следующие результаты:
2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) ================================================== 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) CPUtime / GPUtime = 84.983 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The time to calculate PI was 14.617 seconds 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The value of PI is 3.141592653590 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The time to calculate PI was 14.040 seconds 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The value of PI is 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: gone = 0.172 sec. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) read = 20000 elements 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) CLProgramCreate: неопознанная ошибка. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) ==================================================
6. Заключительная фантазия
Вот еще один кернел (он расположен в файле OCL_pi_double_several_simple_kernels.mq5, приложенном ниже, но здесь не показанном).
В скрипте был реализован как раз тот вариант, когда автор временно отказался от написания "единого" кернела и написал четыре простых кернела для разных размеров векторов (4, 8, 16, 32):
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _itInKern ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" " \r\n" "typedef struct \r\n" "{ \r\n" " double16 lo; \r\n" " double16 hi; \r\n" "} double32; \r\n" " \r\n" "inline double32 convert2double32( double a ) \r\n" "{ \r\n" " double32 b; \r\n" " b.lo = ( double16 )( a ); \r\n" " b.hi = ( double16 )( a ); \r\n" " return b; \r\n" "} \r\n" " \r\n" "inline double dot32( double32 a, double32 b ) \r\n" "{ \r\n" " double32 c; \r\n" " c.lo = a.lo * b.lo; \r\n" " c.hi = a.hi * b.hi; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo + c.lo.hi.hi + \r\n" " c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo + c.hi.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// определяем векторные константы \r\n" " double32 _v32; \r\n" " _v32.lo = ( double16 ) ( 0., 1., 2., 3., 4., 5., 6., 7., \r\n" " 8., 9., 10., 11., 12., 13., 14., 15. ); \r\n" " _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23., \r\n" " 24., 25., 26., 27., 28., 29., 30., 31. ); \r\n" " \r\n" " /// все векторное с неопределенным типом \r\n" " double32 xVect; \r\n" " double32 sumVect = convert2double32( 0.0 ); \r\n" " double32 double1Vect = convert2double32( 1.0 ); \r\n" " \r\n" " double32 in; \r\n" " /// в цикле работаем только с 16-векторами! \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j ); \r\n" " in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j ); \r\n" " xVect.lo = ( in.lo + 0.5 ) * _STEP; \r\n" " xVect.hi = ( in.hi + 0.5 ) * _STEP; \r\n" " sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. ); \r\n" " sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. ); \r\n" " } \r\n" " out[ i ] = dot32( sumVect, double1Vect ); \r\n" "} \r\n";
Именно в этом кернеле реализована размерность вектора, равная 32. Определение нового векторного типа и несколько необходимых inline функций находятся вне основной функции кернела. Кроме того (это важно!), все вычисления внутри основного цикла намеренно выполняются только со стандартными векторными типами данных, а нестандартные типы обрабатываются уже вне цикла. Это существенно ускоряет исполнение кода.
Для нашего вычисления этот кернел работает не медленнее, чем для векторов с шириной 16, но, правда, и не существенно быстрее.
Согласно данным MetaDriver'а, исполнение скрипта с этим кернелом (_ch=32) показывает следующие результаты:
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec. 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: неопознанная ошибка или ее отсутствие. 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; каналов векторизации - 32 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================
Заключение и выводы
Автор прекрасно понимает, что задача, выбранная здесь для демонстрации возможностей OpenCL, не слишком характерна для этого языка.
Гораздо проще взять учебник, списать с него стандартный пример о перемножении больших матриц и выложить его здесь. Да, пример будет несомненно впечатляющим. Однако... много ли участников форума mql5.com проводят такие финансовые вычисления, при которых нужно перемножать большие матрицы? Сомнительно. Автору захотелось выбрать свой собственный пример и пройти все трудности самостоятельно, а заодно и попытаться рассказать о них. Судить, конечно, только вам, уважаемые форумяне.
Выигрыш в производительности на эмуляции OpenCL (на "голом" CPU) оказался очень небольшим - в сравнении с сотнями и даже тысячами, полученными на скриптах MetaDriver'а. Но на приличном GPU выигрыш минимум на порядок больше, чем на эмуляции, - даже если сбросить со счета несколько большее время исполнения на CPU в случае CPU AMD. OpenCL все же стоит изучить хотя бы ради такого скачка в скорости вычислений!
В следующей статье автор предполагает заняться вопросами, связанными с особенностями отображения абстрактных моделей OpenCL на реальное "железо". Знание этого иногда позволяет дополнительно существенно ускорить расчеты.
Автор выражает особую благодарность MetaDriver'у за ценнейшие советы по программированию и оптимизации быстродействия, а также Support Team за саму возможность работать с Intel OpenCL SDK.
Содержание приложенных файлов:
- pi.mq5 - скрипт на чистом MQL5 с двумя способами вычисления числа "пи";
- OCl_pi_float.mq5 - первая реализация скрипта с кернелом OpenCL при вещественных вычислениях с типом float;
- OCL_pi_double.mq5 - то же самое, но вещественные вычисления - с типом double;
- OCL_pi_double_several_simple_kernels.mq5 - скрипт с несколькими специфичными кернелами для разной "ширины" векторов (4, 8, 16, 32);
- OCL_pi_double_parallel_straight.mq5 - скрипт с единым кернелом для нескольких случаев "ширины" векторов (4, 8, 16).
Ядерная оценка неизвестной плотности вероятности
Безграничные возможности с MetaTrader 5 и MQL5
Создай торгового робота за 6 шагов!
Несколько советов для начинающих заказчиков
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Запрашиваемая страница не найдена
Проверьте правильность пути и попробуйте заново
не могу скачать файлы с статьи
Да, действительно. Скачанный файл оказывается html-страницей, но не файлом mq5.
Спасибо, сообщу в Сервисдеск.
Да, действительно. Скачанный файл оказывается html-страницей, но не файлом mq5.
Спасибо, сообщу в Сервисдеск.
Исправлено.
Автор или знатоки ответьте пожалуйста:
Где быстрее отработает код представленный ниже на основном камне или в видике ? И есть ли какие то специфические моменты ?
void OnStart()
{
long total= 1000000000;
for(long i=0;i<total;i++)
for(long q=0;q<total;q++)
for(long w=0;w<total;w++)
for(long e=0;e<total;e++)
for(long r=0;r<total;r++)
for(long t=0;t<total;t++)
for(long y=0;y<total;y++)
for(long u=0;u<total;u++)
func(i,q,w,e,r,t,y,u);
}