
OpenCL: The Bridge to Parallel Worlds
Introduction
This article is the first in a short series of publications on programming in OpenCL, or Open Computing Language. The MetaTrader 5 platform in its current form, prior to providing support for OpenCL, did not allow to directly, i.e. natively use and enjoy the advantages of multi-core processors to speed up computations.
Obviously, the developers could endlessly repeat that the terminal is multithreaded and that "every EA/script runs in a separate thread", yet the coder was not given an opportunity for a relatively easy parallel execution of the following simple loop (this is a code to calculate the pi value = 3.14159265...):
long num_steps = 1000000000; double step = 1.0 / num_steps; double x, pi, sum = 0.0; for (long i = 0; i<num_steps; i++) { x = (i + 0.5)*step; sum += 4.0/(1.0 + x*x); } pi = sum*step;
However, as far back as 18 months ago, a very interesting work entitled "Parallel Calculations in MetaTrader 5" appeared in the "Articles" section. And yet...one gets the impression that despite the ingenuity of the approach, it is somewhat unnatural - an entire program hierarchy (the Expert Advisor and two indicators) written to speed up calculations in the above loop would have been too much of a good thing.
We already know that there are no plans to support OpenMP and are aware of the fact that adding OMP requires a drastic reprogramming of the compiler. Alas, there will be no cheap and easy solution for a coder where no thinking is required.
The announcement of native support for OpenCL in МQL5 was therefore very welcome news. Starting on page 22 of the same news thread, MetaDriver began posting scripts allowing to evaluate the difference between implementation on CPU and GPU. OpenCL aroused tremendous interest.
The author of this article first opted out of the process: a quite low end computer configuration (Pentium G840/8 Gb DDR-III 1333/No video card) did not seem to provide for effective use of OpenCL.
However, following the installation of AMD APP SDK, a specialized software developed by AMD, the first script proposed by MetaDriver that had been run by others only if a discrete video card was available, was successfully run on the author's computer and demonstrated a speed increase that was far from being trifling in comparison with a standard script runtime on one processor core, being approximately 25 times faster. Later, acceleration of the same script runtime reached 75, due to Intel OpenCL Runtime being successfully installed with the help of the Support Team.
Having carefully studied the forum and materials provided by ixbt.com, the author found out that Intel's Integrated Graphics Processor (IGP) supports OpenCL 1.1, only starting with Ivy Bridge processors and up. Consequently, the acceleration achieved on the PC with the above configuration could not have anything to do with IGP and the OpenCL program code in this particular case was executed only on х86 core CPU.
When the author shared the acceleration figures with ixbt experts, they answered instantly and all at once that this all was a result of a substantial under-optimization of the source language (MQL5). In the community of OpenCL professionals, it is a known fact that a correct optimization of a source code in С++ (of course, subject to use of a multi-core processor and SSEx vector instructions) can at its best result in a gain of several dozen percent on OpenCL emulation; in the worst case scenario, you can even lose, e.g. due to extremely high spending (of time) when passing data.
Hence - another assumption: 'miraculous' acceleration figures in MetaTrader 5 on pure OpenCL emulation should be treated adequately without being attributed to "coolness" of OpenCL itself. A really strong advantage of GPU over a well-optimized program in С++ can only be gained using a quite powerful discrete video card since its computing capabilities in some algorithms are far beyond the capabilities of any modern CPU.
The developers of the terminal state that it has not yet been properly optimized. They also dropped a hint about the degree of acceleration which will be several times over following the optimization. All acceleration figures in OpenCL will be accordingly reduced by the same "several times". However, they will still be considerably greater than unity.
It is a good reason to learn the OpenCL language (even if your video card does not support OpenCL 1.1 or is simply missing) with which we are going to proceed. But first let me say a few words about the essential basis - software that supports Open CL and the appropriate hardware.
1. Essential Software and Hardware
1.1.AMD
The appropriate software is produced by AMD, Intel and NVidia, the members of the nonprofit industry consortium - the Khronos Group that develops different language specifications in relation to computations in heterogeneous environments.
Some useful materials can be found in the official website of the Khronos Group, e.g.:
These documents will have to be used quite often in the process of learning OpenCL as the terminal does not yet offer Help information on OpenCL (there is only a brief summary of OpenCL API). All the three companies (AMD, Intel and NVidia) are video hardware suppliers and each of them has their own OpenCL Runtime implementation and respective software development kits - SDK. Let us go into the peculiarities of choosing video cards, taking AMD products as an example.
If your AMD video card is not very old (first released into production in 2009-2010 or later), it is going to be quite simple - an update of your video card driver should be enough to get to work immediately. A list of OpenCL compatible video cards can be found here. On the other hand, even a video card which is pretty good for its time, like Radeon HD 4850 (4870), will not save you the trouble when dealing with OpenCL.
If you do not yet have an AMD video card but feel up to getting one, have a look at its specifications first. Here you can see a fairly comprehensive Modern AMD Video Cards Specification Table. The most important for us are the following:
- On-board Memory — the amount of local memory. The bigger it is, the better. 1 GB would usually be enough.
- Core Clock — operating core frequency. It is also clear: the higher the operating frequency of GPU multiprocessors, the better. 650-700 MHz is not bad at all.
- [Memory] Type — video memory type. The memory should ideally be fast, i.e. GDDR5. But GDDR3 would also be fine although around twice as worse in terms of memory bandwidth.
- [Memory] Clock (Eff.) - operating (effective) frequency of video memory. Technically, this parameter is closely related to the previous one. The GDDR5 operating effective frequency is on the average twice as high as the frequency of GDDR3. It has nothing to do with the fact that "higher" memory types work on higher frequencies but is due to the number of data transfer channels used by the memory. In other words, it has to do with memory bandwidth.
- [Memory] Bus - bus data width. It is advisable to be at least 256 bit.
- MBW — Memory BandWidth. This parameter is actually a combination of all three of the above video memory parameters. The higher it is, the better.
- Config Core (SPU:TMU(TF):ROP) — configuration of GPU core units. What is of importance to us, i.e. for non-graphical calculations, is the first number. 1024:64:32 stated would mean that we need number 1024 (the number of unified streaming processors or shaders). Obviously, the higher it is, the better.
- Processing Power — theoretical performance in floating point computations (FP32 (Single Precision) / FP64 (Double Precision). Whereas specification tables always contain a value corresponding to FP32 (all video cards can handle single-precision calculations), this is far from being the case with FP64 since double precision is not supported by every video card. If you are sure that you will never need double precision (double type) in GPU calculations, you may disregard the second parameter. But whatever the case, the higher this parameter is, the better.
- TDP — Thermal Design Power. This is, roughly speaking, the maximum power the video card dissipates in the most difficult calculations. If your Expert Advisor will be frequently accessing GPU, the video card will not only consume a lot of power (which is not bad if it pays off) but will also be quite noisy.
Now, the second case: there is no video card or the existing video card does not support OpenCL 1.1 but you have an AMD processor. Here you can download AMD APP SDK which apart from runtime also contains SDK, Kernel Analyzer and Profiler. Following the installation of AMD APP SDK, the processor should be recognized as an OpenCL device. And you will be able to develop fully featured OpenCL applications in emulation mode on CPU.
The key feature of SDK, as opposed to AMD, is that it is also compatible with Intel processors (although when developing on Intel CPU, native SDK is yet significantly more efficient as it is capable of supporting the SSE4.1, SSE4.2 and AVX instruction sets that have only recently become available on AMD processors).
1.2. Intel
Before getting to work on Intel processors, it is advisable to download Intel OpenCL SDK/Runtime.
We should point out the following:
- If you intend to develop OpenCL applications only using CPU (OpenCL emulation mode), you should know that Intel CPU graphics kernel does not support OpenCL 1.1 for processors older than and including Sandy Bridge. This support is only available with Ivy Bridge processors but it will hardly make any difference even for the ultra powerful Intel HD 4000 integrated graphics unit. For the processors older than Ivy Bridge, this would mean that the acceleration achieved in the MQL5 environment is only due to SS(S)Ex vector instructions used. Yet it also appears to be significant.
- After the installation of Intel OpenCL SDK, the registry entry HKEY_LOCAL_MACHINE\SOFTWARE\Khronos\OpenCL\Vendors is required to be amended as follows: replace IntelOpenCL64.dll in the Name column with intelocl.dll . Then reboot and start MetaTrader 5. The CPU is now recognized as an OpenCL 1.1 device.
To be quite honest, the issue regarding Intel's OpenCL support has not yet been fully resolved so we should expect some clarifications from the developers of the terminal in the future. Basically, the point is that nobody is going to be watching for kernel code errors (OpenCL kernel is a program executed on GPU) for you - it is not the MQL5 compiler. The compiler will merely take in a whole big line of the kernel and try to execute it. If, for example, you did not declare some internal variable х used in the kernel, the kernel will still be technically executed, albeit with errors.
However all errors that you will get in the terminal come down to less than a dozen out of those described in Help on API OpenCL for the functions CLKernelCreate() and CLProgramCreate(). Language syntax is very similar to that of C, enhanced with vector functions and data types (in fact this language is C99 which was adopted as the ANSI С standard in 1999).
It is Intel OpenCL SDK Offline Compiler that the author of this article uses to debug code for OpenCL; it is much more convenient than to blindly look for kernel errors in MetaEditor. Hopefully, in the future the situation will change for the better.
1.3. NVidia
Unfortunately, the author did not search for information on this subject. The general recommendations nevertheless remain the same. Drivers for new NVidia video cards automatically support OpenCL.
Basically, the author of the article does not have anything against NVidia video cards but the conclusion drawn based on the knowledge gained from looking for information and forum discussions is as follows: for non-graphical calculations, AMD video cards appear to be more optimal in terms of price/performance ratio than NVidia video cards.
Let us now move to programming.
2. The First MQL5 Program Using OpenCL
To be able to develop our first, very simple program, we need to define the task as such. It must have become customary in parallel programming courses to use calculation of the pi value which is approximately equal to 3.14159265 as an example.
For this purpose, the following formula is used (the author has never come across this particular formula before but it seems to be true):
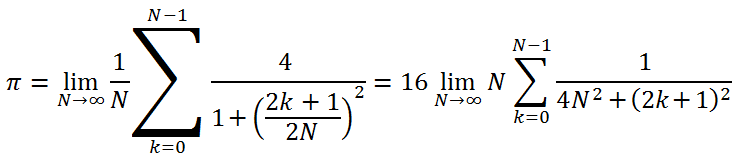
We want to calculate the value accurate to 12 decimal places. Basically, such precision can be obtained with around 1 million iterations but this number will not enable us to evaluate the benefit of calculations in OpenCL as the duration of calculations on GPU gets too short.
GPGPU programming courses suggest selecting the amount of calculations so that the GPU task duration is at least 20 milliseconds. In our case, this limit should be set higher due to significant error of the GetTickCount() function comparable to 100 ms.
Below is the MQL5 program where this calculation is implemented:
//+------------------------------------------------------------------+ //| pi.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" long _num_steps = 1000000000; long _divisor = 40000; double _step = 1.0 / _num_steps; long _intrnCnt = _num_steps / _divisor; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { uint start,stop; double x,pi,sum=0.0; start=GetTickCount(); //--- first option - direct calculation for(long i=0; i<_num_steps; i++) { x=(i+0.5)*_step; sum+=4.0/(1.+x*x); } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); //--- calculate using the second option start=GetTickCount(); sum=0.; long divisor=40000; long internalCnt=_num_steps/divisor; double partsum=0.; for(long i=0; i<divisor; i++) { partsum=0.; for(long j=i*internalCnt; j<(i+1)*internalCnt; j++) { x=(j+0.5)*_step; partsum+=4.0/(1.+x*x); } sum+=partsum; } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); Print("_______________________________________________"); return(0); } //+------------------------------------------------------------------+Having compiled and run this script, we get:
2012.05.03 02:02:23 pi (EURUSD,H1) The time to calculate PI was 8.783 seconds 2012.05.03 02:02:23 pi (EURUSD,H1) The value of PI is 3.141592653590 2012.05.03 02:02:15 pi (EURUSD,H1) The time to calculate PI was 7.940 seconds 2012.05.03 02:02:15 pi (EURUSD,H1) The value of PI is 3.141592653590
The pi value ~ 3.14159265 is calculated in two slightly different ways.
The first one can almost be considered a classical method for demonstration of capabilities of multi-threading libraries like OpenMP, Intel TPP, Intel MKL and others.
The second one is the same calculation in the form of a double loop. The entire calculation consisting of 1 billion iterations is broken down into large blocks of the outer loop (there are 40000 of them there) where every block executes 25000 "basic" iterations making up the inner loop.
You can see that this calculation runs a little slower, by 10-15%. But it is this particular calculation that we are going to use as a base when converting to OpenCL. The main reason is the kernel (the basic computing task executed on GPU) selection that would carry out a reasonable compromise between the time spent on transferring data from one area of memory to another and calculations as such run in the kernel. Thus, in terms of the current task, the kernel will be, roughly speaking, the inner loop of the second calculation algorithm.
Let us now calculate the value using OpenCL. A complete program code will be followed by short comments on functions characteristic of the host language (MQL5) binding to OpenCL. But first, I would like to highlight a few points related to typical "obstacles" that could interfere with coding in OpenCL:
- The kernel does not see variables declared outside the kernel. That is why the global variables _step and _intrnCnt had to be declared again at the beginning of the kernel code (see below). And their respective values had to be transformed into strings to be read properly in the kernel code. However, this peculiarity of programming in OpenCL proved very useful later on, e.g. when making vector data types that are natively absent from C.
- Try to give as many calculations to the kernel as possible while keeping their number reasonable. This is not very critical for this code as the kernel is not very fast in this code on the existing hardware. But this factor will help you speed up the calculations if a powerful discrete video card is used.
So, here is the script code with the OpenCL kernel:
//+------------------------------------------------------------------+ //| OCL_pi_float.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs; input int _device=0; /// OpenCL device number (0, I have CPU) #define _num_steps 1000000000 #define _divisor 40000 #define _step 1.0 / _num_steps #define _intrnCnt _num_steps / _divisor string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(int arg) { return IntegerToString(arg); } const string clSrc= "#define _step "+d2s(_step,12)+" \r\n" "#define _intrnCnt "+i2s(_intrnCnt)+" \r\n" " \r\n" "__kernel void pi( __global float *out ) \r\n" // type float "{ \r\n" " int i = get_global_id( 0 ); \r\n" " float partsum = 0.0; \r\n" // type float " float x = 0.0; \r\n" // type float " long from = i * _intrnCnt; \r\n" " long to = from + _intrnCnt; \r\n" " for( long j = from; j < to; j ++ ) \r\n" " { \r\n" " x = ( j + 0.5 ) * _step; \r\n" " partsum += 4.0 / ( 1. + x * x ); \r\n" " } \r\n" " out[ i ] = partsum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt)); int clCtx=CLContextCreate(_device); int clPrg = CLProgramCreate( clCtx, clSrc ); int clKrn = CLKernelCreate( clPrg, "pi" ); uint st=GetTickCount(); int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float CLSetKernelArgMem(clKrn,0,clMem); const uint offs[ 1 ] = { 0 }; const uint works[ 1 ] = { _divisor }; bool ex=CLExecute(clKrn,1,offs,works); //--- Print( "CL program executed: " + ex ); float buf[]; // type float ArrayResize(buf,_divisor); uint read=CLBufferRead(clMem,buf); Print("read = "+i2s(read)+" elements"); float sum=0.0; // type float for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt]; float pi=float(sum*_step); // type float Print("pi = "+d2s(pi,12)); CLBufferFree(clMem); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); double gone=(GetTickCount()-st)/1000.; Print("OpenCl: gone = "+d2s(gone,3)+" sec."); Print("________________________"); return(0); } //+------------------------------------------------------------------+
A more detailed explanation of the script code will be given a bit later.
In the meantime, compile and start the program to get the following:
2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) ________________________ 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) OpenCl: gone = 5.538 sec. 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) pi = 3.141622066498 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) read = 40000 elements 2012.05.03 02:20:15 OCl_pi_float (EURUSD,H1) FLOAT: _step = 0.000000001000; _intrnCnt = 25000
As can be seen, the runtime has slightly reduced. But this is not enough to make us happy: the value of pi ~ 3.14159265 is obviously accurate only up to the 3rd digit after the decimal point. Such roughness of the calculations is due to the fact that in real calculations the kernel uses float type numbers the accuracy of which is clearly below the required precision accurate to 12 decimal places.
According to MQL5 Documentation, the precision of a float type number is only accurate to 7 significant figures. While the precision of a double type number is accurate to 15 significant figures.
Therefore, we need to make real data type "more accurate". In the above code, the lines where the float type should be replaced with double type are marked with the comment ///type float. After compilation using the same input data, we get the following (new file with the source code - OCL_pi_double.mq5):
2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) OpenCl: gone = 12.480 sec. 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.03 03:25:23 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
The runtime has significantly increased and even exceeded the time of the source code without OpenCL (8.783 sec).
"It is clearly the double type that slows down calculations",- you would think. Yet let us experiment and substantially change the input parameter _divisor from 40000 to 40000000:
2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) OpenCl: gone = 5.070 sec. 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) read = 40000000 elements 2012.05.03 03:26:50 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25
It has not impaired the accuracy and the runtime has got even slightly shorter than in the case with float type. But if we simply change all integer types from long to int and restore the previous value of the _divisor = 40000, the kernel runtime will decrease by over a half:
2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) OpenCl: gone = 2.262 sec. 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.16 00:22:44 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
You should always remember: if there is a quite "long" but "light" loop (i.e. a loop consisting of a lot of iterations every one of each does not have much arithmetic), a mere change in data types from "heavy" ones (long type - 8 bytes) to "light" ones (int - 4 bytes) can drastically decrease the kernel runtime.
Let us now stop our programming experiments for a short while and focus on the meaning of the entire "binding" of the kernel code to get some understanding of what we are doing. By the kernel code "binding" we provisionally mean OpenCL API, i.e. a system of commands allowing the kernel to communicate with the host program (in this case, with the program in MQL5).
3. OpenCL API Functions
3.1. Creating a context
A command given below creates context, i.e. an environment for the management of OpenCL objects and resources.
int clCtx = CLContextCreate( _device );
First, a few words about the platform model.
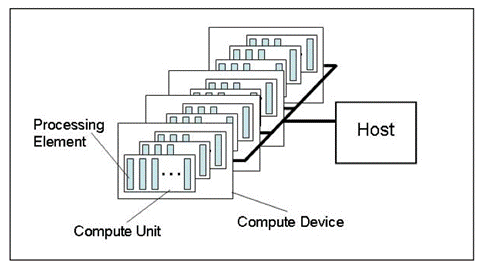
Fig. 1. Abstract model of a computing platform
The figure shows an abstract model of a computing platform. It is not a very detailed depiction of the structure of the hardware with relation to video cards but is fairly close to reality and gives a good general idea.
Host is the main CPU controlling the entire program execution process. It can recognize a few OpenCL devices (Compute Devices). In most cases, when a trader has a video card for calculations available in the system unit, a video card is considered as a device (a dual-processor video card will be considered as two devices!). Besides that, the host per se, i.e. CPU is always considered as an OpenCL device. Every device has its unique number within the platform.
There are several Compute Units in every device that in case with CPU correspond to х86 cores (including the Intel CPU "virtual" cores, i.e. "cores" created via Hyper-threading); for a video card, these would be SIMD Engines, i.e. SIMD cores or mini-processors in terms of the article GPU Computing. AMD/ATI Radeon Architectural Features. Powerful video cards typically have around 20 SIMD cores.
Every SIMD core contains stream processors, e.g. Radeon HD 5870 video card has 16 stream processors in every SIMD Engine.
Finally, every stream processor has 4 or 5 processing elements, i.e. ALU, in the same card.
It should be noted that terminology used by all major graphics vendors for hardware is quite confusing especially for beginners. It is not always obvious what is meant by "bees" so commonly used in a popular forum thread about OpenCL. Nevertheless, the number of threads, i.e. simultaneous threads of computations, in modern video cards is very large. E.g. the estimated number of threads in Radeon HD 5870 video card is over 5 thousand.
The figure below shows standard technical specifications of this video card.

Fig. 2. Radeon HD 5870 GPU features
Everything specified further below (OpenCL resources) should necessarily be associated with the context created by the CLContextCreate() function:
- OpenCL devices, i.e. hardware used in computations;
- Program objects, i.e. program code executing the kernel;
- Kernels, i.e. functions run on the devices;
- Memory objects, i.e. data (e.g. buffers, 2D and 3D images) manipulated by the device;
- Command queues (current implementation of the terminal language does not provide for a respective API).
The context created can be illustrated as an empty field with devices attached to it below.
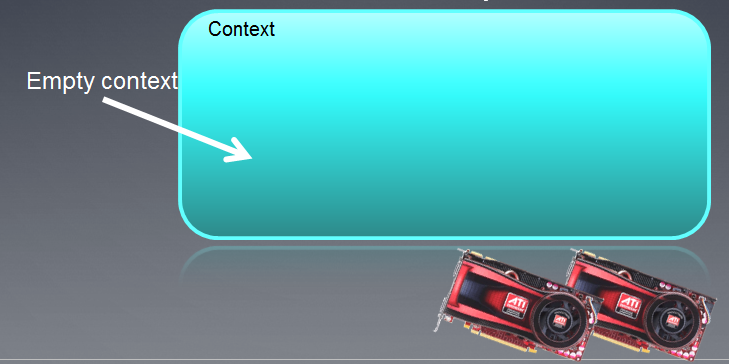
Fig. 3. OpenCL Context
Following the execution of the function, the context field is currently empty.
It should be noted that OpenCL context in MQL5 works with only one device.
3.2. Creating a program
int clPrg = CLProgramCreate( clCtx, clSrc );
The CLProgramCreate() function creates a resource "OpenCL program".
The object "Program" is in fact a collection of OpenCL kernels (that are going to be discussed in the next clause) but in MetaQuotes implementation, there apparently can only be one kernel in the OpenCL program. In order to create the object "Program", you should ensure that the source code (here - clSrc) is read into a string.
In our case it is not necessary as the clSrc string has already been declared as a global variable:

The figure below shows the program being a part of the context created earlier.

Fig. 4. Program is a part of the context
If the program failed to compile, the developer should independently initiate a request for data at the output of the compiler. A fully featured OpenCL API has the API function clGetProgramBuildInfo() after calling which a string is returned at the output of the compiler.
The current version (b.642) does not support this function which should probably be worth being included in OpenCL API to provide an OpenCL developer with more information on the kernel code correctness.
"Tongues" coming from the devices (video cards) are command queues that are apparently not going to be supported in MQL5 on API level.
3.3. Creating a kernel
The CLKernelCreate() function creates an OpenCL resource "Kernel".
int clKrn = CLKernelCreate( clPrg, "pi" );
Kernel is a function declared in the program that is run on the OpenCL device.
In our case, it is the pi() function with the name "pi". The object "kernel" is the function of the kernel together with respective arguments. The second argument in this function is the function name which should be in exact accordance with the function name within the program.

Fig. 5. Kernel
Objects "kernel" can be used as many times as may be necessary when setting different arguments for one and the same function declared as the kernel.
We should now move to the functions CLSetKernelArg() and CLSetKernelArgMem() but let us first say a few words about objects stored in the memory of the devices.
3.4. Memory objects
First of all, we should understand that any "big" object processed on GPU shall first be created in the memory of GPU itself or moved from the host memory (RAM). By a "big" object we mean either a buffer (one-dimensional array) or an image that can be two- or three-dimensional (2D or 3D).
A buffer is a large area of memory containing separate adjacent buffer elements. These may be either simple data types (char, double, float, long, etc.) or complex data types (structures, unions, etc.). Separate buffer elements can be accessed directly, read and written.
We are not going to look into images at the moment as it is a peculiar data type. The code provided by the developers of the terminal on the first page of the thread about OpenCL suggests that the developers did not engage in the use of images.
In the introduced code, the function creating the buffer appears to be as follows:
int clMem = CLBufferCreate( clCtx, _divisor * sizeof( double ), CL_MEM_READ_WRITE );
The first parameter is a context handle with which the OpenCL buffer is associated as a resource; the second parameter is the memory allocated for the buffer; the third parameter shows what can be done with this object. The value returned is a handle to the OpenCL buffer (if successfully created) or -1 (if creation failed due to an error).
In our case, the buffer was created directly in the memory of GPU, i.e. OpenCL device. If it was created in RAM without using this function, it should be moved to the OpenCL device memory (GPU) as illustrated below:
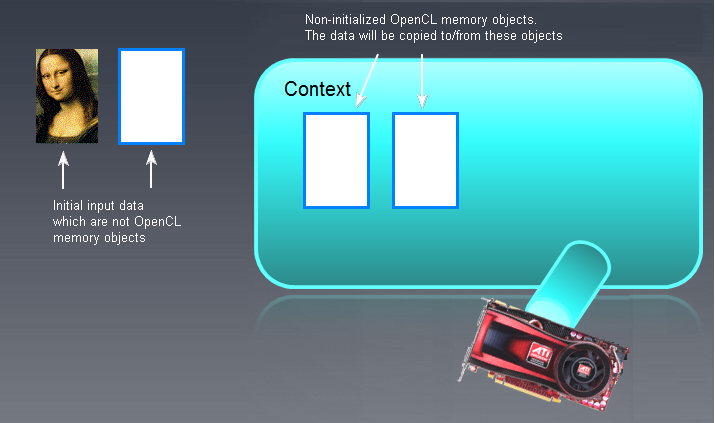
Fig. 6. OpenCL memory objects
Input/output buffers (not necessarily images - the Mona Lisa is here for illustration purposes only!) that are not OpenCL memory objects are shown on the left. Empty, uninitialized OpenCL memory objects are displayed more to the right, in the main context field. The initial data "the Mona Lisa" will subsequently be moved to the OpenCL context field and whatever is output by the OpenCL program will need to be moved back to the left, i.e. into RAM.
The terms used in OpenCL for copying data from/into host/OpenCL device are as follows:
- Copying of data from host into the device memory is called writing (CLBufferWrite() function);
- Copying of data from the device memory into host memory is called reading (CLBufferRead() function, see below).
The write command (host -> device) initializes a memory object by data and at the same time places the object in the device memory.
Bear in mind that the validity of memory objects available in the device is not specified in the OpenCL specification as it depends on the vendor of hardware corresponding to the device. Therefore, be careful when creating memory objects.
After the memory objects have been initialized and written to devices, the picture appears to be something like this:
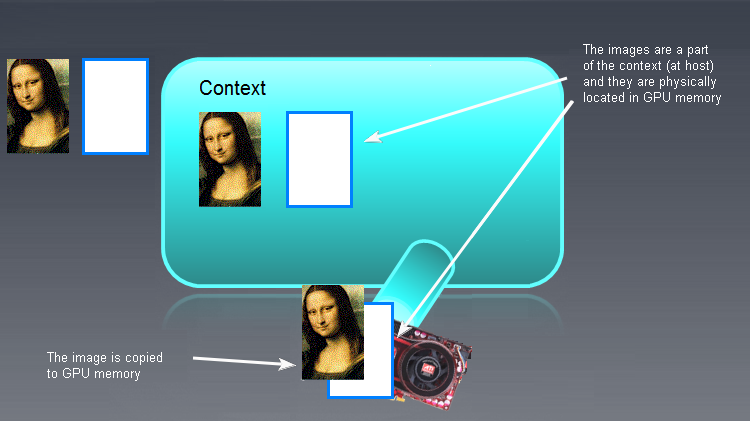
Fig. 7. Result of initialization of the OpenCL memory objects
We can now proceed to functions that set parameters of the kernel.
3.5. Setting parameters of the kernel
CLSetKernelArgMem( clKrn, 0, clMem );
The CLSetKernelArgMem() function defines the buffer created earlier as a zero parameter of the kernel.
If we now take a look at the same parameter in the kernel code, we can see that it appears as follows:
__kernel void pi( __global float *out )
In the kernel, it is the out[ ] array that has the same type as created by the API function CLBufferCreate().
There is a similar function to set non-buffer parameters:
bool CLSetKernelArg( int kernel, // handle to the kernel of the OpenCL program uint arg_index, // OpenCL function argument number void arg_value ); // function argument value
If, for example, we decided to set some double x0 as a second parameter of the kernel, it would first need to be declared and initialized in the MQL5 program:
double x0 = -2;
and the function will then need to be called (also in the MQL5 code):
CLSetKernelArg( cl_krn, 1, x0 );
Following the above manipulations, the picture will be as follows:
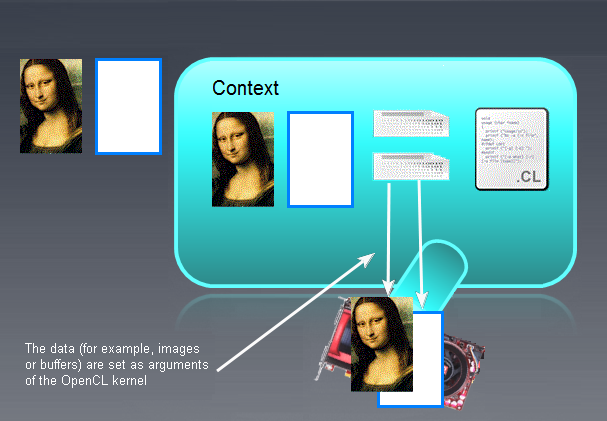
Fig. 8. Results of setting parameters of the kernel
3.6. Program execution
bool ex = CLExecute( clKrn, 1, offs, works );
The author did not find a direct analog of this function in the OpenCL specification. The function executes the kernel clKrn with the given parameters. The last parameter 'works' sets the number of tasks to be executed per every calculation of the computing task. The function demonstrates SPMD (Single Program Multiple Data) principle: one call of the function creates kernel instances with their own parameters in the number equal to the works parameter value; these kernel instances are, conventionally speaking, executed simultaneously but on different stream cores, in AMD terms.
The generality of OpenCL consists in the fact that the language is not bound to the underlying hardware infrastructure involved in the code execution: the coder does not have to know the hardware specifications in order to properly execute an OpenCL program. It will still be executed. Yet it is strongly advisable to know these specifications to improve the efficiency of the code (e.g. speed).
For example, this code is executed just fine on the author's hardware lacking a discrete video card. That said, the author has a very vague idea of the structure of CPU itself where the entire emulation is taking place.
So, the OpenCL program has finally been executed and we can now make use of its results in the host program.
3.7. Reading the output data
Below is a fragment of the host program reading data from the device:
float buf[ ]; ArrayResize( buf, _divisor ); uint read = CLBufferRead( clMem, buf );
Remember that reading data in OpenCL is copying this data from the device into the host. These three lines show how this is done. It will suffice to declare the buf[] buffer of the same type as the read OpenCL buffer in the main program and call the function. The type of the buffer created in the host program (here - in the MQL5 language) can be different from the type of the buffer in the kernel but their sizes shall be an exact match.
The data has now been copied into the host memory and is fully available to us within the main program, i.e. the program in MQL5.
After all the required calculations on the OpenCL device have been made, the memory should be freed from all objects.
3.8. Destruction of all OpenCL objects
This is done using the following commands:
CLBufferFree( clMem ); CLKernelFree( clKrn ); CLProgramFree( clPrg ); CLContextFree( clCtx );
The main peculiarity of these series of functions is that the objects should be destroyed in the order reverse to the order of their creation.
Let us now have a quick look at the kernel code itself.
3.9. Kernel
As can be seen the whole kernel code is one single long string consisting of multiple strings.
The kernel header looks like a standard function:
__kernel void pi( __global float *out )
There are a few requirements to the kernel header:
- The type of a returned value is always void;
- The specifier __kernel does not have to include two underline characters; it can as well be kernel;
- If an argument is an array (buffer), it is passed only by reference. Memory specifier __global (or global) means that this buffer is stored in the device global memory.
- Arguments of simple data types are passed by value.
The body of the kernel is not in any way different from the standard code in C.
Important: the string:
int i = get_global_id( 0 );
means that i is a number of a computational cell within GPU which determines the calculation result within that cell. This result is further written to the output array (in our case, out[]) following which its values are added up in the host program after reading the array from the GPU memory into CPU memory.
It should be noted that there may be more than one function in the OpenCL program code. E.g. a simple inline function situated outside the pi() function can be called inside the "main" kernel function pi(). This case will be considered further.
Now that we have briefly familiarized ourselves with OpenCL API in the MetaQuotes implementation, we can continue experimenting. In this article, the author did not plan to go deep into details of hardware that would allow to optimize the runtime to its maximum. The main task at the moment is to provide a starting point for programming in OpenCL as such.
In other words, the code is rather naive as it does not take into account the hardware specifications. At the same time, it is quite general so that it could be executed on any hardware - CPU, IGP by AMD (GPU integrated into CPU) or a discrete video card by AMD / NVidia.
Before considering further naive optimizations using vector data types, we will first have to familiarize ourselves with them.
4. Vector Data Types
Vector data types are the types specific to OpenCL, setting it apart from C99. Among these are any types of (u)charN, (u)shortN, (u)intN, (u)longN, floatN, where N = {2|3|4|8|16}.
These types are supposed to be used when we know (or assume) that the built-in compiler will manage to additionally parallelize calculations. We need to note here that this is not always the case, even if kernel codes only differ in the value of N and are identical in all other respects (the author could see it for himself).
Below is the list of built-in data types:

Table 1. Built-in vector data types in OpenCL
These types are supported by any device. Each of these types has a corresponding type of API for communication between the kernel and the host program. This is not provided for in the current MQL5 implementation but it is not a big deal.
There are also additional types but they should be explicitly specified in order to be used as they are not supported by every device:

Table 2. Other built-in data types in OpenCL
In addition, there are reserved data types which are yet to be supported in OpenCL. There is quite a long list of them in the language Specification.
To declare a constant or a variable of vector type, you should follow simple, intuitive rules.
A few examples are set forth below:
float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f); uint4 u = ( uint4 ) ( 1 ); /// u is converted to a vector (1, 1, 1, 1). float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) ); float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f ); float4 f = ( float4 ) ( 1.0f, 2.0f ); /// error
As can be seen, it is sufficient to match the data types on the right, put together, with the "width" of the variable declared on the left (here, it is equal to 4). The only exception is the conversion of a scalar to a vector with the components equal to the scalar (line 2).
There is a simple mechanism of addressing vector components for every vector data type. On the one hand, they are vectors (arrays), while on the other they are structures. So, for example the first component of vectors having width 2 (e.g., float2 u) can be addressed as u.x and the second one as u.y.
The three components for a vector of long3 u type will be: u.x, u.y, u.z.
For a vector of float4 u type, those will be, accordingly, .xyzw, i.e. u.x, u.y, u.z, u.w.
float2 pos; pos.x = 1.0f; // valid pos.z = 1.0f; // invalid because pos.z does not exist float3 pos; pos.z = 1.0f; // valid pos.w = 1.0f; // invalid because pos.w does not exist
You can select multiple components at once and even permute them (group notation):
float4 c; c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); c.z = 1.0f; c.xy = ( float2 ) ( 3.0f, 4.0f ); c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f ); float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 swiz= pos.wzyx; // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f ) float4 dup = pos.xxyy; // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )The component group notation, i.e. specification of several components, can occur on the left side of the assignment statement (i.e. l-value):
float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); pos.xw = ( float2 ) ( 5.0f, 6.0f ); // pos = ( 5.0f, 2.0f, 3.0f, 6.0f ) pos.wx = ( float2 ) ( 7.0f, 8.0f ); // pos = ( 8.0f, 2.0f, 3.0f, 7.0f ) pos.xyz = ( float3 ) ( 3.0f, 5.0f, 9.0f ); // pos = ( 3.0f, 5.0f, 9.0f, 4.0f ) pos.xx = ( float2 ) ( 3.0f, 4.0f ); // invalid as 'x' is used twice pos.xy = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // mismatch between float2 and float4 float4 a, b, c, d; float16 x; x = ( float16 ) ( a, b, c, d ); x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw ); x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz ); // invalid as the component a.xxxxxxx is not a valid vector type
Individual components can be accessed using another notation - the letter s (or S) which is inserted before a hexadecimal digit or several digits in a group notation:
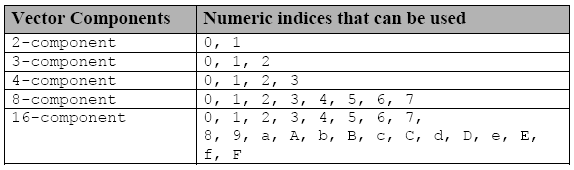
Table 3. Indices that are used to access individual components of vector data types
If you declare a vector variable f
float8 f;then f.s0 is the 1st component of the vector and f.s7 is the 8th component.
Equally, if we declare a 16-dimensional vector x,
float16 x;then x.sa (or x.sA) is the 11th component of the vector x and x.sf (or x.sF) refers to the 16th component of the vector x.
Numeric indices (.s0123456789abcdef) and letter notations (.xyzw) cannot be intermixed in the same identifier with the component group notation:
float4 f, a; a = f.x12w; // invalid as numeric indices are intermixed with the letter notations .xyzw a.xyzw = f.s0123; // valid
And finally, there is yet another way to manipulate vector type components using .lo, .hi, .even, .odd.
These suffixes are used as follows:
- .lo refers to the lower half of a given vector;
- .hi refers to the upper half of a given vector;
- .even refers to all even components of a vector;
- .odd refers to all odd components of a vector.
For example:
float4 vf; float2 low = vf.lo; // vf.xy float2 high = vf.hi; // vf.zw float2 even = vf.even; // vf.xz float2 odd = vf.odd; // vf.yw
This notation can be used repeatedly until a scalar (non-vector data type) appears.
float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f ); float2 s = u.lo.lo; // ( 1.0f, 2.0f ) float2 t = u.hi.lo; // ( 5.0f, 6.0f ) float2 q = u.even.lo; // ( 1.0f, 3.0f ) float r = u.odd.lo.hi; // 4.0f
The situation is slightly more complicated in a 3-component vector type: technically it is a 4-component vector type with the value of the 4th component undefined.
float3 vf = (float3) (1.0f, 2.0f, 3.0f); float2 low = vf.lo; // ( 1.0f, 2.0f ); float2 high = vf.hi; // ( 3.0f, undefined );
Brief rules of arithmetic (+, -, *, /).
All of the specified arithmetic operations are defined for vectors of the same dimension and are done component-wise.
float4 d = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 w = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f ); float4 _sum = d + w; // ( 6.0f, 10.0f, 13.0f, 3.0f ) float4 _mul = d * w; // ( 5.0f, 16.0f, 30.0f, -4.0f ) float4 _div = w / d; // ( 5.0f, 4.0f, 3.333333f, -0.25f )
The only exception is when one of the operands is a scalar and the other is a vector. In this case, the scalar type is cast to the type of data declared in the vector while the scalar itself is converted to a vector with the same dimension as the vector operand. This is followed by an arithmetic operation. The same is true for the relational operators (<, >, <=, >=).
Derived, C99 native data types (e.g., struct, union, arrays and others) that can be made up of the built-in data types listed in the first table of this section are also supported in the OpenCL language.
And the last thing: if you want to use GPU for exact calculations, you will inevitably have to use the double data type and consequently doubleN.
For this purpose, just insert the line:
#pragma OPENCL EXTENSION cl_khr_fp64 : enable
at the beginning of the kernel code.
This information should already be enough to understand much of what follows. Should you have any questions, please see the OpenCL 1.1 Specification.
5. Implementation of the Kernel with Vector Data Types
To be quite honest, the author did not manage to write a working code with vector data types off-hand.
At the beginning, the author did not pay much attention reading the language specification thinking that everything will work out by itself as soon as a vector data type, for example double8, is declared within the kernel. Moreover, the author's attempt to declare only one output array as an array of double8 vectors also failed.
It took a while to realize that this is absolutely not sufficient to effectively vectorize the kernel and achieve real acceleration. The problem will not be solved by outputting results in the vector array as the data does not only require to be quickly input and output but also quickly calculated. The realization of this fact sped up the process and increased its efficiency making it possible to finally develop a much faster code.
But there is more to it than that. While the kernel code set forth above could be debugged almost blindly, looking for errors has now become quite difficult due to the use of vector data. What constructive information can we get from this standard message:
ERR_OPENCL_INVALID_HANDLE - invalid handle to the OpenCL program
or this one
ERR_OPENCL_KERNEL_CREATE - internal error while creating an OpenCL object
?
Therefore, the author had to resort to SDK. In this case, given the hardware configuration available to the author, it happened to be Intel OpenCL SDK Offline Compiler (32 bit) provided in Intel OpenCL SDK (for CPUs/GPUs other than by Intel, SDK should also contain relevant offline compilers). It is convenient because it allows to debug the kernel code without binding to the host API.
You simply insert the kernel code into the compiler window, although not in the form used within the MQL5 code but instead without external quote characters and "\r\n" (carriage return characters) and press the Build button with a gear wheel icon on it.
In so doing, the Build Log window will display information on the Build process and its progress:
Fig. 9. Program compilation in Intel OpenCL SDK Offline Compiler
In order to obtain the kernel code without quote characters, it would be useful to write a simple program in the host language (MQL5) that would output the kernel code into a file - WriteCLProgram(). It is now included in the host program code.
Messages of the compiler are not always very clear but they provide much more information than MQL5 currently can. The errors can immediately be fixed in the compiler window and once you make sure that there are no more of them, the fixes can be transferred to the kernel code in MetaEditor.
And the last thing. The author's initial idea was to develop a vectorized code capable of working with double4, double8 and double16 vectors by way of setting a single global parameter "number of the channels". This was eventually accomplished, after a few days of having a hard time with token-pasting operator ## that, for some reason, was refusing to work within the kernel code.
During this time, the author successfully developed a working code of the script with three kernel codes every one of which is suitable for its dimension - 4, 8 or 16. This intermediate code will not be provided in the article but it was worth mentioning in case you might want to write a kernel code without having too much trouble. The code of this script implementation (OCL_pi_double_several_simple_kernels.mq5) is attached below at the end of the article.
And here is the code of the vectorized kernel:
"/// enable extensions with doubles \r\n" "#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _intrnCnt ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" "#define _CH " + i2s( _ch ) + " \r\n" "#define _DOUBLETYPE double" + i2s( _ch ) + " \r\n" " \r\n" "/// extensions for 4-, 8- and 16- scalar products \r\n" "#define dot4( a, b ) dot( a, b ) \r\n" " \r\n" "inline double dot8( double8 a, double8 b ) \r\n" "{ \r\n" " return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi ); \r\n" "} \r\n" " \r\n" "inline double dot16( double16 a, double16 b ) \r\n" "{ \r\n" " double16 c = a * b; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot4( c.lo.lo + c.lo.hi + c.hi.lo + c.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double16 v16 = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 ); \r\n" " double8 v8 = v16.lo; \r\n" " double4 v4 = v16.lo.lo; \r\n" " double2 v2 = v16.lo.lo.lo; \r\n" " \r\n" " /// all vector-related with the calculated type \r\n" " _DOUBLETYPE in; \r\n" " _DOUBLETYPE xVect; \r\n" " _DOUBLETYPE sumVect = ( _DOUBLETYPE ) ( 0.0 ); \r\n" " _DOUBLETYPE doubleOneVect = ( _DOUBLETYPE ) ( 1.0 ); \r\n" " _DOUBLETYPE doubleCHVect = ( _DOUBLETYPE ) ( _CH + 0. ); \r\n" " _DOUBLETYPE doubleSTEPVect = ( _DOUBLETYPE ) ( _STEP ); \r\n" " \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in = v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j ); \r\n" " xVect = ( in + 0.5 ) * doubleSTEPVect; \r\n" " sumVect += 4.0 / ( xVect * xVect + 1. ); \r\n" " } \r\n" " out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n" "} \r\n";
The external host program has not changed much, except for the new global constant _ch setting the number of "vectorization channels" and the global constant _intrnCnt that has become _ch times smaller. That is why the author decided not to show the host program code here. It can be found in the script file attached below at the end of the article (OCL_pi_double_parallel_straight.mq5).
As can be seen, apart from the "main" function of the kernel pi(), we now have two inline functions that determine scalar product of the vectors dotN( a, b ) and one macro substitution. These functions are involved due to the fact that the dot() function in OpenCL is defined with regard to vectors whose dimension does not exceed 4.
The dot4() macro redefining the dot() function is there only for the convenience of calling the dotN() function with the calculated name:
" out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n"
Had we used the dot() function in its usual form, without index 4, we would not have been able to call it as easily as it is shown here, when _ch = 4 (number of vectorization channels being equal to 4).
This line illustrates another useful feature of the specific kernel form lying in the fact that the kernel as such is treated within the host program as a string: we can use calculated identifiers in the kernel not only for functions but also for data types!
The complete host program code with this kernel is attached below (OCL_pi_double_parallel_straight.mq5).
Running the script with the vector "width" being 16 ( _ch = 16 ), we get the following:
2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) ================================================== 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) CPUtime / GPUtime = 4.130 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The time to calculate PI was 8.830 seconds 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The value of PI is 3.141592653590 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The time to calculate PI was 8.002 seconds 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The value of PI is 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: gone = 2.138 sec. 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: pi = 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) read = 20000 elements 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) CLProgramCreate: unknown error. 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) ==================================================
You can see that even the optimization using vector data types did not make the kernel faster.
But if you run the same code on GPU, the speed gain will be much more considerable.
According to the information provided by MetaDriver (video card - HIS Radeon HD 6930, CPU - AMD Phenom II x6 1100T), the same code yields the following results:
2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) ================================================== 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) CPUtime / GPUtime = 84.983 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The time to calculate PI was 14.617 seconds 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The value of PI is 3.141592653590 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The time to calculate PI was 14.040 seconds 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The value of PI is 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: gone = 0.172 sec. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) read = 20000 elements 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) CLProgramCreate: unknown error. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) ==================================================
6. The Finishing Touch
Here is another kernel (it can be found in the OCL_pi_double_several_simple_kernels.mq5 file attached hereto below which is however not demonstrated here).
The script is an implementation of the idea that the author had when he temporarily abandoned an attempt to write a "single" kernel and thought of writing four simple kernels for different vector dimensions (4, 8, 16, 32), :
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _itInKern ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" " \r\n" "typedef struct \r\n" "{ \r\n" " double16 lo; \r\n" " double16 hi; \r\n" "} double32; \r\n" " \r\n" "inline double32 convert2double32( double a ) \r\n" "{ \r\n" " double32 b; \r\n" " b.lo = ( double16 )( a ); \r\n" " b.hi = ( double16 )( a ); \r\n" " return b; \r\n" "} \r\n" " \r\n" "inline double dot32( double32 a, double32 b ) \r\n" "{ \r\n" " double32 c; \r\n" " c.lo = a.lo * b.lo; \r\n" " c.hi = a.hi * b.hi; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo + c.lo.hi.hi + \r\n" " c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo + c.hi.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double32 _v32; \r\n" " _v32.lo = ( double16 ) ( 0., 1., 2., 3., 4., 5., 6., 7., \r\n" " 8., 9., 10., 11., 12., 13., 14., 15. ); \r\n" " _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23., \r\n" " 24., 25., 26., 27., 28., 29., 30., 31. ); \r\n" " \r\n" " /// all vector-related with undefined type \r\n" " double32 xVect; \r\n" " double32 sumVect = convert2double32( 0.0 ); \r\n" " double32 double1Vect = convert2double32( 1.0 ); \r\n" " \r\n" " double32 in; \r\n" " /// work only with 16-vectors in the loop! \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j ); \r\n" " in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j ); \r\n" " xVect.lo = ( in.lo + 0.5 ) * _STEP; \r\n" " xVect.hi = ( in.hi + 0.5 ) * _STEP; \r\n" " sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. ); \r\n" " sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. ); \r\n" " } \r\n" " out[ i ] = dot32( sumVect, double1Vect ); \r\n" "} \r\n";
This very kernel implements vector dimension 32. The new vector type and a few necessary inline functions are defined outside the main function of the kernel. Besides that (and this is important!), all calculations within the main loop are intentionally made only with standard vector data types; non-standard types are handled outside the loop. This allows to substantially speed up the code execution time.
In our calculation, this kernel does not seem to be slower than when used for vectors with a width of 16, yet it is not much faster either.
According to the information provided by MetaDriver, the script with this kernel (_ch=32) yields the following results:
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec. 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: unknown error or no error. 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; vectorization channels - 32 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================
Summary and Conclusions
The author understands perfectly well that the task chosen for demonstration of the OpenCL resources is not quite typical of this language.
It would have been much easier to take a textbook and crib a standard example of multiplication of large matrices to post it here. That example would obviously be impressive. However, are there many mql5.com forum users who are engaged in financial computations requiring multiplication of large matrices? It is quite doubtful. The author wanted to choose his own example and overcome all difficulties encountered on the way on his own, while at the same time trying to share his experience with others. Of course, you are the ones to judge, dear forum users.
The gain in efficiency on OpenCL emulation (on "bare" CPU) has turned out to be quite small in comparison with hundreds and even thousands obtained using MetaDriver's scripts. But on an adequate GPU, it will be at least an order of magnitude greater than on emulation, even if we ignore a slightly longer runtime on CPU with CPU AMD. OpenCL is still worth learning, even if the gain in computation speed is only that big!
The author's next article is expected to address issues related to peculiarities of displaying OpenCL abstract models on real hardware. The knowledge of these things sometimes allows to further speed up calculations to a considerable extent.
The author would like to express his special thanks to MetaDriver for very valuable programming and performance optimization tips and to the Support Team for the very possibility of using Intel OpenCL SDK.
Contents of the attached files:
- pi.mq5 - a script in pure MQL5 featuring two ways of calculating the "pi" value;
- OCl_pi_float.mq5 - the first implementation of the script with the OpenCL kernel involving real calculations with the float type;
- OCL_pi_double.mq5 - the same, only involving real calculations with the double type;
- OCL_pi_double_several_simple_kernels.mq5 - a script with several specific kernels for various vector "widths" (4, 8, 16, 32);
- OCL_pi_double_parallel_straight.mq5 - a script with a single kernel for some vector "widths" (4, 8, 16).
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/405
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Kernel Density Estimation of the Unknown Probability Density Function
Kernel Density Estimation of the Unknown Probability Density Function
 MetaTrader 5 - More Than You Can Imagine!
MetaTrader 5 - More Than You Can Imagine!
 Get 200 usd for your algorithmic trading article!
Get 200 usd for your algorithmic trading article!
 A Few Tips for First-Time Customers
A Few Tips for First-Time Customers
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article OpenCL: A Bridge to a Parallel World has been released:
By Sceptic Philozoff
OpenCL support is a very good choice, now and in the future of the computing platform heterogeneity is very obvious, but now the same algorithms under the conditions of using OpenCL than CUDA performance is much lower, perhaps CUDA than OpenCL is more underlying, better optimised for its own GPU. NVIDIA's GPUs have better performance, better momentum, and the CUDA compiler has adopted LLVM. NVIDIA's GPU performance is better, the development momentum is better, and CUDA compiler has adopted LLVM, there will be more and more languages to support CUDA, Python can now support, especially CUDA6.0 in the programming ease of use is more prominent, especially Unified Memory technology, in the future, with the CUDA runtime support for automatic data migration is better, the performance of the programme and programming productivity will be better. MQL5 support for OpenCL is a good start, and there may be some things that can be done on CUDA in the future.
Author or experts answer please:
Where will the code below work faster on the main stone or in the vidicon ? And are there any specifics ?
void OnStart()
{
long total= 1000000000;
for(long i=0;i<total;i++)
for(long q=0;q<total;q++)
for(long w=0;w<total;w++)
for(long e=0;e<total;e++)
for(long r=0;r<total;r++)
for(long t=0;t<total;t++)
for(long y=0;y<total;y++)
for(long u=0;u<total;u++)
func(i,q,w,e,r,t,y,u);
}
For example :
Pi = 4*atan(1);
or
Pi = acos(-1);
I don't think that more than 7sec to get the value of PI on 12 decimals is the top efficiency.
I have heard of OpenCV for Python and Machine Learning which can be of use even in highly psychological field which is trading but never of OpenCL. On these grounds, there is a nice interface environment which is ZeroMQ today. Well, I guess that communication between platform MTx and Python environment can take the bit of time especially if there is a lot of data that must pass through.
Thanks for the article indeed.