ディープニューラルネットワーク(その8)バギングアンサンブルの分類品質の向上
MetaTrader 5
—
トレーディング
| 19 11月 2018, 13:06
456
1
内容
- はじめに
- 初期データの準備
- pretrainサブセットでのノイズサンプルの処理
- ノイズが除去された初期データに関するニューラルネットワーク分類器のアンサンブルの訓練と、テストサブセットでのニューラルネットワーク連続予測の計算
- 得られた連続予測の閾値の特定、クラスラベルへの変換、ニューラルネットワークメトリックの計算
- アンサンブルのテスト
- ニューラルネットワーク分類器アンサンブルハイパーパラメータの最適化
- 処理後パラメータの最適化
- 複数の最良アンサンブルと出力のスーパーアンサンブルへの結合
- 実験結果の分析
- 終わりに
- 添付ファイル
はじめに
これまでの2つの記事(1、2)では、ELMニューラルネットワーク分類器のアンサンブルを作成しまし、分類品質をどのように改善できるかを議論しました。多くの解決策が可能な中で、ノイズサンプルの影響を減らし、最適な閾値を選択するという2つが選択されました。これによって、アンサンブルのニューラルネットワークの連続予測がクラスラベルに変換されます。本稿では、分類品質が以下によってどのように影響を受けるかを実験的に調べることを提案します。
- データノイズ除去法
- 閾値の種類
- アンサンブルのニューラルネットワークと後処理のハイパーパラメータの最適化
次いで、分類の平均化によって得られた品質と最適化結果に続いた最良のアンサンブルからなるスーパーアンサンブルの単純多数決によって得られた品質とを比較します。すべての計算はR 3.4.4環境で実行されます。
1. 初期データの準備
初期データの準備には前に説明したスクリプトを使用します。
1番目のブロック(ライブラリ)で必要なライブラリと関数を読み込みます。
2番目のブロック(準備)では、端末から渡されたタイムスタンプ付きの相場を使用して、指標値(この場合はデジタルフィルタ)とOHLCに基づく追加変数を計算します。このデータセットをデータフレームdtに結合します。次に、これらのデータの外れ値のパラメータを定義し、それらを補完します。次に、正規化パラメータを定義し、データを正規化します。入力データの結果セットDTcap.nが得られます。
3番目のブロック(データX1)では、下記の2つのセットを生成します。
- data1 — DataタイムスタンプとClass目標を持つすべての13指標を含む
- X1 — 同じ予測変数のセット(タイムスタンプなし)。目標は数値(0、1)に変換される。
4番目のブロック(データX2)でも2つのセットを生成します。
- data2 — 7つの予測変数(Data、CO、HO、LO、HL、dC、dH、dL)とタイムスタンプ
- Х2 — 同じ予測変数のセット(タイムスタンプなし)
#--1--ライブラリ------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-準備---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-データX1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-データ-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
5番目のブロック(bestF)では、Х1セットの予測変数を重要度の昇順で並べ替え(orderX1)、係数が0.5以上のものを選択します(featureX1)。選択した予測変数の係数と名前を出力します。
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
2番目のデータセットХ2でも同じ計算を行い、orderX2とfeatureX2を得ます。
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"
これで実験の初期データの作成は完了です。重要度で並び替えられた2つのデータセットX1/data1、X2/data2と予測変数orderX1、orderX2が用意されました。上記のスクリプトはすべてPrepare_VIII.Rファイルにあります。
2. pretrainサブセットでのノイズサンプルの処理
私自身を含む多くの著者は、ノイズ予測変数フィルタリングの研究に専念してきました。ここでは、データセット内のノイズサンプルの識別と処理という、等しく重要であってもあまり使用されていない別の機能を探求することを提案します。質問は、データセットのいくつかの例が何故ノイズとみなされ、それらを処理するためにどのような方法が使用されるかということでしょう。ここで説明を試みます。
分類の課題に直面している一方、予測変数と目標の訓練セットは既にあります。目標は訓練セットの内部構造によく対応すると考えられます。しかし実際には、予測変数セットのデータ構造は、提案されている目標の構造よりはるかに複雑です。セットには目標によく対応するサンプルが含まれていますが、中にはまったく対応しないものもあり、学習時にモデルを大きく歪ませています。結果として、これはモデル分類の質の低下につながります。ノイズサンプルを特定して処理するアプローチは既に検討されています。ここでは、3つの処理方法によってどのように分類品質が影響を受けるかを確認します。
- 誤ってラベル付けされた例の修正
- セットからの除去
- 別のクラスへの割り当て
ノイズサンプルはNoiseFiltersR::GE()関数を使用して識別及び処理されます。これは、ノイズサンプルを探し、ラベルを修正します(誤ったラベリングを修正します)。ラベルを変更できない例は削除されます。特定されたノイズサンプルは、手動でセットから削除することも、別のクラスに移動して新しいラベルを割り当てることもできます。上記のすべての計算は、アンサンブルを訓練するために使用されるため、「pretrain」サブセットで実行されます。関数の結果を参照してください。
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameters:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
.......
以下はout関数の出力構造体です。
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
ここで
- out$cleanData — ノイズサンプルのラベリングを修正した後のデータセット
- out$remIdx — 除去されたサンプルのインデックス(例ではなし)
- out$repIdx — 目標が再ラベル付けされたサンプルのインデックス
- out$repLab — これらのノイズサンプルの新しいラベル。したがって、out$repIdxを使用して、それらをセットから削除したり、新しいラベルを割り当てることができます。
ノイズサンプルのインデックスが決まったら、denoiseX1pretrain構造体に結合されたアンサンブルを訓練するための4つのデータセットを準備します。
- denoiseX1pretrain$origin — 元のpretrainingセット
- denoiseX1pretrain$repaired — ノイズサンプルのラベリングを修正したデータセット
- denoiseX1pretrain$removed — ノイズサンプルを削除したデータセット
- denoiseX1pretrain$relabeled — 新しいラベルが割り当てられたノイズサンプルを含むデータセット(すなわち、目標は現在3つのクラスを有する)
#--2-データXrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env)
サブセットdenoiseX1pretrain$origin|repaired|relabeledには同一の予測変数хがありますが、目標уはセットごとに違います。構造をみてみましょう。
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
セットdenoiseX1pretrain$removedのサンプル数が変更されているため、予測変数の重要性がどのように変更されたかを確認します。
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci"
最良の予測変数の順序と構成が変更されました。アンサンブルを訓練するときはこれを考慮する必要があります。
よって、denoiseX1pretrain$origin、repaired、removed、relabeledの4つのサブセットが用意されています。これらはELMアンサンブルを訓練するために使用されます。データをのノイズを除去するためのスクリプトはDenoise.Rファイルにあります。初期データХ1とdenoiseX1pretrainの構造は次のようになります。
図1 初期データの構造
3. ノイズが除去された初期データに関するニューラルネットワーク分類器のアンサンブルの訓練と、テストサブセットでのニューラルネットワーク連続予測の計算
アンサンブルを訓練し、スタッキングアンサンブルの訓練可能な結合器の入力データとして後で機能する予測を受け取る関数を記述しましょう。
このような計算は既に前の記事で行われているので、詳細は説明しません。概要すると、
- ブロック1(Input)で、定数を定義する
- ブロック2(createEns)で、一定のパラメータと再現可能な初期化を備えた個々のニューラルネットワーク分類器のアンサンブルを作成する関数CreateEns()を定義する。
- ブロック3(GetInputData)でGetInputData()関数がアンサンブルEnsを使って3つのサブセットХ1$ train/test/test1を計算する
#--1--入力------------- evalq({ #活性化関数の種類 Fact <- c("sig", #: シグモイド "sin", #: 正弦 "radbas", #: 放射基底関数 "hardlim", #: ハードリミット "hardlims", #: 対称ハードリミット "satlins", #: satlins "tansig", #: 接線シグモイド "tribas", #: 三角基底関数 "poslin", #: 正の線形 "purelin") #: 線形 n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #--- アンサンブルを作成する--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---アンサンブルを作成する--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---予測-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---予測--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---予測--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---結果------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
訓練アンサンブルのためには、既に4グループ(オリジナル(origin),、訂正されたラベル(repaired)、ノイズサンプル削除済み(removed)、ノイズサンプル再ラベル付け(relabeled))のデータを持つdenoiseX1pretrainセットがあります。これらのデータ群のそれぞれについてアンサンブルを訓練した後、4つのアンサンブルが得られます。GetInputData()関数でこれらのアンサンブルを使用して、train、test、test1の3つのサブセットで4つの予測グループを取得します。以下は、展開された形式のアンサンブルごとの別々のスクリプトです(デバッグと理解の容易さのためだけです)。
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
アンサンブル予測結果の構造を以下に示します。
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
これらの出力/入力の分布がどのように見えるかを見てみましょう。InputTrain[ ,1:10]セットの初めの10つの出力を見ましょう。
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
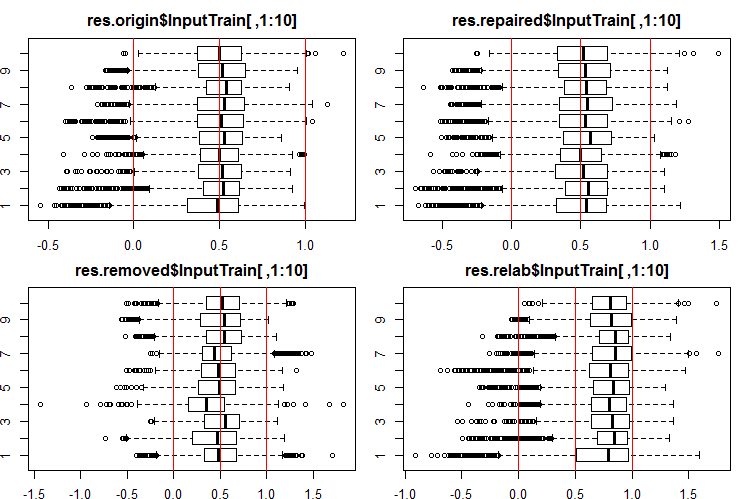
図2 4つの異なるアンサンブルを使用したInputTrain出力の予測の分布
InputTest[ ,1:10]セットの初めの10つの出力を見ましょう。
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
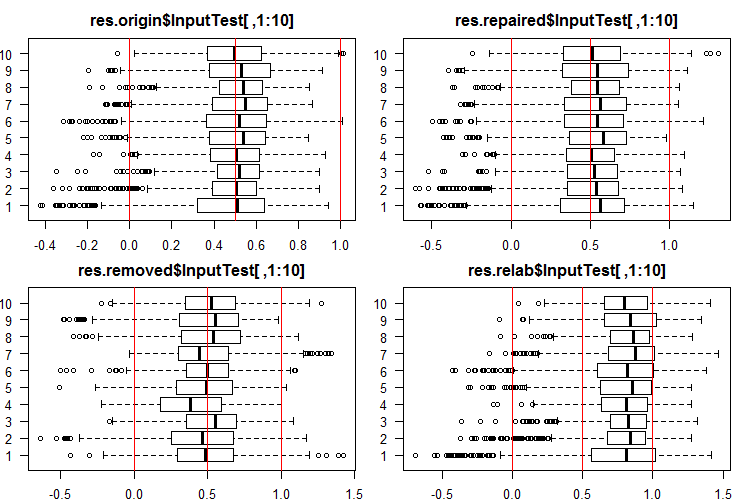
図3 4つの異なるアンサンブルを使用したInputTest出力の予測の分布
InputTest1[ ,1:10]セットの初めの10つの出力を見ましょう。
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
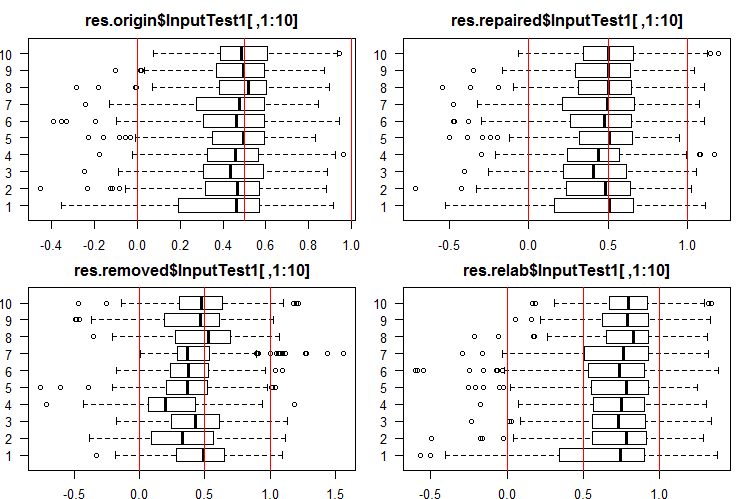
図4 4つの異なるアンサンブルを使用したInputTest1出力の予測の分布
予測の分布はすべて、以前の実験のSpatialSignメソッドで正規化したデータから得られた予測とは大きく異なります。ご自分でも異なる正規化方法をお試しになれます。
各アンサンブルを使用してサブセットX1$train/test/test1の予測を計算すると、図2 - 4に示すような分布を持つ4つのデータ群(res.origin、res.repaired、res.removed、res.relab)が得られます。
連続予測をクラスラベルに変換し、各アンサンブルの分類品質を決定しましょう。
4. 得られた連続予測の閾値の特定、クラスラベルへの変換、ニューラルネットワークメトリックの計算
連続データをクラスラベルに変換するには、これらのクラスへの分割の1つまたは複数の閾値が使用されます。すべてのアンサンブルの5番目のニューラルネットワークから得られたInputTrainセットの連続予測は次のようになります。
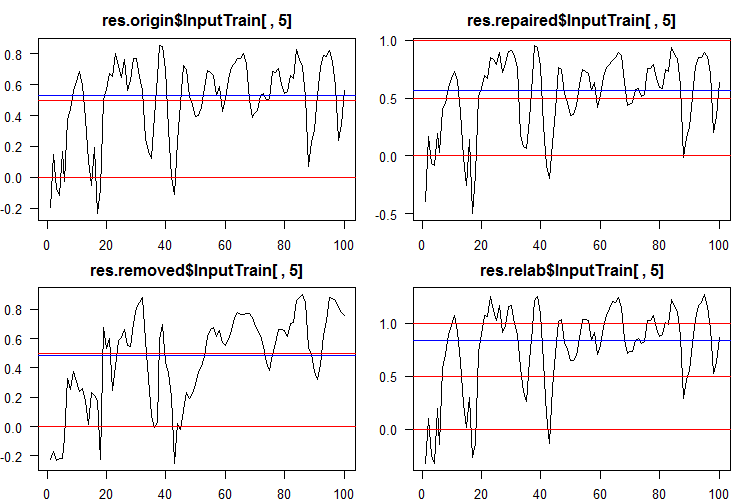
図5 様々なアンサンブルの第5ニューラルネットワークの連続予測
ご覧のとおり、origin、repaired、relabeledモデルの連続予測のグラフは、形状は似ていますが、範囲が異なります。removedモデルの予測の線は、かなり異なっています。
後続の計算を簡素化するために、すべてのモデルとその予測を1つの構造体predX1で収集します。これを行うには、ループ内ですべての計算を繰り返すコンパクトな関数を記述します。下記はスクリプトとpredX1の構造の画像です。
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env)
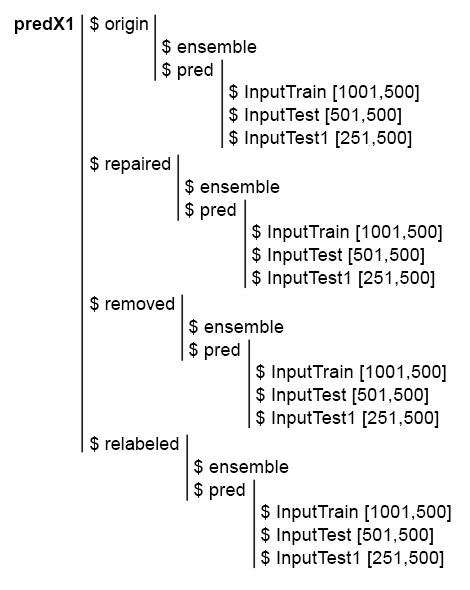
図6 predX1セットの構造
アンサンブルの予測品質のメトリックを得るには、刈り込みと平均化(または単純多数決)の2つの操作が必要です。刈り込みを行うには、アンサンブルのすべてのニューラルネットワークのすべての出力を連続形式からクラスラベルに変換する必要があります。次に、各ニューラルネットワークのメトリックを定義し、最良のスコアでそれらの特定の数を選択します。次に、これらの最良のニューラルネットワークの連続予測を平均して、アンサンブルの連続平均予測を得ます。もう一度、閾値を定義し、平均化された予測をクラスラベルに変換し、アンサンブルの分類品質の最終スコアを計算します。
従って、連続予測をクラスラベルに2回変換する必要があります。これら2つの段階での変換閾値は、同じであっても異なっていてもかまいません。どのような種類の閾値を使用できるのでしょうか。
- デフォルト閾値(ここでは0.5)
- 中央値に等しい閾値。私はこれの信頼性がより高いと思います。しかし中央値は検証セットでのみ決定できる一方、後続のサブセットをテストする場合にのみ適用できます。たとえば、InputTrainサブセットで閾値を定義し、これはInputTest及びInputTest1サブセットで後に使用されます。
- さまざまな基準に合わせて最適化された閾値。 例えば、最小分類誤差、最大精度「1」、または「0」などとすることができます。最適閾値は、常にInputTrainサブセットで決定され、InputTestとInputTest1サブセットで使用されます。
- 最良のニューラルネットワークの出力を平均するときには較正を使用することができます。一部の著者は、較正された出力のみを平均化できると書いています。この主張を確認することは、本稿の範囲を超えています。
最適な閾値は、InformationValue::optimalCutoff()関数を使用して決定されます。詳細はパッケージに記載されています。
ポイント1及び2の閾値を決定するには、追加の計算は必要ありません。ポイント3の最適な閾値を計算するには、関数GetThreshold()を記述します。
#--関数------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
この関数で説明されている最初の4種類の閾値(half、med、mce、both)のみが計算されます。最初の2つは、半分と中央値の閾値です。mce閾値は、最小分類エラーを提供します。both閾値は係数youdensIndex = (sensitivity + specificity —1)の最大値を提供します。計算の順序は次のようになります。
1. predX1セットでは、InputTrainサブセットでアンサンブルの500個のニューラルネットワークのそれぞれの4種類の閾値を計算します。これは各データ群(origin 、repaired、removed、relabeled)で別々に行われます。
2. 次に、これらの閾値を使用して、すべてのサブセット(train/test/test1) iのすべてのニューラルネットワークアンサンブルの連続予測をクラスに変換し、平均値F1を決定します。それぞれ3つのサブセットを含む4つのメトリックグループが得られます。以下は、 originグループのステップごとのスクリプトです。
predX1$origin$pred$InputTrainサブセットに4種類の閾値を定義します。
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env)
各計算で2つのネストループを使用します。外部ループでは、閾値タイプを選択し、クラスタを作成し、計算を4つのコアに並列化します。内部ループでは、アンサンブルを構成する500個のニューラルネットワークのそれぞれのInputTrain予測を反復処理します。それぞれに4種類の閾値が定義されています。得られたデータの構造は次のようになります。
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
得られた閾値を使用して、サブセット train、test 、test1のoriginグループの連続予測をクラスラベルに変換し、メトリック(mean(F1))を計算します。
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)
originグループと3つのサブセットのメトリックの分布を参照してください。下のスクリプトはoriginグループ用です。
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
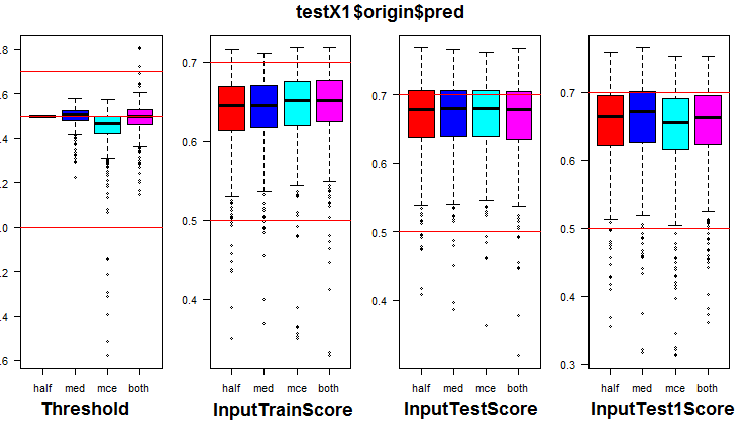
図7 originグループ内の閾値及びメトリックの分布<
視覚化によって、origin データ群の閾値として「med」を使用しても「half」の閾値と比較して目に見える品質の向上は得られないことが示されました。
すべてのグループで4種類の閾値をすべて計算します(かなりの時間とメモリが必要です)。
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
取得した閾値を使用して、すべてのグループとサブセットのメトリックを計算します。
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
各データ群に対して、アンサンブルの500個のニューラルネットワークそれぞれのメトリックを3つのサブセットに4つの異なる閾値を追加しました。
各グループとサブセットでどのようにメトリックが分布しているかを見てみましょう。スクリプトは、repairedサブセット用に提供されています。他のグループでも同様で、グループ番号のみが変更されます。わかりやすくするために、すべてのグループのグラフを1つに示します。
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
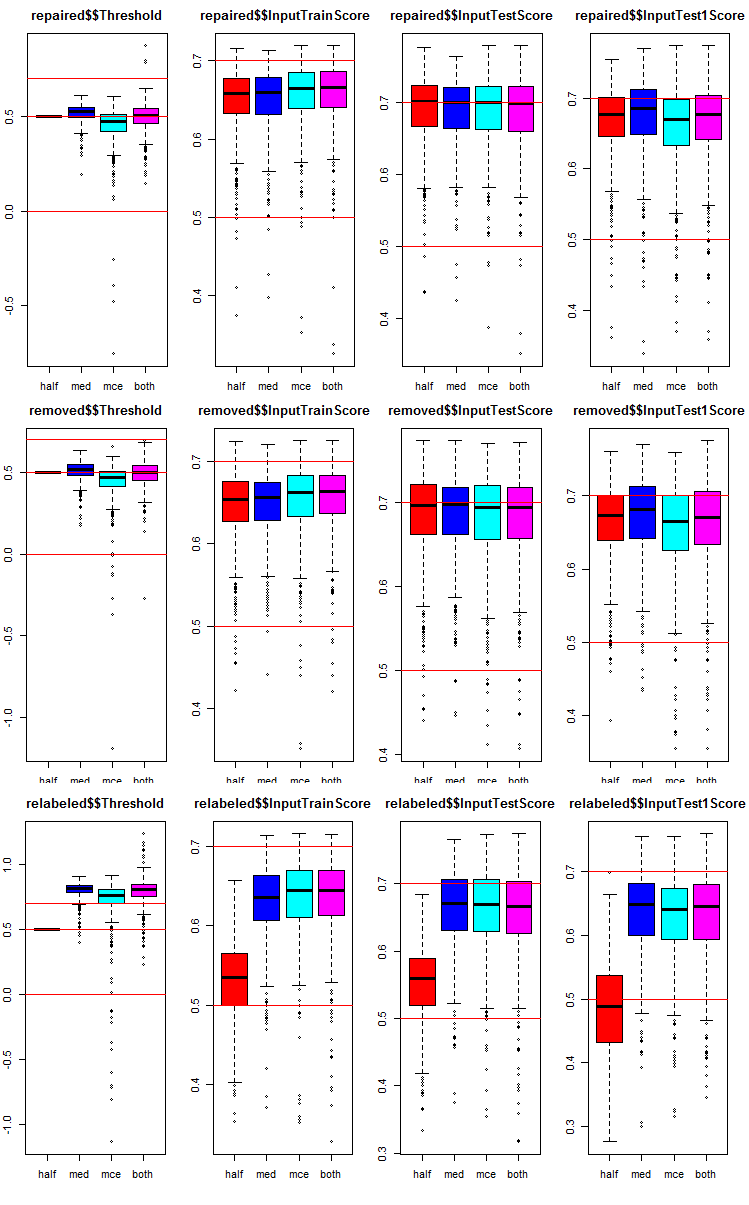
図8 3つのサブセットと4つの異なる閾値を持つ3つのデータ群におけるアンサンブルの各ニューラルネットワークの予測メトリックの分布グラフ
下記はすべてのグループに共通です。
- テストセットのメトリック(InputTestScore) は、検証セットのメトリック(InputTrainScore)よりも優れている
- 2番目のテストサブセットのメトリック(InputTest1Score) は、1番目のテストサブセットのメトリックよりも著しく劣っている
- 「half」型の閾値の結果は、「relabeled」型を除いたすべてのサブセットで他のものより悪くない
5. アンサンブルのテスト
5.1. InputTrainサブセット内の各アンサンブルと各データ群で最良のメトリックを持つ7つのニューラルネットワークの決定
刈り込みを実行します。testX1サブセットの各データ群では、平均F1の最大値を持つ7つのInputTrainScore値を選択する必要があります。それらのインデックスは、アンサンブル内の最良のニューラルネットワークのインデックスになります。スクリプトは以下の通りで、Test.Rファイルにもあります。
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
4つのデータ群(origin、repaired、removed、relabeled)で最良スコアを有するニューラルネットワークのインデックスを取得しました。それらを詳しく見て、これらの最良のニューラルネットワークがデータのグループと閾値タイプによってどのくらい異なるかを比較しましょう。
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
「mce」と「both」の両方のタイプのニューラルネットワークのインデックスが頻繁に一致することがわかります。
5.2. これら7つの最良のニューラルネットワークの連続予測の平均化
7つの最良のニューラルネットワークを選択した後、サブセットInputTrain、InputTest、InputTest1、及び各閾値タイプによってデータの各グループ内で平均します。以下は InputTrainサブセットを4つのグループで処理するためのスクリプトです。
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
データ群repairedで得られた平均連続予測の構造と統計スコアを見てみましょう。
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
最後の2つの閾値タイプの統計はここでも同じです。残りの2つのサブセットInputTest、InputTest1のスクリプトは次のとおりです。
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
repairedデータ群のInputTestサブセットの統計を見てみましょう。
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
最後の2つの閾値タイプの統計はここでも同じです。
5.3. 平均化された連続予測の閾値の定義
今度は、各アンサンブルの平均予測を行います。すべてのデータ群と閾値タイプについて、クラスラベルと品質の最終メトリックに変換する必要があります。これを行うには、前の計算と同様に、InputTrainサブセットのみを使用して最良の閾値を決定します。以下のスクリプトは、各グループと各サブセットの閾値を計算します。
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. アンサンブルの平均予測のクラスラベルへの変換と、すべてのデータ群のInputTrain、InputTest、InputTest1サブセットでのアンサンブルのメトリックの計算
上記で計算されたth_averの閾値を使用して、メトリックを決定します。
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
要約表を作成し、得られたメトリックを分析します。originグループから始めましょう(ノイズサンプルは未処理)。TestScoreとTest1Scoreのスコアを探します。TestTrainサブセットのスコアは指標であり、テストスコアとの比較に必要です。
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
提案された表は何を示すのでしょうか。
TestScoreの0.750という最良の結果は、両方の変換(刈り込みと平均化の両方)に「half」閾値を持つバリアントによって示されました。ただし、 Test1Scoreサブセットの品質は0.735に低下します。
両方のサブセットで約0.745のより安定した結果が、刈り込み時には閾値変形(med、mce,both)、平均化時にはmedで表示されます。
次のデータ群repaired(ノイズサンプルの訂正されたラベル付き)をご覧ください。
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
最良の結果はhalf/halfの組み合わせで示され、0.759です。両方のサブセットで〜0.750のより安定した結果が、刈り込みの際の閾値変形(half、med、mce、both)によって示され、平均化されるときにmedが示されます。
次のデータ群removedをご覧ください(ノイズサンプルをセットから削除)。
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
表を分析します。TestScoreの0.769という最良の結果は、med/half閾値を持つバリアントによって示されました。ただし、 Test1Scoreサブセットの品質は0.732に低下します。TestScoreサブセットでは、刈り込み閾値(half、med、mce、both)と、平均化閾値halfが最高の組み合わせで、すべてのグループの中で最高のスコアを生成します。
最後のデータ群relabeledをご覧ください(ノイズサンプルを別クラスに分離)
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
このグループの最良の結果は、刈り込み時には(med、mce、both)、平均化時には両方またはmedである以下の閾値の組み合わせによって生成されます。
値は異なる可能性があることに留意してください。
下の図は、上記の計算をすべて行った後のtestX1のデータ構造を示しています。
図9 testX1のデータ構造体
6. ニューラルネットワーク分類器アンサンブルハイパーパラメータの最適化
これまでの計算はすべて、個人的経験に基づいて設定されたニューラルネットワークの同じハイパーパラメータを持つアンサンブルで実行されています。ご存知のように、他のモデルと同様に、ニューラルネットワークのハイパーパラメータは、より良い結果を得るために特定のデータセットに対して最適化する必要があります。訓練には、ノイズを除去したデータを4つのグループ (origin、repaired、removed、 relabeled)に分けて使います。したがって、これらの集合に対してアンサンブルのニューラルネットワークの最適なハイパーパラメータを正確に得る必要があります。ベイズ最適化に関するすべての質問は前回の記事で徹底的に議論されているので、その詳細はここでは考慮しません。
ニューラルネットワークの4つのハイパーパラメータが最適化されます。
- 予測変数数numFeature = c(3L, 13L)の値は3～13
- 訓練で使用されるサンプルのパーセンテージr = c(1L, 10L)の値は10～100％
- 隠れ層のニューロン数nh = c(1L, 51L)の値は1～51
- アクティベーション関数のタイプは、 Fact活性化関数のリストのインデックスfact = c(1L, 10L)
定数を設定します。
##===OPTIM=============================== evalq({ #活性化関数の種類 Fact <- c("sig", #: シグモイド "sin", #: 正弦 "radbas", #: 放射基底関数 "hardlim", #: ハードリミット "hardlims", #: 対称ハードリミット "satlins", #: satlins "tansig", #: 接線シグモイド "tribas", #: 三角基底関数 "poslin", #: 正の線形 "purelin") #: 線形 bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
品質指標Score = meаn(F1)とクラスラベルのアンサンブル予測を返す適合関数を記述します。刈り込み(アンサンブルにおける最良のニューラルネットワークの選択)と連続予測の平均化は、同じ閾値= 0.5を用いて行われます。それは、最初の近似のために、以前は非常に良い選択肢だったことが判明しました。下記がスクリプトです。
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
コメントアウトされたSEED変数には値が2つあります。これは、このパラメータが結果に及ぼす影響を実験的に確認するのに必要です。私はSEEDの2つの異なる値で、同じ初期データとパラメータで最適化を実行しました。最良の結果はSEED = 1235809でみられました。この値は、以下のスクリプトで使用されます。しかし、得られたハイパーパラメータ及び分類品質スコアは、SEEDの両方の値に対して提供されます。他の値もお試しください。
適合関数が機能しているかどうかとその計算の1回のパスがどれくらい時間がかかるかを確認し、結果をみましょう。
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741
以下は、ノイズを除去したデータ群ごとにニューラルネットワークのハイパーパラメータを連続的に最適化するためのスクリプトです。初期ランダム初期化の20ポイントを使用し、20回反復します。
#---Optimアンサンブル----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
スクリプトの実行を開始したら、およそ30分(ハードウェアによって異なります)待ちます。得られたスコア値を降順で並べ替え、3つのスコア値を選択します。これらのスコアはbest.res(SEED = 12345)及びbest.res1(SEED = 1235809)変数に割り当てられます。
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env)
best.resスコアを見てください。
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
次はbest.res1スコアです。
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
ご覧の通り、これらの結果はより良好です。最初の3つの結果ではなく10の違いを出力すると、違いはさらに顕著になります。
最適化を実行するたびに、異なるハイパーパラメータ値と結果が生成されます。ハイパーパラメータは、さまざまな初期RNG設定を使用して、また特定の開始初期化を使用して最適化することができます。
4つのデータ群についてアンサンブルのニューラルネットワークの最良のハイパーパラメータを収集しましょう。後で最適なハイパーパラメータでアンサンブルを作成するために必要になります。
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)
The hyperparameters:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
すべてのスクリプトはOptim_VIII.R fileにあります。
7. 処理後ハイパーパラメータ(刈り込みと平均化のための閾値)の最適化
ニューラルネットワークのハイパーパラメータの最適化は、分類品質にわずかな増加をもたらします。前述のように、刈り込みと平均化の際の閾値タイプの組み合わせは、分類品質に強い影響を与えます。
既に、half/half閾値の一定の組み合わせで、ハイパーパラメータを最適化しています。多分、この組み合わせは最適ではありません。さらに最適化された2つのパラメータ(アンサンブルを刈り込むときの閾値タイプ(最適なニューラルネットワークを選択する)であるth1 = c(1L, 2L)、アンサンブルの平均予測をクラスラベルに変換するときの閾値タイプであるth2 = c(1L, 4L) )を使用して最適化を繰り返します。最適化するハイパーパラメータの定数と値の範囲を定義します。
##===OPTIM=============================== evalq({ #活性化関数の種類 Fact <- c("sig", #: シグモイド "sin", #: 正弦 "radbas", #: 放射基底関数 "hardlim", #: ハードリミット "hardlims", #: 対称ハードリミット "satlins", #: satlins "tansig", #: 接線シグモイド "tribas", #: 三角基底関数 "poslin", #: 正の線形 "purelin") #: 線形 bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
次は適合関数についてです。これはわずかに修正され、2つの仮パラメータth1、th2が追加されました。関数本体とbestブロックで、th1に応じて閾値を計算します。test-averageブロックで、閾値タイプth2に応じてGetThreshold()関数を使用して閾値を決定します。
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
この関数の反復に時間がどれくらいかかるか確認します。
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
関数の実行時間はあまり変わっていません。その後、最適化を実行し、結果を待ちます。
#---Optimアンサンブル----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
各データ群に対して得られた10の最適なハイパーパラメータを選択します。
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758
品質に若干の改善があります。各データ群の最良のハイパーパラメータは、以前の閾値の組み合わせを考慮しない最適化で得られたハイパーパラメータとは異なります。最高の品質スコアは、ノイズサンプルが再ラベル付けされた(repaired)または除去された(removed) データ群によって示されます。
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
このセクションで使用されたスクリプトはすべてOptim_mVIII.Rファイルにあります。
8. 複数の最良アンサンブルと出力のスーパーアンサンブルへの結合
いくつかの最高のアンサンブルを組み合わせてスーパーアンサンブルとし、それらの出力を単純多数決でカスケードします。
まず、最適化の間に得られたいくつかの最良アンサンブルの結果を組み合わせます。最適化の後、関数は最良のハイパーパラメータだけでなく、すべての反復でクラスラベル内の予測の履歴も返します。各データ群の5つのベストアンサンブルからスーパーアンサンブルを生成し、単純多数決を使用して、そのバリエーションで分類品質スコアが向上するかどうかを確認します。
計算は次の順序で実行されます。
- ループ内の4つのデータ群を順番に繰り返す
- 各データ群内の5つの最良予測のインデックスを決定します。
- これらのインデックスとの予測をデータフレームに結合します。
- すべての予測でクラスラベルを「0」から「-1」に変更します。
- これらの予測を行ごとに合計します。
- これらの合計値を、条件に従ってクラスラベル(-1,0,1)に変換します。値が3より大きい場合はclass = 1、-3より小さい場合はclass = -1、それ以外の場合はclass = 0にします。
これらの計算を実行するスクリプトは次のとおりです。
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env)
追加の第3のクラス「0」があります。「-1」の場合は「売り」、「1」の場合は「買物」、「0」の場合は「わからない」です。エキスパートアドバイザーがこのシグナルにどのように反応するかは、ユーザーの責任です。それは市場から離れても、市場に出ていても何もしないで、新しい行動を促すのを待つことができます。エキスパートをテストするときは、ビヘイビアモデルを構築して確認する必要があります。
メトリックを取得するには、次のことが必要です。
- ループ内の各データ群を順次反復する
- ターゲットYtest1の実際の値では「0」クラスラベルをラベル「-1」で置き換える
- 上記で得られた実際のターゲットprVotと予測されたターゲットprVotとをデータフレームに結合する
- データフレームからprVot = 0の値を持つ行を削除する
- メトリックを計算する
計算して結果を見ます。
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#---------------------------------------
すべてのグループで品質が大幅に向上しました。最良のバランス精度はremoved(0.8227)とrepaired(0.8209)のグループで得られました。
単純な多数決を使ってグループの予測を組み合わせます。結合をカスケード式に実行します。
- ループ内のすべてのデータ群を反復処理する
- 最良の結果を持つパスのインデックスを決定する
- これらのベストパスの予測を選択する
- 各列で、クラスラベル「0」をラベル 「-1」に置き換える
- グループの予測を行ごとに合計する
結果をご覧ください。
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209
投票の最大値のみを残し、メトリックを計算します。
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1
これは、バランスのとれた精度= 0.8362という非常に優れたスコアをもたらしました。
このセクションで説明するスクリプトはVoting.Rファイルにあります。
しかし、1つのことを忘れてはなりません。ハイパーパラメータを最適化するときは、InputTestテストセットを使用しました。つまり、次のテストセットInputTest1で作業を開始できます。カスケード式にアンサンブルを組み合わせると、ハイパーパラメータの最適化なしに同じ正の効果を生み出す可能性が最も高いです。先に得られた平均結果を確認してください。
セクション5.2で得られたアンサンブルの平均出力を結合します。
1つの変更でセクション5.4で説明した計算を再現します。連続平均予測をクラスラベルに変換するとき、これらのラベルは[-1、0、1]になります。各サブセットtrain/test/test1の計算順序は次のとおりです。
- ループ内の4つのデータ群を順番に繰り返す
- 4タイプの刈り込み閾値による
- 4タイプの平均化閾値による
- アンサンブルの連続平均予測をクラスラベル[-1,1]に変換する
- 4種類の平均化閾値でそれらを合計する
- 新しいラベル[-1、0、1]で合計したラベルを付け直す
- 得られた結果をVotAver構造体に追加する
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
サブセットとグループの再ラベル付けされた平均予測が決定されたら、それらのメトリックを計算します。以下は計算のシーケンスです。
- ループ内のグループを反復処理する
- 4種類の平均化閾値を反復処理する
- 実際の予測のクラスラベルを "0"から "-1"に変更する
- 実際の及び再ラベル付けされた予測をデータフレームに結合する
- データフレームから予測が0に等しい行を削除する
- メトリックを計算してVotAver構造に追加する
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
読み取り可能な形式でデータを収集し、表示します。
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
最良の結果は、ノイズサンプルの処理を伴う、「removed」データ群の試験サブセットに示されました。
もう一度、タイプを平均化して、各データ群の各サブセットで結果を結合します。
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
読み取り可能な形式で結果を収集します。
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711
テストセットの結果を検討してください。意外なことに、relabeledメソッドが最良の結果でした。すべてのグループの結果は、5.4で得られた結果よりもはるかに優れています。単純多数決によるアンサンブル出力をカスケード式に組み合わせる方法は、分類品質(精度)を5％から7％に向上させます。
このセクションのスクリプトはVoting_aver.Rファイルにあります。得られたデータの構造を下の図に示します。
図10 VotAverのデータ構造体
以下の図は、すべての計算の簡略化されたスキームで、ステージ、使用されているスクリプト、データ構造を示しています。
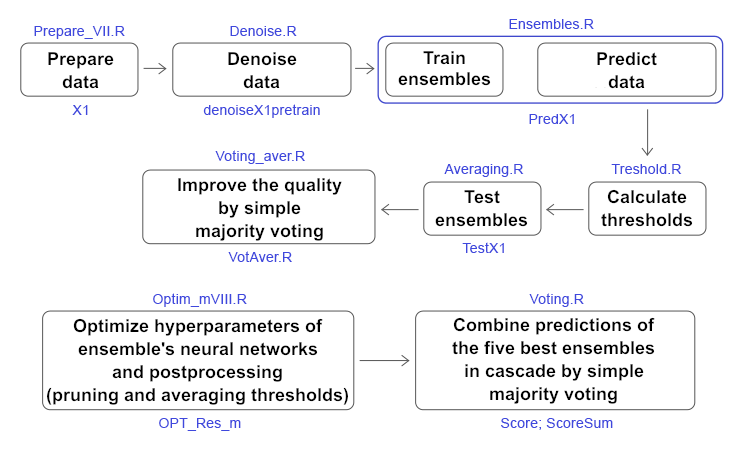
図11 記事中の主な計算の構造と順序
8. 実験結果の分析
pretrainサブセットの初期データセットから次の3つの方法でノイズサンプルを処理しました。
- クラスの数を変更せずに(誤って)ラベル付けされたデータを再割り当てた
- サブセットから「ノイズ」サンプルを除去(除去)した
- 別のクラス(再ラベル付け)で "ノイズ"サンプルを分離した
4つのデータ群(origin、repaired、removed、relabeled) がdenoiseX1pretrain構造体に取得されます。それらを使用して、500 ELMニューラルネットワーク分類器からなるアンサンブルを訓練します。4つのアンサンブルが得られます。これらの4つのアンサンブルを使用して3つのサブセットХ1$train/test/test1の連続予測を計算し、それらをpredX1構造に集めます。
次に、InputTrainサブセット上の各アンサンブルの500個のニューラルネットワークのそれぞれの連続予測のための4種類の閾値を計算します。これらの閾値を使用して、連続予測をクラスラベル(0,1)に変換します。アンサンブルの各ニューラルネットワークのメトリック(mean(F1))を計算し、構造体 testX1$$(InputTrainScore|InputTestScore|InputTest1Score)に集めます。4つのデータ群と3つのサブセットでのメトリックの分布の可視化によって下記がわかります。
- まず、最初のテストサブセットのメトリックは、すべてのグループのInputTrainSのメトリックよりも高い
- 次に、repairedグループとremovedグループは、他の2つのグループよりも視覚的に高い評価を得ている
各アンサンブルにおけるmean(F1)の最大値を有する7つの最良ニューラルネットワークを選択し、それらの連続予測を平均します。それらの値をtestX1$$(TrainYpred|TestYpred|Test1Ypred)構造体に追加します。サブセットTrainYpredの閾値th_averを計算し、平均化されたすべての連続予測のメトリックを決定し、それらをtestX1$$(TrainScore|TestScore|Test1Score)構造体に追加します。分析が可能になります。
さまざまなデータ群の刈り込みと平均化の閾値の異なる組み合わせを使用して、0.75〜0.77の範囲でメトリックを取得します。removed グループでは、「ノイズ」サンプルが削除された状態で最良の結果が得られました。
ニューラルネットワークのハイパーパラメータの最適化は、すべてのグループにおいて0.77+のメトリックの安定した増加を提供します。
ニューラルネットワークのハイパーパラメータ及び後処理(刈り込み及び平均化)閾値の最適化は、処理された「ノイズ」サンプルを有するすべてのグループにおいて約0.78+の安定した高い結果をもたらします。
最適なハイパーパラメータでいくつかのアンサンブルからスーパーアンサンブルを作成し、これらのアンサンブルの予測を取って、各データ群で簡単な多数決を組み合わせます。その結果、repaired、removedグループのメトリックを0.82+の範囲で取得します。これらのスーパーアンサンブルの予測を単純多数決で組み合わせると、0.836という最終的なメトリック値が得られます。したがって、カスケード式に予測を単純多数決で組み合わせると、品質が6〜7％改善されます。
受け取ったアンサンブルの平均予測に関するこのステートメントを早期に確認します。グループの計算とコンバージョンを繰り返した後、テストサブセットのremovedグループで0.8+のメトリックを受け取ります。カスケード式の結合を続けると、すべてのデータ群のTestサブセットで0,8 +の値を持つメトリックが得られます。
単純投票によってカスケード式にアンサンブル予測を組み合わることは実際に分類品質を改善すると結論付けることができます。
終わりに
本稿では、アンサンブルのニューラルネットワークのハイパーパラメータと後処理の最適化と同様に、バギングアンサンブルの品質を改善する3つの方法が検討されています。実験の結果に基づいて、以下の結論を導くことができます。
- repaired及びremovedメソッドを使用してノイズサンプルを処理すると、アンサンブルの分類品質が大幅に向上します。
- 刈り込み及び平均化の閾値タイプを選択すると、その組み合わせも分類品質に大きな影響を与えます。
- いくつかのアンサンブルを組み合わせて、それらの予測を単純多数決でカスケード結合したスーパーアンサンブルに分類すると、分類品質が最も向上します。
- アンサンブルのニューラルネットワーク及び後処理のハイパーパラメータを最適化することにより、分類品質スコアがわずかに改善されます。新しいデータに対して最初の最適化を実行し、品質が低下したときに定期的に最適化を繰り返すことをお勧めします。周期性は実験的に決定されます。
添付ファイル
GitHub/PartVIIIには下記のファイルが含まれています。
- Importar.R — パッケージインポート関数
- Library.R — 必要なライブラリ
- FunPrepareData_VII.R — 初期データを準備する関数
- FunStacking_VIII.R — アンサンブルを作成してテストする関数
- Prepare_VIII.R — 訓練可能な結合器の初期データを準備するための関数とスクリプト
- Denoise.R — ノイズサンプルを処理するスクリプト
- Ensemles.R — アンサンブルを作成するスクリプト
- Threshold.R — 閾値を決定するスクリプト
- Test.R — アンサンブルをテストするスクリプト
- Averaging.R — アンサンブルの連続出力を平均化するスクリプト
- Voting_aver.R — 単純多数決でカスケード式に平均出力を組み合わせるスクリプト
- Optim_VIII.R — ニューラルネットワークのハイパーパラメータを最適化するスクリプト
- Optim_mVIII.R — ニューラルネットワークと後処理のハイパーパラメータを最適化するスクリプト
- Voting.R — スーパーアンサンブルの出力をカスケードで簡単な多数決で組み合わせるスクリプト
- SessionInfo_VII.txt — 記事スクリプトで使用されているパッケージのリスト
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/4722
添付されたファイル |
PartVIII.zip
(23.24 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
ディープニューラルネットワーク(その7)ニューラルネットワークのアンサンブル: スタッキング
アンサンブルの構築を続けます。今回は、以前に作成したバギングアンサンブルに、訓練可能な結合器、つまりディープニューラルネットワークが追加されます。ニューラルネットワークの1つは、刈り込み後に7つの最良アンサンブル出力を組み合わせます。2つ目はアンサンブルの500個の出力をすべて入力として取り込み、刈り込んで結合します。ニューラルネットワークは、Python用のKeras/TensorFlowパッケージを使用して構築されます。このパッケージの特徴には簡単に触れます。テストが実行されて、バギングアンサンブルとスタッキングアンサンブルの分類品質が比較されます。
EAのリモートコントロールの方法
トレーディングロボットの主な利点は、リモートの VPS サーバー上で24時間動作できることです。 しかし、時にはサーバーに直接アクセスすることができず、タスクに介入する必要があります。 EAをリモートで管理することは可能でしょうか。 この記事では、外部コマンドを使用してEAを制御するオプションの1つを提案します。
MQL5レシピ - オープンヘッジポジションのプロパティを取得しましょう
MetaTrader 5プラットフォームでは、マルチマーケットだけでなく、さまざまなポジション計算システムの使用も可能です。このような機能は、取引アイデアの実装と形式化のためのツールを大幅に拡大します。この記事では、ポジションが独立してカウントされたとき（『ヘッジ』）のポジションのプロパティの処理と考慮の方法について説明します。派生クラスの提案と、ヘッジポジションのプロパティの処理と取得の例を提示します。
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
Обсуждение и вопросы по коду можно сделать в ветке
Удачи