
機械学習モデルの評価と変数の選択
イントロダクション
この記事では、機械学習モデルで使用するための入力変数の選択、前処理および評価の詳細に焦点を当てています。複数の正規化のメソッド及びその関数は、ここで説明します。トレーニングモデルの最終結果に影響を与える重要なプロセスも明らかにします。入力データの情報伝達性と可視化を決定する、あまり知られていないメソッドを評価します。
"RandomUniformForests"のパッケージで、重要な予測因子の対応や目標、相互作用、および最適なセットを分析します。
"ラフ集合"のパッケージで、別の角度からの予測因子を選択するのと同じ問題を見ていきます。最適な予測変数のセットを表示し、例のセットも最適化することができます。
Revolution R Open 3.2.1で - すべての計算は、R言語で実行されます。
1. 入力変数(signs, predictors)
すべての変数、入力(予測因子)と出力(ターゲット)は、以下のタイプの可能性があります。
バイナリ - 二つの値です {0,1}, {-1,1}, {"yes", "no"}, {"male", "female"}.。
レベルの有限数の公称(要因)。例えば、係数「曜日」は、7レベルを有し、それらの各々は(月曜日、火曜日など)をとることができます。要因は、順番、またはランダムにすることができます。例えば、一日の時間は24のレベルを持っているいうことになります。すべてのレベルが等しく重要なので、都市の地区の因子は32レベルになります。並べた要因を宣言するときには、明示的に指定する必要があります。
定量的(数値)の連続。+ Int. の(無限大)からの連続変数の範囲。
「生の」データ(OHLC)は、数値の入力変数として使用されていません。差分対数や引用率の対数が適用されます。しかし、セットに合わせた様々なインジケーターが最も頻繁に使用されます。典型的には、すべての変数は、各列が可変であることを特徴とするデータフレームが均一である場合、ラインは特定の時点での変数の状態です。ターゲット変数が、最後の(または最初の)列に配置されています。
1.1. クリーンアップ
クリーンアップは次のことを意味します。
a)除去または(不確定)データ「NA」が欠落して変換。
多くのモデルは、入力データのギャップを許可していません。したがって、いずれかの欠損データを持つ行を削除するか、補間データとのギャップを埋めます。このような目的のため、それぞれの関数は、多くのパッケージで提供されます。不確実なデータを削除するNAは、一般的に、デフォルトで組み込まれていますが、それは na.omit(dt)を通じて自分で行う方が良いでしょう。
b) 「ゼロ・オプション」の変数の除去。
いくつかのケースでは(特に、変数の変換中に)予測因子は、一意の値が表示される場合があります。多くのモデルの場合は、不安定な動作につながる可能性があります。これらのゼロに近い分散予測因子を同定し、シミュレーションの前に除去しなければなりません。「キャレット」パッケージ特別な関数caret:: nearZeroVar()で、このような予測因子を特定し、使用することができます。この点の議論が必要です。
c)同定と相関予測因子の除去(数字)。
一部のモデルは非常によく相関した予測因子を処理しながら(例えばPLS、LARSと正則L1)、他のモデル予測変数間の相関レベルを低下させる効果を得ることができます。強い相関予測因子を除去するために、「キャレット」パッケージから関数キャレット:: findCorrelationを使用します。(相関係数の閾値は、例えば>0.9に)非常に強力なパッケージです。
d)同定と線形依存性の除去(要因)。
caret::findLinearCombos() 関数は、線形結合を設定する行列転送のQR拡張(存在する場合)を使用しています。たとえば、次の行列を分析してみましょう:
ltfrDesign <- matrix(0, nrow = 6, ncol = 6) ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1) ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0) ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1) ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0) ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0) ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)
2、3列は最初の列への追加であることに注意してください。同様に、列4、5、6は、第一列に形成されています。caret:: findLinearCombos()関数は、線形依存関係を削除することができ、これらの依存関係を列挙するリストを返します。
comboInfo <- findLinearCombos(ltfrDesign) comboInfo $linearCombos $linearCombos[[1]] [1] 3 1 2 $linearCombos[[2]] [1] 6 1 4 5 $remove [1] 3 6 ltfrDesign[, -comboInfo$remove] [,1] [,2] [,3] [,4] [1,] 1 1 1 0 [2,] 1 1 0 1 [3,] 1 1 0 0 [4,] 1 0 1 0 [5,] 1 0 0 1 [6,] 1 0 0 0
バイナリ予測因子を多数使用した場合、このタイプが発生する因子予測因子は、ダミーに変換されます。
1.2. 変換、データの前処理
多くのモデルは、数値入力データがある範囲(正規化、標準化)にあるように、特定のメソッド(要因)に変換することが求められています。例えば、ニューラルネットワークおよびサポートベクターマシンで、(SVM)の入力データを受け入れる範囲は[-1、1]、[0,1]です。R言語の多くのパッケージは、このような変換の関数を提供したり、変換自体を実行します。前処理のパラメータの定義は、入力データのトレーニングセットを実行するということを覚えておいてください。テストと検証セット、新しいデータが、入ってくる予測モデルは、トレーニングセットで得られたパラメータに変換されます。
標準化 (スケーリング)
範囲{+ h、-l}に変換する一般式。範囲H=+1に応じ l =(-1または0)。一部のリソースでは、活性化関数(tanh/ sig)のセクションを使用しないように、範囲を狭くすることをお勧めします。 {-0.9;0.9}または{0.1。 0.9}これは、ニューラルネットワーク、SVMの活性化関数を持つ他のモデルを指します。
Xn = (x - min(x)) / (max(x) - min(x)) * (h - l) + l;
逆変換(非正規化)は、式に基づいて実行されます。
x = (x - l) / (h - l) * (max(x) - min(x)) + min(x);
標準化
変数分布が正常に近いことを知って、以下の式を用いて正規化することが可能です。
x = (x - mean(x)) / sd(x)
いくつかのパッケージでは、前処理のために提供される特別な関数があります。したがって、preProcess() の関数"caret"パッケージは、前処理の次のメソッドを提供しています:: "BoxCox", "YeoJohnson", "expoTrans", "center", "scale", "range", "knnImpute", "bagImpute", "medianImpute", "pca", "ica" , "spatialSign".
"BoxCox", "YeoJohnson", "expoTrans"
Yeо-Johnson変換は、ゼロまたは負の値(ボックス・コックス変換の予測値が厳密に正である必要あり)との予測因子を受け入れ、ボックス・コックスモデルに少し似ています。マンリー(1976)の指数関数変換は、正と負のデータに使用することができます。
"範囲"変換スケールデータ[0、1]。これは重要です!新しいサンプルがトレーニングセットで使用されるものより高い値を持っている場合は、値がこの範囲外となり、予測結果が不正になります。
"センター" - は、平均値が差し引かれ、"スケール"は、標準偏差(スケーリング)により分割されています。通常、それらは「標準化」と呼ばれ、一緒に使用されます。
"knnImpute", "bagImpute", "medianImpute" - 異なるアルゴリズムを使用した、未定義のデータの計算。
"spatialSign" - 変換は、р予測変数の数であるр寸法で単位円に予測データを投影します。本質的に、ベクトルデータは、そのノルムで除算します。変換前に、中心とスケーリングされるべきです。
"PCA" - 主成分分析は、新しい変数が互いに相関しない小さな部分空間へのデータ変換に使用されます。センタリングとスケーリングは、このメソッドを使用して自動的に行われ、列名はPC1、PC2等に変更されます
"isa" - 同様に、独立成分分析は、コンポーネントと(PCAに無相関とは異なり)独立している元のセットの線形結合である新しい変数を検索するために使用することができます。新しい変数は等IC1、IC2、としてマークされます
最適なデータ・クラスタリングの手順を見つけるために割り当てられた"clusterSim"パッケージには、列と行の両方で18のメソッドでデータを正規化する dataNormalization()関数を有しています。一覧表示です:
n1 — standardization ((x – mean) / sd);
n2 — positional standardization ((x – median) / mad);
n3 — unitization ((x – mean) / range);
n3а — positional unitization ((x – median) / range);
n4 — unitization with zero minimum ((x – min) / range);
n5 — normalization in range <-1, 1> ((x – mean) / max(abs(x – mean)));
n5a — positional normalization in range <-1,1> ((x – median) / max(abs(x-median)));
n6 — quotient transformation (x/sd);
n6a — positional quotient transformation (x/mad);
n7 — quotient transformation (x/range);
n8 — quotient transformation (x/max);
n9 — quotient transformation (x/mean);
n9a — positional quotient transformation (x/median);
n10 — quotient transformation (x/sum);
n11 — quotient transformation (x/sqrt(SSQ));
n12 — normalization ((x-mean)/sqrt(sum((x-mean)^2)));
n12a — positional normalization ((x-median)/sqrt(sum((x-median)^2)));
n13 - ゼロは、中央点との正規化((x-midrange)/(range/2))。
「ダミー変数」 - 多くのモデルが「ダミー」に係数予測値を変換。関数dummyVar() から「カレット」パッケージは、この目的に使用できます。この関数は、式やデータのセットを取得し、ダミー変数を作成するために使用できるオブジェクトを表示します。
2. 出力データ(目的変数)
分類問題なので、ターゲット変数がレベル(クラス)の数が要因です。二つのクラスを使用してターゲットにしたときのモデルの大半は、より良好な結果を示しています。特別なクラスの多くの追加的措置は、このような問題に対処するために取られています。ターゲット変数は、トレーニングデータ準備の過程で符号化され、予測の後に復号されます。
クラスは、いくつかのメソッドで符号化されます。 decodeClassLabels()クラスに対応する列が含まれている行列のベクトルクラスをコード化し、また、 - "シュトゥットガルト大学でのニューラルネットワークのシミュレーション"のRSNNSパッケージには2つの予測モデルの後に逆変換を行います。 encodeClassLabels()、。具体例:
> data(iris) > labels <- decodeClassLabels(iris[,5]) > class <- encodeClassLabels(labels) > head(labels) setosa versicolorのvirginicaの [1,] 1 0 0 [2,] 1 0 0 [3,] 1 0 0 [4,] 1 0 0 [5,] 1 0 0 [6,] 1 0 0 > head(class) [1] 1 1 1 1 1 1
モデル出力の数は、ターゲット・クラスの数に等しくなります。これは、ターゲットに適用されるだけの符号化方式(一対一)ではありません。ターゲットが2つのクラスを持っている場合は、1出力で管理することができます。マトリックス中のターゲット変数の符号化は、間違いなく多くの利点があります。
3. 評価と予測因子の選択
入力データ(予測)の増加は、必ずしもモデルの改善つながらないことを示しています。結果は、実際には3-5予測因子の影響を受けます。「rminer」、「caret」、「SuperLearner」、「mlr」のような集約・パッケージ、内蔵された関数があります。ほとんどのアプローチでの予測変数の数は(John, Kohavi and Pfleger, 1994)2つのカテゴリに分けることができます。:
- フィルタリング。フィルタリングメソッドは、予測モデルの外の予測因子の関連性を評価し、そして、最終的には、一定の基準を満たす予測因子を使用しています。例えば、分類タスクについて各予測値は、個別に予測と観察クラス間の妥当な関係が存在するかどうかを確認するために、評価することができます。重要な依存関係を持つ予測因子は、その後、分類モデルに含まれます。
ラッパー。ラッピングメソッドは、モデルの効率を最適化し、最適な組み合わせを見つけるために、予測因子を追加および/または削除する手順を使用して、異なるモデルを評価します。本質的には、メソッドが最適化される必要がある出力と入力と使用モデルの効率として、予測因子を考慮する探索アルゴリズムです。予測因子を反復処理する多くのメソッド(再帰的削除/遺伝的アルゴリズム、シミュレーテッドアニーリング、他)があります。
この記事では、上記のすべての欠点を述べ、新たなメソッドとフィルタリングメソッドのアプローチを分析します。
3.1. フィルタリング
外部メソッドや基準を使用すると、予測因子の重要性(情報関数)が確立されます。各変数の寄与の重要性は、ここで暗示されています。
通常は、3つの利用可能性があります。
予測因子の数を取ります。
最も重要な予測因子の合計数の割合を取ります。
- その閾値を超えた予測因子を取ります。
すべてのケースは、量、パーセンテージの最適化を可能にします。
特定のメソッドを考慮し、実験を行う入力および出力データのセットを形成してみましょう。
入力データ
入力セット内で11のインジケーター(オシレータ)が含まれます。いくつかのインジケーターからいくつかの変数を得ようとしています。その後、17の変数の入力セットを形成する関数を記述します。
最後の4000のバーからの引用はTF = M30 / EURUSDがとられます。
In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp -DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>% as.data.frame() %>% mutate(., oscK = fastK - fastD)%>% transmute(.,slowD, oscK)%>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144) In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol) return(In) }
これらのインジケーターは非常によく知られており、広く適用されているので、それらを議論するつもりはありません。「パイプ」(%>%)の計算で許容可能なMACDインジケータの例に基づいて "magrittr" パッケージをコメントします。書き込み順序は次のようになります。
二つの変数(macd, signal)を返します。
得られた行列は、データフレームに変換されます。
新しい変数vsigは、(書き込み順)データフレームに追加されます。
- signal変数が取得されます。
- 第1の差分が算出されます。
- 第1の差分を計算する際、ベクトルが元の数の単位なのでNAベクタルは、最初に追加されます。
- それは10で乗算されます。
必要な変数(列)がvsig, signalデータフレームから選択されます。
データフレームは、マトリックスに変換されます。
中間結果が必要とされない場合、この計算メソッドは、非常に便利です。また、式が読みやすく、理解しやすくなります。
入力データの行列を取得し、内容を見ていきます。
x <- In(p = 16) > summary(x) DX ADX oscDX Min. : 0.02685 Min. : 5.291 Min. :-93.889 1st Qu.: 8.11788 1st Qu.:14.268 1st Qu.: -9.486 Median :16.63550 Median :18.586 Median : 5.889 Mean :20.70162 Mean :20.716 Mean : 4.227 3rd Qu.:29.90428 3rd Qu.:24.885 3rd Qu.: 19.693 Max. :79.80812 Max. :59.488 Max. : 64.764 NA's :16 NA's :31 NA's :16 ar tr atr Min. :-100.0000 Min. :0.0000000 Min. :0.000224 1st Qu.: -50.0000 1st Qu.:0.0002500 1st Qu.:0.000553 Median : -6.2500 Median :0.0005600 Median :0.000724 Mean : -0.8064 Mean :0.0008031 Mean :0.000800 3rd Qu.: 50.0000 3rd Qu.:0.0010400 3rd Qu.:0.000970 Max. : 100.0000 Max. :0.0150300 Max. :0.003104 NA's :16 NA's :1 NA's :16 cci chv cmo Min. :-515.375 Min. :-0.67428 Min. :-88.5697 1st Qu.: -84.417 1st Qu.:-0.33704 1st Qu.:-29.9447 Median : -5.674 Median : 0.03057 Median : -2.4055 Mean : -1.831 Mean : 0.11572 Mean : -0.6737 3rd Qu.: 83.517 3rd Qu.: 0.44393 3rd Qu.: 28.0323 Max. : 387.814 Max. : 3.25326 Max. : 94.0649 NA's :15 NA's :31 NA's :16 sign vsig rsi Min. :-0.38844 Min. :-0.43815 Min. :12.59 1st Qu.:-0.07124 1st Qu.:-0.05054 1st Qu.:39.89 Median :-0.00770 Median : 0.00009 Median :49.40 Mean :-0.00383 Mean :-0.00013 Mean :49.56 3rd Qu.: 0.05075 3rd Qu.: 0.05203 3rd Qu.:58.87 Max. : 0.38630 Max. : 0.34871 Max. :89.42 NA's :33 NA's :34 NA's :16 slowD oscK SMI Min. :0.0499 Min. :-0.415723 Min. :-74.122 1st Qu.:0.2523 1st Qu.:-0.043000 1st Qu.:-33.002 Median :0.4720 Median : 0.000294 Median : -5.238 Mean :0.4859 Mean :-0.000017 Mean : -4.089 3rd Qu.:0.7124 3rd Qu.: 0.045448 3rd Qu.: 22.156 Max. :0.9448 Max. : 0.448486 Max. : 75.079 NA's :19 NA's :17 NA's :25 signal vol Min. :-71.539 Min. :0.003516 1st Qu.:-31.749 1st Qu.:0.008204 Median : -5.319 Median :0.011274 Mean : -4.071 Mean :0.012337 3rd Qu.: 19.128 3rd Qu.:0.015312 Max. : 71.695 Max. :0.048948 NA's :33 NA's :16
Output data (target)
ターゲット変数として、ZZから受信したシグナルを使用します。以下はジグザグとシグナルを計算するための式です。
ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) if(ch > 1) ch <- ch/(10 ^ (Dig - 1)) if(mode == "m"){pr <- pr[ ,'Med']} if(mode == "hl") {pr <- pr[ ,c("High", "Low")]} if(mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]} dz <- zz %>% diff %>% c(0,.) sig <- sign(dz) return(cbind(zz, sig)) }
関数パラメータ:
- pr = price — matrix of OHLCMed quotations;
- ch — minimum length of a zigzag bend in points (4 signs);
- mode — applied price (m — average, hl — High and Low, cl — Close). 平均値がデフォルトで使用されます。
関数は、範囲[-1; 1]におけるジグザグの傾きに基づいて得られるジグザグとシグナルの2つの変数を持つ行列を返す - -。
さまざまな長さを持つ2つのZZのシグナルを計算します。
out1 <- ZZ(ch = 25) out2 <- ZZ(ch = 50)
チャートは、次に応じます。
> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")
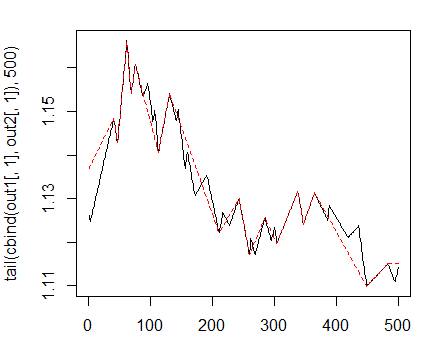
図1。曲がり最小25/75 pのジグザグ
次に、短い最初のZZを使用します。一般的なデータフレームで入力変数とターゲットを組み合わせた条件を="0"と定義し、ターゲットからクラス「0」を削除します。
> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% + na.omit > data <- data[data$Class != 0, ] > data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")
対象のクラスの分布を見てください:
> table(data$Class) -1 1 1980 1985
このクラスは十分にバランスがとれています。入力および出力データ準備のセットを持っているので、予測因子の重要性を評価するために始めることができます。
まず、入力データがどのような相関かチェックします:
> descCor <- cor(data[ ,-ncol(data)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03803 0.26310 0.31750 0.57240 0.95730
入力変数は、90%以上の相関関係がありますか?
> highCor <- caret::findCorrelation(descCor, cutoff = .90) > highCor [1] 12 15
答えは - RSIと SMI。これら2つのデータのセットを形成し、残りの相関が表示されます。
> data.f <- data[ ,-highCor] > descCor <- cor(data.f[ ,-ncol(data.f)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03219 0.21610 0.27060 0.47820 0.89880
変数の重要度(VI)を評価するには、、深い分析と可視化の幅広い選択を持つ新しいパッケージ「Random Uniform Forests」を使用します。パッケージの開発者の意図どおりに、変数の重要性を決定する主な目的は、いつ、どこで、どのようにを評価することである。
このパッケージには、深さが可変の重要なインジケーターがあります。より深い評価に入る前に検討していきます。
グローバル変数の重要最大限の予測誤差を低減し、変数を設定しますが、重要な変数は、応答に影響を与えます。
例えば、変数が別のクラスの上に強い影響力を持っている、または変数間の相互作用は何でしょう。
変数の重要性は、すべてのユニットによって測定され、切断点が偶発的であるように、すべての変数に値を持つことができています。そのため、各変数は選択されているチャンスを持っていますが、それは主に各エントロピーを減少させるものである場合にのみ、重要性を取得します。
Local Variable Importance
定義:同じ観察、終端ノードで発生頻度が最も高いものであれば、最初のオーダーで局所的に重要である。
Partial importance
定義:端末ノードの出現の最高周波数を有するものである同一の観測、クラスのオーダーであれば、予測は部分的に重要である。
相互作用
これを考慮するとき、どのように影響するでしょうか。例えば、いくつかの変数は、より関連性の高い変数の問題に強烈なインパクトを持つことができ、この変数が影響力になり相互作用の多くを持つことができます。それでは、相互作用が何であるかを定義してみましょう。
定義:第一および終端ノードで発生した2番目に高い数、持って両方とも同じ観測上の場合、すべての予測は、他との相互作用です。
部分的な依存関係
変数(または変数の組)は、他のすべての変数の値を知ること、レスポンスの値にどのように影響するかを決定することを可能にするツールです。具体的には、部分的な依存性は、可変の最大影響効果は応答の値に基づいて行使されます。部分的な依存性の概念は、異なるメソッドで実装されたRandom Uniform Forests で、グラデーションマシン(GBM)でフリードマン(2002)から派生しました。
Importance = contribution + interaction:Random Uniform Forestsパッケージのアイデアによると、以下のスキームに基づいて、変数の重要性を決定することができます。ただし、寄与は、予測誤差に(すべてに影響する点で)変数の影響があり、相互作用プロセッサー他の変数への影響があります。
実験に進みましょう
モデルをテストし、 data.f[]データセットに分割します。比2/3でセットをテストし、-1;1の範囲に正規化。分離のため、rminer::holdout() function を使用します。正規化のためにcaret::preProcess() と method = c("spatialSign").を使用します。モデルを訓練するとき、パッケージは、" doParallel"パッケージで自動的に利用可能なプロセッサコアマイナス1の間の計算を並列化します。コアの特定の数を示すことができるのは、「スレッド」オプションを使用して計算するために使用されます。> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+ method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train,
+ Y = y.train,
+ xtest = x.test,
+ ytest = y.test,
+ mtry = 1, ntree = 300,
+ threads = 2,
+ nodesize = 2
+ )
ラベル-11は、計算を容易にするため1〜2に変換され、代替として内部的に使用されます。
> print(ruf)
Call:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test,
ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)
ランダムで均一な種類:分類
paramsObject
ntree 300
mtry 1
nodesize 2
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
Out-of-bag (OOB) evaluation
OOB estimate of error rate: 20.2%
OOB error rate bound (with 1% deviation): 21.26%
OOB confusion matrix:
Reference
Prediction -1 1 class.error
-1 1066 280 0.2080
1 254 1043 0.1958
OOB estimate of AUC: 0.798
OOB estimate of AUPR: 0.7191
OOB estimate of F1-score: 0.7962
OOB (adjusted) estimate of geometric mean: 0.7979
Breimanの境界
(約バランスの取れたクラスの下の)期待予測誤差:18.42パーセント
Upper bound: 27.76%
平均相関:0.0472
強さ(マージン):0.4516
強度の標準偏差:0.2379
テストセット
エラー率:19.97パーセント
混同行列:
Reference
Prediction -1 1 class.error
-1 541 145 0.2114
1 119 517 0.1871
ROC曲線下面積:0.8003
精密リコール曲線下面積:0.7994
F1 score: 0.7966
幾何平均:0.8001
これを解読します。
- 誤差は、(内部エラー)偏差の1%=21.26パーセントです。
- Breimanの境界 - Breiman(2001)によって提案された理論的な性質。ランダムフォレストのプロパティを継承しているので、ここにも適用可能です。分類のため、予測誤差、強さの標準偏差と平均相関の2つの境界を提供します。
- 予想される予測誤差=18.42パーセント。上限誤差=27.76パーセント。
- テストエラー=19.97パーセント(外部エラー)。(Breimanの境界の上限よりも、内部評価と少ない場合、再トレーニングは発生しません。)
誤差チャートを見てみましょう:
> plot(ruf)
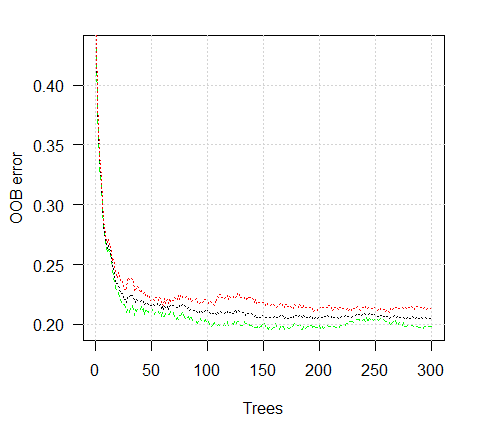
図2。数に応じたトレーニングエラー
> summary(ruf) Global Variable importance: 注:ほとんどの予測関数は、 'スコア' によって順序付けしてプロットされています。 ほとんどの判別式を見ることによって、 'クラス' にアカウントを取られるべきです。 and 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 平均ツリーサイズ(ノード数)概要: Min. 1st Qu. Median Mean 3rd Qu. Max. 3 1044 1313 1213 1524 1861 平均リーフ・ノード(端末ノード数)概要: Min. 1st Qu. Median Mean 3rd Qu. Max. 2 522 657 607 762 931 リーフサイズ(リーフノードあたりの観測数)要約ノード: Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 4.355 3.000 2632.000 平均ツリーの深さ:10 理論(バランス)ツリーの深さ:11
すべての入力変数は、重大かつ重要であることがわかり、。変数が最も頻繁に出現するクラスで示されています。
より多くの統計情報:
> pr.ruf <- predict(ruf, x.test, type = "response"); > ms.ruf <- model.stats(pr.ruf, y.test) テストセット Error rate: 19.97% 混同行列: Reference Prediction -1 1 class.error -1 540 144 0.2105 1 120 518 0.1881 エリアの下でROC曲線:0.8003 精密リコール曲線下面積:0.7991 F1-score: 0.7969 幾何平均:0.8001
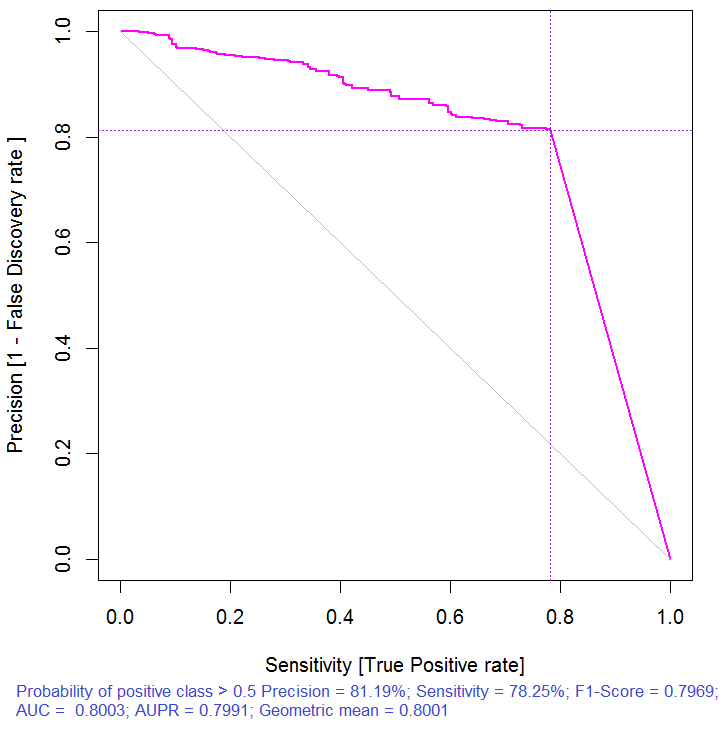
図3. 精密リコール曲線
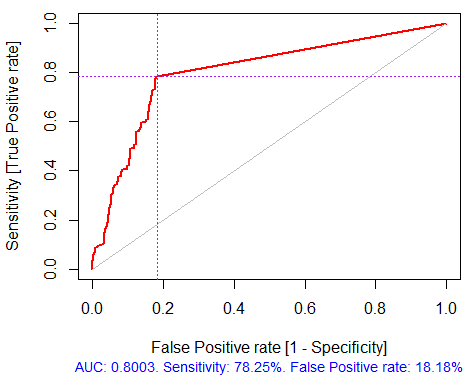
図4。ROC曲線や誤差曲線
多くのフィルタパッケージによって提供されており、ここで停止した場合、世界的に最高のインジケーターにはいくつかの予測因子を選択する必要があります。考慮に入れた予測因子の相互の影響をとらないように、良好な結果を提供していません。
> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3) 1 - Global Variable Importance (15 most important based on information gain) : 注:ほとんどの予測関数は、 'スコア' によって順序付けしてプロットされています。 ほとんどの判別式を見ることによって、 'クラス' にアカウントを取られるべきです。 and 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 2 - ローカル変数の重要性 変数間の相互作用(10の(列で最も重要な変数)と第2(行)の順序): (各オーダーにおける)各変数について、他との相互作用は、計算されます。 cci cmo slowD oscK signal atr chv cmo 0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062 cci 0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899 slowD 0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744 signal 0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698 atr 0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619 ADX 0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596 ar 0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581 oscK 0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570 DX 0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536 oscDX 0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524 avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612 ADX tr ar vsig DX oscDX sign cmo 0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964 cci 0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802 slowD 0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647 signal 0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601 atr 0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522 ADX 0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499 ar 0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484 oscK 0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473 DX 0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439 oscDX 0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427 avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515 vol avg2ndOrder cmo 0.0889 0.1173 cci 0.0726 0.1010 slowD 0.0571 0.0855 signal 0.0526 0.0810 atr 0.0447 0.0730 ADX 0.0424 0.0707 ar 0.0409 0.0692 oscK 0.0397 0.0681 DX 0.0363 0.0647 oscDX 0.0352 0.0636 avg1rstOrder 0.0439 0.0000 相互作用に基づく変数の重要度(10最も重要): cmo cci slowD signal oscK atr ADX ar 0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 chv DX 0.0520 0.0485 最も重要なラベル(10変数の重要性 conditionally to each label) : Class -1 Class 1 cci 0.16 0.23 cmo 0.20 0.18 slowD 0.09 0.10 oscK 0.09 0.07 signal 0.05 0.07 tr 0.02 0.07 ADX 0.06 0.03 chv 0.06 0.04 atr 0.05 0.06 ar 0.05 0.03
他との相互作用に基づいて、変数の重要性はグローバルな重要性の順序と一致しません。そして最後に、クラスによって、変数の重要性の寄与を考慮します。グローバルな重要の変数に基づいた tr,は、放棄されている必要があり、最後の場所にあったプロセッサーと強い相互作用します。
トップ10の変数:
> best <- Cs(cci, cmo, slowD, oscK, signal, tr, ADX. chv, atr, ar)モデルの品質が重要な予測因子のセットが改善されているか、確認してみましょう。
> x.tr <- x.train[ ,best] > x.tst <- x.test[ ,best] > ruf.opt <- randomUniformForest(X = x.tr, + Y = y.train, + xtest = x.tst, + ytest = y.test, + ntree = 300, + mtry = "random", + nodesize = 1, + threads = 2) ラベル-1 1は、計算を容易にするために1〜2に変換されました そして代替として内部に使用されます。 > ruf.opt Call: randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, threads = 2) ランダムで均一な種類:分類 paramsObject ntree 300 mtry random nodesize 1 maxnodes Inf replace TRUE bagging FALSE depth Inf depthcontrol FALSE OOB TRUE importance TRUE subsamplerate 1 classwt FALSE classcutoff FALSE oversampling FALSE outputperturbationsampling FALSE targetclass -1 rebalancedsampling FALSE randomcombination FALSE randomfeature FALSE categorical variables FALSE featureselectionrule entropy Out-of-bag (OOB) evaluation OOB estimate of error rate: 18.69% OOB error rate bound (with 1% deviation): 19.67% OOB confusion matrix: Reference Prediction -1 1 class.error -1 1079 253 0.1899 1 241 1070 0.1838 OOB推定 AUC:0.8131 AUPRのOOB推定値:0.7381 F1スコアのOOB推定値:0.8125 幾何平均のOOB(調整)の推定値:0.8131 Breimanの境界 (バランスの取れたクラスの下の)期待予測誤差:14.98パーセント 上限:28.18パーセントを 平均相関:0.0666 強さ(マージン):0.5548 強度の標準偏差:0.2945 > pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response") > ms.ruf.opt <- model.stats(pr.ruf.opt, y.test) テストセット Error rate: 17.55% 混同行列: Reference Prediction -1 1 class.error -1 552 124 0.1834 1 108 538 0.1672 ROC曲線下面積:0.8245 精密リコール曲線下面積:0.8212 F1-score: 0.8226 幾何平均:0.8244
図5。ROC曲線や誤差曲線
図6。精密リコール曲線
この品質は明らかに改善されました。試験上の予測誤差は、17.55パーセント、上位レベルの28.18パーセント未満です。したがって、再トレーニングはほとんどありません。モデルは、そのチューニングモデルの品質の更なる向上を可能にすることができます。しかし、これは今回の目標ではありません。
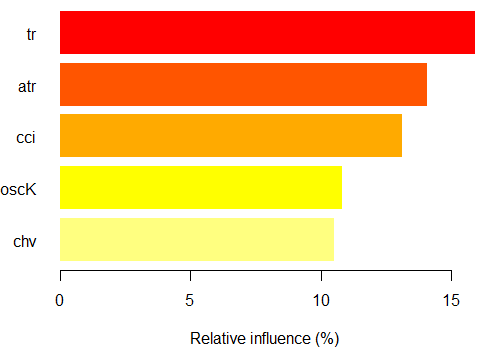
> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst) 関連する変数が抽出されています。 1 - グローバル変数の重要性(10最も重要な情報に基づいて): 注:ほとんどの予測関数は、 'スコア' によって順序付けしてプロットされています。 ほとんどの判別式を見ることによって、 'クラス' にアカウントを取られるべきです。 and 'class.frequency'. variables score class class.frequency percent 1 atr 3556 -1 0.50 100.00 2 oscK 3487 -1 0.51 98.07 3 chv 3465 1 0.51 97.45 4 signal 3432 1 0.51 96.51 5 cci 3424 1 0.50 96.30 6 slowD 3415 1 0.51 96.04 7 ADX 3397 -1 0.50 95.52 8 ar 3369 -1 0.50 94.76 9 tr 3221 1 0.53 90.59 10 cmo 3177 -1 0.50 89.36 percent.importance 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 9 10 9 2 - ローカル変数の重要性 変数間の相互作用(10の(列で最も重要な変数)と第2(行)の順序): (各オーダーにおける)各変数について、他との相互作用は、計算されます。 atr cci oscK slowD ADX tr chv cci 0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349 atr 0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251 oscK 0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186 chv 0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099 ar 0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050 signal 0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024 ADX 0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997 slowD 0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986 cmo 0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876 tr 0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842 avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066 signal ar cmo avg2ndOrder cci 0.1282 0.1182 0.1087 0.1412 atr 0.1184 0.1084 0.0989 0.1313 oscK 0.1120 0.1020 0.0925 0.1249 chv 0.1033 0.0933 0.0838 0.1162 ar 0.0984 0.0884 0.0789 0.1113 signal 0.0957 0.0857 0.0762 0.1086 ADX 0.0931 0.0831 0.0736 0.1060 slowD 0.0919 0.0819 0.0724 0.1049 cmo 0.0810 0.0710 0.0615 0.0939 tr 0.0776 0.0676 0.0581 0.0905 avg1rstOrder 0.0999 0.0900 0.0804 0.0000 相互作用に基づく変数の重要度 (10 最重要) : atr cci oscK chv slowD ADX signal ar 0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 tr cmo 0.0802 0.0672 ラベル上の変数の重要度 (10最も重要な変数、条件付きで各ラベルへ): Class -1 Class 1 atr 0.17 0.14 oscK 0.16 0.11 tr 0.03 0.16 cci 0.14 0.13 slowD 0.12 0.09 ADX 0.10 0.10 chv 0.08 0.10 signal 0.09 0.07 cmo 0.07 0.03 ar 0.06 0.06
図7. 情報利得に基づいた変数の重要性
グローバル変数の重要ほぼ横ばいでしたが、クラスによって変数の重要性が異なるランク付けされています。tr変数は、3回起こります。
予測を超える部分的な依存性
最も重要な変数の部分依存性が考慮されます。
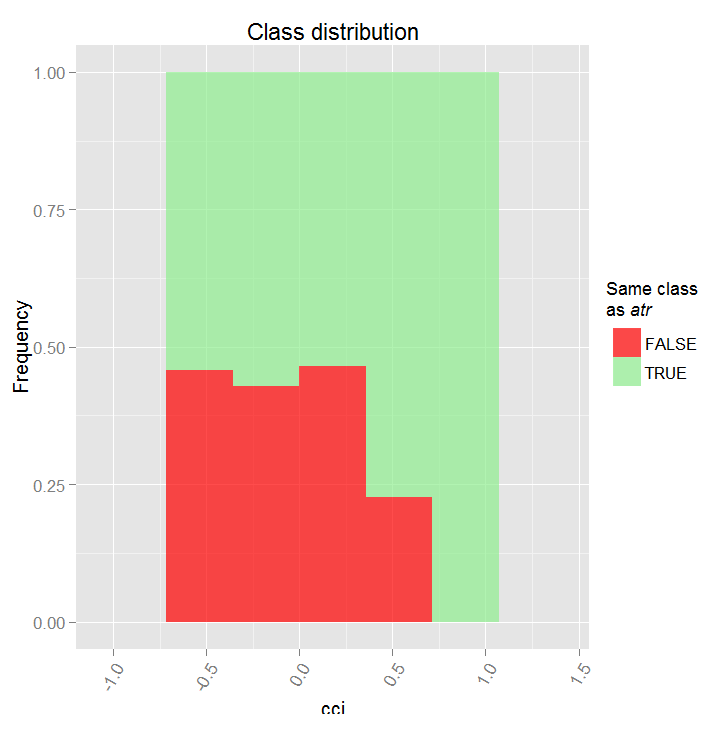
> plot(imp.ruf.opt, Xtest = x.tst)
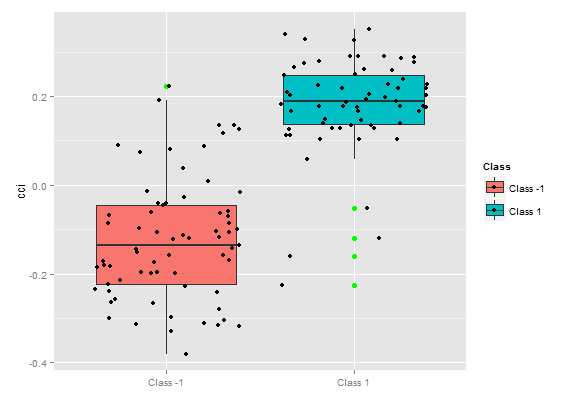
図8. CCI変数の部分的な依存性
> pd.signal <- partialDependenceOverResponses(x.tst, + imp.ruf.opt, + whichFeature = "signal", + whichOrder = "all" + )
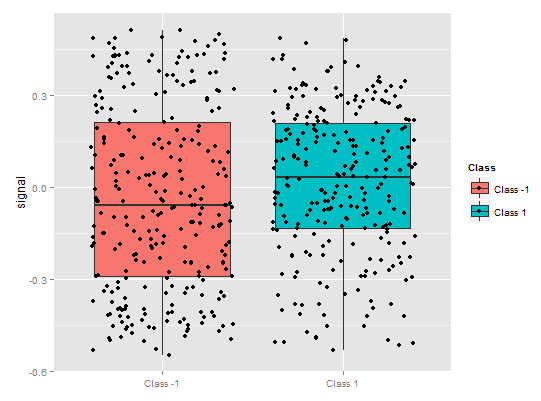
図9. シグナル変数の部分依存性
記号の部分依存性が全く異なる図が上の図です。両方のクラスのほぼ完全なデータを観察できます。
> pd.tr <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "tr",
whichOrder = "all"
)
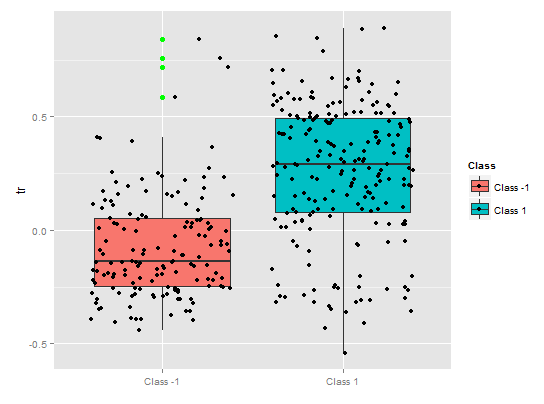
部分依存関係tr予測、クラスによる合理的な分離は、まだここで大きく取り上げる存在であることを示しています。
図10. tr変数の部分依存性
> pd.chv <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "chv",
whichOrder = "all")
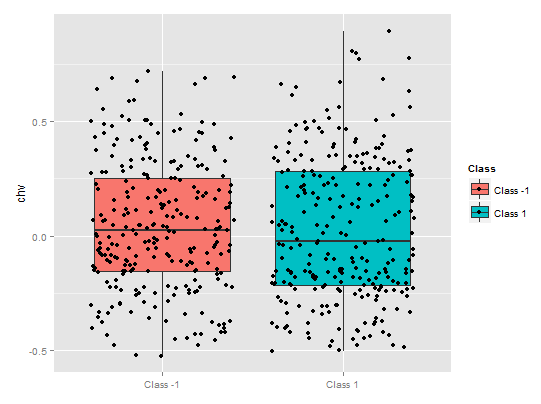
部分依存性chvの予測は嘆かわしいものです。クラスによって、完全なデータ・カバレッジが観察されます。
図11. chv 変数の部分依存性
この予測データは、クラスにリンクされている視覚判断のメソッドと分離可能。
クラス以上の変数の重要性
"変数の重要性は、ローカルな視点を提供します。クラスが固定され、最初は重要な変数を考慮したクラスの修正であることを意味し、最終的には、各クラスの重要な変数が考慮されます。他のクラスが存在しなかったかのように、すべての変数は重要性があります。
ここでは後者が選択されるときに、重要となるクラスを選択する変数を持っていません。変数の順序は、クラスの重要性を考慮することなく、各クラスに関するランキングを提供します。
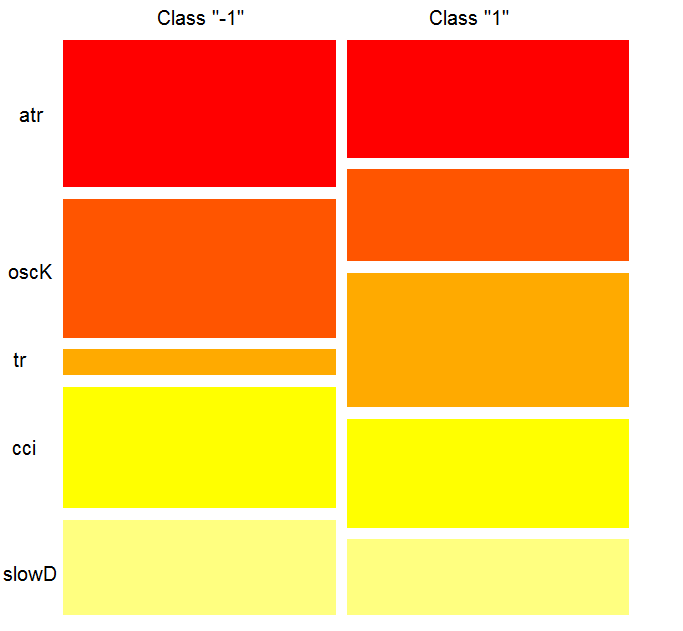
チャートは何を示しているのでしょう?tr予測は、「-1」クラスの「1」よりもかなり重要です。そしてその逆も重要です。予測因子は、異なるクラスで異なる重要性を持っています。
図12。クラスによって変数の重要性
相互作用に基づいた変数の重要性
各変数が他の変数と共同相互作用に提示されているかを示したグラフです。一つの重要な点は:最初の変数は、他との相互影響を有するものである必要はありません。変数の相互作用
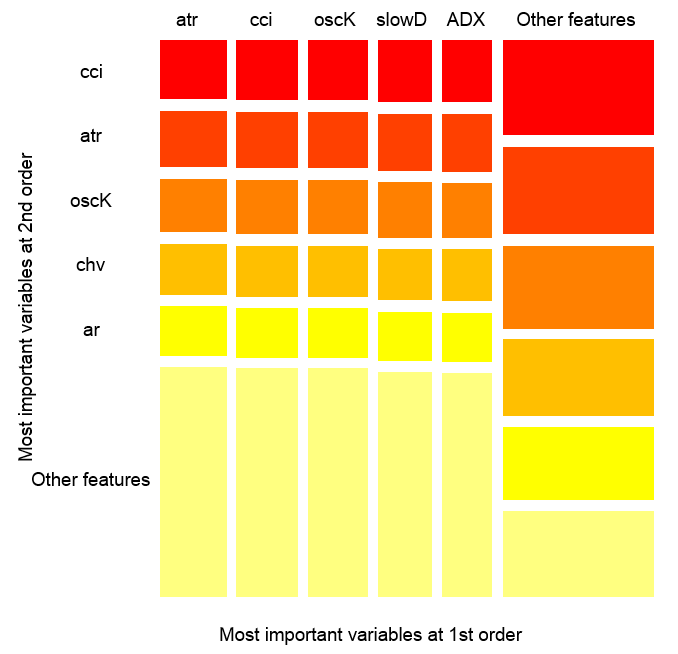
図14。観測値を超える変数の重要性
上の図は、相互作用に与えた定義に従って、内のすべての予測因子の第一及び第二のオーダーの相互作用を示しています。これは、面積が単位に等しいです。最初のオーダーは、アカウント1つの変数のみを考慮して行う必要があり、(降順影響でソート)の変数は、最も重要であることを示しています。未知の変数がすでに最初の順序で選択されている場合、2番目に重要な変数は一つになることを示しています。
明確にするために、相互作用は、順序付けられた関数のテーブルを提供します。最初のオーダーは、最も重要な変数を与えます。2番目のオーダーは、2番目に重要な変数を与えます。変数のペアの交点は、可能な相互影響のうち、相対的な相互影響を与えます。これらの測定は、モデルとデータの両方に依存することに注意してください。そのため、測定中は、直接予測に依存します。また、「他のサイン」と呼ばれるメタ変数は、グループ化された変数の可視化のデフォルトのビューを表示することを可能にすることを意味します。
部分的な重要性
クラス「-1」を超えるx.tstの観察に基づいて部分的な重要性を見ることができます。
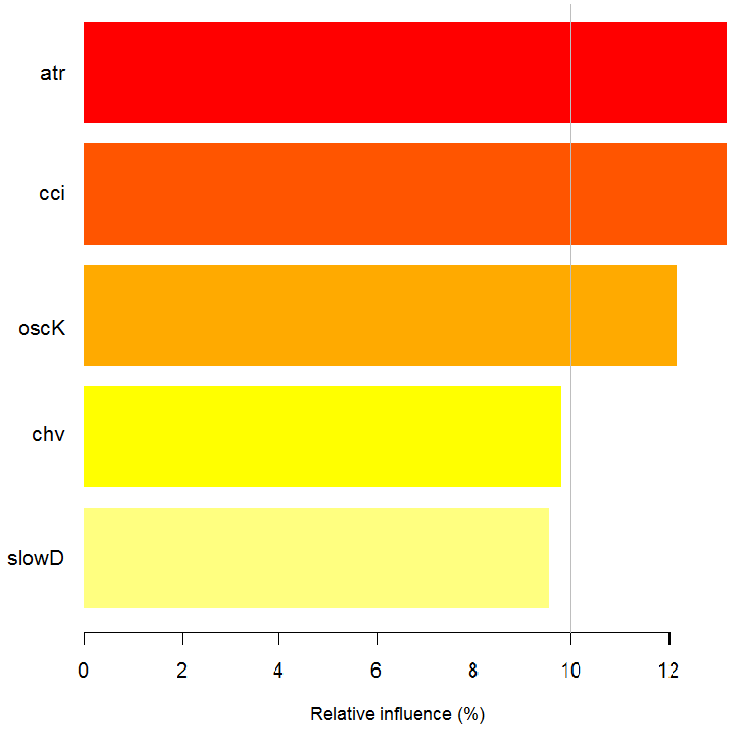
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "-1") 相対的影響:67.41 z.testとクラスに基づいて« - 1»
図15. クラス以上の観察に基づいた変数の部分的な重要性"-1"
クラス「-1」の最も重要な予測因子は、上の図に示す5予測因子です。
クラス「1」に同じ
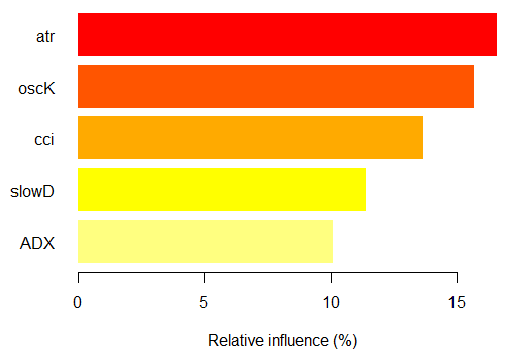
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "1") 相対的影響:64.45%
図16。クラス「1」以上の観察に基づいて、変数の部分的な重要性
予測因子は、構造やランキングの両方が異なっていることを参照してください。
CCIと ATRの予測変数間の部分的な依存関係を見てみましょう。。
> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst, + imp.ruf.opt, + features = Cs(atr, cci), + whichOrder = "all", + perspective = T) 最初のオーダーでのATRとCCIの間の相互作用のレベル:0.1748 (99.97の%)最大レベル ATRとCCIの間の相互作用のレベル:0.1526 (87.28関数の%)最大レベル) クラス分布:ペアの変数は推定を表示します 確率変数が他よりもclassに有します。 classがTRUEになる場合、変数はおそらく影響を与えます。 その他(カテゴリまたは値)ラベルを予測する。 依存性は:変数のペアの形状を表示します。 依存性と同じクラスの予測推定合意 依存性を定義する値。カテゴリ変数の場合 クロス集計が使用されています。 Heatmap:変数のペアの領域が表示されます これは、最も効果的です。 強い依存性が暗い色です。 変数のペア、は、 (「グローバル変数の重要性')を判別します。 相互作用の高いレベルを有するもの。 '相互作用に基づいた変数の重要' )。
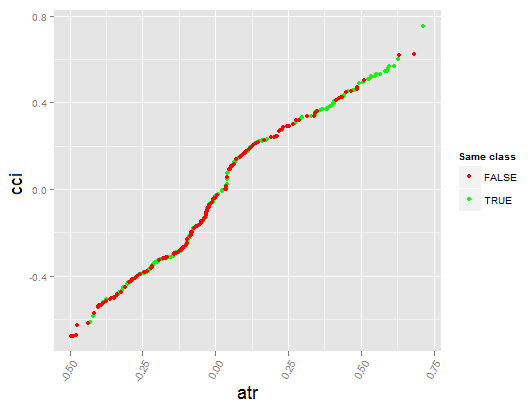
図17. 予測因子間の部分的依存関係 CCIと ATR
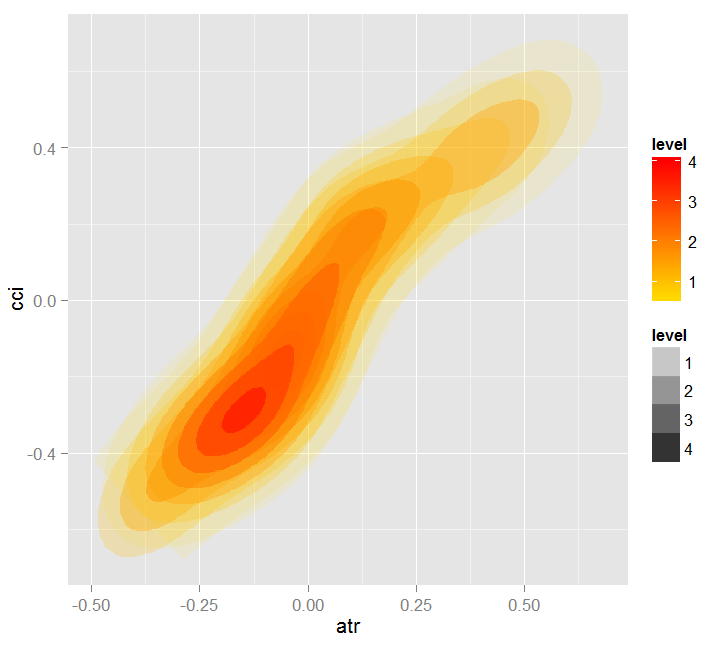
図18. 予測因子間の依存関係 ATRと CCI
図19. 予測因子間の依存関係のヒートマップ ATRと CCI
グローバル変数の重要性を記述するために決定されたグローバル変数は、予測誤差を低減することに最大の影響力があります。
ローカル変数の重要性は、他者との相互作用を使用して、影響力があります。
これにつながる部分的な重要性は、変数がより重要であるときです。変数の重要性を分析する最後のステップは、部分的な依存性であるメソッド プロセッサーに関連付けられています。
要約すると:ランダムにおける変数の重要度は、ディテールと最低レベルのものから行きます。まず、変数の重要性を見つけると、各クラスに重みを与えます。その後、影響力のそれらの相互作用を見つけると、最初の1のようにすべてのクラスを考慮して変数を選択します。次のステップは、 - 影響力が固定されているときに各クラス内の考慮を得るところです。最後に、変数がどのようになるか/「部分的な依存関係」を見ることが重要です。すべてのグローバル変数は、任意のトレーニングやテストセットで動作します。
予測因子のマルチレベル評価は、最も重要な予測因子を選択して、大幅にデータの次元を削減し、予測の質を改善することにより、最適なセットを作成することができます。
予測因子でなく、最も有益な観測項目を選択することができます。
別の興味深いパッケージを見てみましょう - 。「RoughSet」
簡単な説明:ラフ集合理論(RST)及び(FRST)ファジィラフ集合):このパッケージに2つのメインセクションがあります。RSTはZ. Pawlak(1982、1991)によって提案された、異質と不正確さを含むモデリングと情報システムのための高度な数学です。オブジェクト間の識別不能な関係RSTは、情報を抽出するために追加のパラメータを必要としません。
FRST理論、RSTの拡張子は、D.デュボアとH.プラーデ(1990)によって提案され、L.A.によって提案されたファジィ集合で表現されている不確実性と識別不能の概念を組み合わせました。Zadeh (1965) and RST. この概念では、予備的なデータを離散化せずに連続属性(変数)で分析することができます。上述した概念に基づいて、多くのメソッドが提案されています。課題を解決するためのメソッドは、識別不能の関係と近似の概念を使用します。
少し余談です。
知識表現のメソッドは、通常、情報システムにおいて主要な役割を果たしています。誘導性概念形成のシステムの知識を提示する最もよく知られているメソッドは、生成規則、決定木、述語の計算と意味ネットワークです。
実際の情報アレイに格納された場合、次の問題が表示されます。:
- このデータは、(構造的、定性的、定量的)に異種です。
- 通常、大規模なので、実際のデータベースが容認できないことがあり、データベースからの知識を取得するため、指数関数的な複雑さのアルゴリズムです。
- 実際のデータ配列に含まれる情報は、歪んだ、過度の、不完全であることがあり、いくつかの値が完全に存在しなくてもよいです。したがって、分類規則の構成は、唯一の既存の属性を使用する必要があります。
現在、データベース(データマイニング)から知識を抽出するためのラフ集合論は、理論的枠組みと実践的なメソッドのセットとして使用されています。
おおよそのセットは、正確に利用可能な関数のセットによって記述することができない、すなわち、未定義の境界を有します。
この集合論は、1982年にZdzislaw Pawlakによって提案され、不完全な情報のための新しい数学的な基盤となりました。この理論の最も重要な概念は、可能性または要素の所属する「ファジー」の境界とセットの必要性を評価する近似です。
下の近似は決定的な高い近似は要素が含まれ、Xに属する不明確な境界領域を上位と下位の差がある近似に属するX集合の要素があります。
だいたいのセットの、シンプルでありながら強力なコンセプトは、複数の理論的研究のための拠点となりました。 - ロジック、代数、トポロジーおよび研究適用 - 人工知能、近似推論、知的データ分析、決定理論、画像処理とパターン認識。
情報の「粒度」に関連する「データ不完全性」と「近似セット」の概念。この概念は、本質的にトポロジーであり、そのようなファジィ集合、ベイズ推論、ニューラルネットワーク、進化的アルゴリズム、データ分析の統計的メソッドとして、不完全な情報を操作するアプローチを補完します。
次に進みましょう。このパッケージで提供されるすべてのメソッドは、それに応じてグループ分けすることができます。
RSTとFRSTの基本概念。下限と上限の近似値、正の領域とdiscernibility行列:このパートでは、4つの異なるタスクを観察することができます。
離散化。名目に物理データを変換するために使用されます。RSTの観点から、このタスクは、オブジェクト間のdiscernibilityを維持しようとします。
特徴選択。これは、予測変数の完全なセットと同じ品質を得るために予測因子のサブセットを見つけるプロセスです。言い換えると、この目的は、本質的な特徴を選択し、それらの依存を排除することです。複数の関数を含むデータセットに直面している場合に有効かつ必要です。RSTとFRSTの面で予測因子の選択はsuperreductsの検索に関するものです。
インスタンスの選択。このプロセスは、コヒーレントを節約しながら、トレーニングデータセットから、不要なコピーを除去することを目的としています。従って、良好な分類精度は、積極的な貢献を与えない試験片を除去することによって達成されます。
ルールの誘導。すでに述べたように、誘導ルールのタスクは、ルールを生成するソリューションテーブルの知識を提供するために使用されます。典型的には、このメソッドは、機械学習の訓練段階と呼ばれます。
予測/分類。このタスクは、新たなデータセット(テストセット)の変数の値を予測するために使用されます。
予測因子の選択とサンプルの選択 - このリストから2つのカテゴリを探求します。
入力および出力データのセットを形成してみましょう。以前に取得した同じデータを使用しますが、パッケージで動作する「DecisionTable」クラスに変換します。> library(RoughSets) 必要なパッケージをロード:Rcpp > require(magrittr) > data.tr <- SF.asDecisionTable(data.f[idx$tr, ], + decision.attr = 16, + indx.nominal = 16) > data.tst <- SF.asDecisionTable(data.f[idx$ts, ], + decision.attr = 16, + indx.nominal = 16 + ) > true.class <- data.tst[ ,ncol(data.tst)]以前に述べたように、RSTは、名目上のデータを使用しています。継続的な数値データを持っているので、パッケージから入手できる特殊な離散化機能を使用して、公称データに変換しようとしています。
> cut.values <- D.global.discernibility.heuristic.RST(data.tr) > data.tr.d <- SF.applyDecTable(data.tr, cut.values)
結果として得られるか見てみましょう:
> summary(data.tr.d) DX ADX (12.5,20.7]: 588 (17.6,19.4]: 300 (20.7, Inf]:1106 (19.4,25.4]: 601 [-Inf,12.5]: 948 (25.4,31.9]: 294 (31.9, Inf]: 343 [-Inf,17.6]:1104 oscDX ar (1.81, Inf]:1502 (-40.6,40.6]:999 [-Inf,1.81]:1140 (40.6,71.9] :453 (71.9, Inf] :377 [-Inf,-40.6]:813 tr atr (0.000205,0.000365]:395 (0.00072,0.00123]:1077 (0.000365,0.0005] :292 (0.00123, Inf] : 277 (0.0005,0.00102] :733 [-Inf,0.00072] :1288 (0.00102,0.00196] :489 (0.00196, Inf] :203 [-Inf,0.000205] :530 cci chv (-6.61, Inf]:1356 (-0.398,0.185]:1080 [-Inf,-6.61]:1286 (0.185,0.588] : 544 (0.588, Inf] : 511 [-Inf,-0.398] : 507 cmo sign (5.81,54.1]: 930 [-Inf, Inf]:2642 (54.1, Inf]: 232 [-Inf,5.81]:1480 vsig slowD (0.0252, Inf]:1005 [-Inf, Inf]:2642 [-Inf,0.0252]:1637 oscK signal (-0.0403,0.000545]:633 (-11.4, Inf]:1499 (0.000545,0.033] :493 [-Inf,-11.4]:1143 (0.033, Inf] :824 [-Inf,-0.0403] :692 vol Class (0.0055,0.00779]:394 -1:1319 (0.00779,0.0112]:756 1 :1323 (0.0112,0.0154] :671 (0.0154, Inf] :670 [-Inf,0.0055] :151
予測因子が離散化されていることがわかります。slowD, sign がすべて分離されていないです。変数シグナル、vsig、cci、oscDXは、単に2つの領域に分割されています。他の変数は3と6クラスの間で分割されています。
重要な変数を選択します:
> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list()) > best1 <- reduct1$reduct > best1 DX ADX oscDX ar tr atr cci 1 2 3 4 5 6 7 chv cmo vsig oscK signal vol 8 9 11 13 14 15
分割されなかったデータセットから削除されます(slowD, sign)。テストセットの離散化を行い、減少に応じて変換します。
> data.tst.d <- SF.applyDecTable(data.tst, cut.values) > new.data.tr <- SF.applyDecTable(data.tr.d, reduct1) > new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)
さて、「誘導ルール」と呼ばれるパッケージの優れた点を使用して、予測因子と標的に結合する一連のルールを抽出します。次のいずれかのオプションが使用されます。
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)
これらのルールが予測でどのように動作するかチェックします。
> pred.vals <- predict(rules, new.data.tst) > table(pred.vals) pred.vals -1 1 655 667
Metrics:
> caret::confusionMatrix(true.class, pred.vals[ ,1]) 混同マトリックスと統計 Reference 予測 -1 1 -1 497 163 1 158 504 精度:0.7572 95% CI : (0.7331, 0.7801) No情報レート:0.5045 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5144 マクネマーの検定p値:0.8233 精度:0.7588 特異性:0.7556 Pos Pred値:0.7530 Neg Pred値:0.7613 プレバレンス : 0.4955 検出率:0.3759 検出プリバレンス:0.4992 バランス精度:0.7572 'Positive' Class : -1
意義の例の選択:
> ##-----Instance Selection----------- > res.1 <- IS.FRIS.FRST(decision.table = data.tr, control = list(threshold.tau = 0.5, alpha = 1, type.aggregation = c("t.tnorm", "lukasiewicz"), t.implicator = "lukasiewicz")) > new.data.tr <- SF.applyDecTable(data.tr, res.1) > nrow(new.data.tr) [1] 2353約300の例は、破棄と評価されました。このセットからルールセットを抽出し、前のセットで予測品質を比較します。
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9,
timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
-1 1
638 684
> caret::confusionMatrix(true.class, pred.vals[ ,1])
混同マトリックスと統計
Reference
予測 -1 1
-1 506 154
1 132 530
Accuracy : 0.7837
95% CI : (0.7605, 0.8056)
No情報レート:0.5174
P-Value [Acc > NIR] : <2e-16
Kappa : 0.5673
マクネマーの検定のp値:0.2143
精度:0.7931
特異性:0.7749
順位Pred値:0.7667
Neg Pred値: 0.8006
プリバレンス:0.4826
検出率:0.3828
検出プリバレンス:0.4992
バランス精度:0.7840
'Positive' Class : -1
品質は、以前の場合よりも良くなります。RandomUniformForestsの場合と同様に、反復実験で再現性のある結果を得ることは不可能であることに留意すべきです。それぞれわずかに異なる結果を与えます。
ルールはどのように見えるでしょうか?見ていきましょう:> head(rules) [[1]] [[1]]$idx [1] 6 4 11 [[1]]$values [1] "(85.1, Inf]" "(0.00137, Inf]" "(0.0374, Inf]" [[1]]$consequent [1] "1" [[1]]$support [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454 [11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661 [21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877 [31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981 [41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191 [51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396 [61] 2472 2489 2497 2531 2564 2583 2602 2643 [[1]]$laplace 1 0.9857143
データを含むリストは、次のとおりです。
- $idx - このルールのインデックス予測因子。上記の例では、6(" atr")、4("ar")、11(vsig)があります。
- $values - このルールがインジケーターの範囲です。
- $consequent - ソリューション:class="1"。理解できるようにするには:" atr"の範囲(85.1 Inf]" ANDarの範囲"(0.00137 Inf]" AND"Vsig"の範囲(0.0374 Inf]"、クラス="1"にします。
- $support - このソリューションをサポートするインデックス。
- $laplace - このルールの信頼度の評価。
ルールの計算は、かなりの時間を要します。
結論
最も貴重な選択することに基づいて新たな機会を検討しています。また、予測の依存関係と応答への影響の異なるレベルを検討しました。実験の結果は、RBMとディープネットワークを検討する次の記事で適用されます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/2029
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 自己組織化特徴マップ(Kohonenマップ) - サブジェクトリビジッティング
自己組織化特徴マップ(Kohonenマップ) - サブジェクトリビジッティング
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
リアルタイムで「直近300バー抜き」を 使うのか!
リアルタイムで使えるのか?
あなたの記事はすべて間違っています。なぜなら、あなたのターゲット定義が間違っているからです。あなたの指摘に従えば、300小節後にシンガルが起こるので、リアルタイムではすべて機能しません。
あなたの指摘に従えば、300小節後にシンガルが発生します。
リアルタイムで「直近300バー抜き」を 使うのか!
リアルタイムで使えるのか?
あなたの記事はすべて間違っています。なぜなら、あなたのターゲット定義が間違っているからです。あなたの指摘に従えば、300小節後にシンガルが起こるので、リアルタイムではすべて機能しません。
あなたの指摘に従えば、シンガルは300小節後に起こるでしょう。
あなたは著者のビジョンを本当に理解していないし、自分の想像に甘すぎるし、あなたの言っていることの愚かさは、自分自身に重ね合わされているだけだ。
ウラジーミル・ペレヴェンコへ:素晴らしい記事をありがとう ! フリーウォーク」のこのバカげたこと、すべての中国人が彼を好きなわけではない。
次のブランチでお答えします。
こんにちは、ウラジミール、
この質問に関するあなたの回答は見つかりませんでした。また、Digの値が何なのかもわかりません!
親愛なる皆さん、
ZZ関数の 変数で 定義されている--Dig--は何を意味するのか、どなたか教えてください。もしそうなら、この定数の値はどうすればいいのでしょうか?
Dig--小数点以下の桁数。たぶん5か3。
返信が遅れて申し訳ない。質問を見ていませんでした。議論は多くの枝に散らばっている。私はそれを追跡する時間がありません。
すみません。
この記事はボリュームがあり、労をねぎらった。
しかし、疑問がある:
1.各バーにラベル付けされた選択されたターゲットで層別化を使っている。代表的でない2つのサンプルを混合すると、通常、結果が改善されるが、それは歪む。
2- 構築されたモデルに基づく特徴選択、特に最初の分割ランダムと貪欲法を考慮すると、モデル構築法のための特徴削減法である。貪欲な方法は常に正しく安定しているとは限りません。この場合、少なくとも異なるサブサンプルを使用する必要があるでしょう。
2番目の方法は最後まで理解できませんでした。ランダムな最初の予測因子と同じで、それからリーフを構築しようとするのでしょうか、それともツリーを構築して最良のリーフを残し、それを評価に使用するのでしょうか?