スタックRBMとディープニューラルネットワーク。セルフトレーニング、及びセルフコントロール

この記事では、ディープニューラルネットワークと予測の選択に関する以前の記事の続きです。ここでは、スタックRBMによって開始されたニューラルネットワークの関数を扱い、「darch」パッケージの実装をします。ニューラルネットワークの予測性能を改善するため、マルコフモデルの可能性も明らかにします。最後に、プログラムでEAを実装します。

コンテンツ

• 1. DBNの構造
• 2. 調製およびデータの選択
• 2.1. エントリー変数
• 2.2。出力変数
• 2.3。初期データフレーム
• 2.3.1。高い相関変数を削除
• 2.4. 最も重要な変数の選択
• 3. 実験パート。
• 3.1。構築モデル
• 3.1.1。「darch」パッケージの簡単な説明
• 3.1.2. DNAモデルを構築。パラメーター。
• 3.2。トレーニングおよびテストサンプルの形成。
• 3.2.1。バランシングクラスと前処理。
• 3.2.2。ターゲット変数のコーディング
• 3.3。モデルのトレーニング
• 3.3.1。事前トレーニング
• 3.3.2。微調整
• 3.4。モデルをテスト。マトリクス
• 3.4.1。デコード予測。
• 3.4.2。予測結果を改善
• 較正
• マルコフ連鎖モデルのスムージング
• 理論的なバランス曲線上の予測シグナルを修正
• 3.4.3。マトリクス
• 4. EAの構造
• 4.1。EA操作の説明
• 4.2。セルフコントロール。セルフトレーニング
• インストールと起動
• メソッドおよび定性的なインジケーターを改善するメソッド。
• 結論

イントロダクション

実験を行うためのデータの準備では、予測因子の選択について前の記事から変数を使用します。最初のサンプルを形成し、きれいにし、重要な変数を選択します。

テストと検証サンプルに初期サンプルを分割するメソッドを検討します。

"darch"パッケージのDBNネットワークのモデルを構築し、データセットにトレーニングします。モデルをテストした後、モデルの品質を評価するために、メトリックを取得します。パッケージには、ニューラルネットワークの設定を構成するため、多くの機会を検討していきます。

また、マルコフモデルは、ニューラルネットワークの予測を向上させることができ、メソッドについて説明します。

モデルが継続的なモニタリングの結果に基づいて、トレードを中断することなく、その場で定期的にトレーニングされるEAを開発します。「darch」パッケージからのDBNモデルは、EAに使用されます。また、EAは前の記事からSAE DBNを使用して構築されます。

さらに、さまざまなメソッドとモデルの定性的なインジケーターを改善するメソッドを示します。

1. スタックRBMによる初期化、ディープニューラルネットワークの構造（DN_SRBM）

DN_SRBMは、基本的には、ニューラルネットワークの隠れた層の数に等しく、RBMのn個で構成されていることに注意してください。トレーニングには、二つの段階があります。

第一段階は、事前トレーニングを必要とします。すべてのRBMは、体系的に（ターゲットなし）設定エントリーにスーパーバイザーなしでトレーニングされています。隠された層のこの重み付けの後、RBMは、ニューラルネットワークの関連する隠れ層に転送されます。

第２段階、ニューラルネットワークは、スーパーバイザーでトレーニングされて微調整を伴います。それについての詳細は、前回の記事で提供されていたので、ここでは繰り返す必要はありません。単に前回の記事で使用していた「deepnet」パッケージとは異なり、「darch」パッケージモデルを構造の広い実装およびチューニングに言及します。モデルを作成する際に、より詳細が提供されます。図1は、構造及びDN_SRBMのトレーニングプロセスを示しています

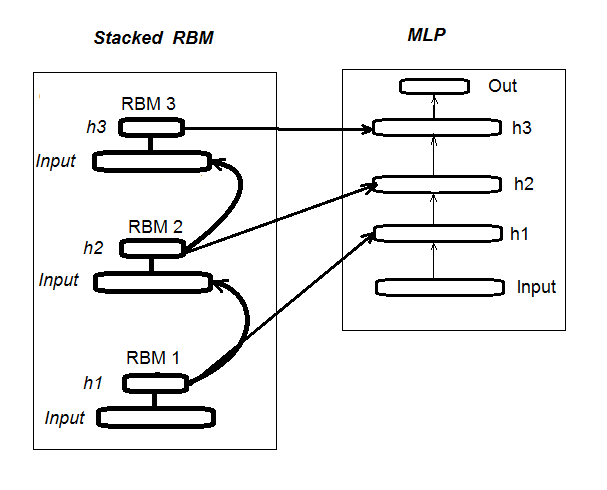
図1。DN SRBMの構造

2. 調製およびデータの選択

2.1. エントリー変数（看板、予測変数）

前回の記事では、すでに予測因子の評価と選択を検討し、今回は、追加情報を提供する必要はありません。11のインジケーター（：ADX、アルーン、ATR、CCI、ボラティリティをチェイキン、CMO、MACD、RSI、ストフ、SMI、ボラティリティすべてオシレーター）を使用します。いくつかの変数は、いくつかのインジケーターから選択しました。このように、17の変数のエントリーセットを形成しています。EURUSD、14.02.16時点のМ30の最後の6000の足からのクオートを取る、とIn()関数を使用してインジケーターの値を計算してみましょう。

#---2---------------------------------------------
In <- function(p = 16){
  require(TTR)
  require(dplyr)
  require(magrittr)
  adx <- ADX(price, n = p) %>% as.data.frame %>% 
    mutate(.,oscDX = DIp - DIn) %>% 
    transmute(.,DX, ADX, oscDX) %>% 
    as.matrix()
  ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% 
    extract(,3)
  atr <- ATR(price, n = p, maType = "EMA") %>%
    extract(,1:2)
  cci <- CCI(price[ ,2:4], n = p)
  chv <- chaikinVolatility(price[ ,2:4], n = p)
  cmo <- CMO(price[ ,'Med'], n = p)
  macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% 
    as.data.frame() %>% 
    mutate(., vsig = signal %>% 
             diff %>% c(NA,.) %>% multiply_by(10)) %>% 
    transmute(., sign = signal, vsig) %>% 
    as.matrix()
  rsi <- RSI(price[ ,'Med'], n = p)
  stoh <- stoch(price[ ,2:4], nFastK = p, 
                nFastD =3, nSlowD = 3, 
                maType = "EMA") %>%
                                as.data.frame() %>% 
                                mutate(., oscK = fastK - fastD) %>%
                                transmute(.,slowD, oscK) %>% 
                                as.matrix()
  smi <- SMI(price[ ,2:4],n = p, nFast = 2, 
             nSlow = 25, nSig = 9)
  kst <- KST(price[ ,4])%>% as.data.frame() %>% 
                                mutate(., oscKST = kst - signal) %>%
                                select(.,oscKST) %>% as.matrix()
  In <- cbind(adx, ar, atr, cci, chv, cmo, macd, 
              rsi, stoh, smi, kst)
  return(In)
}

出力上のエントリーデータ行列を取得します。

2.2出力データ（目的変数）

ターゲット変数として、ZZで得られたシグナルを取ります。ジグザグとシグナルを計算する関数：

#----3------------------------------------------------
ZZ <- function(pr = price, ch = ch , mode="m") {
  require(TTR)
  require(magrittr)
  if (ch > 1) ch <- ch/(10 ^ (Dig - 1))
  if (mode == "m") {pr <- pr[ ,'Med']}
  if (mode == "hl") {pr <- pr[ ,c("High", "Low")]}
  if (mode == "cl") {pr <- pr[ ,c("Close")]}
  zz <- ZigZag(pr, change = ch, percent = F, 
               retrace = F, lastExtreme = T)
  n <- 1:length(zz)
  dz <- zz %>% diff %>% c(., NA)
  sig <- sign(dz)
  for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]}
  return(cbind(zz, sig))
}

関数のパラメータ：

pr = price – matrix of OHLCMed quotes;

ch – minimum length of the zigzag bend in the points (4 signs) or in real terms (for example, ch = 0.0035);

mode – applied price ("m" - medium, "hl" - High and Low, "cl" - Close), medium used by default.

この関数は、2つの変数を持つ行列を返します - 実際には、ジグザグやシグナルの範囲でジグザグ角のベースに得られます[-1;1]。左側に1つの足分シグナルをシフトします。このシグナルは、ニューラルネットワークをトレーニングするために使用されます。

少なくとも37ポイント（4sign）の曲げ長さとZZするためのシグナルを計算します。

> out <- ZZ(ch = 37, mode = "m")
必要なパッケージをロードする：TTR
読み込みに必要なパッケージ：magrittr
> table(out[ ,2])

  -1    1 
2828 3162

ご覧の通り、このクラスは少しアンバランスです。モデルのトレーニングのサンプルを形成する場合、横ばいに必要な措置を講じます。

2.3。初期データフレーム

初期データフレームを作成する不確実なデータ（NA）からきれいにし、２つのクラス「-1」と「1」の要因にターゲット変数を変換する関数を書いてみましょう。この関数は、In()およびZZ()で関数を書か兼ね備えています。すぐにモデルの予測の品質を評価するために、最後の500バーをトリミングします。

#-----4---------------------------------
form.data <- function(n = 16, z = 37, len = 500){
  require(magrittr)
  x <- In(p = n)
  out <- ZZ(ch = z, mode = "m")
  data <- cbind(x, y = out[ ,2]) %>% 
    as.data.frame %>% head(., (nrow(x)-len))%>%
        na.omit
  data$y <- as.factor(data$y)
  return(data)
}

2.3.1。高い相関変数を削除

初期設定から0.9以上の相関係数を持つ変数を削除します。初期データフレームを形成相関の高い変数を削除し、クリーンなデータを返す関数を記述します。

変数が0.9以上の相関関係を持ち、確認することができます。

> data <- form.data(n = 16, z = 37) # prepare data frame
> descCor <- cor(data[ ,-ncol(data)])# remove a target variable
> summary(descCor[upper.tri(descCor)])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-0.1887  0.0532  0.2077  0.3040  0.5716  0.9588 
> highCor <- caret::findCorrelation(descCor, cutoff = 0.9)
> highCor
[1] 12  9 15
> colnames(data[ ,highCor])
[1] "rsi" "cmo" "SMI"

したがって、上記の変数は削除の対象となります。データフレームから削除します。

> data.f <- data[ ,-highCor]
> colnames(data.f)
 [1] "DX"     "ADX"    "oscDX"  "ar"     "tr"    
 [6] "atr"    "cci"    "chv"    "sign"   "vsig"  
[11] "slowD"  "oscK"   "signal" "vol"    "Class" 

1つの関数にコンパクトに書き込みます：

#---5-----------------------------------------------
cleaning <- function(n = 16, z = 37, cut = 0.9){
  data <- form.data(n, z)
  descCor <- cor(data[ ,-ncol(data)])
  highCor <- caret::findCorrelation(descCor, cutoff = cut)
  data.f <- data[ ,-highCor]
  return(data.f)
}
> data.f <- cleaning()

相関の高いデータがセットから削除されるべきであることに同意するものとします。しかし、両方のオプションを使用して、結果がここで比較すべきです。このケースでは、オプションで削除を選択します。

2.4. 最も重要な変数の選択

グローバルな重要性、ローカルとクラスによる重要性：変数は、3つのインジケーターに基づいて選択されます。前回の記事で詳述したように、randomUniformForestパッケージのチャンスをつかむでしょう。次のアクションは、コンパクトに1つの関数に収集されます。実行されると、結果として3セットを取得します。

• 相互作用で最高の変数を持ちます。
• クラス「-1」の最良の変数です。
• クラス「1」の最良の変数を持ちます。

#-----6------------------------------------------------
prepareBest <- function(n, z, cut, method){
  require(randomUniformForest) 
  require(magrittr)
  data.f <<- cleaning(n = n, z = z, cut = cut)
  idx <- rminer::holdout(y = data.f$Class)
  prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method)
  x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
  x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
  y.train <- data.f[idx$tr, ncol(data.f)]
  y.test <- data.f[idx$ts, ncol(data.f)]
#---------
  ruf <- randomUniformForest( X = x.train, Y = y.train,
                              xtest = x.test, ytest = y.test,
                              mtry = 1, ntree = 300,
                              threads = 2, nodesize = 1
                       ）
  imp.ruf <- importance(ruf, Xtest = x.test)
  best <- imp.ruf$localVariableImportance$classVariableImportance %>% 
                  head(., 10) %>% rownames()
#-----partImport
  best.sell <- partialImportance(X = x.test, 
                                imp.ruf, 
                                whichClass = "-1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  best.buy <- partialImportance(X = x.test,
                                   imp.ruf,
                                   whichClass = "1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  dt <- list(best = best, buy = best.buy, sell = best.sell)
  return(dt)
}

関数計算のオーダーを明確にします。公式パラメータ：

n – インプットデータパラメータ;

z – アウトプットデータパラメータ;

cut – 変数の相関閾値;

method - エントリーデータ前処理メソッド。

計算のオーダー：

• 変数が削除に相関しているdata.fの初期セットを作成し、保存します。
• idxのトレーニングおよびテストサンプルのインデックスを特定します。
• 準備の前処理パラメータを決定します。
• トレーニングおよびテストサンプルを、正規化されたエントリーデータに初期サンプルに分割。
• 取得したセットのrufモデルをテストします。
• imp.of変数の重要度を計算します。
• 相互作用の点で10の最も重要な変数を選択する - best。
• 最も重要な各クラスの変数「-1」と「+1」を選択 - best.buy、best.sell。
• best.sell、best.buy - 予測の3セットでリストを作成します。
  

これらのサンプルを計算し、選択された変数の、グローバルローカルおよび部分的な重要性の値を評価します。

> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign"))
読み込んで必要なパッケージ：randomUniformForest
Labels -1 1 は 1 2 に変換されます。for 
       as交換。

1 - グローバル変数の重要度（14最も重要な情報に基づいて）：
注：ほとんどの予測機能は、 'スコア' によってプロットされています。判別式
は、考慮に入れなければならない。'class' 及び 'class.frequency'.

   変数スコア class class.frequency percent
1        cci  4406    -1            0.51  100.00
2     signal  4344    -1            0.51   98.59
3        ADX  4337    -1            0.51   98.43
4       sign  4327    -1            0.51   98.21
5      slowD  4326    -1            0.51   98.18
6        chv  4296    -1            0.52   97.51
7       oscK  4294    -1            0.52   97.46
8        vol  4282    -1            0.51   97.19
9         ar  4271    -1            0.52   96.95
10       atr  4237    -1            0.51   96.16
11     oscDX  4200    -1            0.52   95.34
12        DX  4174    -1            0.51   94.73
13      vsig  4170    -1            0.52   94.65
14        tr  4075    -1            0.50   92.49
   percent.importance
1                   7
2                   7
3                   7
4                   7
5                   7
6                   7
7                   7
8                   7
9                   7
10                  7
11                  7
12                  7
13                  7
14                  7


2 - ローカル変数の重要性
変数間の相互作用（10最初の（列で最も重要な変数）と第２（行）のオーダー）：
（各オーダーにおける）各変数について、他との相互作用は計算されます。

                cci  slowD    atr     tr     DX
atr          0.1804 0.1546 0.1523 0.1147 0.1127
cci          0.1779 0.1521 0.1498 0.1122 0.1102
slowD        0.1633 0.1375 0.1352 0.0976 0.0956
DX           0.1578 0.1319 0.1297 0.0921 0.0901
vsig         0.1467 0.1209 0.1186 0.0810 0.0790
oscDX        0.1452 0.1194 0.1171 0.0795 0.0775
tr           0.1427 0.1168 0.1146 0.0770 0.0750
oscK         0.1381 0.1123 0.1101 0.0725 0.0705
sign         0.1361 0.1103 0.1081 0.0704 0.0685
signal       0.1326 0.1068 0.1045 0.0669 0.0650
avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775
               vsig  oscDX   oscK signal     ar
atr          0.1111 0.1040 0.1015 0.0951 0.0897
cci          0.1085 0.1015 0.0990 0.0925 0.0872
slowD        0.0940 0.0869 0.0844 0.0780 0.0726
DX           0.0884 0.0814 0.0789 0.0724 0.0671
vsig         0.0774 0.0703 0.0678 0.0614 0.0560
oscDX        0.0759 0.0688 0.0663 0.0599 0.0545
tr           0.0733 0.0663 0.0638 0.0573 0.0520
oscK         0.0688 0.0618 0.0593 0.0528 0.0475
sign         0.0668 0.0598 0.0573 0.0508 0.0455
signal       0.0633 0.0563 0.0537 0.0473 0.0419
avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545
                chv    vol   sign    ADX avg2ndOrder
atr          0.0850 0.0850 0.0847 0.0802      0.1108
cci          0.0824 0.0824 0.0822 0.0777      0.1083
slowD        0.0679 0.0679 0.0676 0.0631      0.0937
DX           0.0623 0.0623 0.0620 0.0576      0.0881
vsig         0.0513 0.0513 0.0510 0.0465      0.0771
oscDX        0.0497 0.0497 0.0495 0.0450      0.0756
tr           0.0472 0.0472 0.0470 0.0425      0.0731
oscK         0.0427 0.0427 0.0424 0.0379      0.0685
sign         0.0407 0.0407 0.0404 0.0359      0.0665
signal       0.0372 0.0372 0.0369 0.0324      0.0630
avg1rstOrder 0.0497 0.0497 0.0495 0.0450      0.0000


相互作用に基づく変数の重要度（10最重要）：
   cci    atr  slowD     DX     tr   vsig  oscDX 
0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 
  oscK signal   sign 
0.0599 0.0509 0.0464 

ラベルの上に変数の重要度（10各ラベルへの条件付きで最も重要な変数）：
       Class -1 Class 1
cci        0.17    0.23
slowD      0.20    0.09
atr        0.14    0.15
tr         0.04    0.12
oscK       0.08    0.03
vsig       0.06    0.08
oscDX      0.04    0.08
DX         0.07    0.08
signal     0.05    0.04
ar         0.04    0.02

結果

1. グローバルな重要性の点で、14の変数は等しいです。
2. 最高の10は、全体（グローバルな重要性）との相互作用（ローカルの重要性）によって定義されています。
3. 各クラスの部分的な重要性が７つの変数は以下のチャートに表示されます。

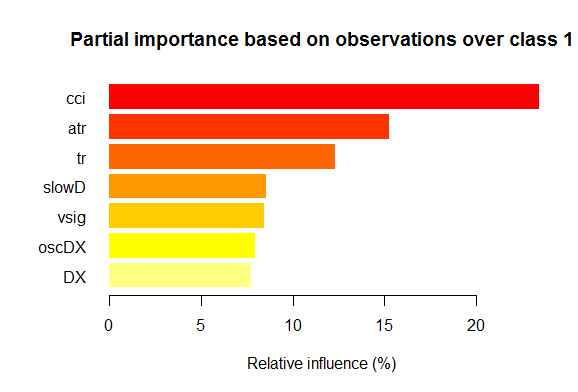
図2。「1」クラスの変数の部分的な重要性

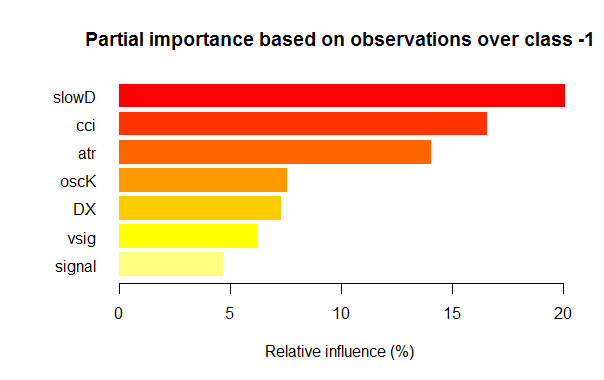
図3。「-1」クラスの変数の部分的な重要性

ご覧の通り、異なるクラスの最も重要な変数は、構造とランキングの双方で異なっています。slowD変数が最も重要である「-1」クラスの場合、その後4位にあります。

そこで、データのセットの準備ができています。実験を続行することができます。

3. 実験パート。

実験は、R言語で行われます - Rオープン、バージョン3.2.2。http://www.revolutionanalytics.com/revolution-r-open

正規のR3.2.2以上で利点があります。

• マルチスレッド処理を適用し、より定性的な計算Intel® Math Kernel Library。
  
• 再現性のRツールキットの高度な関数。明確化：R言語は、常に既存のパッケージを改善し、新しいものを追加しています。このような進歩は、再現性の損失を伴います。数ヶ月前に書かれたパッケージは、突然うまく機能しなくなる可能性があります。多くの時間は、パッケージの変化による誤差を識別し、無駄になります。例えば、EAは、作成の時点で、ディープニューラルネットワーク上の最初の記事に添付されています。しかし、数ヶ月後にユーザーは、その非操作性について訴えるでしょう。「svSocket」パッケージの更新はEAの故障につながります。最終的なEAは、この記事に添付されます。この問題は課題となり、簡単に解決しました。新しいディストリビューションがリリースされたときにCRANリポジトリ内のすべてのパッケージは、コピーすることによって、リリース日に固定されています。この日付の後のCRANの変化は、「凍結」パッケージに影響を与えることはできません。さらに、2014年10月から開始し、毎日CRANのスナップショット、関連する状態を固定されたパッケージのバージョンになります。独自の「チェックポイント」パッケージで、必要とする日における関連する必要なパッケージをダウンロードすることができます。言い換えれば、いくつかの種類を操作します。

また、別のニュース。MicrosoftはRevolution Analyticsを買収したとき、開発サポートすることを約束し、無料でご利用できるRevolutionRオープン（RRO）を公開しました。RROとRevolutionR Enterpiseでノベルティに関する多数のメッセージが続きました。（Rと SQL Server、 PowerBI、Azure、コCortana Analiticsの統合を言及しないように、）。MicrosoftRサーバー - 次のRROの更新がMicrosoft R Open、およびRevolution R Enterpriseに呼び出されるという情報があります。前にMicrosoftはVisual Studioで利用できるようになることを発表しました。Visual Studio用のRツール（RTVS）は、以下の Visual Studioのモデル用のPythonツールを編集するRの完全なIDEを提供するVisual Studioのに自由に加えてもよく、スクリプトをデバッグします。

この記事を書き終わった時点では、Microsoft Rオープン（R3.2.3）は、リリースされました。

3.1。構築モデル

3.1.1。「darch」パッケージの簡単な説明

「darch」版。0.10.0パッケージだけ作成し、モデルのトレーニングが、自分の好みに合わせて調整することができない関数の広い範囲を提供しています。先に示したように、ディープニューラルネットワークは層の数、RBM（N=層-1）およびMLPニューラルネットワークのn個から成ります。RBMの層状事前トレーニングがスーパーバイザーなしでフォーマットされていないデータに対して実行されます。ニューラルネットワークの微調整は、フォーマットされたデータの監督を行います。トレーニングステージを割ると、ボリューム内のさまざまなデータを使用し（ただし、構造ではない！）、単独の事前トレーニングに基づいて、さまざまな微調整モデルを得るための機会を与えてくれます。事前トレーニングや微調整用データが同じであればさらに、２つの段階に分割し、一度にトレーニングすることが可能です。もしくは、ニューラルネットワークを使用せず、RBMを使用し、事前にトレーニングをスキップして、多層ニューラルネットワークを使用することができます。同時に、すべての内部パラメータへのアクセス権があります。パッケージは、上級ユーザーを対象としています。事前トレーニングと微調整：さらに、分割プロセスを分析します。

3.1.2. DNAモデルを構築。パラメーター。

トレーニングを構築し、DBNモデルをテストするプロセスを説明します。

1. 必要なパラメータでコンストラクタを使用して「Darch'という名前のディープ構造オブジェクトを作成します

newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),

ただし:

• layers：各層の層とニューロンの数を示す配列。 たとえば、layers = c(5,10,10,2)　－　5ニューロン（可視）、および2出力を備えた1出力層との2の隠れ層とエントリー層。
• BatchSize：トレーニング中のミニサンプルのサイズ。
• ff：ff形式は重み、偏差のために使用するかどうかを示します。ff形式は圧縮で大量のデータを保存するために適用されます。
• LogLevel：ログおよび出力のレベルこの関数を実行します。
• GenWeightFunction：RBMの重みの行列を生成する関数。ユーザの活性化関数を使用する機会があります。

ニューラルネットワークを事前にトレーニングするために使用される蓄積ネットワークに結合 - darch-オブジェクトは、（1層）含まれています。２つの属性 fineTuneFunctionと executeFunctionは、微調整の関数(バックプロパゲーション）および（ runDarch）。preTrainDArch()とfineTuneDArch()は2つのトレーニング機能を用いて行われます。最初の関数は対照的発散法を用いて、スーパーバイザせずにRPMネットワークをトレーニングします。第2の関数は、ニューラルネットワークの微調整関数属性で示された関数を使用しています。ニューラルネットワークのパフォーマンスの後、すべての層の出力は、実行出力属性で実行する出力属性のみ出力層で見つけることができます。

2. 事前トレーニングdarchオブジェクトの関数

preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),

ただし:

• darch: instance of the 'Darch' class;
• dataSet: data set for training;
• numEpoch: number of training epochs;
• numCD : number of sampling iterations. 通常、1つで十分です。
• ...転送することができる追加のパラメータトレーナー関数。
• trainOutputLayer：論理値RBMの出力層をトレーニングする必要があるかどうかを示します。

この関数はtrainRBM() の関連するニューラルネットワーク層へのトレーニング重みとバイアスの後にコピーします。

3. darchオブジェクトの微調整関数

fineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T, 
              isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101, 
              stopValidErr = -Inf, stopValidClassErr = 101, ...),

ただし:

• darch: 「Darch」クラスのサンプル;
• dataSet: トレーニング用データセットとテスト（検証に使用することができます）;
• dataSetValid : データのセット;
• numxEpoch: トレーニングエポック数;
• bootstrap: 論理検証データを作成するときに、ブートストラップを適用するために必要です;
• isBin：出力データが論理値として解釈されるべきであるかどうかを示します。By default — FALSE. TRUEの場合、0.5以上のすべての値は1として解釈されます。
• isClass：は、分類トレーニングされている場合を示しています。TRUEの場合は、分類の統計情報が決定されます。デフォルトはTRUE。
• stopErr：ニューラルネットワークのトレーニングをストップするための基準は、トレーニング中に発生します。-Inf by default;
• stopClassErr：ニューラルネットワークのトレーニングをストップするための基準は、トレーニング中に発生します。101 by default;
• stopValidErr：検証データにエラーが発生し、ニューラルネットワークをストップさせるための基準。-Inf by default;
• stopValidClassErr：ニューラルネットワークをストップさせるための基準。101 by default;
• ...トレーニング関数に渡すことができる追加のパラメータ。

この関数は微調整関数に保存された関数を持つネットワークをトレーニングします。エントリーデータ(trainData, validData, testData) 、それらに属するクラス（targetDataは、validTargets、testTargets）は、データセットまたはFF-マトリックスとして転送することができます。検証およびテスト用のデータとクラスは必須ではありません。提供されている場合には、ニューラルネットワークは、データセットを用いて実行され、統計情報が計算されます。isBin出力データをバイナリとして解釈されるべきであるならば、属性を示しています。isBin=TRUEの場合、0.5以上のすべての出力値は、1として解釈されるまた、エラー（stopErr、stopValidErr）またはトレーニングまたは検証セットの正しい分類（stopClassErr、stopValidClassErr）に基づいて、トレーニングのストップ基準を設定することができます。

すべての関数のパラメータは、デフォルト値を有します。しかし、他の値も利用可能です。例えば：

ニューラルネットを活性化する関数 - sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivativeをご利用いただけます。sigmoidUnitDerivativeはデフォルトで使用されます。

ニューラルネットワークの微調整の関数 - 弾力性 rpropagationによってバックプロパゲーションでは、4つのバリエーションが提供されています。（「Rprop-"" RPROP+"、" iRprop+"、" iRprop-」）及び minimizeClassifier（この関数は非線形共役勾配法を用いてトレーニングされています）。最後の2つのアルゴリズムに、サブジェクトの知識を持っている人に、複数のパラメータの設定とニューラルネットワークの微調整の個別の実装が提供されています。具体例：

rpropagation(darch, trainData, targetData, method="iRprop+",
             decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
             minDelta=0.000001, maxDelta=50, ...),

ただし:

• darch – トレーニングのdarchオブジェクト;
• trainData – エントリーデータは、トレーニングに設定します;
• targetData – トレーニングセットの予想出力;
• メソッド - トレーニングメソッド。"iRprop+" by default. "Rprop+", "Rprop-", "iRprop-" are possible;
• deFact - トレーニングの要因を減少させます。0.5 by default;
• incFact - トレーニングの要因を増やします。1.2 by default;
• weightDecay - トレーニングで重みを減少させます。0 by default;
• initDelta - アップデートで初期設定値。0.0125 by default;
• minDelta - ステップサイズの最小境界線。0.000001 by default;
• maxDelta - ステップサイズの上限境界線。デフォルトでは50。

この関数は、トレーニングされたニューラルネットワークとdarchオブジェクトを返します。

3.2。トレーニングおよびテストサンプルの形成。

データの最初のサンプルを形成しています。検証とテストサンプルに分割する必要があります。デフォルトで比率が2/3です。パッケージは、サンプルを分割するために使用される多くの関数を有しています。 rminer::holdout()トレーニングに初期サンプルを破壊し、サンプルをテストするためのインデックスを計算します。。

holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
        seed = NULL, window=10, increment=1),

ただし:

• y - 目的のターゲット変数、数値ベクトルまたは因子、この場合には、成層分離（クラス間割合はすべての部分で同じ）が適用されます。
• ratio - 分離の割合（百分率で - 学習サンプルのサイズが確立され;　サンプルの総数に - テストサンプルのサイズに確立されています）。
• 内部分割 - TRUEの場合、トレーニングデータが再びトレーニングと検証サンプルに分離される。同じ比率は、内部分離に適用されます。
• モード - モードサンプリング。利用可能なオプション：
• stratified – 層状ランダム分割（у要因であれば、標準的なランダム分割）;
• random – 標準のランダム分割。
• order - 最初の例は、トレーニングに使用され、残りのものは静的モードに適用されます。
• rolling - 一般的に（株式や金融相場の予測に適用される）スライディングウィンドウとして知られているウィンドウorder、のウィンドウサイズを指し除きます。テストサンプルが最後の反復を除いて、割合に相当しながら、各反復のトレーニングサンプルの大きさは、ウィンドウに固定されています。
• インクリメンタル - インクリメンタル反復回数とインクリメント - - また、そのウィンドウを除いて、増加ウィンドウとして知られている再トレーニングの増分モードは、初期ウィンドウサイズ、ITERであるすべての反復で追加されます。テストセットのサイズは、それが小さくできる最後の反復を除いて、割合に相当するのに対し、学習サンプルの大きさは、各反復においてインクリメントを増大します。
• iter - 再トレーニングの増分モデルの反復回数（モード=「ローリング」や、ITERは通常ループ内で設定されている「増分」場合にのみ使用）。
• seed - NULLの場合、ランダムシードを使用している以外のシードは（さらに計算が常に同じ結果を返す必要があります）固定されます。
• window - トレーニング・ウィンドウのサイズ（モード=「ローリング」の場合）、またはトレーニングウィンドウの初期サイズ（もしモード="増分"）;
• インクリメント - すべての反復でトレーニングウィンドウに追加された番号（モード=「増分」またはモード=「ローリング」）。

3.2.1。バランシングクラスと前処理。

多数のサンプルでクラスの数を揃えるトレーニングおよびテストサンプルにサンプルを分割し、前処理を実行する関数の書き込み（正規化を、必要に応じて）および関連するサンプルのリストを返します。 - train, test。バランスを達成するために、caret::upSample()クラスの分布が等しくなって、ランダムに交換して採取します。すべては、必要なクラスのバランスをとるために見つけます。しかし、すでに知られているように、実際には、真実の基準である実験の結果は、バランスのとれたサンプルは常にトレーニングでより良い結果を示しています。自身で実験をストップしません。

前処理にcaret::preProcess()関数を使用します。前処理のパラメータは、prepr変数に保存されます。すでに考慮され、以前の記事でそれらを適用しているので、ここでのさらなる説明はありません。

#---7----------------------------------------------------
prepareTrain <- function(x , y, 
                         rati, mod = "stratified", 
                         balance = F, 
                         norm, meth)
{
  require(magrittr)
  require(dplyr)
  t <- rminer::holdout(y = y, ratio = rati,
                       mode = mod)
  train <- cbind(x[t$tr, ], y = y[t$tr])
  if(balance){
    train <- caret::upSample(x = train[ ,best], 
                             y = train$y, 
                             list = F)%>% tbl_df
    train <- cbind(train[ ,best], select(train, y = Class))
  }
  test <- cbind(x[t$ts, ], y = y[t$ts])
  if (norm) {
    prepr <<- caret::preProcess(train[ ,best], method = meth)
    train = predict(prepr, train[ ,best])%>% cbind(., y = train$y)
    test =  predict(prepr, test[ ,best] %>% cbind(., y = test$y))
  }
  DT <- list(train = train,
             test = test)
  return(DT)
}

前処理に関するコメントは：エントリー変数の範囲に正規化されます（-1、1）。

3.2.2。ターゲット変数のコーディング

分類タスクを解くときに、ターゲット変数が複数のレベル（クラス）を有する因子です。このモデルでは、後続の目標状態から成るベクトル（列）として設定されています。例えば、 y = с("1", "1", "2", "3", "1"). ニューラルネットワークをトレーニングするためには、ターゲット変数は、符号化されなければなりません。この行列のすべての行では、1つの列のみ1を含んでもよいです。softmax() を使用して、出力層の活性化関数は、すべてのクラスでは、予測対象変数の状態の確率を得ることができます。classvec2classmat()関数は、符号化に使用されます。ターゲット変数、を符号化するための最良のメソッドは簡単なので、それを使用します。目標の予測値の逆変換（デコード）変数は、さまざまなメソッドによって達成されます。

3.3。モデルのトレーニング

3.3.1。事前トレーニング

前述したように、まず、デフォルトで予備トレーニングのパラメータを持つRBMの必要数、およびランダムな重みとニューロンの活性化関数のセットで開始するニューラルネットワークを含む DArchという名前のディープ構造オブジェクトを作成します。必要に応じて、オブジェクトの作成段階で、事前トレーニングパラメータは、変更することができます。その後、RPMネットワークが出力する（ターゲット変数なし）トレーニングサンプルを送信することにより、スーパーバイザーなしで事前にトレーニングされます。完了した後、 DАrchのトレーニング中に得られた重みとバイアスがニューラルネットワークに転送されます。（例えば）ベクターの形態で事前に隠されたニューロンの分布を設定する必要があります。

L<- c( 14, 50, 50, 2)

エントリー層のニューロンの数は、エントリー変数の数に等しいです。隠れ層、出力層は、2層を持つことになり、50ニューロンが含まれています。最後のビットを説明しましょう。ターゲット変数（要因）は、2つのレベル（クラス）がある場合、実際には、一つの出力で十分です。しかし、それぞれが一つのクラスに対応した行列にベクトルを変換し、出力層に分類タスクでよく動作するsoftmax活性化関数を、適用することができます。また、クラス確率の形での出力が、その後の分析で、追加の機会を与えます。この対象は、すぐにカバーされます。

エポック数は、通常、10から50の範囲内で、実験的に設定されています。

サンプリングの繰り返しの数は、デフォルトですが、このパラメータは、実験したい場合増加させることができます。これは、別の関数で定義されます：

#----8--------------------------------------------------------------
pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9)
{
  require(darch)
# create object DArch
  dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5)
＃設定された初期 
  setInitialMomentum(dbn) <- InM 
＃最終的な瞬間を設定   
  setFinalMomentum(dbn) <- FinM
＃最終的に初期から瞬間を切り替える設定した時間    
  setMomentumSwitch(dbn) <- round(0.8 * nE)
  dbn <- preTrainDArch(dbn, dataSet = dS, 
                  numEpoch = nE,
                  numCD = nCD, 
                  trainOutputLayer = T)
  return(dbn)
}

3.3.2。微調整

前述したように、パッケージはbackpropagation()、rpropagation()、 minimizeClassifier()、微調整のminimizeAutoencoder()を提供します。。十分パッケージに記載されていませんし、適用するメソッドのない例が存在しないので、最後は考慮されません。実験でこれらの関数は、良い結果を示しませんでした。

また、パッケージのアップデートについて何かを追加したいと思います。この記事を書き始めたとき、バージョンは0.9で、複数の変更を含む新しい0.10バージョンがリリースされました。すべての計算をやり直さなければなりませんでした。短いテストの結果に基づいて、動作速度が大幅に（ユーザーの場合、パッケージのより障害である）結果の品質とは異なり、増加しています。

第一の関数を考えてみましょう。（backpropagation） DАrchオブジェクトにデフォルトで設定され、トレーニングニューラルネットワークパラメータがここで使用されています。第二の関数（rpropagation）も、デフォルトパラメータとデフォルトで「iRprops」の4つのトレーニングメソッド（上述）を有しています。パラメータやトレーニングメソッドの両方を変更することができます。これらの関数を適用することは簡単です：微調整関数を変更するFineTuneDarch()

setFineTuneFunction(dbn) <- rpropagation  

（必要な場合）微調整の設定に加えて、すべての層におけるニューロンを活性化する関数を設定する必要があります。sigmoidUnitは、デフォルトではすべてのレイヤに設定されています。これはパッケージ sigmoidUnitDerivative、linearUnitDerivative、tanSigmoidUnitDerivative、softmaxUnitDerivativeで利用可能です。微調整は微調整関数を選択する能力を持つ別の関数で定義されます。別のリスト内の活性化可能な関数を収集します。

actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)

トレーニングし、ニューラルネットワークを生成する微調整関数を記述します：最初 トレーニングを受けたbackpropagation関数を使用してrpropagation：

#-----9-----------------------------------------
fineMod <- function(variant=1, dbnin, dS, 
                    hd = 0.5, id = 0.2,
                    act = c(2,1), nE = 10)
{
  setDropoutOneMaskPerEpoch(dbnin) <- FALSE
  setDropoutHiddenLayers(dbnin) <- hd
  setDropoutInputLayer(dbnin) <- id
  layers <<- getLayers(dbnin)
  stopifnot(length(layers)==length(act))
  if(variant < 0 || variant >2) {variant = 1}
  for(i in 1:length(layers)){
    fun <- actFun %>% extract2(act[i])
    layers[[i]][[2]] <- fun
  }
  setLayers(dbnin) <- layers
  if(variant == 1 || variant == 2){ # backpropagation
    if(variant == 2){# rpropagation
      #setDropoutHiddenLayers(dbnin) <- 0.0
      setFineTuneFunction(dbnin) <- rpropagation
    }
    mod = fineTuneDArch(darch = dbnin, 
                        dataSet = dS, 
                        numEpochs = nE,
                        bootstrap = T)
    return(mod)
  }
}

関数の仮パラメータに関するいくつかの明確化。

• variant - 微調整関数の選択（backpropagation1-、2-rpropagation）。
• dbnin - モデルは、事前トレーニングから生じました。
• dS - 微調整に設定されたデータ（dataSet）。
• hd - ニューラルネットワークの隠れ層におけるサンプリング（hiddenDropout）の係数。
• id - サンプリングの係数（inputDropout）ニューラルネットワークのエントリー層
• act - ニューラルネットワークのすべての層におけるニューロンの活性化の関数のインジケーターとベクトル。ベクトルの長さは、層の数よりも1単位短いです。
• nE - トレーニングエポック数。

dataSet - このバージョンで登場した新しい変数。その背後にある理由を理解していません。通常、言語モデルに変数を転送する２つのメソッドがあり -(y~., data)のペア（x、y）のまたは式を使用しています。この変数の導入品質を向上させるが、ユーザーの代わりに混同していません。しかし、知られていない理由を有することができます。

3.4。モデルをテスト。マトリクス

トレーニングされたモデルのテストは、テストサンプルに対して行われます。正式な精度と定性的K.は、関連する情報を以下に提供されます。2つのインジケーターを計算することを考慮しなければなりません。この目的に、2つの異なるデータのサンプルが必要になります。精度を計算するために、最も頻繁に最後のバーで定義されていない、ターゲット変数の値、およびジグザグを必要としています。そのため、テストprepareTrain()と質的なインジケーターに、次の関数を使用します。

＃---10-------------------------------------------
prepareTest <- function(n, z, norm, len = 501)
{
  x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% 
    tail(., len)
  CO <- price[ ,"CO"] %>% tail(., len)
  if (norm) {
    x <- predict(prepr,x)
  }
  dt <- cbind(x = x, CO = CO) %>% as.data.frame()
  return(dt)
}

モデルは、ヒストリーの最後の500バーにテストされます。

実際のテスト、testAcc()とtestBal()について適用されます。

#---11-----
testAcc <- function(obj, typ = "bin"){
  x.ts <- DT$test[ ,best] %>% as.matrix()
  y.ts <- DT$test$y %>% as.integer() %>% subtract(1)
  out <- predict(obj, newdata = x.ts, type = typ) 
  if (soft){out <- max.col(out)-1} else {out %<>% as.vector()}               
  acc <- length(y.ts[y.ts == out])/length(y.ts) %>% 
    round(., digits = 4)
  return(list(Acc = acc, y.ts = y.ts, y = out))
}
#---12-----
testBal <- function(obj, typ = "bin") {
  require(fTrading)
  x <- DT.test[ ,best]
  CO <- DT.test$CO
  out <- predict(obj, newdata = x, type = typ) 
  if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} 
  sig <- ifelse(out == 0, -1, 1)
  sig1 <- Hmisc::Lag(sig) %>% na.omit
  bal <- cumsum(sig1 * tail(CO, length(sig1)))
  K <- tail(bal, 1)/length(bal) * 10 ^ Dig
  Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
  dd <- maxDrawDown(bal)
  return(list(sig = sig, bal = bal, K = K, 
              Kmax = Kmax, dd = dd))
}

最初の関数が返すAccおよび目標変数の値（実数または予測）。第２の関数が予測シグナルを返すsig に、バランスはシグナルに基づいて得られる(bal),品質係数(К)、この係数の最大値(Kmax)と最大ドローダウン、同じエリア内の(dd)。

バランスを計算する場合、最後の予測シグナルはまだ、計算時に削除されるべきである形成されていない将来のバーを参照しています。右のバーによって SIGベクトルを移動させることで行っています。

3.4.1。デコード予測。

得られた結果は、「WTA」メソッドを使用して（ベクトル行列から変換）復号することができます。確率の最大値を有する列番号に等しく、この確率の閾値は、クラスが決定されていない設定にすることができます。

out <- classmat2classvec(out, threshold = 0.5) 
or
out <- max.col(out)-1

閾値を0.5とし、列の最大の確率がこのしきい値を下回っている場合は、（「定義されていない」）、追加のクラスを取得します。精度のようなインジケーターを計算するときに、それを考慮に入れる必要があります。

3.4.2。予測結果を改善

受信した後に予測結果を改善することが可能ですか？適用できる3つの可能なメソッドがあります。

• 較正

キャリブレーションは、実際のデータで最も正確な互換性を与える可能性の範囲の計算です。このため、 CORElearnパッケージに特別な関数があります：

CORElearn::calibrate(correctClass, predictedProb, class1 = 1,  
                     method = c("isoReg", "binIsoReg", "binning", "mdlMerge"),  
                     weight=NULL, noBins=10, assumeProbabilities=FALSE)

ただし:

• correctClass — 分類のクラスの正しいラベルを持つベクトル;
• predictedProb — 正しいクラスと同じ長さの予測クラス1（確率）を有するベクター;
• method — ("isoReg", "binIsoReg", "binning", "mdlMerge"). 詳細については、パッケージの説明をお読みください。
• weight - ベクトル（示されている場合）以外のすべての重みは、デフォルトでは1に等しく、correctClassと同じ長さと重みを提供する必要があります。
• noBins - パラメータの値がメソッドに依存し、チャネルの初期数を決定します。
• assumeProbabilities - の場合TRUE、、値はpredictedProbが範囲[0、1]にされていました。e. 可能性の評価として、アルゴリズムは、シンプルな回帰として使用することができます。

このメソッドは、ベクターによって設定された2つのレベルのターゲット変数に適用されます。

• マルコフ連鎖モデルによる予測結果を平滑化

従って、理論的に、最も基本的な情報を提供することはありません。これは新たな記事に値する広大で複雑なテーマです。

マルコフのプロセスは、以下の関数を持つランダムなプロセスです。：任意の時点t0で、将来のシステムのいずれかの確率にのみ存在する状態に依存し、システムがこの状態に達したとき、依存しません。

ランダムマルコフ過程の分類：

• 離散状態と離散時間（マルコフ連鎖）;
• 連続状態と離散時間（マルコフ一貫性）を持ちます。
• 離散状態と連続時間（連続マルコフ連鎖）;
• 連続状態と連続時間。

唯一のマルコフはS1, S2, ..., Sn. でさらに考えられています。

マルコフ連鎖。離散状態と離散時間でランダムマルコフ過程
モーメント t1、t2、... Sシステムがその状態を変更することができたときに、次のステップとして考えられています。t時間が、ステップ番号1,2k、ではないプロセスが依存する引数として使用されます。

ランダムプロセスは、状態Sの配列によって特徴づけられ、 S（1）、S（2）、... S（k）は、...、 S（0）（最初のステップの前に）初期状態があります。最初のステップ後の状態は S（K） - K-工程後のシステムの状態です。

マルコフ連鎖の状態の確率はPi(K)であるk個のステップとK+1の Sシステムは Si（=1、2、...、 n）のプロセッサーになります。

マルコフ連鎖確率の初期分布 - 。プロセスの開始時における状態の確率の分布
遷移確率から K個のステップ（遷移確率）のSiの状態Sjと状態 - S K個のステップを条件に、 Sjの状態で表示され、条件付き確率は K-1ステップ）の前にSiの状態にありました。

Uniformマルコフ連鎖 - 。マルコフ連鎖の遷移確率は、ステップ数に依存しませんが、上のどの間にトランジションををとります。

正方行列サイズn個のхnから均一なマルコフ連鎖Рijの移行確率。次の関数があります。

1. 各行には、システムの選択状態を説明し、その要素から1ステップですべての可能な遷移の確率状態からi個をとります。
2. 列の要素 - セット（j）の状態にワンステップで可能な遷移の確率。
3. 各行の確率の合計は1に等しいです。
4. 対角線上に - Рij確率は、システムがSiの状態に残るでしょう。

マルコフ過程を観察し、非表示にすることができます。マルコフモデル（HMM）が離散確率過程のペア{聖}と{Xtの}で構成されています。観察プロセス{Xt}は、いわゆる条件付き分布を通じて状態の観察されない（隠された）マルコフ過程{セント}とリンクされています。

目標時間シリーズの状態が観察されたマルコフ過程（クラス）は均一ではありません。明らかに、1つの状態から別の状態への遷移確率は、現在の状態で費やされた時間に依存します。これは、状態変化後の最初のステップの間に、変更される可能性が低く、この状態で費やした時間の増加に伴って増大することを意味します。これらのモデルはセミマルコフ（HSMM）と呼ばれています。深く追及はしません。

ジグザグから得られる理想的なシグナル（ターゲット）の離散的なオーダーに基づいたНММのパラメータがあります。考え方は以下の通りです。ニューラルネットワークによって予測シグナルを持つ、НММを使用して滑らかにします。

何をもたらすのでしょうか？通常は、ニューラルネットワークの予測における「排出量」、1-2バーの長さである状態を変化させる領域がされています。ターゲット変数がこのような小さな長さを持っていないことがあります。予測されたターゲット変数に得られたモデルを適用することにより、それ以上の可能性の遷移をもたらすことができます。

これらの計算の隠れマルコフおよび半マルコフモデルを計算するために設計された"mhsmm"パッケージを使用します。単に離散値の時系列を平滑化する smooth.discrete()関数を使用します。

obj <- smooth.discrete(y)

状態の可能性が高い順にViterbiアルゴリズム（グローバルデコーディング）を使用して得られたデフォルトでは、最終的に得られる状態のスムーズな順になります。個々の最も可能性の高い状態が識別され、平滑化、のメソッドを使用するオプションもあります。

標準的なメソッドは、新たな時系列を平滑化するために適用されます

sm.y <- predict(obj, x = new.y)

• 理論的なバランス曲線上の予測シグナルを修正

このコンセプトは以下の通りです。バランスラインで、平均からの偏差を計算することができます。補正シグナルを計算し、これらの偏差を使用します。瞬間では偏差がマイナス、予測シグナルのパフォーマンスを無効にする、逆を行います。このアイデアは、一般的には良いですが、欠点があります。ゼロバーは予測シグナルがありますが、バランス値と、補正シグナルがありません。この問題を解決するには、2つのメソッドがあります。補正シグナルと偏差を既存に基づいて補正シグナルを予測するためには、回帰を通して - 新しいバーの偏差を予測し、それに基づいて補正シグナルを識別するために形成されたバー上の既存の偏差を使用します。既に形成されている新たなバーの補正シグナルを取ることができます。

上記のメソッドは、既に知られており、テストされているので、最近登場したマルコフモデルのパラメータの決定を可能にする関数の範囲を持っている「マルコフ連鎖」パッケージの機会を実装しようとする観察離散プロセスを経て、いくつかの将来のバーで状態を予測します。このアイデアは、この記事から取りました。

3.4.3。マトリクス

モデル予測の品質を評価するために、測定基準の全範囲（精度、AUC、ROCおよびその他）が追加されます。前回の記事で、正式なインジケーターが品質を定義することはできません。EAの目標は、許容可能なドローダウンで最大の利益を得ることです。この目的に、K品質インジケーターを導入し、N個の長さの固定されたヒストリーのセグメント上の1つのバーのポイントの平均利益を示しました。N個のセグメントの長さによって累積リターン（記号）を割ることによって算出されます。精度は直説計算されます。

最後に、計算を実行し、テスト結果を取得します。

• 出力データ。すでに price.OHLC()関数を実行した結果として得られる価格[]マトリックスがあります。バーのクオート、平均価格があります。すべての出力データはRstudioの添付ファイルに表示される「アイコン」をダウンロードすることによって得ることができます。

# Find  constanta  
n = 34; z = 37; cut = 0.9; soft = TRUE. 
# 前処理メソッドを探します  
method = c("center", "scale","spatialSign")
＃データの初期セットを形成します
data.f <- form.data(n = n, z = z)
＃重要な予測因子のセットを見つけます 
best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) 
＃約32 - コアプロセッサ上で計算。この段階をスキップすることができます 
＃、将来的に予測変数のセット全体を使用します。したがって、前の行をコメントアウト
# コメントを外し、2つの最低ライン。
# data.f <- form.data(n = n, z = z)
# best <- colnames(data.f) %>% head(., ncol(data.f) - 1)
# トレーニングニューラルネットワークのセットを準備します
DT <- prepareTrain(x = data.f[ , best],
                   y = data.f$y,
                   balance = TRUE,
                   rati = 501, mod = "stratified",
                   norm = TRUE, meth = method) 

＃必要なライブラリのダウンロード
require(darch)
require(foreach)
# 活性化に利用可能な関数を特定します
actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)
# ターゲット変数を変換します
if (soft) { y <- DT$train$y %>% classvec2classmat()} # into matrix
if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # to vector with values [0, 1]
＃トレーニングにデータセットを作成
dataSet <- createDataSet(
  data = DT$train[ ,best] %>% as.matrix(), 
  targets = y ,
  scale = F
）
＃ニューラルネットワークの定数を識別する
＃エントリー層のニューロンの数は、（予測因子の量に等しいです）
nIn <- ncol(dataSet@data)
＃出力層のニューロンの数 
nOut <- ncol(dataSet@targets)
＃ニューラルネットワークのすべての層のニューロンの数とベクトル
＃ニューラルネットワークの他の構成を使用する場合、このベクターは書き直す必要があります
Layers = c(nIn, 2 * nIn , nOut)
＃トレーニングに関連する他のデータ
Bath = 50
nEp = 100
ncd = 1
＃ニューラルネットワークの事前トレーニング
preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd)
＃微調整の追加のパラメータ
Hid = 0.5; Ind = 0.2; nEp = 10
＃他の二つのモデル、バックプロパゲーション
# 結果を比較
model <- foreach(i = 1:2, .packages = "darch") %do% {
  dbn <- preMod
  if (!soft) {act = c(2, 1)}
  if (soft) {act = c(2, 4)}
  fineMod(variant = i, dbnin = dbn, 
          hd = Hid, id = Ind,
          dS = dataSet, act = act, nE = nEp)
}
＃精度を得るためにテスト
resAcc <- foreach(i = 1:2, .packages = "darch") %do% {
  testAcc(model[[i]]) 
}
＃品質係数にテストするデータのサンプルを準備します
DT.test <- prepareTest(n = n, z = z, T)
＃テスト
resBal <- foreach(i = 1:2, .packages = "darch") %do% {
  testBal(model[[i]]) 
}

それでは、結果を見てみましょう

> resAcc[[1]]$Acc
[1] 0.5728543
> resAcc[[2]]$Acc
[1] 0.5728543

両方のモデルで同様に悪いです。

品質係数について：

> resBal[[1]]$K
[1] 5.8
> resBal[[1]]$Kmax
[1] 20.33673
> resBal[[2]]$Kmax
[1] 20.33673
> resBal[[2]]$K
[1] 5.8

良好な性能を示しています。しかし、大きなドローダウンは何とかすべきです

> resBal[[1]]$dd$maxdrawdown
[1] 0.02767

以下の計算から求めた補正シグナルとのドローダウンを修正します

bal <- resBal[[1]]$bal
# signal on the last 500 bars
SIG< - resBal[[1]]$ SIG[1：500</ s2の>]sig <- resBal[[1]]$sig[1:500]
# バランスラインからの平均
ma <- pracma::movavg(bal,16, "t")
＃平均からの勢い 
roc <- TTR::momentum(ma, 3)%>% na.omit
# 平均からのバランスライン偏差
dbal <- (bal - ma) %>% tail(., length(roc))
＃二つのベクトルをまとめます
dbr <- (roc + dbal) %>% as.matrix()
# 補正シグナルを計算します
sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) gives the same result
# 結果として得られるシグナル
S <- sig.cor * tail(sig, length(sig.cor))
＃結果として得られるシグナルの残高
Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S))))
# 補正されたシグナル上の品質係数
Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig
> Kk
[1] 28.30382

補正されたシグナル上の質の結果は非常に良いです。折れ線グラフで表示されるROCとDBRは、補正シグナルを算出するために用いられます。

matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1))
abline(h=0, col=2)
grid()

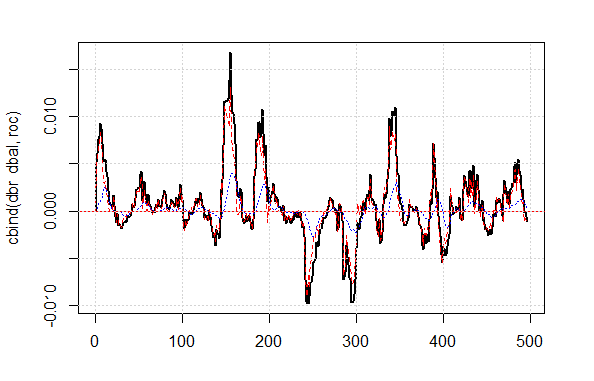
平均値から図4バランスライン偏差

シグナル補正前後のバランスラインは、図５に示されています。

plot(c(NA,NA,NA,Bal), t="l")
lines(bal, col= 2)
lines(ma, col= 4)

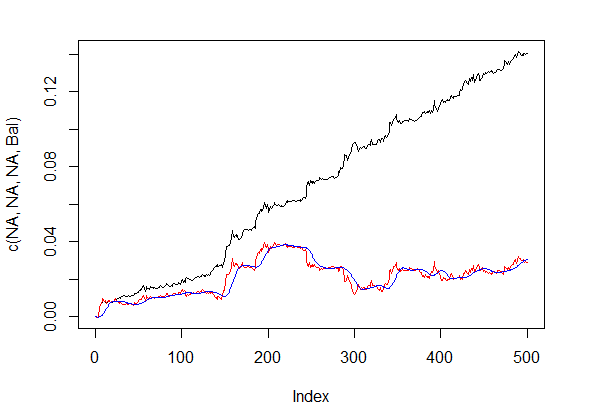
図5　バランスラインとシグナル補正後

シグナルの値がゼロバーのニューラルネットワークによって予測されていますが、補正値を持っていません。このシグナルを予測するためのマルコフモデルを使用します。最後の状態の値を使用して、モデルのパラメータを識別します。補正シグナルの観測された状態に基づいて、1つ先のバーで状態を予測します。まず、予測に基づくシグナル、結果として得られるシグナルとその品質インジケーターを計算します。correct()関数を記述します。言い換えれば、以前に実行された計算を書き留めます。

この記事での「シグナル」は、整数-1と1の配列です。「状態」は、これらのシグナルに対応する整数1及び2の配列です。相互変換に関数を使用します。

#---13----------------------------------
        sig2stat <- function(x) {x %>% as.factor %>% as.numeric}
        stat2sig <- function(x) ifelse(x==1, -1, 1)
        #----14--correct-----------------------------------
        correct <- function(sig){
          sig <- Hmisc::Lag(sig) %>% na.omit
          bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig))))
          ma <- pracma::movavg(bal, 16, "t")
          roc <- TTR::momentum(ma, 3)%>% na.omit
          dbal <- (bal - ma) %>% tail(., length(roc))
          dbr <- (roc + dbal) %>% as.matrix()
          sig.cor <- sign(dbr)
          S <- sig.cor * tail(sig, length(sig.cor))
          bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S))))
          K <- tail(bal, 1)/length(bal) * 10 ^ Dig
          Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
          dd <- fTrading::maxDrawDown(bal)
          corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd)
          return(corr)
         }

先にバールの予測とシグナルベクトルを得るために、「マルコフ連鎖」パッケージと pred.sig()関数を使用します。

#---15---markovchain----------------------------------
pred.sig <- function(sig, prev.bar = 10, nahead = 1){
          require(markovchain)
        ＃観察された補正シグナルを変換します  
          stat <- sig2stat(sig)
        ＃計算モデルパラメータ
        ＃環境でモデルが存在しない場合       
          if(!exists('MCbsp')){
             MCbsp <<- markovchainFit(data = stat, 
                                method = "bootstrap",
                                nboot = 10L,
                                name="Bootstrap MС")
         }
        # Set necessary constants
          newData <- tail(stat, prev.bar)
          pr <- predict(object = MCbsp$estimate, 
                                newdata = newData,
                                n.ahead = nahead)
        ＃エントリーシグナルに対する予測シグナルを添付
          sig.pr <- c(sig, stat2sig(pr))
          return(sig.pr = sig.pr)
}

EAをコンパクトに実行するため、得られたシグナル計算を書き留めます：

sig <- resBal[[1]]$sig
sig.cor <- correct(sig)
sig.c <- sig.cor$sig.c
pr.sig.cor <- pred.sig(sig.c)
sig.pr <- pr.sig.cor$sig.pr
＃ EAのシグナルの結果ベクトル 
S <- sig.pr * tail(sig, length(sig.pr))

• 予測シグナルのスムージング。

マルコフ連鎖のモデルを使用して、離散シグナルを平滑化する関数を記述します。この目的に、"mhsmm"パッケージを使用します。

#---16---smooth------------------------------------
smoooth <- function(sig){
■スムーズな予測シグナル
＃マルコフモデルのパラメータを定義します
＃環境でモデルがまだ存在しない場合
    require(mhsmm)
    if(!exists('obj.sm')){
         obj.sm <<- sig2stat(sig)%>% smooth.discrete()
    }
＃得られたモデルとのシグナルを平滑化
    sig.s <- predict(obj.sm, x = sig2stat(sig))%>% 
             抽出2（1）％>％stat2sig()
＃平滑化シグナルの計算残高
     sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
     bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
     K <- tail(bal, 1)/length(bal) * 10 ^ Dig
     Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
     dd <- fTrading::maxDrawDown(bal)
     return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}

平滑化シグナルに基づいてバランスを計算して比較します。

sig <- resBal[[1]]$sig
sig.sm <- smoooth(sig)
plot(sig.sm$bal, t="l")
lines(resBal[[1]]$bal, col=2)

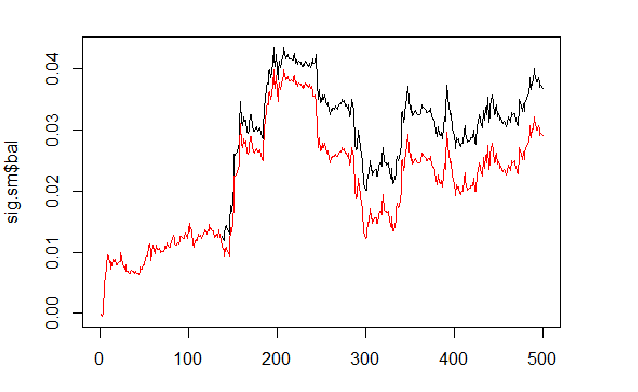
図6　平滑化および予測シグナルに基づいたバランス

ご覧の通り、品質はやや改善したが、ドローダウンはまだ残っています。EAでこのメソッドを使用しません。

sig.sm$dd
$maxdrawdown
[1] 0.02335
$from
[1] 208
$to
[1] 300

4. EAアルゴリズムの構造

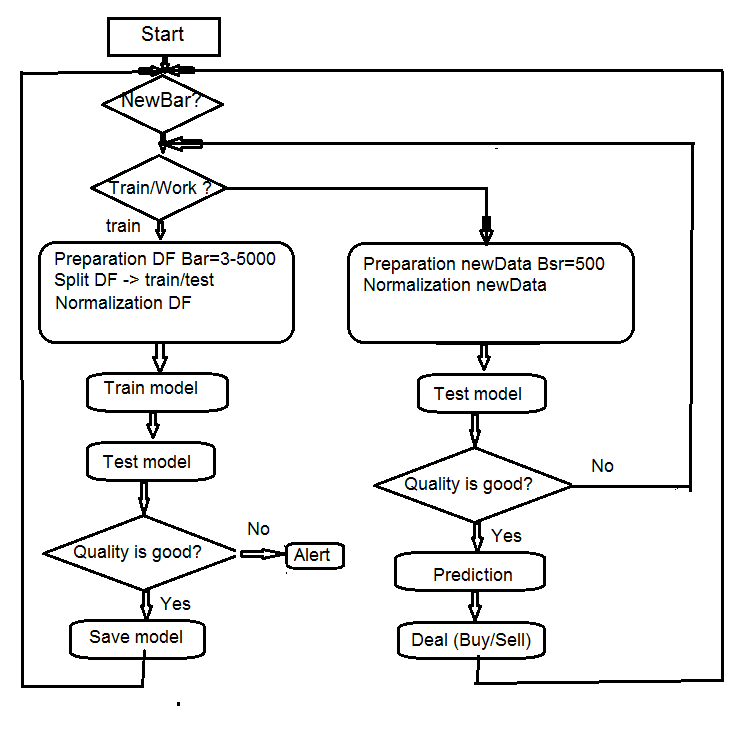
図7　EAアルゴリズムの構造

4.1。EA操作の説明

EAは、2つのストリーム（MQLとターム）で動作するため、相互作用のプロセスを説明します。それぞれ別々のストリームで行われる動作について説明します。

4.1.1 MQL

チャート上のEAを配置した後：

init() 関数内

• ターミナルの設定（DLL、トレード許可）チェックしてください。
• タイマーのセット;
• launch Rterm;
• R-プロセス環境に必要な定数を転送します。
• Rtermかどうかを確認していない場合 - アラート。
• exit from init().
  

deinit()関数内

• タイマーをストップ。
• グラフィックオブジェクトを削除。
• Rtermをストップ。

OnTimer()関数内

• Rterm関数かどうかチェックしてください。
• 新しいバーである場合（最終時間=時間[0]！）：
• これはEAの最初の起動に応じて、ヒストリーを設定します。
• フォームのベクトル (Open, High, Low, Close) とRtermに転送します。
• スクリプトを起動し、その性能の結果を受けずに残します。
• set the get_sig = true flag;
• set LastTime= Time[0].
  
• Rtermが動作すれば、フラグが= get_sig=trueです。
• Rtermから受け取るべきsigベクトルの長さを特定します。
• 元の大きさにベクトルの大きさを調整します。失敗した場合、プロセスはドロップされます。
• シグナルオーダー（ベクトル）を取得。
• 最後のシグナルを使用して実行されなければならない操作を決定。
• シグナルを得る場合、get_sig=falseをリセットします。
  
• 残りは普通です。
• CheckForClose()
• CheckForOpen()

このパートにおけるEAは、オーダーを送信し、「考える」ことができ、得られた命令を実行する「パフォーマー」でそれらを開くときに、エラーの状態を追跡し、標準的なEAの他の多くの関数を実行します。

4.1.2Rterm

オペレーティング・スクリプトは、2つのパートから構成されています。一方は、最初のエントリに実行されます。

• if first:
• インターネット上から必要なライブラリをアップロードし、環境にそれらをインストールします。
• 必要な関数を定義します。
• クオート行列を作成します。
• トレーニングとモデルをテストするためのデータのサンプルを用意;
• 作成したモデルをトレーニングします。
• モデルをテストします。
• パフォーマンスのシグナルを計算します。
• 予測の品質を確認してください。設定された最小値に等しい場合 - 進みます。それ以外の場合 - アラートを送信します。
• if !first:
• テストと予測のデータのサンプルを用意;
• 新しいデータにモデルをテストします。
• パフォーマンスのシグナルを計算します。
• 予測の品質を確認してください。セットの最小値に等しい場合 - 進みます。それ以外の場合は - = TRUE、最初に設定したモデルを再トレーニングするためにリクエストします。

4.2。セルフコントロールとセルフトレーニング

モデルのシグナルを予測する品質管理がК係数を用いて行われます。許容できる品質の限界を識別するための二つのメソッドがあります。まず - その最大値の関係で係数の最大を設定します。К<Kmaxと*0.8の場合、実行シグナルからEAをストップする必要があります。同じアクションを必要とするКの最小値を設定します。EAで第２のメソッドを使用します。

5。インストールと起動

e_DNSAE.mq4とe_DNRBM.mq4：この記事に取り付けられた2つのEAがあります。それらの両方が同じデータのサンプルと関数を使用します。違いは、使用されるディープネットワークモデルです。最初のEAは、DNを使用して、SAEおよび「deepnet」のパッケージを開始します。パッケージの説明はディープニューラルネットワーク上の前回の記事で見つけることができます。第2のEAはDN、RBMと「darch"パッケージを使用しています。

標準ディストリビューションが適用されます。

• *.mq4 in the ~/MQL4/Expert folder
• *.mqh in the ~/MQL4/Include folder
• *.dll in the ~/MQL4/Libraries folder
• *.r in the C:/RData folder

R言語とスクリプトへのパスを修正します。

EAを初めて起動すると、リポジトリから必要なライブラリをダウンロードして、Rterm環境で設定します。また、添付のリストに従って、事前にそれらをインストールします。

通常、Rプロセスは、必要なライブラリが存在しないために、誤ってスクリプトへのパスを示します。

初期データが別々に装着されていると、セッションはすべての関数が動作していることを確認し、同様の実験を行うためにRstudioで開くことができます。

6。メソッドおよび定性的なインジケーターを改善するメソッド。

定性的なインジケーターを改善するためのいくつかのメソッドがあります。

• 評価および予測因子の選択は - 最適化（GA）の遺伝的アルゴリズムを適用します。
• 予測因子の最適なパラメータを決定し、変数をターゲットにします。
• ニューラルネットワークの最適なパラメータを決定。

インジケーターを改善するのに役立つ措置をとります。

結論

「darch"パッケージを用いた実験は、以下の結果を示しています。

• RBM開始ディープニューラルネットワークは、SAEより悪いトレーニングを受けています。これは、ほとんど新規情報ではありません。
• ネットワークを迅速にトレーニングできます。
• このパッケージは、モデルのほぼすべての内部パラメータへのアクセスを提供することによって、予測の品質を向上させる大きな可能性を有します。
• このパッケージは、非常に広いセットでのみニューラルネットワークやRBMを使用することができます。
• 常に進化しており、開発者は、次のリリースで追加の関数を導入します。
• МТ4/МТ5とR言語の統合は、トレーダーに追加のDLLなしで最新のアルゴリズムを使用する機会を提供します。

添付

1. Sess_DNRBM_GBPUSD_30のRセッション
2. Zip file with the "e_DNRBM" Expert Advisor
3. Zip file with the "e_DNSAE" Expert Advisor