ディープニューラルネットワーク(その5)DNNハイパーパラメータのベイズ最適化
1 500
0
内容
- はじめに
- 1. DNN最適ハイパーパラメータの特定 (darch)
- ソースデータセットの生成
- 統計的に重要でない予測子の削除
- 最適化されるDNNハイパーパラメータの特定と値域
- DNNの事前訓練及び微調整機能の定義
- 最適化のための適合関数の定義
- DNN最適のパラメータの計算
- 2. 最適のパラメータを使ったDNNの訓練とテスト
- 3. 最適のパラメータを使ったDNNテストの結果の分析
- 4. 最適のパラメータを使ったモデルのフォワードテスト
- 終わりに
- 適用
はじめに
前の記事では、デフォルトパラメータでの基本的なモデルとDNNモデルが考察され、分類の質が不十分であることが判明しました。分類の質を向上させるためには何ができるのでしょうか。
- DNNハイパーパラメータを最適化する
- DNN正則化を改善する
- 訓練サンプルの数を増やす
- ニューラルネットワークの構造を変更する
上記の、既存のDNNを改善するための機会はすべて本稿及び今後の記事で検討されます。ネットワークのハイパーパラメータの最適化から始めましょう。
1. DNN最適ハイパーパラメータの特定 (darch)
一般的な場合、ニューラルネットワークのハイパーパラメータは、グローバルとローカルの2つのグループに分けることができます。グローバルハイパーパラメータには、隠れ層の数、各層のニューロンの数、学習のレベル、運動量、ニューロンの重みの初期化が含まれます。ローカルハイパーパラメータには、層の種類、アクティベーション機能、ドロップアウト/ドロップコネクト、及びその他の正則化パラメータが含まれます。
ハイパーパラメータの最適化の構造を図に示します。
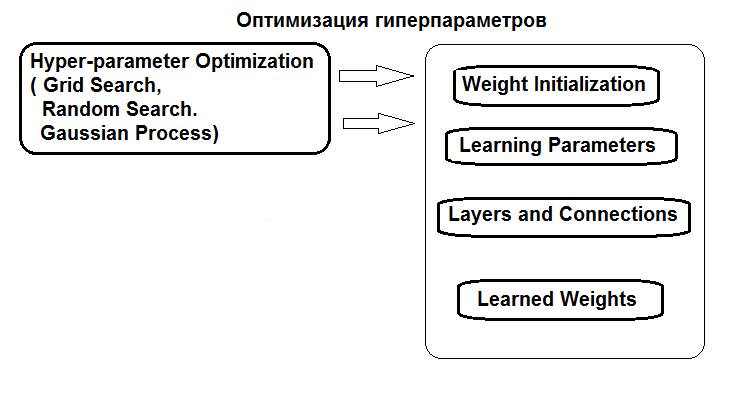
図1 ニューラルネットワークハイパーパラメータの構造と最適化の手法
ハイパーパラメータは3つの方法で最適化できます。
- グリッド検索：各ハイパーパラメータに対して、固定値を持つベクトルがいくつか定義されます。次に、caret::train()関数またはカスタムスクリプトを使用して、モデルがすべてのハイパーパラメータ値の組み合わせについて訓練されます。その後、分類の質の値が最良であるモデルが選択されます。そのパラメータは最適とみなされます。この方法の欠点は、値のグリッドを定義すると最適値を失う可能性が高いことです。
- 遺伝的最適化：遺伝的アルゴリズムを用いて最良のパラメータを確率的に検索します。遺伝的最適化のいくつかのアルゴリズムについては以前に詳しく説明したので、ここでは繰り返しません。
- 最後に、ベイズ最適化。これは本稿で使用されます。
ベイズアプローチには、ガウス過程とMCMCが含まれます。rBayesianOptimization（バージョン1.1.0）パッケージが使用されます。応用法の理論は文献で広く見られますが、例えばこの記事にもあります。
ベイズ最適化を実行するには、次のことが必要です。
- 適合関数を決定する。
- ハイパーパラメータの変更のリストと境界を決定する。
適合関数（FF）は、最適化中に最大化されるべき品質スコア（最適化基準、スカラー）及び目的関数の予測値を返すべきです。FFは2つのクラスのF1の平均値であるmean(F1)の値を返します。DNNモデルは事前訓練で訓練されます。
ソースデータセットの生成
実験には、新しいバージョンのMRO 3.4.2が使用されます。当バージョンでは、以前は使用されていなかったいくつかの新しいパッケージが備えられています。
RStudioを実行し、GitHub/Part_Iに移動して、ターミナルから取得されたクオーツを持つCotir.RDataファイルをダウンロードし、データ準備関数を持つFunPrepareData.RファイルをGitHub/Part_IVからダウンロードします。
以前は、帰結値と正規化データが帰属されたデータセットは、事前訓練を使用した訓練でより良い結果を得ることができました。前に考えた他の前処理オプションもテストすることができます。
事前訓練/訓練/検証/テストサブセットに分割する際には、分類の質を向上させるための最初の機会を使用します。つまり、訓練のサンプル数を増やします。事前訓練サブセットのサンプル数は4000に増やされます。
#---- 準備する ------------- library(anytime) library(rowr) library(darch) library(rBayesianOptimization) library(foreach) library(magrittr) #source(file = "FunPrepareData.R") #source(file = "FUN_Optim.R") #--- 準備する ---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
SplitData()関数でstartパラメータを変えることで、開始量だけ右にシフトしたセットを得ることができます。これにより、将来の価格帯のさまざまな部分の品質を確認し、履歴の変化を判断することができます。
統計的に重要でない予測子の削除
統計的に重要でない2つの変数を削除しますc(v.rstl, v.pcci)。これは当シリーズの前回の記事で特定されました。
##---Data DT-------------- require(foreach) evalq({ foreach(i = 1:4) %do% { DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DT list(pretrain = DT[[1]], train = DT[[2]], val = DT[[3]], test = DT[[4]]) -> DT }, env)
テスト用のデータセット（事前訓練/訓練/テスト/テスト1）を作成し、微調整してテストし、Xリストにまとめます。
#-----データX------------------
evalq({
list(
pretrain = list(
x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$pretrain$Class %>% as.data.frame()
),
train = list(
x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$train$Class %>% as.data.frame()
),
test = list(
x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$val$Class %>% as.data.frame()
),
test1 = list(
x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$test$Class %>% as.vector()
)
) -> X
}, env)
実験のためのセットの用意ができました。
テスト結果からメトリックを計算する関数が必要です。mean(F1) の値は最適化（最大化）基準として使用されます。この関数をenv環境にロードします。
evalq( #input 実際の予測ベクトルまたは予測される混乱行列 # https://github.com/saidbleik/Evaluation/blob/master/eval.R Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){ if (is.null(cm)) { actual = actual[!is.na(actual)] predicted = predicted[!is.na(predicted)] f = factor(union(unique(actual), unique(predicted))) actual = factor(actual, levels = levels(f)) predicted = factor(predicted, levels = levels(f)) cm = as.matrix(table(Actual = actual, Predicted = predicted)) } n = sum(cm) # インスタンス数 nc = nrow(cm) # クラス数 diag = diag(cm) # number of correctly classified instances per クラスごとで正しく分類されたインスタンスの数 rowsums = apply(cm, 1, sum) # クラスごとのインスタンス数 colsums = apply(cm, 2, sum) # クラスごとの予測数 p = rowsums / n # クラスにわたるインスタンスの配布 q = colsums / n # 予測クラスにわたるインスタンスの分布 #精度 accuracy = sum(diag) / n #クラスごと recall = diag / rowsums precision = diag / colsums f1 = 2 * precision * recall / (precision + recall) #マクロ macroPrecision = mean(precision) macroRecall = mean(recall) macroF1 = mean(f1) #1-vs-all matrix oneVsAll = lapply(1:nc, function(i){ v = c(cm[i,i], rowsums[i] - cm[i,i], colsums[i] - cm[i,i], n - rowsums[i] - colsums[i] + cm[i,i]); return(matrix(v, nrow = 2, byrow = T))}) s = matrix(0, nrow = 2, ncol = 2) for (i in 1:nc) {s = s + oneVsAll[[i]]} #平均精度 avgAccuracy = sum(diag(s))/sum(s) #マイクロ microPrf = (diag(s) / apply(s,1, sum))[1]; #majority クラス mcIndex = which(rowsums == max(rowsums))[1] # majority-クラスインデックス mcAccuracy = as.numeric(p[mcIndex]) mcRecall = 0*p; mcRecall[mcIndex] = 1 mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex] mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1) #ランダムな精度 expAccuracy = sum(p*q) #kappa kappa = (accuracy - expAccuracy) / (1 - expAccuracy) #ランダムな推測 rgAccuracy = 1 / nc rgPrecision = p rgRecall = 0*p + 1 / nc rgF1 = 2 * p / (nc * p + 1) #ランダムな重みづけ rwgAccurcy = sum(p^2) rwgPrecision = p rwgRecall = p rwgF1 = p classNames = names(diag) if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "") return(list( ConfusionMatrix = cm, Metrics = data.frame( Class = classNames, Accuracy = accuracy, Precision = precision, Recall = recall, F1 = f1, MacroAvgPrecision = macroPrecision, MacroAvgRecall = macroRecall, MacroAvgF1 = macroF1, AvgAccuracy = avgAccuracy, MicroAvgPrecision = microPrf, MicroAvgRecall = microPrf, MicroAvgF1 = microPrf, MajorityClassAccuracy = mcAccuracy, MajorityClassPrecision = mcPrecision, MajorityClassRecall = mcRecall, MajorityClassF1 = mcF1, Kappa = kappa, RandomGuessAccuracy = rgAccuracy, RandomGuessPrecision = rgPrecision, RandomGuessRecall = rgRecall, RandomGuessF1 = rgF1, RandomWeightedGuessAccurcy = rwgAccurcy, RandomWeightedGuessPrecision = rwgPrecision, RandomWeightedGuessRecall = rwgRecall, RandomWeightedGuessWeightedF1 = rwgF1))) }, env) #-------------------------
この関数は、広範囲のメトリックを返しますが、今のところF1だけが必要です。
本稿の前の部分のように、2つの隠れ層を持つニューラルネットワークが使用されます。DNNは事前訓練との2段階で訓練されます。可能なオプションは次のとおりです。
- 事前訓練:
- SRBMのみを訓練
- SRBM + ニューラルネットワークの最上層を訓練
- 微調整:
- 誤差逆伝播法訓練法を使用
- rpropagation訓練法を使用
4つの訓練オプションのそれぞれは、最適化のための異なるハイパーパラメータのセットを有します。
最適化のためのハイパーパラメータの定義
値が最適化されるハイパーパラメータと値域のリストを定義しましょう。
- n1, n2 — それぞれの隠れ層でのニューロンの数（1～25）。2 の倍数が必要なため、モデルに与える前にこのパラメータに2を掛けます（poolSize）。これは maxout活性化関数のために必要です。
- fact1, fact2 — それぞれの隠れ層の活性化関数のインデックスで、Fact <- c("tanhUnit", "maxoutUnit", "softplusUnit", "sigmoidUnit")ベクトルで定義された活性化関数のリストから選択されます。他の関数を追加することもできます。
- dr1, dr2 — 各層でのドロップアウト値（0～0.5）
- Lr.rbm — StackedRBM訓練のレベル（事前訓練の段階で0.01～1.0）
- Lr.top — 事前訓練段階でのニューラルネットワークの最上層の訓練のレベル（0.01～1.0）。このパラメータは、ニューラルネットワークの最上層を訓練せずに事前訓練を行うためには必要ありません。
- Lr.fine — backpropagationを使用する場合の微調整段階でのニューラルネットワークの訓練レベル（0.01～1.0）。このパラメータはrpropagationを使用する際には必要でありません。
すべてのパラメータの詳細な説明は、以前の記事とパッケージに記載されています。darch()関数のすべてのパラメータにはデフォルト値があります。それらはいくつかのグループに分けることができます。
- グローバルパラメータ: 事前訓練と微調整の両方に使用されます。
- データ処理パラメータ: caret::preProcess()の機能が使用されます。
- SRBMパラメータ: 事前訓練にのみ使用されます。
- NNパラメータ: 事前訓練と微調整の両方に使用されますが、段階によって異なる値を持つ可能性があります。
デフォルトのパラメータ値は、新しい値のリストを指定するか、明示的にdarch()関数に書き込むことで変更できます。次に、最適化するハイパーパラメータの簡単な説明を示します。
まず、事前訓練/訓練段階に共通するDNNのグローバルパラメータを設定します。
Ln <- c(0, 2*n1, 2*n2, 0) — 2つの隠れ層を有する4層ニューラルネットワークが生成されることを示すベクトルです。入力層及び出力層のニューロンの数は入力データから決定され、明示的に指定することはできません。隠れ層のニューロン数は、それぞれ2*n1と2*n2です。
次に、RBM（Lr.rbm）、事前訓練中のDNNの最上層（Lr.top）、微調整中のすべての層（Lr.fine）の訓練レベルを定義します。
fact1/fact2 — Factベクトルで定義されたリストから隠された各層の活性化関数のインデックスです。出力層にはsoftmax関数が使用されます。
dr1/dr2 — それぞれの隠れ層でのドロップアウトレベルです。
darch.trainLayers — 事前訓練を使用して訓練される層と微調整中に訓練される層を示します。
4つの訓練/最適化オプションのそれぞれについて、ハイパーパラメータとその値域を記述しましょう。さらに、最良の訓練オプションを見つける上での便宜のために、パラメータBs.rbm = 100 (rbm.batchSize) 及びBs.nn = 50 (darch.batchSize) を外部パラメータにします。それらが減少すると、分類の質は向上しますが、最適化時間はかなり増加します。
#-2---------------------- evalq({ #--InitParams--------------------- Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit") wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate", "weightDecayWeightUpdate") #---SRBM + RP---------------- bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0)#, ) #---SRBM + BP---------------- bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + 上位層 + BP---- bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + 上位層 + RP----- bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0) ) Bs.rbm <- 100L Bs.nn <- 50L },envir = env)
事前訓練及び微調整関数の定義
DNNは4つのオプションすべてを使って訓練されます。必要な関数はすべてFUN_Optim.Rスクリプトにあるので、Git/PartVで計算を開始する前にダウンロードされるべきです。
各オプションの事前訓練及び微調整関数は下記のとおりです。
- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm ) — SRBMのみを事前訓練
- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — SRBMと上位層を事前訓練（誤差逆伝播法）
- fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — rpropagationを使用したDNNの微調整
- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — 誤差逆伝播法を使用したDNNの微調整
同じような関数の一覧で本稿がいっぱいにならないように、事前訓練（SRBM + topLayer）+ RP（微調整rpropagation）のオプションのみが考慮されます。多くの実験では、このオプションがほとんどの場合に最良の結果を示しました。他のオプションの関数も同様です。
# SRBM + 上位層（誤差逆伝播法）
pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + 上位層（誤差逆伝播法）
{
darch( x = X$pretrain$x, y = X$pretrain$y,
xValid = X$train$x,
yValid = X$train$y,
#=====定数======================================
layers = Ln,
paramsList = list(),
darch = NULL,
shuffleTrainData = T,
seed = 54321,
logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE.
#--最適化パラメータ----------------------------------
darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"),
darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2],
"weightDecayWeightUpdate"),
rbm.learnRate = Lr.rbm,
bp.learnRate = Lr.top,
darch.dropout = c(0, dr1, dr2),
#=== RBMパラメータ ==============
rbm.numEpochs = 30L,
rbm.allData = T,
rbm.batchSize = Bs.rbm,
rbm.consecutive = F,
rbm.errorFunction = mseError, #rmseError
rbm.finalMomentum = 0.9,
rbm.initialMomentum = 0.5,
rbm.momentumRampLength = 1,
rbm.lastLayer = -1,
rbm.learnRateScale = 1,
rbm.numCD = 1L,
rbm.unitFunction = tanhUnitRbm,
rbm.updateFunction = rbmUpdate,
rbm.weightDecay = 2e-04,
#=== NNパラメータ ========================
darch.numEpochs = 30L,
darch.batchSize = Bs.nn,
darch.trainLayers = c(FALSE, FALSE,TRUE ),
darch.fineTuneFunction = "backpropagation", #rpropagation
bp.learnRateScale = 1, #0.99
#--重み-----------------
generateWeightsFunction = generateWeightsGlorotUniform,
# generateWeightsUniform (default),
# generateWeightsGlorotUniform,
# generateWeightsHeUniform.
# generateWeightsNormal,
# generateWeightsGlorotNormal,
# generateWeightsHeNormal,
darch.weightDecay = 2e-04,
normalizeWeights = T,
normalizeWeightsBound = 15,
#--パラメータ正則化-----------
darch.dither = F,
darch.dropout.dropConnect = F,
darch.dropout.oneMaskPerEpoch = T,
darch.maxout.poolSize = 2L,
darch.maxout.unitFunction = "exponentialLinearUnit",
darch.elu.alpha = 2,
darch.returnBestModel = T
#darch.returnBestModel.validationErrorFactor = 0,
)
}
この関数ではX$trainセットの値が検証セットとして使用されます。
rpropagationを使用した微調整関数。パラメータとは別に、事前に訓練された構造体Dnnがこの関数に渡されます。
fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation { darch( x = X$train$x, y = X$train$y, #xValid = X$test$x, yValid = X$test$y, xValid = X$test$x %>% head(250), yValid = X$test$y %>% head(250), #=====定数====================================== layers = Ln, paramsList = list(), darch = Dnn, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. rbm.numEpochs = 0L, #--最適化パラメータ---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), darch.dropout = c(0, dr1, dr2), #=== NNパラメータ ======================== darch.numEpochs = 50L, darch.batchSize = Bs.nn, darch.trainLayers = c(TRUE,TRUE, TRUE), darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation" #=== RPROPパラメータ ====== rprop.decFact = 0.5, rprop.incFact = 1.2, rprop.initDelta = 1/80, rprop.maxDelta = 50, rprop.method = "iRprop+", rprop.minDelta = 1e-06, #--重み----------------- darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--パラメータ正則化----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
ここでは、X$testの最初の250個の値が検証セットとして使用されます。すべての訓練オプションのすべての関数は、env環境に読み込まれる必要があります。
適合関数の定義
これらの2つの関数を使用して、ハイパーパラメータの最適化に必要な適合関数を記述します。これは最適化すべき最適化基準Score = mean(F1)の値と目的関数Ypred の予測値を返します。
#---SRBM + 上位層 + RP---- fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>% mean() return(list(Score = Score, Pred = Ypred) }
DNN最適のパラメータの決定
最適化関数BayesianOptimization()は、ハイパーパラメータのスペース内でランダムに取得された10個の初期点を使用して開始されます。計算がすべてのプロセッサコア（Intel MKL）で並列化されているにもかかわらず、かなりの時間がかかり、反復回数と「バッチサイズ」のサイズに依存します。時間を節約するために10反復から始めます。将来、結果が満足できない場合は、以前の最適化実行の最適値を初期値として使用して最適化を続けることができます。
SRBM + RPを訓練する変形
#---SRBM + RP---------------- evalq( OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) 見つかった最良のパラメータは下記のとおりです。 Round = 7 n1 = 22.0000 n2 = 2.0000 fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 Lr.rbm = 0.7889 Value = 0.7531
得られた最適のパラメータとF1の変形を見てみましょう。BayesianOptimization()関数は、複数の値を返します。これらは、最良のパラメータ値（Best_Par）、これらの最良のパラメータの最適化基準の最適な値（Best_Value）、最適化履歴（History）、すべての反復後に取得された予測（Pred）です。最適化の履歴を見てみましょう。事前に'Value'で降順に並べ替えます。
evalq({
OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 22 2 3 2 0.41136623 0.48175897 0.78886312 0.7531204
2 23 8 4 2 0.16814464 0.16221565 0.08381839 0.7485614
3 19 17 3 3 0.17274258 0.46809117 0.72698789 0.7485614
4 25 25 4 2 0.30039573 0.26894463 0.11226139 0.7473266
5 11 24 3 2 0.31564303 0.11091751 0.40387209 0.7462520
6 1 6 3 4 0.36876218 0.17403265 0.90387675 0.7450260
7 25 25 3 1 0.06872059 0.42459582 0.40072731 0.7447972
8 1 25 4 1 0.24871843 0.18593687 0.31920691 0.7445628
9 18 1 4 3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25 4 1 0.37052548 0.07603925 0.87100360 0.7402597
これは良い結果です。もう1つの最適化を実行しますが、以前の実行best_init1の値を使用して、ハイパーパラメータのスペースで10ポイントを初期化します。
evalq( OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = best.init1, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) 見つかった最良のパラメータは下記のとおりです。 Round = 1 n1 = 4.0000 n2 = 1.0000 fact1 = 1.0000 fact2 = 4.0000 dr1 = 0.1870 dr2 = 0.0000 Lr.rbm = 0.9728 Value = 0.7608
この実行による10の最良の結果を見てみましょう。
evalq({
OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 4 1 1 4 0.18701522 2.220446e-16 0.9728164 0.7607811
2 3 24 1 4 0.12698982 1.024231e-01 0.5540933 0.7549180
3 5 5 1 3 0.07366640 2.630144e-01 0.2156837 0.7542661
4 1 18 1 4 0.41907554 4.641130e-02 0.6092082 0.7509800
5 1 23 1 4 0.25279461 1.365197e-01 0.2957633 0.7504026
6 4 25 4 1 0.09500347 3.083338e-01 0.2522729 0.7488496
7 17 3 3 3 0.36117416 3.162195e-01 0.4214501 0.7458489
8 13 4 3 3 0.22496776 1.481455e-01 0.4448280 0.7437376
9 21 24 1 3 0.36154287 1.335931e-01 0.6749752 0.7435897
10 5 11 3 3 0.29627244 3.425604e-01 0.1251956 0.7423566
最良の結果だけでなく、トップ10の品質構成も改善され、'Value' 統計が増加しました。最適化は、さまざまな初期点を選択して数回繰り返すことができます（たとえば、最悪の10つの値の最適化を試みるなど）。
この訓練変形については、以下の最良のハイパーパラメータを使います。
> env$OPT_Res1.1$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm 4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728
これらを解釈してみましょう。以下の最適のパラメータが得られました。
- 第1隠れ層のニューロン数 - 2*n1 = 8
- 第2隠れ層のニューロン数 - 2*n2 = 2
- 第1隠れ層の活性化関数 Fact[fact1] ="tanhdUnit"
- 第2隠れ層の活性化関数 Fact[fact2] = "sigmoidUnit"
- 第1隠れ層のドロップアウトレベル dr1 = 0.187
- 第2隠れ層のドロップアウトレベル dr2 = 0.0
- 事前訓練時のSRBMの訓練レベル Lr.rbm = 0.9729
概して良好な結果を得ることに加えて、興味深い構造体DNN (10-8-2-2) が形成されました。
SRBM + BPを訓練する変形
#---SRBM + BP---------------- evalq( OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)
10の最良の結果を見てみましょう。
> evalq({
+ OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+ dplyr::select(-Round) -> best.init2
+ best.init2
+ }, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine Value
1 23 24 2 1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2 3 24 4 3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3 15 13 4 1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4 7 18 3 1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5 7 23 3 3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6 21 23 3 1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7 23 8 3 4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8 5 2 1 1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9 1 24 1 2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18 8 4 1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895
結果は良好で、追加の最適化は必要ありません。
この変形の最適なハイパーパラメータは下記のとおりです。
> env$OPT_Res2$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine 23.0000 24.0000 2.0000 1.0000 0.4513 0.1459 0.8990 0.2326
SRBM + 上位層 + BPを訓練する変形
#---SRBM + 上位層 + BP---- evalq( OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)見つかった最良のパラメータは下記のとおりです。 Round = 20 n1 = 24.0000 n2 = 5.0000 fact1 = 1.0000 fact2 = 2.0000 dr1 = 0.4060 dr2 = 0.2790 Lr.rbm = 0.9586 Lr.top = 0.8047 Lr.fine = 0.8687 Value = 0.7697
10の最良の結果を見てみましょう。
evalq({
OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init3
best.init3
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine Value
1 24 5 1 2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2 24 13 1 1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3 7 8 3 3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4 9 15 3 3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5 4 20 3 3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6 21 6 3 1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7 22 3 1 1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8 7 18 3 4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9 25 13 2 1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17 1 1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243
結果は良好で、追加の最適化は必要ありません。
この訓練変形の最適なハイパーパラメータは下記のとおりです。
> env$OPT_Res3$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine 24.0000 5.0000 1.0000 2.0000 0.4060 0.2790 0.9586 0.8047 0.8687
SRBM + 上位層 + RPを訓練する変形
#---SRBM + 上位層 + RP---- evalq( OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)見つかった最良のパラメータは下記のとおりです。 Round = 15 n1 = 23.0000 n2 = 7.0000 fact1 = 3.0000 fact2 = 1.0000 dr1 = 0.3482 dr2 = 0.4726 Lr.rbm = 0.0213 Lr.top = 0.5748 Value = 0.7625
ハイパーパラメータの上位10種類は下記のとおりです。
evalq({
OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init4
best.init4
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Value
1 23 7 3 1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2 24 13 3 1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3 1 1 4 3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4 23 7 3 1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5 19 16 3 3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6 8 12 3 1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7 10 8 3 1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8 6 19 1 2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9 11 10 1 2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21 2 1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324
結果は良好で、追加の最適化は必要ありません。
この訓練変形に最適なハイパーパラメータを取ります。
> env$OPT_Res4$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top 23.0000 7.0000 3.0000 1.0000 0.3482 0.4726 0.0213 0.5748
最適のパラメータを使ったDNNの訓練とテスト
変形をテストして得られたメトリックを考えてみましょう。
変形SRBM + RP
DNNを最適なパラメータでテストするには、特別な関数を作成します。ここでは、この訓練変形のみを示します。他の変形でも似ています。
#---SRBM + RP---------------- test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt)) }
test1.DNN()関数のパラメータは先に取得された最適なハイパーパラメータです。次にpretrainSRBM()関数を使用して事前訓練を行って事前訓練されたDNNを取得します。これは後に微調整関数fineTuneRP()に与えられ、訓練されたDnn.optが取得されます。このDnn.optとX$testセットの最後の250の値を使用して、目的関数Ypredの予想値を取得します。予想されたYpredと目的関数yTestの実際の値を使用して、Evaluate()関数でメトリックの数を計算します。メトリックを選択するための複数のオプションが用意されています。その結果、この関数は、Score（テストメトリック）、Pred（ 目的関数の予測値）、Dnn（ 事前訓練されたDNN）、Dnn.opt（ 完全に訓練されたDNN）オブジェクトを生成します。
追加の最適化後に得られたハイパーパラメータを使用して結果をテストして表示します。
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1.1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---訓練/テスト--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.74 0.718 0.724 0.721
1 0.74 0.759 0.754 0.757
結果は、最初の最適化後の結果よりも悪く、桁外れが明白です。下記はハイパーパラメータの初期値によるテストです。
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---訓練/テスト--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.756 0.757 0.698 0.726
1 0.756 0.755 0.806 0.780
結果は良好です。訓練履歴のグラフをプロットしましょう。
plot(env$Res1$Dnn.opt, type = "class")
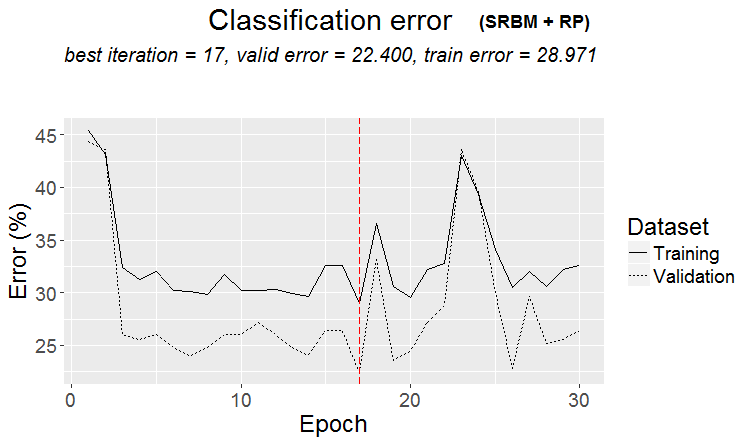
図2 SRBM + RP変形によるDNN訓練の履歴
図からわかるように、検証セットのエラーは訓練セットのエラーよりも小さいものです。これは、モデルが過剰適合されておらず、一般化能力が良好であることを意味します。赤い縦線は、最良と見なされ、訓練後に結果として返されるモデルの結果を示します。
他の3つの訓練変形については、詳細な計算を行わずに計算結果と履歴グラフのみを提供します。すべてが同様に計算されます。
変形SRBM + BP
テスト:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res2$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]; Lr.fine = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#---訓練/テスト--------
Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
}, env)
env$Res2$Score
Accuracy Precision Recall F1
-1 0.768 0.815 0.647 0.721
1 0.768 0.741 0.873 0.801
結果は優れていると言えます。訓練履歴を見てみましょう。
plot(env$Res2$Dnn.opt, type = "class")
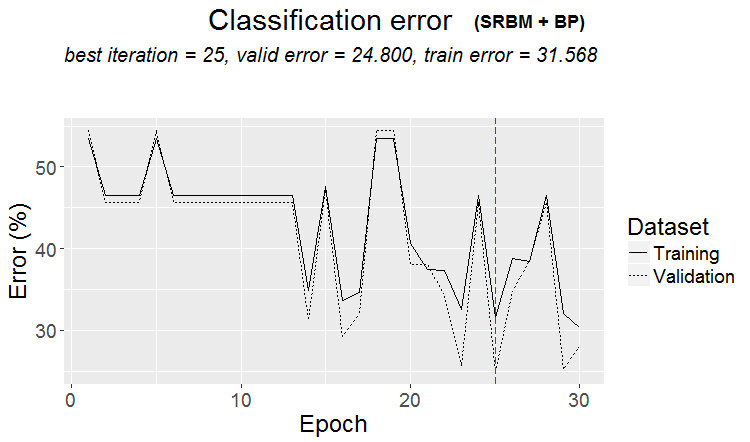
図3 変形SRBM + ВPによるDNN訓練の履歴
変形SRBM + 上位層 + BP
テスト:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res3$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Lr.fine = best.par[9]
Ln <- c(0, 2*n1, 2*n2, 0)
#---訓練/テスト--------
Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
}, env)
env$Res3$Score
Accuracy Precision Recall F1
-1 0.772 0.771 0.724 0.747
1 0.772 0.773 0.813 0.793
結果は優秀です。最適化基準としてF1の平均値を使用すると、両クラスの不均衡にもかかわらず、両方のクラスで同じ品質が得られることに注意してください。
訓練履歴のグラフ:
plot(env$Res3$Dnn.opt, type = "class")
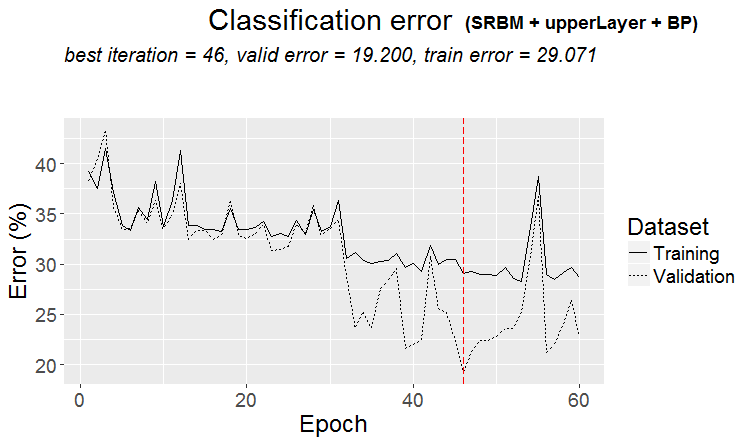
図4 変形SRBM + 上位層 + BPによるDNN訓練の履歴
変形SRBM + 上位層 + RP
テスト:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res4$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#---訓練/テスト--------
Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
}, env)
env$Res4$Score
Accuracy Precision Recall F1
-1 0.768 0.802 0.664 0.726
1 0.768 0.747 0.858 0.799
これは良い結果です。訓練履歴のグラフを見てみましょう。
plot(env$Res4$Dnn.opt, type = "class")
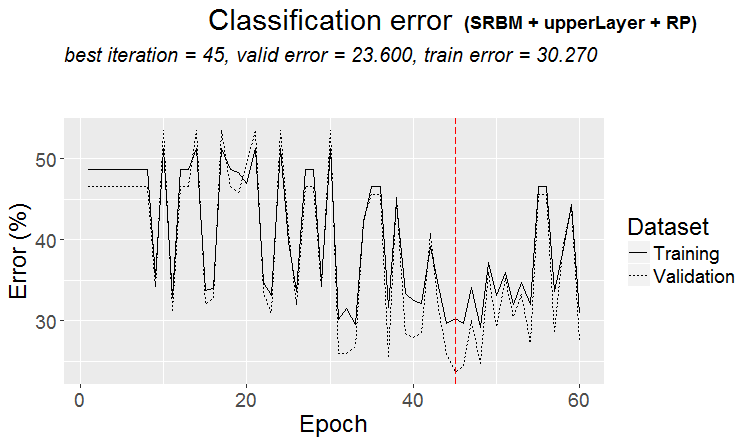
図5 変形SRBM + 上位層 + RPによるDNN訓練の履歴
最適のパラメータを使ったDNNテストの結果の分析
ハイパーパラメータの最適化された値を用いて異なる変形によって訓練されたDNNモデルを訓練して試験した結果、75（±5）％の精度を持つ良好な結果が得られます。25％の分類誤差は安定しており、訓練方法に依存せず、データの構造が4分の1の場合に目的関数の構造と一致しないことを示唆しています。ソースデータセット内のノイズサンプルの存在を調べるときにも同じ結果が観察されました。その数は約25％で、予測変数の変換方法には依存しませんでした。これは普通です。質問：モデルの過剰適合を避けながら予測を改善する方法は何でしょうかオプションがいくつかあります。
- 4つの変形によって訓練された最良のモデルからなるニューラルネットワークのアンサンブルを使用する
- 訓練の各変形による最適化中に得られた10の最良モデルからなるニューラルネットワークのアンサンブルを使用する
- 訓練セットのノイズサンプルを追加クラス"0"にラベル付けし直し、この目的関数（3つのクラスс("-1", "0", "1"）を使用してDNNモデルを訓練する
- 誤分類されたサンプルを追加クラス"0"にラベル付けし直し、この目的関数（3つのクラスс("-1", "0", "1")）を使用してDNNモデルを訓練する
アンサンブルの作成、訓練、使用については、このシリーズの次の記事で詳しく検討します。
ノイズサンプルを再ラベル付けした実験には別の研究が必要で、この記事の範囲を超えています。考え方はシンプルです。前の部分で考慮されたORBoostFilter::NoiseFiltersR関数を使用して、訓練及び検証セットのノイズサンプルを同時に決定します。目的関数では、これらのサンプルに対応するクラス（ "-1"/"1"）の値がクラス "0"に置き換えられます。つまり、目的関数には3つのクラスがあります。このようにして、ノイズサンプルを分類しないようにモデルを教えようとします。このような分類は通常分類エラーの原因となります。同時に、利益の損失は損失ではないという前提に頼ります。
最適のパラメータを使ったモデルのフォワードテスト
DNNの最適なパラメータが、どのくらい長く「将来の」クオーツ値のテストに許容可能な品質で結果を生み出すかを確認しましょう。テストは、以下のように、前の最適化とテストの後に残っている環境で実行されます。
1350バーの移動ウィンドウを使用、訓練 = 1000、テスト = 350（検証には初めの250サンプル、テストには最後の100サンプル）事前訓練に使用される、初めの (4000 + 100) の後はステップ100でデータを処理します。「前方へ」の10ステップ取ります。各ステップでは、2つのモデルが訓練され、テストされます。
- 1 — 事前に訓練されたDNNを使用します。すなわち各ステップで新しい範囲を微調整します
- 2 — 微調整段階での最適化後に得られたDNN.optを新たな範囲で追加的に訓練します。
#--- 準備する ----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
事前訓練されたDNNと、SRBM + 上位層 + BP訓練変形から取得された最適のハイパーパラメータを使用してフォワードテストの最初の部分を実行します。
#----#---SRBM + 上位層 + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #---訓練/テスト-------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
最適化で取得されたDnn.optを使用して2段階目のフォワードテストを行います。
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#---訓練/テスト--------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
テスト結果を比較し、表に配置します。
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Accuracy Precision Recall F1 | Accuracy Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 |
-1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 |
-1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 |
-1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 |
-1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 |
-1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 |
-1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 |
-1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 |
-1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 |
-1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
この表は、最初の2つのステップが良い結果をもたらすことを示しています。品質は実際には両方の変形の最初の2つのステップで同じですが、その後下がります。したがって、最適化とテストの後、DNNはバーに続いて少なくとも200〜250のテストセットのレベルで分類の質を維持すると仮定できます。
以前の記事で述べられたフォワードテストのモデルの追加訓練と多数の調整可能なハイパーパラメータの組み合わせは、他にもたくさんあります。
終わりに
- darch v.0.12パッケージは、DNNハイパーパラメータの巨大なリストにアクセスすることができ、大規模かつ細かい調整が可能です。
- ベイズアプローチを使用してDNNハイパーパラメータを最適化することにより良質のモデルの幅広い選択肢が得られ、アンサンブルを作成するために使用できます。
- ベイズ法を用いたDNNハイパーパラメータの最適化は、分類の質に7～10％の向上をもたらします。
- 最良の結果を得るには、複数の最適化（10〜20）を実行し、その後に最良の結果を選択する必要があります。
- 最適化プロセスは予備工程で得られたパラメータを初期値として供給して段階的に継続することができます。
- DNNにおける最適化の間に得られたハイパーパラメータを使用すると、フォワードテストの分類の品質が、テストセットに等しい長さのセクションのテストレベルで維持されることが保証されます。
さらなる改善には、 最適化されたパラメータをrpropagation訓練の4つの変形、隠れ層でのニューロンの重みの正規化（normalizeWeights(TRUE, FALSE)）、この正規化の上限（ normalizeWeightsBound）で補うことに意味があります。モデルによる分類の質に影響を与えるとおもわれる他のパラメータについてはご自分で実験してみてください。darchパッケージの主な利点の1つは、すべてのニューラルネットワークパラメータへのアクセスが提供されることです。各パラメータがどのように分類の質に影響するかを実験的に決定することが可能です。
相当な時間がかかりますが、ベイズ最適化の使用が推奨されます。
ニューラルネットワークのアンサンブルの使用は、分類の質を改善する別の可能性を与えるようです。異なる変形におけるこの補強のオプションについては、次の記事で説明します。
適用
GitHub/PartVには下記が含まれます。
1. FUN_Optim.R — 本稿で説明しているすべての計算を実行するために必要な関数
2. RUN_Optim.R — 本稿で実行された計算
3. SessionInfo. txt — 計算に使用されるパッケージ
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/4225
自己キャッシング指標の速度比較
トレーダーのハック: 定義と ForEach のブレンド (#define)
オシレーターでZig Zagインジケータ - を作成してみましょう。技術課題の実施例
MetaTrader 5における取引戦略最適化の可視化
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索