ディープニューラルネットワーク(その7)ニューラルネットワークのアンサンブル: スタッキング
1 468
1
内容
- はじめに
- 1. 訓練可能な結合器のための入力データの準備
- 2. 基本比較モデル
- 3. Keras/TensorFlowライブラリ — 一般的な説明とインストール
- 4. バギングアンサンブル出力の結合器 — ニューラルネットワーク
- 5. 実験結果の分析
- 終わりに
- 添付ファイル
はじめに
アンサンブルのベースレベルのモデル(個々の分類器)はフルセットで訓練されています。次に、メタモデルは、テストセットに基づいて予測中に得られたアンサンブル出力に対して訓練されます。この場合、アンサンブルの基本分類器の出力は、それ自体が結合器である新しい訓練済みの分類器の入力データとなります。このアプローチは、「複雑な一般化」、「訓練による一般化」、または単に「スタッキング」と呼ばれています。
この結合器の主な問題の1つは、メタクラシファイアの訓練セットを構築することです。
スタッキングアンサンブルの構築とテストを試してみましょう。これらは、以前に得られた最適なハイパーパラメータを持つELMニューラルネットワーク分類器のアンサンブルを使用します。1番目の実験では刈り込まれたアンサンブルの出力、2番目の実験ではアンサンブルのすべての入力が使用されます。結合器として、両バリエーションは全結合ニューラルネットワークを有しますが、構造は異なります。後の実験では、マルチモードとマルチタスクがどのようにしてニューラルネットワーク分類の品質に影響を与えるかを調べます。
基本比較モデルは、これらのバリエーションの予測品質を推定するために使用されます。
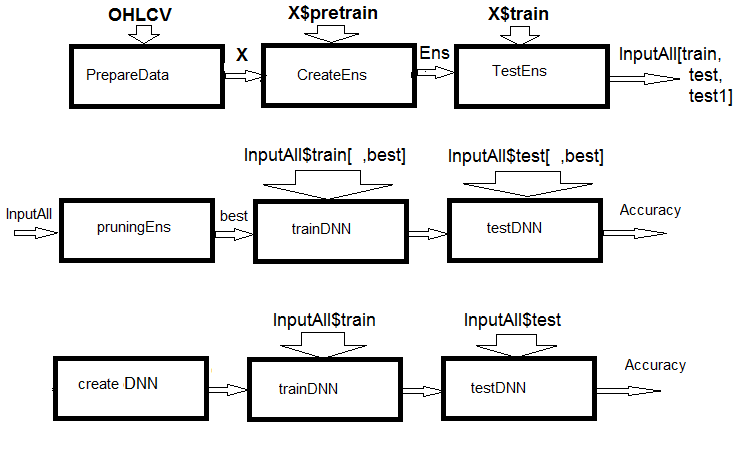
図1 計算の構造図
図から分かるように、実験は3つの部分で構成されています。
- アンサンブルの入力データを準備し、ELMアンサンブルを訓練し、train/test/test1セットの予測を取得します。これらのセットは、訓練可能な結合器のInputAll入力として機能します。
- アンサンブルの刈り込み: 情報の重要性から、最良のELM予測を選択します。基本比較モジュールをテストして基準メトリックを取得します。これらのデータについてDNNを訓練し、テストし、モデルのメトリックを計算し、それらを基本モデルのメトリックと比較します。
- マルチモーダルとマルチタスクニューラルネットワークを作成し、それらを訓練し、InputAllセットでテストします。取得したモデルのメトリックを計算し、ベースモデルのメトリックと比較します。
1. 訓練可能な結合器のための入力データの準備
実験には、Rバージョン3.4.4が使用されます。これにはまだ使われていないいくつかの新しいパッケージが含まれています。
RStudioを実行します。端末相場を含むCotir.RDataをGitHub/Part_Iからダウンロードして、データ準備関数を含むImportar.R、Libary.R、 FunPrepareData_VII.R、FUN_Stacking.RファイルをGitHub/Part_VIIからダウンロードします。注: ダウンロードの順番は重要です。計算を高速化し、スクリプトの読みやすさを向上させるために、関数を少し修正してあります。また、実験に必要な多数の予測変数も追加しました。
同じ相場を使用して、このシリーズの前記事と同じサンプルに分割します。初期データを準備するためのスクリプトを書きましょう。計算の詳細は以前に説明したため、ここでは繰り返されません。変更はdplyrパッケージを使用してパッケージと関数を作業環境にインポートすることに関連しています。dplyr はデータ操作を容易にする非常に便利なパッケージです。しかし、デバッグ中にエラーを検出するのに数時間かかることがあります。
これを明確にしましょう。dplyrライブラリを読み込む際に、以下の警告がコンソールに表示されます。
> library(dplyr) Attaching package: ‘dplyr’ The following objects are masked from ‘package:stats’: filter, lag The following objects are masked from ‘package:base’: intersect, setdiff, setequal, union
関数名の衝突が明白です。この問題を解決するには、特定の関数が呼び出されたパッケージを明示的に指定する必要があります。例えば、dplyr::filter()、dplyr::lagのようにです。2番目の問題は、多くの場合、パッケージの関数は1つまたは2つだけ必要ですが、ライブラリ全体を読み込む必要があるということです。また、特定のパッケージ(例えば、caret)は巨大で、それに必要のない依存パッケージが続きます。この意味で、Pythonで関数やパッケージをインポートするスタイルはより論理的です。下記が例です。
from theano import function, config, shared, tensor import numpy as np import time
1行目ではtheanoパッケージのいくつかの関数がインポートされています。2行目では、numpyパッケージがインポートされ、npというニックネームが付けられます。3行目ではtimeパッケージがインポートされます。Rでは同じ機能はimportarパッケージに実装されています。このパッケージには、import()と import_fun()という2つの関数しかありません。パッケージはimport()でインポートすることができ、関数をインポートするにはimport_fun()を使用します。しかし、import()はreticulate::import()との衝突を避けるためにimport_pack()に改名されました。
さらに新しい変数が導入され、これは実験に必要です。data1とdata2の2つのデータセットを生成します。情報の重要性によって予測変数を配置します。
以下は、実験の初期データを準備するためのスクリプトです。これはPrepare.Rファイルにあります。
#--0--ライブラリ------------- # source(file = "importar.R") # source(file = "Library.R") # source(file = "FunPrepareData_VII.R") # source(file = "FUN_Stacking.R") #--1-準備---- evalq({ # OHLCV、Med、Typ、Wをデータフレームに結合する # 予測変数と目標を計算する dt <- PrepareData(Data, Open, High, Low, Close, Volume) # 初期データをpretrain/train/val/testに分割する DT <- SplitData(dt$feature, 4000, 1000, 500, 250, start = 1) # 外れ値のパラメータを定義する pre.outl <- PreOutlier(DT$pretrain) # すべてのセットで外れ値を補完する DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) # 予想変数を正規化する方法を設定する meth <- "spatialSign" #"expoTrans" "range" "spatialSign", # 正規化パラメータを定義する preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) # すべてのセットで予測変数を正規化する DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
ブロック0 (ライブラリ)で、必要なライブラリと関数をダウンロードします。スクリプトを含む4つのファイルを指定された順序でダウンロードする必要があります。ブロック1 (準備)では、予測値を作成し、それらを正規化して異常値を除去します。正規化方法は変更できます。
次に、data1とdata2の2つのデータセットを作成します。最初のセットでは、デジタルフィルタとその1次差が予測変数として使用され、ジグザグの1次差分の変化の兆候が目標になります。2番目のセットでは、予測変数は高値/安値/終値の一次差分とCO/HO/LO/HL相場の相違の差になり、ジグザグの一次差分が目標になります。スクリプトは以下に示されており、実際にはPrepare.Rファイルにあります。
#--2-Data X------------- evalq({ foreach(i = 1:length(DTcap)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 list(pretrain = X1[[1]] , train = X1[[2]] , test = X1[[3]] , test1 = X1[[4]] ) -> X1 }, env) #----------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 list(pretrain = X2[[1]] , train = X2[[2]] , test = X2[[3]] , test1 = X2[[4]] ) -> X2 }, env)
情報の重要度の高い順に両方のセットの予測変数を配置します。ランク付け方法を見てみましょう。スクリプトは以下に示されており、これもPrepare.Rファイルにあります。
#---3--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX1 }, env) colnames(env$X1$pretrain$x)[env$orderX1] [1] "v.fatl" "v.rbci" "v.ftlm" "fars" "v.satl" "stlm" [7] "rbci" "ftlm" "v.stlm" "v.rftl" "pcci" "v.rstl" [13] "v.pcci evalq({ orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX2 }, env) colnames(env$X2$pretrain$x)[env$orderX2] [1] "dC" "CO" "HO" "LO" "dH" "dL" "HL"
相場予測変数の順序は特に重要です。
結合器の入力データを準備するには、次のことが必要です。
- ELMアンサンブルを作成し、X1$pretrain訓練セットで訓練します。
- 訓練されたアンサンブルを使用してX1$trainセットの予測を行います。これは InputTrain訓練セットになります。
- 訓練されたアンサンブルを使用してX1$testセットの予測を行います。これはInputTestテストセットになります。
- 訓練されたアンサンブルを使用してX1$test1セットの予測を行います。これはInputTest1テストセットになります。
変数と定数を定義し、関数createEns()とGetInputData()を書きます。これは、アンサンブルのすべての出力の値を返します。アンサンブルを最適化した後、createEns()関数のパラメータの値はすでに取得済みです。他の値があるかもしれません。下記のスクリプトは、FUN_Stacking()ファイルにあります。
#----ライブラリ------------- import_fun(rminer, holdout, holdout) #source(file = "FunPrepareData_VII.R") #----入力------------- evalq({ #活性化関数の種類 Fact <- c("sig", #: シグモイド "sin", #: 正弦 "radbas", #: 放射基底関数 "hardlim", #: ハードリミット "hardlims", #: 対称ハードリミット "satlins", #: satlins "tansig", #: 接線シグモイド "tribas", #: 三角基底関数 "poslin", #: 正の線形 "purelin") #: 線形 n <- 500 #---createENS---------------------- createEns <- function(numFeature = 8L, r = 7L, nh = 5L, fact = 7L, order, X){ # 最良の予測変数の指標を決定する bestF <<- order %>% head(numFeature) # 訓練セットの最も良い予測変数を選択する Xtrain <- X$pretrain$x[ , bestF] #setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #--- アンサンブルを作成する--- Ens <<- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #---GetInputData -FUN----------- GetInputData <- function(Ens, X){ #---予測-InputTrain-- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> predEns #[ ,n] #---予測--InputTest---- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---予測--InputTest1---- Xtest2 <- X$test1$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---結果------------------------- return(list(InputTrain = predEns, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
アンサンブルを作成して、訓練可能な結合器の入力を計算します。
#---4--createEns---------------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) createEns(order = orderX1, X = X1) -> Ens GetInputData(Ens, X1) -> res }, env)
以下は結果の構造体です。
> env$res %>% str() List of 3 $ InputTrain: num [1:1001, 1:500] 0.811 0.882 0.924 0.817 0.782 ... $ InputTest : num [1:501, 1:500] 0.5 0.383 0.366 0.488 0.359 ... $ InputTest1: num [1:251, 1:500] 0.32 0.246 0.471 0.563 0.451 ...
2. 基本比較モデル
2つの訓練可能な結合器が作成されます。1つ目はアンサンブルの最良のニューラルネットワークの出力の平均化を置き換え、2つ目は刈り込みと平均化を置き換えます。したがって、両方の選択肢に分類品質スコアが必要になります。
ニューラルネットワークのアンサンブル
1番目のオプションでは、最適なパラメータを持つELMアンサンブルが基本比較モデルになります。
2番目のオプションは500個の入力を意味するので、varbvs パッケージが使用されます。これは、変数を選択し、結果が線形回帰またはロジスティック回帰を使用してモデル化されるベイジアン係数を計算するためのベイジアンモデルを選択する高速アルゴリズムを提供します。これらのアルゴリズムは、"Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies"(回帰におけるベイジアン変数選択のためのスケーラブルな変分推論と遺伝的関連研究におけるその精度)で説明された変分近似に基づいています。このソフトウェアは、100万を超える変数と数千のサンプルを持つ大規模なデータセットでの作業に使用されました。
1番目の選択肢は、追加関数のgetBest()、testAver()、testVot()を書いてメトリックを計算することです。これらの関数はFUN_Stacking.Rファイルにあります。
evalq({
getBest <- function(Ens, x, y, nb){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
predict(Ens[[i]], newdata = x)} -> y.pr
foreach(i = 1:n, .combine = "c") %do% {
median(y.pr[ ,i])} ->> th
foreach(i = 1:n, .combine = "c") %do% {
ifelse(y.pr[ ,i] > th[i], 1, 0) -> Ypred
Evaluate(actual = y, predicted = Ypred)$Metrics$F1 %>%
mean()
} -> Score
Score %>% order(decreasing = TRUE) %>% head(2*nb + 1) -> best
y.pr[ ,best] %>%
apply(1, sum) %>%
divide_by(length(best)) %>%
median() -> med
return(list(Score = Score, bestNN = best, med = med))
}
testAver <- function(Ens, x, y, best, med){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(1, sum) %>% divide_by(length(best)) -> ensPred
ifelse(ensPred > med, 1, 0) -> clAver
Evaluate(actual = y, predicted = clAver)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ensPred, clAver = clAver))
}
testVot <- function(Ens, x, y, best){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(2, function(x) ifelse(x > th[i], 1, -1)) %>%
apply(1, function(x) sum(x)) -> vot
ifelse(vot > 0, 1, 0) -> ClVot
Evaluate(actual = y, predicted = ClVot)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ClVot))
}
}, env)
これらの関数はすでに考察されました。したがって、記述は抜かします。しかし、その出力は注目に値します。
- 関数getBest()はメトリック(Score)、アンサンブルの最高の個々の分類子のインデックス(bestNN)、アンサンブルの平均出力の中央値(med)を返し、これらはモデルのテストに使用されます。すべてのアンサンブルの出力の中央値ベクトルth[500]が環境に挿入されます。
- 関数testAver()はメトリック(Score)、アンサンブルの平均連続予測(Ypred)、アンサンブルの公称予測(clAver)を返します。
- 関数testVot()は、メトリック(Score)とアンサンブルの公称予測(Ypred)を返します。
作成されたアンサンブルを、平均化と多数決を使用して2つのテストセットでテストしてから、メトリックを確認します。
#--2---テスト---- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) Ens <- createEns(order = orderX1, X = X1) #---3------ resBest <- getBest(Ens, x = X1$train$x[ , bestF], y = Ytest, nb = 3) #---4--平均化--- ScoreAver <- testAver(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN, med = resBest$med) ScoreAver1 <- testAver(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN, med = resBest$med) #---5--投票---- ScoreVot <- testVot(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN) ScoreVot1 <- testVot(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN) }, env) > env$ScoreAver$Score Accuracy Precision Recall F1 0 0.75 0.708 0.778 0.741 1 0.75 0.794 0.727 0.759 > env$ScoreAver1$Score Accuracy Precision Recall F1 0 0.753 0.750 0.826 0.786 1 0.753 0.758 0.664 0.708 > env$ScoreVot$Score Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 > env$ScoreVot1$Score Accuracy Precision Recall F1 0 0.741 0.739 0.819 0.777 1 0.741 0.745 0.646 0.692
どちらのテストセットでもパフォーマンスは良好です。以下では、結果を分析する際に分類誤差をバイアス/分散/ノイズに分解し、各要素の合計誤差に対する寄与を推定します。
2番目の選択肢(500件の入力)では、モデルを訓練するためのスクリプトは以下の通りです。これはvarb.Rファイルにあります。
library(varbvs) evalq({ vr <- varbvs(X = res$InputTrain, Z = NULL, y = Ytest, family = "binomial", optimize.eta = TRUE, logodds = seq(-6,-2, 0.25), nr = 250, initialize.params = TRUE, maxiter = 1e5, verbose = FALSE) summary(vr, cred.int = 0.95, nv = 7, nr = 1e5) %>% print() }, env) Summary of fitted Bayesian variable selection model: family: binomial num. hyperparameter settings: 17 samples: 1001 iid variable selection prior: yes variables: 500 fit prior var. of coefs (sa): yes covariates: 1 fit approx. factors (eta): yes maximum log-likelihood lower bound: -579.4602 Hyperparameters: estimate Pr>0.95 candidate values sa 8.09 [7.63,8.54] NA--NA logodds -2.26 [-2.75,-2.00] (-6.00)--(-2.00) Selected variables by probability cutoff: >0.10 >0.25 >0.50 >0.75 >0.90 >0.95 3 3 3 3 3 3 Top 7 variables by inclusion probability: index variable prob PVE coef* Pr(coef.>0.95) X18 18 X18 1.00000 NA 4.529 [+3.861,+5.195] X5 5 X5 1.00000 NA 1.955 [+1.543,+2.370] X255 255 X255 1.00000 NA 2.097 [+1.537,+2.660] X109 109 X109 0.00948 NA -1.033 [-2.008,-0.057] X404 404 X404 0.00467 NA -0.665 [-1.350,+0.024] X275 275 X275 0.00312 NA -0.726 [-1.735,+0.286] X343 343 X343 0.00299 NA -0.604 [-1.353,+0.149] *See help(varbvs) about interpreting coefficients in logistic regression.
得られたモデルを使用して、2つのテストセットの予測を計算し、メトリックを計算します。
env$vr$pip %>% order() %>% tail(7) -> bestNN_vr evalq({ predict(vr, res$InputTest) -> pr.vr1 Evaluate(actual = Ytest1, predicted = pr.vr1)$Metrics[ ,2:5] %>% round(3) -> metr.test confus(table(Ytest1, pr.vr1)) -> cm1 predict(vr, res$InputTest1) -> pr.vr2 Evaluate(actual = Ytest2, predicted = pr.vr2)$Metrics[ ,2:5] %>% round(3) -> metr.test1 confus(table(Ytest2, pr.vr2)) -> cm2 }, env) > env$metr.test Accuracy Precision Recall F1 0 0.78 0.750 0.783 0.766 1 0.78 0.808 0.779 0.793 > env$metr.test1 Accuracy Precision Recall F1 0 0.729 0.765 0.732 0.748 1 0.729 0.689 0.726 0.707
結果は、アンサンブルのメトリックよりもはるかに優れています。
実験を続けるために必要なすべてのデータが用意されています。
Keras/Tensorflowライブラリは将来使用されるため、以下では簡単に検討します。
3. Keras/TensorFlowライブラリ: 一般的な説明とインストール
急速に拡大しているディープニューラルネットワークの分野では、数多くのオープンソースライブラリが補足されています。これらには、TensorFlow(Google)、CNTK(Microsoft)、Apache MXNet他多数が含まれます。これらすべての主要ソフトウェア開発者がRコンソーシアムのメンバーであることから、これらのライブラリにはすべてRのAPIが提供されています。
上記のライブラリはすべて低レベルで、初心者にとっては、学んだり使用するのが難しいです。これを念頭に置いて、RstudioチームはRのkerasパッケージを開発しました。
Kerasは高レベルのニューラルネットワークAPIです。パッケージは、プロトタイプを素早く作成し、モデルの性能を実験的にテストする能力を重視して設計されています。Kerasの主な機能は次のとおりです。
- CPUまたはGPUで同等に動作することができる。
- 親しみやすいAPIで、深層学習モデルのプロトタイプを簡単に作成できる。
- 畳み込みネットワーク(コンピュータビジョン用)、再帰型ネットワーク(シーケンス処理用)、およびそれらの任意の組み合わせのための組み込みサポート。
- 任意のネットワークアーキテクチャをサポート(複数の入力または複数の出力を持つモデル、層の共有、モデルの共有など)。これは、 Keras が本質的にメモリネットワークからニューラルチューリングマシンへの深層モデルの構築に適していることを意味する。
- TensorFlow、CNTK、Theanoなど、いくつかのバックエンドの上で動作することができる。
Kerasは機械ではなくて人のために設計されたAPIです。このパッケージは認知負荷を軽減します。一貫性のあるシンプルなAPIが提供され、ユーザーの行動数を最小限に抑え、ユーザーのエラーに対する効果的なフィードバックが提供されます。これらによってKerasの学習と使用は簡単になります。しかし、これは柔軟性の低下によるものではありません。 Kerasは深層学習の低レベル言語(特に TensorFlow )と統合されているため、 基本言語で作成することができます。
Kerasモデルはいくつかの深層学習モジュールを使用して開発できます。組み込み層のみを使用する Kerasモデルは、これらのバックエンド間で変更なしに転送できます。あるバックエンドでモデルを訓練し、別のバックエンドで読み込むことができます。使用可能なバックエンドは次のとおりです。
- TensorFlowバックエンド(Google)
- CNTKバックエンド(Microsoft)
- Theanoバックエンド
KerasモデルはCPUだけでなくハードウェアプラットフォームで訓練することができます。
- NVIDIA GPU
- Google TPU、TensorFlowバックエンドとGoogle Cloud
- PlaidML Kerasバックエンドを介して、AMDからのOpenCL対応GPU
KerasおよびTensorflowバックエンドのインストール
KerasとTensorFlowはCPUまたはGPUでの作業用に構成できます。CPU版のインストールと設定はより単純なので、このパッケージを使うのが賢明です。TensorFlowウェブサイトにはCPUとGPUバージョンのマニュアルがあります。
- TensorFlow(CPUサポートのみ)。システムにNVIDIA®GPUが搭載されていない場合は、このバージョンをインストールする必要があります。
- TensorFlow(GPUサポート)。TensorFlowプログラムは、通常、GPU上ではCPU上よりもかなり高速で実行されます。したがって、システムにすべての前提条件を満たすNVIDIA®GPUがあり、パフォーマンスが重要なアプリケーションを実行する必要がある場合は、最終的にこのバージョンをインストールする必要があります。
Windowsでサポートされている唯一のインストール方法は "conda"です。つまり、Kerasをインストールする前に、Windows用のAnaconda 3.x(Python 3.5.x / 3.6.x)をインストールする必要があります。私はAnaconda3(Python3.6)をインストールしました。
まず、CRANからkerasパッケージをインストールします。
install.packages("keras")
Keras RインターフェイスはデフォルトでTensorFlowです。メインKerasライブラリとTensorFlowバックエンドを両方インストールするにはinstall_keras()関数を使用します。
# デフォルトインストール library(keras) install_keras()
よってKerasとTensorFlowのCPU版もインストールされます。例えば、NVIDIA GPUなどのカスタム設定が必要な場合は、ドキュメントを参照してください。特定のバージョンまたはGPUサポートのTensorFlowをインストールするには、以下を実行します。
# GPU版TensorFlowのインストール # (注: NVIDIA GPU + CUDAがある場合のみに実行 install_keras(tensorflow = "gpu") # TensorFlowの特定のバージョンをインストール install_keras(tensorflow = "1.5") install_keras(tensorflow = "1.5-gpu")
詳細はこちらでご覧ください。
tfrunsサポートパッケージは、TensorFlowによる実験用に設計されています。これはRからTensorFlowの訓練と実験を管理するためのツールキットです。
- 各訓練実行のハイパーパラメータ、メトリック、出力データ、ソースコードが追跡されます。
- 実行全体でのハイパーパラメータとメトリックを比較して、最高のパフォーマンスを発揮するモデルを探します。
- 個々の訓練の実行や実行間の比較を視覚化するためのレポートを自動的に生成します。
- ソースコードを変更する必要はありません(実行データはすべてのKerasおよびtfestimatorsモデルで自動的にキャプチャされます)。
DNNの訓練プロセスと結果の最高の視覚化品質は、TensorBoardによって提供されます。
深層学習の専門家には、 tensorflowパッケージを使用して、低レベルの TensorFlowライブラリで直接作業する機会が与えられます。
これらのパッケージはすべて、Pythonモジュール、関数、クラスへのRインタフェースであるメインのreticulateパッケージに基づいています。Pythonで呼び出されると、Rデータ型は自動的に同等のPython型に変換されます。Pythonから返された値は、R型に変換されます。
これらのパッケージはすべて文書化されており、数多くの例があり、常に進化しています。これにより、深層学習(DNN、RNN、CNN、LSTM、VAEなど)、強化学習(RL)、その他多くのPython開発を端末のエキスパートと指標で非常に高度なモデルを使用することができます。唯一の制限は、開発者の知識と経験です。
kerasRとkerasformulaの2つの興味深いパッケージがあります。1番目のテストでは、元の"tensorflow-1.5"よりも高い動作速度が確認されています。2番目は、数式を使ったモデルの簡略版を提供します。
本稿では、新しい分野での簡単なスタートの例を示すことを目的としています。その役割は、機会の多様性をすべて対象として、モデルの高品質な得点を得ることではありません。
実験を始める前に、Pythonがインストールされているかどうか、およびRがPythonと相互作用しているかどうかを確認する必要があります。
> library(reticulate)
> py_config()
python: K:\Anaconda3\envs\r-tensorflow\python.exe
libpython: K:/Anaconda3/envs/r-tensorflow/python36.dll
pythonhome: K:\ANACON~1\envs\R-TENS~1
version: 3.6.5 | packaged by conda-forge | (default, Apr 6 2018, 16:13:55)
[MSC v.1900 64 bit (AMD64)]
Architecture: 64bit
numpy: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\numpy
numpy_version: 1.14.2
tensorflow: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow
python versions found:
K:\Anaconda3\envs\r-tensorflow\python.exe
K:\ANACON~1\python.exe
K:\Anaconda3\python.exe
使用されているtensorflowのバージョンを表示します。
> library(tensorflow) > tf_config() TensorFlow v1.5.1 (K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow) Python v3.6 (K:\Anaconda3\envs\r-tensorflow\python.exe)
これで、実験を続行できます。
4. バギングアンサンブル出力の結合器 — ニューラルネットワーク
2つの実験を実行しましょう。1番目では、アンサンブルの最良の出力を平均化するのではなく softmax関数を適用します。2番目では、ニューラルネットワークによる刈り込みと平均化を置き換え、アンサンブルの500個の出力を全て入力として供給します。実験の構造図を下図に示します。
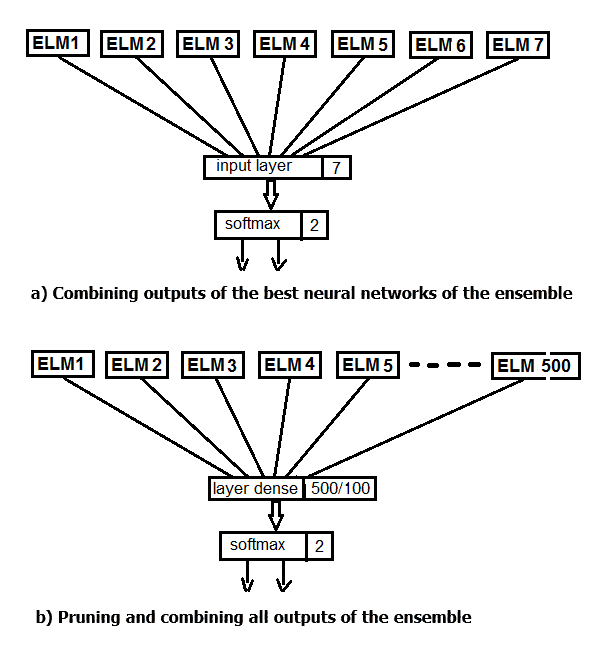
図2 アンサンブル出力の平均化のニューラルネットワークによる置き換え
Kerasの主なデータ構造はモデルであり、層を整理する方法です。もっとも単純なタイプは連続モデルで、これは層の線形スタックを表します。
まず、単純な連続モデルを作成し、パイプ(%>%)演算子を使用して層を追加します。最初の実験では、入力層と出力層のみからなるニューラルネットワークを作成します。テストセットで得られた刈り込み後のアンサンブルの出力は、入力として供給されます。訓練セットの20%が検証に使用されます。このパッケージに含まれるニューラルネットワークの作成、訓練、テストは非常に簡単です。
モデルの定数パラメータを設定し、DNNの訓練とテストセットを定義します。
#===========Keras=========================================== library(keras) num_classes <- 2L batch_size <- 32L epochs <- 300L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical()
モデルを作成します。 スクリプトコードは以下の通りです。構造体NN(7, 2)(入力で7ニューロン、出力で2ニューロン)を持つモデルを定義してコンパイルします。 オプティマイザは"rmsprop"関数、損失関数は"binary__crossentropy"、テスト結果のメトリックは"精度"です。
##----モデル--keras------------------------- # モデルを定義する model <- keras_model_sequential() # 層を追加してコンパイルする model %>% layer_dense(units = num_classes, input_shape = dim(x_train)[2]) %>% layer_activation(activation = 'softmax') %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(), metrics = 'accuracy' )
モデルを訓練してテストします(スクリプトは以下にあります)。訓練履歴を保存します。そして、次を指定します。
- 各繰り返しの結果を端末に出力する必要はありません。
- Viewer/Rstudioにリアルタイムチャートを表示する必要はありません。
- 各訓練エポック後に入力データをシャッフルする必要があります。
検証には、訓練セットの20%を使用します。
## 訓練&評価 --------------------------- # データをモデルに合わせる model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = FALSE, shuffle = TRUE, validation_split = 0.2) -> history # 出力メトリック score <- model %>% evaluate(x_test, y_test, verbose = 0) cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.518 cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.754 #--------------- score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.55 cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.737
定量的な結果は悪くありませんが、アンサンブル平均化の結果と事実上等しいです。このモデルの訓練とテストの履歴を見てみましょう。
#--プロット------------------------
plot(history)
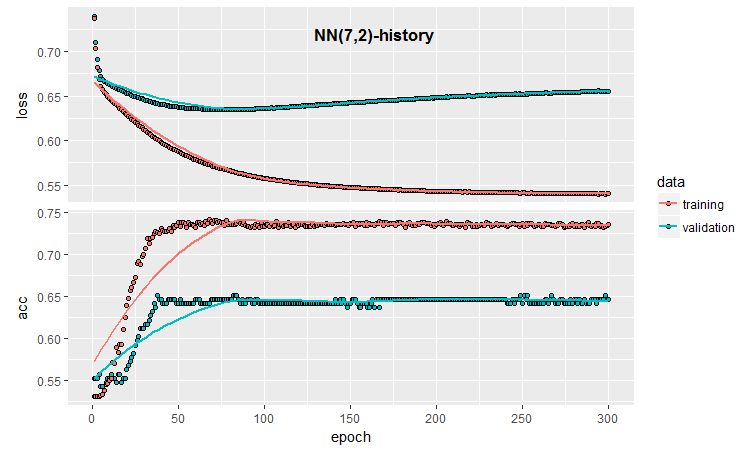
図3 モデル訓練履歴(7, 2)
グラフはモデルが30エポック後に明らかに過剰適合し、50エポック後には精度がプラトーに達することを示します。
覚えていらっしゃるように、ニューラルネットワーク初期化のプロセスはランダムです。つまり、新しく作成され、訓練され、テストされたモデルは、それぞれ異なる結果を生成します。
ニューラルネットワークのこの最小限の構成でも、分類品質および過大適合に影響を及ぼす多くの機会が存在します。早期停止、ニューロン初期化方法、活性化機能の正則化などが一例です。これらのうち、早期停止、入力データへのノイズ追加、起動機能の正則化、および訓練結果のより詳細なグラフィカル表現を出力することのみを確認します。これを行うには、訓練中にkerasが提供するコールバック を適用する機能を使用します。
callback_early_stopping(monitor = "val_loss", min_delta = 0, patience = 0, verbose = 0, mode = c("auto", "min", "max")) callback_tensorboard(log_dir = NULL, histogram_freq = 0, batch_size = 32, write_graph = TRUE, write_grads = FALSE, write_images = FALSE, embeddings_freq = 0, embeddings_layer_names = NULL, embeddings_metadata = NULL)
コールバック関数を定義します。
early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_1") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE)
1番目では、精度値を追跡する必要があることを示しました。この値がpatienteｇエポックでmin_delta 未満になったら、訓練を停止する必要があります。2番目では、後で再生するために訓練結果を保存するディレクトリにパスを設定し、正確に格納する場所を指定しました。これらの関数を使って完全なスクリプトを作成し、その結果を見てみましょう。
##=====バリエーション 早期停止================================= #--データを準備する-------------------------- library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() ##----モデル--keras------------------------- # モデルを定義する model <- keras_model_sequential() # 層を追加してコンパイルする model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## 訓練&評価 --------------------------- # データをモデルに合わせる model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, callbacks = list(early_stopping, tensboard)) -> history
以下は2つのテストセットのメトリックと早期停止による訓練の履歴です。
# 出力メトリック > score <- model %>% evaluate(x_test, y_test, verbose = 0) > cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.539 > cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.756 > #--------------- > score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) > cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.571 > cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.713
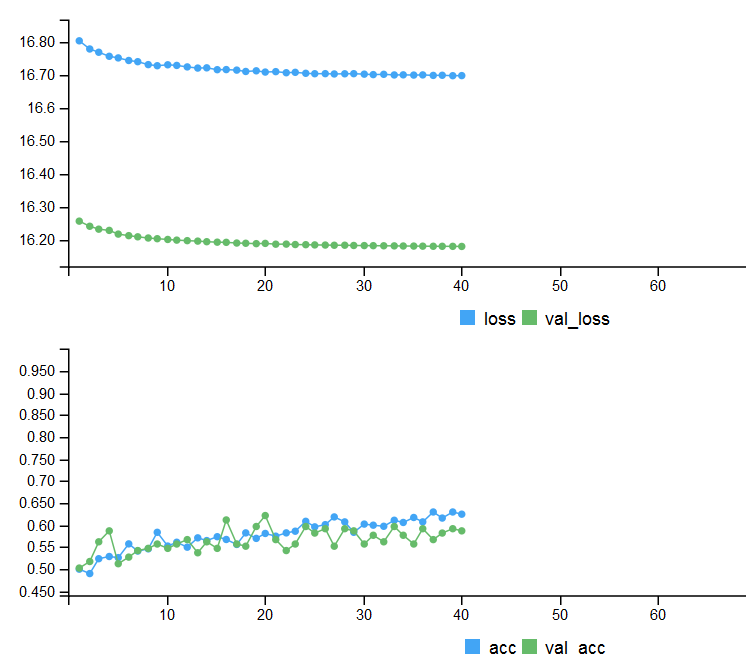
図4 早期停止による訓練の履歴
ニューラルネットワークの訓練プロセスに関する詳細なグラフィック情報を表示するには、tensorboard関数を使用します。
> tensorboard(log_dir = log_dir) TensorBoard 1.7.0 at http://127.0.0.1:7451 (Press CTRL+C to quit) Started TensorBoard at http://127.0.0.1:7451
ブラウザでは、ニューラルネットワークのすべての内部詳細を表示できるページを開きます。サンプルのスクリーンショットは次のとおりです。
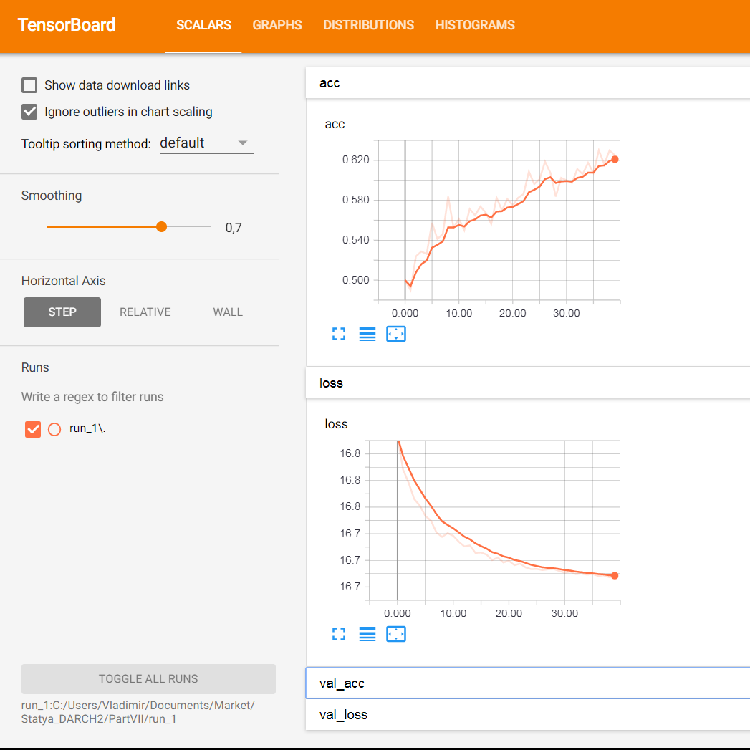
図5 訓練セットの訓練のための損失と精度のグラフ、val_accとval_lossに基づく検証データ
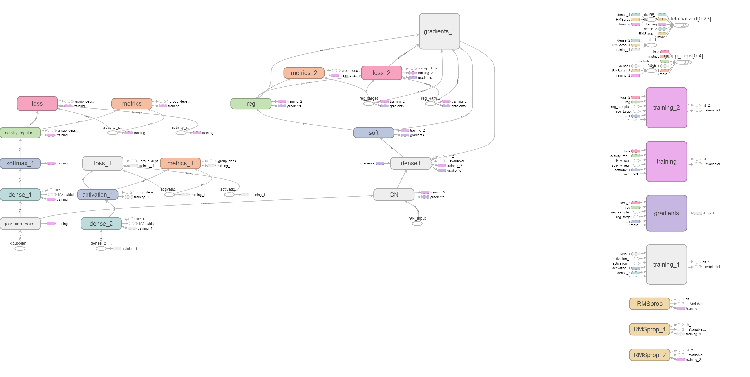
図6 ニューラルネットワークの計算グラフ
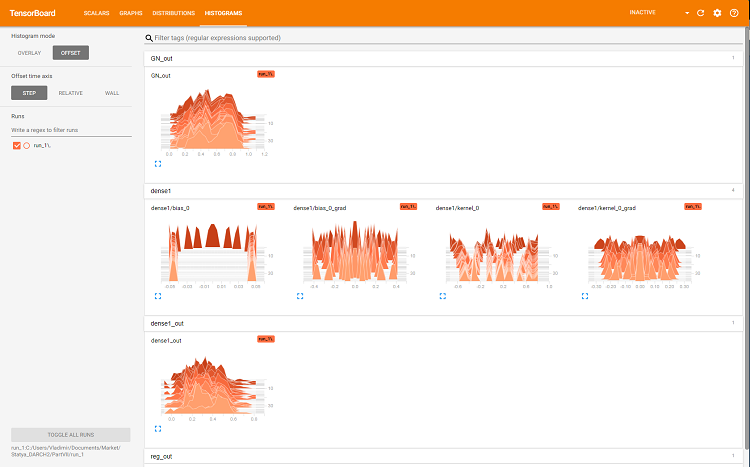
図7 層'dense'のヒストグラム
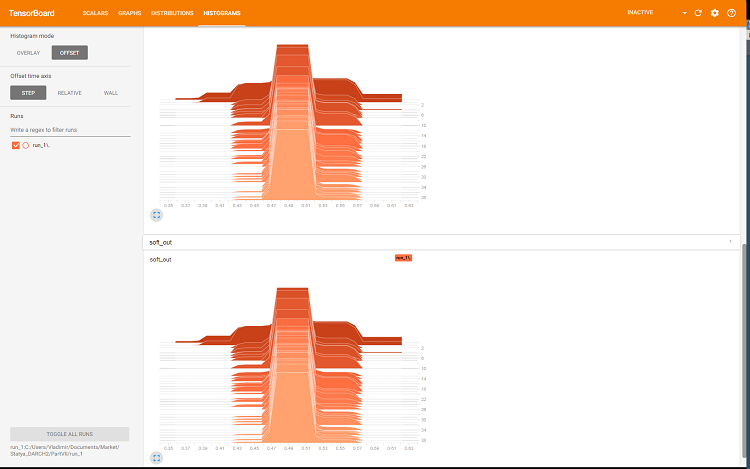
図8 ソフトマックスと正則化出力のヒストグラム
これらのグラフは、ニューラルネットワークのパラメータを調整するための強力なツールですが、詳細な分析は本稿の範囲を超えています。
tensorboardを新しく開始するごとに、保存パスlog_dirを変更するか、以前使用したものを削除する必要があります。
同じパラメータで分類の質がどのように変化するかを見ますが、検証のためにテストセットを使用してみましょう。スクリプトは以下に示され、ファイル内で利用可能です。
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_2") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE) ##----モデル--keras------------------------- # モデルを定義する model <- keras_model_sequential() # 層を追加してコンパイルする model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## 訓練&評価 --------------------------- # データをモデルに合わせる model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_data = list(x_test, y_test), callbacks = list(early_stopping, tensboard)) -> history
2番目のテストセットのメトリックを見てみましょう。
#--model--test1------------------------------------------------- predict(model, x_test1) -> Ypr.test1 Ypr.test1 %>% max.col()-1 -> y_pr_test1 #Ypr.test1 %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test1 evalq(res_mod_test1 <- Eval(Ytest2, y_pr_test1), env) > env$res_mod_test1 $metrics Accuracy Precision Recall F1 0 0.713 0.704 0.826 0.760 1 0.713 0.730 0.575 0.644 $confMatr Confusion Matrix and Statistics predicted actual 0 1 0 114 24 1 48 65 Accuracy : 0.7131 95% CI : (0.6529, 0.7683) No Information Rate : 0.6454 P-Value [Acc > NIR] : 0.013728 Kappa : 0.4092 Mcnemar's Test P-Value : 0.006717 Sensitivity : 0.7037 Specificity : 0.7303 Pos Pred Value : 0.8261 Neg Pred Value : 0.5752 Prevalence : 0.6454 Detection Rate : 0.4542 Detection Prevalence : 0.5498 Balanced Accuracy : 0.7170 'Positive' Class : 0
それらは1番目のバリエーションと実質的に同じです。tensorboardを使用して2つのバリエーションを視覚的に比較できます。
#-----プロット----------------- tensorboard(log_dir = c(paste0(getwd(),"/run_1"), paste0(getwd(),"/run_2")))
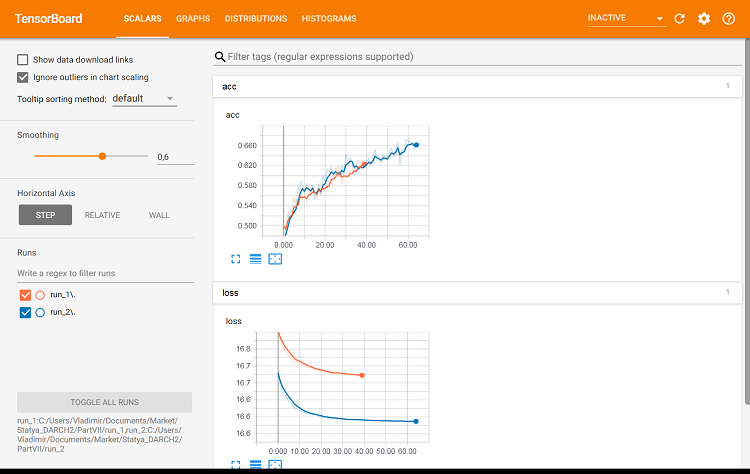
図9 訓練セットのメトリック
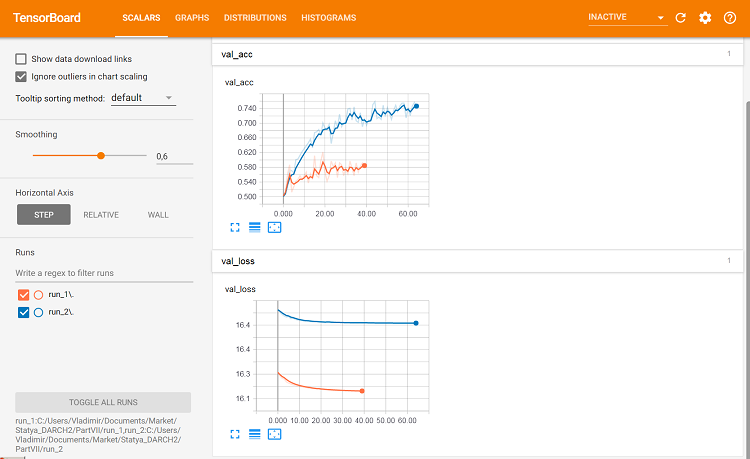
図10 検証セットのメトリック
これで違いがわかります。
最後の実験をしましょう。アンサンブルのすべての500の出力は、入力として多層ニューラルネットワークに供給されます。したがって、ニューラルネットワークは、刈り込みと結合を同時に実行します。このスクリプトは以下に提供されており、modelDNN_500.Rファイルでも使用できます。
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.0001 epochs <- 100L #--------- x_train <- env$res$InputTrain y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1 y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto")
ライブラリと定数をダウンロードし、訓練とテストのためのセットと早期停止機能を定義しました。
##----modelDNN--keras------------------------- # モデルを定義する modDNN <- keras_model_sequential() # 層を追加してコンパイルする modDNN %>% layer_gaussian_noise(stddev = 0.001, input_shape = dim(x_train)[2], name = "GN") %>% layer_batch_normalization() %>% layer_dense(units = 100, activation = "elu", name = "dense1") %>% layer_dropout(rate = 0.5, name = "dp1") %>% layer_batch_normalization() %>% layer_dense(units = 50, activation = "elu", name = "dense2") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.5, name = "dp2") %>% layer_dense(units = 10, activation = "elu", name = "dense3") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.2, name = "dp3") %>% layer_dense(units = num_classes, activation = "softmax", name = "soft") %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.0001), metrics = 'accuracy' )
そこで、ニューラルネットワークを定義し、層のシーケンスとパラメータを指定しました。また、モデルを訓練するときに使用する損失関数、オプティマイザ、およびメトリックについて、コンパイラに指示しました。ここでモデルを訓練します。
## 訓練&評価 --------------------------- # データをモデルに合わせる modDNN %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, #validation_data = list(x_test, y_test), callbacks = list(early_stopping)) -> history
訓練中は、測定データを出力し、入力データをシャッフルします。訓練セットの20%が検証に使用され、早期停止が適用されます。テストセットでモデルをテストします。
#--model--test------------------------- predict(modDNN, x_test) -> Ypr.test Ypr.test %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test evalq(res_mod_test <- Eval(Ytest1, y_pr_test), env)
結果の数値はアンサンブルの平均と同等であることが分かります。
> env$res_mod_test $metrics Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 $confMatr Confusion Matrix and Statistics predicted actual 0 1 0 184 46 1 78 193 Accuracy : 0.7525 95% CI : (0.7123, 0.7897) No Information Rate : 0.523 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5068 Mcnemar's Test P-Value : 0.005371 Sensitivity : 0.7023 Specificity : 0.8075 Pos Pred Value : 0.8000 Neg Pred Value : 0.7122 Prevalence : 0.5230 Detection Rate : 0.3673 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7549 'Positive' Class : 0
訓練履歴をプロットしましょう。
plot(history)
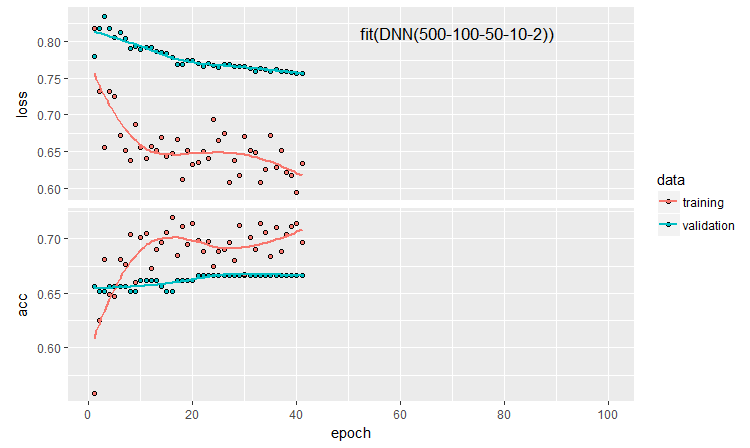
図11 DNN500ニューラルネットワーク訓練履歴
分類品質を向上させるために、ニューロンの初期化方法、ニューロンの活性化の正則化およびその重みなど、多くのハイパーパラメータを変更することができます。ほぼ直観的に選択されたパラメータで得られた結果は、有望な品質を有しますが、失望もあります。最適化なしでは、精度を0.82以上に上げることはできませんでした。結論は、ニューラルネットワークのハイパーパラメータを最適化する必要があるということです。前回の記事では、ベイジアン最適化を実験しました。ここでも同様に適用はできますが、これは別の難しいトピックです。
モデルを順番に定義することで、あらゆる複雑さと深さのモデルをテストし設定することができます。しかし、kerasの機能的APIを使用すると、例えば、多数の入力と出力を持つより複雑なニューラルネットワークの構造を作成することができます。これについては、今後の記事で説明します。
5. 実験結果の分析
5つのモデルの訓練とテストの結果を得ました。
- 平均化を伴うアンサンブル(EnsAver)
- 過半数投票によるアンサンブル(EnsVot)
- ロジスティック回帰モデル(varb)
- ニューラルネットワークDNN(7,2)
- ニューラルネットワークDNN500
これらのすべてのモデルの品質スコアを1つの表に集め、分類エラーをコンポーネントに分解し、全体的なエラーに対する貢献度を見積もりましょう。randomUniformForest::biasVarCov() (Bias-Variance-Covariance Decomposition)関数を使用します。この関数の詳細については、パッケージの説明を参照してください。以下ではEnsAverおよびEnsVotアンサンブルの分類エラーを分解するコードを示します。スクリプトは他のモデルでも同様です。
#---bias--test------------------------------- import_fun(randomUniformForest, biasVarCov, BiasVar) evalq({ target = Ytest1 biasAver <- BiasVar(predictions = ScoreAver$clAver, target = target, regression = FALSE, idx = 1:length(target)) biasVot <- BiasVar(predictions = ScoreVot$ClVot, target = target, regression = FALSE, idx = 1:length(target)) }, env) ----------------------------- Noise: 0.2488224 Squared bias: 0.002107561 Variance of estimator: 0.250475 Covariance of estimator and target: 0.1257046 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2499958 --------------------- Noise: 0.2488224 Squared bias: 0.004079665 Variance of estimator: 0.2499721 Covariance of estimator and target: 0.1274411 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2479918
以下の出力はコンパクトです。
> env$biasAver $predError [1] 0.2499958 $squaredBias [1] 0.002107561 $predictionsVar [1] 0.250475 $predictionsTargetCov [1] 0.1257046
| 95%CI Acc | Precision | Recall | F1 | PredErr | sqBias | predVar | predTargCov | |
|---|---|---|---|---|---|---|---|---|
| EnsAver | 0.7102, 0.7880 (0.7500) | 0.708 0.794 |
0.778 0.727 |
0.741 0.759 |
0.2499 | 0.0021 | 0.2505 | 0.1257 |
| EnsVot | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.248 | 0.0041 | 0.25 | 0.1274 |
| varb | 0.7416, 0.8159 (0.7804) | 0.790 0.808 |
0.783 0.779 |
0.766 0.793 |
0.2199 | 0.000398 | 0.25 | 0.13964 |
| DNN(7, 2) | 0.7165, 0.7935 (0.7565) | 0.765 0.751 |
0.678 0.823 |
0.719 0.785 |
0.2460 | 0.000195 | 0.2498 | 0.1264 |
| DNN500 | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.2779 | 0.01294 | 0.2452 | 0.1145 |
要約表の情報は以下の通りです。
- 基本モデルの中で最高の精度スコアは、アンサンブルの500の出力を組み合わせた varb によって得られました。このスコアによる訓練可能な結合器の中で最良のモデルはDNN(7,2)で、これはアンサンブルの7つの最高出力を組み合わせたものです。
- テストサンプルの最小テスト誤差(PredErr)はvarbとDNN(7,2)によって達成されました。
- 同じ2つのモデルの2乗偏差 (sqBias)は他のモデルよりも一桁良好です。
- すべてのモデルの誤差分散(PredVar)はほぼ同じです。これは奇妙に見えます。アンサンブルによって分散が減少したはずですが、低バイアスが得られました。
- 推定値と応答(predictionTargetCov)の間の最良の共分散は varbによって示されました。それは、個々の変数として単独で何かを意味するものではなく、モデルの比較にのみ使用されます。
- DNN500モデルのすべてのスコアは最低です。結論は、単純なタスクでモデルの複雑さを増やしても、より良い結果につながるわけではないということです。
終わりに
平均化または単純多数決を用いたELMニューラルネットワーク分類器のアンサンブルは、計算速度が非常に高く、良好な分類品質を示します。出力を連続変数から公称変数に変換するためのしきい値を最適化し、平均化する前に出力を較正することによって、品質を改善することが可能です。エラーの分散の顕著な減少は検出されませんでした。
アンサンブル出力の平均化を単純なニューラルネットワークのsoftmax関数に置き換えると、分散が著しく減少することなくバイアスが1桁減少します。刈り込みと平均化の代わりにより複雑なニューラルネットワークモデルを使用しても良い結果は得られませんでした。
ベイジアン変数選択(varbvsパッケージ)の助けを借りて得られたロジスティック回帰モデルは、非常に良い結果を示しています。このパッケージによって決定された最良の出力をニューラルネットワークに使用することができます。
ノイズの24%は、前処理の後では除去できないように見えますが、ノイズサンプルはある段階で別のクラスにラベル付けされる必要がありますす。
kerasの機能を使用し、シーケンス(時系列)データを操作する必要があります。これは、分類品質を改善することができます。
添付ファイル
GitHub/PartVIIには下記のファイルが含まれています。
- Importar.R — パッケージインポート関数
- Library.R — 必要なライブラリ
- FunPrepareData_VII.R — 初期データを準備するための関数
- FunStacking.R — アンサンブルを作成してテストする関数
- Prepare.R — 訓練可能な結合器の初期データを準備するための関数とスクリプト
- Varb.R — varb基本モデルのスクリプト
- model_DNN7_2.R — DNN(7-2)ニューラルネットワークのスクリプト
- model_DNN_500.R — DNN500ニューラルネットワークのスクリプト
- SessionInfo_VII.txt — 記事スクリプトで使用されているパッケージのリスト
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/4228
EAのリモートコントロールの方法
ディープニューラルネットワーク(その8)バギングアンサンブルの分類品質の向上
ギャップ ー 収入戦略か50/50か?
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
Обсуждение и вопросы по коду можно сделать в ветке
Удачи