Algorithmes d'optimisation de la population : Algorithme de type Electro-Magnétique (ЕМ)

Sommaire :

1. Introduction
2. Algorithme
3. Résultats des tests

1. Introduction

Au cours des dernières décennies, les chercheurs du monde entier ont mis au point de nombreuses méthodes de recherche métaheuristiques pour résoudre des problèmes complexes d'optimisation globale, ainsi que des moyens de les améliorer.

L'algorithme ElectroMagnetism-like (ЕМ) est un algorithme de recherche métaheuristique relativement nouveau basé sur la simulation du comportement des particules électromagnétiques dans l'espace physique, introduit pour la première fois par I. Birbil et S.С. Fang en 2003. Il est décrit comme un algorithme évolutionnaire avec un bruit aléatoire et une population basée sur la force électromagnétique de l'interaction entre les particules chargées.

Cet algorithme s'inspire du mécanisme d'attraction et de répulsion des charges dans la théorie de l'électromagnétisme pour résoudre des problèmes d'optimisation non linéaires sans restrictions dans un domaine continu. En raison de sa capacité à résoudre des problèmes complexes d'optimisation globale, la méthode EM est largement utilisée comme outil d'optimisation dans de nombreux domaines.

Faits intéressants sur l'électromagnétisme et les charges électriques :

• Il existe deux types de charges électriques : les charges positives et les charges négatives. Toutes les charges sont soit positives, soit négatives.
• Le champ électromagnétique peut être utilisé pour transmettre des informations sous forme d'ondes radio. Nous utilisons cette fonction tous les jours lorsque nous écoutons la radio ou regardons la télévision.
• Nous avons le champ magnétique terrestre, qui nous protège du vent solaire et des rayons cosmiques.
• Il existe différents matériaux qui peuvent être magnétisés, ce qui permet de créer des électro-aimants. Les électro-aimants sont utilisés dans diverses applications telles que les générateurs d'électricité.
• Il existe de nombreuses applications basées sur l'électromagnétisme. Par exemple, les ordinateurs, les téléphones portables et d'autres appareils utilisent la technologie électromagnétique.
• Tous les objets lumineux (par exemple, les ampoules électriques et les phares de voiture) émettent un rayonnement électromagnétique.
• L'électromagnétisme joue également un rôle important en médecine. Les appareils médicaux tels que l'IRM et le scanner utilisent un champ électromagnétique pour créer des images à l'intérieur du corps.
• Certains animaux, comme les requins et les anguilles électriques, peuvent utiliser l'électromagnétisme pour se déplacer dans l'eau.
• L'électromagnétisme est l'une des 4 forces fondamentales de la nature, avec la force gravitationnelle, la force faible et la force forte.

2. Algorithme

Guidé par la théorie de l'électromagnétisme, EM simule le mécanisme d'attraction-répulsion des charges pour atteindre une solution optimale globale en utilisant des variables limitées. Dans l'algorithme, toutes les solutions sont considérées comme des particules chargées dans l'espace de recherche, et la charge de chaque particule est associée à la valeur de la fonction cible. Les particules ayant une meilleure performance objective appliqueront des forces d'attraction, et les particules ayant des valeurs objectives plus faibles appliqueront des forces de répulsion aux autres particules. Plus la valeur de la fonction objective est élevée, plus le degré d'attraction ou de répulsion entre les particules est important.

Le principe de l'algorithme est qu'au stade initial, une population de solutions aléatoires est formée. Chaque solution est représentée par un vecteur de coordonnées correspondant aux charges des particules électromagnétiques. A chaque itération de l'algorithme, le mouvement de ces charges dans l'espace est également simulé sous l'action des forces électromagnétiques. En se déplaçant, chaque charge interagit avec d'autres charges, ce qui entraîne une modification de la direction du mouvement et de la vitesse. Il en résulte une convergence progressive des solutions vers la valeur optimale de la fonction objective.

Les principaux composants de l'algorithme EM sont les suivants :

1. Formation de la population initiale de solutions (charges), où chaque charge est représentée par un vecteur de coordonnées et correspond à une certaine solution du problème d'optimisation.
2. Calcul de la force électromagnétique d'interaction entre les charges. Le calcul est effectué à chaque itération de l'algorithme et dépend de la distance entre les charges (solutions).
3. Mouvement des charges dans l'espace sous l'influence des forces d'interaction électromagnétiques.
4. Mise à jour de la population de solutions à chaque itération par la fonction objective (la fonction objective peut être, par exemple, la fonction de perte dans les problèmes d'apprentissage automatique).
5. Détermination de la condition d'arrêt de l'algorithme, par exemple l'atteinte d'une certaine valeur de la fonction objective.

Les particules interagissent entre elles, s'attirant ou se repoussant en fonction de leur charge et de la distance qui les sépare. L'algorithme est exécuté en plusieurs itérations, à chacune desquelles les coordonnées et les charges des particules sont mises à jour. Les nouvelles valeurs de la fonction d'aptitude sont calculées.

L'unité logique de l'algorithme d'optimisation EM est la particule. Elle peut être décrite par la structure S_Particle, qui est un agent dans l'espace de recherche. Chaque particule possède des coordonnées c[], qui déterminent sa position dans l'espace de recherche, ainsi que la charge C, qui affecte l'interaction avec les autres particules. Pour chaque particule, on calcule la valeur de la fonction d'aptitude f, qui évalue la qualité de la solution correspondant à la coordonnée donnée. Pour chaque particule, les distances R par rapport aux autres particules et les vecteurs de force F sont également calculés, ce qui détermine la direction du mouvement de la particule dans l'espace de recherche.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

La classe C_AO_EM est une implémentation de l'algorithme d'optimisation électromagnétique. Elle est utilisée pour trouver les valeurs optimales d'une fonction donnée sur un ensemble de nombres réels. L'algorithme est basé sur la simulation des processus d'interaction entre les particules magnétiques et électriques dans un système physique.

La classe contient les champs suivants :

• S_Particle p[] - tableau de particules représentant des solutions potentielles au problème d'optimisation.
• double rangeMax[] - tableau des valeurs maximales de la plage de recherche pour chaque coordonnée.
• double rangeMin[] - tableau des valeurs minimales de la plage de recherche pour chaque coordonnée.
• double rangeStep[] - tableau des étapes de recherche pour chaque coordonnée.
• double cB[] - tableau de coordonnées de la meilleure solution.
• double fB - valeur de la fonction de la meilleure solution.

La classe contient les méthodes suivantes :

• void Init() initialise l'algorithme, en fixant le nombre de coordonnées, le nombre de particules, la constante d'environnement et le pas de déplacement.
• void Moving(int iter) itère l'algorithme en déplaçant les particules conformément aux règles d'interaction des champs magnétiques et électriques.
• void Revision() effectue une révision des particules en vérifiant qu'elles ne sortent pas de la plage de recherche et en ajustant leur position si nécessaire.

La classe contient également des champs privés :

• int coordinatesNumber - nombre de coordonnées.
• int particlesNumber - nombre de particules.
• double envConstant - constante de l'environnement.
• double movConstant - étape du mouvement.
• double exponent - exposant de distance.
• double vect[] - tableau de vecteurs.
• bool revision - drapeau indiquant la nécessité d'une révision de la particule.

La classe contient des méthodes privées :

• double SeInDiSp(double In, double InMin, double InMax, double Step) distribue des points sur une grille uniforme.
• double RNDfromCI(double min, double max) génère un nombre aléatoire dans l'intervalle donné.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode d'initialisation de l'algorithme d'optimisation "algorithme électromagnétique" commence par la réinitialisation du générateur de nombres aléatoires et par la définition de valeurs initiales pour certaines variables. La méthode prend ensuite plusieurs paramètres en entrée : le nombre de coordonnées, le nombre de particules, la valeur de l'environnement et le pas de déplacement. La méthode crée ensuite plusieurs tableaux de la taille requise et les remplit avec des valeurs initiales.

Les tableaux stockent les valeurs maximales et minimales de la plage pour chaque coordonnée, l'étape de modification de la coordonnée, le vecteur et la position actuelle de chaque particule. La méthode crée ensuite un tableau de particules et, pour chaque particule, crée des tableaux pour stocker ses coordonnées, la matrice des distances par rapport aux autres particules, le vecteur de force et la meilleure valeur actuelle de la fonction. À la fin, la méthode crée un tableau pour stocker les meilleures coordonnées de toutes les particules. La méthode initialise ainsi toutes les variables et les tableaux nécessaires au fonctionnement de l'algorithme d'optimisation "algorithme électromagnétique".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

La méthode Moving() est la première à être exécutée à chaque itération. Elle est responsable du mouvement des particules dans l'espace de recherche de la solution. La méthode vérifie en premier si les particules ont déjà été initialisées. Si ce n'est pas le cas, chaque particule reçoit des coordonnées aléatoires dans les limites données et remet à zéro son estimation et sa charge actuelles. Le vecteur des différences vect[] entre les valeurs maximales et minimales dans chaque dimension de l'espace de recherche est également calculé.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

Si l'initialisation a déjà été effectuée, la méthode calcule la charge de chaque particule en fonction de son écart par rapport au maximum global normalisé à la somme des écarts par rapport au maximum global de toutes les particules. Calculer la somme des différences comme suit :

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

La charge des particules est calculée par l'équation :

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));

Comme vous pouvez le constater, la valeur de la charge dans l'équation est positive. Le signe de la charge sera pris en compte plus loin dans l'algorithme. Si la somme des écarts par rapport au maximum global est nulle, la charge de la particule est supposée nulle. La charge calculée de la particule déterminera l'amplitude de la force agissant à partir de la particule sur d'autres particules pertinentes au cours de l'étape de calcul de la force. Le code permettant de calculer la charge d'une particule est le suivant :

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

Avant de commencer à calculer les distances entre les particules, il est nécessaire de réinitialiser le tableau des distances entre la particule et les autres particules, ainsi que le vecteur des forces agissant sur la particule :

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

Les distances entre toutes les paires de particules et les forces agissant entre elles sont ensuite calculées. Une formule basée sur la loi de Coulomb, qui décrit l'interaction entre les particules chargées, est utilisée. Les forces agissant sur chaque particule sont calculées comme la somme vectorielle de toutes les forces agissant sur elle à partir d'autres particules.

Selon la théorie électromagnétique, la force d'action d'une particule sur une autre est inversement proportionnelle à la distance entre les deux particules et directement proportionnelle au produit de leurs charges. Une particule ayant une valeur cible inférieure applique une force de répulsion à une particule ayant une valeur cible relativement plus élevée. Elle éloigne aussi une bonne particule d'une région dont la valeur cible est mauvaise. D'autre part, une particule ayant une valeur cible plus élevée exerce une attraction sur les particules ayant des valeurs relativement plus faibles.

En tenant compte de toutes les forces générées par toutes les autres particules, le vecteur de force total pour la particule est calculé. Ce vecteur de force combiné détermine la direction dans laquelle la particule se déplacera pendant la phase de mouvement de la particule. Les auteurs de l'algorithme recommandent de normaliser le vecteur force de la particule par rapport au vecteur des forces entre toutes les particules. Mes expériences ont montré que sans normalisation, les résultats sont meilleurs. Le code est donc présenté sans normalisation.

En fonction de la particule dont la valeur de la fonction objective est la plus élevée, nous définissons la direction de la force (imitation du signe de la charge).

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

De nouvelles coordonnées sont enfin calculées pour chaque particule en fonction de sa position actuelle et de la force qui agit sur elle. Les particules n'ont pas de masse, ce qui signifie qu'il n'y a pas d'accélération. Contrairement à l'algorithme de recherche gravitationnelle GSA, les particules se déplacent instantanément vers un nouvel emplacement. Les coordonnées de mouvement sont limitées par la portée de la recherche et le pas de changement.

Le code commenté renvoie la particule située de l'autre côté de la plage à une distance de la coordonnée correspondante au cas où la particule serait hors de portée.

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

La méthode Revision(), la deuxième qui doit être exécutée à chaque itération dans l'algorithme d'optimisation EM, est chargée de vérifier la meilleure position de la particule lors de l'itération en cours. La méthode passe en revue toutes les particules et compare la valeur de leur fonction d'aptitude à la meilleure valeur actuelle de fB. Si la valeur de la fonction d'aptitude de la particule actuelle est supérieure à fB, fB est mise à jour et la position de la particule est copiée dans le tableau cB.

La méthode Revision() permet ainsi de suivre la meilleure position de la particule à chaque itération de l'algorithme et de la stocker dans le tableau cB. Cela permet d'optimiser le processus de recherche de la solution optimale et d'accroître l'efficacité de l'algorithme.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

La méthode SeInDiSp() de l'algorithme d'optimisation "electromagnetic algorithm" est utilisée pour limiter les valeurs de la variable In dans un intervalle donné [InMin, InMax] avec un pas. Si In est inférieur ou égal à InMin, la méthode renvoie InMin. Si In est supérieur ou égal à InMax, la méthode renvoie InMax. Si le pas est égal à 0, la méthode renvoie la valeur originale de In. Dans le cas contraire, la méthode calcule une nouvelle valeur In à l'aide de l'équation : InMin + Step * (In - InMin) / Step, où MathRound() est la méthode permettant d'arrondir un nombre à l'entier le plus proche.

Ainsi, la méthode SeInDiSp() permet de contrôler la variation de la valeur de la variable In dans les limites spécifiées et avec un pas spécifié, ce qui permet d'optimiser la fonction plus efficacement et plus rapidement.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————

3. Résultats des tests

Résultats du banc d'essai de l'algorithme ME :

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigin's ; Func runs 10000 result : 59,939529106561224
2023.03.26 18:27:43.215    Score : 0,74268
2023.03.26 18:27:52.960    25 Rastrigin's ; Func runs 10000 result : 59,780143424645416
2023.03.26 18:27:52.960    Score : 0,74071
2023.03.26 18:29:22.856    500 Rastrigin's ; Func runs 10000 result : 63,94951378068386
2023.03.26 18:29:22.856    Score : 0,79237
2023.03.26 18:29:22.856    =============================
2023.03.26 18:29:28.901    5 Forest's ; Func runs 10000 result : 0,28698617113254693
2023.03.26 18:29:28.901    Score: 0,16233
2023.03.26 18:29:38.103    25 Forest's ; Func runs 10000 result : 0,1571444033424823
2023.03.26 18:29:38.103    Score : 0,08889
2023.03.26 18:30:53.341    500 Forest's ; Func runs 10000 result : 0,11734383105881332
2023.03.26 18:30:53.341    Score : 0,06638
2023.03.26 18:30:53.341    =============================
2023.03.26 18:30:58.108    5 Megacity's ; Func runs 10000 result : 1,3599999999999999
2023.03.26 18:30:58.108    Score : 0,11333
2023.03.26 18:31:08.897    25 Megacity's ; Func runs 10000 result : 0,776
2023.03.26 18:31:08.897    Score : 0,06467
2023.03.26 18:32:23.199    500 Megacity's ; Func runs 10000 result : 0,34320000000000006
2023.03.26 18:32:23.199    Score : 0,02860
2023.03.26 18:32:23.199    =============================
2023.03.26 18:32:23.199    All score: 2,79996

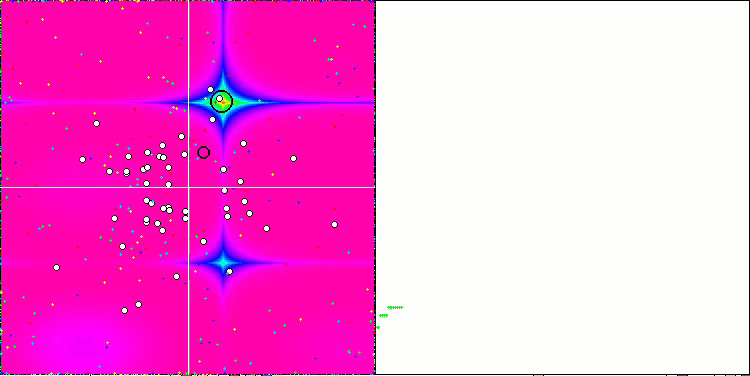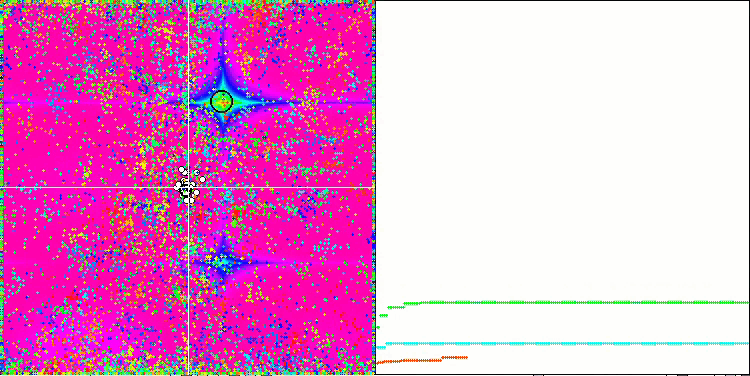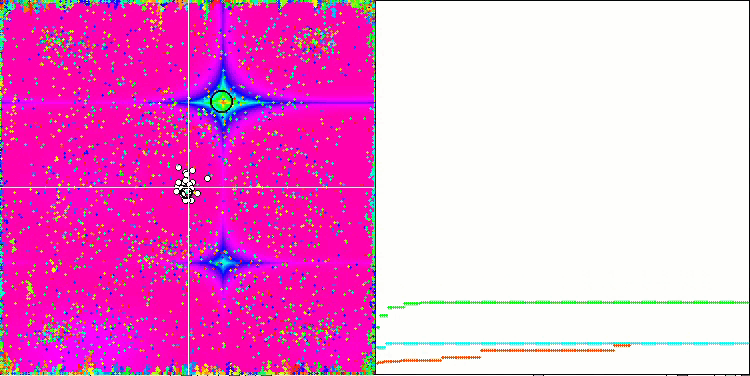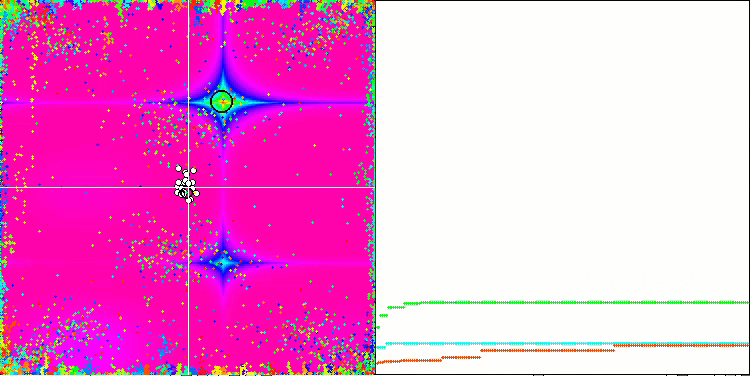
En prêtant attention à l'animation de l'algorithme ME sur les fonctions de test, nous pouvons imaginer une sorte d'"électrification" du champ de l'espace de recherche. Les particules forment des groupes de charges élevées qui suivent les caractéristiques de la surface de la fonction d'essai. Malheureusement, la qualité de la convergence est sensiblement faible, mais l'image est indéniablement belle.

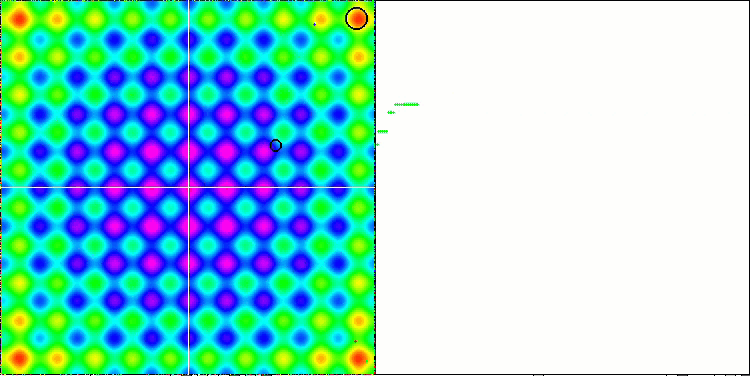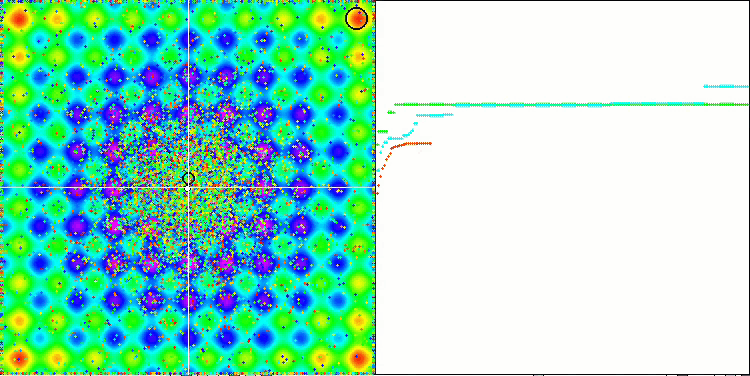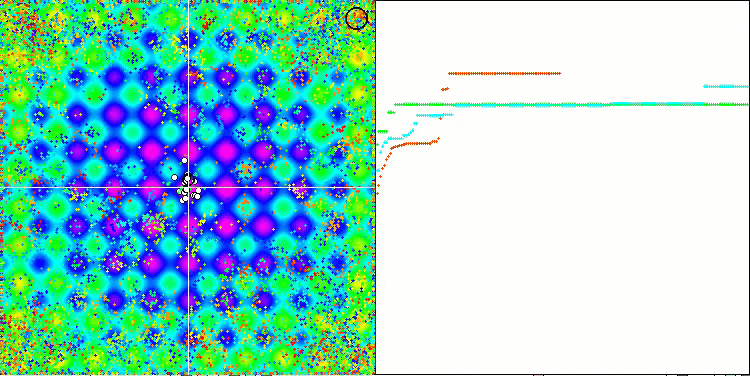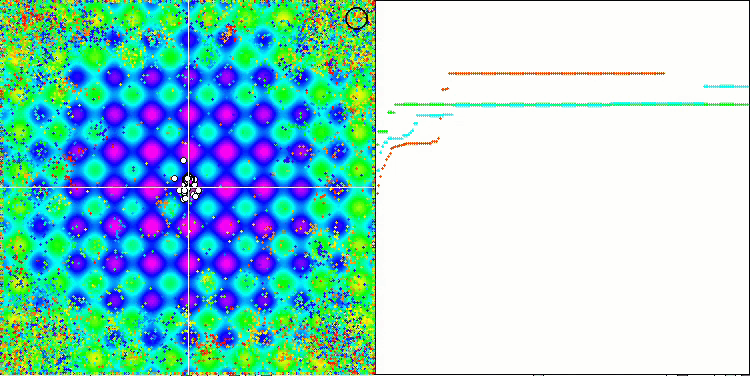
  EM sur la fonction de test de Rastrigin.

  EM sur la fonction de test Forest.

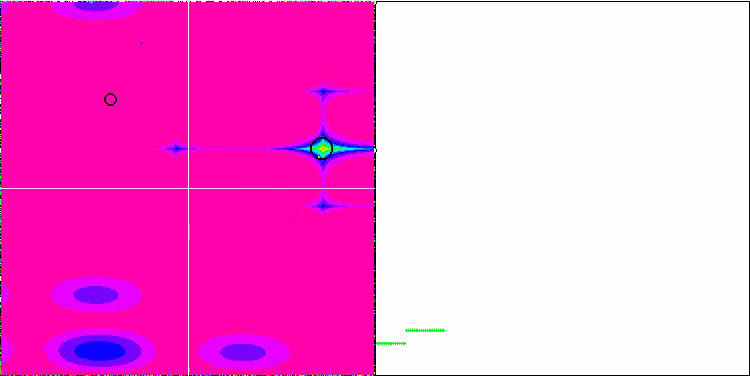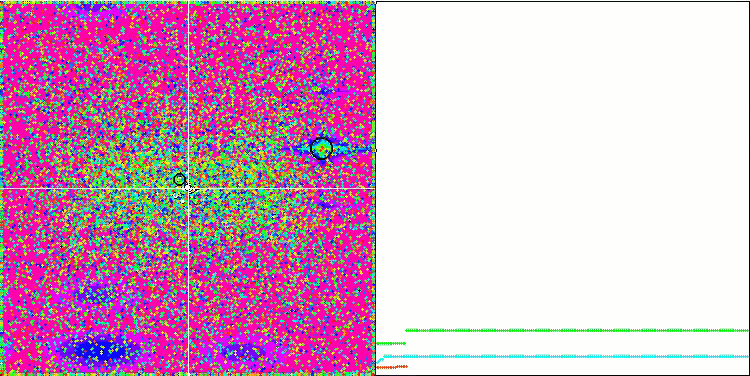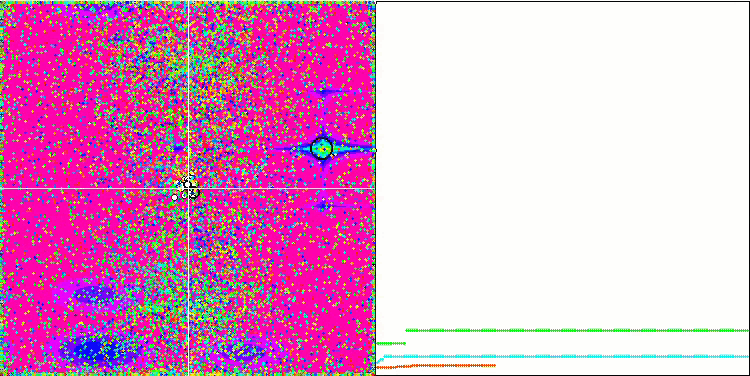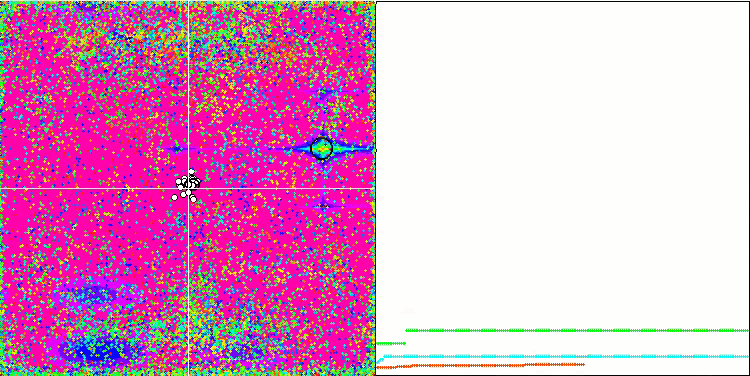
  EM sur la fonction de test Megacity.

Passons maintenant aux résultats des tests de l'algorithme d'optimisation EM. EM a obtenu des résultats inférieurs à la moyenne avec une note finale de 22. L'algorithme a donné de mauvais résultats dans presque tous les tests. L'exception est le test de la fonction de Rastrigin avec 1000 paramètres, pour lequel EM s'est avéré meilleur que des algorithmes aussi puissants que SSG et BA. Les valeurs absolues de la fonction à 1000 paramètres se sont également avérées plus élevées que dans les tests à 10 et 50 paramètres !

C'est la première fois que les résultats de la recherche s'améliorent avec l'augmentation du nombre de paramètres optimisés. Ce phénomène est très probablement lié aux particularités de la stratégie de recherche EM elle-même. Il est nécessaire de noter la sensibilité de l'algorithme EM à la présence d'un gradient et à la différentiabilité sur toute la surface de la définition de la fonction étudiée.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
SSG	semis et croissance des jeunes arbres	1,00000	1,00000	0,55665	2,55665	0,72740	0,94522	1,00000	2,67262	0,76364	0,85977	1,00000	2,62340	100,000
HS	recherche d'harmonie	0,99676	0,95282	0,48178	2,43136	1,00000	0,98931	0,44806	2,43736	1,00000	1,00000	0,41537	2,41537	92,329
ACOm	optimisation par colonies de fourmis M	0,34611	0,17985	0,17044	0,69640	0,86888	1,00000	0,77362	2,64249	1,00000	0,88930	0,05606	1,94536	65,347
IWO	Optimisation des mauvaises herbes envahissantes	0,95828	0,67083	0,29807	1,92719	0,70773	0,46349	0,31773	1,48896	0,80000	0,42067	0,33289	1,55356	61,104
COAm	algorithme d'optimisation coucou M	0,92400	0,46794	0,26004	1,65199	0,58378	0,34034	0,16526	1,08939	0,72727	0,33025	0,17083	1,22835	47,612
FAm	algorithme firefly M	0,59825	0,33980	0,17135	1,10941	0,51073	0,42299	0,49790	1,43161	0,34545	0,28044	0,35258	0,97847	41,537
ABC	colonie d'abeilles artificielles	0,78170	0,32715	0,20822	1,31707	0,53837	0,21455	0,13344	0,88636	0,56364	0,26569	0,13926	0,96858	36,849
GSA	algorithme de recherche gravitationnelle	0,70167	0,45217	0,00000	1,15384	0,31660	0,36416	0,33204	1,01280	0,59395	0,35054	0,00000	0,94448	36,028
BA	algorithme des chauves-souris	0,40526	0,63761	0,84451	1,88738	0,20841	0,17477	0,25989	0,64308	0,29698	0,09963	0,17371	0,57032	35,888
BFO	optimisation du butinage bactérien	0,67203	0,30963	0,11813	1,09979	0,39702	0,26623	0,20652	0,86976	0,52122	0,33211	0,18932	1,04264	34,693
EM	algorithme de type électro-magnétique	0,12235	0,46278	1,00000	1,58513	0,00000	0,03498	0,34880	0,38377	0,00000	0,00000	0,10924	0,10924	22,091
MA	algorithme du singe	0,33192	0,33451	0,14644	0,81287	0,10012	0,07891	0,08932	0,26836	0,21818	0,04243	0,10720	0,36781	13,603
FSS	recherche d'un banc de poissons	0,46812	0,25337	0,11302	0,83451	0,12840	0,05013	0,06516	0,24369	0,16971	0,04796	0,08283	0,30050	12,655
PSO	optimisation par essaims de particules	0,20449	0,08200	0,07160	0,35809	0,18895	0,10486	0,21738	0,51119	0,23636	0,05903	0,01957	0,31496	10,031
RND	aléatoire	0,16826	0,09743	0,08019	0,34589	0,13496	0,04810	0,04715	0,23021	0,16971	0,03875	0,04922	0,25767	5,302
GWO	optimiseur du loup gris	0,00000	0,00000	0,02256	0,02256	0,06570	0,00000	0,00000	0,06570	0,32727	0,07378	0,02557	0,42663	1,000

Résumé

1. L'algorithme EM est une méthode d'optimisation efficace capable de résoudre divers problèmes d'optimisation, en particulier ceux associés au traitement de grandes quantités de données et à la haute dimensionnalité des fonctions lisses.
2. L'algorithme est basé sur la simulation du comportement des particules électromagnétiques dans l'espace physique, ce qui lui permet d'atteindre une grande précision du résultat lorsqu'il travaille avec des fonctions multidimensionnelles complexes.
3. L'algorithme EM ne nécessite pas de calcul de gradient, ce qui le rend plus polyvalent et plus facile à appliquer à différents problèmes, mais il est sensible à la présence d'un gradient dans la fonction à optimiser.
4. L'algorithme peut être modifié et personnalisé en fonction du problème d'optimisation spécifique, ce qui en fait un outil flexible pour l'optimisation de diverses fonctions.
5. Il existe plusieurs modifications de l'algorithme EM qui peuvent être améliorées par rapport à la version de base et adaptées à des problèmes d'optimisation spécifiques.
6. L'algorithme EM peut être utilisé dans divers domaines tels que l'apprentissage automatique, l'intelligence artificielle, l'optimisation des marchés financiers, etc.

Le principal avantage de l'algorithme électromagnétique est sa capacité à résoudre des problèmes d'optimisation dans des espaces multidimensionnels et de grandes dimensions, tout en maintenant une grande précision du résultat.

L'algorithme EM est donc un outil efficace pour optimiser diverses fonctions et peut être utilisé dans un large éventail de problèmes d'optimisation, en particulier lors du traitement d'une grande quantité de données et/ou d'une dimensionnalité élevée.

Cette évaluation peut être utile pour choisir l'algorithme le plus approprié pour résoudre un problème d'optimisation particulier. Mais l'efficacité de l'algorithme dépend de nombreux facteurs, tels que la taille du problème, le type de fonction, le nombre de variables, etc. Par conséquent, le choix d'un algorithme doit être basé sur une analyse approfondie d'un problème particulier.

La figure 1 montre les résultats des tests des algorithmes

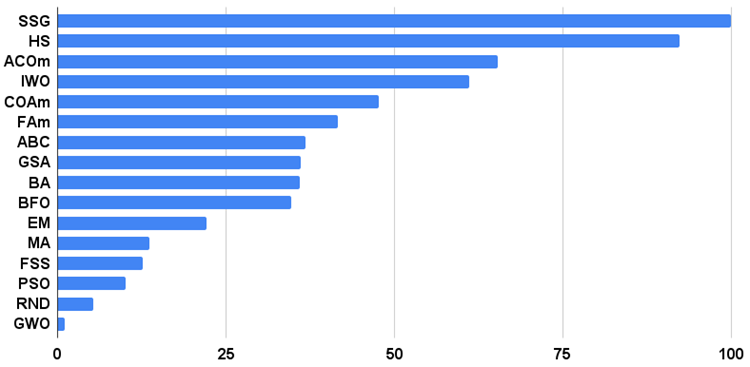
Figure 1. Histogramme des résultats des tests des algorithmes

Avantages et inconvénients de l'algorithme électromagnétique (EM) :

Avantages :
1. Mise en œuvre facile
2. Extensibilité impressionnante pour les fonctions lisses.
3. Nombre réduit de paramètres externes

Inconvénients :
1. Complexité de calcul élevée.
2. Mauvais résultats sur les fonctions discrètes.
3. Se bloquer sur des fonctions avec des "plateformes" horizontales plates.

Chaque article présente une archive contenant les versions actuelles mises à jour des codes algorithmiques de tous les articles précédents. L'article est basé sur l'expérience accumulée par l'auteur et représente son opinion personnelle. Les conclusions et les jugements sont basés sur ses propres expériences.