Utiliser des Cartes de Caractéristiques Auto-Organisatrices (Kohonen Maps) dans MetaTrader 5
304
0
Introduction
Une Self-Organizing Feature Map (SOM) est un type de réseau artificiel et neuronal qui est entrainé à l’aide d’un apprentissage par observation visant à produire une représentation bi-dimensionnelle discrétisée de l’espace d’entrée de l’échantillonnage de formation appelée une carte.
Ces cartes sont utiles pour la classification et la visualisation de vues de faible dimension de données de grande dimension, semblables à une mise à l'échelle multidimensionnelle. Le modèle a d'abord été décrit comme un réseau neuronal et artificiel par le professeur finlandais Teuvo Kohonen, et est parfois appelé carte de Kohonen.
Il existe plusieurs algorithmes disponibles,nous suivrons le code présenté auhttp://www.ai-junkie.com. Pour visualiser les données au terminal client de MetaTrader 5, nous utiliserons lecIntBMP - Une librairie de création d’images BMP. Dans cet article, nous examinerons plusieurs applications simples de Kohonen Maps.
1. Cartes de Caractéristiques Auto-Organisées
Les Cartes de Caractéristiques Auto-Organisatrice étaient décrites pour la première fois parTeuvo Kohonen en 1982 Contrairement à de nombreux réseaux neuronaux, il n'a pas besoin de correspondance un à un entre les données d'entrée et de sortie cible. Ce réseau neuronal est entraîné à l'aide d'un apprentissage non supervisé.
Le SOM peut être formellement décrit comme un mappage non linéaire, ordonné et lisse de données d'entrée de grande dimension sur les éléments d'un tableau régulier de faible dimension. Dans sa forme de base, il produit un graphique de similarité des données d'entrée.
Le SOM convertit les rapports statistiques non linéaires entre les données de grande dimension en une relation géométrique simple de leurs points d'image sur une grille de nœuds bidimensionnelle régulière. Les cartes SOM peuvent être utilisées pour la classification et la visualisation de données de grande dimension.
1.1. Architecture de Réseau
La carte simple de Kohonen sous forme de grille de 16 nœuds(4x4 chacun d'eux est connecté avec un vecteur d'entrée tridimensionnel) est présentée dans la Fig. 1.
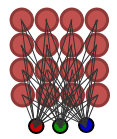
Figure 1. Carte simple de Kohonen (16 nœuds)
Chaque nœud présente des coordonnées (x,y) dans le réseau et un vecteur de poids avec des composants, définis à base du vecteur d'entrée.
1.2. Apprentissage de l’Algorithme
Contrairement à de nombreux autres types de réseaux neuronaux, le SOM n'a pas besoin d’indiquer une sortie cible. Au lieu de cela, lorsque les poids des nœuds correspondent au vecteur d'entrée, cette zone du réseau est sélectivement optimisée pour ressembler plus étroitement aux données de la classe dont le vecteur d'entrée est membre.
A partir d'une distribution initiale de poids aléatoires, et sur de nombreuses itérations, le SOM s'installe dans une carte de zones stables. Chaque zone est en fait un classificateur d'entités, vous pouvez donc considérer la sortie graphique comme un type de carte d'entités de l'espace d'entrée.
La formation se déroule en plusieurs étapes et en plusieurs itérations :
- Les poids de chaque nœud sont initialisés avec des valeurs aléatoires.
- Un vecteur est choisi au hasard depuis l'ensemble des données d'apprentissage.
- Chaque nœud est examiné pour calculer quels poids ressemblent le plus au vecteur d'entrée. Le nœud gagnant est communément appelé Best Matching Unit (BMU).
- Le rayon du voisinage de la BMU est calculé. Initialement, cette valeur est définie sur le rayon du réseau, mais sans gradation à chaque saut de temps.
- Pour tous les nœuds trouvés à l'intérieur du rayon de BMU, les poids du nœud sont ajustés pour les rendre plus semblables au vecteur d'entrée. Plus un nœud est proche de la BMU, plus ses poids sont alertés.
- Répétez l'étape 2 pour les itérations N.
Les détails sont disponibleshttp://www.ai-junkie.com.
2. Études de cas
2.1. Exemple 1: "Bonjour le monde!" dans SOM
L'exemple classique de la carte de Kohonen est un problème de regroupement de couleurs.
Admettons que nous avons un ensemble de 8 couleurs dont chacune est représentée comme un vecteur tri-dimentionnel dansle modèle couleur RGB.
-
Rouge : (255,0,0); 
Vert : (0,128,0);-
Bleu : (0,0,255); -
Vert foncé : (0,100,0); -
Bleu foncé : (0,0,139); -
Jaune : (255,255,0); 
Orange: (255,165,0);-
Violet : (128,0,128).
Quand nous travaillons avec les cartes Kohonen enlangage MQL5,nous suivrons le paradigmeorienté-objet.
Nous avons besoin de deux classes : Classe CSOMNode pour un nœud de la grille régulière et CSOM qui est une classe de réseau de neurones.
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
L'implémentation des méthodes de classe peut être trouvée dans som_ex1.mq5. Le code présente plusieurs commentaires, nous allons nous concentrer sur l'idée.
La description de la classe CSOM se présente comme suit :
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
L'utilisation de la classe CSOM est simple :
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
Le résultat est présenté en Fig 2.
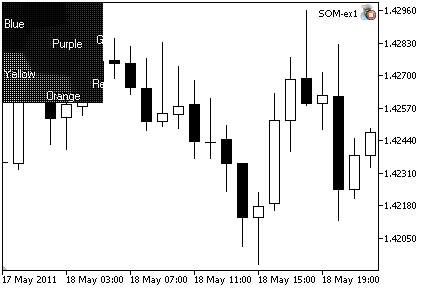
Figure 2. La sortie de SOM_ex1.mq5 Expert Advisor
La dynamique de l'apprentissage de la carte de Kohonen est présentée sur la figure 3 (voir les étapes sous l'image) :
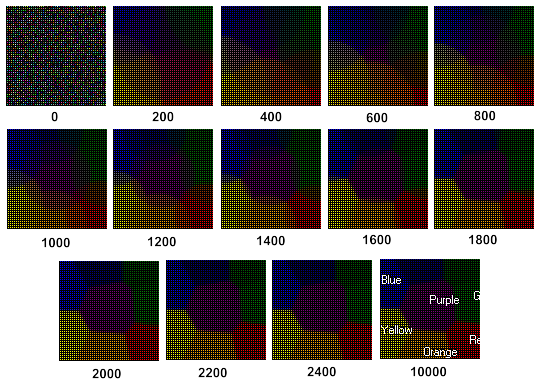
Figure 3. La dynamique de l'apprentissage de Kohonen Map
Nous pouvons constater sur la Fig. 3, la carte de Kohonen est formée après 2400 pas.
Si nous créons le réseau de 300 nœuds et indiquons la taille de l'image comme 400x400 :
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
nous obtiendrons l'image, présentée en figure 4 :
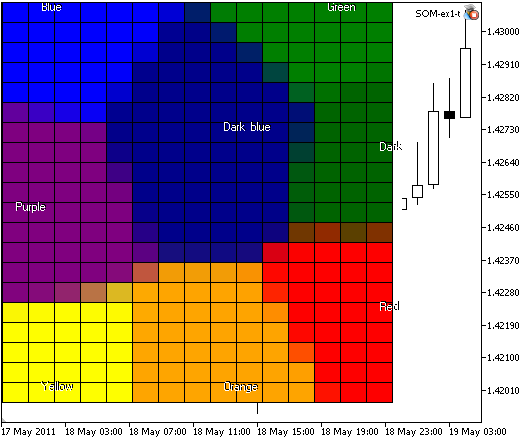
Figure 4. La carte de Kohonen avec 300 nœuds, taille d'image 400x400
Si vous lisez le livre Visual Explorations in Finance: with Self-Organizing Mapsécrit par,Guido Deboeck et Teuvo Kohonen, vous vous rappelez que les nœuds du réseau peuvent être représentés en tant que cellules hexagonales. En modifiant le code de l'Expert Advisor, nous pouvons implémenter une autre visualisation.
Le résultat de SOM-ex1-hex.mq5 est présenté en Fig. 5:
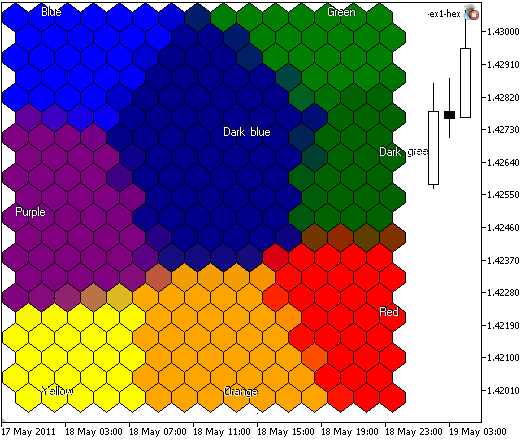
Figure 5. La carte de Kohonen avec 300 nœuds, taille d'image 400x400, les nœuds sont représentés dans des cellules hexagonales
Dans cette version, nous pouvons définir l'affichage des limites des cellules en utilisant les paramètres d'entrée :
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
Dans certains cas, nous n'avons pas besoin d'afficher les limites des cellules, si vous indiquez ShowBorders=false, vous obtiendrez l'image suivante (voir Fig. 6):
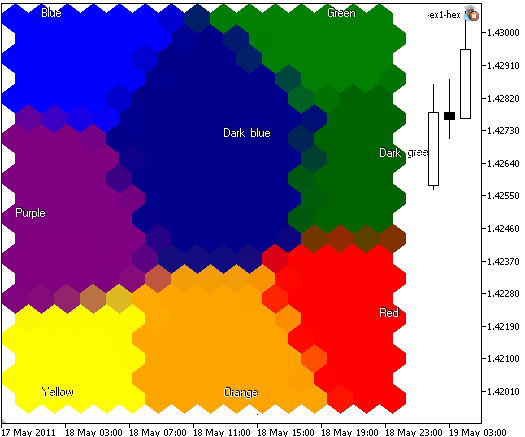
Fig. 6. Carte de Kohonen avec 300 nœuds, image 400x400, nœuds tracés sous forme de cellules hexagonales, limites de cellule désactivées
Dans le premier exemple, nous avons utilisé 8 couleurs dans l'ensemble d'apprentissage avec les composants de couleur spécifiés. Nous pouvons étendre l'ensemble d'apprentissage et simplifier la spécification des composants de couleur en ajoutant deux méthodes à la classe CSOM.
Notez que dans ce cas, les Kohonen Maps sont simples car il n'y a que peu de couleurs, séparées dans l'espace colorimétrique. En conséquence, nous avons les groupes localisés.
Le problème apparaît si l'on considère plus de couleurs avec des composants de couleur plus proches.
2.2. Exemple 2: Utilisation de Web-colors comme exemples d'apprentissage
En langage MQL5 Web-couleurs sont prédéfinies par les constantes.
Figure 7. Couleurs Web
Et si on appliquait l'algorithme de Kohonen à un ensemble de vecteurs avec des composants similaires ?
Nous pouvons créer une classe CSOMWeb, dérivée de la classe CSOM :
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
Comme vous le constatez, pour simplifier le travail avec les couleurs, nous avons ajouté deux nouvelles méthodes, la spécification explicite des composants de couleur n'est plus nécessaire maintenant.
L'implémentation des méthodes de classe se présente comme suit :
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
Toutes les couleurs Web peuvent être combinées dans le tableau web_colors[] :
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
La fonction OnInit() présente une forme simple :
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
Si nous lançons le som-ex2-hex.mq5, nous obtiendrons l'image, présentée dans la Fig 8.
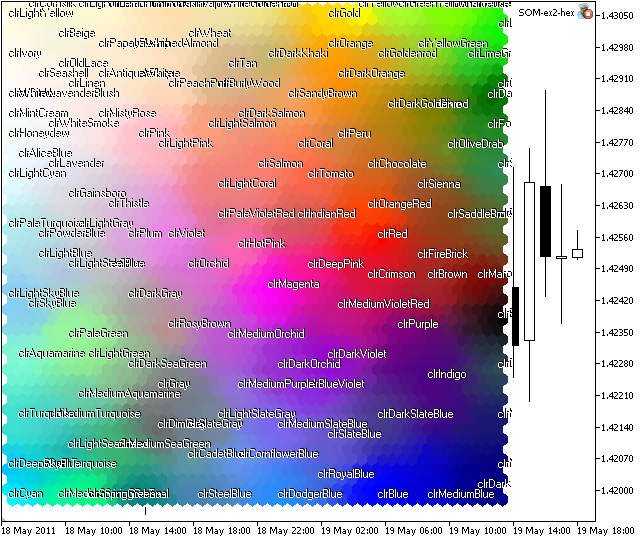
Figure 8. Carte Kohonen pour Web-couleurs
Comme vous le constatez, il existe des groupes, mais certaines couleurs (comme xxxBlue) sont situées dans différentes zones.
La raison de ce fait est la structure de l'ensemble d'apprentissage, il existe de nombreux vecteurs avec des composants proches.
2.3. Exemple 3: Groupement de produits
En suite nous examinerons un simple échantillon qui tentera d’assembler vingt-cinq aliments dans des zones similaires à base de trois paramètres qui sontprotéine, glucides etlipides
| Nourriture | Protéine | Glucides | Lipides | |
|---|---|---|---|---|
| 1 | Pommes | 0.4 | 11.8 | 0.1 |
| 2 | Avocat | 1.9 | 1.9 | 19.5 |
| 3 | Bananes | 1.2 | 23.2 | 0.3 |
| 4 | Steak de bœuf | 20.9 | 0 | 7.9 |
| 5 | Big Mac | 13 | 19 | 11 |
| 6 | Noix du Brésil | 15.5 | 2.9 | 68.3 |
| 7 | Pain | 10.5 | 37 | 3.2 |
| 8 | Beurre | 1 | 0 | 81 |
| 9 | Fromage | 25 | 0.1 | 34.4 |
| 10 | Gâteau au fromage | 6.4 | 28.2 | 22.7 |
| 11 | Biscuits | 5.7 | 58.7 | 29.3 |
| 12 | Flocons de maïs | 7 | 84 | 0.9 |
| 13 | Œufs | 12.5 | 0 | 10.8 |
| 14 | Poulet frit | 17 | 7 | 20 |
| 15 | frites | 3 | 36 | 13 |
| 16 | Chocolat chaud | 3.8 | 19.4 | 10.2 |
| 17 | Pepperoni | 20.9 | 5.1 | 38.3 |
| 18 | Pizza | 12.5 | 30 | 11 |
| 19 | Tarte Au Porc | 10.1 | 27.3 | 24.2 |
| 20 | Pommes de terre | 1.7 | 16.1 | 0.3 |
| 21 | Riz | 6.9 | 74 | 2.8 |
| 22 | Poulet rôti | 26.1 | 0.3 | 5.8 |
| 23 | Sucre | 0 | 95.1 | 0 |
| 24 | Steak de thon | 25.6 | 0 | 0.5 |
| 25 | L'eau | 0 | 0 | 0 |
Tableau 1 Protéines, glucides et lipides pour 25 aliments.
Ce problème est intéressant, car les vecteurs d'entrée ont des valeurs différentes et chaque composant a sa propre plage de valeurs. C'est important pour la visualisation, car nous utilisons le modèle de couleur RGB avec des composants variant de 0 à 255.
Fort heureusement que dans ce cas, les vecteurs d’entrée sont également tri-dimensionnels et nous pouvons utiliser le modèle de couleur RGB destiné à la visualisation de la carte de Kohonen
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
Comme vous le constatez, nous avons ajouté des tableaux m_max_values[] et m_min_values[] pour le stockage des valeurs maximales et minimales de l'ensemble d'entraînement. Pour la visualisation dans un modèle de couleur RGB, la "mise à l'échelle" est nécessaire, nous avons donc surchargé les méthodes Train(), Render() et ShowPattern().
La recherche des valeurs maximales et minimales est implémentée dans la méthode Train().
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
Pour afficher les composants dans le modèle de couleur RVB, nous devons modifier la méthode Render() :
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
Le résultat de som_ex3.mq5 est présenté en Fig 9.
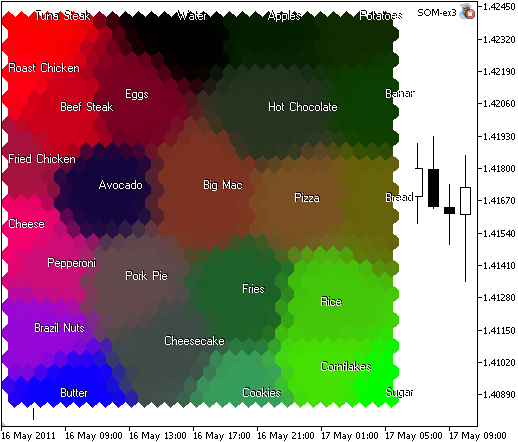
Figure 9. Carte des aliments, regroupée en zones de similitude, basée sur les protéines, les glucides et les lipides
Analyse des composants. Nous pouvons constater sur la carte que le sucre, le riz et les flocons de maïs sont tracés en vert à cause des glucides (2e composant). Le Beurre est en zone verte, il contient beaucoup de lipides (3ème composant). Beaucoup de protéines (1er composant, rouge) sont contenues dans le steak de bœuf, le poulet rôti et le steak de thon.
Vous pouvez étendre l'ensemble d'entraînement en ajoutant de nouveaux aliments à partir desFood Composition Tables (alternative table)
Comme vous le constatez, le problème est résolu pour les directions R,V,B "pures". Qu'en est-il des autres aliments avec plusieurs composants égaux (ou presque égaux) ? Plus loin, nous examinerons les plans de composants, c'est très utile, en particulier pour les cas où les vecteurs d'entrée ont une dimension supérieure à 3.
2.4. Exemple 4. Cas à 4 dimensions. Ensemble de données sur l'iris de Fisher. CMYK
Pour les vecteurs tridimensionnels, il n'y a pas de problème de visualisation. Les résultats sont clairs grâce au modèle de couleur RGB, utilisé pour visualiser les composants de couleur.
Lorsque nous travaillons avec des données de grande dimension, nous devons trouver le moyen de les visualiser. La solution simple consiste à tracer une carte de dégradé (par exemple, Noir/Blanc), avec des couleurs proportionnelles à la longueur du vecteur. L'autre moyen consiste à utiliser un autre espace de couleurs. Dans cet exemple, nous examinerons le modèle de couleur CMYK pour définir les données de Fisher’s Iris. Il y a une meilleure solution, nous l’examinerons plus loin
L'ensemble de données sur les fleurs d'iris ou l'ensemble de données sur l'iris de Fisher est un ensemble de données multivariées présenté par R. Fisher (1936) comme exemple d'analyse discriminante. L’ensemble de données se compose de 50 échantillons de chaque espèce des fleurs iris (Iris setosa, Iris virginicaet Iris versicolor).
Quatre caractéristiques ont été mesurées à partir de chaque échantillon, il s'agit de la longueur et de la largeur du sépale et du pétale, en centimètres.
Figure 10. Iris flower
Chaque échantillon dispose de 4 caractéristiques :
- Longueur du sépale ;
- Largeur des sépales ;
- Longueur des pétales ;
- Largeur des pétales.
L’ensemble de données de la fleur d’irispeut être trouvé dans SOM_ex4.mq5.
Dans cet exemple, nous utiliserons l'espace colorimétrique CMYK intermédiaire pour le traçage, c'est-à-dire que nous considérerons les poids du nœud comme des vecteurs dans l'espace CMYK. Pour visualiser les résultats, la conversion CMYK->RGB est utilisée. Une nouvelle méthode int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k) est ajoutée à la classe CSOM, elle est utilisée dans la méthode CSOM::Render(). Nous devons également modifier les classes pour prendre en charge les vecteurs à 4 dimensions.
Le résultat est présenté sur la Fig 11.
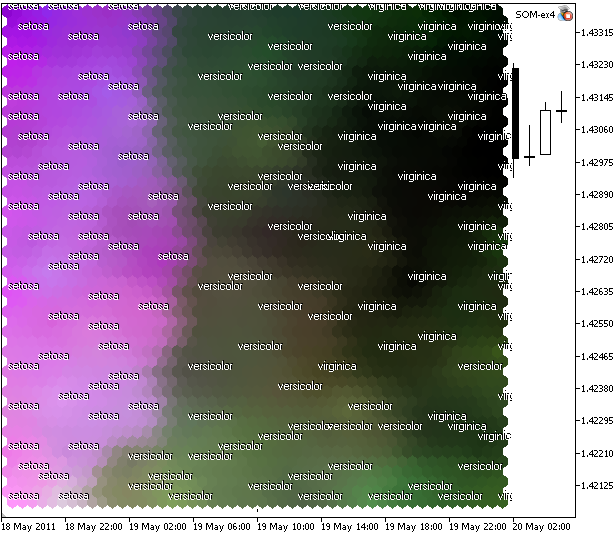
Figure 11. Carte de Kohonen pour l'ensemble de données de fleurs d'iris, tracée dans le modèle de couleur CMJN
Que voit-on ? Nous n’avons pas encore le groupage complet (à cause des caractéristiques du problème) mais nous pouvons voir laséparation linéaire d’iris setosa.
La raison de cette séparation linéaire desetosa est un grand composant «Magenta» 2eme dans l’espace CMYK
2.6. Analyse du Plan des Composants
Nous pouvons constater dans les exemples précédents (regroupement de données sur les aliments et l'iris) qu'il y a un problème avec la visualisation des données.
Par exemple, pour un problème alimentaire, nous avons analysé la carte Kohonen en s’appuyant sur les informations sur certaines couleurs (rouge, vert, bleu). En plus des groupes de base, il y avait des aliments avec plusieurs composants. De plus, l'analyse devenait difficile si les composants étaient pour la plupart égaux..
Les plans composants offrent la possibilité de voir l’intensité relative de chaque aliment.
Nous devons ajouter desCIntBMP instances de classe (m_bmp[]tableau) dans la classe CSOM et modifier les méthodes du rendu correspondantes. Nous avons également besoin d'une carte de dégradé pour visualiser l'intensité de chaque composant (les valeurs les plus basses affichées en bleu, les valeurs les plus élevées affichées en rouge):
Figure 12. Palette de dégradé
Nous avons ajouté le tableau Palette[768], les méthodes GetPalColor() et Blend(). Le dessin d'un nœud est placé dans la méthode RenderCell().
Ensemble de données sur les fleurs d'iris
Les résultats de som-ex4-cpr.mq5 sont présentés sur la Fig 13.
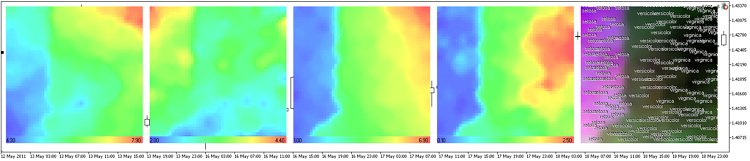
Figure 13. Représentation des plans de composants de l'ensemble de données de la fleur d'iris
Dans ce cas, nous utilisons la grille avec 30x30 nœuds, taille de l'image 300x300.
Les plans composants jouent un rôle important dans la détection de corrélation : en comparant ces plans même partiellement et corrélant des variables éventuellement détectées par inspection visuelle. C'est plus facile si les plans du composant sont réorganisés pour que les corrélés soient proches les uns des autres. De cette façon, il est facile de sélectionner des combinaisons de composants intéressantes pour un complément d’enquête.
Examinons les plans de composants (Fig. 14).
Les valeurs des composants maximaux et minimaux sont indiquées dans le tableau des gradients.
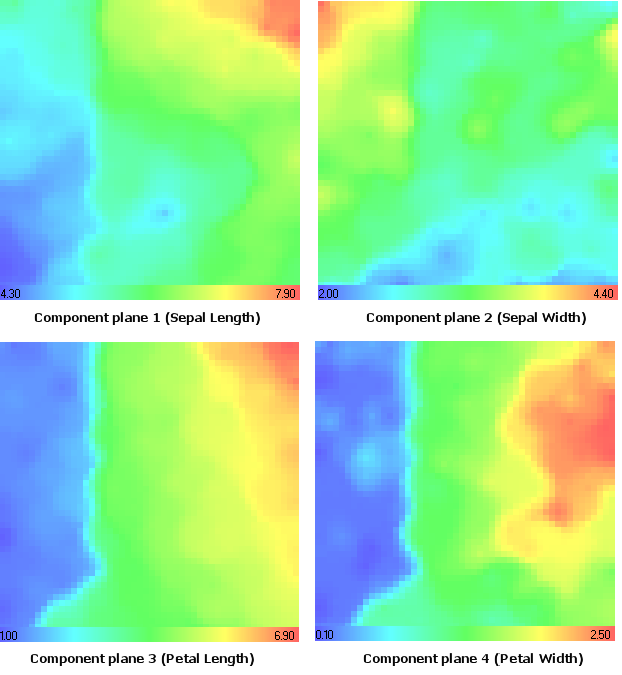
Figure 14. Ensemble de données sur les fleurs d'iris. Plans de composants
Tous ces plans composants, représentés dans le modèle de couleur CMJN, sont illustrés en Fig. 15.
Figure 15. Ensemble de données sur les fleurs d'iris. Carte Kohonen dans le modèle de couleur CMYK
Rappelons-nous du type d’irissetosa En utilisant l'analyse du plan de composant (Fig. 14), nous pouvons constater qu'il a des valeurs minimales dans les 1er (longueur de sépale), 3e (longueur de pétale) et 4e (largeur de pétale).
Il est remarquable qu'il a des valeurs maximales dans le 2ème plan de composant (Sepal Width), le même résultat que nous avons obtenu dans le modèle de couleur CMYK (composant Magenta, Fig. 15).
Regroupement alimentaire
Examinons maintenant le problème de regroupement des aliments en utilisant l'analyse du plan des composants (som-ex3-cpr.mq5).
Le résultat est présenté en Fig. 16 (30x30 nœuds, taille de l'image 300x300, cellules hexagonales sans limites).
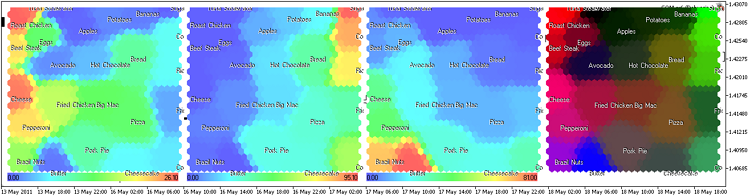
Figure 16. Carte de Kohonen pour la nourriture, représentation du plan des composants
Nous avons ajouté l'option d'affichage des titres dans la méthode ShowPattern() de la classe CSOM (paramètre d'entrée ShowTitles=true).
Les plans de composants (protéines, glucides, lipides) se présentent comme suit :
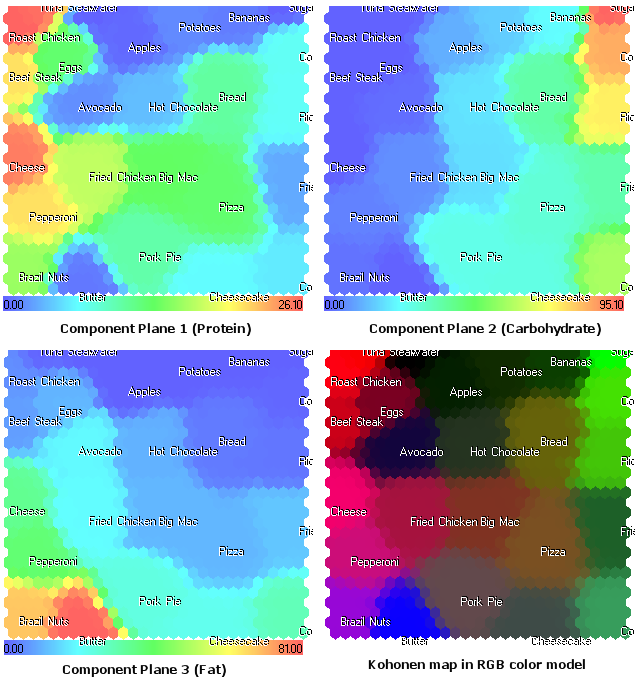
Figure 17. Carte de Kohonen pour les aliments. Plans de composants et modèle de couleur RVB
La représentation du plan des composants, illustrée en Fig 17, ouvre une nouvelle vue sur la structure des composants alimentaires. De plus, elle fournit des informations supplémentaires, qui ne peuvent pas être vues dans le modèle de couleur RGB, présenté en Fig. 9.
Par exemple, nous voyons maintenant le Fromage dans le 1er plan composant (protéine). Dans le modèle de couleur RGB, il est affiché en couleur, proche du magenta, à cause des lipides (2e composant).
2.5. Implémentation des plans composants pour le cas de la dimension arbitraire
Les exemples que nous avons examinés présentent des caractéristiques spécifiques, la dimension a été fixée et l'algorithme de visualisation était différent pour différentes représentations (modèles de couleurs RGB et CMYK).
Nous pouvons maintenant généraliser l'algorithme pour des dimensions arbitraires, mais dans ce cas, nous ne visualiserons que les plans des composants. Le programme doit être en mesure de charger les données arbitraires à partir du fichier CSV.
Par exemple, le fichier food.csv se présente comme suit :
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
La première ligne du fichier comporte les noms (titres) du vecteur de données d'entrée. Les titres sont nécessaires pour distinguer les plans composants, nous imprimerons leurs noms dans le panneau de dégradé.
Le nom du motif se trouve dans la dernière colonne, dans notre cas c'est le nom de l'aliment.
Le code de SOM.mq5 (fonction OnInit) est simplifié :
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
Le nom du fichier avec les modèles d'apprentissage est indiqué dans le paramètre d'entrée DataFileName, dans notre cas "food.csv".
Le résultat est illustré en Fig 18.
Figure 18. Carte de Kohonen de la nourriture en dégradé du schéma de couleurs noir/blanc
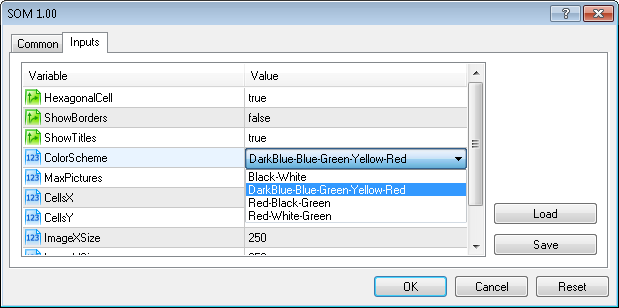
Nous avons également ajouté le paramètre d'entrée ColorScheme pour la sélection du schéma de dégradé.
À l'heure actuelle, il existe 4 schémas de couleurs disponibles (ColorScheme=0,1,2,4=Noir-Blanc,Bleu foncé-Bleu-Vert-Jaune-Rouge,Rouge-Noir-Vert,Rouge-Blanc-Vert).
Vous pouvez facilement ajouter votre propre schéma en ajoutant le dégradé dans la méthode CSOM::InitParameters().
Le schéma de couleurs peut être sélectionné à partir des paramètres d'entrée d'Expert Advisor :
De même, nous pouvons préparer l'ensemble de données sur les fleurs d'iris (iris-fisher.csv) :
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
Le résultat est illustré en Fig 19.
Figure 19. Ensemble de données sur les fleurs d'iris. Plans de composants dans le schéma de couleurs Rouge-Noir-Vert (ColorScheme=2, iris-fisher.csv)
Nous avons maintenant un outil pour les applications réelles.
2.6. Exemple 5: Cartes thermiques du marché
Les Cartes de Caractéristiques Auto-Organisatrices peuvent être utilisées pour les cartes de mouvement du marché. Des fois la vue d’ensemble du marché est nécessaire,la carte thermique du marchées très utile. Les valeurs sont regroupées en fonction des secteurs économiques.
La couleur actuelle du stock dépend du taux de croissance actuel (en %) :
Figure 20. Carte thermique du marché pour les actions du S&P500
Le marché hebdomadaire de la carte thermique des actions depuis S&P (http://finviz.com) est illustré en Fig. 20. La couleur dépend du taux de croissance (en %) :
La taille du rectangle boursier dépend de la capitalisation boursière. La même analyse peut être effectuée dans le terminal client MetaTrader 5 en utilisant les cartes Kohonen.
L'idée est d'utiliser les taux de croissance (en %) sur plusieurs cadres temporels. Nous avons l'outil pour travailler avec les cartes Kohonen, donc le seul nécessaire est le script, qui enregistre les données dans un fichier .csv.
Les données de prix sur les prix CFD des valeurs boursières américaines (#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, # HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT et #XOM) peuvent être trouvés sur le serveur de démonstration MetaQuotes.
Le script, qui prépare le fichier dj.csv est très simple :
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
Les données de l’historique doivent être téléchargées, vous pouvez automatiquement le faire en utilisant le scriptDownloadHistory.
À la suite du script dj.mq5, nous obtiendrons le dj.csv avec les données suivantes :
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
Après avoir lancé le som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv"), nous obtiendrons 8 images, chacune d'elles correspond aux intervalles de temps de 30, 60, 90, 120, 150, 180, 210 et 240 minutes.
Les cartes Kohonen des données de taux de croissance du marché (valeurs boursières américaines) des 4 dernières heures de la séance de bourse du 23 mai 2011 sont présentées en Fig 21.
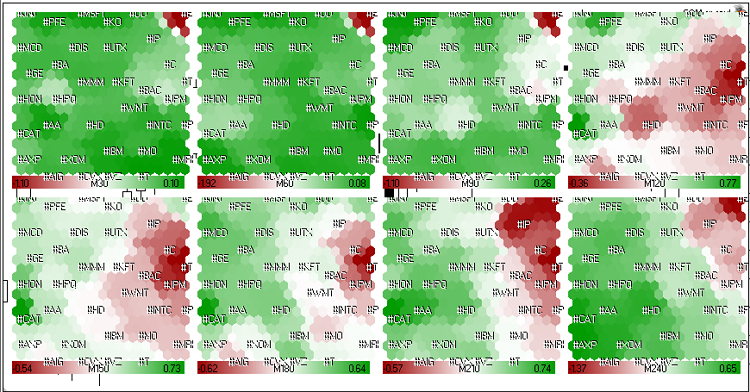
Figure 21. Cartes de Kohonen pour les valeurs boursières américaines (dernières 4 heures de la session de trade du 23 mai 2011).
Nous pouvons constater sur la Fig 21, la dynamique de #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co), #BAC (Bank of America) est similaire. Ils se sont regroupés dans un cluster rouge à long terme.
Au cours de la dernière heure et demi (M30, M60, M90) sa dynamique est devenue verte, mais généralement (M240) les indices boursiers étaient dans la zone rouge.
À l'aide des cartes de Kohonen, nous pouvons visualiser la dynamique relative des indices boursiers, trouver des leaders et des perdants et leur environnement. Les éléments avec des données similaires forment des groupes.
Comme nous le constatons en figure 21a, le prix des actions de Citigroup Inc était le leader de la baisse. Généralement, toutes les actions des sociétés de financières étaient en zone rouge.
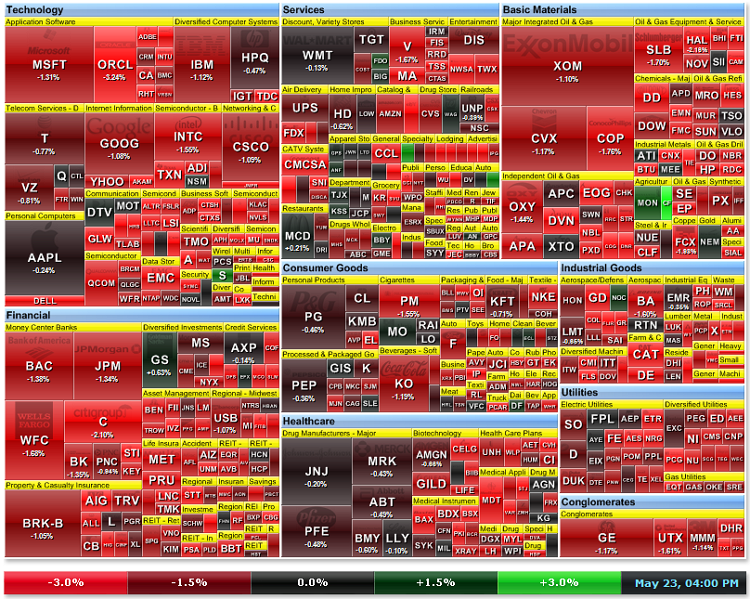
Figure 21a. Carte thermique du marché du 23 mai 2011 (sourcehttp://finviz.com)
De même, on peut calculer les cartes Kohonen du marché FOREX (Fig. 22) :
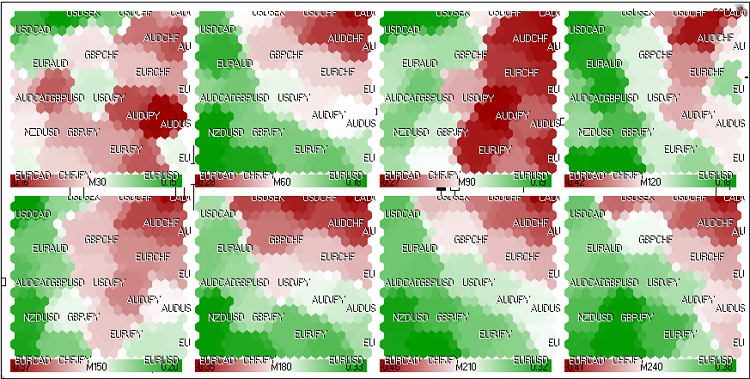
Figure 22. Carte de Kohonen pour le marché FOREX (24 mai 2011, session européenne)
Les paires suivantes sont utilisées : EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.
Les taux de croissance sont exportés vers fx.csv à l'aide du script fx.mq5.
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
En plus des prix, vous pouvez utiliser les valeurs des indicateurs à différentes périodes.
2.6. Exemple 6: Analyse des Résultats d'Optimisation
Le Strategy Tester du terminal client MetaTrader 5 offre la possibilité d'explorer la structure de l'espace des paramètres et de trouver le meilleur ensemble de paramètres de stratégie. Vous pouvez également exporter les résultats d'optimisation à l'aide de l'option "Exporter vers XML (MS Office Excel)" dans le menu contextuel de l'onglet "Résultats d'optimisation".
Les statistiques du testeur sont comprises dans les résultats de l’optimisation (41 colonnes):
- Résultat
- Bénéfice
- Bénéfice brut
- Perte brute
- Retrait
- Gain attendu
- Facteur de bénéfice
- Facteur de reprise
- Rapport de Sharpe
- Niveau de marge
- Personnalisé
- Solde minimal
- Solde DD maximal
- Solde DD Maximum (%)
- Solde Relatif DD
- Solde relatif DD (%)
- Capitaux propres minimaux
- Capitaux propres DD Maximum
- Capitaux propres DD Maximum (%)
- Capitaux propres relatifs DD
- Capitaux propres relatifs DD (%)
- Trades
- Deals
- Courts trades
- Bénéfices de courts trades
- Longs trades
- Bénéfice de longs trades
- Bénéfice trades
- Perte trades
- Trade à bénéfice maximal
- Trade à perte maximale
- Max de gains consécutifs
- Max de gains consécutifs ($)
- Bénéfice consécutif maximum
- Nombre maximal de bénéfices consécutifs
- Pertes consécutives maximales
- Pertes consécutives maximales
- Perte consécutive maximale
- Nombre maximal de pertes consécutives
- Moyenne des gains consécutifs.
- Pertes consécutives maximales
L'utilisation des statistiques du testeur permet d'aider à l'analyse de l'espace des paramètres. Il est remarquable que de nombreux paramètres de la statistique soient étroitement liés et dépendent des résultats des performances de trade.
Par exemple, les meilleurs résultats de trading affichent des valeurs les plus élevées des paramètres Profit, Profit Factor, Recovery Factor et Sharpe Ratio. Ce fait permet de les utiliser dans l'analyse des résultats.
Résultats d'optimisation de MovingAverage.mq5 Expert Advisor
Dans ce chapitre, nous examinerons l'analyse des résultats d'optimisation de MovingAverage.mq5 Expert Advisor, inclus dans le package standard du terminal client MetaTrader 5. Cet Expert Advisor est basé sur le croisement du prix et de l'indicateur de moyenne mobile. Il a deux paramètres d'entrée : MovingPeriod et MovingShift, c'est-à-dire que nous aurons comme résultat le fichier XML avec 43 colonnes.
Nous ne considérerons pas l'espace des paramètres à 43 dimensions, les plus intéressants sont :
- Bénéfice
- Facteur de bénéfice
- Facteur de Reprise
- Rapport de Sharpe
- Trades
- ProfitTrades(%);
- MovingPeriod=12
- MovingShift;
Notez que nous avons ajouté le paramètre ProfitTrades (%) (il est absent dans les résultats), cela indique le pourcentage des deals rentables et calculé comme résultat de la division de ProfitTrades (28) par Trades (22), multiplié par 100..
Préparons le fichier optim.csv avec 9 colonnes pour 400 ensembles de paramètres d'entrée de MetaTrader 5 Strategy Tester.
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
Notez que nous avons utilisé la valeur de MovingPeriod comme colonne de titre, elle sera utilisée pour "marquer" les motifs sur les cartes de Kohonen.
Dans Strategy Tester, nous avons optimisé les valeurs de MovingPeriod et MovingShift avec les paramètres suivants :
- Symbole=EURUSD
- Period_H1
- Mode génération de ticks - "1 Minute OHLC",
- Intervalle de test - 2011.01.01-2011.05.24,
- Optimisation - Rapide (algorithme génétique),
- Optimisation - Solde maximal
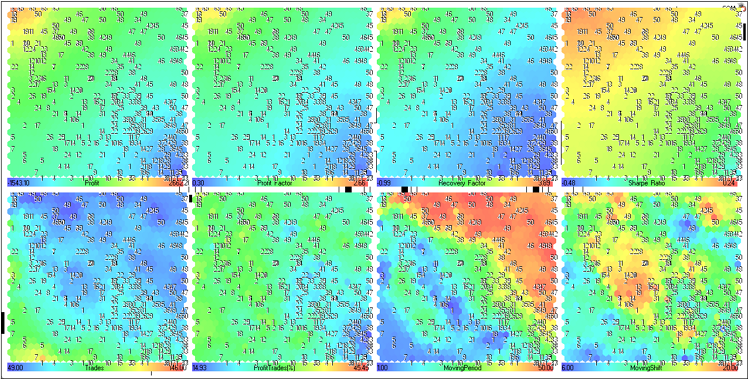
Figure 23. Carte de Kohonen pour les résultats d'optimisation de MovingAverage EA (représentation du plan des composants)
Examinons les plans composants de la rangée supérieure (Profit, Profit Factor, Recovery Factor и Sharpe Ratio).
Ils sont combinés dans la Fig. 24.
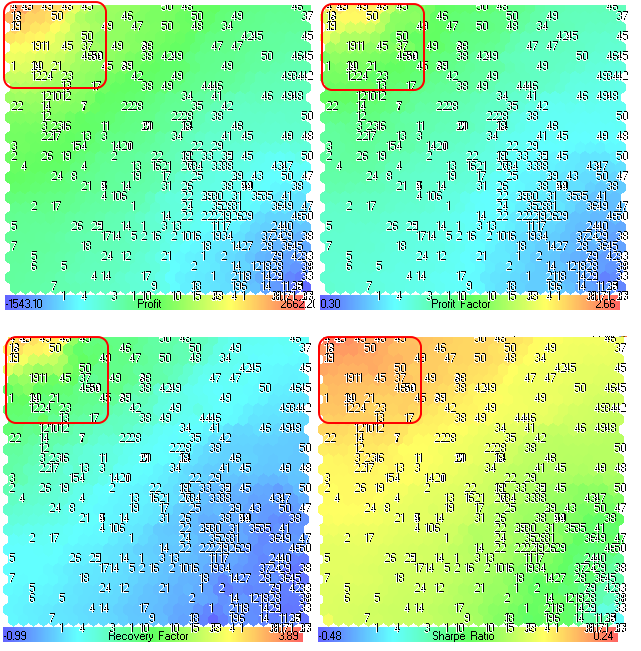
Figure 24. Plans de composants pour les paramètres Profit, Profit Factor, Recovery Factor et Sharpe Ratio
Le premier dont nous avions besoin est de trouver les zones avec les meilleurs résultats d'optimisation.
Nous pouvons constater sur la figure 24, les zones avec des valeurs maximales se trouvent dans le coin supérieur gauche. Les chiffres correspondent à la période de moyennage de l'indicateur de moyenne mobile (paramètre MovingPeriod, nous l'avons utilisé comme titre). L'emplacement des numéros est le même pour tous les plans de composants. Chaque plan composant dispose de sa propre plage de valeurs, les valeurs sont imprimées dans le panneau de dégradé.
Les meilleurs résultats d'optimisation ont les valeurs les plus élevées de Bénéfice, Facteur de Bénéfice, Facteur de Reprise et le Rapport Sharpe, nous avons donc des informations sur les zones sur la carte (décrites dans la Fig. 24).
Les plans des composants pour Trades, ProfitTrades (%), MovingPeriod et MovingShift sont présentés dans la figure 25.
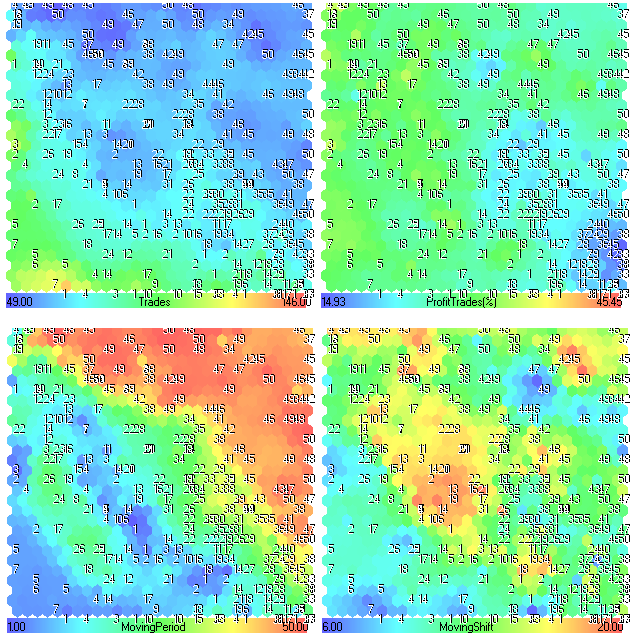
Figure 25. Plans de composants pour les paramètres Trades, ProfitTrades (%), MovingPeriod et MovingShift
Analyse du plan des composants
À première vue, il n'y a pas d'informations intéressantes. Les 4 premiers plans composants (Profit, Profit Factor, Recovery Factor et Sharpe Ratio) semblent similaires, car ils dépendent directement des performances du système du trade.
Nous pouvons constater sur la Fig 24, la région supérieure gauche est très intéressante (par exemple, les meilleurs résultats peuvent être obtenus si nous réglons la MovingPeriod de 45 à 50).
L'Expert Advisor a été testé à la tranche horaire de l' EURUSD, sa stratégie basée sur la tendance, nous pouvons considérer ces valeurs comme une mémoire de "tendance du marché". Si c'est vrai, la mémoire de tendance du marché pour le premier semestre 2011 est égale à 2 jours.
Examinons d'autres plans de composants.
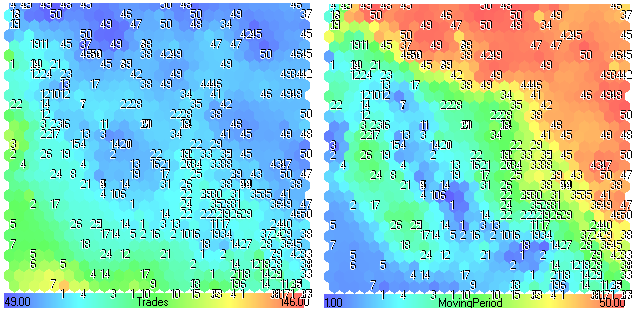
Figure 26. Plans composants Trades-MovingPeriod
En regardant la figure 26,nous pouvons constater que des valeurs inférieures de MovingPeriod (zones bleues) entraînent des valeurs plus élevées de Trades (zones -rouge). Si la période de moyenne mobile est faible, il existe de nombreux croisements (trades).
Nous pouvons également constater ce fait sur le plan des composants des Trades (zones vertes avec des nombres inférieurs à 20).
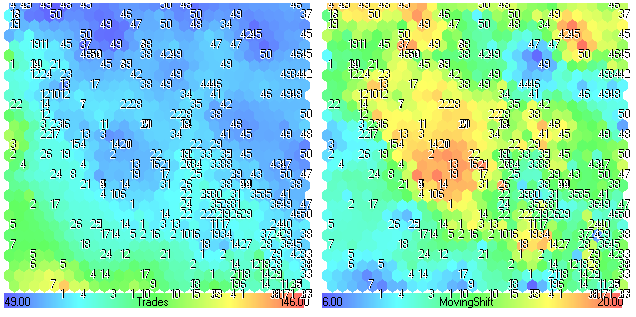
Figure 27. Plans de composants Trades-MovingShift
Le nombre de trades diminue (zones bleues) avec l'augmentation de MovingShift (zones jaune-rouge). En comparant les plans des composants pour MovingShift et Fig.24, nous pouvons constater que le paramètre MovingShift n'est pas très important pour les performances de cette stratégie de trading.
Le pourcentage de trades rentables ProfitTrades (%) ne dépend pas directement de MovingPeriod ou MovingShift, c'est une caractéristique intégrale du système de trade Autrement dit, l'analyse de sa corrélation avec les paramètres d'entrée est insignifiante.
Des stratégies de trade plus complexes peuvent être analysées de la même manière. Vous devez trouver le ou les paramètres les plus importants de votre système de trade et l'utiliser comme titre.
Conclusion
Le principal avantage des Cartes de Caractéristiques Auto-Organisatrices est la possibilité de produire une représentation discrétisée en deux dimensions de données de grande dimension. Les données aux caractéristiques similaires forment des groupes, cela simplifie l'analyse de corrélation.
Les détails et autres applications peuvent être disponibles dans l’excellent livreVisual Explorations in Finance: with Self-Organizing Mapspar Guido Deboeck et Teuvo Kohonen.
Annexe
Après la publication de la version russe, Alex Sergeev a proposé une version améliorée de classes(SOM_Alex-Sergeev_en.zip).
Liste des modifications :
1. L'affichage des images a changé : cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. Ajout de la caractéristique pour ouvrir un dossier avec des images :
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
Modifications dansCSOM class:
- Méthode ajoutée CSOM::HideChart - Cache le graphique.
- Membres de classe ajoutés m_chart, m_wnd, m_x0, m_y0 - (graphique, fenêtre et coordonnées pour afficher les images).
+ ajout de m_sID - préfixe des noms d'objets. Le préfixe utilise le nom de fichier, par défaut le préfixe "SOM" est utilisé. - Toutes les cartes sont sauvegardées au fichier portant le m_sID nom.
- Les fichiers bmp sont nommées par arecolonne de nom des motifs.
- Méthode modifiée CSOM::ShowBMP cartes sauvegardées dans le dossier \ fichiers au lieu d’\ images, ça marche plus rapidement.
- Le CSOM::NetDeinit s’est déplacé vers CSOM::HideBMP.
- Modification de la CSOM::ReadCSVData méthode la premièrecolonne comporte des titres.
- Ajout d’un indicateur pour afficher les cartes intermédiaires dans CSOM::Train(bool bShowProgress)
- L’affichage des cartes intermédiaires dansCSOM::Train est effectué chaque 2 secondes (au lieu d’une itération) l’avancement est affiché dans le graphique à l’aide deCommenire.
- Noms optimisés de certaines variables, méthodes de classe classées par catégorie.
Le dessin de bmp est un processus très lent. Si vous n'en avez pas vraiment besoin, ne le dessinez pas à chaque fois.
L'exemple d'images SOM avec des résultats d'optimisation est compris dans l'archive.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/283
Création de Critères Personnalisés d’Optimisation des Expert Advisors
Estimations Statistiques
Assistant MQL5 pour les Nuls
Traçage, Débogage et Analyse Structurelle du Code Source
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation