Características del Wizard MQL5 que debe conocer (Parte 45): Aprendizaje por refuerzo con Monte-Carlo

Introducción

Este artículo continúa nuestro análisis del aprendizaje por refuerzo considerando otro algoritmo, concretamente el Monte-Carlo. Este algoritmo es muy similar y, de hecho, podría decirse que abarca tanto el Q-Learning como el SARSA, ya que puede ser tanto on-policy como off-policy. Sin embargo, lo que lo distingue es el énfasis en los episodios. Se trata simplemente de una forma de agrupar las actualizaciones del ciclo de aprendizaje por refuerzo, que presentamos en este artículo, de modo que la actualización de los valores Q del mapa Q (Q-Map) se produzca con menos frecuencia.

Con el algoritmo de Monte-Carlo, los valores Q solo se actualizan después de la finalización de un episodio. Un episodio es un lote de ciclos. Para este artículo, hemos asignado a este número de ciclos el parámetro de entrada 'm_episodes_size' y es optimizable o ajustable. Se atribuye al método Monte-Carlo su robustez ante la variabilidad del mercado porque puede simular mejor una amplia gama de posibles escenarios de mercado, lo que permite a los operadores determinar cómo funcionan diferentes estrategias en una variedad de condiciones. Esta variabilidad ayuda a los traders a comprender posibles compensaciones, riesgos y retornos, lo que les permite tomar decisiones más informadas.

Se argumenta que esta ventaja se deriva de su «visión del rendimiento a largo plazo», que contrasta con los métodos tradicionales, que tienden a centrarse en los resultados a corto plazo. Lo que esto significa es que las actualizaciones poco frecuentes que realizan las simulaciones de Monte-Carlo, dado que solo se producen una vez por episodio, evitan el ruido del mercado con el que se topan inevitablemente el Q-Learning y el SARSA, ya que estos ejecutan sus actualizaciones con mayor frecuencia. Por lo tanto, Monte-Carlo se esfuerza por evaluar el rendimiento a largo plazo de las estrategias de negociación mediante la evaluación de las recompensas acumuladas a lo largo del tiempo. Al analizar múltiples episodios de esto, los comerciantes pueden obtener información sobre la rentabilidad general y la sostenibilidad de sus estrategias.

El algoritmo de Monte-Carlo calcula estimaciones del valor de la acción basándose en los retornos promedio de pares estado-acción a lo largo de múltiples ciclos dentro de un solo episodio. Esto permite a los comerciantes evaluar mejor qué acciones (por ejemplo, comprar o vender) tienen más probabilidades de producir resultados favorables en función del desempeño histórico. Esta actualización de los valores Q se debe a que el componente de recompensa de estos valores Q se determina de la siguiente manera:

Donde:

• R t+1 , R t+2 ,…,R T son las recompensas recibidas en cada paso después del tiempo t.
• γ /gamma es el factor de descuento (0 ≤ γ ≤ 1), que establece en qué medida se «descuentan» las recompensas futuras (es decir, se valoran menos que las recompensas inmediatas).
• T representa el intervalo de tiempo en el que finaliza el episodio (estado terminal o tamaño del episodio en ciclos).

Estas consideraciones generales sobre las recompensas, implícitas en la actualización de los valores Q indicada anteriormente, tienden a hacer que Monte-Carlo sea más adaptable, como ya se ha mencionado. Esta adaptabilidad inherente permite a los operadores ajustar sus estrategias en función de las condiciones cambiantes del mercado. Esta adaptabilidad es crucial en los mercados financieros, donde las tendencias pueden cambiar rápidamente y los resultados pasados no siempre permiten predecir los resultados futuros. Esta adaptabilidad es crucial en los mercados financieros, donde las tendencias pueden cambiar rápidamente y los resultados pasados no siempre permiten predecir los resultados futuros. Seguimos un enfoque similar para este artículo.

Por lo tanto, las estrategias que serían adaptables en Monte-Carlo se basarían en muchos aspectos en la elección del Q-Map y los estados. En el último artículo, dado que el algoritmo de aprendizaje por refuerzo era también el principal modelo de previsión del Asesor Experto, a través de una clase de señal personalizada, utilizamos tres estados del entorno cruzados entre un horizonte a corto plazo y otro a largo plazo para crear una cuadrícula/matriz de nueve opciones. Lo que estos estados captaron fue simplemente optimismo, estabilidad y pesimismo, y es relativamente simple/burdo. Sin embargo, tiene potencial para ser más elaborado y sensible a los mercados, no solo aumentando sus dimensiones generales, sino también añadiendo más factores a tener en cuenta. Sin embargo, tiene potencial para ser más elaborado y sensible a los mercados, no solo aumentando sus dimensiones generales, sino también añadiendo más factores a tener en cuenta.

Resumen sobre el aprendizaje por refuerzo (Reinforcement Learning, RL) en el trading

El aprendizaje por refuerzo (RL) está diseñado para funcionar en entornos dinámicos, como los mercados financieros, donde interactúa continuamente con su «entorno» tomando medidas (como comprar, vender o mantener) en función de su estado actual (donde estos estados se definen por los precios o indicadores del mercado, etc.). Cada acción realizada por el agente influye en el estado del entorno, lo que da lugar a nuevas observaciones y posibles recompensas.

Otros ejemplos de conjuntos de estados que pueden adoptar los operadores para sus Q-Maps incluyen los estados basados en indicadores técnicos. Otros ejemplos de conjuntos de estados que pueden adoptar los operadores para sus Q-Maps incluyen los estados basados en indicadores técnicos.

Dado que hemos combinado las perspectivas a corto y largo plazo en un único eje, ahora tenemos la oportunidad de introducir otro eje que abarque diferentes métricas además de las lecturas del indicador MA. Otro indicador que podría utilizarse para ello es el índice de fuerza relativa (Relative Strength Index, RSI). Con ello, consideraríamos los estados de sobrecompra (RSI > 70) que podrían ser una señal de venta, y el estado de sobreventa (RSI < 30) que podría ser una señal de compra, además de un estado transitorio adicional que no ofrece ninguna señal.

O, aún dentro de los estados basados en indicadores, podríamos fijarnos en las bandas de Bollinger, donde un precio cercano o por encima de la banda superior podría indicar un estado bajista, mientras que un precio en la banda inferior o por debajo de ella podría indicar un estado alcista, con un tercer estado neutral implícito para cualquier otra posición.

Además de los estados de los indicadores técnicos, la volatilidad del mercado también podría presentar un eje alternativo a la matriz de estados del entorno. Con esto, la medición se basaría en indicadores como la desviación estándar del precio o el ATR, y aunque se podrían utilizar tres estados posibles (alta volatilidad, baja volatilidad y moderada), se podrían añadir muchas más gradaciones para que el algoritmo fuera más sensible a los mercados. Esta configuración de estado (o eje) ayudaría a orientar al agente sobre si debe operar de forma agresiva o conservadora. También se pueden considerar estados basados en el volumen para las acciones, con una gradación similar.

Además de las tendencias bajistas y alcistas en la acción del precio que hemos utilizado en artículos anteriores y que también estamos considerando para este, existen patrones más específicos de acción del precio, como las rupturas de los niveles de soporte/resistencia. Alternativamente, podría tratarse de patrones de cabeza y hombros tanto para señales alcistas como bajistas, siendo cualquier otro patrón una oscilación. El reconocimiento de tales patrones en la evolución reciente de los precios permitiría al agente anticipar la continuación o la reversión.

Otro posible eje para los estados del Q-Map podrían ser los estados basados en el tiempo. Recuerde que este eje se emparejaría con otro eje, como la acción del precio anterior o los indicadores técnicos mencionados, de modo que se pueda deducir qué acción del precio es más fiable en cada periodo de tiempo. Recuerde que este eje se emparejaría con otro eje, como la acción del precio anterior o los indicadores técnicos mencionados, de modo que se pueda deducir qué acción del precio es más fiable en cada periodo de tiempo. La medición de estos sentimientos dependería de las lecturas del calendario de noticias económicas para un indicador específico, dada la variedad disponible. La gradación de estos estados debe variar de positivo a neutro a negativo, y los estados internos se pueden sumar dependiendo del nivel de detalle que se desee. La incorporación de estados de sentimiento, especialmente con estos métodos, podría ayudar al agente a responder a eventos externos que afectan al mercado.

Similares y alternativos a esto serían los estados económicos basados en eventos. Sin embargo, algo diferente de estos dos que también podría considerarse son los estados basados en cartera. Esta categoría es muy aplicable fuera del mercado Forex y presenta varios ejes potenciales. En primer lugar están los niveles de exposición, donde la cartera de uno se califica en función de la exposición relativa, por ejemplo, de las acciones a los bonos. La gradación podría variar desde 90-10 en un extremo hasta 10-90 en el otro extremo respectivamente. Este eje se puede emparejar con el tiempo o cualquier otra métrica diferente pero relacionada, de modo que el rendimiento de la cartera (que estaría alineado con las recompensas del agente) pueda guiar el proceso de actualización del valor Q.

Otra opción en los estados basados en cartera es el nivel de riesgo. Esto podría considerar porcentajes de asignación de capital para cada inversión, con gradaciones estatales que van desde una pequeña cantidad < 0,5% hasta un límite de, digamos, 10%. Nuevamente, la comparación o el emparejamiento de esto podría ser con otra métrica específica de la cartera y una optimización sobre un conjunto de datos decente debería proporcionar un Q-Map que oriente sobre qué niveles de riesgo usar y cuándo. Otra alternativa podrían ser los estados de reducción, y en resumen estos estados basados en cartera permitirían al agente tener en cuenta el contexto financiero más amplio y no sólo señales aisladas del mercado.

También podría mencionar los estados de macrotendencia; los principios son similares, pero lo más importante es que los ejemplos aquí compartidos no son exhaustivos. La elección de los estados del entorno puede ser fundamental para definir la estrategia y, por lo tanto, para obtener una ventaja competitiva, dependiendo de su singularidad y del esfuerzo invertido no solo en las pruebas, sino también en la validación cruzada.

Además de los estados del entorno, las señales de recompensa después de cada acción proporcionan al agente retroalimentación en forma de indicación del éxito o fracaso de su acción. Las recompensas se pueden cuantificar en términos de ganancias/pérdidas (como lo hemos estado aplicando hasta ahora), retornos ajustados al riesgo o cualquier otra métrica de desempeño relevante que pueda guiar al agente hacia acciones más favorables. Recuerde que las recompensas son un componente clave en la actualización de los valores Q del mapa Q.

RL es quizás más conocido por equilibrar la exploración frente a la explotación al realizar pronósticos. En el papel, el agente a menudo emplea estrategias de exploración para descubrir nuevas acciones que podrían producir mejores recompensas, mientras que alternativamente explota acciones conocidas que anteriormente han demostrado ser exitosas. El equilibrio entre la exploración y la explotación, que está controlado por un parámetro de entrada épsilon, es crucial para que el agente evite óptimos locales y continúe mejorando su toma de decisiones a lo largo del tiempo.

Por lo tanto, a través de ensayo y error, dado que el enfoque épsilon-codicioso para seleccionar acciones adecuadas incorpora una selección aleatoria, el agente aprende de sus experiencias en el entorno y ajusta su política de selección de acciones basándose en resultados pasados. Con cada experiencia, mejora la comprensión del agente de qué acciones conducen a recompensas positivas, lo que le permite tomar mejores decisiones en situaciones futuras similares.

Esta mejora se debe a los valores o la política del Q-Map del agente. El mapa representa una estrategia que vincula estados con acciones y actualiza continuamente las acciones de cada estado basándose en las recompensas observadas. La mejora de la política está guiada por algoritmos de aprendizaje de refuerzo que buscan maximizar las recompensas acumuladas a lo largo del tiempo.

Éstos son los aspectos básicos que hemos visto en los últimos tres artículos sobre RL; sin embargo, todavía hay conceptos más innovadores dentro de RL. Una de ellas es la estimación de la función de valor, donde el agente a menudo estima la función de valor que puede predecir el rendimiento esperado de un estado determinado o de un par estado-acción. Al aproximar la función de valor, el agente puede evaluar los beneficios potenciales a largo plazo de diferentes acciones, facilitando así mejores decisiones.

La asignación de crédito temporal es otro concepto en el que el agente conecta las acciones realizadas en el pasado con las recompensas recibidas en el futuro. En el papel, este enfoque permite al agente comprender cómo sus acciones anteriores afectan los resultados futuros, lo que puede conducir a una mejor planificación o a la configuración preventiva de ciertas políticas que anulen la asociación predeterminada entre acción y estado.

Otro es el de las tasas de aprendizaje adaptativas, un tema que tratamos en este artículo anterior cuando hablamos de los perceptrones multicapa. Estos también pueden activarse como alfa al realizar actualizaciones de valor Q. El agente puede emplearlas para ajustarse en función de la incertidumbre de los valores de estado-acción, lo que permite actualizaciones más agresivas cuando el agente se encuentra en una situación de incertidumbre y actualizaciones más conservadoras a medida que gana confianza. Esta adaptabilidad podría ayudar al agente a aprender de manera eficiente en condiciones de mercado variables.

Otras ideas destacadas relacionadas con el RL incluyen la generalización entre estados para mejorar la eficiencia y el desarrollo de estrategias a largo plazo que van más allá de las recompensas inmediatas.

El algoritmo de Monte-Carlo

El enfoque de aprendizaje adoptado por los métodos Monte-Carlo difiere de los algoritmos RL anteriores que hemos considerado, ya que aprende a partir de episodios completos de experiencia, esperando hasta el final de un episodio para «aprender», pero adoptando un enfoque holístico que abarca múltiples puntos de recompensa recibidos durante el intervalo. Por lo tanto, esto requiere que los valores de recompensa se almacenen en búfer varias veces para que, cuando concluya el episodio, se pueda acceder a todos los valores de recompensa anteriores. Implementamos esto en MQL5 de la siguiente manera, desde la función get output de nuestra clase de señal personalizada:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

Por el contrario, Q-Learning utiliza un método de aprendizaje de diferencia temporal (Temporal-Difference, TD) que actualiza las estimaciones de valores después de cada acción realizada (o después de cada ciclo), utilizando el método de arranque a partir de valores de estado-acción posteriores. Esto es similar a SARSA pero aquí las actualizaciones de las estimaciones de valor se realizan utilizando la acción tomada en el siguiente estado, lo que proporciona un enfoque de aprendizaje basado en políticas.

El mecanismo de actualización de Monte-Carlo se basa en el rendimiento promedio observado después de tomar acciones desde un estado a lo largo de múltiples ciclos en un episodio. Cada par estado-acción se actualiza sólo una vez que se completa el episodio, para reflejar el verdadero rendimiento a largo plazo. Por lo tanto, el valor de recompensa utilizado en esta actualización es una suma ponderada como se muestra en la fórmula ya compartida anteriormente, así como en el código MQL5 en la función de obtención de salida anterior.

Sin embargo, Q-Learning utiliza la recompensa futura máxima del próximo estado (fuera de política) para realizar actualizaciones en el valor de acción del estado actual, lo que puede conducir a un aprendizaje más agresivo ya que considera el mejor resultado posible en cada paso del ciclo dentro de un episodio. De manera similar, SARSA actualiza el valor en función de la acción real tomada en el siguiente estado (según la política), fusionando la política actual del agente en el proceso de aprendizaje, lo que puede generar actualizaciones levemente más conservadoras que Q-Learning, pero aún más agresivas que Monte-Carlo.

Monte-Carlo, por regla general, se basa en una exploración completa del entorno a través de múltiples ciclos en un episodio, para aprender acciones óptimas, lo que permite un muestreo exhaustivo de pares estado-acción antes de realizar actualizaciones. Esto se realiza mediante un enfoque ε-greedy, que presentamos en nuestro artículo introductorio sobre Q-Learning, donde las actualizaciones se vieron influenciadas por acciones no realizadas por el agente.

SARSA también es ε-greedy en su enfoque para equilibrar la exploración y la explotación, sin embargo actualiza los valores en función de la acción realmente tomada en el siguiente estado, lo que lo hace más receptivo a la política actual del agente y a las elecciones de exploración. La diferencia de Monte-Carlo con estos dos, además de tener actualizaciones hechas solo una vez en cada episodio, es que puede ser según la política o fuera de ella. Para este fin, nuestra clase de señal personalizada para Monte-Carlo tiene un parámetro de entrada m_on_policy que es booleano y, como su nombre lo sugiere, orientaría si se utiliza en un estado de política activada o desactivada.

La interfaz de clase para esta clase de señal personalizada se presenta a continuación:

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

La convergencia de Monte-Carlo tiende a ser más lenta ya que requiere episodios completos para las actualizaciones, lo que puede no ser necesariamente eficiente en entornos con episodios largos o recompensas escasas. Esto contrasta con el algoritmo Q-Learning que, en su mayor parte, converge más rápido debido a su naturaleza de bootstrap, pero que seguramente será inestable ya que puede oscilar o divergir en entornos con recompensas no estacionarias o alta varianza. Se promociona SARSA como más estable que Q-Learning en ciertas situaciones, ya que tiene en cuenta la política real del agente durante las actualizaciones, lo que tiende a generar curvas de aprendizaje más suaves.

En lo que respecta a la eficiencia de muestreo, Monte-Carlo suele ser menos eficiente en el muestreo debido a sus requisitos de episodios completos para obtener actualizaciones, lo que puede ser un inconveniente importante en entornos con un gran espacio de acción de estado. Por otro lado, Q-Learning es más eficiente en el uso de muestras ya que actualiza los valores en cada paso, lo que permite modificaciones más rápidas basadas en retroalimentación inmediata. De hecho, se podría decir que es incluso más eficiente que SARSA, ya que este último puede requerir más muestras que Q-Learning porque es sensible a la política actual y a la estrategia de exploración utilizada.

El método Monte-Carlo es adecuado para entornos donde los episodios pueden definirse claramente y los rendimientos a largo plazo tienden a ser más cruciales que los picos de corto plazo, como en las simulaciones comerciales. Esto lo convierte claramente en una estrategia clave para los "comerciantes" de valor o de largo plazo. Q-Learning es eficaz en entornos con una estructura de recompensa clara y transiciones de estados bien definidas, lo que lo hace ideal para tareas como el day trading. Si bien SARSA es beneficioso en situaciones donde el aprendizaje debe reflejar de cerca la política del agente, como en entornos dinámicos o parcialmente observables donde la adaptación es crucial, como en el swing trading.

Implementación de Monte-Carlo en una clase de señal personalizada

Implementamos nuestra señal personalizada que utiliza Monte-Carlo RL como modelo raíz y generador de señales. Los pasos principales para lograr esto ya se compartieron anteriormente con la interfaz de clase y la función de obtención de salida. A continuación se muestran las funciones de condición larga y corta:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

El código fuente completo de esta implementación se adjunta al final, y las guías sobre cómo utilizarlo para ensamblar un asesor experto ensamblado por un asistente se pueden encontrar aquí y aquí. El proceso de decisión de Markov es inherente al uso de Q-Maps, no obstante, hay un parámetro de entrada que presenta la opción de utilizar la ponderación de Markov al realizar actualizaciones del valor Q. Además, podemos optimizar si lo usamos o no según la política, el tamaño de épsilon, nuestro parámetro que guía hasta qué punto exploramos frente a explotamos, y la cantidad de ciclos en un episodio. Realizamos ejecuciones de optimización en el par GBPUSD para el año 2022 en el marco de tiempo de una hora. A continuación se muestran nuestros resultados:

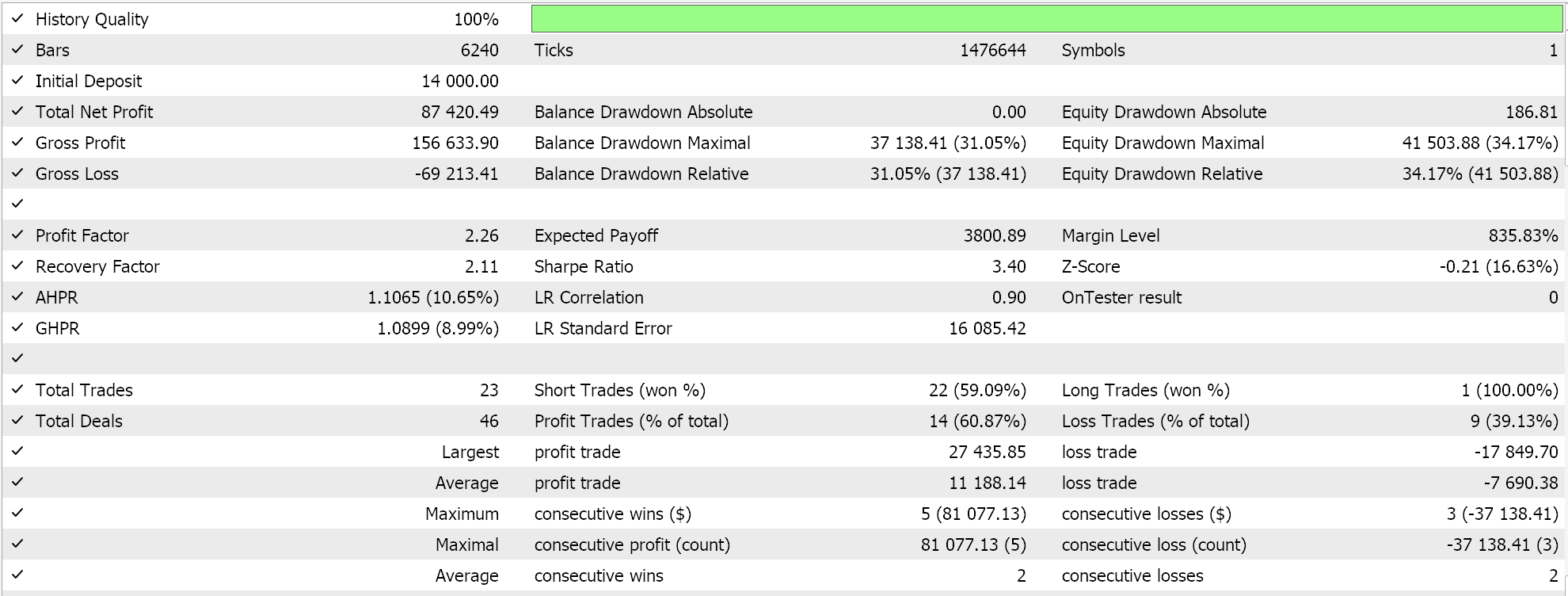
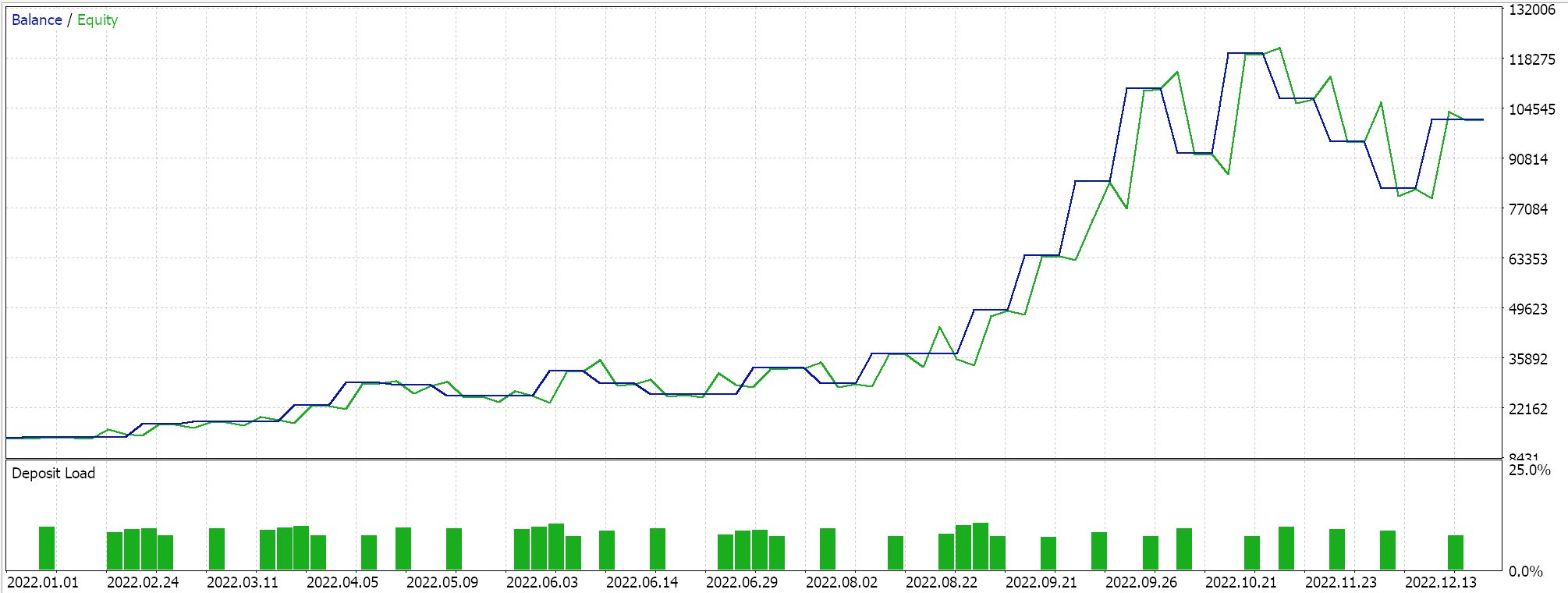
Conclusión y consideraciones adicionales

En resumen, hemos analizado el algoritmo Monte-Carlo del aprendizaje por refuerzo, que toma muchas características de Q-Learning y SARSA, dos algoritmos que ya hemos tratado anteriormente aquí y aquí respectivamente, y presenta una forma de aprendizaje aún más dinámica y adaptable que se centra en los rasgos y atributos a largo plazo de su entorno. Además de utilizar una matriz de entorno más personalizada como se destaca en algunas de las alternativas enumeradas en este artículo, también se puede explotar una escala de acción alternativa, con más de 3 opciones.

También hay algunas consideraciones adicionales al implementar Monte-Carlo (MC) que vale la pena mencionar. MC equilibra el equilibrio entre sesgo y varianza en la forma en que se calcula el valor de recompensa de actualización. En los casos en que el número de ciclos en un episodio es pequeño, tiende a haber un alto sesgo y una baja varianza, mientras que los episodios más largos con un alto número de ciclos tienden a presentar lo opuesto. Por lo tanto, dependiendo de los objetivos de cada uno, esto es algo a tener en cuenta al desarrollar el Q-Map porque un sesgo alto tenderá a hacer que el modelo sea más adaptable a la acción a corto plazo, mientras que una varianza alta se ajustará mejor a la intención del algoritmo de capturar rasgos y atributos a largo plazo.

La exploración más granular del espacio de acción del estado que se obtiene al tener múltiples recompensas de diferentes puntos de tiempo cuando se usan múltiples retornos de n pasos significa que al variar los horizontes de los posibles retornos (que en nuestra clase de señal personalizada estaba controlada por el parámetro de entrada m_episode_cycles), podemos ajustar la intensidad de la señal para las estrategias comerciales. Esta granularidad conduce a decisiones más matizadas a la hora de determinar los puntos de entrada y salida, lo que permite optimizar ambos y realizar ajustes en el tiempo y la intensidad de sus señales.