
Criterios de tendencia en el trading
Introducción
Todos los tráders conocen la frase "La tendencia es tu amiga". De hecho, los movimientos de tendencia de los precios pueden resultar muy rentables. Las operaciones de tendencia se basan en el supuesto de que el movimiento de los precios continuará en la misma dirección. El principal problema de este tipo de operaciones reside en determinar el momento del comienzo y el final de la tendencia con suficiente precisión.
Hoy en día, existen muchos enfoques para definir y calcular los parámetros de la tendencia. En este artículo veremos los más interesantes, y trataremos de ponerlos en práctica.
Suavizado y tendencias
El movimiento de los precios puede representarse mediante un modelo sencillo. Tenemos un componente determinista que depende del tiempo. A este se le une algún componente aleatorio que no depende de nada y se comporta de forma impredecible. Una de las tareas a las que se enfrenta un tráder es reducir de algún modo el impacto de este componente.
Uno de los filtros más sencillos es la media móvil simple, pero este indicador tiene un grave inconveniente: va con retraso. Vamos a modelar una tendencia y a aplicarle una SMA con un periodo 3.
| Tendencia | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| SMA | - | - | 1 | 2 | 3 | 4 |
Ahora vamos a intentar eliminar el retraso. La fórmula de la SMA será la siguiente:
![]()
Ahora le añadiremos un ajuste que será igual a la variación media del precio de una barra:
![]()
Veamos cómo cambian los coeficientes de nuestro nuevo indicador:
![]()
Un indicador con estos coeficientes acertará la tendencia con precisión. Luego generalizaremos este indicador a cualquier número de precios procesados. El cálculo del indicador con un periodo igual a 4 tendrá el aspecto siguiente.
Primero hallaremos el valor de la SMA:
![]()
Las correcciones del cambio de precio medio pasarán a ser dos:
![]()
![]()
Es decir, calcularemos la variación media del precio en relación con el centro de la SMA. Entonces, la fórmula del indicador será como sigue:
![]()
La diferencia entre este indicador y el SMA se hace especialmente notable con periodos pequeños.
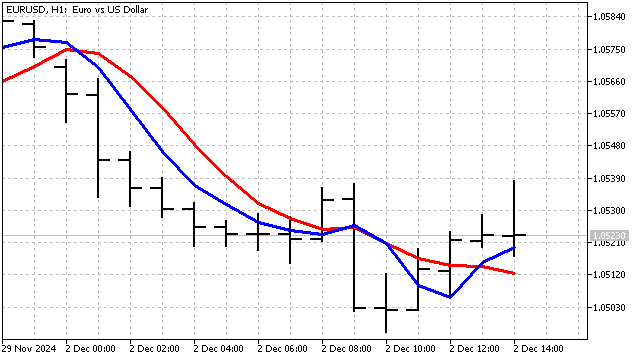
El principal inconveniente de este enfoque es que no existen criterios a la hora de elegir el periodo del indicador. El tráder debe seleccionarlo arbitrariamente, basándose en sus propias consideraciones.
Hoy intentaremos construir un indicador que no dependa del periodo. Supongamos que tenemos una serie temporal V que queremos predecir con un paso de antelación. Para las previsiones usaremos el método más sencillo: lo que haya sido, será. Por ejemplo, tenemos un valor inicial V, entonces la predicción un paso por delante será igual a ese valor:
![]()
Cuando aparezca el nuevo valor V, hallaremos la semisuma entre la previsión y V. El valor obtenido será la previsión para el siguiente paso:
![]()
Es decir, la previsión se ajustará a medida que aparezcan nuevos valores de la serie temporal. Este método de predicción conduce a un suavizamiento exponencial con un coeficiente de 0,5.
Ahora cambiaremos un poco el enfoque de las previsiones. Supongamos que los cambios previstos se producen con la misma intensidad:
![]()
Es decir, todos los valores previstos pertenecerán a una tendencia lineal. La fórmula del indicador construido sobre este principio tendrá el aspecto siguiente:
![]()
Tenemos un indicador recursivo: para calcular el valor actual del indicador, se utilizarán sus valores pasados. Pero, en esta forma sería inestable, pues uno de los coeficientes es 1. Para superar este obstáculo, aplicaremos la misma recursión a Indicator[i+1]:
![]()
El indicador ahora constará de dos partes: una SMA con un periodo de 2 y la mitad de la velocidad del indicador en los recuentos anteriores. Haremos un cambio más para que el indicador resulte más estable:
![]()
Y así es como se verá nuestro nuevo indicador comparado con la EMA similar con un periodo igual a 3.
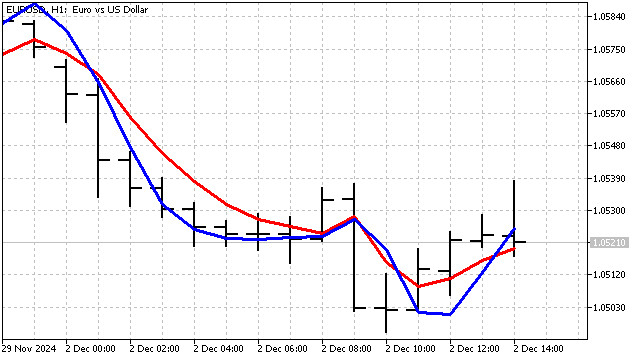
Por desgracia, suprimir el ruido por completo será una tarea casi imposible. Pero resulta más que posible destacar el componente de tendencia en el movimiento de los precios. Ambos indicadores resultan sensibles a los cambios en los parámetros de tendencia. En este caso, su retraso se reducirá al mínimo posible. Estos indicadores pueden usarse de forma independiente (para suavizar los precios) y también como fuente de datos para otros indicadores.
Criterios de tendencia
Los criterios de tendencia se denominan más bien criterios de aleatoriedad. La esencia de su aplicación es muy sencilla. Con la ayuda del criterio, comprobaremos si una fila con precios es aleatoria. Si el criterio nos muestra que la serie no es aleatoria, podremos decir que se trata de una tendencia. Veamos cuáles son los criterios y cómo pueden aplicarse al análisis técnico.
Criterio de Abbe. Este criterio se basa en calcular la varianza de dos formas distintas. La varianza selectiva resulta sensible a las tendencias, mientras que en la varianza de Allan, la influencia de la tendencia tiende a cero. Comparando estas dispersiones entre sí, podemos estimar la contribución del componente de tendencia a la variación de los precios.
Para las aplicaciones comerciales, modificaremos ligeramente el cálculo de este criterio:
![]()
Este criterio solo indica la presencia de una tendencia. La dirección de la tendencia deberá determinarse por otros medios.
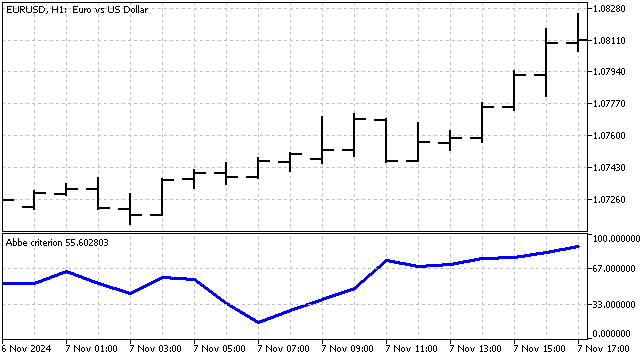
Este criterio puede ayudarnos a identificar los momentos de cambio de tendencia.
Criterio de signo para las primeras diferencias. Este criterio es muy sencillo e intuitivo. Tomamos N precios y los dividimos en pares consecutivos, que serán N-1. Luego aplicamos una función de signo a cada par:
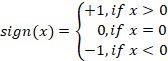
Después, obtenemos el valor del criterio:
![]()
El indicador RSI usa el mismo enfoque, solo que los movimientos alcistas y bajistas del precio se calculan por separado, sin tener en cuenta los signos.
Esta estadística tiene un inconveniente: no diferencia la secuencia de aparición de los signos. Es decir, podemos intercambiar los precios y obtener el mismo resultado. Para evitar este inconveniente, podemos asignar pesos a cada signo, en función del momento en que aparezca. Entonces, el cálculo del criterio tendrá el aspecto que sigue:
![]()
En este caso, la secuencia de signos se hará única, y el mismo resultado solo será posible cuando dos series temporales sean similares.
Veamos cómo podemos usar este criterio para el análisis técnico. Los valores que pueden obtenerse utilizando este criterio se sitúan dentro de unos límites estrictamente delimitados. La intuición sugiere que los valores cercanos a cero pueden ser más comunes, pero será mejor comprobarlo aquí.
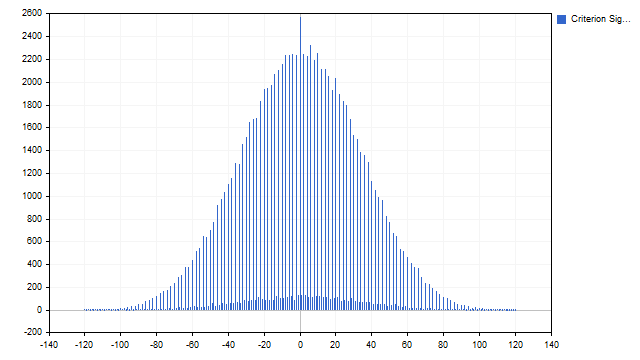
La suposición ha resultado correcta. Hablando en términos estrictos: hemos obtenido una función de probabilidad empírica. ¿Qué se puede aprender de esta función? Podemos obtener los niveles de sobrecompra/sobreventa. Hemos fijado este nivel en el 33%, es decir, el indicador filtrará el tercio más bajo y el tercio más alto de los valores. El tercio que queda en medio será el movimiento lateral. Y el indicador en sí tendrá este aspecto:
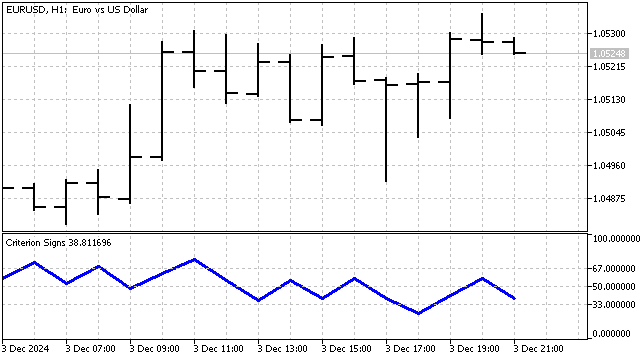
El criterio del signo se refiere al criterio no paramétrico. La principal ventaja de estos criterios reside en su estabilidad e insensibilidad a las variaciones bruscas de los precios.
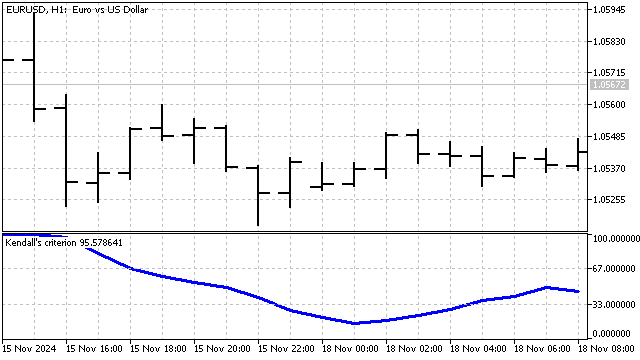
Criterio de Kendall. Este criterio también se basa en la función de los signos. Pero la aplicación de esta función será un poco diferente.
El cálculo de este criterio puede realizarse en dos pasos. En primer lugar, para cada precio, hallaremos la suma de los signos con todos los precios que la preceden:
![]()
A continuación, hallaremos la suma total de estos valores:
![]()
Utilizando este criterio, compararemos el número de movimientos de precios alcistas y bajistas para todas las combinaciones de precios por pares. Gracias a ello, podremos evaluar con mayor precisión la dirección y la fuerza de la tendencia.
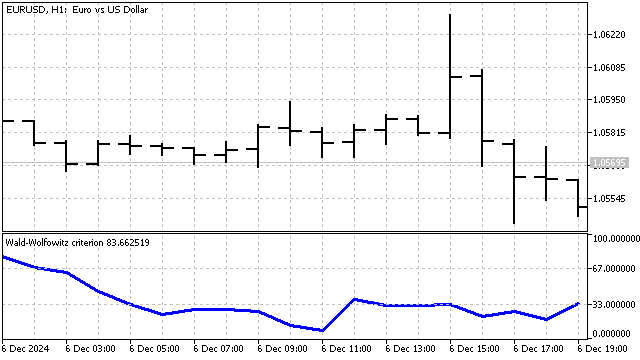
Criterio de clasificación de Wald-Wolfowitz. Para calcular este criterio, necesitaremos conocer el rango de cada precio. El rango es el número de precios que se hallan por debajo del precio actual. Para este ejemplo, tomaremos 5 valores de precio:
| Índice | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Precio | 1.05702 | 1.05910 | 1.05783 | 1.05761 | 1.05657 |
| Rango | 1 | 4 | 3 | 2 | 0 |
El precio con índice 0 es superior a un único precio con índice 4. Así que el rango de este precio será 1. El precio con el índice 1 será mayor que todos los demás y su rango será 4. Los rangos de todos los demás precios se calcularán del mismo modo.
La esencia de este criterio es muy sencilla: si los precios forman una tendencia, sus rangos también se ordenarán. Y si los rangos están mal mezclados, entonces los precios estarán mal mezclados. En este ejemplo, los precios están parcialmente ordenados, lo cual puede sugerir una tendencia.
El valor de este criterio se calcula según la fórmula:
![]()
En esencia, este criterio es una versión robusta de la función de autocorrelación. Y el indicador construido sobre su base tendrá este aspecto:
Criterio Foster-Stewart. Este criterio permite evaluar simultáneamente la presencia de una tendencia en la media y la varianza. Se basa en el cálculo del número de registros superiores e inferiores. Para cada referencia de precio, determinaremos el valor de dos variables H y L.
La variable H será igual a 1 si el precio actual es superior a todos los precios anteriores. La variable L será igual a 1 si el precio es inferior a todos los precios anteriores. En todos los demás casos, estas variables serán cero. Los parámetros del criterio se calcularán del siguiente modo:
![]()
![]()
El parámetro T muestra la fuerza y la dirección de la tendencia. El parámetro D resulta similar al criterio de Abbe y solo indica la presencia de una tendencia. Estos parámetros pueden usarse solos o combinados entre sí.
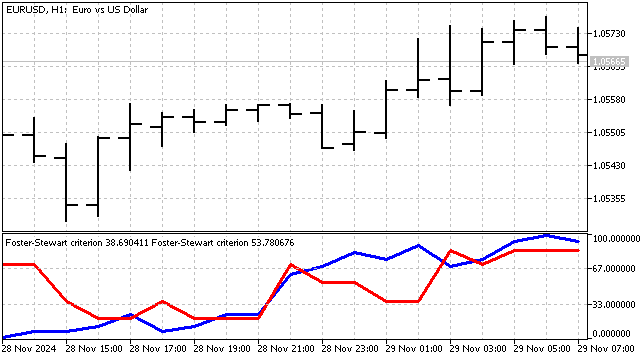
Este criterio puede modernizarse para considerar ambos parámetros al mismo tiempo. En la versión clásica, una tendencia puede considerarse establecida si el valor de T o D resulta lo suficientemente grande (para T, por supuesto, deberemos tomar el valor absoluto). De ello se deduce que el producto de estos parámetros se desvía de cero en la medida de lo posible cuando haya tendencia. Este enfoque nos permite identificar las tendencias más marcadas.
Veamos ahora cómo podemos usar estos criterios en el trading.
Estrategias comerciales
Desgraciadamente, los criterios de tendencia no dicen nada sobre el inicio de una tendencia, solo indican que la tendencia se ha producido. Precisamente esta propiedad se puede utilizar en el trading; después de una fuerte tendencia será posible cambiar la dirección del movimiento del precio a la opuesta.
Partiendo de este supuesto, podemos crear una estrategia sencilla. Si el criterio de tendencia ha alcanzado un valor mínimo, deberemos abrir una posición de compra. Para abrir posiciones de venta, el criterio deberá alcanzar un máximo. Es decir, utilizaremos los criterios de tendencia para determinar la sobrecompra/sobreventa. Este enfoque parece prometedor.
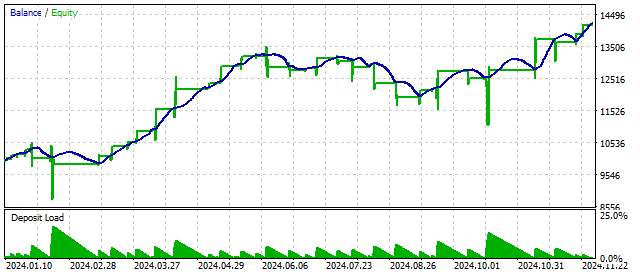
La aplicación de filtros adicionales puede mejorar el rendimiento de la estrategia. El criterio de Abbe puede usarse como un filtro de este tipo. Permítame recordarle que este criterio solo determina la presencia de una tendencia. Pero la dirección de la tendencia deberá determinarse por otros medios. Por ejemplo, definiremos una tendencia utilizando la velocidad media de movimiento de los precios:
![]()
Si el valor resultante está por encima o por debajo de un determinado nivel, consideraremos que se ha establecido una tendencia. Para confirmar dicha hipótesis, utilizaremos el criterio de Abbe. Si su valor está por encima de un determinado nivel, la hipótesis de tendencia será cierta. Dejaremos la apertura y el cierre de posiciones igual que en el ejemplo anterior. El resultado de esta estrategia será el siguiente:
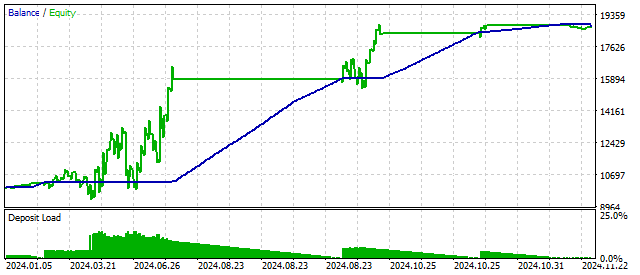
El criterio Foster-Stewart permite evaluar directamente tanto la presencia de una tendencia como su dirección. Es decir, este criterio puede servir de señal y de filtro al mismo tiempo. La aplicación de este criterio puede ofrecer estos resultados:
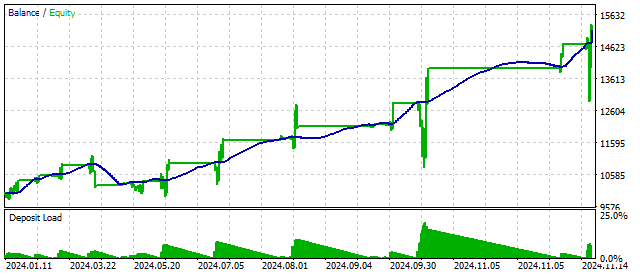
Una versión modernizada de este criterio producirá resultados diferentes.
La aplicación de criterios de tendencia está justificada, pero conlleva algunas dificultades:
- En primer lugar, deberemos utilizar filtros adicionales para reducir el número de señales falsas.
- En segundo lugar, necesitaremos normas independientes para el cierre de posiciones a fin de reducir el riesgo y la carga de los depósitos.
- En tercer lugar, los criterios de tendencia pueden resultar sensibles al número de precios procesados. Por lo tanto, podría ser necesario suavizar previamente las series temporales al aplicarlos. Y con periodos pequeños, el suavizamiento debería ser obligatorio.
Conclusión
Hoy existen varias decenas de criterios de tendencia. La aplicación de estos puede resultar útil tanto para analizar situaciones de mercado como para negociar.
En la redacción de este artículo hemos utilizado los siguientes programas.
| Nombre | Tipo | Descripción |
|---|---|---|
| tSMA | indicador | SMA análogo de tendencia
|
| tEMA | indicador | Análoga de tendencia de EMA con periodo 3 |
| Criterio de Abbe | indicador | Criterio de Abbe |
| Criterion Signs | indicador | Criterio de signo para las primeras diferencias |
| scr Criterion Signs | script | El script permite estimar la distribución de valores del criterio de signos
|
| Kendall's criterion | indicador | Criterio de Kendall |
| Foster-Stewart criterion | indicador | Criterio Foster-Stewart
|
| Foster-Stewart criterion I | indicador | Versión modernizada del criterio Foster-Stewart |
| Wald-Wolfowitz criterion | indicador | Criterio Wald-Wolfowitz |
| EA 3 criterions | asesor | El asesor experto comercia según 3 criterios
|
| EA Abbe criterion | asesor |
|
| Criterio EA Foster-Stewart | asesor |
|
| EA Foster-Stewart criterion I | asesor |
|
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16678
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Ingeniería de características con Python y MQL5 (Parte I): Predicción de medias móviles para modelos de IA de largo plazo
Ingeniería de características con Python y MQL5 (Parte I): Predicción de medias móviles para modelos de IA de largo plazo
 Algoritmo de Tribu Artificial (Artificial Tribe Algorithm, ATA)
Algoritmo de Tribu Artificial (Artificial Tribe Algorithm, ATA)
 Robot comercial multimodular en Python y MQL5 (Parte I): Creamos la arquitectura básica y los primeros módulos
Robot comercial multimodular en Python y MQL5 (Parte I): Creamos la arquitectura básica y los primeros módulos
 Solicitudes en Connexus (Parte 6): Creación de una solicitud y respuesta HTTP
Solicitudes en Connexus (Parte 6): Creación de una solicitud y respuesta HTTP
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Lo intentaré... hay otros criterios interesantes, como la definición de punto de giro. Tengo que averiguar cómo explicarlos de forma más sencilla.
No sé cuál es el problema con el probador. Me sale esto.
Gracias, lo intentaré. ¿Y dónde buscas explicaciones de los criterios y mecanismos matemáticos para detectarlos? Parecen fuentes científicas ...
Gracias, lo intentaré. ¿Y dónde buscar explicaciones de los criterios y mecanismos matemáticos para su detección? Parece que las fuentes científicas ...
hay un montón de literatura, pero todos los criterios son en su mayoría dispersos aquí y allá. Aquí hay una buena selección de diferentes criterios
Estoy trabajando en la aplicación práctica del criterio de tendencia de Wald-Wolfowitz descrito en su artículo. Según tengo entendido, el criterio de Wald-Wolfowitz comprueba la hipótesis de aleatoriedad/estacionariedad de los datos. En el código de los Asesores Expertos de trading, ¿es importante entender qué devuelve exactamente el indicador?
¿Entiendo correctamente que el indicador calcula la probabilidad (en porcentaje) de que la secuencia de precios (en este caso - los valores de apertura) es al azar sobre la base del criterio de Wald-Wolfowitz.
El resultado se almacena en el buffer buffer[0] y representa el porcentaje de probabilidad (de 0 a 100).
Cuanto más se acerque el valor al 100%, mayor será la probabilidad de aleatoriedad (sin tendencia).
Cuanto más se acerque al 0%, mayor será la probabilidad de no aleatoriedad (presencia de tendencia o agrupación)...
Lógica de cálculo:
El indicador clasifica los valores de apertura para un periodo seleccionado ( iPeriod ), luego calcula estadísticas basadas en las clasificaciones y las convierte en un valor porcentual mediante CDF (función de distribución empírica):
Niveles en el gráfico:
indicador_nivel1 = 33 e indicador_nivel2 = 67 son puntos de referencia para la interpretación:
<33% - fuerte no aleatoriedad (posible tendencia).
>67% - alta aleatoriedad (plano).
¿Entiendo correctamente la interpretación del indicador presentada en su artículo?
Estoy trabajando en la aplicación práctica del criterio de tendencia de Wald-Wolfowitz descrito en su artículo. Según tengo entendido, el criterio de Wald-Wolfowitz comprueba la hipótesis de aleatoriedad/estacionariedad de los datos. En el código de los Asesores Expertos de trading es importante entender ¿qué devuelve exactamente el indicador?
¿Entiendo correctamente que el indicador calcula la probabilidad (en porcentaje) de que la secuencia de precios (en este caso - los valores abiertos) es al azar sobre la base del criterio de Wald-Wolfowitz.
El resultado se almacena en el buffer buffer[0] y representa el porcentaje de probabilidad (de 0 a 100).
Cuanto más se acerque el valor al 100%, mayor será la probabilidad de aleatoriedad (sin tendencia).
Cuanto más se acerque el valor al 0%, mayor será la probabilidad de no aleatoriedad (presencia de una tendencia o agrupación)...
Lógica de cálculo:
El indicador clasifica los valores abiertos para un periodo seleccionado ( iPeriod ), luego calcula estadísticas basadas en las clasificaciones y las convierte en un valor porcentual mediante CDF (función de distribución empírica):
Niveles en el gráfico:
indicador_nivel1 = 33 e indicador_nivel2 = 67 son puntos de referencia para la interpretación:
<33% - fuerte no aleatoriedad (posible tendencia).
>67% - alta aleatoriedad (tendencia plana).
¿Entiendo correctamente la interpretación del indicador presentado en su artículo?
Sí, usted entiende todo correctamente. Lo único es que fijé los niveles 33 y 67 sólo porque necesitaba algunos niveles. Puede establecer otros niveles, por ejemplo, 25 y 80.
Sí, lo has entendido todo correctamente. Lo único es que fijé los niveles 33 y 67 simplemente porque necesitaba algunos niveles. Puede establecer otros niveles, por ejemplo, 25 y 80.
Gracias por su respuesta.