Si he entendido bien, queremos encontrar el máximo de la función Hill igual a 1.
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //máximo global + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //global min. - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
Esta función sólo tiene dos parámetros.
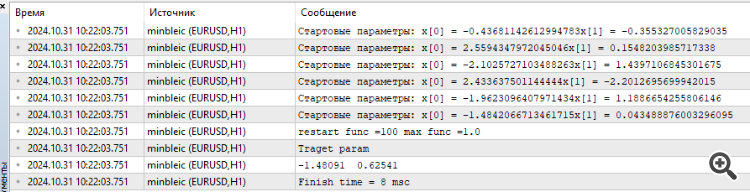
He conectado MinBleic
Me parece que debemos contar no el resultado medio dado por el optimizador, pero el máximo. Y, por supuesto, se puede ver el tiempo, fenomenal 8 milisegundos.
1. Si he entendido bien, queremos encontrar el máximo de la función Hill igual a 1.
2. Esta función sólo tiene dos parámetros.
3. MinBleic conectado
Me parece que no hay que contar el resultado medio que produce el optimizador, sino el máximo. Y por supuesto se puede ver el tiempo, fenomenal 8 milisegundos.
Gracias por tu comentario.
1. Sí, es cierto. Todas las funciones de prueba están unificadas y sus valores se encuentran en el intervalo [0,0; 1,0].
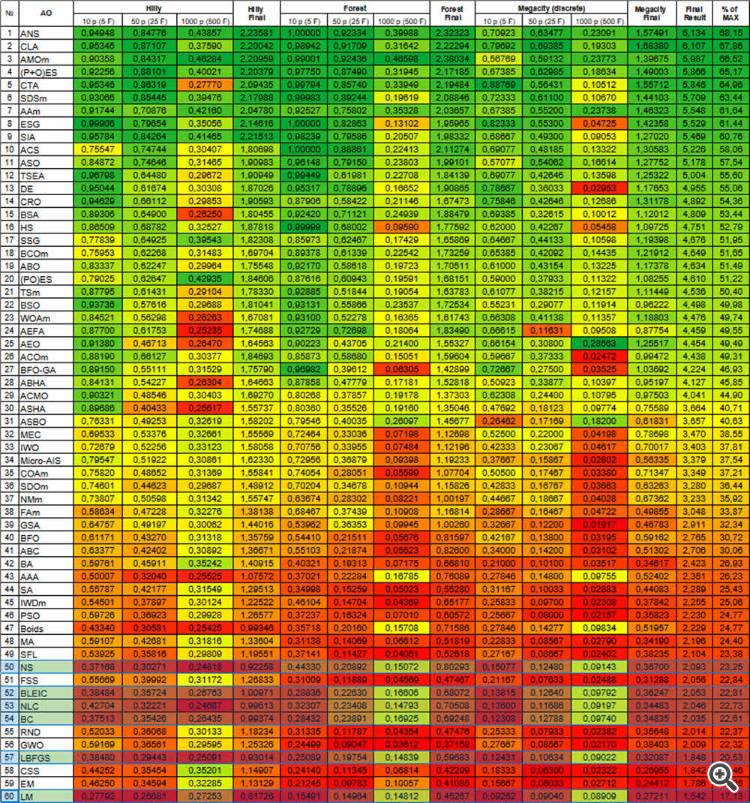
2. Todas las funciones de prueba tienen sólo dos parámetros. Pero cuando probamos algoritmos, utilizamos un espacio de búsqueda multidimensional (tres tipos de pruebas, 5*2=10, 25*2=50, 500*2=1000 parámetros para evaluar la capacidad de escalado de AO) duplicando repetidamente una función bidimensional.
3. El problema con dos parámetros es demasiado simple para comparar adecuadamente los algoritmos entre sí, casi todos los algoritmos resuelven dicho problema instantáneamente con una convergencia del 100%. 4. Los algoritmos tienen dificultades con los espacios multidimensionales.
¿Debemos tomar el resultado máximo? La cuestión es que la dispersión de los resultados en distintas ejecuciones de los algoritmos importa. En todos los algoritmos en la primera iteración valores aleatorios de puntos de siembra, que puede ser completamente al azar muy cerca del valor del extremo global, en este caso el algoritmo irrazonablemente rápido encontrar el mejor resultado, por lo que el valor medio de los resultados de las carreras refleja mejor la característica del algoritmo para excluir la dependencia aleatoria en el "éxito" del algoritmo.
Esto está relacionado con la teoría de la probabilidad. No importa lo compleja que sea la función objetivo, si sólo hay un parámetro, incluso después de generar 10 valores aleatorios, uno de ellos estará muy cerca del extremo global. Los métodos ALGLIB (variaciones del descenso de gradiente) son sensibles a la posición inicial de los puntos en el espacio, por lo que su naturaleza es determinista. A medida que aumenta la dimensionalidad del espacio de búsqueda, la complejidad del espacio aumenta exponencialmente, no hay forma de llegar al extremo global generando números aleatorios.
La prueba es la dificultad de estos métodos para converger incluso en un paraboloide monótono, suave y unimodal si aumenta la dimensionalidad del problema.
Cuantos más resultados estables muestre AO independientemente de los valores iniciales en el espacio de búsqueda, más fiable se puede considerar este método para resolver problemas. Por eso en las pruebas elegimos el valor medio de varias ejecuciones de AO.
La realidad actual es tal que muchas tareas requieren la optimización de millones e incluso miles de millones de parámetros (IA, LLM, redes generativas, tareas complejas de control en producción y empresas), y no podemos hablar de suavidad y unimodalidad de las tareas.
Gracias por su comentario.
1. Sí, correcto. Todas las funciones de prueba están unificadas y sus valores se encuentran en el intervalo [0,0; 1,0].
2. Todas las funciones de prueba tienen sólo dos parámetros. Pero cuando probamos algoritmos, utilizamos un espacio de búsqueda multidimensional (tres tipos de pruebas, 5*2=10, 25*2=50, 500*2=1000 parámetros para evaluar la capacidad de escalado de AO) duplicando repetidamente una función bidimensional.
3. El problema con dos parámetros es demasiado simple para comparar adecuadamente los algoritmos entre sí, casi todos los algoritmos resuelven dicho problema instantáneamente con una convergencia del 100%. 4. Los algoritmos tienen dificultades con los espacios multidimensionales.
¿Debemos tomar el resultado máximo? La cuestión es que la dispersión de los resultados en distintas ejecuciones de los algoritmos importa. En todos los algoritmos en la primera iteración, los valores aleatorios de los puntos de siembra, que puede ser completamente al azar muy cerca del valor del extremo global, en cuyo caso el algoritmo irrazonablemente rápido encontrar el mejor resultado, por lo que el valor medio de los resultados de las carreras refleja mejor la característica del algoritmo para excluir la dependencia aleatoria en el "éxito" del algoritmo.
Esto está relacionado con la teoría de la probabilidad. No importa lo compleja que sea la función objetivo, si sólo hay un parámetro, incluso después de generar 10 valores aleatorios, uno de ellos estará muy cerca del extremo global. Los métodos ALGLIB (variaciones del descenso de gradiente) son sensibles a la posición inicial de los puntos en el espacio, por lo que su naturaleza es determinista. A medida que aumenta la dimensionalidad del espacio de búsqueda, la complejidad del espacio aumenta exponencialmente, no hay forma de llegar al extremo global generando números aleatorios.
La prueba es la dificultad de estos métodos para converger incluso en un paraboloide monótono, suave y unimodal si aumenta la dimensionalidad del problema.
Cuantos más resultados estables muestre AO independientemente de los valores iniciales en el espacio de búsqueda, más fiable se puede considerar este método para resolver problemas. Por eso en las pruebas elegimos el valor medio de varias ejecuciones de AO.
La realidad actual es tal que muchas tareas requieren la optimización de millones e incluso miles de millones de parámetros (IA, LLM, redes generativas, tareas complejas de control en producción y empresas), y no podemos hablar de suavidad y unimodalidad de las tareas.
Se ha tomado una función muy compleja en sí misma. A medida que aumenta el número de parámetros, encontrar los parámetros óptimos para la suma de dichas funciones tiene, en mi opinión, un interés puramente teórico. Para el comercio, un modelo matemático predictivo puede tener muchos parámetros, pero la función de pérdida en sí es muy simple, por lo que la búsqueda es mucho más fácil allí. Y desde luego no puede haber mil millones de parámetros, sino unos modestos 10-100, si no nos interesa el kurvafitting, claro, imho.
Si miramos desde el punto de vista del resultado. Me interesan los parámetros que encuentran el máximo de la función, ¿por qué necesito un resultado medio? Me interesa el óptimo y el tiempo para alcanzar este óptimo. Si este tiempo es aceptable, entonces no me importa cuánto esfuerzo gastó el ordenador para seleccionar el vector inicial de parámetros, lo principal es que obtuve el resultado.
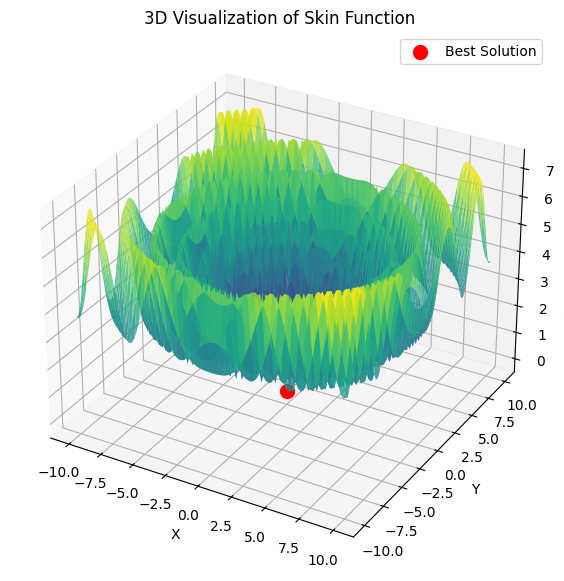
He aquí un ejemplo para la suma de 5 funciones Hilly
15 segundos de tiempo y el resultado es 0,76. No está mal, creo. Especialmente teniendo en cuenta el tema de comercio, cuando simplemente no sabemos lo que el óptimo global es igual y nunca lo sabrá.
De todos modos, gracias por el artículo. Hay mucho que pensar aquí. Voy a probar los otros algoritmos un poco más tarde y publicar los resultados.
1) Has tomado una función muy compleja en sí misma. A medida que aumenta el número de parámetros, la búsqueda de parámetros óptimos para la suma de tales funciones es de interés puramente teórico en mi opinión.
2) Para el comercio, un modelo matemático predictivo puede tener muchos parámetros, pero la función de pérdida en sí es muy simple, por lo que la búsqueda es mucho más fácil allí. Y desde luego no puede haber mil millones de parámetros, sino unos modestos 10-100, si no nos interesa el kurvafitting, claro, imho.
3) Si miramos desde el punto de vista del resultado. Me interesan los parámetros que encuentran el máximo de la función, ¿por qué necesito un resultado medio? Me interesa el óptimo y el tiempo para alcanzar este óptimo. Si este tiempo es aceptable, entonces no me importa cuánto esfuerzo ha empleado el ordenador para seleccionar el vector inicial de parámetros, lo principal es que he obtenido el resultado.
4) He aquí un ejemplo para la suma de 5 funciones Hilly
15 segundos de tiempo y el resultado es 0,76. No está mal, creo. Especialmente teniendo en cuenta el tema de comercio, cuando simplemente no sabemos lo que el óptimo global es igual y nunca lo sabrá.
5) De todos modos, gracias por el artículo. Hay mucho que pensar aquí. Voy a probar el resto de los algoritmos un poco más tarde y publicar los resultados.
1) En los artículos consideramos los OEAs no por sí mismos como un caballo en el vacío (ejemplo - PSO, muy famoso y por lo tanto popular, pero no potente, y el mismo OEA - no conocido por nadie en absoluto, pero pica el espacio liso y discreto tan rápido como vuelan los chips), sino que junto con el análisis de su lógica y dispositivo consideramos sus capacidades de búsqueda en comparación con los demás. Esto nos permite comprender en profundidad sus potencialidades en tareas prácticas. Y es con el crecimiento de la dimensionalidad cuando se pueden revelar las verdaderas posibilidades y es en la comparación de los algoritmos entre sí. En la vida real prácticamente no hay tareas sencillas, a menos, claro está, que hablemos de tareas que puedan resolverse analíticamente.
Antes he explicado por qué es necesario utilizar el valor medio de los resultados finales al comparar algoritmos, para excluir la influencia del "éxito aleatorio" y revelar directamente las capacidades de búsqueda de los algoritmos.
Y cuando se trata de la aplicación práctica de AO (no para comparar AOs), entonces sí, se recomienda utilizar varias ejecuciones de optimizaciones para elegir el mejor resultado. Pero, si un algoritmo débil tiene que reiniciarse repetidamente, desperdiciando preciosas ejecuciones de la función objetivo, entonces otro algoritmo conseguirá el mismo resultado en muchas menos ejecuciones de la función objetivo. ¿Por qué pagar más si el resultado puede ser el mismo? Los algoritmos débiles se atascarán, se empantanarán en el espacio de búsqueda, requerirán múltiples reinicios y nunca estarás seguro de que no estás atascado elementalmente al principio de la optimización. Supongo que a nadie le interesa una situación así en la práctica.
2) Intente visualizar la función de pérdida en un problema práctico con al menos dos parámetros con algún Asesor Experto, la superficie resultará no ser suave y no unimodal en absoluto. Debido a la naturaleza discreta de las tareas de negociación, los objetivos simples y suaves simplemente no existen. Por lo tanto, los métodos que tengan dificultades incluso en un paraboloide liso serán ineficaces en el trading.
3) El resultado medio se utiliza para comparar algos entre sí, no en la práctica (véase el punto 1). Si usted no se preocupa por el tiempo y la energía gastada en la búsqueda, a continuación, hacer una búsqueda completa, no tiene sentido utilizar AO en absoluto. Pero en la práctica esto ocurre muy raramente, siempre estamos limitados en tiempo y recursos computacionales.
4) Los resultados presentados carecen de información sobre el número de ejecuciones de la función objetivo necesarias para alcanzar el resultado especificado. Este indicador es la clave para evaluar la eficacia de la AO. La elección del AO debería basarse en maximizar la eficacia (minimizando el número de ejecuciones) y minimizar la probabilidad de quedarse atascado, especialmente en tareas prácticas de negociación.
5) Gracias, me alegro de que los artículos sirvan para razonar. Sería genial si pudieras proporcionar el código de las pruebas que has realizado, aunque todo el código ya está proporcionado en el artículo (aparentemente, utilizas algún método de prueba propio). Lo miraremos y lo resolveremos.
Estoy trabajando en otro artículo sobre las cuestiones planteadas en esta discusión.
Pruebe diferentes algoritmos, hemos considerado muchos, compárelos entre sí. Los métodos Alglib son muy rápidos y creo que son muy buenos para resolver problemas formulados analíticamente (este es un tema aparte), pero cuando no se conoce la fórmula analítica, hay otras opciones.
Para aquellos que necesiten resolver problemas formulados analíticamente - los artículos también serán muy útiles, ya que describen los principios mismos del trabajo con los métodos ALGLIB.
No es correcto comparar de este modo los solucionadores metaevr. y de gradiente. Deberían ponerse en igualdad de condiciones.
Metaevr. ya ha sembrado puntos, mientras que los solucionadores de gradiente empiezan desde un punto.
Para crear condiciones de igualdad, tenemos que hacer un lote para este último. O inicialización múltiple.
Por eso los de gradiente necesitan ser evaluados por el mejor resultado, no por el resultado medio. Y por eso se ejecutan más rápido. Así se consigue un equilibrio entre velocidad y precisión en el entrenamiento de redes neuronales.
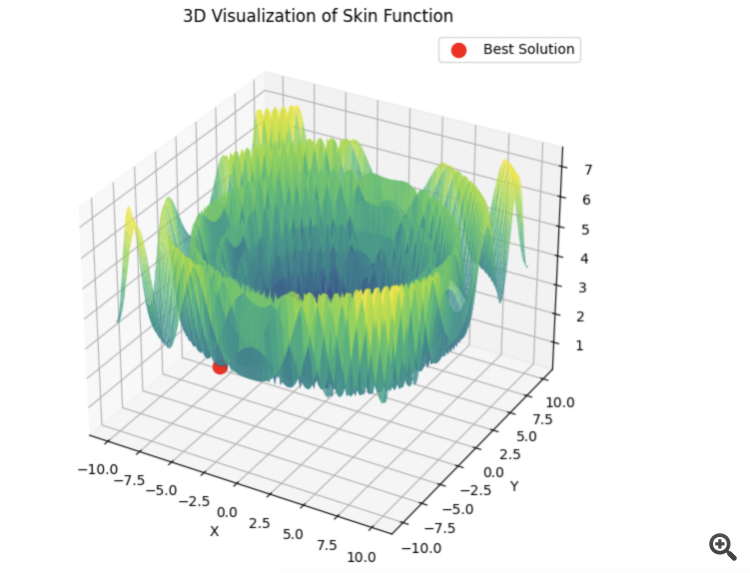
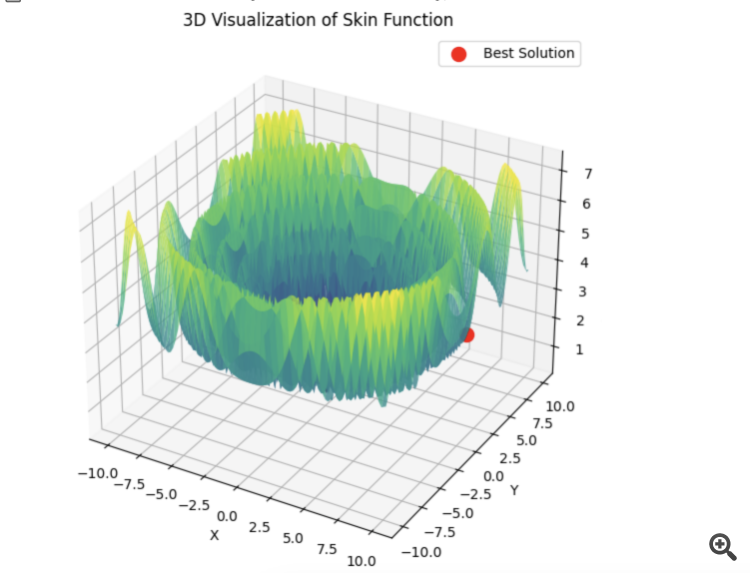
Si PSO elige el mínimo correcto de inmediato:
Entonces lbfgs saltará de localidad en localidad, y este es un comportamiento normal para él. Pero es rápido y puede saltar un número configurable de veces, dividiendo la función optimizada en lotes.
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso

Artículo publicado Métodos de optimización de la biblioteca ALGLIB (Parte II):
En la primera parte de nuestro estudio, dedicada a los algoritmos de optimización de la biblioteca ALGLIB en el paquete estándar del terminal MetaTrader 5, nos familiarizamos con los algoritmos: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno) y NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). No solo analizamos sus fundamentos teóricos, sino que también deconstruimos una forma sencilla de aplicarlos a problemas de optimización.
En este artículo seguiremos investigando los métodos restantes del arsenal ALGLIB. Prestaremos especial atención a su prueba con funciones multivariantes complejas, lo cual nos permitirá hacernos una visión holística de la eficacia de cada método. Concluiremos con un análisis exhaustivo de los resultados obtenidos y presentaremos recomendaciones prácticas para seleccionar el algoritmo óptimo para determinados tipos de problemas.
Autor: Andrey Dik