Redes neuronales en el trading: Representación adaptativa de grafos (NAFS)

Introducción

En los últimos años, el aprendizaje de representación de grafos se ha aplicado ampliamente en diversos escenarios, como la clusterización de nodos, la predicción de enlaces, la clasificación de nodos y la clasificación de grafos. El objetivo del aprendizaje de la representación de grafos consiste en codificar la información del grafo en la incorporación de nodos. Los métodos tradicionales de aprendizaje de representaciones de grafos se han centrado en preservar la información sobre la estructura del grafo. Sin embargo, estos métodos tienen dos grandes limitaciones:

1. Arquitectura superficial. Aunque las redes de grafos convolucionales (GCN) emplean múltiples capas superpuestas para captar información estructural profunda, el aumento del número de capas suele dar lugar a un suavizado excesivo y a incorporaciones indistinguibles.
2. Baja escalabilidad. Los métodos de aprendizaje de representación de grafos basados en GNN no pueden ampliarse a grafos de gran tamaño debido a su elevado coste computacional y al elevado uso de memoria.

Los problemas indicados fueron abordados por los autores del artículo "NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning", en el que se presenta un nuevo método para representar grafos simplemente suavizando las características de los nodos seguido de combinatoria adaptativa. El método (Node-Adaptive Feature Smoothing — NAFS) crea mejores incorporaciones de nodos que integran información tanto de la estructura del grafo como de las características de los nodos. Basándose en la observación de que distintos nodos tienen "índices de suavizado" muy diferentes, el NAFS suaviza de forma adaptativa cada característica de los nodos y utiliza la información de vecindad de bajo y alto orden de cada nodo. Además, el conjunto de características también se usa para combinar las características suavizadas extraídas mediante distintos operadores de suavizado. Como el NAFS no requiere entrenamiento, reduce significativamente los costes de formación y se adapta mejor a grandes grafos.

1. El algoritmo NAFS

Muchos investigadores han propuesto separar el suavizado y la transformación de características en cada capa de GCN para una clasificación de nodos escalable. En concreto, realizan operaciones de suavizado de características por adelantado y, a continuación, introducen las características procesadas en un MLP sencillo para generar las etiquetas de nodos predichas finales.

Estas GNN desacopladas constan de dos partes: el suavizado de características y el entrenamiento del MLP. El suavizado de características tiene como objetivo combinar la información estructural del grafo y las características de los nodos en las mejores características para el MLP posterior. Durante el entrenamiento, el MLP solo aprende características suavizadas.

Existe otra rama de las GNN que también separa el suavizado y la transformación de características. En ellas, las características brutas de los nodos se pasan primero a un MLP para crear incorporaciones intermedias. Luego se realizan operaciones de propagación personalizadas sobre las incorporaciones obtenidas para obtener los resultados finales de la predicción. Sin embargo, esta rama de las GNN todavía tiene que realizar recursivamente operaciones de propagación en cada época de entrenamiento, lo cual hace imposible su ejecución en grafos a gran escala.

La forma más sencilla de obtener información estructural detallada de un grafo consiste simplemente en apilar varias capas de GNN. No obstante, un gran número de operaciones de suavizado de características en el modelo GNN dará lugar a incorporaciones de nodos indistinguibles, es decir, a un problema de sobresuavizado.

El análisis cuantitativo muestra empíricamente que el grado de cada nodo desempeña un papel sustancial en el paso óptimo de suavizado. De forma intuitiva, los nodos de alto grado deberían tener pasos de suavizado relativamente más pequeños que los nodos de bajo grado.

Aunque el uso de operaciones de suavizado de características dentro de las GNN no conectadas es escalable a la hora de entrenar la representación de grafos grandes, esto provocará una representación subóptima de los nodos, y es que no resulta óptimo realizar el suavizado de características para todos los nodos indiscriminadamente: los nodos con diferentes propiedades estructurales tienen diferentes índices de suavizado. Por ello, deberemos utilizar un suavizado de características adaptado al nodo que cumplirá las diversas necesidades de nivel de suavizado de cada nodo.

Al aplicar sistemáticamente 𝐗l=Â𝐗l−1, la matriz de incorporaciones 𝐗l−1 de los nodos suavizados acumula información estructural más profunda sobre el grafo a medida que l aumenta. A continuación, las matrices de incorporación de nodos multiescala {𝐗0, 𝐗1, …, 𝐗K} (donde K es el paso de suavizado máximo) se combinan en una única matriz Ẋ que combina información local y global sobre los nodos vecinos.

El análisis realizado por los autores del método NAFS demuestra que la velocidad a la que cada nodo alcanza el estado estacionario resulta muy variable. Y esto significa que será necesario un enfoque personalizado para considerar los nodos. Para ello, los autores del NAFS introducen el concepto de "peso de suavizado", basado en la distancia entre los vectores de características locales y suavizados de cada nodo. Esto nos permite adaptar el proceso de suavizado a cada nodo por separado.

Una alternativa más eficaz sería sustituir la matriz de suavizado  por la similitud coseno. Una mayor similitud coseno entre los vectores de características locales y suavizadas significa que el nodo vi estará más lejos del estado estacionario y [Âk𝐗]i contendrá intuitivamente más información relevante sobre el nodo. Por consiguiente, para el nodo vi, la característica suavizada con mayor similitud coseno debería contribuir más a la incorporación final del nodo.

Los distintos operadores de suavizado actúan en realidad como diferentes extractores de conocimiento. Esto permite captar su estructura de grafos de conocimiento a distintas escalas y dimensiones. Para lograr el mismo efecto, la operación de conjunto de características cuenta con múltiples extractores de conocimiento. Dichos extractores de conocimiento se utilizan como parte de la operación de suavizado de características para crear diferentes características suavizadas.

El NAFS genera incorporaciones de nodos sin entrenamiento, lo cual lo hace muy eficiente y escalable. Además, la estrategia de suavizado adaptativo de las características de los nodos permite captar información estructural profunda.

A continuación le presentamos la visualización del método NAFS por parte del autor.

2. Implementación con MQL5

Tras considerar los aspectos teóricos del framework NAFS, pasaremos a la aplicación práctica de los planteamientos propuestos usando MQL5. Y antes de empezar a aplicar el framework, aclararemos sus principales pasos.

1. Formación de una matriz de representaciones multiescala de nodos.
2. Determinación de los pesos de suavizado considerando la similitud coseno entre el vector de características del nodo y las representaciones suavizadas.
3. Cálculo de las medias ponderadas de incorporación total.

Aquí vale la pena señalar que podemos cubrir algunas de las operaciones anteriores con la funcionalidad existente de nuestra biblioteca. Por ejemplo, las operaciones de determinación de la similitud coseno y de cálculo de las medias ponderadas pueden realizarse fácilmente mediante la operación de multiplicación de dos matrices. La capa SoftMax nos ayudará a calcular los coeficientes de suavizado.

La cuestión de la formación de una matriz de representaciones multiescala de nodos sigue abierta.

2.1 Matriz de representación multiescala de nodos

Para formar una matriz de representaciones multiescala de nodos, utilizaremos una media simple de los valores de las características individuales de un nodo con los parámetros similares de sus vecinos más próximos. En este caso, lograremos una gran escalabilidad utilizando una ventana de promediado de diferentes tamaños.

Permítame recordarle que situaremos el proceso de cálculo principal en un contexto OpenCL. Como consecuencia, también situaremos el proceso de entrenamiento de matrices en la esfera de los cálculos paralelos. Para ello, crearemos un nuevo kernel en el programa OpenCL FeatureSmoothing.

__kernel void FeatureSmoothing(__global const float *feature,
                               __global float *outputs,
                               const int smoothing
                              )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_global_size(1);

En los parámetros de este kernel, obtendremos los punteros a dos búferes de datos (datos de origen y resultados) y una constante del número de escalas de suavizado. En este caso no definiremos el paso de escala de suavizado ya que lo tomaremos como igual a "1". En este caso, la ventana de promediado se ampliará en 2 elementos. Al fin y al cabo, la aumentaremos por igual antes y después del elemento analizado.

También cabe señalar que el número de escalas de suavizado no podrá ser un número negativo. Y cuando el valor sea cero, simplemente transferiremos los datos de origen.

Planeamos ejecutar este kernel en un espacio de tareas bidimensional de flujos completamente independientes sin crear grupos de trabajo locales. La primera dimensión se corresponderá con el tamaño de la secuencia original a analizar, mientras que la segunda indicará el número de características del vector de descripción de un elemento de la secuencia.

En el cuerpo del kernel, identificaremos directamente el flujo actual a lo largo de todas las dimensiones del espacio de tareas y definiremos sus dimensionalidades.

A partir de los datos obtenidos, determinaremos el desplazamiento de los búferes de datos.

   const int shift_input = pos * dimension + d;
   const int shift_output = dimension * pos * smoothing + d;

Con esto completaremos la fase preparatoria y pasaremos directamente a la formación de representaciones de diferentes escalas. Y lo primero que haremos es trasladar los datos de origen, que es una representación de promediado cero.

   float value = feature[shift_input];
   if(isinf(value) || isnan(value))
      value = 0;
   outputs[shift_output] = value;

A continuación, organizaremos el ciclo de formación de valores medios de características individuales dentro de la ventana de promediado. Como comprenderá, aquí deberemos recoger la suma de todos los valores dentro de la ventana promedio y luego dividir la suma obtenida por el número de elementos sumados.

Observe que las ventanas de promediado de todas las escalas se forman en torno a un único elemento analizado. Por consiguiente, cada escala sucesiva usará todos los elementos de la escala anterior. Aprovecharemos esta propiedad y, para minimizar los accesos a la costosa memoria global, en cada iteración solo añadiremos nuevos valores a la suma acumulada previamente y luego dividiremos la suma acumulada actual por el número de elementos de la ventana de promediado que se analiza.

   for(int s = 1; s <= smoothing; s++)
     {
      if((pos - s) >= 0)
        {
         float temp = feature[shift_input - s * dimension];
         if(isnan(temp) || isinf(temp))
            temp = 0;
         value += temp;
        }
      if((pos + s) < total)
        {
         float temp = feature[shift_input + s * dimension];
         if(isnan(temp) || isinf(temp))
            temp = 0;
         value += temp;
        }
      float factor = 1.0f / (min((int)total, (int)(pos + s)) - max((int)(pos - s), 0) + 1);
      if(isinf(value) || isnan(value))
         value = 0;
      float out = value * factor;
      if(isinf(out) || isnan(out))
         out = 0;
      outputs[shift_output + s * dimension] = out;
     }
  }

También conviene señalar que, por extraño que parezca, no todas las ventanas de promediado de la misma escala tienen el mismo tamaño. Al fin y al cabo, existen elementos extremos de una secuencia cuando la ventana de promediación se sale de la secuencia por un lado u otro. Por consiguiente, en cada iteración, determinaremos el número real de elementos de promediado.

Del mismo modo, construiremos un algoritmo para distribuir el gradiente de error a través de las operaciones anteriores en el kernel FeatureSmoothingGradient, con el que le sugiero que se familiarice. En el archivo adjunto encontrará el código completo del programa OpenCL.

2.2 Construyendo la clase NAFS

Tras realizar las adiciones necesarias en el programa OpenCL, procederemos a trabajar en el lado del programa principal, donde crearemos una nueva clase de formación de incorporación adaptativa de nodos CNeuronNAFS. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronNAFS :  public CNeuronBaseOCL
  {
protected:
   uint                 iDimension;
   uint                 iSmoothing;
   uint                 iUnits;
   //---
   CNeuronBaseOCL       cFeatureSmoothing;
   CNeuronTransposeOCL  cTranspose;
   CNeuronBaseOCL       cDistance;
   CNeuronSoftMaxOCL    cAdaptation;
   //---
   virtual bool      FeatureSmoothing(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing);
   virtual bool      FeatureSmoothingGradient(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

public:
                     CNeuronNAFS(void) {};
                    ~CNeuronNAFS(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronNAFS; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Como puede ver, declararemos 3 variables y 4 capas internas en la nueva estructura de la clase. Nos familiarizaremos con su funcionalidad durante la implementación de los algoritmos de los métodos virtuales redefinidos.

También cabe destacar la presencia de 2 métodos de envoltorio de los kernels homónimos del programa OpenCL descrito anteriormente. Se basan en el algoritmo básico de llamada al kernel. Así que le sugiero que se familiarice con ellos.

Todos los objetos internos de la nueva clase se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de todos los objetos declarados y heredados se realizará en el método Init.

bool CNeuronNAFS::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint dimension, uint smoothing, uint units_count,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * units_count,
                            optimization_type, batch))
      return false;

En los parámetros del método obtendremos las constantes principales que nos permitirán definir de forma inequívoca la arquitectura del objeto creado. En este caso tendremos:

• dimension — tamaño del vector de descripción de un elemento de la secuencia;
• smoothing — número de escalas de promediado (en el valor cero se copiarán los datos de origen);
• units_count — tamaño de la secuencia analizada.

Tenga en cuenta que todos los parámetros tienen el tipo de valores enteros sin signo. Este enfoque excluye la posibilidad de obtener valores negativos en los parámetros. 

Como es habitual, en el cuerpo del método llamaremos primero al método homónimo de la clase padre, en el que, como sabrá, ya está organizado el proceso de control de los parámetros obtenidos y de inicialización de los objetos heredados. Se supone que el tamaño del tensor de resultados será igual al tensor de valores iniciales y se definirá como el producto del número de elementos de la secuencia analizada por el tamaño del vector de descripción de un elemento.

Una vez ejecutadas con éxito las operaciones de los métodos de la clase padre, almacenaremos los parámetros recibidos del programa externo en variables internas con los nombres correspondientes.

   iDimension = dimension;
   iSmoothing = smoothing;
   iUnits = units_count;

Y luego inicializaremos los objetos recién declarados. Y primero declararemos una capa interna para registrar la matriz de representación multiescala de nodos. Su tamaño deberá ser suficiente para registrar la matriz completa. Por consiguiente, será (iSmoothing + 1) veces el tamaño de los datos de origen.

   if(!cFeatureSmoothing.Init(0, 0, OpenCL, (iSmoothing + 1) * iUnits * iDimension, optimization, iBatch))
      return false;
   cFeatureSmoothing.SetActivationFunction(None);

Tras determinar las representaciones multiescala de nodos (en nuestro caso, formaremos representaciones de patrones de velas de diferentes escalas), tendremos que determinar la similitud de coseno entre las representaciones obtenidas y el vector de características de la barra analizada. Para ello, multiplicaremos el tensor de los datos de origen por el tensor de la representación multiescala de nodos. Sin embargo, para realizar esta operación, primero tendremos que realizar una transposición del tensor de la representación multiescala.

   if(!cTranspose.Init(0, 1, OpenCL, (iSmoothing + 1)*iUnits, iDimension, optimization, iBatch))
      return false;
   cTranspose.SetActivationFunction(None);

La operación de multiplicación de matrices ya está implementada dentro de nuestra clase base de capas neuronales y heredada de la clase padre. Y para registrar los resultados de la operación, inicializaremos el objeto interno cDistance.

   if(!cDistance.Init(0, 2, OpenCL, (iSmoothing + 1)*iUnits, optimization, iBatch))
      return false;
   cDistance.SetActivationFunction(None);

Aquí me gustaría recordarle que como resultado de la multiplicación de vectores unidireccionales obtendremos valores positivos, y como resultado de la multiplicación de vectores multidireccionales, obtendremos valores negativos. Obviamente, si la barra analizada tiene la dirección de la tendencia general, el resultado de la operación de multiplicación del vector de representación de barras y valores promediados será positivo. En caso contrario, obtendremos un valor negativo. En caso de movimiento plano (flat), el vector de valores promediados será próximo a "0". Como consecuencia, el resultado del producto también tenderá a cero. Usaremos la función SoftMax para normalizar los valores obtenidos y determinar los coeficientes de influencia adaptativa de las distintas escalas.

   if(!cAdaptation.Init(0, 3, OpenCL, cDistance.Neurons(), optimization, iBatch))
      return false;
   cAdaptation.SetActivationFunction(None);
   cAdaptation.SetHeads(iUnits);

Ahora, para determinar la incorporación final del nodo analizado (barra), solo tenemos que multiplicar el vector de coeficientes adaptativos de cada nodo por la matriz de representación multiescala correspondiente. Escribiremos el resultado de esta operación en el búfer de la interfaz de intercambio de datos de la capa subsiguiente heredada de la clase padre. Por consiguiente, no crearemos un objeto interno adicional. Solo desactivaremos de manera forzosa la función de activación y finalizaremos el método de inicialización transmitiendo el resultado lógico de las operaciones al programa que realiza la llamada.

   SetActivationFunction(None);
//---
   return true;
  }

Una vez inicializado el nuevo objeto, construiremos el método feedForward. En los parámetros del método, obtendremos un puntero a los datos de origen, como es habitual.

bool CNeuronNAFS::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject()))
      return false;

A partir de los datos obtenidos, primero generaremos un tensor de representaciones multiescala llamando al método de envoltorio del kernel FeatureSmoothing presentado anteriormente.

   if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject()))
      return false;

Como hemos mencionado al describir el algoritmo del método de inicialización, transpondremos la matriz de representación de nodos multiescala resultante.

   if(!cTranspose.FeedForward(cFeatureSmoothing.AsObject()))
      return false;

A continuación, la multiplicaremos por el tensor de datos de origen para obtener los coeficientes de similitud de coseno.

   if(!MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), 1, iDimension,
                                                                           iSmoothing + 1, iUnits))
      return false;

Y normalizaremos el valor obtenido utilizando la función SoftMax.

   if(!cAdaptation.FeedForward(cDistance.AsObject()))
      return false;

Ahora solo tendremos que multiplicar el tensor de coeficientes adaptativo obtenido por la matriz de representación multiescala formada anteriormente.

   if(!MatMul(cAdaptation.getOutput(), cFeatureSmoothing.getOutput(), Output, 1, iSmoothing + 1, 
                                                                             iDimension, iUnits))
      return false;
//---
   return true;
  }

Como resultado de esta operación, obtendremos las incorporaciones finales de los nodos, que almacenaremos en el búfer de la interfaz de interacción de capas neuronales dentro del modelo. Después finalizaremos el método transmitiendo el resultado lógico de las operaciones al programa que realiza la llamada.

La siguiente etapa de nuestro trabajo consistirá en organizar los algoritmos de pasada inversa de nuestra nueva clase de framework NAFS. Y aquí hay dos peculiaridades. En primer lugar, nuestro nuevo objeto no contiene parámetros entrenables, como se menciona en la parte teórica de este artículo. Por consiguiente, redefiniremos el método de actualización de parámetros updateInputWeights con un stub con un resultado positivo constante.

   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

Pero el método de distribución de gradientes de error calcInputGradients merece especial atención. A pesar de la simplicidad del método de pasada directa, existe un doble uso tanto de los datos de origen como de la matriz de representación multiescala. Por consiguiente, tendremos que pasar cuidadosamente el gradiente de error a través de todas las rutas de información del algoritmo que se está construyendo con el fin de pasar el gradiente de error a la capa de datos de origen.

bool CNeuronNAFS::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En los parámetros del método obtendremos el puntero al objeto de la capa anterior al que tenemos que pasar el gradiente de error según la influencia de los datos de origen en el resultado del modelo. En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido, porque de lo contrario todas las operaciones posteriores carecerán de sentido.

Primero tendremos que distribuir el gradiente de error obtenido de la capa posterior entre los coeficientes adaptativos y la matriz de representación multiescala. Sin embargo, después planeamos transferir el gradiente de error a la matriz de representación multiescala y a lo largo del flujo de información de los coeficientes adaptativos. Por consiguiente, en esta etapa, almacenaremos el gradiente de error del tensor de representación multiescala en un búfer temporal.

   if(!MatMulGrad(cAdaptation.getOutput(), cAdaptation.getGradient(),
                  cFeatureSmoothing.getOutput(), cFeatureSmoothing.getPrevOutput(),
                  Gradient, 1, iSmoothing + 1, iDimension, iUnits))
      return false;

A continuación, trabajaremos con el flujo de información de los coeficientes adaptativos. Aquí, primero transferiremos el gradiente de error al nivel del tensor de similitud de coseno llamando al método de distribución del gradiente del objeto correspondiente.

   if(!cDistance.calcHiddenGradients(cAdaptation.AsObject()))
      return false;

En el siguiente paso, distribuiremos el gradiente de error entre los datos de origen y el tensor transpuesto de representaciones multiescala. Aquí asumiremos también la adquisición posterior del gradiente de error al nivel de los datos de origen en el segundo flujo de información. Por consiguiente, en esta fase almacenaremos el gradiente de error correspondiente en el búfer temporal.

   if(!MatMulGrad(NeuronOCL.getOutput(), PrevOutput,
                  cTranspose.getOutput(), cTranspose.getGradient(),
                  cDistance.getGradient(), 1, iDimension, iSmoothing + 1, iUnits))
      return false;

A continuación, transpondremos el gradiente de error de la matriz de representación multiescala y lo sumaremos con los datos almacenados anteriormente.

   if(!cFeatureSmoothing.calcHiddenGradients(cTranspose.AsObject()) ||
      !SumAndNormilize(cFeatureSmoothing.getGradient(), cFeatureSmoothing.getPrevOutput(),
                       cFeatureSmoothing.getGradient(), iDimension, false, 0, 0, 0, 1)
     )
      return false;

Y ahora solo nos quedará pasar el gradiente de error a la capa de datos de origen. Primero transferiremos el gradiente de error desde la matriz de representación multiescala.

   if(!FeatureSmoothingGradient(NeuronOCL, cFeatureSmoothing.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cFeatureSmoothing.getPrevOutput(),
                       NeuronOCL.getGradient(), iDimension, false, 0, 0, 0, 1) ||
      !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                    (ENUM_ACTIVATION)NeuronOCL.Activation())
     )
      return false;
//---
   return true;
  }

Luego añadiremos los datos guardados anteriormente y realizaremos una corrección del gradiente de error por la derivada de la función de activación de la capa de datos de origen. Y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

Aquí concluiremos el análisis de los principios de construcción de los métodos de la clase CNeuronNAFS. Podrá ver el código de esta clase y todos sus métodos en el archivo adjunto.

2.3 Arquitectura del modelo

Ahora debemos decir unas palabras sobre la arquitectura de los modelos entrenados. Ya hemos implementado la nueva función de suavizado adaptativo en el modelo de Codificador de estados del entorno. El modelo en sí lo hemos tomado prestado del artículo anterior sobre el framework AMCT. Así, nuestro nuevo modelo aprovechará los enfoques de ambos frameworks. La arquitectura del modelo se representará en el método CreateEncoderDescriptions.

Nos mantendremos fieles a los planteamientos generales de construcción de modelos y crearemos primero una capa completamente conectada para pasar los datos de entrada al modelo.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí vale la pena decir que el algoritmo NAFS nos permite aplicar el suavizado adaptativo directamente a los datos de origen. Sin embargo, recordemos que nuestro modelo recibe los datos brutos ofrecidos por el terminal. Por consiguiente, las características analizadas pueden tener distribuciones de valores diferentes. Siempre hemos utilizado una capa de normalización para minimizar el impacto negativo de este factor. Y en este caso, estamos adoptando el mismo enfoque.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y después, aplicaremos una capa de suavizado adaptativo de características. Este es el orden recomendado para nuestros experimentos, ya que las diferencias significativas en las distribuciones de las características individuales pueden provocar la dominancia de la característica con la mayor amplitud de valores en la generación de coeficientes de atención adaptativa respecto a las escalas de suavizado.

La mayoría de los parámetros del nuevo objeto entrarán en la representación ya conocida de la descripción de la capa neuronal.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronNAFS;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;

En este caso, utilizaremos 5 escalas de promediado, lo cual se corresponde con la formación de ventanas {1, 3, 5, 7, 9, 11}.

   descr.window_out = 5;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

La arquitectura del codificador adicional permanecerá inalterada y contendrá una capa AMCT.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAMCT;
   descr.window = BarDescr;                           // Window (Indicators to bar)
     {
      int temp[] = {HistoryBars, 50};                // Bars, Properties
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = EmbeddingSize / 2;              // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Seguida de una capa totalmente conectada de dimensionalidad decreciente.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

La arquitectura de los modelos del Actor y el Crítico permanecerá inalterada. En su lugar, hemos trasladado los programas de interacción medioambiental y formación de modelos de artículos anteriores. Su código completo se halla en el archivo adjunto. Allí se presentará el código completo de todos los programas y clases utilizados en la elaboración del artículo.

3. Simulación

Más arriba hemos realizado un trabajo serio sobre la implementación de los enfoques propuestos por los autores del framework NAFS usando MQL5. Y ahora es el momento de probar su eficacia para resolver nuestros problemas. Para ello, entrenaremos los modelos usando los enfoques propuestos con datos reales del instrumento EURUSD para todo el año 2023. Durante el entrenamiento usaremos los datos históricos del marco temporal H1.

Al igual que antes, emplearemos el entrenamiento offline del modelo con una actualización periódica de la muestra de entrenamiento para mantenerla al día en el dominio de valores de la política actual del Actor.

Ya hemos mencionado antes que el nuevo modelo de Codificador del estado del entorno se ha construido sobre la base del Transformador contrastivo de patrones. Para comparar los resultados con claridad, probaremos el nuevo modelo conservando íntegramente los parámetros de prueba del modelo básico. Los resultados de las pruebas de los 3 primeros meses de 2024 se muestran a continuación.

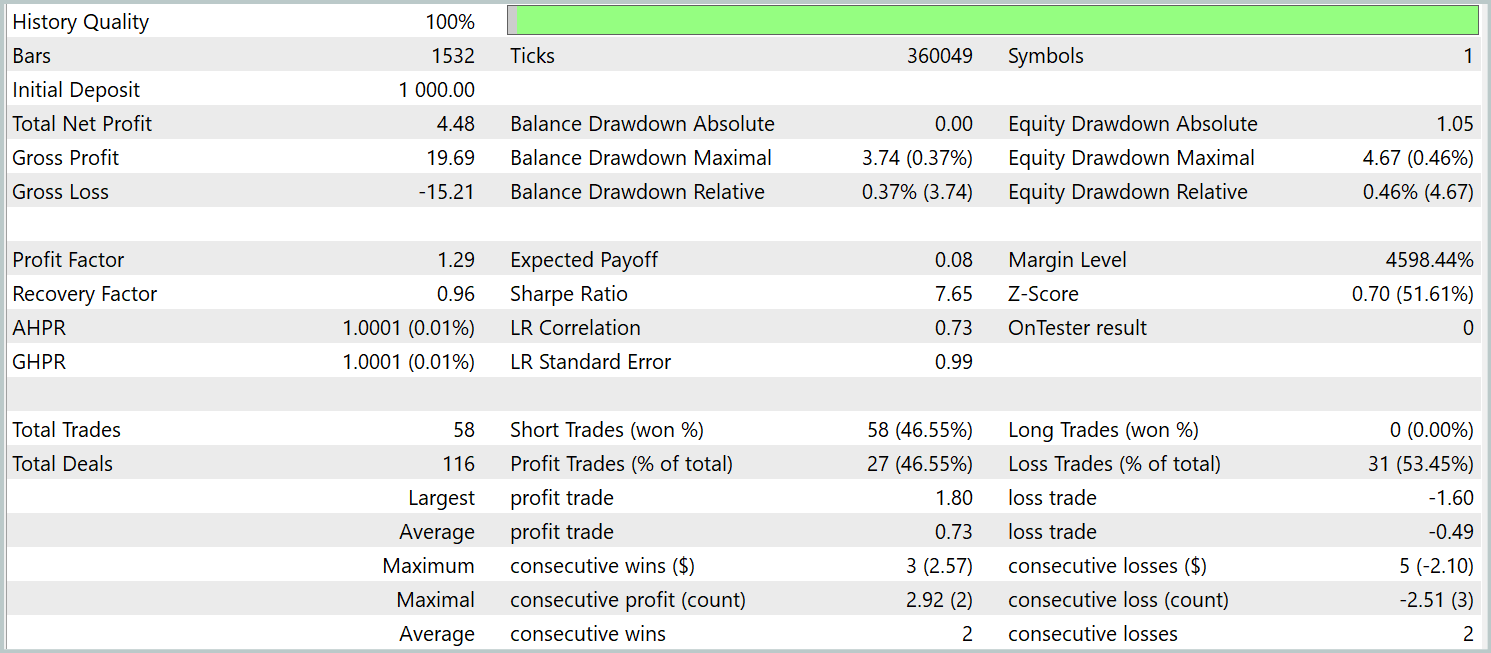
Digamos de entrada que la comparación de los resultados de las pruebas del modelo actual y del modelo básico evoca sentimientos ambiguos. Por un lado, vemos una disminución del factor de beneficio de 1,4 a 1,29. Por otro lado, gracias al aumento del número de transacciones comerciales en 2,5 veces, tenemos un aumento proporcional del beneficio total durante el mismo periodo de prueba.

Además, en contraste con el modelo básico, observamos una tendencia ascendente continuada en el balance durante todo el periodo de prueba. Sin embargo, solo se ejecutan posiciones cortas. Esto puede deberse a un mayor énfasis en las tendencias globales de los valores suavizados. Algunas tendencias locales también se ignoran durante el filtrado del ruido.

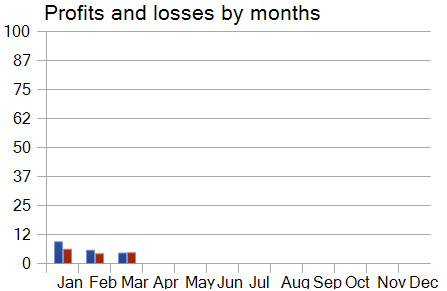
Sin embargo, cuando observamos el gráfico del rendimiento del modelo por meses, vemos un descenso gradual. Esta observación no hace sino confirmar nuestra suposición, formulada en el artículo anterior, de que la representatividad de la muestra de entrenamiento disminuye conforme aumenta el periodo de prueba.

Conclusión

En este artículo, nos hemos familiarizado con el método NAFS (Node-Adaptive Feature Smoothing), que supone un enfoque no paramétrico simple y eficiente para construir representaciones de nodos en grafos sin necesidad de entrenar parámetros. Este combina características suavizadas de los nodos vecinos, al tiempo que el uso de conjuntos de diferentes estrategias de suavizado mejora las representaciones finales, haciéndolas robustas e informativas.

En el artículo práctico, hemos implementado nuestra visión de los enfoques propuestos mediante MQL5. También hemos entrenado los modelos construidos con datos históricos reales. Y los hemos probado fuera de la muestra de entrenamiento. A partir de los resultados de nuestros experimentos, podemos concluir que los enfoques propuestos poseen cierto potencial. Podemos combinar los planteamientos propuestos con otros frameworks. Al mismo tiempo, la aplicación de los planteamientos propuestos permite mejorar la eficacia de los modelos básicos.

Enlaces

• NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL