Redes neuronales: así de sencillo (Parte 34): Función cuantílica totalmente parametrizada

MetaTrader 5 — Asesores Expertos | 15 marzo 2023, 13:39

491

Dmitriy Gizlyk

Contenido

1.1. Redes cuantílicas implícitas (Implicit Quantile Networks - IQN)
1.2. Función cuantílica totalmente parametrizada (Fully Parameterized Quantile Function - FQF)

2. Aplicación usando MQL5

Introducción

Seguimos analizando los algoritmos de aprendizaje Q distribuidos. En artículos anteriores, ya hemos examinado 2 algoritmos. En el primero [4], nuestro modelo enseñaba las probabilidades de obtener una recompensa dentro de un determinado rango de valores. En el segundo [5], modificamos el planteamiento para resolver el problema, y entrenamos el modelo para predecir el nivel de recompensa con una probabilidad dada.

Obviamente, en ambos algoritmos necesitaremos algún conocimiento a priori sobre la naturaleza de la distribución de recompensas para resolver el problema, y mientras que en el primer algoritmo deberemos transmitir los niveles de recompensa esperados al modelo, en el segundo se facilitará un poco la tarea del usuario. Eso sí, necesitaremos especificar un número de cuantiles cuyo tamaño esté normalizado entre 0 y 1, y que estén clasificados de forma ascendente. No obstante, sin conocer la verdadera distribución de los valores de recompensa, resultará difícil determinar el número de cuantiles necesarios y el volumen de cada uno.

Aquí hay que decir que hemos introducido el supuesto de una distribución uniforme de la secuencia estudiada, y también hemos tomado intervalos iguales de cuantiles. En este caso, además, el principal hiperparámetro regulador es el número de estos cuantiles, que se determina de forma experimental con una muestra de validación.

1. Aspectos teóricos de la parametrización completa

Los dos métodos mencionados requieren tanto el aprendizaje previo de la muestra de entrenamiento como la optimización de los hiperparámetros. No obstante, cabe señalar que, a la hora de optimizar los hiperparámetros, elegiremos algunos valores medios. En otras palabras, elegiremos algo que nos acerque lo más posible al objetivo deseado: los parámetros seleccionados, además, deberán cumplir al máximo todos los estados posibles del sistema estudiado. Recordemos también que hemos supuesto una distribución uniforme, y que obtendremos un modelo rebosante de todo tipo de compromisos. Resulta sencillo ver que un modelo así distará mucho de ser óptimo.

Para maximizar la verosimilitud y minimizar el error de predicción, nos veremos obligados a aumentar el número de cuantiles a entrenar. Esto conllevará un aumento del tamaño del modelo y del tiempo de aprendizaje del mismo. En la mayoría de los casos, este enfoque resultará ineficaz, pero nuestro objetivo consiste en explorar el entorno todo lo posible, así que surge el deseo de alejarse de alguna forma de las categorías fijas de valores en el primer algoritmo y de los cuantiles fijos en el segundo algoritmo.

1.1. Redes cuantílicas implícitas (Implicit Quantile Networks - IQN)

También en este caso, el uso de cuantiles parece más progresivo. Al fin y al cabo, estará de acuerdo con que, para definir categorías, necesitaremos explorar a fondo la distribución original definiendo sus límites, y el modelo no está preparado para valores que se salgan del rango especificado. El modelo de categorías no es universal y cambia de una tarea a otra.

Al mismo tiempo, las probabilidades de que sucedan los eventos tienen límites claros que van de 0 a 1. Sin embargo, el uso de una distribución uniforme de cuantiles limitará nuestras libertades y la gama de funciones que se pueden optimizar, y nos gustaría encontrar un algoritmo en el que el propio modelo determine la distribución cuantílica óptima sin aumentar el número de cuantiles.

El primer algoritmo de este tipo se propuso en julio de 2018 en el artículo "Implicit Quantile Networks for Distributional Reinforcement Learning". Hay que decir que los autores adoptaron un enfoque ligeramente distinto respecto al problema de los cuantiles óptimos: basaron su algoritmo en el QR-DQN del que hablamos antes. Pero en lugar de buscar los cuantiles óptimos, los autores decidieron generarlos aleatoriamente e introducirlos en la entrada del modelo junto con los datos iniciales que describen el estado del entorno. La idea es que, durante el aprendizaje, se introduzcan en la entrada del modelo los mismos estados del sistema con diferentes distribuciones cuantílicas. Como resultado, el modelo se verá forzado a utilizar no un corte concreto de la función cuantílica, sino una aproximación completa de la misma.

Este enfoque permite entrenar un modelo menos sensible al hiperparámetro del número de cuantiles, y su distribución aleatoria permitirá ampliar la gama de funciones aproximadas a las funciones distribuidas de forma no uniforme.

Antes de suministrarla a la entrada del modelo, crearemos una integración de cuantiles generados aleatoriamente usando la fórmula siguiente.

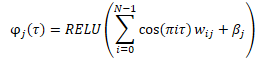
Durante la combinación de la integración resultante con el tensor de datos original, es posible que se produzcan variaciones. Puede ser una simple concatenación de 2 tensores o una multiplicación adamar (por elementos) de 2 matrices.

A continuación, le ofrecemos una comparación de las arquitecturas analizadas tal como las presentan los autores del artículo.

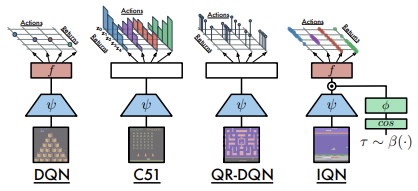
La eficacia del modelo queda confirmada por las pruebas efectuadas con 57 juegos de Atari. A continuación, podrá ver una tabla comparativa del artículo original [8]

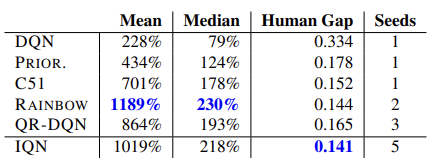
Hipotéticamente, dado el tamaño ilimitado del modelo, este enfoque permitirá aprender cualquier distribución de la recompensa prevista.

1.2. Función cuantílica totalmente parametrizada (Fully Parameterized Quantile Function - FQF)

El modelo presentado de redes cuantílicas implícitas es capaz de aproximar diversas funciones, pero este proceso está vinculado al crecimiento del propio modelo. En la práctica, sin embargo, disponemos de recursos limitados, y al generar cuantiles aleatorios, siempre existe el riesgo de producir valores subóptimos, tanto en el entrenamiento como en la explotación industrial.

Y en noviembre de 2019, se propuso un modelo de función cuantílica totalmente parametrizado "Fully Parameterized Quantile Function for Distributional Reinforcement Learning".

Básicamente, es el mismo modelo IQN, solo que en lugar de un generador de cuantiles aleatorio, se utiliza una capa neuronal totalmente conectada que retorna una distribución de cuantiles basada en el estado actual del entorno suministrado a la entrada. El modelo genera una distribución cuantílica para cada par de valores «estado-acción», lo cual nos permite aproximar la distribución óptima de la recompensa esperada para cada acción en un estado concreto del sistema. Precisamente de esto hablamos al principio de este artículo.

Obviamente, en este caso, se mantienen los requisitos básicos para los cuantiles: aumentar en el rango entre 0 y 1. Este efecto se logrará normalizando los datos a la salida de la capa neuronal usando la función SoftMax, seguida de la suma acumulativa de elementos del vector normalizado.

En el artículo original, los autores citan los resultados de la prueba del nuevo algoritmo en 55 juegos de Atari. A continuación, podemos ver una table resumen con los resultados del artículo original. Los datos presentados demuestran la superioridad del algoritmo de parametrización de la función cuantílica completa sobre otros algoritmos de aprendizaje Q distribuido. Por supuesto, esto se logró sacrificando el rendimiento del modelo. Un modelo adicional de generación de cuantiles requerirá recursos informáticos adicionales.

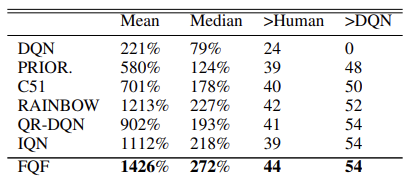
Además, los autores del método han experimentaron con el número óptimo de cuantiles y propusieron utilizar una distribución de 32 cuantiles.

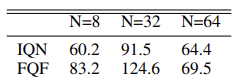
Sugerimos al lector que aprenda el algoritmo del método directamente mientras lo implementa.

2. Implementación usando MQL5

En su artículo, los autores del método de parametrización completa de la función cuantílica hablan del uso de 2 redes neuronales: una para generar la distribución cuantílica, y otra para la aproximación de la función cuantílica. En la práctica, el algoritmo descrito anteriormente también utiliza una tercera red convolucional que crea una integración del estado del entorno. Esta integración del estado supone la información de origen del algoritmo en cuestión.

No obstante, la biblioteca que hemos construido antes se centra en la construcción de modelos coherentes, y nosotros no hemos creado un algoritmo para transferir el gradiente de error entre modelos, cosa que podría resultar necesaria al entrenar varios modelos consecutivos.

Obviamente, podemos utilizar el mecanismo de Transfer Learning y entrenar cada modelo individual de forma coherente, pero hemos decidido implementar todo el algoritmo en un único modelo.

Los modelos de convolución con los que ya estamos familiarizados se usan para crear una integración del estado del entorno [1]. Por consiguiente, podemos construir fácilmente un modelo de este tipo con las herramientas existentes.

A continuación, deberemos aplicar el algoritmo FQF. En mi opinión, la forma más fácil de implementarlo dentro de nuestro concepto de biblioteca sería crear una nueva clase de capa neuronal. El agente recibirá la integración del estado actual del sistema analizado y suministrará a la salida la acción del agente. Así, podremos construir un agente de nuestro modelo dentro de la nueva clase.

Vamos a crear la nueva clase CNeuronFQF como descendiente de la clase básica de la capa neuronal CNeuronBaseOCL. La nueva clase redefinirá el conjunto de métodos ya estándar, y, en el bloque protegido, declarará los objetos internos que utilizaremos al implementar el algoritmo FQF. La finalidad de los objetos la iremos conociendo a medida que construyamos el algoritmo.

class CNeuronFQF : protected CNeuronBaseOCL
  {
protected:
   //--- Fractal Net
   CNeuronBaseOCL    cFraction;
   CNeuronSoftMaxOCL cSoftMax;
   //--- Cosine embeding
   CNeuronBaseOCL    cCosine;
   CNeuronBaseOCL    cCosineEmbeding;
   //--- Quantile Net
   CNeuronBaseOCL    cQuantile0;
   CNeuronBaseOCL    cQuantile1;
   CNeuronBaseOCL    cQuantile2;
   //--- 
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override; 
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; 

public:
                     CNeuronFQF();
                    ~CNeuronFQF();
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint actions, uint quantiles, uint numInputs, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override        const { return defNeuronFQF; }
   virtual CLayerDescription* GetLayerInfo(void) override;
  };

En nuestra clase, utilizaremos objetos internos estáticos, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos.

La clase y los objetos internos se inicializarán en el método Init. Para el proceso de inicialización de los objetos internos, necesitaremos los siguientes parámetros:

numOutputs — número de neuronas en la siguiente capa
myIndex — índice de la neurona actual en la capa
open_cl — puntero al objeto de trabajo con OpenCL
actions — número de acciones posibles que puede realizar un agente,
quantiles — número de cuantiles
numInputs — tamaño de la capa neuronal anterior
optimization_type — función usada para optimizar los parámetros del modelo
batch — tamaño del lote de actualización de los parámetros del modelo.

bool CNeuronFQF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                      uint actions, uint quantiles, uint numInputs,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, actions, optimization, batch))
      return false;
   SetActivationFunction(None);

En el cuerpo del método, no definiremos un bloque para comprobar los parámetros obtenidos. En su lugar, llamaremos directamente a un método similar de la clase padre que ya contendrá todos los controles necesarios. El método de la clase padre controlará los parámetros externos e inicializará los objetos heredados. Por lo tanto, una vez que se haya ejecutado correctamente, solo tendremos que inicializar los objetos recién declarados.

Recuerde también deshabilitar la función de activación del objeto. Todas las funciones de activación necesarias serán definidas por el algoritmo y se especificarán para los objetos internos.

Recordemos que, según el algoritmo FQF, la integración del estado del sistema se introducirá en la entrada de la red de generación cuantílica. Para ello, los autores del método utilizaron una única capa totalmente conectada con normalización de datos usando la función SoftMax. En nuestra versión, serán 2 objetos: una capa completamente conectada sin función de activación y una capa SoftMax.

Como generaremos una distribución cuantílica para cada acción posible, también definiremos el tamaño de las capas usadas como el producto del número de acciones posibles por el número dado de cuantiles. En el caso de SoftMax, también normalizaremos los datos en cuanto a las acciones.

//---
   if(!cFraction.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cFraction.SetActivationFunction(None);
//---
   if(!cSoftMax.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cSoftMax.SetHeads(actions);
   cSoftMax.SetActivationFunction(None);

A continuación, según el algoritmo, deberemos crear una integración de los cuantiles resultantes. La crearemos en dos etapas. Primero prepararemos los datos y los guardaremos en el búfer de la capa neuronal cCosine. Luego los pasaremos a través de la capa cCosineEmbeding con la función de activación ReLU. Otra función que ejecuta la capa cCosineEmbeding es la alineación del tamaño del tensor de integración con el tamaño de los datos originales para la posterior multiplicación de Hadamard de los tensores.

   if(!cCosine.Init(numInputs, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cCosine.SetActivationFunction(None);
//---
   if(!cCosineEmbeding.Init(0, myIndex, open_cl, numInputs, optimization, batch))
      return false;
   cCosineEmbeding.SetActivationFunction(LReLU);

Por último, deberemos pasar los datos por un modelo de función cuantil que contendrá 1 capa oculta totalmente conectada con 4 veces el producto del número de acciones por el número de cuantiles y una función de activación ReLU, así como una capa completamente conectada sin función de activación en la salida. El tamaño de la capa de resultados será igual al producto del número de acciones posibles por el número de cuantiles.

   if(!cQuantile0.Init(4 * actions * quantiles, myIndex, open_cl, numInputs, optimization, batch))
      return false;
   cQuantile0.SetActivationFunction(None);
//---
   if(!cQuantile1.Init(actions * quantiles, myIndex, open_cl,
                       4 * actions * quantiles, optimization, batch))
      return false;
   cQuantile1.SetActivationFunction(LReLU);
//---
   if(!cQuantile2.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cQuantile2.SetActivationFunction(None);
//---
   return true;
  }

Al aplicar el método, no olvide supervisar las operaciones, y cuando todos los objetos internos se hayan inicializado correctamente, salir del método con un resultado positivo.

2.1. Pasada directa

Una vez inicializados los objetos, procederemos a construir el proceso de pasada directa. Pero antes de empezar a crear el método CNeuronFQF::feedForward, deberemos crear los kernels que faltan en el programa OpenCL. Ya hemos implementado al completo el funcionamiento de las capas neuronales, pero aún nos queda por implementar la nueva funcionalidad.

Según el algoritmo FQF, los datos de origen en forma de integración del estado actual se introducirán en el modelo de generación de cuantiles. El funcionamiento de las dos capas neuronales (cFraction completamente conectada y cSoftMax) ya ha sido implementado. Sin embargo, de SoftMax saldrá un tensor con una suma de los valores de cada acción igual a 1. Nosotros, en cambio, necesitaremos fracciones crecientes de los cuantiles. A continuación, deberemos crear las integraciones de estos cuantiles usando la fórmula siguiente.

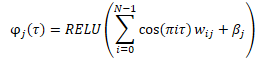
La fórmula anterior es exactamente igual a la de una capa neuronal totalmente conectada con una función de activación ReLU. Como datos de entrada, solo se utilizará cos(πit). El tensor de dichos cosenos será lo que prepararemos en el búfer de resultados de la capa neuronal cCosine.

Para implementar esta funcionalidad, crearemos el kernel FQF_Cosine. Luego suministraremos a la entrada del kernel los dos punteros a los búferes de datos. Uno contendrá los datos de la capa SoftMax. En el segundo, registraremos los resultados de nuestro kernel.

Recordemos que el algoritmo FQF presupone la creación de cuantiles para cada acción posible. En consecuencia, construiremos el algoritmo del kernel considerando un espacio de problemas bidimensional. En una dimensión se dispondrán los cuantiles y en la otra las posibles acciones del agente.

En el cuerpo del kernel, determinaremos directamente el identificador del hilo en ambas dimensiones. Asimismo, solicitaremos el número total de hilos en la primera dimensión, lo cual nos ayudará a determinar el desplazamiento en los tensores hasta el primer cuantil de la acción analizada.

A continuación, deberemos calcular la fracción acumulada del cuantil actual, lo cual haremos en un ciclo.

En este caso, merece la pena prestar atención. Al igual que con el algoritmo QR-DQN, no determinaremos el límite superior del cuantil, sino su valor medio. Por consiguiente, sumaremos la fracción de todos los cuantiles anteriores determinados por SoftMax en el paso anterior y añadiremos la mitad de la fracción del cuantil actual.

Por último, escribiremos el coseno del producto del valor medio resultante del cuantil actual, el número de pi y el número ordinal del cuantil.

__kernel void FQF_Cosine(__global float* softmax,
                         __global float* output)
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;
//---
   float result = 0;
   for(int it = 0; it < i; it++)
      result += softmax[shift + it];
   result += softmax[shift + i] / 2.0f;
   output[shift + i] = cos(i * M_PI_F * result);
  }

Las operaciones posteriores para crear la integración cuantílica las realizaremos usando la funcionalidad de la capa interna cCosineEmbeding. Sin embargo, entonces deberemos realizar la operación de multiplicación de Hadamar del tensor de integración cuantílica por el tensor de datos de origen (la incrustación del estado del sistema). Para llevar a cabo dicha operación, necesitaremos otro kernel más. Pero antes de crear un nuevo kernel, hemos mirado los kernels ya preparados para las redes neuronales creadas anteriormente, y nos ha llamado la atención el kernel que creamos para la capa Dropout. Recordemos que para que la capa anterior funcionara, creamos un kernel en el que multiplicamos por elementos el tensor de coeficientes por los datos de origen. Ahora deberemos realizar una operación matemática similar, pero con datos diferentes y el significado lógico de la operación. Como podemos ver, esto no influirá en el proceso de las operaciones matemáticas. Así que usaremos con seguridad una solución ya preparada.

A continuación, describiremos las operaciones de la red cuantílica que hemos implementado como un perceptrón con una capa oculta. En la salida de este perceptrón, obtendremos una distribución de la recompensa esperada similar a la del modelo QR-DQN. Solo que, a diferencia del método anterior, usaremos una distribución de probabilidad diferente para cada posible acción del agente. Para obtener un valor de recompensa discreto, deberemos multiplicar el nivel de recompensa de cada cuantil por su probabilidad, y luego sumar los valores obtenidos según las acciones del agente.

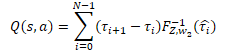
En nuestro caso particular, todos los deltas de la probabilidad ya se han calculado en el búfer de resultados de la capa cSoftMax. Ahora solo tendremos que multiplicar el valor del búfer especificado por el búfer de resultados del perceptrón de la función cuantílica de la capa neuronal cQuantile2. Luego sumaremos el resultado de la operación en cuanto a las posibles acciones del agente,

y crearemos el nuevo kernel FQF_Output para realizar las operaciones especificadas. En los parámetros del kernel, transmitiremos los punteros a tres búferes de datos: los resultados de la función cuantílica, el delta de probabilidad y el búfer de resultados. También indicaremos el número de cuantiles.

Después ejecutaremos el kernel en un espacio de tareas unidimensional que se corresponderá con el número de acciones posibles del agente.

En el cuerpo del kernel, primero solicitaremos el identificador del hilo y determinaremos el desplazamiento en los búferes de datos hasta el vector de distribución cuantílica correspondiente.

A continuación, en un ciclo, realizaremos la multiplicación del vector de probabilidades por el vector de distribución cuantílica, y escribiremos el resultado de la operación en el búfer de resultados correspondiente.

Tenga en cuenta que el búfer de resultados será mucho más pequeño que los búferes de datos de origen, ya que solo contiene un valor discreto para cada posible acción del agente, mientras que los datos de originen contienen un vector entero de valores para cada acción. Como consecuencia, el desplazamiento en el búfer de resultados también será igual al identificador del hilo actual.

__kernel void FQF_Output(__global float* quantiles,
                         __global float* delta_taus,
                         __global float* output,
                         uint total)
  {
   size_t action = get_global_id(0);
   int shift = action * total;
//---
   float result = 0;
   for(int i = 0; i < total; i++)
      result += quantiles[shift + i] * delta_taus[shift + i];
   output[action] = result;
  }

A continuación, ejecutaremos el algoritmo FQF completo de pasada directa y crearemos los kernels que faltaban. Ahora podremos trabajar de nuevo en nuestra clase y repetir el algoritmo completo utilizando MQL5. Como de costumbre, redefiniremos el método CNeuronFQF::feedForward para realizar una pasada directa.

En los parámetros, el método de pasada directa recibirá el puntero a la capa neuronal anterior, cuyo búfer de resultados (esperamos) contendrá la integración del estado actual del sistema.

En el cuerpo del método, no crearemos el bloque de control de datos de origen, sino que llamaremos directamente a los métodos de pasada directa de las capas neuronales internas cFraction y cSoftMax. La exclusión del bloque de control de datos de origen en este caso no planteará ningún riesgo, ya que cada uno de los métodos llamados tendrá su propio bloque de control. Todo lo que deberemos hacer es comprobar el resultado de las operaciones de los métodos a los que llamamos.

bool CNeuronFQF::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFraction.FeedForward(NeuronOCL))
      return false;
   if(!cSoftMax.FeedForward(GetPointer(cFraction)))
      return false;

A continuación, deberemos crear la integración de los niveles de probabilidad de los cuantiles. En este punto, primero llamaremos al kernel de preparación de datos FQF_Cosine creado anteriormente. Este kernel se ejecutará en un espacio de tareas bidimensional. En la primera dimensión, especificaremos el número de cuantiles, mientras que en la segunda dimensión indicaremos el número de acciones posibles que puede realizar un agente.

Observe aquí que no hemos creado variables internas para los hiperparámetros indicados. Sin embargo, el tamaño del búfer de resultados de nuestra capa CNeuronFQF será igual al número de acciones posibles del agente, mientras que podremos definir el número de cuantiles como la relación entre el búfer de resultados de la capa cSoftMax y el número de acciones.

Luego transmitiremos los punteros del búfer a los parámetros del kernel y enviaremos este a la cola de ejecución. Al hacerlo, deberemos necesariamente supervisar el progreso de las operaciones en cada paso.

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2];
      global_work_size[1] = Output.Total();
      global_work_size[0] = cSoftMax.Neurons() / global_work_size[1];
      OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_softmax, cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_outputs, cCosine.getOutputIndex());
      if(!OpenCL.Execute(def_k_FQF_Cosine, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_Cosine: %d", GetLastError());
         return false;
        }
     }

A continuación, llamaremos al método cCosineEmbeding de la capa neuronal interna, que completará el proceso de integración de cuantiles.

   if(!cCosineEmbeding.FeedForward(GetPointer(cCosine)))
      return false;

En el siguiente paso del algoritmo FQF, deberemos combinar la integración del estado actual del sistema (datos de origen) con la integración de cuantiles. Como recordará, para esta operación decidimos utilizar el kernel de la capa neuronal Dropout. En el cuerpo de este kernel, utilizaremos operaciones vectoriales sobre vectores de 4 elementos. Por lo tanto, el número de hilos será 4 veces inferior al tamaño de los búferes de datos.

Luego transmitiremos los datos requeridos en los parámetros del kernel. A continuación, colocaremos el kernel en la cola de ejecución.

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = {(cCosine.Neurons() + 3) / 4};
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cCosineEmbeding.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cQuantile0.getOutputIndex());
      OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, (int)cCosine.Neurons());
      if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel Dropout: %d", GetLastError());
         return false;
        }
     }

Ahora deberemos determinar los niveles de la distribución cuantílica. Para ello, llamaremos secuencialmente a los métodos de las capas neuronales de pasada directa de nuestro perceptrón de función cuantílica,

   if(!cQuantile1.FeedForward(GetPointer(cQuantile0)))
      return false;
//---
   if(!cQuantile2.FeedForward(GetPointer(cQuantile1)))
      return false;

y tras completar el método de pasada directa, llamaremos al kernel para convertir la distribución cuantílica en el valor discreto de la recompensa esperada para cada posible acción del agente FQF_Output. El procedimiento de colocación del kernel en la cola de ejecución seguirá siendo el mismo:

definimos el espacio de tareas
transmitimos los punteros a los búferes y la otra información necesaria a los parámetros del kernel
llamamos a los procedimientos para ejecutar el kernel.

Y, por supuesto, no deberemos olvidarnos de supervisar el proceso de las operaciones en cada paso.

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = { Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_quantiles, cQuantile2.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_delta_taus, cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_output, getOutputIndex());
      OpenCL.SetArgument(def_k_FQF_Output, def_k_fqfout_total, 
                         (uint)(cQuantile2.Neurons() / global_work_size[0]));
      if(!OpenCL.Execute(def_k_FQF_Output, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_Output: %d", GetLastError());
         return false;
        }
     }
//---
   return true;
  }

Con esto, podemos dar por concluida la pasada directa de nuestra clase: ahora procederemos a sobrescribir los métodos de la pasada inversa, que en nuestra clase estará representada por 2 métodos: calcInputGradients y updateInputWeights.

2.2. Pasada inversa

El primer método que veremos es calcInputGradients, que transferirá el gradiente a todas las capas internas y a la capa neuronal anterior.

El método indicado resulta exactamente igual al método directo, solo que en sentido contrario. Como consecuencia, para todos los kernels creados con una pasada directa, deberán crearse kernels con operaciones "invertidas", y, puesto que todo el proceso inverso se organiza en la secuencia inversa de la pasada directa, construiremos los kernels de manera similar.

A la salida del método de pasada directa, convertiremos la distribución cuantílica en un valor discreto para cada posible acción del agente. A la entrada del método de pasada inversa, esperaremos obtener un gradiente de error para cada acción, y después deberemos asignar el gradiente resultante tanto al valor de la función cuantílica como a los deltas de las probabilidades de los rangos cuantílicos.

Implementaremos esta función en el kernel FQF_OutputGradient. En los parámetros del kernel, transmitiremos los punteros a los 5 búferes de datos a la vez. 3 de ellos contendrán los datos de origen y 2 servirán para registrar los resultados del kernel.

Recordemos que nuestros tensores de deltas de probabilidad y los resultados de la función cuantílica estarán estructurados mediante lógica tabular en cuanto a los cuantiles y las posibles acciones de los agentes. Del mismo modo, ejecutaremos el kernel en el espacio de tareas bidimensional en cuanto a los cuantiles y las acciones del agente.

En el cuerpo del kernel, solicitaremos inmediatamente los identificadores de los hilos en ambas dimensiones y el número de hilos en la primera dimensión, y también determinaremos el desplazamiento en los búferes de datos.

__kernel void FQF_OutputGradient(__global float* quantiles,
                                 __global float* delta_taus,
                                 __global float* output_gr,
                                 __global float* quantiles_gr,
                                 __global float* taus_gr
                                )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;

A continuación, deberemos distribuir el gradiente de error. En la pasada directa, obteníamos el resultado multiplicando 2 variables. La derivada de la operación de multiplicación será el segundo multiplicador. En consecuencia, para transmitir el gradiente, necesitaremos multiplicar el gradiente de error resultante por el elemento correspondiente del tensor opuesto.

Nótese aquí que deberemos multiplicar un elemento del búfer de los gradientes resultantes por los elementos correspondientes de los 2 tensores. Esto significa que tendremos que acceder dos veces al mismo elemento del búfer global. No obstante, debemos recordar que acceder a los elementos de la memoria global resulta "caro", y para reducir el tiempo total de ejecución, primero tendremos que mover el valor del elemento del búfer global a la variable de memoria privada más rápida. Las operaciones posteriores ya se realizarán con esta variable "rápida".

Los resultados de las operaciones los guardaremos en los elementos correspondientes de los dos búferes de resultados.

   float gradient = output_gr[action];
   quantiles_gr[shift + i] = gradient * delta_taus[shift + i];
   taus_gr[shift + i] = gradient * quantiles[shift + i];
  }

El siguiente kernel que llamaremos directamente desde nuestro método de pasada directa será el kernel Dropout. En él realizaremos la multiplicación de Hadamar de los dos tensores de integración. Integración del estado del entorno e integración de cuantiles. Y si antes utilizábamos el kernel Dropout creado anteriormente para la pasada directa, ahora necesitaremos llamar al kernel 2 veces sucesivamente con diferentes datos de entrada para distribuir el gradiente de error en las dos direcciones. No obstante, nosotros estamos buscando el máximo paralelismo en las operaciones para que el tiempo de aprendizaje del modelo resulte lo más corto posible. Así que vamos a gastar algo de nuestro tiempo en crear el nuevo kernel FQF_QuantileGradient.

Podemos ver que el algoritmo de este kernel es exactamente el mismo que el del kernel anterior. No hay nada extraño en ello, al fin y al cabo, ambos kernels desempeñan una función similar. La única diferencia es el desplazamiento a través del búfer de los gradientes resultantes. Si en el caso anterior, el tamaño del búfer de gradiente obtenido era diferente al de los demás búferes, ya que solo tenía un valor discreto para cada posible acción del agente, en este caso, todos los búferes tendrán el mismo tamaño, y, en consecuencia, en el búfer de gradiente utilizaremos un desplazamiento similar al del resto de los búferes.

__kernel void FQF_QuantileGradient(__global float* state_embeding,
                                   __global float* taus_embeding,
                                   __global float* quantiles_gr,
                                   __global float* state_gr,
                                   __global float* taus_gr
                                  )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;
//---
   float gradient = quantiles_gr[shift + i];
   state_gr[shift + i] = gradient * taus_embeding[shift + i];
   taus_gr[shift + i] = gradient * state_embeding[shift + i];
  }

El último kernel que deberemos analizar es el kernel FQF_CosineGradient, que realiza el procedimiento inverso a la preparación de datos para integrar cuantiles. La derivada de la operación de preparación de datos será la siguiente.

Como resultado de las operaciones de este kernel, esperamos obtener un gradiente de error a la salida de la capa SoftMax del modelo de predicción de probabilidad de cuantiles. También en este caso deberemos tener en cuenta que cada cuantil utiliza el valor acumulado del tensor de resultados SoftMax, por lo que cada elemento del tensor tenía un efecto sobre todos los cuantiles posteriores, y lo lógico sería que cada elemento del tensor recibiera su parte del gradiente según su participación en el resultado final. Por consiguiente, recopilaremos el gradiente de error de todos los elementos del búfer de gradiente obtenido que hayan sido influidos por el elemento del tensor de resultados SoftMax analizado.

Vamos a considerar la implementación del kernel. En los parámetros, transmitiremos los punteros a 3 búferes de datos:

Resultados de la capa SoftMax
Gradientes de error obtenidos
Búfer de resultados — gradientes de error a nivel del búfer de resultados de la capa SoftMax.

Como la mayoría de los kernels tratados en este artículo, este kernel se ejecutará en un espacio de tareas bidimensional. Una dimensión será cuantílica, la otra será la de posibles acciones de los agentes.

En el cuerpo del kernel, solicitaremos los identificadores de hilo en ambas dimensiones y determinaremos el desplazamiento en los búferes de datos. Todos los búferes de datos tendrán el mismo tamaño, en consecuencia, el desplazamiento también será el mismo para todos los búferes de datos.

__kernel void FQF_CosineGradient(__global float* softmax,
                                 __global float* output_gr,
                                 __global float* softmax_gr
                                )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;

Cada elemento influirá solo en su propio cuantil y en los siguientes. Así que primero contaremos simplemente la suma de los elementos anteriores,

   float cumul = 0;
   for(int it = 0; it < i; it++)
      cumul += softmax[shift + it];

y luego calcularemos el gradiente a partir del elemento correspondiente.

Aquí debemos señalar que en la pasada directa transmitiremos a la integración el valor cuantílico medio. Como consecuencia, calcularemos el gradiente de error usando el valor medio de la probabilidad cuantílica.

   float result = -M_PI_F * i * sin(M_PI_F * i * (cumul + softmax[shift + i] / 2)) * output_gr[shift + i];

A continuación, realizaremos un ciclo similar para determinar el gradiente de error a partir de los cuantiles posteriores. Al hacerlo, ajustaremos el efecto del gradiente según la proporción del elemento actual en la probabilidad total del cuantil del gradiente.

   for(int it = i + 1; it < total; it++)
     {
      cumul += softmax[shift + it - 1];
      float temp = cumul + softmax[shift + it] / 2;
      result += -M_PI_F * it * sin(M_PI_F * it * temp) * output_gr[shift + it] * 
                                                         softmax[shift + it] / temp;
     }
   softmax_gr[shift + i] += result;
  }

Una vez completadas las iteraciones del ciclo, escribiremos el resultado de las operaciones en el elemento correspondiente del búfer de resultados.

En esta fase, hemos preparado todos los kernels para organizar la pasada inversa de nuestra clase, por lo que ahora podremos proceder a crear directamente el método de distribución de gradientes de error calcInputGradients.

En los parámetros, el método obtendrá el puntero al objeto de la capa neuronal anterior a la que vamos a transmitir el gradiente de error; luego organizaremos un bloque de controles directamente en el método. Aquí comprobaremos los punteros al objeto obtenido y a los búferes de datos internos.

bool CNeuronFQF::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !Gradient || !Output)
      return false;

Tenga en cuenta que, a diferencia de lo que sucede en el método de pasada directa, aquí crearemos un bloque de control. Esto se debe a que las operaciones de este método comenzarán con una llamada al kernel OpenCL, y al transmitirles los punteros a los búferes de datos, deberemos estar seguros de que existen. De lo contrario, correremos el riesgo de cometer un error crítico en la ejecución de las operaciones.

Una vez superado con éxito el bloque de control, procederemos a la ejecución directa de las operaciones de distribución del gradiente de error. Primero llamaremos al kernel FQF_OutputGradient, en el que distribuiremos el gradiente de error al perceptrón de función cuantílica y al bloque de predicción cuantílica. Las operaciones de cola del kernel serán similares a las operaciones de pasada directa correspondientes. El kernel se ejecutará en un espacio de tareas bidimensional. La primera dimensión se corresponderá con los cuantiles y la segunda con las posibles acciones de los agentes.

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles,
                                                              cQuantile2.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus,
                                                                 cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_output_gr,
                                                                 getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles_gr,
                                                             cQuantile2.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus_gr,
                                                               cSoftMax.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_OutputGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
         return false;
        }
     }

A continuación, transmitiremos el gradiente de error a través del perceptrón de función cuantílica. Para ello, llamaremos secuencialmente a los métodos de pasada inversa de las capas neuronales internas del bloque especificado.

   if(!cQuantile1.calcHiddenGradients(GetPointer(cQuantile2)))
      return false;
   if(!cQuantile0.calcHiddenGradients(GetPointer(cQuantile1)))
      return false;

El gradiente de error de la función cuantílica deberemos asignarlo a la integración del estado actual del sistema (la capa neuronal anterior) y a la integración de las probabilidades cuantílicas. Para ejecutar esta función, hemos creado el kernel FQF_QuantileGradient. Luego llamaremos al kernel anterior usando un procedimiento de eficacia probada.

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cCosineEmbeding.Neurons(), 1 };
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_enbeding,
                                                                  NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_embedding,
                                                            cCosineEmbeding.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_quantiles_gr,
                                                               cQuantile0.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_gr,
                                                                NeuronOCL.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_gr,
                                                          cCosineEmbeding.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_QuantileGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
         return false;
        }
     }

El siguiente paso consistirá en realizar un gradiente de error usando la integración de cuantiles. Aquí llamaremos primero al método de pasada inversa de la capa neuronal interna cCosine,

   if(!cCosine.calcHiddenGradients(GetPointer(cCosineEmbeding)))
      return false;

y luego llamaremos al kernel FQF_CosineGradient usando el procedimiento que ya hemos elaborado.

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax,
                                                                  cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_output_gr,
                                                                  cCosine.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax_gr,
                                                                 cSoftMax.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_CosineGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_CosineGradient: %d", GetLastError());
         return false;
        }
     }

Al final del método, ejecutaremos el gradiente de error a través de la capa interna cSoftMax llamando a su método de pasada inversa.

   if(!cSoftMax.calcInputGradients(GetPointer(cFraction)))
      return false;
//---
   return true;

Nótese que no transmitiremos a la capa anterior el gradiente de error del bloque de predicción de probabilidad cuantílica. Esto tiene que ver con el carácter prioritario de la determinación de la recompensa esperada en lugar de la distribución de probabilidades.

El segundo método de pasada inversa updateInputWeights, que vamos a redefinir, será responsable de la funcionalidad de actualización de los parámetros de nuestro modelo. Aquí todo será bastante sencillo. Simplemente llamaremos uno a uno a los métodos internos de la capa neuronal del mismo nombre y comprobaremos el resultado de la operación.

bool CNeuronFQF::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFraction.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cCosineEmbeding.UpdateInputWeights(GetPointer(cCosine)))
      return false;
   if(!cQuantile1.UpdateInputWeights(GetPointer(cQuantile0)))
      return false;
   if(!cQuantile2.UpdateInputWeights(GetPointer(cQuantile1)))
      return false;
//---
   return true;
  }

Con esto daremos por completada la funcionalidad básica de nuestra nueva clase CNeuronFQF. Más arriba hemos analizado la organización de los procesos de pasada directa e inversa. En la clase también se han redefinido los métodos para guardar los datos en un archivo y restaurar la funcionalidad de la clase después de guardarlos. En ellos, simplemente llamaremos uno a uno a los métodos correspondientes de los objetos internos. Le invitamos a familiarizarse con su construcción. Encontrará el código completo de todas las clases y métodos utilizados en el archivo adjunto al artículo.

Continuemos. Más arriba hemos construido una clase para organizar el algoritmo de aprendizaje del modelo usando la parametrización completa de la función cuantílica, pero esto es solo una parte del proceso. Sigue siendo el mismo aprendizaje Q con el uso de un búfer de datos y una Target Net, y para facilitar el proceso de uso del método descrito directamente durante el aprendizaje Q, hemos creado la clase CFQF como clase descendiente de la clase básica de nuestros modelos CNet.

class CFQF : protected CNet
  {
private:
   uint              iCountBackProp;
protected:
   uint              iUpdateTarget;
   //---
   CNet              cTargetNet;
public:
                     CFQF(void);
                     CFQF(CArrayObj *Description)  { Create(Description); }
   bool              Create(CArrayObj *Description);
                    ~CFQF(void);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
                     { return        CNet::feedForward(inputVals, window, tem); }
   bool              backProp(CBufferFloat *targetVals, float discount = 0.9f,
                              CArrayFloat *nextState = NULL, int window = 1, bool tem = true);
   void              getResults(CBufferFloat *&resultVals);
   int               getAction(void);
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; }
   bool              Save(string file_name, datetime time, bool common = true)
     { return CNet::Save(file_name, getRecentAverageError(), (float)iUpdateTarget, 0, time, common); }
   virtual bool      Save(const int file_handle);
   virtual bool      Load(string file_name, datetime &time, bool common = true);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)   const   {  return defFQF;   }
   virtual bool      TrainMode(bool flag) { return CNet::TrainMode(flag); }
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result)
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual void      SetUpdateTarget(uint batch)   { iUpdateTarget = batch; }
   virtual bool      UpdateTarget(string file_name);
  };

Hemos creado la clase de forma similar a la clase CQRDQN del artículo anterior, y su estructura será casi igual a la estructura de la clase en cuestión. Solo hemos eliminado las variables no utilizadas y la matriz de probabilidades. Al fin y al cabo, nuestras capas neuronales individuales serán responsables de ello. Como consecuencia, hemos introducido cambios en los métodos de la clase. No vamos a detallar ahora todos los métodos de la clase: podrá leerlos usted mismo en el archivo adjunto. Destacaremos solo algunos de ellos.

Para empezar, le proponemos centrarnos primero en el método de pasada inversa. El método obtiene en los parámetros los valores objetivo y el siguiente estado del sistema. El siguiente estado del sistema será un parámetro opcional. Podemos utilizar esto para entrenar un nuevo modelo, ya que el uso de un modelo no entrenado para predecir las recompensas futuras solo añadirá ruido y complicará el proceso de aprendizaje.

En el cuerpo del método, comprobaremos directamente que exista un parámetro obligatorio en forma de búfer de valores objetivo.

bool CFQF::backProp(CBufferFloat *targetVals, float discount = 0.9f,
                    CArrayFloat *nextState = NULL, int window = 1, bool tem = true)
  {
//---
   if(!targetVals)
      return false;

A continuación, comprobaremos la disponibilidad del parámetro opcional y, si fuera necesario, haremos una predicción de las recompensas futuras. Aquí también ajustaremos los valores objetivo según la magnitud de la recompensa futura considerando el factor de descuento.

   if(!!nextState)
     {
      vectorf target;
      if(!targetVals.GetData(target) || target.Size() <= 0)
         return false;
      if(!cTargetNet.feedForward(nextState, window, tem))
         return false;
      cTargetNet.getResults(targetVals);
      if(!targetVals)
         return false;
      target = target + discount * targetVals.Maximum();
      if(!targetVals.AssignArray(target))
         return false;
     }

A continuación, comprobaremos si es necesario actualizar la Target Net,

   if(iCountBackProp >= iUpdateTarget)
     {
#ifdef FileName
      if(UpdateTarget(FileName + ".nnw"))
#else
      if(UpdateTarget("FQF.upd"))
#endif
         iCountBackProp = 0;
     }
   else
      iCountBackProp++;

y al final del método, llamaremos al método de pasada inversa de la clase padre.

   return CNet::backProp(targetVals);
  }

También hemos modificado el método de selección codiciosa de acciones. Aquí simplemente identificaremos el elemento con la máxima recompensa del búfer de resultados del modelo.

int CFQF::getAction(void)
  {
   CBufferFloat *temp;
   CNet::getResults(temp);
   if(!temp)
      return -1;
//---
   return temp.Maximum(0, temp.Total());
  }

También hemos introducido cambios en el método de muestreo de la acción getSample. En él, primero obtendremos el resultado de la última pasada directa del modelo.

int CFQF::getSample(void)
  {
   CBufferFloat* resultVals;
   CNet::getResults(resultVals);
   if(!resultVals)
      return -1;

Luego copiaremos estos datos del búfer a un vector y aplicaremos la función SoftMax. A continuación, calcularemos las sumas acumuladas de los valores vectoriales.

   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return -1;
     }
   delete resultVals;
//---
   if(!temp.Activation(temp, AF_SOFTMAX))
      return -1;
   temp = temp.CumSum();

El vector resultante será una especie de distribución cuantílica de las probabilidades de acción de los agentes. Partiendo de esta distribución, muestrearemos un único valor y lo retornaremos al programa que ha realizado la llamada.

   int err_code;
   float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
   if(random >= 1)
      return (int)temp.Size() - 1;
   for(int i = 0; i < (int)temp.Size(); i++)
      if(random <= temp[i] && temp[i] > 0)
         return i;
//---
   return -1;
  }

En cada paso, comprobaremos el resultado de las operaciones. Si se produce un error, retornaremos "-1" al programa que ha realizado la llamada.

Con esto daremos por finalizado nuestro análisis de los algoritmos de construcción de las nuevas clases para implementar el algoritmo FQF. El código completo de todas las clases y sus métodos se encuentra en el archivo adjunto.

3. Simulación

En lo que respecta a la simulación, hemos creado el asesor electrónico "FQF-learning.mq5" para entrenar el modelo utilizando un método de función cuantílica totalmente parametrizada. Este ha repetido casi exactamente el algoritmo del asesor experto "QRDQN-learning.mq5" del artículo anterior. Solo hemos cambiado el nombre del archivo y los objetos usados, así que no nos detendremos en la arquitectura de sus algoritmos. En el archivo adjunto se muestra el código completo del asesor.

El modelo se ha entrenado con los datos históricos de EURUSD de los últimos 2 años y el marco temporal H1. Los parámetros de todos los indicadores se han tomado por defecto. Como podemos ver, estos son los parámetros de prueba invariables de todos los modelos de nuestra serie.

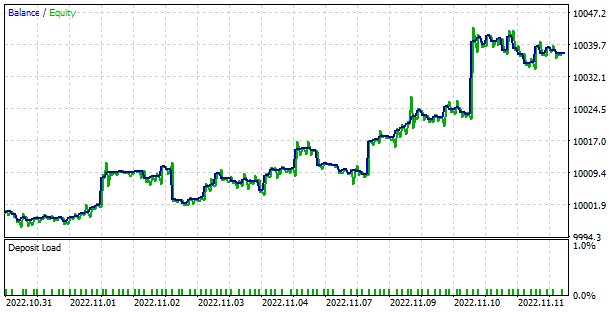
Diremos de entrada que durante la curva de aprendizaje, el modelo nos ha alegrado con su progresión bastante uniforme y constante hacia la reducción de errores, lo cual es un buen indicador de la estabilidad del aprendizaje de los modelos.

El modelo entrenado se ha puesto a prueba en el simulador de estrategias. Para ello, hemos creado el asesor"FQF-learning-test.mq5", que es una copia del asesor «QRDQN-learning-test.mq5» del artículo anterior. Como es natural, no vamos a analizar ahora mismo su algoritmo, pues solo hemos cambiado el nombre del archivo y la clase del modelo. Podrá encontrar el código completo del asesor en el archivo adjunto.

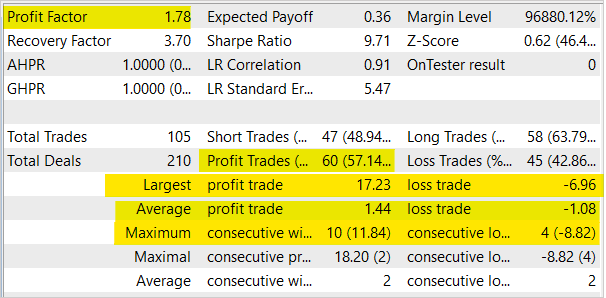
Durante las pruebas, el modelo ha demostrado su capacidad para generar beneficios. El modelo ha mostrado un factor de beneficio de 1,78 y un factor de recuperación de 3,7. Al mismo tiempo, la proporción de transacciones rentables supera el 57%, y la operación rentable máxima es casi 2,5 veces superior a la operación perdedora máxima. La serie máxima rentable ha sido de 10 transacciones, mientras que la serie perdedora máxima no ha superado las 4 transacciones. En general, la media de transacciones rentables es ⅓ superior a la media de transacciones perdedoras.

Gráfico de la prueba del modelo en el simulador de estrategias

Resultados de la prueba del modelo en el simulador de estrategias

Conclusión

En este trabajo, hemos continuado nuestro estudio de los algoritmos de aprendizaje distribuido por refuerzo, y también hemos construido las clases necesarias para implementar el método de aprendizaje de la función cuantílica totalmente parametrizada en el aprendizaje por refuerzo. Asimismo, hemos entrenado el modelo con este método, y hemos puesto a prueba el rendimiento del modelo entrenado en el simulador de estrategias. Hay que decir que el método ha mostrado una tendencia constante a la reducción de errores durante el proceso de entrenamiento, y al probar el modelo entrenado en el simulador de estrategias, hemos podido observar la capacidad del modelo para generar beneficios.

Una vez más, querríamos recordarle que el comercio bursátil es un método de inversión de alto riesgo, y los programas presentados en el artículo solo pretenden mostrar el funcionamiento de los métodos y algoritmos analizados. Dichos programas no están listos para su uso en el comercio real. Sin embargo, es posible construir herramientas comerciales que funcionen sobre su base. Aun así, antes de utilizar estas herramientas, deberá probarlas de forma exhaustiva. Los riesgos que conlleva el uso de programas en el comercio real deberán ser evaluados y aceptados por el usuario.

Enlaces

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	FQF-learning.mq5	Asesor	Asesor para la optimización de modelos
2	FQF-learning-test.mq5	Asesor	Asesor Experto para probar modelos en el Simulador de Estrategias
3	FQF.mqh	Biblioteca de clases	Clase de organización del modelo FQF
4	NeuroNet.mqh	Biblioteca de clases	Biblioteca para organizar modelos de redes neuronales
5	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL para organizar modelos de redes neuronales
6	NetCreator.mq5	Asesor	Herramienta de construcción de modelos
7	NetCreatotPanel.mqh	Biblioteca de clases	Biblioteca de clases para crear una herramienta

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/11804

Archivos adjuntos |

Descargar ZIP

MQL5.zip (106.93 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Algoritmos de optimización de la población: Optimización del Lobo Gris (Grey Wolf Optimizer - GWO)

Hoy analizaremos uno de los algoritmos de optimización más modernos: la Optimización del Lobo Gris. El original comportamiento de las funciones de prueba hace que este sea uno de los algoritmos más interesantes entre los analizados anteriormente. Uno de los líderes para la aplicación en el entrenamiento de redes neuronales y funciones suaves con muchas variables.

Algoritmos de optimización de la población: Colonia de abejas artificiales (Artificial Bee Colony - ABC)

Hoy estudiaremos el algoritmo de colonia de abejas artificiales. Asimismo, complementaremos nuestros conocimientos con nuevos principios para el estudio de los espacios funcionales. En este artículo hablaremos sobre mi interpretación de la versión clásica del algoritmo.

DoEasy. Elementos de control (Parte 28): Estilos de barra en el control «ProgressBar»

El artículo desarrollará los estilos de visualización y el texto de descripción para la barra de progreso del control ProgressBar.

Indicadores no lineales

En este artículo, intentaremos analizar algunas formas de construir indicadores no lineales, así como su uso en el trading. Existen bastantes indicadores en la plataforma comercial MetaTrader que utilizan enfoques no lineales.