Нейросети — это просто (Часть 34): Полностью параметризированная квантильная функция
Содержание
- Введение
- 1. Теоретические аспекты полной параметризации
- 1.1. Неявные квантильные сети (Implicit Quantile Networks - IQN)
- 1.2. Полностью параметризованная квантильная функция (Fully Parameterized Quantile Function - FQF)
- 2. Реализация средствами MQL5
- 3. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Мы продолжаем изучение алгоритмов распределенного Q-обучения. В предыдущих статьях мы уже рассмотрели 2 алгоритма. В первом [4], наша модель учила вероятности получения вознаграждения в заданном диапазоне значений. Во втором [5], мы изменили подход к решению задачи. И обучали модель прогнозировать уровень вознаграждения с заданной вероятностью.
Очевидно, что в обоих алгоритмах для решения задачи нам необходимы некие априорные знания о природе распределения вознаграждения. И если в первом алгоритме нам необходимо передать модели уровни ожидаемого вознаграждения, то во втором алгоритме задача пользователя немного упрощается. Нам необходимо указать модели ряд квантилей, размер которых нормализован в диапазоне от 0 до 1, и они расположены в порядке возрастания. Тем не менее, без знаний об истинном распределении значений вознаграждения сложно определить количество необходимых квантилей и объемы каждого.
Здесь надо сказать, что мы ввели допущение о равномерном распределении изучаемой последовательности. И взяли равномерные интервалы квантилей. При этом основным регулирующим гиперпараметром стало количество таких квантилей. Которое определяется опытном путем на валидационной выборке.
1. Теоретические аспекты полной параметризации
Оба упомянутых метода требуют предварительное изучение обучающей выборки и оптимизацию гиперпараметров. При этом стоит заметить, что при оптимизации гиперпарметров мы выбираем некие средние значения. Иными словами, мы выбираем нечто, способное максимально приблизить нас к желаемой цели. И выбранные нами параметры должны максимально удовлетворять всем возможным состояниям изучаемой системы. Вспомним ещё о сделанном нами допущении равномерного распределения. И получим модель, переполненную всевозможными компромиссами. Легко понять, что такая модель будет далека от оптимальной.
С целью получения максимального правдоподобия и минимизации ошибки прогнозирования мы вынуждены увеличивать количество обучаемых квантилей. Что ведет к увеличению размера и времени обучения модели. В большинстве случаев такой подход малоэффективен. Но мы же стремимся к максимальному изучению окружающей среды. И возникает желание каким-то образом уйти от фиксированных категорий значений в первом алгоритме и фиксированных квантилей во втором алгоритме.
1.1. Неявные квантильные сети (Implicit Quantile Networks - IQN)
И здесь использование квантилей выглядит более прогрессивно. Ведь согласитесь, для определения категорий нам необходимо полностью изучить исходное распределение, определив его границы. И при этом модель не готова к выпадам значений за пределы указанного диапазона. Модель категорий не универсальна и меняется от задачи к задаче.
В то же время вероятности появления событий имеют четкие границы в диапазоне от 0 до 1. Но использование равномерного распределения квантилей ограничивает наши свободы и круг оптимизируемых функций. И нам бы хотелось найти такой алгоритм, когда модель сама бы определяла оптимальное квантильное распределение без увеличения числа квантилей.
И первый подобный алгоритм был предложен в июле 2018 года в статье "Implicit Quantile Networks for Distributional Reinforcement Learning". Надо сказать, что авторы немного иначе подошли к решению задачи оптимальных квантилей. Они построили свой алгоритм на базе ранее рассмотренного нами QR-DQN. Но вместо поиска оптимальный квантилей, авторы решили генерировать их случайным образом и подавать на вход модели вместе с исходными данными описания состояния среды. Идея состоит в том, что в процессе обучения на вход модели будут подаваться одни и те же состояния системы с различными квантильными распределениями. В результате модель будет вынуждена использовать не определенный срез квантильной функции, а полное её приближение.
Такой подход позволяет обучить модель менее чувствительную к гиперпараметру количества квантилей. А случайное их распределение позволяет расширить круг аппроксимируемых функций на неравномерно распределенные.
Перед подачей на вход модели создаётся эмбединг случайно сгенерированных квантилей по представленной ниже формуле.
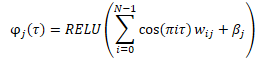
В процессе объединения полученного эмбединга с тензором исходных данных возможны варианты. Это может быть как простая конкатенация 2 тензоров, так и адамарное (поэлементное) умножение 2 матриц.
Ниже приведено сравнение рассмотренных архитектур, представленное авторами статьи.
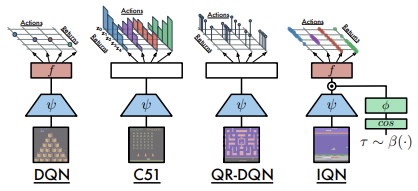
Эффективность модели подтверждается проведенными тестами на 57 играх Atari. Ниже представлена сравнительная таблица из оригинальной статьи [8]
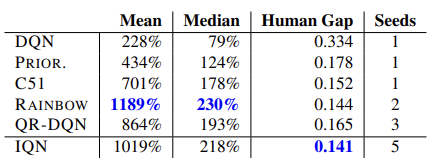
Гипотетически, при неограниченности размера модели такой подход позволяет выучить любое распределение прогнозируемого вознаграждения.
1.2. Полностью параметризованная квантильная функция (Fully Parameterized Quantile Function - FQF)
Представленная модель неявных квантильных сетей способна аппроксимировать различные функции. Но этот процесс связан с ростом самой модели. На практике же мы имеем ограниченные ресурсы. А при генерация случайных квантилей всегда присутствует риск получения неоптимальных значений. Как в процессе обучения, так и в процессе промышленной эксплуатации.
И в ноябре 2019 года была предложена модель полностью параметризированной квантильной функции "Fully Parameterized Quantile Function for Distributional Reinforcement Learning".
По существу, это таже модель IQN. Только вместо генератора случайных квантилей используется полносвязный нейронный слой, который возвращает распределение квантилей на основании поданного на вход текущего состояния среды. Модель генерирует распределение квантилей для каждой пары значений "состояние—действиe". Что позволяет аппроксимировать оптимальное распределение ожидаемого вознаграждения для каждого действия в конкретном состоянии системы. Именно об этом мы говорили в начале данной статьи.
При этом, конечно, сохраняются основные требования к квантилям — возрастание в диапазоне от 0 до 1. Для достижения этого эффекта используется нормализация данных на выходе нейронного слоя с помощью функции SoftMax и последующим кумулятивным (накопительным) сложением элементов нормализованного вектора.
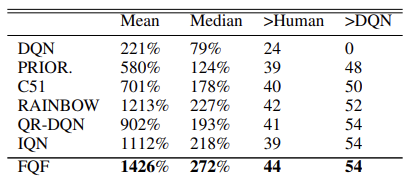
В оригинальной статье авторами приводятся результаты тестирования нового алгоритма на 55 играх Atari. Ниже приведена обобщенная таблица результатов из оригинальной статьи. Представленные данные демонстрируют превосходство алгоритма полной параметризации квантильной функции над другими алгоритмами распределенного Q-обучения. Конечно, за это пришлось заплатить производительностью модели. Дополнительная модель генерации квантилей требует дополнительных вычислительных ресурсов.
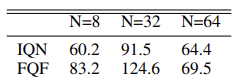
Кроме того, авторы метода провели эксперименты по выбору оптимального количества квантилей и предлагают использовать распределение из 32 квантилей.
Непосредственно с алгоритмом метода я предлагаю познакомиться в процессе его реализации.
2. Реализация средствами MQL5
В своей статье авторы метода полной параметризации квантильной функции говорят об использовании 2 нейронных сетей. Одна для генерации распределения квантилей. Вторая аппроксимации квантильной функции. Фактически же описанный алгоритм использует еще и третью сверточную сеть, которая создаёт эмбединг состояния среды. Именно этот эмбединг состояния является исходными данными рассматриваемого алгоритма.
Однако, построенная нами ранее библиотека ориентирована на построение последовательных моделей. И мы не создавали алгоритм для передачи градиента ошибки между моделями. Который может потребоваться при обучении нескольких последовательных моделей.
Конечно, мы можем воспользоваться механизмом Transfer Learning и последовательно обучить каждую отдельно взятую модель. Но я решил реализовать весь алгоритм в рамках одной модели.
Для создания эмбединга состояния среды используются сверточные модели, с которыми мы уже знакомы [1]. Следовательно, мы без труда сможем построить подобную модель существующими средствами.
Далее нам предстоит реализовать алгоритм FQF. На мой взгляд, наиболее простым способом реализации в рамках концепции нашей библиотеки будет создание нового класса нейронного слоя. Который на вход получит эмбединг текущего состояния анализируемой системы и выдаст на выходе действие агента. Таким образом, внутри нового класса мы построим агента нашей модели.
Создадим новый класс CNeuronFQF наследником базового класса нейронного слоя CNeuronBaseOCL. В новом классе будут переопределен уже стандартный набор методов. А в защищенном блоке объявим внутренние объекты, которые будем использовать при реализации алгоритма FQF. С назначением объектов мы познакомимся в процессе построения алгоритма.
class CNeuronFQF : protected CNeuronBaseOCL { protected: //--- Fractal Net CNeuronBaseOCL cFraction; CNeuronSoftMaxOCL cSoftMax; //--- Cosine embeding CNeuronBaseOCL cCosine; CNeuronBaseOCL cCosineEmbeding; //--- Quantile Net CNeuronBaseOCL cQuantile0; CNeuronBaseOCL cQuantile1; CNeuronBaseOCL cQuantile2; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronFQF(); ~CNeuronFQF(); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint actions, uint quantiles, uint numInputs, ENUM_OPTIMIZATION optimization_type, uint batch); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronFQF; } virtual CLayerDescription* GetLayerInfo(void) override; };
В нашем классе мы используем статические внутренние объекты, что позволяет нам оставить пустыми конструктор и деструктор класса.
Инициализации класса и внутренних объектов осуществляется в методе Init. Для процесса инициализации внутренних объектов нам потребуются нижеследующие параметры:
- numOutputs — количество нейронов в следующем слое
- myIndex — индекс текущего нейрона в слое
- open_cl — указатель на объект работы с OpenCL устройством
- actions — количество возможных действий агента
- quantiles — количество квантилей
- numInputs — размер предыдущего нейронного слоя
- optimization_type — используемая функция оптимизации параметров модели
- batch — размер пакета обновления параметров модели.
bool CNeuronFQF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint actions, uint quantiles, uint numInputs, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, actions, optimization, batch)) return false; SetActivationFunction(None);
В теле метода мы не определяем блок проверки полученных параметров. Вместо этого мы сразу вызываем аналогичный метод родительского класса, который уже содержит все необходимые контроли. В методе родительского класса осуществляется контроль внешних параметров и инициализация унаследованных объектов. Поэтому, после его успешного выполнения нам останется лишь инициализировать только вновь объявленные объекты.
Также не забываем отключить функцию активации объекта. Все необходимые функции активации определены алгоритмом и будут указаны для внутренних объектов.
Напомню, что согласно алгоритму FQF эмбединг состояния системы подается на вход сети генерации квантилей. Для данных целей авторами метода использовался один полносвязный слой с нормализацией данных с помощью функции SoftMax. В нашем исполнении это будут 2 объекта: полносвязный слой без функции активации и слой SoftMax.
Так как мы будем генерировать распределение квантилей для каждого возможного действия, то и размер используемых слоёв определим равным произведению числа возможных действий на заданное количество квантилей. А в случае SoftMax мы будем и нормализацию данных осуществлять в разрезе действий.
//--- if(!cFraction.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch)) return false; cFraction.SetActivationFunction(None); //--- if(!cSoftMax.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch)) return false; cSoftMax.SetHeads(actions); cSoftMax.SetActivationFunction(None);
Далее согласно алгоритму нам предстоит создать эмбединг полученных квантилей. Его мы будем создавать в 2 этапа. Сначала мы подготовим данные и сохраним их в буфер нейронного слоя cCosine. А затем проведем через полносвязный слой cCosineEmbeding с функцией активацией ReLU. Ещё одна функция, которую выполняет слой cCosineEmbeding является выравнивание размера тензора эмбединга с размером исходных данных для последующего адамарного умножения тензоров.
if(!cCosine.Init(numInputs, myIndex, open_cl, actions * quantiles, optimization, batch)) return false; cCosine.SetActivationFunction(None); //--- if(!cCosineEmbeding.Init(0, myIndex, open_cl, numInputs, optimization, batch)) return false; cCosineEmbeding.SetActivationFunction(LReLU);
В завершениe нам предстоит провести данные через модель квантильной функции. Которая будет содержать 1 скрытый полносвязный слой с количеством нейронов в 4 раза больше произведения количества действий на количество квантилей и функцией активации ReLU. И полносвязный слой без функции активации на выходе. Размер слоя результатов равен произведению числа возможных действий на количество квантилей.
if(!cQuantile0.Init(4 * actions * quantiles, myIndex, open_cl, numInputs, optimization, batch)) return false; cQuantile0.SetActivationFunction(None); //--- if(!cQuantile1.Init(actions * quantiles, myIndex, open_cl, 4 * actions * quantiles, optimization, batch)) return false; cQuantile1.SetActivationFunction(LReLU); //--- if(!cQuantile2.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch)) return false; cQuantile2.SetActivationFunction(None); //--- return true; }
В процессе реализации метода не забываем осуществлять контроль выполнения операций. И после успешной инициализации всех внутренних объектов выходим из метода с положительным результатом.
2.1. Прямой проход
После инициализации объектов мы переходим к построению процесса прямого прохода. Но прежде, чем приступить к созданию метода прямого прохода CNeuronFQF::feedForward, нам предстоит создать недостающие кернелы в программе OpenCL. Работа нейронных слоёв у нас полностью реализована. А вот новый функционал нал предстоит реализовать.
В соответствии с алгоритмом FQF исходные данные в виде эмбединга текущего состояния попадают в модель генерации квантилей. Работа двух нейронных слоёв (полносвязного cFraction и cSoftMax) реализована. Но из SoftMax выходит тензор с суммой значений по каждому действию равным 1. Нам же нужны возрастающие доли квантилей. После чего необходимо будет создать эмбединги этих квантилей по формуле ниже.
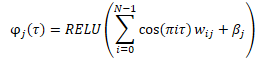
Приведенная формула полностью повторяет формулу полносвязного нейронного слоя с функцией активации ReLU. Только в качестве исходных данных служит cos(πiт). Тензор таких косинусов мы и подготовим в буфер результатов нейронного слоя cCosine.
Для реализации этого функционала создадим кернел FQF_Cosine. На вход кернела подадим 2 указатели на буферы данных. В одном будут данные от слоя SoftMax. Во второй мы будем записывать результаты работы нашего кернела.
Напомню, алгоритмом FQF предусматривается создание квантилей для каждого возможного действия. Следовательно, выстраивать алгоритм кернела мы будем с учетом двухмерного пространства задач. По одному измерению расположатся квантили, а по второму — возможные действия агента.
В теле кернела мы сразу определяем идентификатор потока в обоих измерениях. Также запросим общее количество потоков в первом измерении, которое поможет нам определить смещение в тензорах до первого квантиля анализируемого действия.
Далее нам необходимо посчитать накопительную долю текущего квантиля. Что мы и сделаем в цикле.
При этом стоит обратить внимание. Как и в алгоритме QR-DQN мы определяем не верхнюю границу квантиля, его среднее значение. Поэтому, мы складываем долю всех предыдущих квантилей, определенную SoftMax на предыдущем этапе, и прибавляем половину доли текущего квантиля.
В завершение записываем косинус из произведения полученного среднего значения текущего квантиля, числа Пи и порядкового номера квантиля.
__kernel void FQF_Cosine(__global float* softmax, __global float* output) { size_t i = get_global_id(0); size_t total = get_global_size(0); size_t action = get_global_id(1); int shift = action * total; //--- float result = 0; for(int it = 0; it < i; it++) result += softmax[shift + it]; result += softmax[shift + i] / 2.0f; output[shift + i] = cos(i * M_PI_F * result); }
Дальнейшие операции создания эмбединга квантилей мы выполним с помощью функционала внутреннего слоя cCosineEmbeding. Однако, затем нам предстоит операция адамарного умножения тензора эмбединга квантилей на тензор исходных данных (эмбединга состояния системы). Для реализации этой операции нам потребуется ещё кернел. Но перед созданием нового кернела я посмотрел на уже готовые к ранее созданным нейронным сетям. И моё внимание привлек кернел, который мы создавали для слоя Dropout. Помните, для функционирования указанного слоя мы создавали кернел в котором поэлементно умножали тензор коэффициентов на исходные данные. Сейчас нам предстоит выполнить аналогичные математическую операцию, но с другими данными и логическим смыслом операции. Как вы понимаете, на процесс математических операций это не влияет. Поэтому мы смело воспользуемся готовым решением.
Далее идут операции квантильной сети, которую мы реализовали в виде перцептрона с одним скрытым слоем. На выходе данного перцептрона мы получим распределение ожидаемого вознаграждения аналогичное модели QR-DQN. Только в отличие от ранее рассмотренного метода для каждого возможного действия агента используется свое распределение вероятностей. Для получения дискретного значения вознаграждения нам необходимо умножить уровень вознаграждения по каждому квантилю на его вероятность и полученные значения сложить в разрезе действий агента.
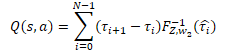
В нашем конкретном случае все дельты вероятностей уже посчитаны в буфере результатов слоя cSoftMax. И сейчас нам достаточно поэлементно умножить значение указанного буфера на буфер результатов перцептрона квантильной функции из нейронного слоя cQuantile2. Результат операции мы сложим в разрезе возможных действий агента.
Для выполнения указанных операций мы создадим новый кернел FQF_Output. В параметрах кернела мы будем передавать указатели на 3 буфера данных: результаты квантильной функции, дельты вероятностей и буфер результатов. Также укажем количество квантилей.
Запускать кернел мы будем в одномерном пространстве задач, которое соответствует количеству возможных действий агента.
В теле кернела мы сначала запрашиваем идентификатор потока и определяем сдвиг в буферах данных до соответствующего вектора квантильного распределения.
Далее в цикле мы осуществляем умножение вектора вероятностей на вектор квантильного распределения. И результат операции записываем в соответствующий буфер результатов.
Обратите внимание, что буфер результатов будет значительно меньше буферов исходных данных. Так как содержит только одно дискретное значение для каждого возможного действия агента. В то время как исходные данные содержат по целому вектору значений для каждого действия. Соответственно и смещение в буфере результатов равно идентификатору текущего потока.
__kernel void FQF_Output(__global float* quantiles, __global float* delta_taus, __global float* output, uint total) { size_t action = get_global_id(0); int shift = action * total; //--- float result = 0; for(int i = 0; i < total; i++) result += quantiles[shift + i] * delta_taus[shift + i]; output[action] = result; }
Мы проговорили весь алгоритм прямого прохода FQF и создали недостающие кернелы. Теперь мы можем вернуться к работе над нашим классом и повторить весь алгоритм средствами MQL5. Как обычно, для осуществления прямого прохода мы переопределяем метод CNeuronFQF::feedForward.
В параметрах метод прямого прохода получает указатель на предыдущий нейронный слой, буфер результатов которого (по нашим ожиданиям) содержит эмбединг текущего состояния системы.
В теле метода мы не создаем блок контроля исходных данных. А сразу вызываем методы прямых проходов внутренних нейронных слоёв cFraction и cSoftMax. Исключения блока контролей исходных данных в данном случае не несет никаких рисков, так как каждый из вызываемых метод имеет свой блок контролей. Нам лишь достаточно проверить результат выполнения операций вызываемых методов.
bool CNeuronFQF::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cFraction.FeedForward(NeuronOCL)) return false; if(!cSoftMax.FeedForward(GetPointer(cFraction))) return false;
Далее нам предстоит создать эмбединг вероятностных уровней квантилей. И в этом месте мы сначала вызываем выше созданный кернел подготовки данных FQF_Cosine. Данный кернел запускается в двухмерном пространстве задач. По первому измерению мы указываем количество квантилей. А по второму измерению — количество возможных действий агента.
Здесь надо обратить внимание, что мы не создавали внутренних переменных для указанных гиперпараметров. Но при этом размер буфера результатов нашего слоя CNeuronFQF равен количеству возможных действий агента. А количество квантилей мы можем определить как отношения буфера результатов слоя cSoftMax к количеству действий.
Передаем указатели на буферы в параметры кернела и отправляем кернел в очередь выполнения. При этом не забываем на каждом шаге контролировать процесс выполнения операций.
{
uint global_work_offset[2] = {0, 0};
uint global_work_size[2];
global_work_size[1] = Output.Total();
global_work_size[0] = cSoftMax.Neurons() / global_work_size[1];
OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_softmax, cSoftMax.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_outputs, cCosine.getOutputIndex());
if(!OpenCL.Execute(def_k_FQF_Cosine, 2, global_work_offset, global_work_size))
{
printf("Error of execution kernel FQF_Cosine: %d", GetLastError());
return false;
}
}
Далее мы вызываем метод прямого прохода внутреннего нейронного слоя cCosineEmbeding, чем и завершаем процесс эмбединга квантилей.
if(!cCosineEmbeding.FeedForward(GetPointer(cCosine))) return false;
На следующем этапе алгоритма FQF нам предстоит объединить эмбединг текущего состояния системы (исходные данные) с эмбедингом квантилей. Как вы помните, для этой операции мы решили использовать кернел нейронного слоя Dropout. В теле данного кернела мы использовали векторные операции над векторами из 4 элементов. Поэтому количество потоков будет в 4 раза меньше размеров буферов данных.
Передадим необходимые данные в параметрах кернела. После чего поставим кернел в очередь выполнения.
{
uint global_work_offset[1] = {0};
uint global_work_size[1] = {(cCosine.Neurons() + 3) / 4};
OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, NeuronOCL.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cCosineEmbeding.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cQuantile0.getOutputIndex());
OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, (int)cCosine.Neurons());
if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size))
{
printf("Error of execution kernel Dropout: %d", GetLastError());
return false;
}
}
Теперь нам необходимо определить уровни квантильного распределения. Для этого мы последовательно вызываем методы прямого прохода нейронных слоёв нашего перцептрона квантильной функции.
if(!cQuantile1.FeedForward(GetPointer(cQuantile0))) return false; //--- if(!cQuantile2.FeedForward(GetPointer(cQuantile1))) return false;
И завершении метода прямого прохода мы вызовем кернел перевода квантильного распределения в дискретное значение ожидаемого вознаграждения для каждого возможного действия агента FQF_Output. Процедура постановки кернела в очередь выполнения остаётся прежней:
- определяем пространство задач
- передаем указатели на буферы и другую необходимую информацию в параметры кернела
- вызываем процедуры выполнения кернела.
И не забываем контролировать процесс выполнения операций на каждом шаге.
{
uint global_work_offset[1] = {0};
uint global_work_size[1] = { Neurons() };
OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_quantiles, cQuantile2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_delta_taus, cSoftMax.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_output, getOutputIndex());
OpenCL.SetArgument(def_k_FQF_Output, def_k_fqfout_total,
(uint)(cQuantile2.Neurons() / global_work_size[0]));
if(!OpenCL.Execute(def_k_FQF_Output, 1, global_work_offset, global_work_size))
{
printf("Error of execution kernel FQF_Output: %d", GetLastError());
return false;
}
}
//---
return true;
}
На этом мы завершаем работу над прямым проходом нашего класса и переходим к переопределению методов обратного прохода. Который в нашем классе будет представлен 2 методами: calcInputGradients и updateInputWeights.
2.2. Обратный проход
Первым мы рассмотрим метод calcInputGradients, в котором осуществляется передача градиента до всех внутренних слоёв и предыдущего нейронного слоя.
Указанный метод полностью повторяет метод прямого прохода, только в обратном направлении. Соответственно, для всех кернелов, которые были созданы при прямом проходе, необходимо создать кернелы с «зеркальными» операциями. И так как весь процесс обратного прохода организован в обратной последовательности прямого прохода, то и построение кернелов мы будем осуществлять в аналогичном порядке.
На выходе метода прямого прохода мы преобразовывали квантильное распределение в дискретное значение по каждому возможному действию агента. На входе метода обратного прохода мы ожидаем получить градиент ошибки по каждому действию. И нам предстоит распределить полученный градиент на как на значение квантильной функции, так и на дельты вероятностей квантильных диапазонов.
Указанный функционал мы будем выполнять в кернеле FQF_OutputGradient. В параметрах кернела мы будем передавать указатели сразу на 5 буферов данных. 3 из них будут содержать исходные данные и 2 для записи результатов работы кернела.
Напомню, что тензоры дельт вероятностей и результатов квантильной функции у нас структурированы с табличной логикой в разрезе квантилей и возможных действий агента. Аналогично, мы будем запускать кернел в 2 мерном пространстве задач в разрезе квантилей и действий агента.
В теле кернела мы сразу запрашиваем идентификаторы потока в обоих измерениях, количество потоков в первом измерении и определяем смещение в буферах данных.
__kernel void FQF_OutputGradient(__global float* quantiles, __global float* delta_taus, __global float* output_gr, __global float* quantiles_gr, __global float* taus_gr ) { size_t i = get_global_id(0); size_t total = get_global_size(0); size_t action = get_global_id(1); int shift = action * total;
Далее нам предстоит распределить градиент ошибки. При прямом проходе результат мы получали путем умножения 2 переменных. Производной операции умножения является второй множитель. Следовательно, для передачи градиента нам необходимо умножить полученный градиент ошибки на соответствующий элемент противоположного тензора.
Тут надо обратить внимание, что один элемент буфера полученных градиентов нам предстоит умножить на соответствующие элементы 2 тензоров. То есть нам предстоит 2 раза обращаться к одному и тому же элементу глобального буфера. Но мы помним, что обращение к элементам глобальной памяти «дорогое удовольствие». И чтобы сократить общее время выполнения операций мы сначала перенесем значение элемента глобального буфера в переменную наиболее быстрой частной памяти. И дальнейшие операции уже будем выполнять с этой «быстрой» переменной.
Результаты операций сохраняем в соответствующие элементы 2 буферов результатов.
float gradient = output_gr[action];
quantiles_gr[shift + i] = gradient * delta_taus[shift + i];
taus_gr[shift + i] = gradient * quantiles[shift + i];
}
Следующий кернел, который мы вызывали непосредственно из нашего метода прямого прохода является кернел Dropout. В нем мы осуществляли адамарное умножение 2 тензоров эмбедингов. Эмбединга состояния среды и эмбединга квантилей. И если при прямом проходе мы воспользовались ранее созданным кернелом Dropout, то сейчас для распределения градиента ошибки в 2 направлениях нам потребовалось бы вызывать указанный кернел последовательно 2 раза с разными исходными данными. Но мы же стремимся к максимальному параллелизму операций с целью максимально сократить время обучения модели. Поэтому мы потратим немного своего времени и создадим новый кернел FQF_QuantileGradient.
Можно заметить, что алгоритм данного кернела полностью повторяет алгоритм предыдущего кернела. В этом нет ничего странного. Ведь оба кернела выполняют похожую функцию. Разница лишь в смещении по буферу полученных градиентов. Если в предыдущем случае размер буфера полученных градиентов отличался от остальных буферов, так как имел только одно дискретное значение для каждого возможного действия агента, то в данном случае все буферы имеют один размер. И, соответственно, в буфере поученных градиентов мы используем смещение аналогичное остальным буферам.
__kernel void FQF_QuantileGradient(__global float* state_embeding, __global float* taus_embeding, __global float* quantiles_gr, __global float* state_gr, __global float* taus_gr ) { size_t i = get_global_id(0); size_t total = get_global_size(0); size_t action = get_global_id(1); int shift = action * total; //--- float gradient = quantiles_gr[shift + i]; state_gr[shift + i] = gradient * taus_embeding[shift + i]; taus_gr[shift + i] = gradient * state_embeding[shift + i]; }
Последний кернел, который нам предстоит рассмотреть — это кернел FQF_CosineGradient, который выполняет процедуру, обратную подготовке данных для эмбединга квантилей. Производная операции подготовки данных имеет нижеследующий вид.
![]()
В результате выполнения операций данного кернела мы ожидаем получить градиент ошибки на выходе слоя SoftMax модели прогнозирования вероятностей квантилей. И здесь следует обратить внимание на тот факт, что каждый квантиль использовал накопительное значение тензора результатов SoftMax. А значит каждый элемент тензора оказывал влияние на все последующие квантили. И логично было бы, чтобы каждый элемент тензора получил свою долю градиента в соответствии со своим участием в конечном результате. Поэтому мы будем собирать градиент ошибки со всех элементов буфера полученных градиентов, на которые оказывал влияние анализируемый элемент тензора результатов SoftMax.
Рассмотрим реализацию кернела. В параметрах мы передаем указатели на 3 буфера данных:
- результаты слоя SoftMax
- полученные градиенты ошибки
- буфер результатов — градиенты ошибки на уровне буфера результатов слоя SoftMax.
Как и большинство рассмотренных в данной статье кернелов, данные кернел будет запускаться в двухмерном пространстве задач. Одно измерение квантилей, второе — возможных действий агента.
В теле кернела мы запрашиваем идентификаторы потока в обоих измерениях и определяем смещение в буферах данных. Все буфера данных имеют одинаковый размер. Следовательно, и смещение будет одно для всех буферов данных.
__kernel void FQF_CosineGradient(__global float* softmax, __global float* output_gr, __global float* softmax_gr ) { size_t i = get_global_id(0); size_t total = get_global_size(0); size_t action = get_global_id(1); int shift = action * total;
Каждый элемент оказывает влияние только на свой и последующие квантили. Поэтому мы сначала просто посчитаем сумму предшествующих элементов.
float cumul = 0; for(int it = 0; it < i; it++) cumul += softmax[shift + it];
А затем посчитаем градиент от соответствующего элемента.
Здесь надо обратить внимание, что при прямом проходе мы на эмбединг передавали среднее значение квантиля. Соответственно и градиент ошибки мы считаем по среднему значению вероятности квантиля.
float result = -M_PI_F * i * sin(M_PI_F * i * (cumul + softmax[shift + i] / 2)) * output_gr[shift + i];
Далее мы в цикле аналогичным образом определим градиент ошибки от последующих квантилей. При этом мы будем корректировать влияние градиента в соответствии с долей текущего элемента в суммарной вероятности квантиля градиента.
for(int it = i + 1; it < total; it++) { cumul += softmax[shift + it - 1]; float temp = cumul + softmax[shift + it] / 2; result += -M_PI_F * it * sin(M_PI_F * it * temp) * output_gr[shift + it] * softmax[shift + it] / temp; } softmax_gr[shift + i] += result; }
После завершения итераций цикла результат операций запишем в соответствующий элемент буфера результатов.
На данном этапе мы подготовили все кернелы для организации обратного прохода нашего класса. И можно приступить к непосредственному созданию метода распределения градиента ошибки calcInputGradients.
В параметрах метод получает указатель на объект предыдущего нейронного слоя, которому нам предстоит передать градиент ошибки. И сразу в метода мы организовываем блок контролей. Здесь мы проверяем указатели на полученный объект и внутренние буфера данных.
bool CNeuronFQF::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !Gradient || !Output) return false;
Обратите внимание, в отличии от метода прямого прохода здесь создаем контрольный блок. Это связано с тем, что операции данного метода начинаются с вызова кернела программы OpenCL. И при передаче ему указателей на буферы данных мы должны быть уверены в их существовании. В противном случае мы рискуем получить критическую ошибку в процессе выполнения операций.
После успешного прохождения блока контролей мы переходим к непосредственному выполнению операций распределения градиента ошибки. И первым мы вызываем кернел FQF_OutputGradient, в котором распределим градиент ошибки на перцептрон квантильной функции и блок прогнозирования квантилей. Операции постановки кернела в очередь аналогичны соответствующим операция прямого прохода. Кернел запускается в 2 мерном пространстве задач. Первое измерение соответствует квантилям, а второе — возможным действиям агента.
{
uint global_work_offset[2] = {0, 0};
uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles,
cQuantile2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus,
cSoftMax.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_output_gr,
getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles_gr,
cQuantile2.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus_gr,
cSoftMax.getGradientIndex());
if(!OpenCL.Execute(def_k_FQF_OutputGradient, 2, global_work_offset, global_work_size))
{
printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
return false;
}
}
Далее мы проведем градиент ошибки через перцептрон квантильной функции. Для этого мы последовательно вызовем методы обратного прохода внутренних нейронных слоёв указанного блока.
if(!cQuantile1.calcHiddenGradients(GetPointer(cQuantile2))) return false; if(!cQuantile0.calcHiddenGradients(GetPointer(cQuantile1))) return false;
Градиент ошибки от квантильной функции нам предстоит распределить на эмбединг текущего состояния системы (предыдущий нейронный слой) и эмбединг вероятностей квантилей. Для выполнения этого функционала мы создали кернел FQF_QuantileGradient. Мы осуществляем вызов указанного кернела по уже отработанной процедуре.
{
uint global_work_offset[2] = {0, 0};
uint global_work_size[2] = { cCosineEmbeding.Neurons(), 1 };
OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_enbeding,
NeuronOCL.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_embedding,
cCosineEmbeding.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_quantiles_gr,
cQuantile0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_gr,
NeuronOCL.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_gr,
cCosineEmbeding.getGradientIndex());
if(!OpenCL.Execute(def_k_FQF_QuantileGradient, 2, global_work_offset, global_work_size))
{
printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
return false;
}
}
Следующим этапом мы проводим градиент ошибки через эмбединг квантилей. Здесь мы сначала вызываем метод обратного прохода внутреннего нейронного слоя cCosine.
if(!cCosine.calcHiddenGradients(GetPointer(cCosineEmbeding))) return false;
А потом по уже отработанной процедуре вызываем кернел FQF_CosineGradient.
{
uint global_work_offset[2] = {0, 0};
uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax,
cSoftMax.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_output_gr,
cCosine.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax_gr,
cSoftMax.getGradientIndex());
if(!OpenCL.Execute(def_k_FQF_CosineGradient, 2, global_work_offset, global_work_size))
{
printf("Error of execution kernel FQF_CosineGradient: %d", GetLastError());
return false;
}
}
В завершении метода проведем градиент ошибки через внутренний слой cSoftMax, путем вызова его метода обратного прохода.
if(!cSoftMax.calcInputGradients(GetPointer(cFraction))) return false; //--- return true;
Обратите внимание, мы не передаем на предыдущий слой градиент ошибки от блока прогнозирования вероятностей квантилей. Это связано с приоритетностью задачи определения ожидаемого вознаграждения, а не вероятностного распределения.
Второй метод обратного прохода updateInputWeights, который нам предстоит переопределить, отвечает за функционал обновления параметров нашей модели. И здесь все довольно просто. Мы лишь поочередно вызываем одноименные методы внутренних нейронных слоёв и проверяем результат выполнения операций.
bool CNeuronFQF::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cFraction.UpdateInputWeights(NeuronOCL)) return false; if(!cCosineEmbeding.UpdateInputWeights(GetPointer(cCosine))) return false; if(!cQuantile1.UpdateInputWeights(GetPointer(cQuantile0))) return false; if(!cQuantile2.UpdateInputWeights(GetPointer(cQuantile1))) return false; //--- return true; }
На этом мы завершаем работу с основным функционалом нашего нового класса CNeuronFQF. Выше мы рассмотрели организацию процессов прямого и обратного проходов. В классе ещё были переопределены методы сохранения данных в файл и восстановление работоспособности класса после сохранения. В них мы лишь поочередно вызывали соответствующие методы внутренних объектов. И я предлагаю Вам самостоятельно познакомиться с их построением. Полный код всех используемых классов и их методов вы можете найти во вложении к статье.
А мы двигаемся дальше. Выше мы построили класс для организации алгоритма обучения модели методом полной параметризации квантильной функции. Но это лишь часть процесса. Это по-прежнему остаётся всё то же Q-обучение с использование буфера данных и Target Net. И для облегчения процесса использования описанного метода непосредственно в процессе Q-обучения был создан класс CFQF наследником базового класса наших моделей CNet.
class CFQF : protected CNet { private: uint iCountBackProp; protected: uint iUpdateTarget; //--- CNet cTargetNet; public: CFQF(void); CFQF(CArrayObj *Description) { Create(Description); } bool Create(CArrayObj *Description); ~CFQF(void); bool feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { return CNet::feedForward(inputVals, window, tem); } bool backProp(CBufferFloat *targetVals, float discount = 0.9f, CArrayFloat *nextState = NULL, int window = 1, bool tem = true); void getResults(CBufferFloat *&resultVals); int getAction(void); int getSample(void); float getRecentAverageError() { return recentAverageError; } bool Save(string file_name, datetime time, bool common = true) { return CNet::Save(file_name, getRecentAverageError(), (float)iUpdateTarget, 0, time, common); } virtual bool Save(const int file_handle); virtual bool Load(string file_name, datetime &time, bool common = true); virtual bool Load(const int file_handle); //--- virtual int Type(void) const { return defFQF; } virtual bool TrainMode(bool flag) { return CNet::TrainMode(flag); } virtual bool GetLayerOutput(uint layer, CBufferFloat *&result) { return CNet::GetLayerOutput(layer, result); } //--- virtual void SetUpdateTarget(uint batch) { iUpdateTarget = batch; } virtual bool UpdateTarget(string file_name); };
Класс был создан аналогично классу CQRDQN из предыдущей статьи. И его структура практически полностью повторяет структуру указанного класса. Мы лишь удалили неиспользуемые переменные и матрицу вероятностей. Ведь за это у нас отвечает отдельные нейронные слои. И, соответственно, внесли изменения в методы класса. Я не буду сейчас подробно останавливаться на всех методах класса. Вы сможете ознакомиться с ними самостоятельно во вложении. Остановлюсь лишь на некоторых из них.
Вначале предлагаю остановиться на методе обратного прохода. В параметрах метод получает целевые значения и следующее состояние системы. При этом следующее состояние системы является необязательным параметром. Это может быть использовано при обучении новой модели, когда использование необученной модели для прогнозирования будущих вознаграждений добавит лишь шума и усложнит процесс обучения.
В теле метода мы сразу поверяем наличие обязательного параметра в виде буфера целевых значений.
bool CFQF::backProp(CBufferFloat *targetVals, float discount = 0.9f, CArrayFloat *nextState = NULL, int window = 1, bool tem = true) { //--- if(!targetVals) return false;
Затем проверяем наличие необязательного параметра и, при необходимости, сделаем прогноз будущих вознаграждений. Здесь же мы скорректируем целевые значения на величину будущего вознаграждения с учетом коэффициента дисконтирования.
if(!!nextState) { vectorf target; if(!targetVals.GetData(target) || target.Size() <= 0) return false; if(!cTargetNet.feedForward(nextState, window, tem)) return false; cTargetNet.getResults(targetVals); if(!targetVals) return false; target = target + discount * targetVals.Maximum(); if(!targetVals.AssignArray(target)) return false; }
После чего мы проверим необходимость обновления Target Net.
if(iCountBackProp >= iUpdateTarget) { #ifdef FileName if(UpdateTarget(FileName + ".nnw")) #else if(UpdateTarget("FQF.upd")) #endif iCountBackProp = 0; } else iCountBackProp++;
И в завершении метода вызовем метод обратного прохода родительского класса.
return CNet::backProp(targetVals);
}
Также был изменен метод жадного выбора действия. Здесь мы просто определяем элемент с максимальным вознаграждением из буфера результатов модели.
int CFQF::getAction(void) { CBufferFloat *temp; CNet::getResults(temp); if(!temp) return -1; //--- return temp.Maximum(0, temp.Total()); }
Изменения были внесены и в метод семплирования действия getSample. В нем мы сначала получаем результат последнего прямого прохода модели.
int CFQF::getSample(void) { CBufferFloat* resultVals; CNet::getResults(resultVals); if(!resultVals) return -1;
Полученные данные копируем из буфера в вектор и применяем к ним функцию SoftMax. После чего посчитаем кумулятивные суммы значений вектора.
vectorf temp; if(!resultVals.GetData(temp)) { delete resultVals; return -1; } delete resultVals; //--- if(!temp.Activation(temp, AF_SOFTMAX)) return -1; temp = temp.CumSum();
Полученный вектор является своеобразным квантильным распределением вероятностей действий агента. Из этого распределения мы семплируем одно значение. И возвращаем его вызывающей программе.
int err_code; float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code); if(random >= 1) return (int)temp.Size() - 1; for(int i = 0; i < (int)temp.Size(); i++) if(random <= temp[i] && temp[i] > 0) return i; //--- return -1; }
На каждом шаге мы проверяем результат выполнения операций. В случае возникновения ошибки возвращаем вызывающей программе значение «-1».
Этим мы завершаем рассмотрение алгоритмов построения новых классов для реализации алгоритма FQF. С полным кодом всех классов и их методов можно ознакомиться во вложении.
3. Тестирование
Для обучения модели методом полностью параметризированной квантильной функции был создан электронный советник «FQF-learning.mq5». Он практически полностью повторил алгоритм советника "QRDQN-learning.mq5" из предыдущей статьи. Мы лишь изменили название файла и используемые объекты. Поэтому позвольте не останавливаться на архитектуре его алгоритмов. Полный код советника приведен во вложении.
Обучение модели осуществлялось на исторических данных инструмента EURUSD за последние 2 года и таймфрейм H1. Параметры всех индикаторов использовались заданные по умолчанию. Как можно заметить, это неизменные параметры тестирования всех моделей в рамках нашей серии статей.
Сразу скажу, что в процессе обучения модель порадовала довольно ровной и стабильной динамикой к снижению ошибки. Что является довольно хорошим маркером стабильности обучения модели.
Обученная модель была протестирована в тестере стратегий. Для этого был создан советник «FQF-learning-test.mq5». Который является копией советника «QRDQN-learning-test.mq5» из предыдущей статьи. И мы не будем сейчас разбирать его алгоритм. Так как мы лишь изменили название файла и класс модели. С полным кодом советника можно ознакомиться во вложении.
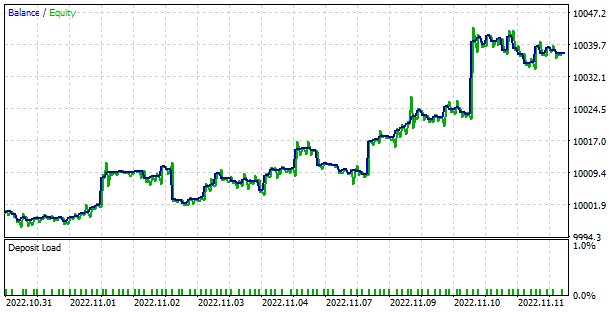
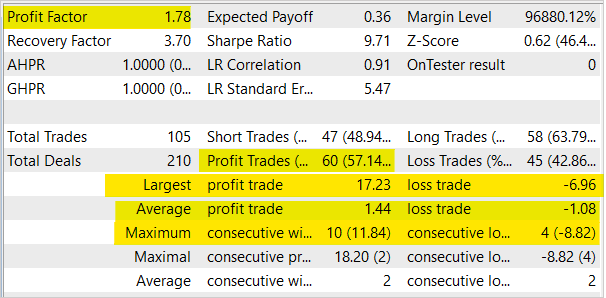
В процессе тестирования модель продемонстрировала способность к генерированию прибыли. По результатам тестирования модель показала профит-фактор на уровне 1.78 и фактор восстановления 3.7. При этом доля прибыльных сделок превышает 57%. А максимальная прибыльная сделка практически в 2.5 раза превышает максимальную убыточную сделку. Максимальная прибыльная серия составила 10 сделок. В то время как максимальная убыточная серия не превышает 4 сделок. В целом средняя прибыльная сделка на ⅓ превышает среднюю убыточную сделку.
Заключение
В данной статье мы продолжили изучение алгоритмов распределенного обучения с подкреплением и построили классы для реализации метода обучения полностью параметризированной квантильной функции в обучении с подкреплением. Мы провели обучение модели данным методом. И проверили работоспособность обученной модели в тестере стратегий. Надо сказать, что в процессе обучения метод продемонстрировал устойчивую динамику к снижению ошибки. И в процессе тестирования обученной модели в тестере стратегий мы могли наблюдать способность модели к генерированию прибыли.
Ещё раз хочу напомнить, что торговля на бирже относится к высокорискованным методам инвестирования. А представленные в статье программы призваны лишь продемонстрировать работу методов и алгоритмов. Они не готовы для использования в реальной торговле. Тем не менее на их базе можно создать рабочие торговые инструменты. Но перед их использование необходимо тщательное и всесторонне тестирование разработанных инструментов. Риски использования программ в реальной торговле должны быть оценены и приняты пользователем.
Ссылки
- Нейросети — это просто (Часть 3): Сверточные сети
- Нейросети — это просто (Часть 12): Dropout
- Нейросети — это просто (Часть 26): Обучение с подкреплением
- Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
- Нейросети — это просто (Часть 28): Policy gradient алгоритм
- Нейросети — это просто (Часть 32): Распределенное Q-обучение
- Нейросети — это просто (Часть 33): Квантильная регрессия в распределенном Q-обучении
- A Distributional Perspective on Reinforcement Learning
- Distributional Reinforcement Learning with Quantile Regression
- Implicit Quantile Networks for Distributional Reinforcement Learning
- Fully Parameterized Quantile Function for Distributional Reinforcement Learning
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | FQF-learning.mq5 | Советник | Советник для оптимизации модели |
| 2 | FQF-learning-test.mq5 | Советник | Советник для тестирования модели в тестере стратегий |
| 3 | FQF.mqh | Библиотека классов | Класс организации модели FQF |
| 4 | NeuroNet.mqh | Библиотека классов | Библиотека для организации моделей нейронных сетей |
| 5 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL для организации моделей нейронных сетей |
| 6 | NetCreator.mq5 | Советник | Инструмент создания моделей |
| 7 | NetCreatotPanel.mqh | Библиотека классов | Библиотека класса для создания инструмента |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торгового советника с нуля (Часть 30): CHART TRADE теперь как индикатор?!
Разработка торгового советника с нуля (Часть 30): CHART TRADE теперь как индикатор?!
 Разработка торговой системы на основе Awesome Oscillator
Разработка торговой системы на основе Awesome Oscillator
 Разработка торговой системы на основе Accelerator Oscillator
Разработка торговой системы на основе Accelerator Oscillator
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо!
Ваша "производительность" поражает. Не останавливайтесь!
На таких как Вы всё держится!
P.S.
Я читал новости НейроСетей...
"Нейросети тоже нуждаются в состояниях, напоминающих сны.
К такому выводу пришли исследователи из Национальной лаборатории Лос-Аламоса..."
Доброго времени.
По Вашему коду сделал подобие "Сна" НейроСети.
Процент "спрогнозированных" увеличился на 3%. Для моего "СуперКомпа" - это полет в космос!
Применял эту функцию в конце каждой эпохи обучения:
Вы могли бы протестировать и потом прокомментировать как Вы это делаете? Вдруг "Сны" помогут ИИ?
P.S.
SleepPerriod=1;
Я добавлял к
где Дельта=0. Но мой компьютер Очень, очень слабый... :-(
Похожа ли архитектура nn на архитектуру из предыдущей статьи, за исключением последнего слоя?
да