ニューラルネットワークが簡単に（第34部）：FQF（Fully Parameterized Quantile Function、完全にパラメータ化された分位数関数）

MetaTrader 5 — エキスパートアドバイザー | 26 4月 2023, 09:32

218

Dmitriy Gizlyk

内容

2.MQL5での実装

はじめに

分散型Q学習アルゴリズムの研究を続けます。これまでに、すでに2つのアルゴリズムを検討しました。最初のアルゴリズム[4]のモデルは、与えられた値の範囲で報酬を受け取る確率を学習しました。2番目のアルゴリズム[5]では、問題を解決するために別の方法を使用しました。与えられた確率で報酬レベルを予測するようにモデルを訓練しました。

明らかに、どちらのアルゴリズムでも、問題を解決するには、報酬の分配の性質に関するアプリオリな知識が必要です。最初のアルゴリズムでは、予想される報酬レベルをモデルに入力しますが、2番目のアルゴリズムでは、ユーザーのタスクが少し簡単になります。モデルに入力する必要があるのは一連の分位数です。そのサイズは0から1の範囲で正規化され、昇順に並べられています。ただし、報酬値の真の分布を知らなければ、必要な分位数とそれぞれのボリュームを決定することは困難です。

なお、調査したシーケンスの一様分布を仮定したので、一様な範囲の分位数を使用しました。主な調整ハイパーパラメータは、そのような分位数で、検証データセットで経験的に決定されます。

1.完全なパラメータ化の理論的側面

上記の方法はどちらも、訓練データセットの予備調査とハイパーパラメータの最適化を必要とします。同時に、ハイパーパラメータを最適化するとき、いくつかの平均値を選択することに注意してください。言い換えれば、望ましい目標にできるだけ近づくことができるものを選択します。選択したパラメータは、調査中のシステムの可能なすべての状態を可能な限り満たす必要があります。また、一様分布を仮定しました。したがって、実際にあるモデルにはさまざまな妥協点があります。明らかに、そのようなモデルは最適なものとはほど遠いでしょう。

信頼性を高め、予測誤差を最小限に抑えるには、訓練する分位数の数を増やす必要があります。これにより、モデルの訓練時間とモデルのサイズが増加します。ほとんどの場合、この方法は効果的ではありません。ただし、ここでの目的は、環境を可能な限り徹底的に研究することなので、最初のアルゴリズムで固定値カテゴリを放棄して2番目のアルゴリズムで固定分位数を放棄するという方法は適切なように思われます。

1.1.IQN（Implicit Quantile Networks、暗黙的分位数ネットワーク）

ここでは、分位数の使用がより有望に見えます。カテゴリを決定するには、元の分布を十分に調査し、その制限を定義する必要があるためです。ただし、このモデルは、指定された範囲外の値に対して準備されていません。カテゴリモデルは普遍的なものではなく、タスクごとに異なります。

同時に、イベントの発生確率には0から1の明確な限界がありますが、分位数の一様分布を使用すると、自由度と最適化可能な関数の範囲が制限されます。分位数の数を増やすことなく、モデル自体が最適な分位数分布を決定できるようなアルゴリズムを見つけるとよいでしょう。

このような最初のアルゴリズムは、2018年7月の記事「Implicit Quantile Networks for Distributional Reinforcement Learning」で提案されましたが、著者らは、最適分位数の問題に少し異なる方法でアプローチしました。アルゴリズムは、前に説明したQR-DQNに基づいて構築されていますが、最適な分位数を探す代わりに、それらをランダムに生成し、環境の状態を説明する初期データとともにモデルに入力しています。考え方は次のとおりです。訓練プロセス中に、異なる分位数分布を持つ同じシステム状態がモデルに入力されます。その結果、モデルは分位数関数の特定のスライスではなく、その完全な近似を使用することを余儀なくされます。

この方法により、「分位数」ハイパーパラメータの影響を受けにくいモデルの訓練が可能になります。それらのランダムな分布により、近似関数の範囲を不均一に分布する関数に拡張できます。

データがモデルに入力される前に、以下の式に従って、ランダムに生成された分位数の埋め込みが作成されます。

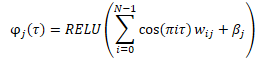
結果の埋め込みを元のデータのテンソルと組み合わせるには、さまざまなオプションがあります。これは、2つのテンソルの単純な連結、または2つの行列のアダマール（要素ごと）積のいずれかです。

以下は、記事の著者らによって提示された、考慮されたアーキテクチャの比較です。

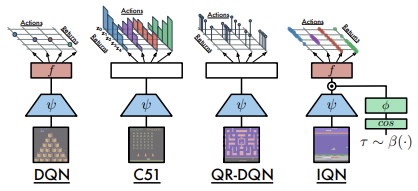
モデルの有効性は、57のアタリゲームで実施されたテストによって確認されています。以下は、元の記事[8]にある比較表です。

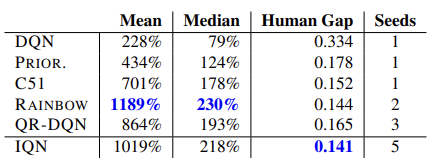
仮説的には、モデルのサイズに制限がない場合、この方法により、予測された報酬の分布を学習できます。

1.2.FQF（Fully Parameterized Quantile Function、完全にパラメータ化された分位数関数）

提示されたIQNのモデルは、さまざまな関数を近似することができますが、このプロセスはモデルの成長に関連しています。しかし、リソースは実際には限られています。ランダム分位数を生成する場合、訓練時とモデルの使用時の両方で、最適でない値が得られるリスクが常にあります。

Fully Parameterized Quantile Function for Distributional Reinforcement Learningは2019年11月に提案されました。

基本的に、これは同じIQNモデルですが、ランダム分位数ジェネレーターの代わりに全結合ニューラル層を使用します。これは、入力として与えられた環境の現在の状態に基づいて分位数の分布を返します。このモデルは、「状態と行動」の値のペアごとに分位数分布を生成します。これにより、特定のシステム状態での各行動に対して期待される報酬の最適な分布の近似が可能になります。これは、この記事の冒頭でお話ししたことです。

分位数の主な要件は引き続き保持されます。これらには、0から1の範囲が含まれます。この効果を実現するために、アルゴリズムはニューラル層の出力でデータの正規化を使用します。データはSoftmax関数を使用して正規化され、正規化されたベクトルの要素の累積加算が適用されます。

元の記事では、著者は55のアタリゲームでのアルゴリズムテストの結果を示しています。以下は、元の記事の結果をまとめた表です。提示されたデータは、分位数関数の完全なパラメータ化アルゴリズムが他の分散Q学習アルゴリズムよりも優れていることを示していますが、その代償はモデルのパフォーマンスです。追加の分位数生成モデルには、追加の計算リソースが必要です。

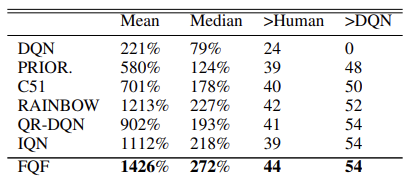
手法の作成者は、最適な分位数を選択するための実験をおこなって32の分位数の分布を使用することを提案しました。

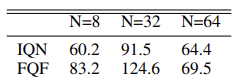
さらなるトピックで実装しながら、メソッドアルゴリズムをより詳細に検討します。

2.MQL5での実装

手法の作成者はその記事で2つのニューラルネットワークの使用法について説明しています。1つは分位数の分布を生成、もう1つは分位数関数の近似です。ただし、説明されているアルゴリズムでは、実際には、環境状態の埋め込みを作成する3番目の畳み込みネットワークも使用します。この状態埋め込みは、検討中のアルゴリズムのソースデータです。

ただし、以前に作成したライブラリは、シーケンシャルモデルの構築に重点を置いています。複数の連続モデルを訓練するときに必要になる可能性がある、モデル間で誤差勾配を渡すアルゴリズムは含まれていません。

もちろん、転移学習メカニズムを使用して、個々のモデルを順次訓練することもできますが、アルゴリズム全体を1つのモデルに実装することにしました。

環境状態の埋め込みを作成するために、以前に説明した畳み込みモデルを使用します[1]。したがって、既存のツールを使用してそのようなモデルを簡単に構築できます。

次に、FQFアルゴリズムを実装する必要があります。私の意見では、ライブラリの概念内でこれを実装する最も簡単な方法は、新しいニューラル層クラスを作成することです。分析中のシステムの現在の状態の埋め込みを入力すると、層がエージェントの行動を出力します。したがって、新しいクラス内で、モデルのエージェントを構築します。

ニューラル層の基本クラスCNeuronBaseOCLから派生した新しいクラスCNeuronFQFを作成します。新しいクラスは、通常のメソッドセットをオーバーライドします。保護ブロックでは、FQFアルゴリズムを実装するときに使用する内部オブジェクトを宣言します。アルゴリズムを構築する過程で、オブジェクトの目的についてさらに学習します。

class CNeuronFQF : protected CNeuronBaseOCL
  {
protected:
   //--- Fractal Net
   CNeuronBaseOCL    cFraction;
   CNeuronSoftMaxOCL cSoftMax;
   //--- Cosine embeding
   CNeuronBaseOCL    cCosine;
   CNeuronBaseOCL    cCosineEmbeding;
   //--- Quantile Net
   CNeuronBaseOCL    cQuantile0;
   CNeuronBaseOCL    cQuantile1;
   CNeuronBaseOCL    cQuantile2;
   //--- 
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override; 
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; 

public:
                     CNeuronFQF();
                    ~CNeuronFQF();
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint actions, uint quantiles, uint numInputs, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override        const { return defNeuronFQF; }
   virtual CLayerDescription* GetLayerInfo(void) override;
  };

私たちのクラスでは、静的な内部オブジェクトを使用しているため、クラスのコンストラクタとデストラクタを空のままにすることができます。

クラスと内部オブジェクトはInitメソッドで初期化されます。内部オブジェクトを初期化するには、次のパラメータが必要です。

numOutputs：次の層のニューロンの数
myIndex：現在のニューロンの層内インデックス
open_cl：OpenCLデバイスを操作するためのオブジェクトへのポインタ
actions：可能なエージェント行動の数
quantiles：分位数の数
numInputs：前のニューラル層のサイズ
Optimization_type：モデルパラメータの最適化に使用される関数
batch：パラメータ更新のバッチサイズ

bool CNeuronFQF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                      uint actions, uint quantiles, uint numInputs,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, actions, optimization, batch))
      return false;
   SetActivationFunction(None);

受け取ったパラメータを確認するためのブロックはメソッド本体では定義せず、代わりに、必要なすべてのコントロールが既に含まれている親クラスの同様のメソッドを呼び出します。親クラスのメソッドは、外部パラメータを制御し、継承されたオブジェクトを初期化します。したがって、実行が成功した後は、新しく宣言されたオブジェクトを初期化するだけで済みます。

また、オブジェクトの活性化関数を無効にすることを忘れないでください。必要な活性化関数はすべてアルゴリズムによって定義され、内部オブジェクトに対して指定されます。

FQFアルゴリズムによれば、システム状態の埋め込みが分位数生成ネットワークに入力されます。これらの目的のために、手法の作成者は、Softmax関数を使用してデータを正規化しながら、1つの全結合層を使用しています。私たちの実装では、これは活性化関数のない全結合層とSoftmax層の2つのオブジェクトになります。

可能な行動ごとに分位数の分布を生成するため、使用される層のサイズは、可能な行動数と指定された分位数の積に等しくなるように定義されます。Softmaxの場合、データの正規化も行動のコンテキストで実装されます。

//---
   if(!cFraction.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cFraction.SetActivationFunction(None);
//---
   if(!cSoftMax.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cSoftMax.SetHeads(actions);
   cSoftMax.SetActivationFunction(None);

さらに、アルゴリズムに従って、取得した分位数の埋め込みを作成する必要があります。これは2段階で作成されます。まず、データを準備し、cCosineニューラル層バッファに保存します。次に、ReLU活性化関数を使用して、全結合層cCosineEmbeddingに渡します。さらに、cCosineEmbeding層は、後続のテンソルのアダマール積のために、埋め込みテンソルのサイズをソースデータのサイズと等しくします。

   if(!cCosine.Init(numInputs, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cCosine.SetActivationFunction(None);
//---
   if(!cCosineEmbeding.Init(0, myIndex, open_cl, numInputs, optimization, batch))
      return false;
   cCosineEmbeding.SetActivationFunction(LReLU);

最後に、分位数関数モデルを介してデータを渡す必要があります。これには、行動数と分位数の積の4倍のニューロン数を持つ1つの隠れ全結合層と、ReLU活性化関数が含まれます。出力に活性化関数のない全結合層もあります。結果層のサイズは、可能な行動の数と分位数の積に等しくなります。

   if(!cQuantile0.Init(4 * actions * quantiles, myIndex, open_cl, numInputs, optimization, batch))
      return false;
   cQuantile0.SetActivationFunction(None);
//---
   if(!cQuantile1.Init(actions * quantiles, myIndex, open_cl,
                       4 * actions * quantiles, optimization, batch))
      return false;
   cQuantile1.SetActivationFunction(LReLU);
//---
   if(!cQuantile2.Init(0, myIndex, open_cl, actions * quantiles, optimization, batch))
      return false;
   cQuantile2.SetActivationFunction(None);
//---
   return true;
  }

メソッドを実装するときは、操作の実行を制御することを忘れないでください。すべての内部オブジェクトの初期化が成功したら、肯定的な結果でメソッドを終了します。

2.1.フィードフォワード

オブジェクトを初期化した後、フィードフォワードプロセスの構築に進みます。ただし、CNeuronFQF::feedForwardメソッドの作成に進む前に、OpenCLプログラムで必要なカーネルを作成する必要があります。ニューラル層の実装は完了しましたが、まだ新しい機能性を実装する必要があります。

FQFアルゴリズムによれば、ソースデータは現在の状態の埋め込みとして分位数生成モデルに入力されます。2つのニューラルネットワーク（全結合のcFractionとcSoftMax）の操作は既に実装されていますが、Softmaxは、各行動の値の合計が1に等しいテンソルを出力します。分位数の割合を増やす必要がありますが。その後、以下の式を使用してこれらの分位数の埋め込みを作成する必要があります。

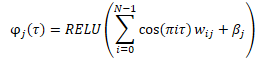
上記の式は、ReLU活性化関数を使用して全結合ニューラル層の式を完全に繰り返します。ここでの違いは、ソースデータがcos(πi)であることです。そのため、そのような余弦のテンソルをニューラル層の結果cCosineのバッファに準備します。

この機能性を実装するために、FQF_Cosineカーネルを作成します。データバッファへの2つのポインタをカーネルに入力します。1つはSoftmax層からデータを提供し、もう1つはカーネル操作の結果を書き込むために使用されます。

FQFアルゴリズムに従って、可能な行動ごとに分位数を作成する必要があります。したがって、2次元の問題空間を考慮してカーネルアルゴリズムを構築します。1次元目は分位数に使用され、2次元目は可能なエージェント行動に使用されます。

カーネル本体で、両方の次元でスレッドIDを決定します。また、最初の次元のスレッドの総数を要求します。これに基づいて、分析された行動の最初の分位までのテンソルのオフセットを決定できます。

次に、現在の分位数の累積シェアを計算する必要があります。これはループでおこなわれます。

次の点に注意してください。QR-DQNアルゴリズムと同様に、分位数の上限ではなく、その平均値を決定します。したがって、前のステップでSoftmaxによって決定された以前のすべての分位数のシェアを合計し、現在の分位数のシェアの半分を追加します。

次に、得られた現在の分位数の平均値、数Pi、および分位数の序数の積から余弦を書き留めます。

__kernel void FQF_Cosine(__global float* softmax,
                         __global float* output)
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;
//---
   float result = 0;
   for(int it = 0; it < i; it++)
      result += softmax[shift + it];
   result += softmax[shift + i] / 2.0f;
   output[shift + i] = cos(i * M_PI_F * result);
  }

分位数埋め込みを作成するためのさらなる操作は、cCosine Embedding内層の機能性を使用して実装されます。ただし、その後、初期データテンソル（システム状態の埋め込み）による分位数埋め込みテンソルのアダマール積を実行する必要があります。この操作を実装するには、別のカーネルが必要です。ただし、新しいカーネルを作成する前に、以前に作成したニューラルネットワークのカーネルを調べたところ、Dropout層用に作成したカーネルに注目しました。この層では、要素ごとに係数テンソルを元のデータで乗算するカーネルを作成しました。ここでは同様の数学演算を実行する必要があります。データと演算の論理的意味は異なりますが、これは数学演算のプロセスには影響しません。したがって、この既製の解決策を使用することにします。

これに続いて、1つの隠れ層を持つパーセプトロンとして実装した分位数ネットワークの操作がおこなわれます。パーセプトロンは、QR-DQNモデルと同様の期待報酬の分布を出力します。ただし、前述の手法とは異なり、エージェントの可能な行動ごとに独自の確率分布が使用されます。個別の報酬値を取得するには、各分位数の報酬レベルにその確率を掛ける必要があります。次に、取得した値をエージェントの行動のコンテキストに追加する必要があります。

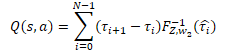
私たちの特定のケースでは、すべての確率デルタは、層の結果を含むcSoftMaxバッファで既に計算されています。これで、指定されたバッファの値を、cQuantile2ニューラル層からの分位数関数パーセプトロンの結果バッファで要素ごとに乗算するだけで済みます。エージェントの可能な行動のコンテキストで操作の結果を要約します。

これらの操作を実行するために、新しいカーネルFQF_Outputを作成します。カーネルパラメータでは、分位数関数の結果、確率デルタ、および結果バッファの3つのデータバッファへのポインタを渡します。分位数も示します。

可能なエージェント行動の数に対応する1次元のタスク空間でカーネルを実行します。

カーネル本体では、最初にスレッド識別子を要求し、対応する分位分布ベクトルへのデータバッファのシフトを決定します。

次に、ループ内で確率ベクトルに分位数分布ベクトルを掛けます。演算の結果は、対応する結果バッファに書き込まれます。

結果バッファには可能な行動ごとに1つの離散値しか含まれていないため、元のデータバッファよりも大幅に小さくなります。対照的に、ソースデータには、各行動の値のベクトル全体が含まれています。したがって、結果バッファ内のオフセットは、現在のスレッドの識別子と等しくなります。

__kernel void FQF_Output(__global float* quantiles,
                         __global float* delta_taus,
                         __global float* output,
                         uint total)
  {
   size_t action = get_global_id(0);
   int shift = action * total;
//---
   float result = 0;
   for(int i = 0; i < total; i++)
      result += quantiles[shift + i] * delta_taus[shift + i];
   output[action] = result;
  }

フィードフォワードアルゴリズムFQF全体について説明し、不足しているカーネルを作成しました。ここで、クラスに戻り、MQL5を使用してアルゴリズム全体を再現できます。いつものように、フィードフォワードパスを実行するには、CNeuronFQF::feedForwardメソッドをオーバーライドします。

フィードフォワードメソッドは、前のニューラル層へのポインタをパラメータで受け取ります。その結果バッファには、(予想どおり）現在のシステム状態の埋め込みが含まれています。

メソッド本体ではソースデータコントロールブロックを作成せずに、代わりに、内部ニューラル層cFractionおよびcSoftMaxのフィードフォワードメソッドを呼び出します。呼び出されたメソッドのそれぞれに独自のコントロールブロックがあるため、ソースデータコントロールブロックを除外してもリスクはありません。呼び出されたメソッドの結果を確認するだけです。

bool CNeuronFQF::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFraction.FeedForward(NeuronOCL))
      return false;
   if(!cSoftMax.FeedForward(GetPointer(cFraction)))
      return false;

次に、分位数の確率レベルの埋め込みを作成する必要があります。ここではまず、上記で作成したデータ準備カーネルFQF_Cosineを呼び出します。このカーネルは、2次元のタスク空間で実行されます。最初の次元では、分位数を示します。2番目の次元は、可能なエージェント行動の数です。

指定されたハイパーパラメータの内部変数は作成していません。ただし、CNeuronFQF層の結果バッファのサイズは、可能なエージェント行動の数と同じです。また、分位数は、cSoftMax層の結果バッファと行動数の比率として定義できます。

バッファへのポインタをカーネルパラメータに渡し、カーネルを実行キューに追加します。各ステップで操作を制御することを忘れないでください。

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2];
      global_work_size[1] = Output.Total();
      global_work_size[0] = cSoftMax.Neurons() / global_work_size[1];
      OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_softmax, cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Cosine, def_k_fqf_cosine_outputs, cCosine.getOutputIndex());
      if(!OpenCL.Execute(def_k_FQF_Cosine, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_Cosine: %d", GetLastError());
         return false;
        }
     }

次に、cCosineEmbeding内部ニューラル層フィードフォワードメソッドを呼び出します。これにより、分位数の埋め込みプロセスが完了します。

   if(!cCosineEmbeding.FeedForward(GetPointer(cCosine)))
      return false;

FQFアルゴリズムの次のステップでは、現在のシステム状態(初期データ)の埋め込みと分位数の埋め込みを組み合わせる必要があります。ご存じのように、この操作ではDropoutニューラル層カーネルを使用することにしました。このカーネルの本体では、40要素のベクトルに対してベクトル演算を使用しました。したがって、スレッドの数は、データバッファのサイズの4分の1になります。

カーネルパラメータで必要なデータを渡します。次に、カーネルを実行キューに入れます。

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = {(cCosine.Neurons() + 3) / 4};
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cCosineEmbeding.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cQuantile0.getOutputIndex());
      OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, (int)cCosine.Neurons());
      if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel Dropout: %d", GetLastError());
         return false;
        }
     }

ここで、分位分布のレベルを決定する必要があります。これには、分位数関数パーセプトロンでニューラル層のフィードフォワードメソッドを順次呼び出します。

   if(!cQuantile1.FeedForward(GetPointer(cQuantile0)))
      return false;
//---
   if(!cQuantile2.FeedForward(GetPointer(cQuantile1)))
      return false;

フィードフォワードパスメソッドの後、カーネルを呼び出して、分位数分布を可能なエージェント行動FQF_Outputごとに期待される報酬の離散値に変換します。カーネルを実行キューに入れる手順は同じです。

タスクスペースを定義する
バッファへのポインタとその他の必要な情報をカーネルパラメータに渡す
カーネル実行手順を呼び出す

各ステップで結果を制御することを忘れないでください。

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = { Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_quantiles, cQuantile2.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_delta_taus, cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_Output, def_k_fqfout_output, getOutputIndex());
      OpenCL.SetArgument(def_k_FQF_Output, def_k_fqfout_total, 
                         (uint)(cQuantile2.Neurons() / global_work_size[0]));
      if(!OpenCL.Execute(def_k_FQF_Output, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_Output: %d", GetLastError());
         return false;
        }
     }
//---
   return true;
  }

これでフィードフォワードカーネルの作業は終了です。次に、勾配逆伝播カーネルの作成に移ります。これは、クラスのcalcInputGradientsとupdateInputWeightsの2つのメソッドによって表されます。

2.2.フィードバックワード

まず、勾配がすべての内部層と前のニューラル層に伝播されるcalcInputGradientsメソッドを見ていきます。

このメソッドは、逆方向にのみ、フィードフォワード方法を完全に繰り返します。したがって、ダイレクトパスで作成したすべてのカーネルについて、「ミラー」操作でカーネルを作成する必要があります。勾配逆伝播プロセス全体がフィードフォワードパスの逆であるため、同じ順序でカーネルを構築します。

フィードフォワードメソッドの出力で、分位分布をエージェントの可能な各行動の離散値に変換しました。勾配逆伝播メソッドの入力で、各行動の誤差勾配を受け取ることが期待されます。次に、分位数関数の値と分位範囲の確率デルタの両方によって、結果の勾配を分配する必要があります。

これらすべてをFQF_OutputGradientカーネルに実装します。カーネルパラメータでは、5つのデータバッファへのポインタを渡します。そのうちの3つはソースデータを含み、残りの2つはカーネル操作の結果を書き込むために使用されます。

確率のデルタテンソルと分位数関数の結果は、分位と可能なエージェント行動のコンテキストで表形式のロジックで構造化されます。同様に、分位数とエージェント行動の2次元タスク空間でカーネルを実行します。

カーネル本体では、両方の次元のスレッドID、最初の次元のスレッド数を要求し、データバッファのオフセットを決定します。

__kernel void FQF_OutputGradient(__global float* quantiles,
                                 __global float* delta_taus,
                                 __global float* output_gr,
                                 __global float* quantiles_gr,
                                 __global float* taus_gr
                                )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;

次に、誤差勾配を伝播する必要があります。フィードフォワードパス中に、2つの変数を乗算して結果を取得しました。乗算演算の微分が2番目の因数です。したがって、勾配を伝播するには、結果の誤差勾配に反対のテンソルの対応する要素を乗算する必要があります。

取得した勾配のバッファの1つの要素を2つのテンソルの対応する要素で乗算する必要があることに注意してください。つまり、グローバルバッファの同じ要素に2回アクセスする必要があるということです。しかし、グローバルメモリの要素へのアクセスは「コストがかかる」ことはご存じの通りです。操作の全体的な実行時間を短縮するために、まずグローバルバッファ要素の値をより高速なプライベートメモリ変数に転送します。以降の操作は、この高速変数を使用して実行されます。

操作の結果は、2つの結果バッファの対応する要素に保存されます。

   float gradient = output_gr[action];
   quantiles_gr[shift + i] = gradient * delta_taus[shift + i];
   taus_gr[shift + i] = gradient * quantiles[shift + i];
  }

フィードフォワードメソッドから直接呼び出した次のカーネルはDropoutです。環境状態の埋め込みと分位数の埋め込みという2つの埋め込みテンソルのアダマール積を実行しました。フィードフォワードパスでは、以前に作成したDropoutカーネルを使用しました。ここで、誤差勾配を2方向に伝播するには、このカーネルを異なる入力で連続して呼び出す必要があります。ただし、モデルの訓練時間を最小限に抑えるために、操作の最大の並列処理を目指しています。したがって、時間をかけて新しいカーネルFQF_QuantileGradientを作成しましょう。

このカーネルのアルゴリズムは、以前のカーネルのアルゴリズムを完全に繰り返します。これについて変なことは何もありません。どちらのカーネルも同様の機能を実行します。違いは、結果の勾配バッファ内のオフセットのみです。前のケースでは、取得された勾配バッファのサイズは、可能なエージェント行動ごとに1つの離散値しかなかったため、残りのバッファとは異なりました。この場合、すべてのバッファは同じサイズになります。したがって、受信した勾配バッファでは、残りのバッファと同様にオフセットを使用します。

__kernel void FQF_QuantileGradient(__global float* state_embeding,
                                   __global float* taus_embeding,
                                   __global float* quantiles_gr,
                                   __global float* state_gr,
                                   __global float* taus_gr
                                  )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;
//---
   float gradient = quantiles_gr[shift + i];
   state_gr[shift + i] = gradient * taus_embeding[shift + i];
   taus_gr[shift + i] = gradient * state_embeding[shift + i];
  }

考慮しなければならない最後のカーネルはFQF_CosineGradientです。これは、分位数埋め込み用のデータの準備とは逆の手順を実行します。データ準備操作の導関数は次のとおりです。

このカーネルの操作の結果として、分位確率予測モデルのSoftmax層の出力で誤差勾配が得られると予想されます。なお、各分位数がSoftmax結果テンソルの累積値を使用しています。つまり、テンソルの各要素が後続のすべての分位数に影響を与えています。テンソルの各要素が、最終結果への関与に応じて勾配のシェアを受け取ることは論理的です。したがって、Softmax結果テンソルの分析された要素によって影響を受けた、受信した勾配バッファのすべての要素から誤差勾配を収集します。

カーネルの実装を考えてみましょう。パラメータでは、3つのデータバッファへのポインタを渡します。

Softmax層の結果
得られた誤差勾配
resultsbuffer：Softmax層の結果バッファレベルでの誤差勾配

この記事で説明するほとんどのカーネルと同様に、これらのカーネルは2次元のタスク空間で実行されます。1つは分位数用で、もう1つは可能なエージェント行動用です。

カーネルの本体では、両方の次元でスレッドIDを要求し、データバッファのオフセットを決定します。すべてのデータバッファは同じサイズです。したがって、オフセットはすべて同じになります。

__kernel void FQF_CosineGradient(__global float* softmax,
                                 __global float* output_gr,
                                 __global float* softmax_gr
                                )
  {
   size_t i = get_global_id(0);
   size_t total = get_global_size(0);
   size_t action = get_global_id(1);
   int shift = action * total;

各要素は、それ自体と後続の分位数にのみ影響します。したがって、最初に前の要素の合計を計算します。

   float cumul = 0;
   for(int it = 0; it < i; it++)
      cumul += softmax[shift + it];

次に、対応する要素から勾配を計算します。

フィードフォワードパス中に、分位数の平均値を埋め込みに渡したことに注意してください。したがって、分位確率の平均値に基づいて誤差勾配を計算します。

   float result = -M_PI_F * i * sin(M_PI_F * i * (cumul + softmax[shift + i] / 2)) * output_gr[shift + i];

次に、ループで、後続の分位数から誤差勾配を決定します。そうすることで、勾配分位数の全確率における現在の要素のシェアに従って、勾配の影響も調整します。

   for(int it = i + 1; it < total; it++)
     {
      cumul += softmax[shift + it - 1];
      float temp = cumul + softmax[shift + it] / 2;
      result += -M_PI_F * it * sin(M_PI_F * it * temp) * output_gr[shift + it] * 
                                                         softmax[shift + it] / temp;
     }
   softmax_gr[shift + i] += result;
  }

すべてのループ反復の後、結果バッファの対応する要素に結果を書き込みます。

クラスの勾配逆伝播パスを編成するためのすべてのカーネルを準備しました。これで、勾配逆伝播メソッドcalcInputGradientsの作成に進むことができます。

このメソッドは、パラメータで、エラーが伝搬される前のニューラル層のオブジェクトへのポインタを受け取ります。コントロールのブロックは、メソッドで実装されます。ここでは、受信したオブジェクトへのポインタと内部データバッファをチェックします。

bool CNeuronFQF::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !Gradient || !Output)
      return false;

フィードフォワード方式とは異なり、ここではコントロールブロックを作成しています。これは、このメソッドの操作がOpenCLプログラムのカーネル呼び出しで開始されるためです。データバッファへのポインタを渡すときは、それらが存在することを確認する必要があります。そうしないと、操作の実行中に重大なエラーが発生する可能性があります。

コントロールのブロックを正常に通過した後、誤差勾配逆伝播操作に進みます。まず、FQF_OutputGradientカーネルを呼び出します。ここで、誤差勾配を分位数関数パーセプトロンと分位予測ブロックに伝播します。カーネルを実行キューに入れる手順は、フィードフォワードの手順と似ています。カーネルは、2次元のタスク空間を実行します。最初の次元は分位数に対応し、2番目の次元はエージェントの可能な行動に対応します。

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles,
                                                              cQuantile2.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus,
                                                                 cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_output_gr,
                                                                 getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_quantiles_gr,
                                                             cQuantile2.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_OutputGradient, def_k_fqfoutgr_taus_gr,
                                                               cSoftMax.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_OutputGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
         return false;
        }
     }

次に、分位数関数のパーセプトロンに誤差勾配を渡します。これをおこなうには、指定されたブロックの内部ニューラル層の逆伝播メソッドを順番に呼び出します。

   if(!cQuantile1.calcHiddenGradients(GetPointer(cQuantile2)))
      return false;
   if(!cQuantile0.calcHiddenGradients(GetPointer(cQuantile1)))
      return false;

分位数関数からの誤差勾配を、現在のシステム状態の埋め込み（前のニューラル層）と分位確率の埋め込みに分配する必要があります。この機能を実行するために、FQF_QuantileGradientカーネルが作成されました。すでに同様の手順に従って、このカーネルを呼び出します。

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cCosineEmbeding.Neurons(), 1 };
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_enbeding,
                                                                  NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_embedding,
                                                            cCosineEmbeding.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_quantiles_gr,
                                                               cQuantile0.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_state_gr,
                                                                NeuronOCL.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_QuantileGradient, def_k_fqfqgr_taus_gr,
                                                          cCosineEmbeding.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_QuantileGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_OutputGradient: %d", GetLastError());
         return false;
        }
     }

次のステップでは、分位数の埋め込みによって誤差勾配を渡します。ここでは、最初に内部ニューラル層cCosineの勾配逆伝播メソッドを呼び出します。

   if(!cCosine.calcHiddenGradients(GetPointer(cCosineEmbeding)))
      return false;

次にFQF_CosineGradientを呼び出します。

     {
      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2] = { cSoftMax.Neurons() / Neurons(), Neurons() };
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax,
                                                                  cSoftMax.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_output_gr,
                                                                  cCosine.getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_FQF_CosineGradient, def_k_fqfcosgr_softmax_gr,
                                                                 cSoftMax.getGradientIndex());
      if(!OpenCL.Execute(def_k_FQF_CosineGradient, 2, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel FQF_CosineGradient: %d", GetLastError());
         return false;
        }
     }

メソッドの最後で、その勾配逆伝播メソッドを呼び出して、内部層cSoftMaxを介して誤差勾配を伝播します。

   if(!cSoftMax.calcInputGradients(GetPointer(cFraction)))
      return false;
//---
   return true;

分位数確率予測ブロックから前の層に誤差勾配を渡さないことにご注意ください。これは、確率分布ではなく、期待される報酬の決定に関連するタスクの優先度によるものです。

オーバーライドする必要がある2番目の逆伝播メソッドupdateInputWeightsは、モデルパラメータの更新を担当します。これは非常に簡単です。内側のニューラル層の関連するメソッドを交互に呼び出し、操作の結果を確認します。

bool CNeuronFQF::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFraction.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cCosineEmbeding.UpdateInputWeights(GetPointer(cCosine)))
      return false;
   if(!cQuantile1.UpdateInputWeights(GetPointer(cQuantile0)))
      return false;
   if(!cQuantile2.UpdateInputWeights(GetPointer(cQuantile1)))
      return false;
//---
   return true;
  }

これで、新しいCNeuronFQFクラスの主な機能性に関する作業は終了です。フィードフォワードおよび勾配逆伝播プロセスの構成を検討しました。データをファイルに保存し、クラスを復元するメソッドも、クラスでオーバーライドされています。これらのメソッドでは、内部オブジェクトの対応するメソッドを呼び出しました。ご自分で勉強なさってください。使用されているすべてのクラスとそのメソッドの完全なコードは、添付ファイルにあります。

先に進みます。分位数関数の完全なパラメータ化という手法により、モデル学習アルゴリズムを整理するためのクラスを構築しました。ただし、これはプロセスの一部にすぎません。これは、データバッファとTargetNetを使用した同じQ学習です。説明した方法をQ学習プロセスで直接使用するプロセスを容易にするために、モデルの基本クラスCNetから派生したCFQFクラスを作成しました。

class CFQF : protected CNet
  {
private:
   uint              iCountBackProp;
protected:
   uint              iUpdateTarget;
   //---
   CNet              cTargetNet;
public:
                     CFQF(void);
                     CFQF(CArrayObj *Description)  { Create(Description); }
   bool              Create(CArrayObj *Description);
                    ~CFQF(void);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
                     { return        CNet::feedForward(inputVals, window, tem); }
   bool              backProp(CBufferFloat *targetVals, float discount = 0.9f,
                              CArrayFloat *nextState = NULL, int window = 1, bool tem = true);
   void              getResults(CBufferFloat *&resultVals);
   int               getAction(void);
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; }
   bool              Save(string file_name, datetime time, bool common = true)
     { return CNet::Save(file_name, getRecentAverageError(), (float)iUpdateTarget, 0, time, common); }
   virtual bool      Save(const int file_handle);
   virtual bool      Load(string file_name, datetime &time, bool common = true);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)   const   {  return defFQF;   }
   virtual bool      TrainMode(bool flag) { return CNet::TrainMode(flag); }
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result)
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual void      SetUpdateTarget(uint batch)   { iUpdateTarget = batch; }
   virtual bool      UpdateTarget(string file_name);
  };

クラスは前回の記事のCQRDQNに似ています。その構造は、そのクラスの構造とほぼ同じです。未使用の変数と確率行列を削除しました。これはすべて別のニューラルネットワークでおこなわれます。クラスメソッドにも必要な変更を加えました。ここでは、クラスのすべてのメソッドについて説明するつもりはありません。添付ファイルでご自身でご確認ください。ここではそれらのいくつかについてのみ言及します。

逆伝播メソッドから始めましょう。このメソッドは、パラメータで目標値とシステムの次の状態を受け取ります。nexStateはオプションのパラメータで、新しいモデルを訓練するときに使用できます。未訓練のモデルを使用して将来の報酬を予測するとノイズが発生し、学習プロセスが複雑になる場合に使用できます。

メソッド本体で、目標値のバッファの形式で必須パラメータの存在を確認します。

bool CFQF::backProp(CBufferFloat *targetVals, float discount = 0.9f,
                    CArrayFloat *nextState = NULL, int window = 1, bool tem = true)
  {
//---
   if(!targetVals)
      return false;

次に、オプションのパラメータの存在も確認し、必要に応じて将来の報酬を予測します。ここで、割引率を考慮して、将来の報酬額の目標値も調整します。

   if(!!nextState)
     {
      vectorf target;
      if(!targetVals.GetData(target) || target.Size() <= 0)
         return false;
      if(!cTargetNet.feedForward(nextState, window, tem))
         return false;
      cTargetNet.getResults(targetVals);
      if(!targetVals)
         return false;
      target = target + discount * targetVals.Maximum();
      if(!targetVals.AssignArray(target))
         return false;
     }

その後、TargetNetを更新する必要があるかどうかを確認します。

   if(iCountBackProp >= iUpdateTarget)
     {
#ifdef FileName
      if(UpdateTarget(FileName + ".nnw"))
#else
      if(UpdateTarget("FQF.upd"))
#endif
         iCountBackProp = 0;
     }
   else
      iCountBackProp++;

メソッドの最後で、親クラスのコールバックメソッドを呼び出します。

   return CNet::backProp(targetVals);
  }

貪欲な行動の選択方法も変更されました。ここでは、モデルの結果バッファから最高の報酬を持つアイテムを単純に決定します。

int CFQF::getAction(void)
  {
   CBufferFloat *temp;
   CNet::getResults(temp);
   if(!temp)
      return -1;
//---
   return temp.Maximum(0, temp.Total());
  }

行動サンプリングメソッドgetSampleにも変更が加えられました。このメソッドでは、最初にモデルの最後のフィードフォワードパスの結果を取得します。

int CFQF::getSample(void)
  {
   CBufferFloat* resultVals;
   CNet::getResults(resultVals);
   if(!resultVals)
      return -1;

受信したデータをバッファからベクトルにコピーし、Softmax関数を適用します。次に、ベクトル値の累積和を計算します。

   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return -1;
     }
   delete resultVals;
//---
   if(!temp.Activation(temp, AF_SOFTMAX))
      return -1;
   temp = temp.CumSum();

結果のベクトルは、エージェントの行動の一種の分位確率分布です。次に、この分布から1つの値をサンプリングし、呼び出し元に返します。

   int err_code;
   float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
   if(random >= 1)
      return (int)temp.Size() - 1;
   for(int i = 0; i < (int)temp.Size(); i++)
      if(random <= temp[i] && temp[i] > 0)
         return i;
//---
   return -1;
  }

ステップごとに、操作の結果を確認します。エラーが発生した場合は、呼び出しプログラムに-1を返します。

これで、FQFアルゴリズムを実装するためのクラスの説明を終了します。すべてのクラスとそのメソッドの完全なコードは、添付ファイルにあります。

3.テスト

FQF手法でモデルを訓練するために、FQF-learning.mq5 EAを作成しました。そのアルゴリズムは、前回の記事のQRDQN-learning.mq5のアルゴリズムと非常によく似ています。変更したのはファイル名と使用するオブジェクトのみなので、そのアーキテクチャについては詳しく説明しません。EAの完全なコードは以下に添付されています。

モデルは、過去2年間のEURUSDの履歴データで、H1時間枠で訓練されました。すべての指標はデフォルトのパラメータで使用されました。ご覧のとおり、この連載内のすべてのモデルをテストするときに使用するパラメータと同じです。

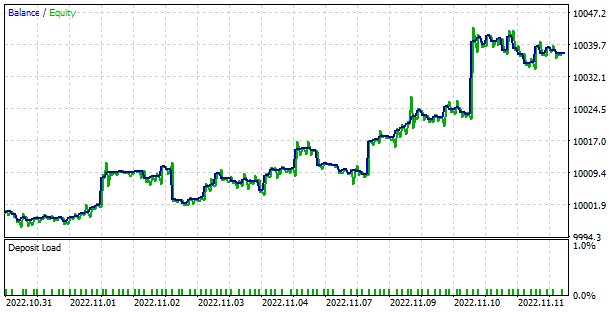
訓練プロセス中、モデルはかなりスムーズで安定した誤差削減ダイナミクスを示しました。これは、モデル訓練の安定性のかなり良いマーカーです。

訓練済みモデルは、ストラテジーテスターでテストされました。別のEAFQF-learning-test.mq5がテスト目的で作成されました。これは、前回の記事のQRDQN-learning-test.mq5のコピーなので、ここではそのアルゴリズムについては考慮しません。ファイル名とモデルクラスのみが変更されています。完全なEAコードは添付ファイルにあります。

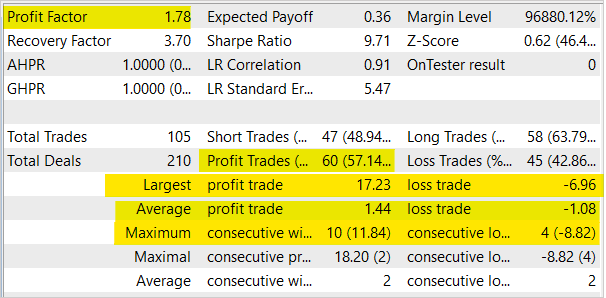
テスト中、モデルは利益を生み出す能力を示しました。テスト結果に基づいて、モデルは1.78のプロフィットファクターと3.7のリカバリーファクターを示しました。勝ちトレードの割合は57%を超えています。最大の勝ちトレードは、最大の負けトレードよりもほぼ2.5倍高くなっています。最長の勝ち組では10回の取引があり、最長の負け組では4回の取引がありました。一般に、平均的な勝ちトレードは、平均的な負けトレードよりも1/3高くなります。

モデルテストグラフ

モデルのテスト結果

結論

この記事では、分散型強化学習アルゴリズムの研究を続け、FQF学習法を強化学習に実装するためのクラスを構築しました。この手法を使用してモデルを訓練し、ストラテジーテスターで訓練済みモデルのパフォーマンスを確認しました。学習プロセス中、この方法は誤差減少に向けた安定した傾向を示しました。ストラテジーテスターでの訓練済みモデルのテストでは、モデルが利益を生み出す能力があることが示されました。

繰り返しになりますが、金融市場取引は非常にリスクの高い投資方法であることを覚えておいてください。この記事で紹介するプログラムは、メソッドとアルゴリズムの動作を示すことのみを目的としています。ライブ取引での使用を意図したものではありませんが、実用的な取引ツールを作成するための基礎としては使用できます。とにかく、使用する前に、開発されたツールの徹底的かつ包括的なテストを実行する必要があります。何にしても、実際の取引でプログラムを使用するリスクを理解し、受け入れてください。

参照文献

記事で使用されているプログラム

#	ファイル名	タイプ	詳細
1	FQF-learning.mq5	EA	モデルを最適化するためのEA
2	FQF-learning-test.mq5	EA	ストラテジーテスターでモデルをテストするためのEA
3	FQF.mqh	クラスライブラリ	FQFモデルクラス
4	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークモデルを作成するためのライブラリ
5	NeuroNet.cl	コードベース	ニューラルネットワークモデルを作成するためのOpenCLプログラムコードライブラリ
6	NetCreator.mq5	EA	モデル構築ツール
7	NetCreatotPanel.mqh	クラスライブラリ	ツールを作成するためのクラスライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11804

添付されたファイル |

ZIPをダウンロード

MQL5.zip (106.93 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークが簡単に（第35回）：ICM（Intrinsic Curiosity Module、内発的好奇心モジュール）

強化学習アルゴリズムの研究を続けます。これまで検討してきたすべてのアルゴリズムでは、あるシステム状態から別の状態への遷移ごとに、エージェントがそれぞれの行動を評価できるようにするための報酬方策を作成する必要がありました。しかし、この方法はかなり人工的なものです。実際には、行動と報酬の間には、ある程度の時間差があります。今回は、行動から報酬までの様々な時間の遅れを扱うことができるモデル訓練アルゴリズムに触れてみましょう。

自動で動くEAを作る（第08回）：OnTradeTransaction

今回は、受注システムに関する問題を迅速かつ効率的に処理するためのイベント処理システムの使用方法について紹介します。このシステムにより、EAは必要なデータを常に検索する必要がなくなり、より速く動作するようになります。

取引における道徳的期待値

この記事は、道徳的期待値についてです。取引でのその使用のいくつかの例と、その助けを借りて達成できる結果を見ていきます。

データサイエンスと機械学習（第10回）：リッジ回帰

リッジ回帰は、モデルの複雑さを軽減し、単純な線形回帰に起因する過学習を防ぐためのシンプルな手法です。