Redes neuronales: así de sencillo (Parte 15): Clusterización de datos usando MQL5

MetaTrader 5 — Sistemas comerciales | 29 julio 2022, 16:01

432

Dmitriy Gizlyk

Contenido

Introducción

En el artículo anterior, nos familiarizamos con el método de clusterización de k-medias y observamos su implementación utilizando el lenguaje Python. Sin embargo, el uso de la integración impone con frecuencia ciertas restricciones y costes adicionales. En particular, el estado actual de la integración no permite el uso de datos de programas integrados como indicadores o la gestión de eventos del terminal. Y si implementamos un gran número de indicadores clásicos en varias bibliotecas, deberemos repetir el algoritmo de los indicadores personalizados en nuestro script. ¿Y qué hacemos si no tenemos el código fuente del indicador y no comprendemos su algoritmo de acción? ¿O si planeamos usar los resultados de la clusterización en otros programas MQL5? En estos casos nos ayudará la implementación del método de clusterización usando las herramientas de MQL5.

1. Principios de construcción de los modelos

Vamos a recordar el algoritmo del método de clusterización de k-medias:

Determinamos k puntos aleatorios de la muestra de entrenamiento como los centros de los clústeres.
Organizamos un ciclo de operaciones:
- Determinamos la distancia de cada punto respecto a cada centro;
- Según el centro más cercano, determinamos si el punto pertenece al clúster;
- Usando la media aritmética, determinamos un nuevo centro para cada clúster.
Repetimos las operaciones en un ciclo hasta que los centros del clúster "se detengan".

Antes de comenzar a escribir el código del método, vamos a hablar un poco sobre los puntos principales de nuestra implementación.

Las operaciones principales del algoritmo anteriormente analizado se llevan a cabo dentro de un ciclo. Al comienzo del cuerpo del ciclo, necesitamos encontrar la distancia desde cada elemento de la muestra de entrenamiento hasta el centro de cada clúster. Como podemos ver, esta operación para cada elemento de la muestra de entrenamiento es absolutamente independiente de los otros elementos. Por consiguiente, podemos usar la tecnología OpenCL para organizar los cálculos paralelos. Además, las operaciones también son independientes para calcular la distancia respecto a los centros de diferentes clústeres. Esto significa que podemos paralelizar las operaciones en un espacio de tareas bidimensional.

El siguiente paso será determinar si un elemento de la secuencia pertenece a un clúster concreto. Al realizar esta operación, también se monitoreará la independencia de los cálculos para cada elemento de la secuencia. Y aquí podemos usar la tecnología OpenCL de cálculos paralelos en el contexto de los elementos individuales de la muestra de entrenamiento.

Así, al concluir las operaciones en el cuerpo del ciclo, definimos los nuevos centros de los clústeres. Para hacer esto, necesitamos iterar todos los elementos de la muestra de entrenamiento y calcular los valores medios aritméticos en el contexto de cada elemento del vector que describe el estado del sistema y cada clúster. Cabe señalar que solo los elementos que pertenecen a dicho clúster se tienen en cuenta al calcular el centro del clúster. El resto de los elementos son ignorados. Por lo tanto, los valores de cada elemento se usan solo una vez. Y aquí también podemos usar la tecnología de cálculos paralelos en un espacio bidimensional. En un eje tendremos los elementos del vector que describen el estado del sistema, y en el segundo, los clústeres analizados.

Después de realizar la clusterización de los datos para evaluar el rendimiento de nuestro modelo, tenemos que calcular la función de pérdida. Para hacer esto, como hemos mencionado anteriormente, necesitamos calcular la desviación media aritmética del estado del sistema respecto al centro del clúster correspondiente. Obviamente, no podemos dividir explícitamente en hilos el cálculo de la media aritmética, pero luego podemos dividir esta tarea en 2 subtareas. Primero calculamos la distancia hasta los respectivos centros. Podemos paralelizar fácilmente esta tarea en el contexto de un solo estado del sistema. Solo entonces calcularemos la media aritmética del vector de distancia resultante.

2. Creamos un programa OpenCL

De esta forma, tenemos cuatro subtareas separadas para organizar los cálculos paralelos. Gracias a los anteriores artículos de esta serie, sabemos que para organizar los cálculos paralelos usando la tecnología OpenCL, necesitamos crear un programa aparte para cargar y realizar operaciones en el lado del contexto OpenCL. Vamos a crear los núcleos ejecutables del programa en un archivo separado "unsupervised.cl" en el orden de las tareas mencionadas anteriormente.

Comenzaremos este trabajo escribiendo el kernel KmeansCulcDistance, en el que organizaremos las operaciones para calcular las distancias desde los estados del sistema hasta los centros actuales de todos los clústeres. Como hemos mencionado anteriormente, iniciaremos la ejecución de este kernel en un espacio de tareas bidimensional. En una dimensión, tendremos los estados separados del sistema de la muestra de entrenamiento. Y en la segunda, los clústeres de nuestro modelo.

En los parámetros para la entrada del kernel, indicamos los punteros a los 3 búferes de datos y el tamaño del vector que describe un estado del sistema analizado. Dos de los búferes indicados contendrán los datos originales. Esta es la muestra de entrenamiento en sí y el array de vectores de los centros de clústeres. El tercer búfer de datos es el tensor de resultados.

En el cuerpo del kernel, primero obtenemos los identificadores del hilo de trabajo actual en ambas dimensiones y el número total de clústeres por cantidad de subprocesos en ejecución en la segunda dimensión. Necesitamos estos datos para determinar el desplazamiento de los elementos necesarios en todos los tensores anteriormente mencionados. De inmediato, determinamos los desplazamientos en los tensores de los datos iniciales e inicializamos con una variable cero para calcular la distancia hasta el centro del clúster.

A continuación, organizamos un ciclo con un número de iteraciones igual al tamaño del vector de descripción del estado del sistema analizado. En el cuerpo de este ciclo, sumamos las distancias al cuadrado entre los valores de los elementos correspondientes de los vectores de estado del sistema y el centro del clúster.

Después de completar todas las iteraciones del ciclo, solo hay que guardar el valor obtenido en el elemento correspondiente del búfer de resultados. No olvidemos que desde un punto de vista matemático, para determinar la distancia entre dos puntos en el espacio, necesitamos extraer la raíz cuadrada del valor resultante. No obstante, en este caso, no nos interesa la distancia exacta entre los dos puntos. Solo necesitamos definir las distancias más pequeñas. Por consiguiente, para ahorrar recursos, no extraeremos la raíz cuadrada.

__kernel void KmeansCulcDistance(__global double *data,
                                 __global double *means,
                                 __global double *distance,
                                 int vector_size
                                )
  {
   int m = get_global_id(0);
   int k = get_global_id(1);
   int total_k = get_global_size(1);
   double sum = 0.0;
   int shift_m = m * vector_size;
   int shift_k = k * vector_size;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_k + i], 2);
   distance[m * total_k + k] = sum;
  }

Bien, ya hemos implementado el comienzo: hemos escrito el código para el primer kernel y estamos trabajando en el siguiente subproceso. De acuerdo con el algoritmo de nuestro método, tenemos que determinar a cuál de los clústeres pertenece cada estado de los presentados en la muestra de entrenamiento. Para lograr esto, necesitaremos determinar cuál de los centros del clúster está más cerca del estado analizado. Ya hemos calculado las distancias en el kernel anterior. Ahora solo necesitamos determinar el número con el valor mínimo. Por supuesto, realizaremos todas las operaciones en el contexto de un solo estado del sistema.

Para organizar este proceso, crearemos elkernel KmeansClustering. Al igual que el kernel anterior, en los parámetros recibirá los punteros a los 3 búferes de datos y el número total de clústeres. Por extraño que parezca, de los 3 búferes, solo un búfer distance portará los datos originales. Los otros dos contendrán los resultados de las operaciones. Para almacenar losclústeres en un búfer, anotaremos el índice del clúster al que pertenece el estado analizado del sistema.

En las banderasdel tercer búfer, registraremos la bandera de cambio de clúster en comparación con el estado anterior. El análisis de estas banderas nos indicará el punto de ruptura del proceso de entrenamiento del modelo. La lógica detrás de este proceso resulta bastante simple. Si ningún estado del sistema cambia la pertenencia a un clúster, entonces, como consecuencia, los centros de los clústeres tampoco cambiarán. Y esto significará que continuar las operaciones cíclicas no tiene ningún sentido. Este es el punto de parada para el entrenamiento del modelo.

Pero volvamos a nuestro algoritmo del kernel. Ejecutaremos su inicio en un espacio de tareas unidimensional en el contexto de los estados de sistema analizados. Por lo tanto, en el cuerpo del kernel, determinaremos el número ordinal del estado analizado y el desplazamiento correspondiente en los búferes de datos. Debemos decir que ambos búferes de resultados contienen un valor para cada estado. Por ello, el desplazamiento en los búferes especificados será igual al identificador del hilo. Esto significa que solo nos queda determinar el desplazamiento en el búfer de datos inicial que contiene las distancias calculadas hasta los centros de los clústeres.

Aquí vamos a preparar 2 variables privadas. En la variable valueregistraremos la distancia hasta el centro. Y en la segunda, la variable result, el número de clúster. En la etapa inicial, guardaremos en ellas los valores del clúster con el identificador "0".

Luego organizamos un ciclo con la iteración de las distancias hasta los centros de todos los clústeres. Como ya hemos guardado los valores del clúster con el índice "0" en las variables, iniciamos el ciclo desde el siguiente clúster.

En el cuerpo del ciclo, comprobamos la distancia hasta el siguiente centro. Y si es mayor o igual que el previamente almacenado en la variable, se verificará el siguiente clúster.

Al encontrar un centro más cercano, reescribiremos el valor de nuestras variables privadas. En ellas guardaremos la distancia menor y el número ordinal del clúster correspondiente.

Después de completar todas las iteraciones de nuestro ciclo, el identificador del clúster más cercano al estado analizado se almacenará en la variable result. A esta referiremos el estado actual. Pero antes de guardar el valor obtenido en el elemento correspondiente del búfer de resultados, verificaremos si el número de clúster ha cambiado en comparación con la iteración anterior y guardaremos el resultado de la comparación en el búfer de banderas.

__kernel void KmeansClustering(__global double *distance,
                               __global double *clusters,
                               __global double *flags,
                               int total_k
                              )
  {
   int i = get_global_id(0);
   int shift = i * total_k;
   double value = distance[shift];
   int result = 0;
   for(int k = 1; k < total_k; k++)
     {
      if(value <= distance[shift + k])
         continue;
      value =  distance[shift + k];
      result = k;
     }
   flags[i] = (double)(clusters[i] != (double)result);
   clusters[i] = (double)result;
  }

Al final del algoritmo de clusterización, necesitaremos actualizar los valores de los vectores centrales de todos los clústeres recopilados en la matriz means. Para realizar esta tarea, crearemos otro kernel KmeansUpdating. Al igual que los kernels anteriormente analizados, el considerado en los parámetros obtendrá los punteros a los 3 búferes de datos y una constante. Dos búferes contienen los datos originales, mientras que el otro búfer contiene los resultados. Como hemos mencionado antes, iniciaremos este kernel para que se ejecute en un espacio de tareas bidimensional. Sin embargo, a diferencia del kernel KmeansCulcDistance, en la primera dimensión del espacio de tareas iteraremos los elementos del vector de descripción de un estado del sistema, mientras que en la constante total_m especificaremos el número de elementos en la muestra de entrenamiento.

En el cuerpo del kernel, primero definiremos los identificadores de los hilos en ambas dimensiones. Como antes, los usaremos para determinar los elementos analizados y los desplazamientos en los búferes de datos. Aquí mismo, determinaremos la longitud del vector de descripción del estado del sistema, que será igual al número total de hilos en ejecución en la primera dimensión. Además, inicializaremos 2 variables privadas en las que sumaremos los valores de los elementos correspondientes de la descripción del estado del sistema y su cantidad.

Las operaciones de suma las realizaremos directamente en el siguiente ciclo organizado, cuyo número de iteraciones resultará igual al número de elementos de la muestra de entrenamiento. No olvidemos que vamos a realizar la suma solo de aquellos elementos que pertenezcan al clúster analizado. Para hacer esto, en el cuerpo del ciclo, primero comprobaremos a qué clúster pertenece el elemento actual, y si no se corresponde con el analizado, pasaremos al siguiente elemento.

Cuando el elemento supera nuestra verificación de conformidad con el clúster analizado, añadimos el valor del elemento correspondiente del vector de descripción del estado del sistema y aumentamos el contador en "1".

Después de salir del ciclo, solo nos quedará dividir la suma acumulada por el número de elementos sumados. Pero aquí debemos recordar que existe la posibilidad de obtener un error crítico de división por cero. Eso sí, obviamente, dada la organización del algoritmo, tal situación resulta poco probable. No obstante, para dotar de mayor fiabilidad a nuestro programa, añadiremos esta verificación. Y ojo, si no existen elementos pertenecientes al clúster analizado, no resetearemos su valor, sino que lo dejaremos igual.

__kernel void KmeansUpdating(__global double *data,
                             __global double *clusters,
                             __global double *means,
                             int total_m
                            )
  {
   int i = get_global_id(0);
   int vector_size = get_global_size(0);
   int k = get_global_id(1);
   double sum = 0;
   int count = 0;
   for(int m = 0; m < total_m; m++)
     {
      if(clusters[m] != k)
         continue;
      sum += data[m * vector_size + i];
      count++;
     }
   if(count > 0)
      means[k * vector_size + i] = sum / count;
  }

En esta etapa, ya hemos creado 3 kernels para implementar el algoritmo de clusterización de datos de las k-medias. Pero antes de proceder a la creación de los objetos del programa principal, tendremos que crear otro kernel para calcular la función de pérdida.

Determinaremos el valor de la función de pérdida en 2 etapas. Primero, determinamos la desviación de cada elemento individual de la muestra de entrenamiento respecto al centro del clúster correspondiente. Y a continuación, calcularemos la desviación media aritmética para toda la muestra. Podemos dividir las operaciones de la primera etapa en hilos y realizar cálculos paralelos usando herramientas OpenCL. Para implementar esta funcionalidad, crearemos el kernel KmeansLoss, que obtendrá los punteros a 4 búferes y una constante en sus parámetros. Tres búferes portarán los datos originales, y el búfer restante escribirá los resultados.

Vamos a iniciar el kernel en un espacio de tareas unidimensional con un número de hilos igual al número de elementos en la muestra de entrenamiento. En el cuerpo del kernel, primero determinaremos el número ordinal del patrón analizado de la muestra de entrenamiento. Luego determinamos a qué clúster pertenece. Esta vez no recalcularemos las distancias hasta los centros de todos los clústeres. En su lugar, simplemente extraeremos el valor correspondiente del búfer clusters según el número ordinal. Precisamente en este búfer guardamos el número de clúster en el kernel KmeansClustering analizado anteriormente.

Ahora podemos determinar el desplazamiento al inicio de los vectores que necesitamos en los tensores de la muestra de entrenamiento y la matriz de centros de clústeres.

Después, solo tenemos que calcular la distancia entre los dos vectores. Para ello, inicializaremos una variable privada para acumular la suma de las desviaciones y organizar un ciclo con la enumeración de todos los elementos del vector de descripción del estado del sistema analizado. En el cuerpo de este ciclo, sumaremos el cuadrado de las desviaciones de los elementos correspondientes de los vectores.

Tras completar todas las iteraciones del ciclo, transferiremos la suma acumulada al elemento correspondiente del búfer de resultados loss

__kernel void KmeansLoss(__global double *data,
                         __global double *clusters,
                         __global double *means,
                         __global double *loss,
                         int vector_size
                        )
  {
   int m = get_global_id(0);
   int c = clusters[m];
   int shift_c = c * vector_size;
   int shift_m = m * vector_size;
   double sum = 0;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_c + i], 2);
   loss[m] = sum;
  }

Bueno, ya hemos analizado los algoritmos para construir todos los procesos del lado del contexto OpenCL. Ahora podemos comenzar a organizar los procesos del lado del programa principal.

3. Trabajo preparatorio del lado del programa principal.

Del lado del programa principal, tenemos que crear la nueva clase CKmeans. El código de esta clase se guardará en el archivo "kmeans.mqh". Sin embargo, antes de comenzar a trabajar en la nueva clase, haremos un pequeño trabajo preparatorio. En primer lugar, para trasladar los datos al contexto de OpenCL, usaremos el objeto de clase CBufferDouble que ya conocemos de esta serie de artículos. No vamos a reescribir el código de la clase especificada: simplemente incluiremos la biblioteca creada anteriormente.

#include "..\NeuroNet_DNG\NeuroNet.mqh"

Luego cargaremos como recurso el código del programa OpenCL creado anteriormente.

#resource "unsupervised.cl" as string cl_unsupervised

A continuación, comenzaremos a crear las constantes con nombre. En este artículo, necesitaremos un número considerable de ellas. Aquí hay que decir que, para tener más tarde la posibilidad de usar estas de forma conjunta con la biblioteca creada previamente, deberemos cuidar la unicidad de las constantes creadas.

Primero, necesitaremos una constante para identificar la nueva clase.

#define defUnsupervisedKmeans    0x7901

En segundo lugar, necesitaremos constantes para identificar los kernels y sus parámetros. Los kernels se identificarán usando numeración continua dentro del programa OpenCL. Al mismo tiempo, los parámetros se numerarán dentro de un solo kernel. Para mejorar la legibilidad del código, hemos decidido agrupar las constantes según los kernels a los que pertenecen.

#define def_k_kmeans_distance    0
#define def_k_kmd_data           0
#define def_k_kmd_means          1
#define def_k_kmd_distance       2
#define def_k_kmd_vector_size    3

#define def_k_kmeans_clustering  1
#define def_k_kmc_distance       0
#define def_k_kmc_clusters       1
#define def_k_kmc_flags          2
#define def_k_kmc_total_k        3

#define def_k_kmeans_updates     2
#define def_k_kmu_data           0
#define def_k_kmu_clusters       1
#define def_k_kmu_means          2
#define def_k_kmu_total_m        3

#define def_k_kmeans_loss        3
#define def_k_kml_data           0
#define def_k_kml_clusters       1
#define def_k_kml_means          2
#define def_k_kml_loss           3
#define def_k_kml_vector_size    4

Después de crear las constantes con nombre, procedemos al siguiente paso del trabajo preparatorio. Cuando hablamos de la implementación de cálculos multihilo en los modelos de aprendizaje supervisado, inicializamos el objeto para trabajar con el contexto de OpenCL en el constructor de la clase de administración de redes neuronales. En el marco de este artículo, planeamos usar la clase de clusterización CKmeans sin utilizar ningún otro modelo. Y parecería que podemos trasladar la función de inicialización del ejemplar del objeto COpenCLMy dentro de nuestra nueva clase CKmeans. Sin embargo, no excluyo el uso de la clusterización como parte de otros modelos más complejos. Pero esto queda fuera del ámbito del presente artículo: volveremos a este tema en artículos posteriores de esta serie. No obstante, debemos considerar esta posibilidad. Así que hemos decidido crear una función aparte para inicializar un ejemplar de la clase de objeto COpenCLMy.

Echemos un vistazo al algoritmo de la función OpenCLCreate. Está construida de tal forma que recibe la prueba del programa OpenCL en los parámetros y retorna el puntero a un ejemplar del objeto inicializado. En el cuerpo de la función, primero crearemos un nuevo ejemplar de la clase COpenCLMy. E inmediatamente después, verificaremos el resultado de la operación de creación de un nuevo objeto.

COpenCLMy *OpenCLCreate(string programm)
  {
   COpenCL *result = new COpenCLMy();
   if(CheckPointer(result) == POINTER_INVALID)
      return NULL;

Luego llamaremos al método de inicialización del nuevo objeto, transmitiéndole en los parámetros una variable de cadena con el texto del programa OpenCL. Una vez más, comprobaremos el resultado de la operación. Si de repente obtenemos un error al realizar esta operación, eliminaremos el objeto creado anteriormente y saldremos del método, retornando un puntero vacío.

   if(!result.Initialize(programm, true))
     {
      delete result;
      return NULL;
     }

Tras inicializar el programa con éxito, procederemos a crear los kernels en el contexto de OpenCL. Primero, especificaremos el número de kernels que se crearán y luego crearemos todos los kernels descritos anteriormente uno a uno. Al mismo tiempo, no debemos olvidarnos de controlar el proceso, comprobando el resultado de cada operación.

El siguiente código muestra un ejemplo de cómo inicializar solo un kernel. Los demás se inicializan de la misma manera. Podrá encontrar el código completo de todos los métodos y funciones en el archivo adjunto.

   if(!result.SetKernelsCount(4))
     {
      delete result;
      return NULL;
     }
//---
   if(!result.KernelCreate(def_k_kmeans_distance, "KmeansCulcDistance"))
     {
      delete result;
      return NULL;
     }
//---
...........
//---
   return result;
  }

Después de crear con éxito todos los kernels, saldremos del método retornando el puntero al ejemplar del objeto creado.

Esto completará el trabajo preparatorio, por lo que podremos comenzar directamente a trabajar en la nueva clase de clusterización de datos.

4. Construyendo una clase de organización para el algoritmo de k-medias

Antes de comenzar a trabajar en la nueva clase de clusterización de datos CKmeans, vamos a analizar su contenido. ¿Qué funcionalidad debería tener? ¿Y qué métodos y variables necesitaremos para implementar esta funcionalidad? Declararemos todas las variables en el bloque protected.

En primer lugar, necesitaremos variables para almacenar los hiperparámetros del modelo: el número de clústeres creados (m_iClusters) y el tamaño del vector de descripción de un estado aparte del sistema (m_iVectorSize).

Al evaluar la calidad del modelo entrenado, calcularemos la función de pérdida, cuyo valor se guarda en la variablem_dLoss.

Además, para entender el estado del modelo (si está entrenado o no), necesitaremos la bandera m_bTrained.

Creo que esta lista de variables será suficiente para implementar la funcionalidad necesaria. A continuación, comenzamos a declarar los objetos utilizados. No tardaremos mucho aquí, ya que declararemos un ejemplar de clase para trabajar con el contexto OpenCL (c_OpenCL). También necesitaremos búferes de datos para almacenar la información e intercambiarla con el contexto de OpenCL. Haremos que sus nombres estén en consonancia con los usados anteriormente al desarrollar el programa OpenCL:

c_aDistance;
c_aMeans;
c_aClasters;
c_aFlags;
c_aLoss.

Después de declarar las variables, comenzaremos a trabajar con los métodos de clase. Aquí no ocultaremos nada: haremos públicos todos los métodos.

Y, obviamente, comenzaremos con el constructor y el destructor de clases. En el primero, crearemos los ejemplares de los objetos usados y estableceremos los valores iniciales para las variables.

void CKmeans::CKmeans(void)   :  m_iClusters(2),
                                 m_iVectorSize(1),
                                 m_dLoss(-1),
                                 m_bTrained(false)
  {
   c_aMeans = new CBufferDouble();
   if(CheckPointer(c_aMeans) != POINTER_INVALID)
      c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0);
   c_OpenCL = NULL;
  }

Y en el destructor de clases, limpiaremos la memoria y eliminaremos todos los objetos creados en la clase.

void CKmeans::~CKmeans(void)
  {
   if(CheckPointer(c_aMeans) == POINTER_DYNAMIC)
      delete c_aMeans;
   if(CheckPointer(c_aDistance) == POINTER_DYNAMIC)
      delete c_aDistance;
   if(CheckPointer(c_aClasters) == POINTER_DYNAMIC)
      delete c_aClasters;
   if(CheckPointer(c_aFlags) == POINTER_DYNAMIC)
      delete c_aFlags;
   if(CheckPointer(c_aLoss) == POINTER_DYNAMIC)
      delete c_aLoss;
  }

A continuación, crearemos el método de inicialización para nuestra clase, en los parámetros a los que transmitiremos el puntero al objeto de trabajo con los hiperparámetros de contexto y modelo de OpenCL. En el cuerpo del método, primero organizaremos un pequeño bloque de controles en el que comprobaremos los datos recibidos en los parámetros.

Después de eso, guardaremos los hiperparámetros obtenidos en las variables correspondientes e inicializaremos el búfer de la matriz de vectores de clústeres promedio con valores cero. Al mismo tiempo, no deberemos olvidarnos de comprobar el resultado de las operaciones de inicialización del búfer.

bool CKmeans::Init(COpenCLMy *context, int clusters, int vector_size)
  {
   if(CheckPointer(context) == POINTER_INVALID || clusters < 2 || vector_size < 1)
      return false;
//---
   c_OpenCL = context;
   m_iClusters = clusters;
   m_iVectorSize = vector_size;
   if(CheckPointer(c_aMeans) == POINTER_INVALID)
     {
      c_aMeans = new CBufferDouble();
      if(CheckPointer(c_aMeans) == POINTER_INVALID)
         return false;
     }
   c_aMeans.BufferFree();
   if(!c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0))
      return false;
   m_bTrained = false;
   m_dLoss = -1;
//---
   return true;
  }

Después de la inicialización, tendremos que entrenar el modelo. Organizaremos esta funcionalidad en el método Study. En los parámetros del método, transmitiremos la muestra de entrenamiento y la bandera de inicialización de la matriz de centros de clústeres. La introducción de la bandera hace posible desactivar la inicialización de la matriz al continuar entrenando un modelo total o parcialmente preentrenado cargado desde un archivo.

En el cuerpo del método, organizaremos el bloque de controles. Primero, verificaremos la validez de los punteros de los objetos recibidos en los parámetros de la muestra de entrenamiento y el contexto de OpenCL.

Luego verificaremos la presencia de datos en la muestra de entrenamiento, y también comprobaremos que su número sea múltiplo del tamaño del vector de descripción del estado aparte del sistema indicado durante la inicialización.

También añadiremos una verificación que se encargará de comprobar que la cantidad de elementos en la muestra de entrenamiento sea al menos 10 veces mayor que el número de clústeres.

bool CKmeans::Study(CBufferDouble *data, bool init_means = true)
  {
   if(CheckPointer(data) == POINTER_INVALID || CheckPointer(c_OpenCL) == POINTER_INVALID)
      return false;
//---
   int total = data.Total();
   if(total <= 0 || m_iClusters < 2 || (total % m_iVectorSize) != 0)
      return false;
//---
   int rows = total / m_iVectorSize;
   if(rows <= (10 * m_iClusters))
      return false;

El siguiente paso consistirá en inicializar la matriz de centros de clústeres. Por supuesto, antes de inicializar la matriz, comprobaremos el estado de la bandera de inicialización que hemos obtenido en los parámetros del método.

A continuación, inicializaremos la matriz con los vectores seleccionados aleatoriamente del conjunto de entrenamiento. Aquí necesitamos crear un algoritmo que excluya la inicialización de varios clústeres con el mismo estado del sistema. Para lograr esto, crearemos una matriz de banderas con un número de elementos igual al número de estados del sistema en el conjunto de entrenamiento. En la etapa inicial, inicializaremos esta matriz con valores false. A continuación, organizaremos un ciclo con un número de iteraciones igual al número de clústeres de nuestro modelo. En el cuerpo del ciclo, generaremos aleatoriamente un número dentro del tamaño de la muestra de entrenamiento y compararemos la bandera con el índice obtenido. Si el estado del sistema dado ya ha inicializado algún clúster, reduciremos los estados del contador de iteraciones y pasaremos a la siguiente iteración del ciclo.

Si el elemento seleccionado aún no ha participado en la inicialización de clústeres, determinaremos el desplazamiento en la muestra de entrenamiento al comienzo del estado dado del sistema en la muestra de entrenamiento y la matriz de vectores centrales. Luego organizaremos un ciclo anidado para copiar los datos. Y antes de pasar a la siguiente iteración del ciclo, cambiaremos la bandera con el índice trabajado.

   bool flags[];
   if(ArrayResize(flags, rows) <= 0 || !ArrayInitialize(flags, false))
      return false;
//---
   for(int i = 0; (i < m_iClusters && init_means); i++)
     {
      Comment(StringFormat("Cluster initialization %d of %d", i, m_iClusters));
      int row = (int)((double)MathRand() * MathRand() / MathPow(32767, 2) * (rows - 1));
      if(flags[row])
        {
         i--;
         continue;
        }
      int start = row * m_iVectorSize;
      int start_c = i * m_iVectorSize;
      for(int c = 0; c < m_iVectorSize; c++)
        {
         if(!c_aMeans.Update(start_c + c, data.At(start + c)))
            return false;
        }
      flags[row] = true;
     }

Después de inicializar la matriz de centros, procederemos a verificar la validez de los punteros y, si fuera necesario, crearíamos nuevos ejemplares de los objetos de búfer para registrar la matriz de distancia (c_aDistance), el vector de identificación del clúster para cada estado del sistema (c_aClasters) y el vector de banderas de cambio de clúster para los estados individuales del sistema (c_aFlags). Al mismo tiempo, no debemos olvidarnos de controlar la ejecución de las operaciones.

   if(CheckPointer(c_aDistance) == POINTER_INVALID)
     {
      c_aDistance = new CBufferDouble();
      if(CheckPointer(c_aDistance) == POINTER_INVALID)
         return false;
     }
   c_aDistance.BufferFree();
   if(!c_aDistance.BufferInit(rows * m_iClusters, 0))
      return false;

   if(CheckPointer(c_aClasters) == POINTER_INVALID)
     {
      c_aClasters = new CBufferDouble();
      if(CheckPointer(c_aClasters) == POINTER_INVALID)
         return false;
     }
   c_aClasters.BufferFree();
   if(!c_aClasters.BufferInit(rows, 0))
      return false;

   if(CheckPointer(c_aFlags) == POINTER_INVALID)
     {
      c_aFlags = new CBufferDouble();
      if(CheckPointer(c_aFlags) == POINTER_INVALID)
         return false;
     }
   c_aFlags.BufferFree();
   if(!c_aFlags.BufferInit(rows, 0))
      return false;

Finalmente, crearemos los búferes en el contexto de OpenCL.

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aMeans.BufferCreate(c_OpenCL) ||
      !c_aDistance.BufferCreate(c_OpenCL) ||
      !c_aClasters.BufferCreate(c_OpenCL) ||
      !c_aFlags.BufferCreate(c_OpenCL))
      return false;

En este punto, completaremos la etapa de trabajo preparatorio y procederemos a organizar las operaciones cíclicas directamente en el proceso de entrenamiento del modelo. Recordemos los puntos esenciales del algoritmo analizado:

Determinamos las distancias de cada elemento de la muestra de entrenamiento hasta cada centro del clúster;
Distribuimos los estados del sistema por clústeres (según la distancia mínima);
Actualizamos los centros del clúster.

Veamos estos pasos del algoritmo. Para cada paso anterior, ya hemos creado kernels en el programa OpenCL. Por consiguiente, nos quedará organizar una llamada cíclica de los kernels correspondientes.

Organizamos un ciclo de entrenamiento y, en el cuerpo del ciclo, llamaremos en primer lugar el kernel para calcular las distancias hasta los centros del clúster. Ya hemos cargado todos los búferes necesarios en la memoria del contexto OpenCL. Por ello, procederemos directamente a especificar los parámetros del kernel. Aquí indicaremos los punteros a los búferes de datos usados y el tamaño del vector que describe el estado del sistema. Tenga en cuenta que para indicar un parámetro específico, usaremos la pareja de constantes "identificador de kernel - identificador de parámetro"

   int count = 0;
   do
     {
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_distance, def_k_kmd_vector_size, m_iVectorSize))
         return false;

A continuación, deberemos indicar la dimensionalidad del espacio de tareas y el desplazamiento de cada uno. Planeamos iniciar este kernel en un espacio de tareas bidimensional. Vamos a crear 2 arrays estáticos con un número de elementos igual al espacio de la tareas:

global_work_size: para indicar la dimensionalidad del espacio de tareas;
global_work_offset: para indicar el desplazamiento en cada dimensión.

En ellos indicaremos un desplazamiento cero en ambas dimensiones. La dimensionalidad de la primera dimensión será igual al número de estados individuales del sistema en la muestra de entrenamiento. E indicamos una dimensionalidad de la segunda dimensión igual al número de clústeres en nuestro modelo.

      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2];
      global_work_size[0] = rows;
      global_work_size[1] = m_iClusters;

Después de ello, solo tendremos que iniciar el kernel para su ejecución y leer los resultados de las operaciones.

      if(!c_OpenCL.Execute(def_k_kmeans_distance, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aDistance.BufferRead())
         return false;

De forma similar, llamaremos al segundo kernel, que determinará si los estados del sistema pertenecen a clústeres específicos. Tenga en cuenta que este kernel se iniciará en un espacio de tareas unidimensional. Por consiguiente, necesitaremos otros arrays para indicar la dimensionalidad y el desplazamiento.

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_flags, c_aFlags.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_clustering, def_k_kmc_total_k, m_iClusters))
         return false;
      uint global_work_offset1[1] = {0};
      uint global_work_size1[1];
      global_work_size1[0] = rows;
      if(!c_OpenCL.Execute(def_k_kmeans_clustering, 1, global_work_offset1, global_work_size1))
         return false;
      if(!c_aFlags.BufferRead())
         return false;

Tenga en cuenta que después de poner el kernel en cola de ejecución, solo leeremos los datos del búfer de bandera. Ahora tendremos suficientes datos para determinar el final del entrenamiento del modelo. Entre tanto, la carga de los datos intermedios de los índices de los clústeres no conllevará una carga semántica, pero requerirá costes adicionales. Por eso, en esta etapa, hemos renunciado a ello.

Tras distribuir los elementos de la muestra de entrenamiento por clústeres, comprobaremos si ha habido una redistribución de los elementos por clústeres. Para hacer esto, comprobaremos el valor máximo del búfer de datos de bandera. Como recordará, en el código del kernel correspondiente, rellenamos el búfer de banderas con el resultado booleano de la comparación de los identificadores de clúster de la iteración anterior y el nuevo asignado. Si es igual, escribimos "0" en el búfer. Si el clúster ha cambiado, - "1". No importa cuántos elementos han cambiado el clúster. Nos basta con conocer su presencia. Por ello, comprobaremos el valor máximo, y si es igual a "0" (es decir, ninguno de los elementos ha cambiado el clúster), consideraremos el entrenamiento del modelo terminado. Leemos el búfer de identificación de clústeres de cada elemento de la secuencia y salimos del ciclo.

      m_bTrained = (c_aFlags.Maximum() == 0);
      if(m_bTrained)
        {
         if(!c_aClasters.BufferRead())
            return false;
         break;
        }

Si el proceso de aprendizaje aún no se ha finalizado, procederemos a organizar la llamada del 3er kernel, actualizando los vectores centrales de los clústeres. Después, ejecutaremos este kernel, al igual que el primero, en un espacio de tareas bidimensional. Por consiguiente, usaremos los arrays creados cuando se llamó al primer kernel. Cambiaremos solo la dimensionalidad de la primera dimensión.

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_updates, def_k_kmu_total_m, rows))
         return false;
      global_work_size[0] = m_iVectorSize;
      if(!c_OpenCL.Execute(def_k_kmeans_updates, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aMeans.BufferRead())
         return false;
      count++;
      Comment(StringFormat("Study iterations %d", count));
     }
   while(!m_bTrained && !IsStopped());

Después de ejecutar el kernel para el control visual del proceso de entrenamiento, mostraremos el número de iteraciones de entrenamiento completadas en el campo de comentarios del gráfico y pasaremos a la siguiente iteración del ciclo.

Tenga en cuenta que durante todo el entrenamiento del modelo, no hemos borrado la memoria del contexto de OpenCL y no hemos vuelto a copiar los datos en él. Recordemos que estas operaciones también requieren recursos. Y para aumentar la eficiencia en el uso de los recursos y reducir el tiempo total de entrenamiento del modelo, hemos eliminado estos costes. Pero este enfoque solo resulta posible si la memoria de contexto es suficiente para almacenar todos los datos. De lo contrario, tendremos que reconsiderar el uso de la memoria de contexto, descargando datos antiguos y cargando datos nuevos antes de ejecutar cada kernel.

Sin embargo, una vez completado el proceso de aprendizaje, antes de salir del método, podemos borrar la memoria de contexto y eliminar algunos de los búferes.

   data.BufferFree();
   c_aDistance.BufferFree();
   c_aFlags.BufferFree();
//---
   return true;
  }

Hay que decir que el entrenamiento del modelo no es un fin en sí mismo. Entrenamos el modelo para aprovechar los resultados del entrenamiento y aplicarlos a los nuevos datos. Para ejecutar esta funcionalidad, crearemos el método Clustering. De hecho, su algoritmo es una versión algo acortada del método de entrenamiento analizado anteriormente, en el que se excluyen el ciclo de aprendizaje y el tercer kernel. Solo los 2 primeros kernels se llaman una vez. Podrá familiarizarse con su código en el archivo adjunto.

El siguiente método que veremos es el método para calcular el valor de la función de pérdida GetLoss. Aquí tenemos que decir que para ahorrar recursos al entrenar el modelo, no calcularemos los valores de la función de pérdida. Por eso, el método recibe en los parámetros el puntero a la muestra de datos para la cual se calculará el error. Pero si antes organizábamos al comienzo del método un bloque de controles, ahora llamaremos al método de clusterización. Y, por supuesto, no debemos olvidarnos de comprobar el resultado de la ejecución del método.

double CKmeans::GetLoss(CBufferDouble *data)
  {
   if(!Clustering(data))
      return -1;

Este enfoque nos permitirá resolver 2 tareas a la vez con una sola acción. En primer lugar, hablamos de la clusterización de la nueva muestra en sí. Después de todo, para calcular las desviaciones, deberemos comprender a qué clústeres pertenecen los elementos de la muestra.

En segundo lugar, entendemos que el método Clustering ya contiene todos los controles necesarios, por lo que no necesitaremos repetirlos.

A continuación, contaremos el número de estados del sistema en la muestra e inicializaremos el búfer para determinar las desviaciones parciales.

   int total = data.Total();
   int rows = total / m_iVectorSize;
//---
   if(CheckPointer(c_aLoss) == POINTER_INVALID)
     {
      c_aLoss = new CBufferDouble();
      if(CheckPointer(c_aLoss) == POINTER_INVALID)
         return -1;
     }
   if(!c_aLoss.BufferInit(rows, 0))
      return -1;

Asimismo, trasladaremos los datos iniciales a la memoria de contexto. Tenga en cuenta que no transmitiremos los búferes de promedio y los identificadores de clúster a la memoria de contexto. La razón es que ya se encuentran en la memoria del contexto de OpenCL. No los eliminaremos después de realizar la clusterización de datos y, en esta etapa, podremos ahorrar algunos recursos.

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aLoss.BufferCreate(c_OpenCL))
      return -1;

A continuación, llamaremos al kernel correspondiente. El procedimiento para llamar al kernel es completamente idéntico a los ejemplos anteriormente analizados, así que no nos detendremos en ello. Podrá encontrar el código completo de todos los métodos y funciones en el archivo adjunto.

Sin embargo, hemos calculado en el kernel la desviación para cada estado individual. Ahora tendremos que determinar la desviación media. Para ello, organizaremos un ciclo en el que simplemente sumaremos todos los valores del búfer. Luego realizaremos la división por el número total de elementos en la muestra analizada.

   m_dLoss = 0;
   for(int i = 0; i < rows; i++)
      m_dLoss += c_aLoss.At(i);
   m_dLoss /= rows;

Al final del método, borraremos la memoria de contexto y retornaremos el valor resultante.

   data.BufferFree();
   c_aLoss.BufferFree();
   return m_dLoss;
  }

En esta etapa, hemos creado toda la funcionalidad necesaria para entrenar el modelo y realizar la posterior clusterización de datos. Pero sabemos que el entrenamiento de un modelo es un proceso bastante laborioso y no se repetirá antes de cada inicio del uso práctico del modelo. Por lo tanto, deberemos organizar el proceso de guardado del modelo en un archivo y restaurar su funcionamiento completo desde el mismo. Esta funcionalidad se implementará en los métodos Save yLoad, respectivamente. Ya hemos creado métodos similares más de una vez como parte de nuestra serie de artículos, porque dichos métodos están presentes en todas las clases. Podrá encontrar su código en el archivo adjunto: estaremos encantados de responder a todas sus preguntas en el foro, en el hilo dedicado a este artículo.

Como resultado, la estructura final de nuestra clase tomará la siguiente forma. Y el código completo de todos los métodos y clases se podrá encontrar en el archivo adjunto.

class CKmeans  : public CObject
  {
protected:
   int               m_iClusters;
   int               m_iVectorSize;
   double            m_dLoss;
   bool              m_bTrained;

   COpenCLMy         *c_OpenCL;       
   //---
   CBufferDouble     *c_aDistance;
   CBufferDouble     *c_aMeans;
   CBufferDouble     *c_aClasters;
   CBufferDouble     *c_aFlags;
   CBufferDouble     *c_aLoss;

public:
                     CKmeans(void);
                    ~CKmeans(void);
   //---
   bool              SetOpenCL(COpenCLMy *context);
   bool              Init(COpenCLMy *context, int clusters, int vector_size);
   bool              Study(CBufferDouble *data, bool init_means = true);
   bool              Clustering(CBufferDouble *data);
   double            GetLoss(CBufferDouble *data);
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedKmeans; }
  };

5. Simulación

Bien, ya estamos alcanzando el punto culminante del proceso. Hemos creado una nueva clase de clusterización de datos y nos gustaría evaluar su valor práctico. Vamos a entrenar el modelo. Para ello, crearemos el asesor ”kmeans.mq5". El código de asesor se encuentra en el archivo adjunto.

Los parámetros externos del asesor se trasladarán al completo de los usados anteriormente. Solo aumentaremos el periodo de estudio a 15 años. Al fin y al cabo, lo más destacado del aprendizaje no supervisado es precisamente la posibilidad de utilizar un gran conjunto de datos sin etiquetar. No hemos mostrado en los parámetros el número de clústeres en el modelo, ya que hemos organizado el proceso de aprendizaje en un ciclo con un amplio espectro de clústeres. Para encontrar el número óptimo de clústeres, hemos probado varias opciones que van desde 50 a 1000 clústeres. En concreto, hemos usado un paso de 50 clústeres. Recuerde: estas son las configuraciones de clusterización que usamos en el artículo anterior al probar el script de Python. También hemos tomado los parámetros de prueba de experimentos anteriores:

Instrumento EURUSD;
Marco temporal H1.

Como resultado del entrenamiento, se ha construido un gráfico de dependencia de la función de pérdida respecto al número de clústeres, que se muestra a continuación.

Gráfico de dependencia de los valores de la función de pérdida respecto al número de clústeres

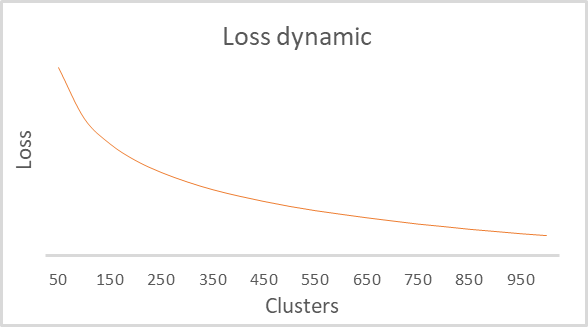
Como podrá ver en el gráfico, la ruptura resultó ser bastante amplia en el rango de 100 a 500 clústeres. Al mismo tiempo, hay que decir que hemos analizado más de 92 mil estados del sistema, y la forma del gráfico en sí es completamente idéntica a la creada por el script de Python en el artículo anterior. Esto confirma indirectamente que la clase que hemos construido funciona de forma correcta.

Conclusión

En este artículo, hemos creado una nueva clase CKmeans para implementar uno de los métodos de clusterización de k-medias más extendidos. E incluso hemos logrado entrenar el modelo con una cantidad diferente de clústeres. Según los resultados de la prueba, el modelo ha podido identificar alrededor de 500 patrones. Hemos obtenido un resultado similar realizando pruebas semejantes en Python. Y esto significa que hemos repetido correctamente el algoritmo del método. En el próximo artículo, discutiremos los posibles métodos de uso práctico de los resultados de la clusterización.

Enlaces

Programas utilizados en el artículo.

#	Nombre	Tipo	Descripción
1	kmeans.mq5	Asesor	Asesor para el entrenamiento de modelos
2	kmeans.mqh	Biblioteca de clases	Biblioteca para organizar el método de k-medias
3	unsupervised.cl	Biblioteca	Biblioteca de código del programa OpenCL para organizar el método de k-medias
4	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
5	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/10947

Archivos adjuntos |

Descargar ZIP

MQL5.zip (63.7 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Aprendiendo a diseñar un sistema de trading con OBV

En este nuevo artículo de nuestra serie para principiantes en programación MQL5, aprenderemos a construir sistemas de trading usando los indicadores más populares. En esta ocasión, analizaremos el indicador On Balance Volume (OBV), aprenderemos a utilizarlo y también a crear un sistema comercial basado en él.

Aprendiendo a diseñar un sistema comercial basado en Parabolic SAR

Esta es la continuación de una serie de artículos en los que aprendemos cómo crear sistemas comerciales usando los indicadores más populares. En el presente artículo, analizaremos el indicador Parabolic SAR. También desarrollaremos un sistema comercial para la plataforma MetaTrader 5 usando algunas estrategias simples.

Redes neuronales: así de sencillo (Parte 16): Uso práctico de la clusterización

En el artículo anterior, creamos una clase para la clusterización de datos. En este artículo, queremos compartir con el lector diferentes opciones de uso de los resultados obtenidos para resolver problemas prácticos en el trading.

Aprendiendo a diseñar un sistema de trading con ATR

En este artículo, analizaremos una nueva herramienta técnica que puede usarse en el trading. Esta es una continuación de nuestra serie para aprender a diseñar sistemas de trading sencillos. En esta ocasión, trabajaremos con otro popular indicador técnico, el rango medio verdadero (Average True Range, ATR).