Neural networks made easy (Part 15): Data clustering using MQL5

MetaTrader 5 — Trading systems | 20 July 2022, 12:58

5 044

Dmitriy Gizlyk

Introduction

In the previous article, we considered the k-means clustering method and studied its implementation using the Python language. However, the use of integration often imposes certain restrictions and additional costs. In particular, the current integration state does not allow the use of data of built-in applications such as indicators or terminal event handling. A lot of classic indicators are implemented in various libraries, but when we talk about custom indicators, we will need to reproduce their algorithms in our scripts. What to do if there is no source code of the indicator and we do not understand the algorithm of its action? Or if you are going to use the clustering results in other MQL5 programs? In such cases, we can benefit from the implementation of the clustering method using MQL5 tools.

1. Model construction principles

We have already considered the k-means clustering method, which is implemented as follows:

Determine k random points from the training sample as cluster centers.
Create a loop of operations:
- Determine the distance from each point to each center
- Find the nearest center and assign a point to this cluster
- Using the arithmetic mean, determine a new center for each cluster
Repeat the operations in a loop until cluster centers "stop moving".

Before we proceeding to writing the method code, let's discuss briefly the main points of our implementation.

The main operations of the earlier considered algorithm are implemented in a loop. At the beginning of the loop body, we need to find the distance from each element of the training sample to the center of each cluster. This operation for each element of the training sample is absolutely independent of other elements. Therefore, we can use the OpenCL technology to implement parallel computing. Furthermore, the operations for calculating the distance to the centers of different clusters are also independent. Therefore, we can parallelize operations in a two-dimensional task space.

In the next step, we need to determine whether an element of the sequence belongs to a particular cluster. This operation also implies independence of calculations for each element of the sequence. Here, we can use the OpenCL technology for parallel computing applied to individual elements of the training set.

In the end of the loop body, we define new centers of clusters. To do this, we need to loop through all the elements of the training sample and to calculate the arithmetic mean values in the context of each element of the vector describing the state of the system and of each cluster. Please note that only the elements belonging to this cluster are used to calculate the cluster center. Other elements are ignored. Therefore, the values of each element are used only once. In this case, it is also possible to use parallel computing technologies in a two-dimensional space. On one axis, we have vector elements describing the state of the system, and on the second one we have the analyzed clusters.

After data clustering is performed, we will need to calculate the loss function in order to evaluate the performance of the model. As mentioned above, this can be done by calculating the arithmetic mean deviation of the system state from the center of the corresponding cluster. Of course, it is not possible to explicitly divide the calculation of the arithmetic mean into threads. However, this task can be divided into two subtasks. First, we calculate the distance to the respective centers. This task can be easily parallelized in the context of a single state of the system. And after that we can calculate the arithmetic mean of the resulting distance vector.

2. Creating an OpenCL program

Thus, we have four separate subtasks for organizing parallel computing. As we discussed in previous articles, in order to implement parallel computing using OpenCL we should create a separate program which will download and execute this operation on the OpenCL context side. The executable program kernels will be creates in the separate file entitled "unsupervised.cl" in the order of the tasks mentioned above.

Let's start this work by writing the kernel KmeansCulcDistance, in which we will implement operations related to the calculation of distances from system states to the current centers of all clusters. This kernel will be executed in a two-dimensional task space. One dimension will be used for separate states of the system from the training sample. The second one, for the clusters of our model.

In the kernel input parameters, we indicate pointers to three data buffers and the size of the vector describing one state of the analyzed system. Two of the specified buffers will contain the source data. This is the training sample and the matrix of cluster center vectors. The third data buffer is the result tensor.

In the kernel body, we get the identifiers of the current operation thread in both dimensions and the total number of clusters by the number of running threads in the second dimension. We need these data to determine the offset to the desired elements in all the mentioned tensors. Here we also determine the offsets in the source data tensors and initialize the variable to zero to calculate the distance to the cluster center.

Next, we implement a loop with the number of iterations equal to the size of the vector describing one state of our system. In the body of this loop, we summarize the squared distances between the values of the corresponding elements of the system state vectors and the cluster center.

After all loop iterations, we only have to save the received value to the corresponding element of the result buffer. From a mathematical point of view, to determine the distance between two points in space, we need to extract the square root of the resulting value. But in this case, we are not interested in the exact distance between the two points. We only need to find the smallest distances. Therefore, to save resources, we will not take the square root.

__kernel void KmeansCulcDistance(__global double *data,
                                 __global double *means,
                                 __global double *distance,
                                 int vector_size
                                )
  {
   int m = get_global_id(0);
   int k = get_global_id(1);
   int total_k = get_global_size(1);
   double sum = 0.0;
   int shift_m = m * vector_size;
   int shift_k = k * vector_size;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_k + i], 2);
   distance[m * total_k + k] = sum;
  }

The code of the first kernel is ready, and we can move on to working on the next subprocess. According to the algorithm of our method, in the next step we need to determine to which of the clusters each state from the training sample belongs. To do this, we will determine which of the cluster centers is closer to the analyzed state. We have already calculated the distances in the previous kernel. Now, we only need to determine the number with the lowest value. All operations will be performed in the context of a single state of the system.

To implement this process, let us create a kernel KmeansClustering. Like the previous kernel, this one will receive pointers to 3 data buffers and the total number of clusters via parameters. Strange as it may seem, but only one buffer distance out of the three available will contain the original data. The other two buffers will contain the results of operations. To the clusters buffer, we will write the index of the cluster to which the analyzed system state belongs.

The third buffer - flags - will be used to write the cluster change flag compared to the previous state. By analyzing these flags we can define the breakpoint of the model training process. The logic behind this process is quite simple. If no state of the system changes its cluster, then, as a consequence, the centers of clusters will not change either. This means that further continuation of the operations loop does not make any sense. There the model training will stop.

Now let us get back to our kernel algorithm. We will launch it in a one-dimensional task space in the context of the analyzed system states. In the kernel body, we define the ordinal number of the analyzed state and the relevant shift in the data buffers. Each of the two result buffers contains one value for each state. Therefore, the shift in the specified buffers will be equal to the thread ID. Therefore, we only need to determine the shift in the source data buffer which contains calculated distances to cluster centers.

Here we will prepare two private variables. Into value we will write the distance to the center. The cluster number will be written to the second one - result. At the initial stage, they will store the values of the cluster with the index "0".

Then we will loop through distances to all cluster centers. Since we have already saved value of "0" cluster to the variables, let us start with the next cluster.

In the loop body, we check the distance to the next center. And if it is greater than or equal to the one already stored in the variable, proceed to check the next cluster.

If a closer center is found, we will overwrite the values of the private variables. We will save a shorter distance and the serial number of the corresponding cluster in them.

Once all loop iterations are complete, the result variable will store the identifier of the cluster closest to the analyzed state. The current state will be referred to it. But before saving the received value to the corresponding element of the result buffer, we need to check whether the cluster number has changed compared to the previous iteration. The result of the comparison will be saved to the flags buffer.

__kernel void KmeansClustering(__global double *distance,
                               __global double *clusters,
                               __global double *flags,
                               int total_k
                              )
  {
   int i = get_global_id(0);
   int shift = i * total_k;
   double value = distance[shift];
   int result = 0;
   for(int k = 1; k < total_k; k++)
     {
      if(value <= distance[shift + k])
         continue;
      value =  distance[shift + k];
      result = k;
     }
   flags[i] = (double)(clusters[i] != (double)result);
   clusters[i] = (double)result;
  }

At the end of the clustering algorithm, we need to update the values of the central vectors of all clusters which are collected in the means matrix. To implement this task, we will create another kernel KmeansUpdating. Like the kernels discussed above, the one considered in the parameters will receive pointers to three data buffers and one constant. Two buffers contain the original data and one buffer contains results. As mentioned above, we will execute this kernel in a two-dimensional task space. But unlike the KmeansCulcDistance kernel, in the first dimension of the task space we will iterate over the elements of the vector describing one system state, while in the total_m constant, we will indicate the number of elements in the training set.

In the kernel body, we will first define the thread IDs in both dimensions. As before, we will use them to determine parsed elements and offsets in data buffers. Here we will determine the length of the vector describing one system state, which is equal to the total number of running threads in the first dimension. In addition, we initialize two private variables in which we will sum up the values of the relevant elements of the system state description and their count.

The summation operations will be implemented in the loop that we are going to create; its number of iterations will be equal to the number of elements in the training sample. Do not forget, that we summarize only those elements that belong to the analyzed cluster. In the loop body, we first check to which cluster the current element belongs. If it does not correspond to the analyzed one, move on to the next element.

If the element passes the validation, i.e. it belongs to the analyzed cluster, we will add the value of the relevant element of the system state description vector and increase the counter by 1.

After exiting the loop, we only need to divide the accumulated sum by the number of summed elements. However, we should remember here about the possibility of getting a critical error: division by zero. Of course, given the organization of the algorithm, such a situation is unlikely. However, to ensure program reliability, we will add this check. Pay attention that if no elements belonging to the cluster are found, we do not rest its value but leave it the same.

__kernel void KmeansUpdating(__global double *data,
                             __global double *clusters,
                             __global double *means,
                             int total_m
                            )
  {
   int i = get_global_id(0);
   int vector_size = get_global_size(0);
   int k = get_global_id(1);
   double sum = 0;
   int count = 0;
   for(int m = 0; m < total_m; m++)
     {
      if(clusters[m] != k)
         continue;
      sum += data[m * vector_size + i];
      count++;
     }
   if(count > 0)
      means[k * vector_size + i] = sum / count;
  }

By this stage, we have created three kernels to implement the k-means data clustering algorithm. But before we proceeding to creating objects of the main program, we have to create another kernel for calculating the loss function.

The value of the loss function will be determined in two stages. First, we find the deviation of each individual element of the training sample from the center of the corresponding cluster. Then we calculate the arithmetic mean deviation for the entire sample. The operations of the first stage can be divided into threads to perform parallel computations using OpenCL tools. To implement this functionality, let us create the KmeansLoss kernel which receives in parameters pointers to four buffers and one constant. Three buffers will contain the source data and one buffer will be used for the results.

We will launch the kernel in a one-dimensional task space with the number of threads equal to the number of elements in the training set. In the kernel body, we first determine the ordinal number of the analyzed pattern from the training set. Then we determine to which cluster it belongs. This time we will not recalculate the distances to the centers of all clusters. Instead, we simply retrieve the relevant value from the clusters buffer according to the element's ordinal number. In the KmeansClustering kernel that we have considered earlier the ordinal number of the cluster was saved to this buffer.

Now we can determine the offset to the beginning of the required vectors in the tensors of the training sample and the matrix of cluster centers.

Next, we only need to calculate the distance between the two vectors. To do this, we initialize a private variable to accumulate the sum of deviations and create a loop through all elements of the vector describing one system state. In the loop body, we will sum the squared deviations of the corresponding elements of the vectors.

After all loop iterations, we will move the accumulated sum to the corresponding element of the loss result buffer.

__kernel void KmeansLoss(__global double *data,
                         __global double *clusters,
                         __global double *means,
                         __global double *loss,
                         int vector_size
                        )
  {
   int m = get_global_id(0);
   int c = clusters[m];
   int shift_c = c * vector_size;
   int shift_m = m * vector_size;
   double sum = 0;
   for(int i = 0; i < vector_size; i++)
      sum += pow(data[shift_m + i] - means[shift_c + i], 2);
   loss[m] = sum;
  }

We have considered the algorithms for constructing all processes on the OpenCL context side. Now we can move on to organizing processes on the side of the main program.

3. Preparatory work on the main program side

On the side of the main program, we will create a new class CKmeans. The class code will be saved to the kmeans.mqh file. But before proceeding directly to the new class, we need to implement some preparatory work. First, to transfer data to the OpenCL context, we will use the class object which we have already discussed in this series of articles: CBufferDouble. We will not rewrite the code of the specified class, but simply include the library created earlier.

#include "..\NeuroNet_DNG\NeuroNet.mqh"

Then, connect the the code of the OpenCL program created above as a resource.

#resource "unsupervised.cl" as string cl_unsupervised

Next, we create named constants. This time we need a number of such constants. To provide future compatibility and use with the previously created library, we should ensure that the created constants are unique.

First, we need a constant to identify the new class.

#define defUnsupervisedKmeans    0x7901

Second, we need constants to identify kernels and their parameters. Kernels are identified through continuous numbering within one OpenCL program. However, parameters are numbered within a single kernel. To improve code readability, I decided to group the constants according to the kernels they belong to.

#define def_k_kmeans_distance    0
#define def_k_kmd_data           0
#define def_k_kmd_means          1
#define def_k_kmd_distance       2
#define def_k_kmd_vector_size    3

#define def_k_kmeans_clustering  1
#define def_k_kmc_distance       0
#define def_k_kmc_clusters       1
#define def_k_kmc_flags          2
#define def_k_kmc_total_k        3

#define def_k_kmeans_updates     2
#define def_k_kmu_data           0
#define def_k_kmu_clusters       1
#define def_k_kmu_means          2
#define def_k_kmu_total_m        3

#define def_k_kmeans_loss        3
#define def_k_kml_data           0
#define def_k_kml_clusters       1
#define def_k_kml_means          2
#define def_k_kml_loss           3
#define def_k_kml_vector_size    4

After creating the named constants, let us move on to the next step of the preparatory work. When we discussed the implementation of multithreaded calculations in supervised learning models, we initialized an object for working with the OpenCL context in the constructor of the dispatch class of the neural network. In this article, we will use the CKmeans clustering class without any other models. Well, we could move the initialization function of the COpenCLMy object instance inside our new class CKmeans. However, clustering might someday be used as part of other more complex models. This is beyond the scope of this article, but we will get back to it in further articles within this series. Anyway, we should provide for this possibility. Therefore, I decided to create a separate function to initialize an instance of the COpenCLMy object class.

Take a look at the OpenCLCreate function algorithm. It is constructed in such a way that it receives the test of the OpenCL program as parameters and returns a pointer to an instance of an initialized object. In the function body, we will first create a new instance of the COpenCLMy class. Immediately check the result of the new object creation operation.

COpenCLMy *OpenCLCreate(string programm)
  {
   COpenCL *result = new COpenCLMy();
   if(CheckPointer(result) == POINTER_INVALID)
      return NULL;

Then call the new object initialization method, passing it a string variable with the OpenCL program text in the parameters. Again, check the result of the operation. If the operation results in an error, delete the object created above and exit the method, returning an empty pointer.

   if(!result.Initialize(programm, true))
     {
      delete result;
      return NULL;
     }

Upon successful initialization of the program, we proceed to creating kernels in the context of OpenCL. First, we specify the number of kernels to be created, and then we create all the previously described kernels, one by one. Do not forget to control the process, checking the result of each operation.

The code below shows an example of initializing only one kernel. The rest are initialized in the same way. The full code of all methods and functions is available in the attachment.

   if(!result.SetKernelsCount(4))
     {
      delete result;
      return NULL;
     }
//---
   if(!result.KernelCreate(def_k_kmeans_distance, "KmeansCulcDistance"))
     {
      delete result;
      return NULL;
     }
//---
...........
//---
   return result;
  }

After successfully creating all the kernels, exit the method by returning a pointer to the created object instance.

This completes the preparatory work, and we can proceed directly to working on a new data clustering class.

4. Constructing an organization class for the k-means algorithm

Starting to work on the new data clustering class CKmeans, let us discuss its content. What functionality should it have? Which methods and variables will we need to perform this functionality? All variables will be implemented in the protected block.

We will need separate variables to store model hyperparameters: the number of clusters to be created (m_iClusters) and the size of the description vector of one individual system state (m_iVectorSize).

To assess the quality of the trained model, we will calculate the loss function, the value of which will be stored in the m_dLoss variable.

In addition, to understand the model state (trained or not), we need the m_bTrained flag.

I think this list is enough to implement the desired functionality. Next, we move on to declaring the objects used. Here we declare one instance of the class to work with the OpenCL context (c_OpenCL). We also need data buffers to store information and to exchange it with the OpenCL context. We will make their names consonant with those used earlier when developing the OpenCL program:

c_aDistance;
c_aMeans;
c_aClasters;
c_aFlags;
c_aLoss.

After declaring variables, let us proceed to class methods. We will not hide anything here, and thus all methods will be public.

Naturally, we start with the class constructor and destructor. In the constructor, we create instances of the objects we use and set the initial variable values.

void CKmeans::CKmeans(void)   :  m_iClusters(2),
                                 m_iVectorSize(1),
                                 m_dLoss(-1),
                                 m_bTrained(false)
  {
   c_aMeans = new CBufferDouble();
   if(CheckPointer(c_aMeans) != POINTER_INVALID)
      c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0);
   c_OpenCL = NULL;
  }

In the class destructor, we clean up the memory and delete all objects created in the class.

void CKmeans::~CKmeans(void)
  {
   if(CheckPointer(c_aMeans) == POINTER_DYNAMIC)
      delete c_aMeans;
   if(CheckPointer(c_aDistance) == POINTER_DYNAMIC)
      delete c_aDistance;
   if(CheckPointer(c_aClasters) == POINTER_DYNAMIC)
      delete c_aClasters;
   if(CheckPointer(c_aFlags) == POINTER_DYNAMIC)
      delete c_aFlags;
   if(CheckPointer(c_aLoss) == POINTER_DYNAMIC)
      delete c_aLoss;
  }

Next, we create our class initialization method,to which, in parameters, we pass a pointer the object of operations with the OpenCL context and model hyperparameters. In the method body, we first create a small block of controls in which we check the data received in the parameters.

After that, save the obtained hyperparameters into the corresponding variables and initialize the buffer of the matrix of mean cluster vectors with zero values. Do not forget to check the result of the buffer initialization operations.

bool CKmeans::Init(COpenCLMy *context, int clusters, int vector_size)
  {
   if(CheckPointer(context) == POINTER_INVALID || clusters < 2 || vector_size < 1)
      return false;
//---
   c_OpenCL = context;
   m_iClusters = clusters;
   m_iVectorSize = vector_size;
   if(CheckPointer(c_aMeans) == POINTER_INVALID)
     {
      c_aMeans = new CBufferDouble();
      if(CheckPointer(c_aMeans) == POINTER_INVALID)
         return false;
     }
   c_aMeans.BufferFree();
   if(!c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0))
      return false;
   m_bTrained = false;
   m_dLoss = -1;
//---
   return true;
  }

After initialization, we have to train the model. We implement this functionality in the Study method. In method parameters, we will pass the training sample and the initialization flag of the matrix of cluster centers. By using the flag, we enable the possibility to disable matrix initialization when continuing training a fully or partially pretrained model loaded from a file.

The block of controls is implemented in the method body. First, check the validity of the object pointers received in the parameters of the training sample and the OpenCL context.

Then check the availability of data in the training sample. Also, make sure that their number is a multiple of the size of the description vector of a single system state specified during initialization.

Furthermore, make check whether the number of elements in the training sample is at least 10 times greater than the number of clusters.

bool CKmeans::Study(CBufferDouble *data, bool init_means = true)
  {
   if(CheckPointer(data) == POINTER_INVALID || CheckPointer(c_OpenCL) == POINTER_INVALID)
      return false;
//---
   int total = data.Total();
   if(total <= 0 || m_iClusters < 2 || (total % m_iVectorSize) != 0)
      return false;
//---
   int rows = total / m_iVectorSize;
   if(rows <= (10 * m_iClusters))
      return false;

The next step is to initialize the matrix of cluster centers. Of course, before initializing the matrix, we will check the state of the initialization flag that we received in the method parameters.

The matrix will be initialized with vectors randomly selected from the training sample. Here, we need to create an algorithm that prevents several clusters from being initialized with the same system state. To do this, we will create an array of flags with the number of elements equal to the number of system states in the training set. At the initial stage, we initialize this array with the false values. Next, implement a loop with the number of iterations equal to the number of clusters in the model. In the loop body, we randomly generate a number within the size of the training sample and check the flag at the obtained index. If this system state has already initialized any cluster, we will decrement the iteration counter states and move on to the next iteration of the loop.

If the selected element has not yet participated in the cluster initialization, then we determine the offset in the training sample to the beginning of the given system state in the training sample and the matrix of central vectors. After that, we implement a nested loop for copying data. Before moving on to the next iteration of the loop, we will change the flag with the processed index.

   bool flags[];
   if(ArrayResize(flags, rows) <= 0 || !ArrayInitialize(flags, false))
      return false;
//---
   for(int i = 0; (i < m_iClusters && init_means); i++)
     {
      Comment(StringFormat("Cluster initialization %d of %d", i, m_iClusters));
      int row = (int)((double)MathRand() * MathRand() / MathPow(32767, 2) * (rows - 1));
      if(flags[row])
        {
         i--;
         continue;
        }
      int start = row * m_iVectorSize;
      int start_c = i * m_iVectorSize;
      for(int c = 0; c < m_iVectorSize; c++)
        {
         if(!c_aMeans.Update(start_c + c, data.At(start + c)))
            return false;
        }
      flags[row] = true;
     }

After initializing the matrix of centers, we proceed to validating the pointers and, if necessary, creating new instances of buffer objects to write the distance matrix (c_aDistance), the cluster identification vector for each state of the system (c_aClusters) and the vector of cluster change flags for individual system states (c_aFlags). Remember to control the execution of operations.

   if(CheckPointer(c_aDistance) == POINTER_INVALID)
     {
      c_aDistance = new CBufferDouble();
      if(CheckPointer(c_aDistance) == POINTER_INVALID)
         return false;
     }
   c_aDistance.BufferFree();
   if(!c_aDistance.BufferInit(rows * m_iClusters, 0))
      return false;

   if(CheckPointer(c_aClasters) == POINTER_INVALID)
     {
      c_aClasters = new CBufferDouble();
      if(CheckPointer(c_aClasters) == POINTER_INVALID)
         return false;
     }
   c_aClasters.BufferFree();
   if(!c_aClasters.BufferInit(rows, 0))
      return false;

   if(CheckPointer(c_aFlags) == POINTER_INVALID)
     {
      c_aFlags = new CBufferDouble();
      if(CheckPointer(c_aFlags) == POINTER_INVALID)
         return false;
     }
   c_aFlags.BufferFree();
   if(!c_aFlags.BufferInit(rows, 0))
      return false;

Finally, we will create buffers in the OpenCL context.

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aMeans.BufferCreate(c_OpenCL) ||
      !c_aDistance.BufferCreate(c_OpenCL) ||
      !c_aClasters.BufferCreate(c_OpenCL) ||
      !c_aFlags.BufferCreate(c_OpenCL))
      return false;

This completes the preparatory stage. Now we can proceed to implementing loop operations directly related to the model training process. So, as we previously considered, the main milestones of the algorithm are as follows:

Determining the distances from each element of the training sample to each cluster center
Distributing system states by clusters (by minimum distance)
Updating cluster centers

Look at these stages of the algorithm. We have already created kernels in the OpenCL program to execute each stage. Therefore, now we need to implement a loop call of the corresponding kernels.

We implement a training loop and in the loop body we first call the kernel for calculating distances to cluster centers. We have already loaded all the necessary buffers into the memory of the OpenCL context. Therefore, we can immediately go to specifying the kernel parameters. Here we indicate pointers to the data buffers we use and the size of the vector describing one system state. Note that to specify a specific parameter, we use a pair of constants "kernel identifier — parameter identifier"

   int count = 0;
   do
     {
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_distance, def_k_kmd_vector_size, m_iVectorSize))
         return false;

Next, we need to specify the dimension of the task space and the offset in each of them. We were going to run this kernel in a two-dimensional task space. Let us create two static arrays with the number of elements equal to the task space:

global_work_size — to specify the dimension of the task space
global_work_offset — to specify the offset in each dimension

In them, we will indicate the zero offset in both dimensions. The size of the first dimension will be equal to the number of individual states of the system in the training set. The size of the second dimension will be equal to the number of clusters in our model.

      uint global_work_offset[2] = {0, 0};
      uint global_work_size[2];
      global_work_size[0] = rows;
      global_work_size[1] = m_iClusters;

After that, we just have to run the kernel for execution and read the results of the operations.

      if(!c_OpenCL.Execute(def_k_kmeans_distance, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aDistance.BufferRead())
         return false;

Similarly, we call the second kernel — determining whether the system states belong to specific clusters. Note that this kernel will be launched in a one-dimensional task space. Therefore, we need other arrays to indicate the dimension and offset.

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_flags, c_aFlags.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_distance, c_aDistance.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_clustering, def_k_kmc_total_k, m_iClusters))
         return false;
      uint global_work_offset1[1] = {0};
      uint global_work_size1[1];
      global_work_size1[0] = rows;
      if(!c_OpenCL.Execute(def_k_kmeans_clustering, 1, global_work_offset1, global_work_size1))
         return false;
      if(!c_aFlags.BufferRead())
         return false;

Please note that after the kernel is queued for execution, we only read the flag buffer data. AT this point, this data is enough to determine the end of model training. Loading of intermediate data of cluster indices does not provide any meaning, but requires additional costs. Therefore, it is not used at this stage.

Once all elements of the training sample have been distributed by clusters, we check whether there was a redistribution of elements by clusters. To do this, we check the maximum value of the flag data buffer. As you remember, in the relevant kernel code we filled the flags buffer with the boolean result of comparison of cluster IDs from the previous iteration and the new assigned one being. If equal, 0 was written to the buffer. If the cluster has changed, we wrote 1. We are not interested in the exact number of elements that changed the cluster. It is enough to know that there are such elements. Therefore, we check the maximum value. If it is equal to 0, i.e. none of the elements changed the cluster, we consider the training of the model completed. We read the cluster identification buffer of each element of the sequence and exit the loop.

      m_bTrained = (c_aFlags.Maximum() == 0);
      if(m_bTrained)
        {
         if(!c_aClasters.BufferRead())
            return false;
         break;
        }

If the learning process has not yet completed, we proceed to the call of the 3rd kernel, which updates the central vectors of clusters. This kernel will also tun in a two-dimensional task space. Therefore, we will use the arrays created at the call of the first kernel. We will only change the size of the first dimension.

      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_data, data.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_means, c_aMeans.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_clusters, c_aClasters.GetIndex()))
         return false;
      if(!c_OpenCL.SetArgument(def_k_kmeans_updates, def_k_kmu_total_m, rows))
         return false;
      global_work_size[0] = m_iVectorSize;
      if(!c_OpenCL.Execute(def_k_kmeans_updates, 2, global_work_offset, global_work_size))
         return false;
      if(!c_aMeans.BufferRead())
         return false;
      count++;
      Comment(StringFormat("Study iterations %d", count));
     }
   while(!m_bTrained && !IsStopped());

After executing kernel, for the visual control of the training process, we will print the number of completed training iterations in the comments field of the chart and move on to the next iteration of the loop.

Note that during the entire model training process, we did not clear the memory of the OpenCL context and did not re-copy the data into it. Because such operations would also require resources. To increase the efficiency of resource use and to reduce the overall model training time, we have eliminated these costs. But this approach is possible only if the context memory is sufficient to store all the data. If not, we will need to reconsider the use of context memory, unloading old data and loading new data before executing each kernel.

Nevertheless, after the training process is completed, before exiting the method, we clear the context memory and delete some of the buffers from it.

   data.BufferFree();
   c_aDistance.BufferFree();
   c_aFlags.BufferFree();
//---
   return true;
  }

Model training is not an end in itself. We train the model to take advantage of the training results and to apply them to new data. To implement this functionality, we will create the Clustering method. In fact, its algorithm is a somewhat truncated version of the learning method discussed above, in which we excluded the learning loop and the third kernel. Only the first 2 kernels are called once. You can study its code yourself in the attachment.

The next method we will look at is the method for calculating the value of the loss function — getloss. To save resources during model training, we did not calculate the values of the loss function. Therefore, in the parameters, the method receives a pointer to the data sample, for which the error will be calculated. But if earlier, at the beginning of the method, we implemented a block of controls, now instead we call the clustering method. And, of course, do not forget to check the method execution result.

double CKmeans::GetLoss(CBufferDouble *data)
  {
   if(!Clustering(data))
      return -1;

This approach allows us to solve 2 tasks at once with one action. The first task is the clustering of the new sample itself. In order to calculate the deviations, we need to understand which clusters the sample elements belong to.

Second, the Clustering clustering method already contains all the necessary controls, so we do not need to repeat them.

Next, we count the number of system states in the sample and initialize the buffer to determine deviations.

   int total = data.Total();
   int rows = total / m_iVectorSize;
//---
   if(CheckPointer(c_aLoss) == POINTER_INVALID)
     {
      c_aLoss = new CBufferDouble();
      if(CheckPointer(c_aLoss) == POINTER_INVALID)
         return -1;
     }
   if(!c_aLoss.BufferInit(rows, 0))
      return -1;

Then we transfer the initial data to the context memory. Note that we do not pass buffers of average values and cluster IDs into the context memory. This is because they already exist in the OpenCL context memory. We did not delete them after data clustering, and thus we can save some resources at this stage.

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aLoss.BufferCreate(c_OpenCL))
      return -1;

Next, we call the corresponding kernel. The kernel call procedure is completely identical to the examples discussed above. So let us not dwell on it. The full code of all methods and functions is available in the attachment.

But in this kernel, we determined the deviation of each individual state. Now we have to determine the mean deviation. To do this, we create a loop in which we simply sum up all the values of the buffer. Then we divide the result by the total number of elements in the analyzed sample.

   m_dLoss = 0;
   for(int i = 0; i < rows; i++)
      m_dLoss += c_aLoss.At(i);
   m_dLoss /= rows;

At the end of the method, we clear the context memory and return the resulting value.

   data.BufferFree();
   c_aLoss.BufferFree();
   return m_dLoss;
  }

By now, we have created the entire functionality require for model training followed by data clustering. But we know that training a model is a resource-intensive process and will not be repeated before each launch of the practical model use. Therefore, we should add the saving of the model to a file and the ability to restore its full functioning back from the file. These features are implemented via the Save and Load methods. As part of this series of articles, we have already created similar methods multiple times, since they are used in every class. The relevant code is available in the attachment. If you have any questions, please write them in comments to the article.

The final structure of our class will be as follows. The complete code of all methods and classes is available in the attachment below.

class CKmeans  : public CObject
  {
protected:
   int               m_iClusters;
   int               m_iVectorSize;
   double            m_dLoss;
   bool              m_bTrained;

   COpenCLMy         *c_OpenCL;       
   //---
   CBufferDouble     *c_aDistance;
   CBufferDouble     *c_aMeans;
   CBufferDouble     *c_aClasters;
   CBufferDouble     *c_aFlags;
   CBufferDouble     *c_aLoss;

public:
                     CKmeans(void);
                    ~CKmeans(void);
   //---
   bool              SetOpenCL(COpenCLMy *context);
   bool              Init(COpenCLMy *context, int clusters, int vector_size);
   bool              Study(CBufferDouble *data, bool init_means = true);
   bool              Clustering(CBufferDouble *data);
   double            GetLoss(CBufferDouble *data);
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedKmeans; }
  };

5. Testing

And here we are moving on to the climax of the process. We have created a new data clustering class. Now, let us evaluate its practical value. We will train the model. To do this, we will create an Expert Advisor entitled "kmeans.mq5". The entire EA code is provided in the attachment below.

The external parameters of the EA are equal to those we used previously. The only difference is that the EA training period is increased to 15 years. This is the advantage of unsupervised learning: we can use a large set of unlabeled data. I did not include the number of model clusters in the parameters, since the learning process is implemented in a loop with a fairly wide range of clusters. To find the optimal number of clusters, we went through several options ranging from 50 to 1000 clusters. The step was 50 clusters. These are the exact clustering parameters that we used in the previous article when testing the Python script. The testing parameters are those we used in previous experiments:

Symbol: EURUSD;
Timeframe H1.

As a result of training, we obtained a graph of the dependence of the loss function on the number of clusters. It is shown below.

Graph of the dependence of the loss function values on the number of clusters

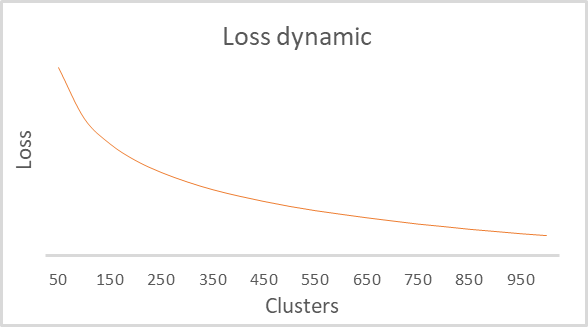
As you can see on the graph, the break turned out to be quite extended — in the range from 100 to 500 clusters. Totally the model analyzed more than 92 thousand system states. The form of the graph is completely identical to the one built by the Python script in the previous article. This indirectly confirms that the class we have built operates correctly.

Conclusions

In this article, we have created a new class CKmeans to implement one of the most common k-means clustering methods. We have even managed to train the model with different numbers of clusters. During tests, the model managed to identify about 500 patterns. A similar result was obtained by similar testing in Python. It means that we have correctly repeated the method algorithm. In the next article, we will discuss possible methods of practical use of clustering results.

References

Programs used in the article

#	Name	Type	Description
1	kmeans.mq5	Expert Advisor	Expert Advisor to train the model
2	kmeans.mqh	Class library	Library for organizing the k-means method
3	unsupervised.cl	Library	OpenCL program code library to implement the k-means method
4	NeuroNet.mqh	Class library	Class library for creating a neural network
5	NeuroNet.cl	Library	OpenCL program code library

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/10947

Attached files |

Download ZIP

MQL5.zip (63.7 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.