
神经网络变得轻松(第十五部分):利用 MQL5 进行数据聚类
内容目录
概述
在上一篇文章中,我们研究了 k-均值聚类方法,并研究了以 Python 语言实现其算法。 然而,使用集成通常会带来某些限制和额外成本。 特别是,当前集成状态不允许使用内置应用程序的数据,如指表或终端事件处理。 许多经典指标都已在各种函数库中实现,但当我们谈到自定义指标时,我们需要在脚本中重现它们的算法。 如果没有指标的源代码,并且我们不了解其行为的算法,那该怎么办? 或者,您是否打算在其它 MQL5 程序中使用聚类结果? 在这种情况下,我们可受益于使用 MQL5 工具实现聚类方法。
1. 模型构造原则
我们已经研究了 k-均值聚类方法,其实现如下:
- 从训练样本中确定 k 个随机点作为聚类中心。
- 创建一个操作循环:
- 判定从每个点到每个中心的距离
- 找到最近的中心,并把一个点分配给该聚类
- 使用算术平均值,为每个聚类判定一个新的中心
- 在循环中重复这些操作,直到聚类中心“停止移动”。
在继续编写方法代码之前,我们简要讨论一下实现的要点。
先前所研究算法的主要操作在循环中实现。 在循环体的伊始,我们需要为训练样本的每个元素找到至每个聚类中心的距离。 对于训练样本的每个元素,该操作与其它元素绝对独立。 如此,我们可以利用 OpenCL 技术来实现并行计算。 甚而,计算至不同聚类中心距离的操作也是独立的。 因此,我们能够在二维任务空间中并行化操作。
在下一步中,我们需要判定序列中的一个元素是否属于特定的聚类。 该操作还意味着序列中每个元素的计算均独立。 在此,我们可以将 OpenCL 技术应用于训练集合中各个元素的并行计算。
在循环主体的末尾,我们定义了新的聚类中心。 为此,我们需要遍历训练样本的所有元素,并在所描述系统和每个聚类状态的向量中每个元素环境下计算其算术平均值。 请注意,只有属于此聚类的元素才会计算聚类中心。 其它元素则被忽略。 因此,每个元素的值仅被使用一次。 在这种情况下,也可以在二维空间中运用并行计算技术。 在一条坐标轴上,我们有描述系统状态的向量元素,在第二条坐标轴上我们有分析的聚类。
执行数据聚类后,我们需要计算损失函数,来评估模型的性能。 如上所述,这可以通过计算系统状态与相应聚类中心的算术平均偏差来实现。 当然,不可能将算术平均值的计算明确划分给线程。 然而,此任务可切分为两个子任务。 首先,我们计算到各个中心的距离。 在系统单个状态环境下,该任务可以容易地并行化。 然后我们可以依据得到的距离向量再计算它们的算术平均值。
2. 创建 OpenCL 程序
因此,我们有四个单独的子任务来组织并行计算。 正如我们在前几篇文章中所讨论的,为了利用 OpenCL 实现并行计算,我们应该创建一个单独的程序,其可下载,并在 OpenCL 环境端执行此操作。 可执行程序内核将按照上述任务的顺序在名为 “unsupervised.cl” 的单独文件中创建。
我们从编写内核 KmeansCulcDistance 开始这项工作,在其中,我们将实现的操作与计算自系统状态到所有聚类当前中心的距离相关。 该内核将在二维任务空间中执行。 一个维度将用于从训练样本中分离系统的状态。 第二个,则针对我们模型中的聚类。
在内核输入参数中,我们指示指向三个数据缓冲区的指针,以及描述所分析系统一个状态的向量大小。 两个指定的缓冲区将包含源数据。 这是训练样本和聚类中心向量矩阵。 第三个数据缓冲区是结果张量。
在内核主体中,我们在两个维度上获得当前操作线程的标识符,并在第二维度上通过运行线程的数量获得聚类的总数。 我们需要这些数据来判定所有上述张量中所需元素的偏移量。 在这里,我们还判定源数据张量中的偏移量,并将变量初始化为零,以便计算到聚类中心的距离。
接下来,我们实现一个循环,迭代次数等于描述系统一个状态的向量大小。 在这个循环的主体中,我们汇总了系统状态向量的相应元素的值至聚类中心之间的平方距离。
在所有循环迭代之后,我们只需要将接收到的值保存到结果缓冲区的相应元素。 从数学角度来看,要判定空间中两点之间的距离,我们需要提取结果值的平方根。 但在这种情况下,我们对两点之间的确切距离不感兴趣。 我们只需要找到最短的距离。 故此,为了节省资源,我们不会取平方根。
__kernel void KmeansCulcDistance(__global double *data, __global double *means, __global double *distance, int vector_size ) { int m = get_global_id(0); int k = get_global_id(1); int total_k = get_global_size(1); double sum = 0.0; int shift_m = m * vector_size; int shift_k = k * vector_size; for(int i = 0; i < vector_size; i++) sum += pow(data[shift_m + i] - means[shift_k + i], 2); distance[m * total_k + k] = sum; }
第一个内核的代码已经准备好,我们可以继续处理下一个子进程。 根据我们的方法算法,在下一步中,我们需要判定训练样本中每个状态属于哪个聚类。 为此,我们将判定哪些聚类中心更接近所分析状态。 我们已经在前面的内核中计算出距离。 现在,我们只需要判定哪个是最小值的数字。 所有操作均在系统单一状态环境下执行。
为了实现这个过程,我们来创建一个内核 KmeansClustering。 与前面的内核一样,这个内核将通过参数接收指向 3 个数据缓冲区的指针和聚类总数。 也许看起来很奇怪,但在三个可用的缓冲区中,只有一个缓冲区 distance 包含原始数据。 其它两个缓冲区则包含操作结果。 至于 clusters 缓冲区中,我们将写入分析系统状态所属聚类的索引。
第三个缓冲区 - flags - 将会写入与先前状态相比较的聚类变更标志。 通过分析这些标志,我们可以定义模型训练过程的断点。 该过程背后的逻辑非常简单。 如果系统的状态没有改变其聚类,那么聚类的中心也不会改变。 这意味着继续循环执行操作没有任何意义。 如此的话,模型训练即将停止。
现在我们返回到我们的内核算法。 我们将在所分析系统状态环境下,在一维任务空间中启动它。 在内核主体中,我们定义了分析状态的序号,和其在数据缓冲区中的相关移位。 两个结果缓冲区中的每一个对于每个状态都包含一个值。 因此,指定缓冲区中的移位即等于线程 ID。 那么,我们只需要判定源数据缓冲区中的偏移量,其中包含到聚类中心的已计算距离。
在此,我们将准备两个私密变量。 我们将在 value 中写入至中心的距离。 聚类编号将写入第二个 - 结果。 在初始阶段,它们存储的聚类索引均为 “0” 值。
然后我们将循环遍历到所有聚类中心的距离。 因为我们已经将 “0” 聚类编号保存到变量当中,所以我们从下一个聚类开始。
在循环主体中,我们依次检查到下一个中心的距离。 如果大于或等于变量中已存储的值,则继续检查下一个聚类。
如果找到更靠近的中心,我们将覆盖私密变量的值。 我们将在其中保存较短距离的相应聚类的编号。
一旦所有循环迭代完成,结果变量将存储最接近分析状态的聚类标识符。 当前状态将作为参考。 但是,在将接收到的值保存到结果缓冲区的相应元素之前,我们需要检查与上一次迭代相比,聚类编号是否发生了变化。 比较结果亦将保存到标志缓冲区。
__kernel void KmeansClustering(__global double *distance, __global double *clusters, __global double *flags, int total_k ) { int i = get_global_id(0); int shift = i * total_k; double value = distance[shift]; int result = 0; for(int k = 1; k < total_k; k++) { if(value <= distance[shift + k]) continue; value = distance[shift + k]; result = k; } flags[i] = (double)(clusters[i] != (double)result); clusters[i] = (double)result; }
在聚类算法结束时,我们需要更新所有聚类的中心向量值,并收集在 means 矩阵当中。 为了实施这项任务,我们将创建另一个内核 KmeansUpdating。 与上面讨论的内核一样,参数中将接收指向三个数据缓冲区和一个常量的指针。 两个缓冲器包含原始数据,一个缓冲器包含结果。 如上所述,我们将在二维任务空间中执行此内核。 但与 KmeansCulcDistance 内核不同,在任务空间的第一维度中,我们将迭代描述一个系统状态的向量元素,而在 total_m 常量中,我们会指示训练集合中的元素数量。
在内核主体中,我们将首先在两个维度中定义线程 ID。 与前面一样,我们将用它们来判定数据缓冲区中已解析的元素和偏移量。 在此,我们将判定描述一个系统状态的向量的长度,该长度等于第一维中运行的线程总数。 此外,我们初始化了两个私密变量,我们将在其中汇总系统状态描述的相关元素的值,及其计数。
求和运算将在我们要创建的循环中实现;其迭代次数将等于训练样本中的元素数量。 不要忘记,我们只汇总那些属于所分析聚类的元素。 在循环体中,我们首先检查当前元素属于哪个聚类。 如果它与所分析元素不一致,则移至下一个元素。
如果元素通过了验证,即它属于所分析聚类,我们将添加系统状态描述向量的相关元素的值,并将计数器加 1。
在退出循环后,我们只需要将累计和除以求和元素的数量。 然而,我们应该记住,这里可能会出现一个关键错误:被零除。 当然,考虑到算法的组织结构,这种情况不太可能发生。 然而,为了确保程序的可靠性,我们将添加相关检查。 请注意,如果找不到属于该聚类的元素,我们则不会保留其值,而是保持不变。
__kernel void KmeansUpdating(__global double *data, __global double *clusters, __global double *means, int total_m ) { int i = get_global_id(0); int vector_size = get_global_size(0); int k = get_global_id(1); double sum = 0; int count = 0; for(int m = 0; m < total_m; m++) { if(clusters[m] != k) continue; sum += data[m * vector_size + i]; count++; } if(count > 0) means[k * vector_size + i] = sum / count; }
在此阶段,我们创建了三个内核来实现 k-均值数据聚类算法。 但在我们继续创建主程序的对象之前,我们必须创建另一个内核来计算损失函数。
损失函数的值将分两个阶段判定。 首先,我们找到训练样本中每个单独元素与相应聚类中心的偏差。 然后我们计算整个样本的算术平均偏差。 第一阶段的操作可以划分到线程,从而利用 OpenCL 工具执行并行计算。 为了实现这一功能,我们创建 KmeansLoss 内核,它在参数中接收指向四个缓冲区和一个常量的指针。 三个缓冲区将包含源数据,一个缓冲区用于结果。
我们将在一维任务空间中启动内核,线程数等于训练集合中的元素数。 在内核主体中,我们首先依据训练集合判定所分析形态的序号。 然后我们再判定它属于哪个聚类。 这次我们不会重新计算至所有聚类中心的距离。 取而代之,我们简单地从聚类缓冲区中根据元素的序号提取相关值。 在我们前面研究过的 KmeansClustering 内核中,聚类的序号被保存到该缓冲区。
现在我们可以判定训练样本张量和聚类中心矩阵中所需向量的起点偏移量。
下一步,我们只需要计算两个向量之间的距离。 为此,我们初始化一个私密变量以累积偏差之和,并依据描述一个系统状态的向量的所有元素创建一个循环。 在循环主体中,我们将取向量相应元素的平方偏差求和。
在所有循环迭代之后,我们将累加和移动到 loss 结果缓冲区的相应元素。
__kernel void KmeansLoss(__global double *data, __global double *clusters, __global double *means, __global double *loss, int vector_size ) { int m = get_global_id(0); int c = clusters[m]; int shift_c = c * vector_size; int shift_m = m * vector_size; double sum = 0; for(int i = 0; i < vector_size; i++) sum += pow(data[shift_m + i] - means[shift_c + i], 2); loss[m] = sum; }
我们已研究了在 OpenCL 环境端构建所有进程的算法。 现在我们可以继续在主程序端组织流程。
3. 主要程序方面的准备工作
在主程序端,我们将创建一个新类 CKmeans。 这个类的代码将保存到 kmeans.mqh 文件当中。 但在直接处理新类之前,我们需要做一些准备工作。 首先,为了将数据传输到 OpenCL 环境,我们将利用我们在本系列文章中已经讨论过的类对象:CBufferDouble。 我们不会重写指定类的代码,而只是简单地包含早前已创建好的函数库。
#include "..\NeuroNet_DNG\NeuroNet.mqh"
然后,连接上面创建的 OpenCL 程序代码作为资源。
#resource "unsupervised.cl" as string cl_unsupervised
接下来,我们创建命名常量。 这次我们需要一些这样的常量。 为提供与先前及未来所创建函数库的兼容性,我们应该确保创建的常量是唯一的。
首先,我们需要一个常量来标识新类。
#define defUnsupervisedKmeans 0x7901
其次,我们需要常量来识别内核及其参数。 内核则由一个 OpenCL 程序中的连续编号来标识。 不过,参数是在单个内核中编号。 为了提高代码的可读性,我决定根据常量所属的内核对其进行分组。
#define def_k_kmeans_distance 0 #define def_k_kmd_data 0 #define def_k_kmd_means 1 #define def_k_kmd_distance 2 #define def_k_kmd_vector_size 3 #define def_k_kmeans_clustering 1 #define def_k_kmc_distance 0 #define def_k_kmc_clusters 1 #define def_k_kmc_flags 2 #define def_k_kmc_total_k 3 #define def_k_kmeans_updates 2 #define def_k_kmu_data 0 #define def_k_kmu_clusters 1 #define def_k_kmu_means 2 #define def_k_kmu_total_m 3 #define def_k_kmeans_loss 3 #define def_k_kml_data 0 #define def_k_kml_clusters 1 #define def_k_kml_means 2 #define def_k_kml_loss 3 #define def_k_kml_vector_size 4
在创建命名常量之后,我们继续下一步的准备工作。 当我们讨论监督学习模型中多线程计算的实现时,我们初始化了一个对象,其用于在神经网络调度类的构造函数中操控 OpenCL 环境。 在本文中,我们将在不使用任何其它模型的情况下使用 CKmeans 聚类类。 好了,我们可以将 COpenCLMy 对象实例的初始化函数移动到我们的新类 CKmeans 内部当中。 不过,有一天聚类也许会被用作其它更复杂模型的一部分。 这超出了本文的范畴,但我们将在本系列的后续文章中继续研讨。 无论如何,我们都应该考虑这种可能性。 因此,我决定创建一个单独的函数来初始化 COpenCLMy 对象类的实例。
看看 OpenCLCreate 函数算法。 它的构造方式是,它接收 OpenCL 程序的测试作为参数,并返回指向初始化对象实例的指针。 在函数主体中,我们将首先创建一个新的 COpenCLMy 类实例。 立即检查创建新对象操作的结果。
COpenCLMy *OpenCLCreate(string programm) { COpenCL *result = new COpenCLMy(); if(CheckPointer(result) == POINTER_INVALID) return NULL;
然后调用新对象的初始化方法,并将 OpenCL 程序文本传递给参数中的字符串变量。 再次检查操作结果。 如果操作导致错误,则删除上面创建的对象,并退出该方法,返回一个空指针。
if(!result.Initialize(programm, true)) { delete result; return NULL; }
直至程序成功初始化后,我们继续在 OpenCL 环境下创建内核。 首先,我们指定要创建的内核数量,然后逐个创建前面描述的所有内核。 不要忘记控制过程,检查每个操作的结果。
下面的代码展示了仅初始化一个内核的示例。 其余的则以相同的方式初始化。 附件中提供了所有方法和函数的完整代码。
if(!result.SetKernelsCount(4)) { delete result; return NULL; } //--- if(!result.KernelCreate(def_k_kmeans_distance, "KmeansCulcDistance")) { delete result; return NULL; } //--- ........... //--- return result; }
成功创建所有内核后,退出该方法,并返回指向所创建对象实例的指针。
准备工作完成,我们可以直接着手处理一个新的数据聚类类。
4. 针对 k-均值算法构造一个组织类
从新的数据聚类类 CKmeans 开始工作,我们讨论一下它的内容。 它应该具有什么功能? 执行此功能需要哪些方法和变量? 所有变量都是在受保护的 模块中实现。
我们需要单独的变量来存储模型超参数:要创建的聚类的数量(m_iClusters),和独立系统状态的描述向量的大小(m_ iVectorSize)。
为了评估训练模型的品质,我们将计算损失函数,其值将存储在 m_dLoss 变量之中。
此外,为了理解模型状态(训练已否),我们需要 m_bTrained 标志。
我认为这份清单足以实现所需的功能。 接下来,我们继续声明要用到的对象。 在此,我们声明了一个类实例来处理 OpenCL 环境(c_OpenCL)。 我们还需要数据缓冲区来存储信息,并与 OpenCL 环境交换信息。 我们应确保它们的名称与开发 OpenCL 程序时所用的名称一致:
- c_aDistance;
- c_aMeans;
- c_aClasters;
- c_aFlags;
- c_aLoss.
声明变量后,我们处理类方法。 我们不会在这里隐藏任何东西,故此所有方法都是公开的。
自然地,我们要从类构造函数和析构函数开始。 在构造函数中,我们创建所用对象的实例,并设置初始变量值。
void CKmeans::CKmeans(void) : m_iClusters(2), m_iVectorSize(1), m_dLoss(-1), m_bTrained(false) { c_aMeans = new CBufferDouble(); if(CheckPointer(c_aMeans) != POINTER_INVALID) c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0); c_OpenCL = NULL; }
在类析构函数中,我们清理内存,并删除由类创建的所有对象。
void CKmeans::~CKmeans(void) { if(CheckPointer(c_aMeans) == POINTER_DYNAMIC) delete c_aMeans; if(CheckPointer(c_aDistance) == POINTER_DYNAMIC) delete c_aDistance; if(CheckPointer(c_aClasters) == POINTER_DYNAMIC) delete c_aClasters; if(CheckPointer(c_aFlags) == POINTER_DYNAMIC) delete c_aFlags; if(CheckPointer(c_aLoss) == POINTER_DYNAMIC) delete c_aLoss; }
接下来,我们创建类初始化方法,在参数中,我们向该方法传递一个指针,该指针指向是带有 OpenCL 环境和模型超参数的操作对象。 在方法主体中,我们首先创建一个小的控制模块,在其中检查参数接收的数据。
之后,将获得的超参数保存到相应的变量之中,并用零值初始化平均聚类向量矩阵的缓冲区。 不要忘记检查缓冲区初始化操作的结果。
bool CKmeans::Init(COpenCLMy *context, int clusters, int vector_size) { if(CheckPointer(context) == POINTER_INVALID || clusters < 2 || vector_size < 1) return false; //--- c_OpenCL = context; m_iClusters = clusters; m_iVectorSize = vector_size; if(CheckPointer(c_aMeans) == POINTER_INVALID) { c_aMeans = new CBufferDouble(); if(CheckPointer(c_aMeans) == POINTER_INVALID) return false; } c_aMeans.BufferFree(); if(!c_aMeans.BufferInit(m_iClusters * m_iVectorSize, 0)) return false; m_bTrained = false; m_dLoss = -1; //--- return true; }
初始化后,我们必须训练模型。 我们已在 Study 方法中实现了此功能。 在方法参数中,我们将传递训练样本和聚类中心矩阵的初始化标志。 通过该标志,在继续完整训练或从文件加载部分预训练模型时,我们就有能力禁用矩阵初始化。
控制模块在方法主体中实现。 首先,检查在训练样本和 OpenCL 环境的参数中接收的对象指针的有效性。
然后检查训练样本中数据的可用性。 此外,确保它们的数量是初始化期间指定的单个系统状态的描述向量大小的倍数。
甚至,检查训练样本中的元素数量是否至少是聚类数量的 10 倍。
bool CKmeans::Study(CBufferDouble *data, bool init_means = true) { if(CheckPointer(data) == POINTER_INVALID || CheckPointer(c_OpenCL) == POINTER_INVALID) return false; //--- int total = data.Total(); if(total <= 0 || m_iClusters < 2 || (total % m_iVectorSize) != 0) return false; //--- int rows = total / m_iVectorSize; if(rows <= (10 * m_iClusters)) return false;
下一步是初始化聚类中心矩阵。 当然,在初始化矩阵之前,我们将检查在方法参数中接收到的初始化标志的状态。
矩阵则用从训练样本中随机选择的向量进行初始化。 在此,我们需要创建一个算法,防止若干个聚类以相同的系统状态初始化。 为此,我们将创建一个标志数组,其元素数量等于训练集合中的系统状态数量。 在初始化阶段,我们采用false 值初始化该数组。 接下来,实现一个循环,迭代次数等于模型中的聚类数量。 在循环主体中,我们在训练样本大小范围内随机生成一个数字,并在获得的索引处检查标志。 如果该系统状态已因任何聚类而被初始化了,我们将减少迭代计数器状态,并继续下一次循环迭代。
如果所选元素尚未参与聚类初始化,则我们要判定训练样本至给定系统状态和中心向量矩阵的偏移量。 之后,我们实现一个用于复制数据的嵌套循环。 在继续循环的下一次迭代之前,我们将采用已处理的索引更改标志。
bool flags[]; if(ArrayResize(flags, rows) <= 0 || !ArrayInitialize(flags, false)) return false; //--- for(int i = 0; (i < m_iClusters && init_means); i++) { Comment(StringFormat("Cluster initialization %d of %d", i, m_iClusters)); int row = (int)((double)MathRand() * MathRand() / MathPow(32767, 2) * (rows - 1)); if(flags[row]) { i--; continue; } int start = row * m_iVectorSize; int start_c = i * m_iVectorSize; for(int c = 0; c < m_iVectorSize; c++) { if(!c_aMeans.Update(start_c + c, data.At(start + c))) return false; } flags[row] = true; }
初始化中心矩阵后,我们继续验证指针,如有必要,创建缓冲区对象的新实例,来写入距离矩阵(c_aDistance)、系统每个状态的聚类标识向量(c_ aClusters)、和单个系统状态的聚类更改标志向量(c_aFlags)。 记住要控制操作的执行。
if(CheckPointer(c_aDistance) == POINTER_INVALID) { c_aDistance = new CBufferDouble(); if(CheckPointer(c_aDistance) == POINTER_INVALID) return false; } c_aDistance.BufferFree(); if(!c_aDistance.BufferInit(rows * m_iClusters, 0)) return false; if(CheckPointer(c_aClasters) == POINTER_INVALID) { c_aClasters = new CBufferDouble(); if(CheckPointer(c_aClasters) == POINTER_INVALID) return false; } c_aClasters.BufferFree(); if(!c_aClasters.BufferInit(rows, 0)) return false; if(CheckPointer(c_aFlags) == POINTER_INVALID) { c_aFlags = new CBufferDouble(); if(CheckPointer(c_aFlags) == POINTER_INVALID) return false; } c_aFlags.BufferFree(); if(!c_aFlags.BufferInit(rows, 0)) return false;
最后,我们将在 OpenCL 环境中创建缓冲区,从而控制操作的执行。
if(!data.BufferCreate(c_OpenCL) || !c_aMeans.BufferCreate(c_OpenCL) || !c_aDistance.BufferCreate(c_OpenCL) || !c_aClasters.BufferCreate(c_OpenCL) || !c_aFlags.BufferCreate(c_OpenCL)) return false;
准备阶段就此完毕。 现在我们可以继续实现与模型训练过程直接相关的循环操作。 那么,正如我们之前所研究的,该算法的主要里程碑如下:
- 判定从训练样本的每个元素到每个聚类中心的距离
- 按聚类分派系统状态(按最小距离)
- 更新聚类中心
查看算法的这些阶段。 我们已在 OpenCL 程序中创建了内核来执行每个阶段。 因此,现在我们需要实现循环调用相应内核。
我们实现了一个训练循环,在循环主体中,我们首先调用内核来计算到聚类中心的距离。 我们已将所有必要的缓冲区加载到 OpenCL 环境的内存中。 因此,我们可以立即开始指定内核参数。 在此,我们指示指向需用到的数据缓冲区的指针,以及描述一个系统状态的向量大小。 请注意,为了指定特定参数,我们用到了一对常量“内核标识符 — 参数标识符”
int count = 0; do { if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_data, data.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_means, c_aMeans.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_distance, c_aDistance.GetIndex())) return false; if(!c_OpenCL.SetArgument(def_k_kmeans_distance, def_k_kmd_vector_size, m_iVectorSize)) return false;
接下来,我们需要指定任务空间的维度,以及每个维度中的偏移量。 我们打算在二维任务空间中运行这个内核。 让我们创建两个静态数组,元素数量等于任务空间:
- global_work_size — 指定任务空间的维度
- global_work_offset — 指定在每个维度中的偏移
在它们中,我们将在两个维度中指定零偏移。 第一维度的大小将等于训练集合中系统单个状态的数量。 第二维度的大小将等于我们模型中的聚类数量。
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = rows; global_work_size[1] = m_iClusters;
之后,我们只需运行内核,执行并读取操作结果。
if(!c_OpenCL.Execute(def_k_kmeans_distance, 2, global_work_offset, global_work_size)) return false; if(!c_aDistance.BufferRead()) return false;
类似地,我们调用第二个内核 — 判定系统状态是否属于特定聚类。 请注意,此内核将在一维任务空间中启动。 因此,我们需要其它数组来指示维度和偏移量。
if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_flags, c_aFlags.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_clusters, c_aClasters.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_clustering, def_k_kmc_distance, c_aDistance.GetIndex())) return false; if(!c_OpenCL.SetArgument(def_k_kmeans_clustering, def_k_kmc_total_k, m_iClusters)) return false; uint global_work_offset1[1] = {0}; uint global_work_size1[1]; global_work_size1[0] = rows; if(!c_OpenCL.Execute(def_k_kmeans_clustering, 1, global_work_offset1, global_work_size1)) return false; if(!c_aFlags.BufferRead()) return false;
请注意,在内核排队等待执行之后,我们仅读取标志缓冲区数据。 在该时刻,这些数据足以判定模型训练是否结束。 装载聚类索引的中间数据没有任何意义,但需要额外的成本。 因此,现阶段未使用。
一旦训练样本的所有元素都按聚类分派好,我们检查是否需要按聚类重新分派元素。 为此,我们检查标志数据缓冲区的最大值。 正如您所记得的,在相关的 内核 代码中,我们在填充标志缓冲区时采用的是上一次迭代的聚类 ID 和新分派聚类 ID 比较后的布尔结果。 如果相等,则将 0 写入缓冲区。 如果聚类发生了变化,我们则写入 1。 我们对聚类变更元素的确切数量不感兴趣。 知道有这样的元素就足够了。 因此,我们检查最大值。 如果它等于 0,即没有任何元素聚类变化,我们认为模型的训练已完成,我们读取序列中每个元素的聚类识别缓冲区,并退出循环。
m_bTrained = (c_aFlags.Maximum() == 0); if(m_bTrained) { if(!c_aClasters.BufferRead()) return false; break; }
如果学习过程尚未完成,我们将继续调用第三个内核,它将更新聚类的中心向量。 该内核还将在二维任务空间中运行。 因此,我们将使用在第一个内核调用时创建的数组。 我们仅会改变第一维度的大小。
if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_data, data.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_means, c_aMeans.GetIndex())) return false; if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_updates, def_k_kmu_clusters, c_aClasters.GetIndex())) return false; if(!c_OpenCL.SetArgument(def_k_kmeans_updates, def_k_kmu_total_m, rows)) return false; global_work_size[0] = m_iVectorSize; if(!c_OpenCL.Execute(def_k_kmeans_updates, 2, global_work_offset, global_work_size)) return false; if(!c_aMeans.BufferRead()) return false; count++; Comment(StringFormat("Study iterations %d", count)); } while(!m_bTrained && !IsStopped());
在内核执行之后,为了对训练过程进行可视化控制,我们将在图表的注释字段中打印完成的训练迭代次数,并进入循环的下一次迭代。
请注意,在整个模型训练过程中,我们没有清除 OpenCL 环境的内存,也没有将数据重新复制到其中。 因为这样的操作也要耗费资源。 为了提高资源利用率,并减少总体模型训练时间,我们剔除了这些成本。 但只有当环境内存足以存储所有数据时,这种方法才可行。 如果没有的话,我们需要重新考虑环境内存的使用,在每个内核执行之前卸载旧数据,并加载新数据。
无论如何,当训练过程完成后,在退出该方法之前,我们都要清除环境内存,并从中删除一些缓冲区。
data.BufferFree(); c_aDistance.BufferFree(); c_aFlags.BufferFree(); //--- return true; }
模特训练本身并不是目的。 我们训练模型是为了利用训练结果,并将其应用于新数据。 为了实现这一功能,我们将创建 Clustering 方法。 事实上,它的算法是上述学习方法的一个略为删节的版本,其中我们剔除了学习循环和第三个内核。 仅调用前 2 个内核一次。 您可以自行研究附件中的代码。
我们将研究的下一种方法是计算损失函数值的方法 — getloss。 为了节省模型训练期间的资源,我们没有计算损失函数的值。 因此,在参数中,该方法接收一个指向数据样本的指针,将为其计算误差。 但若是早前,在方法的开始,我们实现了一个控制模块,现在我们称之为聚类方法。 当然,不要忘记检查方法执行结果。
double CKmeans::GetLoss(CBufferDouble *data) { if(!Clustering(data)) return -1;
这种方法允许我们用一个动作同时解决两个任务。 第一项任务是对新样本本身进行聚类。 为了计算偏差,我们需要了解样本元素属于哪格聚类。
其次,Clustering 聚类方法已经包含了所有必要的控制,因此我们不需要重复它们。
接下来,我们计算样本中系统状态的数量,并初始化缓冲区来判定偏差。
int total = data.Total(); int rows = total / m_iVectorSize; //--- if(CheckPointer(c_aLoss) == POINTER_INVALID) { c_aLoss = new CBufferDouble(); if(CheckPointer(c_aLoss) == POINTER_INVALID) return -1; } if(!c_aLoss.BufferInit(rows, 0)) return -1;
然后我们把初始数据传输到环境内存。 请注意,我们不会将平均值和聚类 ID 的缓冲区传递到环境内存当中。 这是因为它们已经存在于 OpenCL 环境内存当中了。 在数据聚类之后,我们没有删除它们,因此我们可以在这个阶段节省一些资源。
if(!data.BufferCreate(c_OpenCL) || !c_aLoss.BufferCreate(c_OpenCL)) return -1;
接下来,我们调用相应的内核。 内核调用过程与上面讨论的示例完全相同。 既如此,我们究不要纠缠于此。 附件中提供了所有方法和函数的完整代码。
但是在这个内核中,我们判定了每个单独状态的偏差。 现在我们必须要判定平均偏差。 为此,我们创建了一个循环,在这个循环中,我们简单地把缓冲区的所有数值累加。 然后我们将结果除以分析样本中的元素总数。
m_dLoss = 0; for(int i = 0; i < rows; i++) m_dLoss += c_aLoss.At(i); m_dLoss /= rows;
在方法结束时,我们清除环境内存,并返回结果值。
data.BufferFree();
c_aLoss.BufferFree();
return m_dLoss;
}
到目前为止,我们已经创建了模型训练和数据聚类所需的全部功能。 但我们知道,训练一个模型是一个资源密集型的过程,在每次启动实际模型之前不会再重复。 因此,我们应该将模型保存到文件中,并能够从文件中恢复其全部功能。 这些功能则由 Save 和 Load 方法实现。 作为本系列文章的一部分,我们已多次创建过类似的方法,因为它们在每个类中都会用到。 附件中提供了相关代码。 如果您有任何问题,请将其写在文章的评论中。
我们的类最终结构如下。 下面的附件中提供了所有方法和类的完整代码。
class CKmeans : public CObject { protected: int m_iClusters; int m_iVectorSize; double m_dLoss; bool m_bTrained; COpenCLMy *c_OpenCL; //--- CBufferDouble *c_aDistance; CBufferDouble *c_aMeans; CBufferDouble *c_aClasters; CBufferDouble *c_aFlags; CBufferDouble *c_aLoss; public: CKmeans(void); ~CKmeans(void); //--- bool SetOpenCL(COpenCLMy *context); bool Init(COpenCLMy *context, int clusters, int vector_size); bool Study(CBufferDouble *data, bool init_means = true); bool Clustering(CBufferDouble *data); double GetLoss(CBufferDouble *data); //--- virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); //--- virtual int Type(void) { return defUnsupervisedKmeans; } };
5. 测试
在此,我们将进入这个过程的高潮。 我们已创建了一个新的数据聚类类。 现在,我们来评估它的实用价值。 我们将训练模型。 为此,我们将创建一个名为 “kmeans.mq5” 的智能交易系统。 文后附件中提供了整个 EA 代码。
EA 的外部参数与我们之前所用的参数相同。 唯一的区别是 EA 训练周期增加到 15 年。 这就是无监督学习的优势:我们可以使用大量未标记的数据。 我没有在参数中包括模型聚类的数量,因为学习过程是在一个具有相当大范围聚类的循环中实现的。 为了找到最佳的聚类数量,我们选择了 50 到 1000 个聚类。 步长为 50。 这些正是我们在前一篇文章中测试 Python 脚本时所用的聚类参数。 测试参数是我们在先前实验中所用的参数:
- 品种: EURUSD;
- 时间帧 H1。
作为训练的结果,我们得到了损失函数与聚类数量的依赖关系图。 它如下所示。
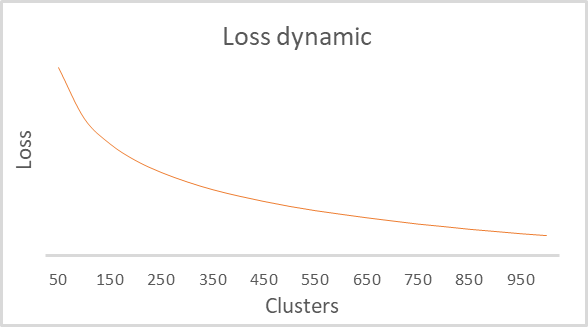
正如您在图表上所看到的那样,拉弯处被证明是相当大的 — 范围从 100 到 500。 该模型总共分析了 92000 多个系统状态。 图形的形式与上一篇文章中 Python 脚本构建的图形完全相同。 这间接地证实了我们构建的类运行正确。
结束语
在本文中,我们创建了一个新类 CKmeans,来实现最常见的 k-均值聚类方法之一。 我们甚至设法用不同数量的聚类来训练模型。 在测试期间,该模型成功地识别了大约 500 种形态。 在 Python 中进行类似的测试,获得了类似的结果。 这意味着我们已经正确地重复了该方法的算法。 在下一篇文章中,我们将讨论实际运用聚类结果的可能方法。
参考
- 神经网络变得轻松
- 神经网络变得轻松(第二部分):网络训练和测试
- 神经网络变得轻松(第三部分):卷积网络
- 神经网络变得轻松(第四部分):循环网络
- 神经网络变得轻松(第五部分):OpenCL 中的多线程计算
- 神经网络变得轻松(第六部分):神经网络学习率实验
- 神经网络变得轻松(第七部分):自适应优化方法
- 神经网络变得轻松(第八部分):关注机制
- 神经网络变得轻松(第九部分):操作归档
- 神经网络变得轻松(第十部分):多目击者关注
- 神经网络变得轻松(第十一部分):自 GPT 获取
- 神经网络变得轻松(第十二部分):舍弃
- 神经网络变得轻松(第十三部分):批次常规化
- 神经网络变得轻松(第十四部分):数据聚类
本文中用到的程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | kmeans.mq5 | 智能交易系统 | 训练模型的智能系统 |
| 2 | kmeans.mqh | 类库 | 组织 k-均值方法的函数库 |
| 3 | unsupervised.cl | 类库 | OpenCL 程序代码库,实现 k-均值方法 |
| 4 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 5 | NeuroNet.cl | 类库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/10947
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 学习如何基于 OBV 设计交易系统
学习如何基于 OBV 设计交易系统
 从头开始开发智能交易系统(第 16 部分):访问 web 上的数据(II)
从头开始开发智能交易系统(第 16 部分):访问 web 上的数据(II)
 视频:简单自动交易 — 如何利用 MQL5 创建简单的智能交易系统
视频:简单自动交易 — 如何利用 MQL5 创建简单的智能交易系统
