Neuronale Netze im Handel: Der Contrastive Muster-Transformer
84
2
Einführung
Bei der Analyse von Marktsituationen mithilfe von maschinellem Lernen konzentrieren wir uns häufig auf einzelne Kerzen und ihre Eigenschaften und übersehen dabei Kerzen-Muster, die häufig aussagekräftigere Informationen liefern. Muster stellen stabile Kerzen-Strukturen dar, die unter ähnlichen Marktbedingungen entstehen und wichtige Verhaltenstendenzen aufzeigen können.
Zuvor erforschten wir Molformer, das aus dem Bereich der Vorhersage molekularer Eigenschaften stammt. Die Autoren des Molformer haben atomare und motivische Darstellungen in einer einzigen Sequenz kombiniert, wodurch das Modell auf strukturelle Informationen über die analysierten Daten zugreifen kann. Dieser Ansatz brachte jedoch die komplexe Herausforderung mit sich, die Abhängigkeiten zwischen Knoten unterschiedlicher Typen zu trennen. Glücklicherweise gibt es alternative Methoden, die dieses Problem umgehen.
Ein solches Beispiel ist der Atom-Motif Contrastive Transformer (AMCT), der in der Veröffentlichung „Atom-Motif Contrastive Transformer for Molecular Property Prediction“ vorgestellt wurde. Um die beiden Ebenen der Interaktion zu integrieren und die Darstellungsfähigkeit von Molekülen zu verbessern, haben die Autoren von AMCT vorgeschlagen, kontrastives Lernen zwischen Atom- und Motivdarstellungen anzuwenden. Da es sich bei der Darstellung von Atomen und Motiven eines Moleküls im Wesentlichen um zwei verschiedene Ansichten desselben Objekts handelt, werden sie beim Training natürlich aufeinander abgestimmt. Durch diesen Abgleich können sie gegenseitig selbstüberwachte Signale liefern und so die Robustheit der erlernten molekularen Darstellungen verbessern.
Es wurde beobachtet, dass identische Motive in verschiedenen Molekülen dazu neigen, ähnliche chemische Eigenschaften aufzuweisen. Dies legt nahe, dass identische Motive in allen Molekülen einheitlich dargestellt werden sollten. Folglich maximiert die Verwendung von kontrastiven Verlusten die Angleichung identischer Motive in verschiedenen Molekülen, was zu besser unterscheidbaren Motivdarstellungen führt.
Um die Motive, die für die Bestimmung der Eigenschaften der einzelnen Moleküle entscheidend sind, effektiv zu identifizieren, haben die Autoren einen Aufmerksamkeitsmechanismus eingebaut, der die Informationen über die Eigenschaften durch ein Kreuzaufmerksamkeits-Modul integriert. Das Kreuzaufmerksamkeits-Modul erfasst insbesondere die Abhängigkeiten zwischen den Einbettungen der molekularen Eigenschaften und den Motivdarstellungen. Auf diese Weise können Schlüsselmotive auf der Grundlage von Kreuzaufmerksamkeitsgewichten identifiziert werden.
1. Der AMCT-Algorithmus
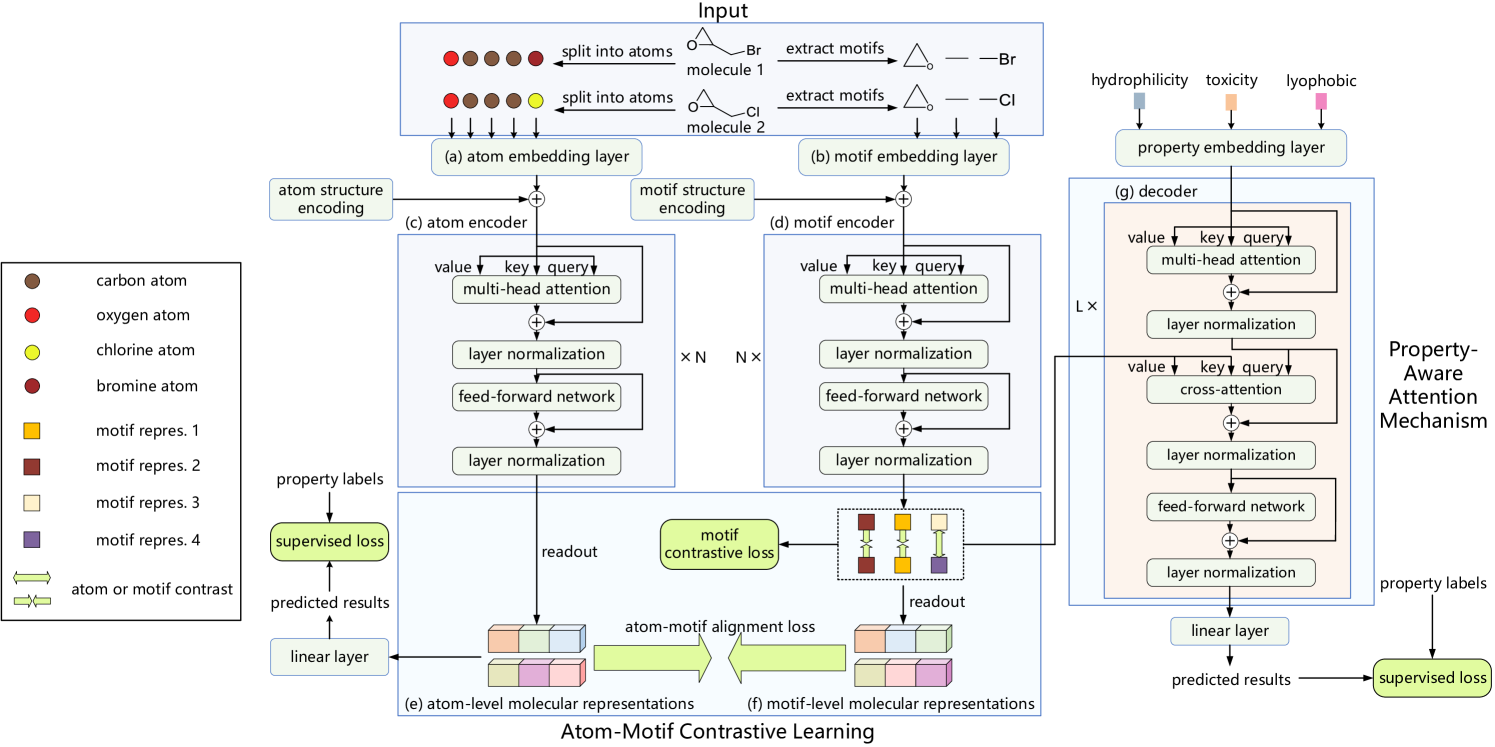
Die in das Modell eingegebenen Molekülbeschreibungen werden zunächst in eine Menge von Atomen zerlegt und in eine Menge von Motiven segmentiert. Diese resultierenden Sequenzen werden dann in parallele Atom- und Motivkodierungsschichten eingespeist, die die jeweiligen Einbettungen erzeugen. Zwei unabhängige Kodierer werden verwendet, um molekulare Darstellungen auf Atom- und Motivebene zu erhalten. Außerdem werden ein Decoder und eine vollständig verbundene Schicht verwendet, um die vorhergesagten Ausgaben zu erzeugen. Während des Modelltrainings umfassen die Verlustfunktionen den Atom-Motiv-Kontrastverlust, den Kontrastverlust auf Motivebene und den Eigenschaftsvorhersageverlust.
Bei der Atomkodierung werden zunächst die Einbettungen der Atome ermittelt. Diese Einbettungen werden dann vom Atom-Encoder verarbeitet, um Abhängigkeiten zwischen einzelnen Atomen innerhalb des Moleküls zu extrahieren. Die Ausgabe ist eine molekulare Darstellung auf Atomebene.
Die Autoren von AMCT verwenden die Knotenzentralität, um strukturelle Informationen zwischen Atomen zu kodieren, insbesondere die Bindungsbeziehungen von Atomen innerhalb eines Moleküls. Da die Zentralität auf jedes Atom angewandt wird, wird sie einfach zu den Atomeinbettungen hinzugefügt.
Während die Abhängigkeiten auf Atomebene effektiv Details auf niedriger Ebene erfassen, übersehen sie strukturelle Informationen auf hoher Ebene zwischen verschiedenen Atomen. Folglich kann dieser Ansatz für eine genaue Vorhersage der molekularen Eigenschaften unzureichend sein. Um dieses Problem zu lösen, führt der AMCT-Rahmen einen parallelen Weg für die molekulare Darstellung auf der Motivebene ein. Bei der Motivkodierung werden die Motive zunächst aus dem Originaldatensatz extrahiert und dann in Einbettungen umgewandelt. Diese Einbettungen werden vom Motivkodierer verarbeitet, um Abhängigkeiten zwischen Motiven zu erfassen.
Der AMCT-Rahmen verwendet die Zentralität auch, um strukturelle Informationen zwischen Motiven zu kodieren, die zu ihren entsprechenden Einbettungen hinzugefügt werden.
Um die zusätzlichen Informationen zu erforschen, die durch Motive bereitgestellt werden, berücksichtigt der Rahmen die Ähnlichkeitsbeziehungen zwischen molekularen Darstellungen auf Atom- und Motivebene. Da Atom- und Motivdarstellungen eines einzelnen Moleküls im Wesentlichen zwei verschiedene Ansichten desselben Wesens sind, gleichen sie sich natürlich an, um beim Modelltraining selbstüberwachte Signale zu erzeugen. Die Autoren verwenden die Kullback-Leibler-Divergenz, um die beiden Darstellungen abzugleichen.
Da der Atom-Motiv-Kontrastverlust innerhalb eines Moleküls wirkt und sich darauf beschränkt, die Konsistenz zwischen Atom- und Motivdarstellungen desselben Moleküls zu erzwingen, wollen die Autoren von AMCT auch den Kontrast zwischen den Molekülen erforschen und die Konsistenz der Darstellungen zwischen verschiedenen Molekülen untersuchen. Da identische Motive in verschiedenen Molekülen in der Regel ähnliche chemische Eigenschaften aufweisen, wird erwartet, dass diese Motive in allen Molekülen einheitliche Darstellungen aufweisen sollten. Um dies zu erreichen, schlagen die Autoren einen motivkontrastiven Verlust vor, der die Konsistenz identischer Motivrepräsentationen über verschiedene Moleküle hinweg maximiert, während er die Repräsentationen von Motiven, die zu unterschiedlichen Klassen gehören, auseinandertreibt.
Ein robuster Dekodierungsprozess ist ebenfalls entscheidend für die Erstellung zuverlässiger Darstellungen. AMCT führt eine eigenschaftsbezogene Dekodierung ein. Zunächst werden Eigenschaftseinbettungen generiert, und dann extrahiert der Decoder molekulare Repräsentationen, die für einzelne Eigenschaften wesentlich sind. Die endgültigen Vorhersagen werden durch lineare Projektion ermittelt.
Der Decoder ist so konzipiert, dass er molekulare Darstellungen extrahiert, die Eigenschaftsinformationen enthalten. Um die Motive zu identifizieren, die für die Bestimmung der Eigenschaften jedes Moleküls am wichtigsten sind, konstruiert AMCT einen eigenschaftsbezogenen Aufmerksamkeitsmechanismus. Konkret wird ein Kreuzaufmerksamkeits-Modul verwendet, wobei Eigenschaftseinbettungen als Werte von Query (Abfrage) und Motivdarstellungen als Key (Schlüssel) dienen. Es wird davon ausgegangen, dass Motive mit höherem Kreuzadhäsionsgewicht einen größeren Einfluss auf die molekularen Eigenschaften haben.
Die Originalvisualisierung des Atom-Motif Contrastive Transformer, wie sie von den Autoren vorgestellt wurde, ist unten zu sehen.
2. Die Implementation in MQL5
Nachdem wir die theoretischen Aspekte des Atom-Motif Contrastive Transformer behandelt haben, gehen wir nun zum praktischen Teil unseres Artikels über, in dem wir unsere eigene Perspektive auf die vorgeschlagenen Ansätze unter Verwendung von MQL5 vorstellen.
AMCT besitzt eine recht komplexe und anspruchsvolle Struktur. Bei näherer Betrachtung der einzelnen Bausteine wird jedoch deutlich, dass die meisten davon in unserer Bibliothek bereits in der einen oder anderen Form implementiert sind. Es bleibt also noch einiges zu tun. Zum Beispiel der Vergleich von Darstellungen auf der Atom- und Motivebene. Ich hoffe, Sie werden mir zustimmen, dass wir nicht nur Diskrepanzen feststellen, sondern auch den Gradienten des Fehlers auf beide Wege verteilen müssen, um diese Diskrepanzen zu minimieren. Es gibt mehrere Möglichkeiten, dieses Problem zu lösen.
Natürlich könnten wir die Ergebnisse aus einem Pfad in den Gradientenpuffer des anderen kopieren und dann den Fehlergradienten mit der grundlegenden Methode calcOutputGradients der neuronalen Schicht berechnen, die wir derzeit zur Berechnung des Modellfehlers verwenden. Der Vorteil dieses Ansatzes liegt in seiner Einfachheit, da er auf bestehende Instrumente zurückgreift. Diese Methode ist jedoch relativ ressourcenintensiv. Während des Modelltrainings müssten zwei Datenpuffer (die Ausgänge beider Pfade) dupliziert und die Gradienten für jede Darstellung sequentiell berechnet werden.
Daher haben wir beschlossen, einen kleinen Kernel auf der Seite von OpenCL zu entwickeln, der es uns ermöglicht, den Fehlergradienten für beide Pfade gleichzeitig zu bestimmen, ohne unnötige Daten zu kopieren.
__kernel void CalcAlignmentGradient(__global const float *matrix_o1, __global const float *matrix_o2, __global float *matrix_g1, __global float *matrix_g2, const int activation, const int add) { int i = get_global_id(0);
In den Kernel-Parametern erhalten wir Zeiger auf vier Datenpuffer. Zwei dieser Puffer enthalten die Ergebnisse der Atom- und Motivwege - in unserem Fall Kerzen und Muster. Zwei weitere Puffer sind für die Speicherung der entsprechenden Fehlergradienten vorgesehen. Außerdem enthalten die Kernel-Parameter einen Zeiger auf die Aktivierungsfunktion, die von beiden Pfaden verwendet wird.
Es ist wichtig zu beachten, dass wir hier ausdrücklich die Verwendung unterschiedlicher Aktivierungsfunktionen für die Pfade einschränken. Der Grund dafür ist, dass für einen korrekten Vergleich der Ergebnisse beider Wege diese im selben Unterraum liegen müssen. Die Aktivierungsfunktion definiert den Ausgaberaum der Schicht. Daher ist die Verwendung einer einzigen Aktivierungsfunktion für beide Pfade ein logischer und notwendiger Ansatz.
An dieser Stelle werden wir auch ein Flag einführen, das angibt, ob der Fehlergradient in die zuvor gespeicherten Daten akkumuliert oder der vorhandene Wert überschrieben werden soll.
Dieser Kernel wird in einem eindimensionalen Aufgabenraum ausgeführt. Folglich wird der im Kernel definierte Thread-Identifikator den erforderlichen Offset in den Datenpuffern angeben.
Als Nächstes werden wir lokale Variablen vorbereiten, um die jeweiligen Ergebnisse der Feedforward-Durchläufe für beide Pfade zu speichern und Nullwerte für die Fehlergradienten zu initialisieren.
const float out1 = matrix_o1[i]; const float out2 = matrix_o2[i]; float grad1 = 0; float grad2 = 0;
Wir prüfen die Gültigkeit der Werte für die Vorwärtsdurchläufe. Wenn wir korrekte numerische Werte haben, berechnen wir die Abweichung, die wir dann um die Ableitung der Aktivierungsfunktion bereinigen. Wir speichern die Ausgabe in den zugewiesenen lokalen Variablen.
if(!isnan(out1) && !isinf(out1) &&
!isnan(out2) && !isinf(out2))
{
grad1 = Deactivation(out2 - out1, out1, activation);
grad2 = Deactivation(out1 - out2, out2, activation);
}
Nun können wir die Fehlergradienten in die entsprechenden globalen Datenpuffer übertragen. Abhängig von der empfangenen Markierung werden entweder Werte zu dem zuvor akkumulierten Gradienten hinzugefügt oder der vorherige Wert wird entfernt und ein neuer Wert geschrieben. Danach schließen wir die Kerneloperationen ab.
if(add > 0) { matrix_g1[i] += grad1; matrix_g2[i] += grad2; } else { matrix_g1[i] = grad1; matrix_g2[i] = grad2; } }
Dies ist unsere einzige Ergänzung zum OpenCL-Programm. Den vollständigen Code finden Sie im Anhang.
Wir gehen nun zum Hauptprogramm über, in dem wir die Architektur des vorgeschlagenen AMCT implementieren werden. Zunächst einmal benötigen wir zwei Verarbeitungswege: einen für Atome (Balken) und einen für Motive (Muster). In ihrer ursprünglichen Arbeit verwendeten die Autoren eine einfache Transformer-Architektur für beide Pfade, die mit struktureller Kodierung von Atomen und Motiven erweitert wurde. Ich schlage jedoch vor, ihn durch einen Transformer zu ersetzen, der die relative Positionskodierung (R-MAT) einbezieht, die wir in einem unserer früheren Artikel untersucht haben. Damit wäre die Frage nach der Architektur des Weges geklärt gewesen. Wäre da nicht ein wichtiges Detail: Der Motiv- (Muster-) Pfad erfordert einen Vorverarbeitungsschritt, um die Muster vorher zu extrahieren. Aus diesem Grund habe ich beschlossen, den Motivpfad in einem separaten Objekt zu implementieren.
2.1 Konstruktion des Motivweges
Wir implementieren den Motivpfad-Algorithmus in der Klasse CNeuronMotifEncoder, deren Struktur unten dargestellt ist.
class CNeuronMotifEncoder : public CNeuronRMAT { public: CNeuronMotifEncoder(void) {}; ~CNeuronMotifEncoder(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronMotifEncoder; } };
Wie aus der Struktur des neuen Objekts ersichtlich ist, verwenden wir CNeuronRMAT als Basisklasse. Diese Klasse implementiert die lineare Modelllogik, bei der die neuronalen Schichten in einem dynamischen Array organisiert sind. Dieses Design ermöglicht es uns, innerhalb der Methode Init auf einfache Weise eine sequentielle Architektur für unseren Muster- (Motiv-) Pfad zu konstruieren. Die gesamte erforderliche Funktionalität wird von der übergeordneten Klasse geerbt.
Die Parameterstruktur der Initialisierungsmethode wird vollständig von der entsprechenden Methode in der Basisklasse geerbt.
bool CNeuronMotifEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(units_count < 3) return false;
Die Extraktion von Mustern setzt jedoch eine Beschränkung der Länge der Eingabedatenfolge voraus, die wir sofort im Hauptteil der Methode überprüfen. Danach bereiten wir ein dynamisches Array vor, um Zeiger auf die neuronalen Schichten zu speichern, die wir erstellen wollen.
cLayers.Clear();
Es ist wichtig zu beachten, dass wir die Methode der Elternklasse noch nicht aufgerufen haben. Dies bedeutet, dass alle geerbten Objekte uninitialisiert bleiben. Andererseits geben die vom externen Programm empfangenen Parameter nicht explizit die Größe des Ergebnispuffers an, der für die Ausführung der übergeordneten Klassenmethode erforderlich ist. Um zu vermeiden, dass die Größe des Ergebnispuffers in dieser Phase berechnet wird, werden zunächst die Schichten initialisiert, die für die Erzeugung der Mustereinbettungen zuständig sind. Da die Größe eines einzelnen Musters nicht in den Methodenparametern angegeben ist, wird sie dynamisch auf der Grundlage der Sequenzlänge festgelegt. Wenn die Sequenzlänge 10 Elemente überschreitet, werden 3-Element-Muster analysiert, ansonsten werden 2-Element-Muster verwendet.
int bars_to_paattern = (units_count > 10 ? 3 : 2);
Wir werden Mustereinbettungen mithilfe einer Faltungsschicht erzeugen, die wir sofort initialisieren. Der Zeiger auf die erstellte neuronale Schicht wird dann zu unserem dynamischen Array hinzugefügt.
CNeuronConvOCL *conv = new CNeuronConvOCL(); int idx = 0; int units = (int)units_count - bars_to_paattern + 1; if(!conv || !conv.Init(0, idx, open_cl, bars_to_paattern * window, window, window, units, 1, optimization_type, batch)|| !cLayers.Add(conv) ) return false; conv.SetActivationFunction(SIGMOID);
Es ist wichtig zu beachten, dass wir Einbettungen von sich überschneidenden Mustern mit einer Schrittweite von einem Balken konstruieren. Die Größe der Einbettung eines einzelnen Musters entspricht der Fenstergröße, die zur Beschreibung eines einzelnen Balkens verwendet wird. Dieser Ansatz ermöglicht eine genauere Analyse der Eingabesequenz auf das Vorhandensein von Mustern.
Wir gehen jedoch noch einen Schritt weiter und analysieren etwas größere Muster - solche, die entweder aus 5 oder 3 Balken bestehen, je nach Länge der Eingabesequenz. Anschließend werden die Einbettungen der Muster auf beiden Ebenen miteinander verknüpft, um dem Modell reichhaltigere Strukturinformationen über die Eingabedaten zu liefern. Um diese Funktionalität zu implementieren, verwenden wir die Schicht CNeuronMotifs, die im Rahmen unserer Arbeit an der Molformer Rahmenwerk entwickelt wurde. Der Hauptvorteil dieser Schicht liegt in ihrer Fähigkeit, den Tensor der extrahierten Muster mit den ursprünglichen Eingabedaten zu verketten. Aus demselben Grund konnten wir sie in der ersten Phase der Musterextraktion nicht verwenden. An diesem Punkt mussten wir die Muster von den Balkenrepräsentationen trennen, die parallel analysiert werden.
idx++; units = units - bars_to_paattern + 1; CNeuronMotifs *motifs = new CNeuronMotifs(); if(!motifs || !motifs.Init(0, idx, open_cl, window, bars_to_paattern, 1, units, optimization_type, batch) || !cLayers.Add(motifs) ) return false; motifs.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Die erzeugten Mustereinbettungen werden in den Pfad von R-MAT eingespeist. Wie Sie wissen, entspricht die Größe des Ausgangsvektors eines Transformer-Pfads der Tensorgröße seiner Eingabedaten. Daher können wir in diesem Stadium die Initialisierungsmethode der neuronalen Basisschicht aufrufen und die Größe des Ergebnispuffers auf der Grundlage der Abmessungen der endgültigen Musterextraktionsschicht festlegen.
if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, motifs.Neurons(), optimization_type, batch)) return false; cLayers.SetOpenCL(OpenCL);
Als Nächstes erstellen wir eine Schleife, um die internen Schichten unseres Decoders zu initialisieren. In jeder Iteration der Schleife werden wir nacheinander eine Schicht der relativen Selbstaufmerksamkeit (CNeuronRelativeSelfAttention) und einen Faltungsblock der Residuen (CResidualConv) initialisieren.
CNeuronRelativeSelfAttention *attention = NULL; CResidualConv *ff = NULL; units = int(motifs.Neurons() / window); for(uint i = 0; i < layers; i++) { idx++; attention = new CNeuronRelativeSelfAttention(); if(!attention || !attention.Init(0, idx, OpenCL, window, window_key, units, heads, optimization, iBatch) || !cLayers.Add(attention) ) { delete attention; return false; } idx++; ff = new CResidualConv(); if(!ff || !ff.Init(0, idx, OpenCL, window, window, units, optimization, iBatch) || !cLayers.Add(ff) ) { delete ff; return false; } }
Wir haben eine ähnliche Schleife in der Initialisierungsmethode der übergeordneten Klasse verwendet. In diesem Fall konnten wir jedoch die Methode der übergeordneten Klasse nicht wiederverwenden, da dies die zuvor erstellte Musterextraktionsschicht löschen würde.
Als Nächstes weisen wir die Datenpufferzeiger neu zu, um übermäßige Kopiervorgänge zu vermeiden.
if(!SetOutput(ff.getOutput()) || !SetGradient(ff.getGradient())) return false; //--- return true; }
Bevor wir die Methode beenden, geben wir das Ergebnis der Operation als booleschen Wert an das aufrufende Programm zurück.
Wie bereits erwähnt, wurde die Funktionalität sowohl für Feed-Forward- als auch für Backpropagation-Durchläufe vollständig von der übergeordneten Klasse geerbt. Damit schließen wir die Implementierung der Klasse des Musterpfads CNeuronMotifEncoder ab.
2.2 Modul Relative Kreuzaufmerksamkeit
Bei der Erstellung der Balken- und Musterpfade haben wir bereits Module zur relativen Selbstaufmerksamkeit verwendet. Der AMCT-Decoder verwendet jedoch einen Kreuzaufmerksamkeits-Mechanismus. Um eine kohärente und einheitliche Architektur für den Rahmen zu gewährleisten, müssen wir nun ein Kreuzaufmerksamkeits-Modul mit relativer Positionskodierung implementieren. Wir werden hier nicht in die theoretischen Details gehen, da alle notwendigen Konzepte in dem Artikel über R-MAT gewidmet sind. Unsere Aufgabe besteht nun darin, eine zweite Eingabequelle in die bestehende Lösung zu integrieren, aus der die Entitäten Key und Value generiert werden. Um diese Aufgabe zu erfüllen, werden wir eine neue Klasse namens CNeuronRelativeCrossAttention erstellen, die den Kreuzaufmerksamkeits-Mechanismus mit relativer Kodierung implementiert. Wie zu erwarten, wird die entsprechende Klasse der Selbstaufmerksamkeit als Basisklasse für diese neue Komponente dienen. Die Struktur des neuen Objekts wird im Folgenden dargestellt.
class CNeuronRelativeCrossAttention : public CNeuronRelativeSelfAttention { protected: uint iUnitsKV; //--- CLayer cKVProjection; //--- //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronRelativeCrossAttention(void) {}; ~CNeuronRelativeCrossAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_kv, uint units_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronRelativeCrossAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Der Code enthält den bereits bekannten Satz von überschreibbaren Methoden. Wir deklarieren hier ein dynamisches Array zur Aufnahme von Zeigern auf weitere Objekte. Darüber hinaus fügen wir eine Variable hinzu, um die Größe der Sequenz in der zweiten Eingabequelle zu erfassen.
Die Initialisierung sowohl geerbter als auch neu deklarierter Mitglieder wird in der Init-Methode durchgeführt.
bool CNeuronRelativeCrossAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_kv, uint units_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
In den Parametern dieser Methode geben wir alle notwendigen Konstanten an, die die Architektur des erstellten Objekts beschreiben. Im Hauptteil der Methode rufen wir sofort die entsprechende Methode der Basisklasse der neuronalen Schicht auf, die die Überprüfung der empfangenen Parameter und die Initialisierung der geerbten Schnittstellen implementiert.
Wir verwenden bewusst nicht die Initialisierungsmethode der direkten Elternklasse, da die Größe der meisten geerbten Objekte unterschiedlich sein wird. Die Ausführung wiederholter Operationen würde nicht nur unsere Arbeitslast nicht verringern, sondern auch die Programmausführungszeit erhöhen. Daher initialisieren wir in dieser Methode auch die in der übergeordneten Klasse deklarierten Objekte.
Sobald die Methode der Basisklasse erfolgreich abgeschlossen ist, speichern wir die vom externen Programm erhaltenen Architekturkonstanten in internen Mitgliedsvariablen unseres Objekts.
iWindow = window; iWindowKey = window_key; iUnits = units_count; iUnitsKV = units_kv; iHeads = heads;
Als Nächstes initialisieren wir gemäß der Transformer-Architektur die Faltungsschichten, in denen die Entitäten von Query, Key und Value erzeugt werden.
int idx = 0; if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; idx++; if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch)) return false; idx++; if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch)) return false;
Beachten Sie, dass wir für die Schichten, die für die Erzeugung von Schlüssel und Wert verantwortlich sind, die Sequenzlänge der zweiten Datenquelle verwenden. Gleichzeitig wird die Vektorgröße jeder Sequenzelementdarstellung aus der ersten Datenquelle übernommen. Die Vektordimensionen der einzelnen Elemente in der zweiten Datenquelle können jedoch unterschiedlich sein. In der Praxis haben wir uns bisher nicht mit dem Alignment von Eingabesequenzdimensionen befasst. Stattdessen haben wir unterschiedliche Fenstergrößen in den Entity-Generierungsschichten verwendet und nur die daraus resultierenden Einbettungsgrößen angeglichen. Im relativen Kodierungsalgorithmus wird jedoch der Begriff des Abstands zwischen Entitäten verwendet, der nur für Entitäten definiert werden kann, die im selben Unterraum liegen. Daher benötigen wir für die Analyse vergleichbare Objekte. Um die Anwendbarkeit des Moduls nicht einzuschränken, werden wir den Mechanismus der trainierbaren Datenprojektion verwenden. Wir werden später auf diesen Punkt zurückkommen, aber jetzt ist es wichtig, diese Anforderung hervorzuheben.
Wie bei der Implementierung der relativen Selbstaufmerksamkeit wird das Produkt zweier Eingabematrizen als Maß für die Entfernung zwischen Entitäten verwendet. Zuvor müssen wir jedoch eine der Matrizen transponieren.
idx++; if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch)) return false;
Lassen Sie uns auch ein Objekt erstellen, um die Ergebnisse der Matrixmultiplikation zu speichern.
idx++; if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnitsKV, optimization, iBatch)) return false;
Als Nächstes organisieren wir den Prozess der Erzeugung der Tensoren BK und BV. Wie wir bereits gesehen haben, werden diese Tensoren mit Hilfe eines MLP mit einer versteckten Schicht erzeugt. Die verborgene Schicht wird von allen Aufmerksamkeitsköpfen gemeinsam genutzt, und die letzte Schicht erzeugt für jeden Aufmerksamkeitskopf eigene Token. Hier werden wir für jede Entität zwei aufeinander folgende Faltungsschichten mit einer hyperbolischen Tangente dazwischen erstellen, um Nichtlinearität zu erzeugen.
idx++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) || !cBKey.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) || !cBKey.Add(conv)) return false;
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) || !cBValue.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) || !cBValue.Add(conv)) return false;
Fügen wir noch 2 weitere MLPs hinzu, um globale Kontext- und Positions-Bias-Vektoren zu erzeugen. Die erste Schicht in den MLPs ist statisch und enthält „1“, die zweite ist trainierbar und erzeugt den notwendigen Tensor. Wir werden Zeiger auf diese Objekte in den Arrays cGlobalContentBias und cGlobalPositionalBias speichern.
idx++; CNeuronBaseOCL *neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false; idx++; CBufferFloat *buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false;
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false; idx++; buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false;
Wir haben Objekte für die vorläufige Vorverarbeitung der Eingabedaten unseres relativen Kreuzaufmerksamkeits-Moduls vorbereitet. Als Nächstes gehen wir zu den Objekten für die Verarbeitung von Kreuzaufmerksamkeits-Ergebnissen über. In diesem Schritt erstellen wir zunächst ein Objekt, das die Ergebnisse der mehrköpfigen Aufmerksamkeit speichert, und fügen seinen Zeiger dem Array cMHAttentionPooling hinzu.
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHAttentionPooling.Add(neuron) ) return false;
Als Nächstes fügen wir eine abhängigkeitsbasierte Pooling-Schicht hinzu. Diese Schicht fasst die Ergebnisse des Mechanismus der mehrköpfigen Aufmerksamkeit zu einer gewichteten Summe zusammen. Die Einflusskoeffizienten werden individuell für jedes Element der Sequenz auf der Grundlage der Analyse der Abhängigkeiten bestimmt.
CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling(); if(!pooling || !pooling.Init(0, idx, OpenCL, iWindowKey, iUnits, iHeads, optimization, iBatch) || !cMHAttentionPooling.Add(pooling) ) return false;
Es ist wichtig zu beachten, dass die Vektorgröße, die jedes Sequenzelement am Ausgang der Pooling-Schicht beschreibt, der internen Dimension entspricht, die von der ursprünglichen Elementvektorlänge in der Eingangssequenz abweichen kann. Daher fügen wir ein zusätzliches MLP-Skalierungsmodul hinzu, um die Ergebnisse auf die ursprüngliche Datendimension zurückzuführen. Dieses Modul besteht aus zwei Faltungsschichten, zwischen denen eine Aktivierungsfunktion LReLU verwendet wird, um Nichtlinearität einzuführen.
//--- idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(LReLU); idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(None);
Danach ersetzen wir den Zeiger auf den Fehlergradientenpuffer in den Datenaustauschschnittstellen mit anderen neuronalen Schichten unseres Modells.
//--- if(!SetGradient(conv.getGradient(), true)) return false;
Kehren wir nun zur Frage der Dimensionalitätsunterschiede zwischen den Eingangsdatenquellen zurück. In unserem aufmerksamkeitsübergreifenden Modul wird die erste Eingabequelle zur Bildung der Abfrage verwendet und dient als primärer Stream im Aufmerksamkeitsmechanismus. Es wird auch in den Residuen-Verbindungen verwendet. Seine Dimensionalität bleibt also unverändert. Um die Dimensionen der beiden Eingangsquellen anzugleichen, führen wir daher eine Projektion der Werte der zweiten Eingangsquelle durch. Um diese lernfähige Datenprojektion zu implementieren, werden wir zwei sequentielle neuronale Schichten erstellen. Die Zeiger auf diese Ebenen werden im Array cKVProjection gespeichert. Die erste Schicht ist eine vollständig verbundene Schicht. Sie ist zunächst für die Verarbeitung und Speicherung der Roheingabe aus der zweiten Datenquelle zuständig.
cKVProjection.Clear(); cKVProjection.SetOpenCL(OpenCL); idx++; neuron = new CNeuronBaseOCL; if(!neuron || !neuron.Init(0, idx, OpenCL, window_kv * iUnitsKV, optimization, iBatch) || !cKVProjection.Add(neuron) ) return false;
Die zweite Faltungsschicht führt eine Datenprojektion in den gewünschten Unterraum durch.
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, window_kv, window_kv, iWindow, iUnitsKV, 1, optimization, iBatch) || !cKVProjection.Add(conv) ) return false;
Nach der Initialisierung aller Objekte, die für die Ausführung der angegebenen Funktionalität erforderlich sind, geben wir das boolsche Ergebnis der Operationen an das aufrufende Programm zurück und beenden die Methode.
//--- SetOpenCL(OpenCL); //--- return true; }
Nachdem die Initialisierung der neuen Objektinstanz abgeschlossen ist, wird der Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward konstruiert. Beachten Sie, dass dieser Algorithmus zwei getrennte Eingangsquellen erfordert. Daher überschreiben wir die geerbte Methode aus der übergeordneten Klasse - diejenige, die nur eine einzige Eingabequelle akzeptiert - so, dass sie immer false zurückgibt, was einen ungültigen oder falschen Methodenaufruf signalisiert. Der korrekte Algorithmus des Vorwärtsdurchlaufs ist in der Version der Methode implementiert, die zwei Eingangsquellen als Parameter annimmt.
bool CNeuronRelativeCrossAttention::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { CNeuronBaseOCL *neuron = cKVProjection[0]; if(!neuron || !SecondInput) return false; if(neuron.getOutput() != SecondInput) if(!neuron.SetOutput(SecondInput, true)) return false;
Innerhalb des Methodenkörpers wird zunächst die Gültigkeit des Zeigers auf die zweite Eingangsdatenquelle überprüft. Wenn der Zeiger gültig ist, wird er an die erste Ebene des Projektionsmodells übergeben, deren Schicht-Zeiger im Array cKVProjection gespeichert sind. Anschließend wird eine Schleife initialisiert, die nacheinander alle Schichten des Projektionsmodells durchläuft. In dieser Schleife wird die Methode des Vorwärtsdurchlaufs jeder Schicht aufgerufen, wobei die Ausgabe der vorherigen neuronalen Schicht als Eingabe für die aktuelle Schicht verwendet wird.
for(int i = 1; i < cKVProjection.Total(); i++) { neuron = cKVProjection[i]; if(!neuron || !neuron.FeedForward(cKVProjection[i - 1]) ) return false; }
Nachdem die Eingabedaten aus der zweiten Quelle erfolgreich projiziert wurden, gehen wir dazu über, die Entitäten Abfrage, Schlüssel und Wert zu erzeugen. Die Abfrage wird anhand der Eingabedaten aus der ersten Quelle erstellt. Für die Entitäten Schlüssel und Wert verwenden wir die Ergebnisse der Projektion der zweiten Quelldaten.
if(!cQuery.FeedForward(NeuronOCL) || !cKey.FeedForward(neuron) || !cValue.FeedForward(neuron) ) return false;
Als Nächstes müssen wir die Koeffizienten der Entfernungen zwischen den Objekten berechnen. Dazu transponieren wir zunächst die Daten aus der ersten Quelle. Dann multiplizieren wir die Ergebnisse der Datenprojektion aus der zweiten Quelle mit den transponierten Daten aus der ersten Quelle.
if(!cTranspose.FeedForward(NeuronOCL) || !MatMul(neuron.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnitsKV, iWindow, iUnits, 1) ) return false;
Auf der Grundlage der resultierenden Datenstrukturkoeffizienten bilden wir die Bias-Tensoren BK und BV. Zunächst übergeben wir Informationen über die Datenstruktur an die Vorwärtsdurchlauf-Methoden der ersten Schichten der entsprechenden Modelle.
if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) || !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject()) ) return false;
Anschließend werden Schleifen durch die Schichten der angegebenen Modelle erstellt, wobei nacheinander die Vorwärtsdurchlauf-Methoden der verschachtelten neuronalen Schichten aufgerufen werden.
for(int i = 1; i < cBKey.Total(); i++) if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1])) return false;
for(int i = 1; i < cBValue.Total(); i++) if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1])) return false;
Als Nächstes erzeugen wir globale Bias-Entitäten. Hier implementieren wir ähnliche Schleifen.
for(int i = 1; i < cGlobalContentBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1])) return false; for(int i = 1; i < cGlobalPositionalBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1])) return false;
Damit ist die vorläufige Datenverarbeitung abgeschlossen. Wir leiten die Ergebnisse also an das Modul der Aufmerksamkeit weiter.
if(!AttentionOut()) return false;
Wir leiten die Ergebnisse der mehrköpfigen Kreuzaufmerksamkeit durch ein Pooling-Modell.
for(int i = 1; i < cMHAttentionPooling.Total(); i++) if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1])) return false;
Dann skalieren wir ihn auf die Größe des ersten Datenquellentensors hoch. Diese Funktion wird von einem internen Skalierungsmodell übernommen.
if(!((CNeuronBaseOCL*)cScale[0]).FeedForward(cMHAttentionPooling[cMHAttentionPooling.Total() - 1])) return false; for(int i = 1; i < cScale.Total(); i++) if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1])) return false;
Als Nächstes müssen wir nur noch die restlichen Verbindungen hinzufügen. Die Ergebnisse der Operation werden in den Datenaustausch-Schnittstellenpuffer mit der nachfolgenden neuronalen Schicht des Modells aufgenommen.
if(!SumAndNormilize(NeuronOCL.getOutput(), ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Bevor die Methode abgeschlossen wird, wird ein boolescher Wert an das aufrufende Programm zurückgegeben, der den Erfolg der Operationen anzeigt.
Nach der Implementierung der Vorwärtsdurchlauf-Methode gehen wir zu den Rückwärtsdurchlauf-Algorithmen über. Wie Sie wissen, ist der Rückwärtsdurchlauf in zwei Stufen unterteilt. Die Verteilung der Fehlergradienten auf alle beteiligten Komponenten entsprechend ihrem Beitrag zum Endergebnis erfolgt in der Methode calcInputGradients. Die Optimierung der Modellparameter zur Minimierung des Modellfehlers ist in der Methode updateInputWeights implementiert. Der Algorithmus für Letzteres ist recht einfach. Es ruft nacheinander die entsprechenden Methoden updateInputWeights aller internen Objekte auf, die trainierbare Parameter enthalten. Der Algorithmus der ersten Methode verdient eine genauere Betrachtung.
In den Parametern der Methode calcInputGradients erhalten wir Zeiger auf zwei Eingabedatenobjekte, die jeweils Puffer für die Aufnahme der entsprechenden Fehlergradienten enthalten.
bool CNeuronRelativeCrossAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondGradient) return false;
Im Hauptteil der Methode wird die Relevanz der empfangenen Zeiger überprüft. Sind die Zeiger ungültig oder veraltet, wären alle weiteren Operationen sinnlos.
Erinnern Sie sich, dass wir während des Vorwärtsdurchlauf einen Zeiger auf den Eingabepuffer der zweiten Datenquelle in der internen Schicht gespeichert haben. Wir führen nun analoge Operationen für den entsprechenden Fehlergradientenpuffer durch und synchronisieren sofort die Aktivierungsfunktionen.
CNeuronBaseOCL *neuron = cKVProjection[0]; if(!neuron) return false; if(neuron.getGradient() != SecondGradient) if(!neuron.SetGradient(SecondGradient)) return false; if(neuron.Activation() != SecondActivation) neuron.SetActivationFunction(SecondActivation);
Nachdem die Vorbereitungsphase abgeschlossen ist, geht es an den eigentlichen Rückwärtsdurchlauf mit den Fehlergradienten, die auf alle Teilnehmer entsprechend ihrem Beitrag zum Endergebnis verteilt wird.
Wir haben den Zeiger auf den Fehlergradientenpuffer während der Initialisierung unseres Objekts ersetzt. Daher beginnt der Rückwärtsdurchlauf direkt in den internen Schichten. An dieser Stelle ist es wichtig, daran zu erinnern, dass der AMCT das kontrastive Lernen auf der Motivebene einführt. Dieser Logik folgend, fügen wir am Ausgang des Kreuzaufmerksamkeits-Blocks Diversitätsverluste hinzu.
if(!DiversityLoss(AsObject(), iUnits, iWindow, true)) return false;
Durch die Einführung von Diversitätsverlusten an dieser Stelle wollen wir die Ausbreitung von Merkmalsrepräsentationen im Einbettungsunterraum maximieren, insbesondere die Ausgaben, die in die nächsten Schichten eingespeist werden. Während wir den Gradienten durch das Objekt des Modells zurückverfolgen, trennen wir gleichzeitig indirekt die Objekte der analysierten Ausgangsdaten, die aus beiden Quellen in unseren Block gelangen.
Anschließend wird der Gesamtgradient durch das interne Modell der Ergebnis-Skalierung geleitet.
for(int i = cScale.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cScale[i]).calcHiddenGradients(cScale[i + 1])) return false; if(!((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).calcHiddenGradients(cScale[0])) return false;
Dann verteilen wir die Aufmerksamkeit nach dem Pooling-Modell auf die Köpfe.
for(int i = cMHAttentionPooling.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).calcHiddenGradients(cMHAttentionPooling[i + 1])) return false;
Bei der Methode AttentionGradient wird der Fehlergradient auf die Entitäten Query, Key und Value sowie auf die Bias-Tensoren entsprechend ihrem Einfluss auf die endgültige Ausgabe übertragen.
if(!AttentionGradient()) return false;
Als Nächstes verteilen wir den Fehlergradienten auf die internen Modelle der trainierbaren globalen Verzerrungen, indem wir eine umgekehrte Iteration durch ihre neuronalen Schichten durchführen.
for(int i = cGlobalContentBias.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).calcHiddenGradients(cGlobalContentBias[i + 1])) return false; for(int i = cGlobalPositionalBias.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).calcHiddenGradients(cGlobalPositionalBias[i + 1])) return false;
In ähnlicher Weise propagieren wir den Fehlergradienten durch die Bias-Entität, die Modelle auf der Grundlage der Struktur der Objekte BK und BV erzeugt.
for(int i = cBKey.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cBKey[i]).calcHiddenGradients(cBKey[i + 1])) return false; for(int i = cBValue.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cBValue[i]).calcHiddenGradients(cBValue[i + 1])) return false;
Anschließend wird sie in die Matrix der Datenstruktur cDistance übertragen. Es gibt jedoch eine wichtige Nuance. Wir haben die Strukturmatrix verwendet, um beide Entitäten zu erzeugen. Der Fehlergradient muss also aus den beiden Informationsströmen ermittelt werden. Daher erhalten wir zunächst den Fehlergradienten von BK.
if(!cDistance.calcHiddenGradients(cBKey[0])) return false;
Und dann ersetzen wir den Zeiger auf den Fehlergradientenpuffer dieses Objekts und nehmen den Gradienten aus BV. Danach summieren wir die Fehlergradienten beider Modelle und setzen die Zeiger auf die Datenpuffer in ihren ursprünglichen Zustand zurück.
CBufferFloat *temp = cDistance.getGradient(); if(!cDistance.SetGradient(GetPointer(cTemp), false) || !cDistance.calcHiddenGradients(cBValue[0]) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iUnits, false, 0, 0, 0, 1) || !cDistance.SetGradient(temp, false) ) return false;
Der auf der Strukturmatrix gesammelte Fehlergradient wird auf die Eingabedatenobjekte verteilt. In diesem Fall verteilen wir die Daten jedoch nicht direkt, sondern über die Transpositionsebene der ersten Datenquelle und das Projektionsmodell der zweiten Quelle.
neuron = cKVProjection[cKVProjection.Total() - 1]; if(!neuron || !MatMulGrad(neuron.getOutput(), neuron.getGradient(), cTranspose.getOutput(), cTranspose.getGradient(), temp, iUnitsKV, iWindow, iUnits, 1) ) return false;
Als Nächstes propagieren wir den Fehlergradienten von der Transpositionsschicht bis hinunter auf die Ebene der ersten Eingabedatenquelle. An diesem Punkt addieren wir die erhaltenen Werte sofort mit dem Gradienten, der aus dem restlichen Verbindungsstrom stammt. Das Ergebnis dieser Operation wird in den Gradientenpuffer der Datenumsetzungsschicht geschrieben. Dieser Puffer ist von der Größe her ideal, und seine zuvor gespeicherten Werte können sicher verworfen werden.
if(!NeuronOCL.calcHiddenGradients(cTranspose.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), Gradient, cTranspose.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Anschließend berechnen wir den Fehlergradienten auf der Ebene der ersten Eingabequelle, die von der Entität Abfrage abgeleitet ist, und fügen ihn zu den kumulierten Daten hinzu. Dieses Mal werden die Ergebnisse der Summierung im Gradientenpuffer der Eingabedaten gespeichert.
if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cTranspose.getGradient(), NeuronOCL.getGradient(), iWindow, false, 0, 0, 0, 1) || !DiversityLoss(NeuronOCL, iUnits, iWindow, true) ) return false;
In dieser Phase fügen wir auch den Diversitätsverlust hinzu.
Damit schließen wir die Gradientenfortpflanzung für die erste Eingabedatenquelle ab und fahren mit dem zweiten Datenstrom fort.
Wir haben zuvor den Fehlergradienten aus der Strukturmatrix im Puffer der letzten Schicht des internen Projektionsmodells für die zweite Eingangsdatenquelle gespeichert. Nun müssen wir den Fehlergradienten aus den Entitäten Schlüssel und Wert hinzufügen. Zu diesem Zweck ersetzen wir zunächst den Gradientenpuffer im Empfängerobjekt. Dann rufen wir nacheinander die Gradientenverteilungsmethoden für die jeweiligen Entitäten auf und addieren die Zwischenergebnisse zu den zuvor akkumulierten Werten.
temp = neuron.getGradient(); if(!neuron.SetGradient(GetPointer(cTemp), false) || !neuron.calcHiddenGradients(cKey.AsObject()) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) || !neuron.calcHiddenGradients(cValue.AsObject()) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) || !neuron.SetGradient(temp, false) ) return false;
An diesem Punkt führen wir einfach eine umgekehrte Iteration durch die Schichten des Projektionsmodells durch, wobei wir die Fehlergradienten nach unten durch das Modell fortschreiben.
for(int i = cKVProjection.Total() - 2; i >= 0; i--) { neuron = cKVProjection[i]; if(!neuron || !neuron.calcHiddenGradients(cKVProjection[i + 1])) return false; } //--- return true; }
Es ist wichtig anzumerken, dass durch das Ersetzen des Zeigers für den Gradientenpuffer in der ersten Schicht des Modells durch den Puffer, der vom externen Programm in den Methodenparametern bereitgestellt wird, die Notwendigkeit des redundanten Kopierens von Daten beseitigt wurde. Wenn Gradienten an die erste Ebene weitergegeben werden, werden sie automatisch in den vom externen System bereitgestellten Puffer geschrieben.
Es bleibt nur noch, das boolesche Ergebnis der Operationen an das aufrufende Programm zurückzugeben und die Methode zu beenden.
Damit ist unsere Implementierung und Diskussion der Methoden im relativen Kreuzaufmerksamkeits-Objekt CNeuronRelativeCrossAttention abgeschlossen. Der vollständige Quellcode für diese Klasse und alle ihre Methoden ist im Anhang enthalten.
Leider haben wir die Volumengrenze dieses Artikels erreicht, bevor wir unsere Implementierung abgeschlossen haben. Daher werden wir eine kurze Pause einlegen und die Arbeit im nächsten Artikel fortsetzen.
Schlussfolgerung
In diesem Artikel haben wir den Atom-Motif Contrastive Transformer (AMCT) vorgestellt, der auf den Konzepten von atomaren Elementen (Kerzen) und Motiven (Mustern) aufbaut. Der Kerngedanke der Methode liegt in der Anwendung kontrastiven Lernens, um dem Modell zu helfen, zwischen informativen und nicht-informativen Mustern über verschiedene Strukturebenen hinweg zu unterscheiden, von grundlegenden Elementen bis hin zu komplexen Gebilden. Auf diese Weise kann das Modell nicht nur lokale Merkmale der Marktbewegungen erfassen, sondern auch aussagekräftige Muster erkennen, die zusätzliche Vorhersagekraft für die Prognose des künftigen Marktverhaltens haben können. Die Transformer-Architektur als Grundlage der Methode ermöglicht die effiziente Modellierung von langfristigen Abhängigkeiten und komplexen Zusammenhängen zwischen Kerzen und Motiven.
Im praktischen Teil haben wir damit begonnen, den vorgeschlagenen Ansatz mit MQL5 zu implementieren. Der Umfang der Arbeit überstieg jedoch die Grenzen eines einzelnen Artikels. Wir werden diese Implementierung im nächsten Artikel fortsetzen, wo wir auch die reale Leistung des vorgeschlagenen Rahmens anhand historischer Marktdaten bewerten werden.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16163
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
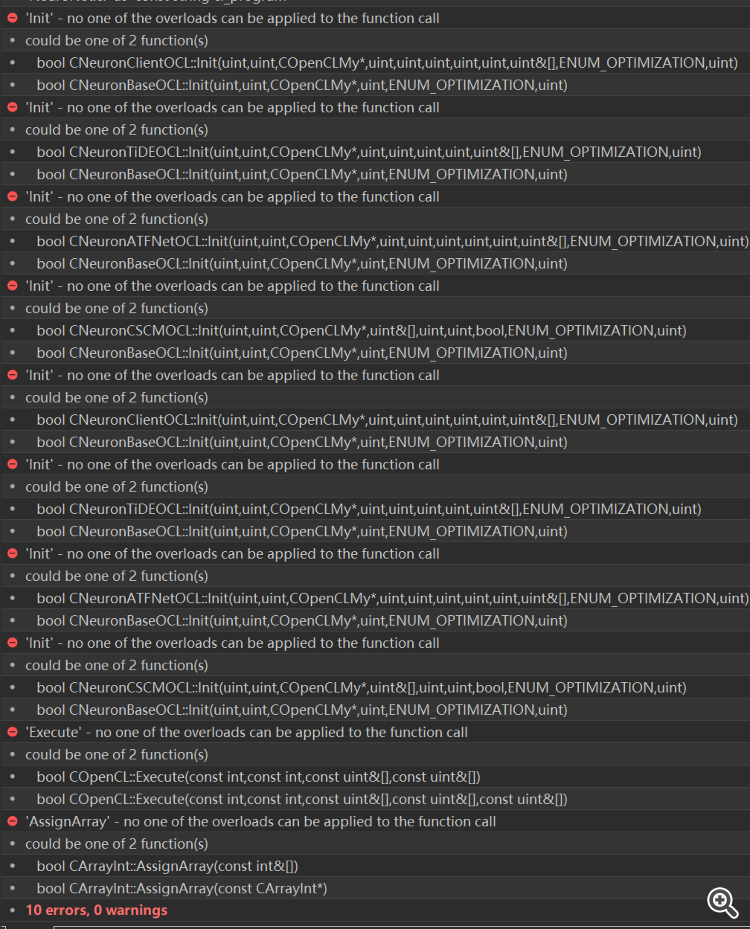
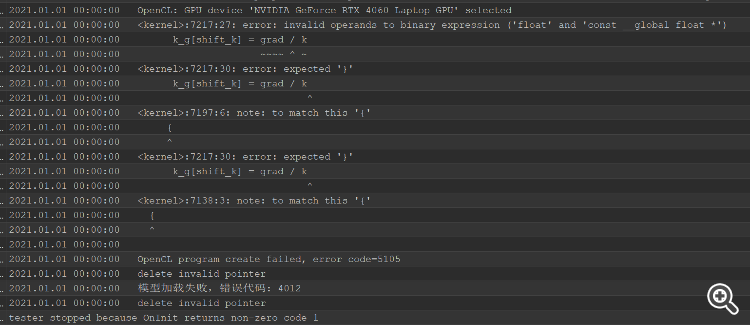Nach der Lösung des Kompilierungsfehlers, gibt es einen Tester Fehler, der ganze Kopf ist verbrannt, kann nicht herausfinden, wo das Problem zu lösen
Entwicklung eines Replay-Systems (Teil 73): Eine ungewöhnliche Kommunikation (II)
Von der Grundstufe bis zur Mittelstufe: Array (IV)
Von der Grundstufe bis zur Mittelstufe: Union (I)
Entwicklung eines Replay-Systems (Teil 72): Eine ungewöhnliche Kommunikation (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.