Neuronale Netze im Handel: Transformer mit relativer Kodierung

Einführung

Kursprognosen und Markttrendvorhersagen sind zentrale Aufgaben für erfolgreiches Handeln und Risikomanagement. Qualitativ hochwertige Prognosen zur Preisentwicklung ermöglichen es den Händlern, rechtzeitig Entscheidungen zu treffen und finanzielle Verluste zu vermeiden. Auf sehr volatilen Märkten können die Möglichkeiten herkömmlicher maschineller Lernmodelle jedoch begrenzt sein.

Der Übergang von der Ausbildung von Modellen von Grund auf zu einem Vortraining auf großen Mengen unbeschrifteter Daten, gefolgt von einer Feinabstimmung für bestimmte Aufgaben, ermöglicht es uns, hochpräzise Vorhersagen zu treffen, ohne große Mengen an neuen Daten sammeln zu müssen. So können beispielsweise Modelle, die auf der Transformer-Architektur basieren und für Finanzdaten angepasst wurden, Informationen über Korrelationen zwischen Vermögenswerten, zeitliche Abhängigkeiten und andere Faktoren nutzen, um genauere Vorhersagen zu treffen. Die Implementierung alternativer Aufmerksamkeitsmechanismen trägt dazu bei, die wichtigsten Marktabhängigkeiten zu berücksichtigen und die Leistung des Modells erheblich zu verbessern. Dies eröffnet neue Möglichkeiten für die Entwicklung von Handelsstrategien und minimiert gleichzeitig die manuelle Abstimmung und die Abhängigkeit von komplexen regelbasierten Modellen.

Ein solcher alternativer Aufmerksamkeitsalgorithmus wurde in der Arbeit „Relative Molecule Self-Attention Transformer“ vorgestellt. Die Autoren haben eine neue Formel der Selbstaufmerksamkeit (Self-Attention) für molekulare Graphen vorgeschlagen, die verschiedene Eingabemerkmale sorgfältig verarbeitet, um eine höhere Genauigkeit und Zuverlässigkeit in vielen chemischen Bereichen zu erreichen. Der Relative Molecule Attention Transformer (R-MAT) ist ein vortrainiertes Modell, das auf der Transformer-Architektur basiert. Sie stellt eine neue Variante der relativen Selbstaufmerksamkeit dar, die Entfernungs- und Nachbarschaftsinformationen effektiv integriert. Der R-MAT bietet modernste, wettbewerbsfähige Leistung für ein breites Spektrum von Aufgaben.

1. Der R-MAT-Algorithmus

Bei der Verarbeitung natürlicher Sprache berücksichtigt die einfache Selbstaufmerksamkeitsschicht die Positionsinformationen der eingegebenen Token nicht, d. h. wenn die Eingabedaten neu angeordnet werden, bleibt das Ergebnis unverändert. Um Positionsinformationen in die Eingabedaten einzubauen, reichert der einfache Transformer diese mit absoluter Positionskodierung an. Im Gegensatz dazu wird bei der relativen Positionskodierung der relative Abstand zwischen den einzelnen Tokenpaaren berücksichtigt, was bei bestimmten Aufgaben zu erheblichen Verbesserungen führt. Der Algorithmus R-MAT verwendet eine relative Token-Positionskodierung.

Die Kernidee besteht darin, die Flexibilität bei der Verarbeitung von Informationen über Graphen und Entfernungen zu erhöhen. Die Autoren der Methode R-MAT haben die Codierung der relativen Position angepasst, um den Selbstaufmerksamkeitsblock mit einer effizienten Darstellung der relativen Positionen der Elemente in der Eingabesequenz anzureichern.

Die gegenseitige Positionierung von zwei Atomen in einem Molekül ist durch drei miteinander verbundene Faktoren gekennzeichnet:

• ihre relative Entfernung,
• ihren Abstand im Moleküldiagramm,
• ihre physikochemische Beziehung.

Zwei Atome werden durch Vektoren 𝒙i und 𝒙j der Dimension D. dargestellt. Die Autoren schlagen vor, ihre Beziehung durch eine Atompaar-Einbettung 𝒃 zu kodierenij der Dimension D′. Diese Einbettung wird dann im Modul der Selbstaufmerksamkeit nach der Projektionsschicht verwendet.

Der Prozess beginnt damit, dass die Nachbarschaftsordnung zwischen zwei Atomen mit Informationen darüber kodiert wird, wie viele andere Knoten sich zwischen den Knoten i und j im ursprünglichen Molekülgraphen befinden. Danach folgt die radiale Basisdistanzkodierung. Schließlich wird jede Bindung hervorgehoben, um die physikochemische Beziehung zwischen den Atompaaren zu verdeutlichen.

Die Autoren weisen darauf hin, dass diese Merkmale zwar leicht während des Vortrainings erlernt werden können, dass aber eine solche Konstruktion für das Training von R-MAT auf kleineren Datensätzen von großem Nutzen sein kann.

Das resultierende Token 𝒃ij für jedes Atompaar im Molekül wird verwendet, um eine neue Selbstaufmerksamkeitsschicht zu definieren, die die Autoren als Relative Selbstaufmerksamkeit der Moleküle bezeichnen.

In dieser neuen Architektur spiegeln die Autoren das Designs Query-Key-Value von der einfachen Selbstaufmerksamkeit wider. Der Token 𝒃ij wird in spezifische Schlüssel- und Werte-Vektoren 𝒃ijV und 𝒃ijK mit Hilfe von zwei neuronalen Netzen φV und φK transformiert. Jedes neuronale Netz besteht aus zwei Schichten. Dazu gehören eine versteckte Schicht, die von allen Aufmerksamkeitsköpfen gemeinsam genutzt wird, und eine Ausgabeschicht, die unterschiedliche relative Einbettungen für die verschiedenen Aufmerksamkeitsköpfe erzeugt. Die relative Selbstaufmerksamkeit kann wie folgt ausgedrückt werden:

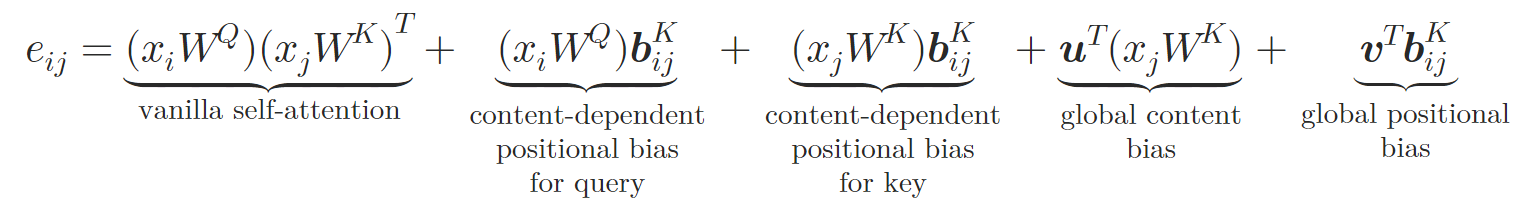
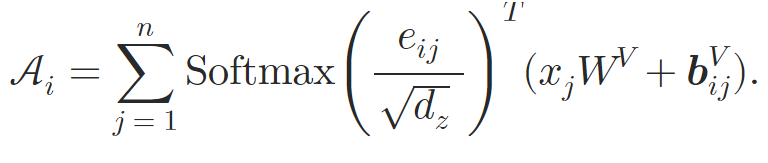
wobei 𝒖 und 𝒗 lernbare Vektoren sind.

Auf diese Weise bereichern die Autoren den Selbstaufmerksamkeits-Block durch die Einbettung atomarer Beziehungen. Bei der Berechnung der Aufmerksamkeitsgewichte führen sie eine inhaltsabhängige Positionsverzerrung, eine globale Kontextverzerrung und eine globale Positionsverzerrung ein, die alle auf der Grundlage von 𝒃ijK berechnet werden. Bei der Berechnung der gewichteten durchschnittlichen Aufmerksamkeit beziehen die Autoren dann auch Informationen aus der alternativen Einbettung 𝒃ijV.

Der Relative Selbstaufmerksamkeits-Block wird verwendet, um den Relativen Aufmerksamkeits-Transformer der Moleküle (R-MAT) zu konstruieren.

Die Eingabedaten liegen in Form einer Matrix der Größe Natoms×36 vor, die von einem Stapel von N Schichten der Relativen Aufmerksamkeits-Transformer der Moleküle verarbeitet wird. Auf jede Aufmerksamkeitsschicht folgt ein MLP mit Residuen-Verbindungen, ähnlich wie beim einfachen Transformer-Modell.

Nach der Verarbeitung der Eingabedaten durch die Aufmerksamkeitsschichten fassen die Autoren die Darstellung zu einem Vektor fester Größe zusammen. Zu diesem Zweck wird das Pooling der Selbstaufmerksamkeit eingesetzt.

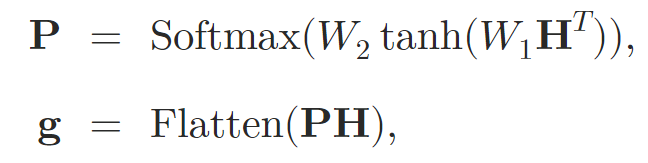
wobei 𝐇 den verborgenen Zustand bezeichnet, der sich aus den Selbstaufmerksamkeitsschichten ergibt, und W1 und W2 die Gewichte für die Zusammenführung der Aufmerksamkeit sind.

Die Grapheneinbettung 𝐠 wird dann in einen zweistufigen MLP mit der Aktivierungsfunktion leaky-ReLU eingespeist, der die endgültige Vorhersage ausgibt.

Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.

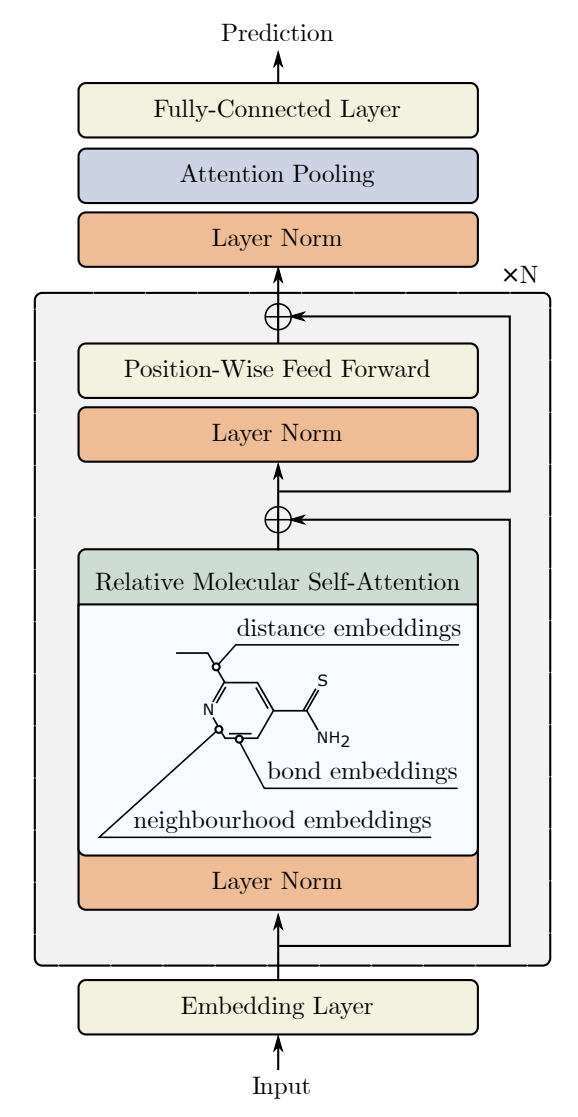
2. Die Implementation in MQL5

Nach der Untersuchung der theoretischen Aspekte der vorgeschlagenen Methode des Relativen Aufmerksamkeits-Transformer der Moleküle (R-MAT) gehen wir dazu über, unsere eigene Interpretation der vorgeschlagenen Ansätze unter Verwendung von MQL5 zu entwickeln. Gleich zu Beginn sollte ich erwähnen, dass ich beschlossen habe, den Aufbau des vorgeschlagenen Algorithmus in einzelne Module zu unterteilen. Wir werden zunächst ein spezielles Objekt für die Implementierung des Attention der relativen Selbstaufmerksamkeit erstellen und dann das R-MAT-Modell in einer separaten High-Level-Klasse zusammenfassen.

2.1 Modul der relativen Selbstaufmerksamkeit

Wie Sie wissen, haben wir den Großteil der Berechnungen in den Kontext von OpenCL verlagert. Wenn wir also mit der Implementierung des neuen Algorithmus beginnen, müssen wir die fehlenden Kernel zu unserem OpenCL-Programm hinzufügen. Der erste Kernel, den wir erstellen, ist der Kernel des Vorwärtsdurchlaufs MHRelativeAttentionOut. Obwohl dieser Kernel auf den zuvor besprochenen Implementierungen des Selbstaufmerksamkeits-Algorithmus basiert, ist die Anzahl der globalen Puffer erheblich gestiegen, deren Zweck wir bei der Entwicklung des Algorithmus untersuchen werden.

__kernel void MHRelativeAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                     __global const float *k,         ///<[in] Matrix of Keys
                                     __global const float *v,         ///<[in] Matrix of Values
                                     __global const float *bk,        ///<[in] Matrix of Positional Bias Keys
                                     __global const float *bv,        ///<[in] Matrix of Positional Bias Values
                                     __global const float *gc,        ///<[in] Global content bias vector
                                     __global const float *gp,        ///<[in] Global positional bias vector
                                     __global float *score,           ///<[out] Matrix of Scores
                                     __global float *out,             ///<[out] Matrix of attention
                                     const int dimension              ///< Dimension of Key
                                    )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Dieser Kernel ist so konzipiert, dass er in einem dreidimensionalen Aufgabenraum arbeitet, wobei jede Dimension einer Abfrage (Query), einem Schlüssel (Key) und Köpfen (Heads) entspricht. Im Rahmen der zweiten Dimension bilden wir Arbeitsgruppen.

Innerhalb des Kernelkörpers identifizieren wir sofort den aktuellen Thread in allen Dimensionen des Aufgabenraums und bestimmen seine Grenzen. Anschließend legen wir konstante Offsets in den Datenpuffern fest, um auf die erforderlichen Elemente zuzugreifen.

   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Dann erstellen wir ein Array im lokalen Speicher für den Austausch von Informationen innerhalb der Arbeitsgruppe.

   __local float temp[LOCAL_ARRAY_SIZE];

Als Nächstes müssen wir gemäß dem Algorithmus für die relative Selbstaufmerksamkeit die Aufmerksamkeitskoeffizienten berechnen. Zu diesem Zweck berechnen wir das Punktprodukt mehrerer Vektoren und summieren die resultierenden Werte. Hier nutzen wir die Tatsache, dass die Dimensionen aller multiplizierten Vektoren gleich sind. Daher reicht eine einzige Schleife aus, um die notwendigen Multiplikationen aller Vektoren durchzuführen.

//--- score
   float sc = 0;
   for(int d = 0; d < dimension; d++)
     {
      float val_q = q[shift_q + d];
      float val_k = k[shift_kv + d];
      float val_bk = bk[shift_kv + d];
      sc += val_q * val_k + 
	    val_q * val_bk + 
            val_k * val_bk + 
            gc[shift_q + d] * val_k + 
            gp[shift_q + d] * val_bk;
     }

Der nächste Schritt besteht darin, die berechneten Aufmerksamkeitskoeffizienten für die einzelnen Abfragen zu normalisieren. Für die Normalisierung verwenden wir wie beim einfachen Algorithmus die Softmax-Funktion. Das Normalisierungsverfahren wird also ohne Änderungen aus unseren bestehenden Implementierungen übernommen. In diesem Schritt wird zunächst der Exponentialwert des Koeffizienten berechnet.

   sc = exp(sc / koef);
   if(isnan(sc) || isinf(sc))
      sc = 0;

Anschließend werden die erhaltenen Koeffizienten innerhalb der Arbeitsgruppe mit Hilfe des zuvor im lokalen Speicher angelegten Arrays summiert.

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Nun können wir den zuvor erhaltenen Koeffizienten durch die Gesamtsumme dividieren und den normalisierten Wert in den entsprechenden globalen Puffer speichern.

//--- score
   float sum = temp[0];
   if(isnan(sum) || isinf(sum) || sum <= 1e-6f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Nach der Berechnung der normalisierten Abhängigkeitskoeffizienten können wir das Ergebnis der Aufmerksamkeitsoperation berechnen. Der Algorithmus hier ist sehr nah am einfachen. Wir addieren einfach die Summe der Vektoren Value und bijV und multiplizieren sie mit dem Aufmerksamkeitsfaktor.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = sc * (val_v + val_bv);
      if(isnan(val) || isinf(val))
         val = 0;
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]);
     }
  }

Es lohnt sich, noch einmal zu betonen, wie wichtig die sorgfältige Platzierung von Barrieren für die Synchronisierung von Operationen zwischen Threads innerhalb einer Workgroup ist. Die Barrieren müssen so angeordnet sein, dass jeder einzelne Thread der Arbeitsgruppe die Barriere gleich oft erreicht. Der Code darf keine Umgehungen der Barrieren oder vorzeitige Beendigungen vor dem Besuch aller Synchronisationspunkte enthalten. Andernfalls riskieren wir ein Blockieren des Kernels, bei dem einzelne Threads an einer Barriere auf einen anderen Thread warten, der seine Operationen bereits abgeschlossen hat.

Der Algorithmus des Rückwärtsdurchlaufs ist im Kernel MHRelativeAttentionInsideGradients implementiert. Diese Implementierung invertiert die Operationen des zuvor besprochenen Vorwärtsdurchlaufs-Kerns vollständig und ist weitgehend an frühere Implementierungen angepasst. Deshalb schlage ich vor, dass Sie es selbst erkunden. Der vollständige Code für das gesamte OpenCL-Programm ist im Anhang enthalten.

Nun geht es an die Umsetzung des Hauptprogramms. Hier werden wir die Klasse CNeuronRelativeSelfAttention erstellen, in der wir den Algorithmus der relativen Selbstaufmerksamkeit implementieren werden. Bevor wir jedoch mit der Umsetzung beginnen, ist es notwendig, einige Aspekte der relativen Positionskodierung zu diskutieren.

Die Autoren von R-MAT haben ihren Algorithmus zur Lösung von Problemen in der chemischen Industrie vorgeschlagen. Sie konstruierten eine Positionsbeschreibung von Atomen in Molekülen, die auf der spezifischen Natur der Aufgabenstellung beruhte. Für uns sind auch der Abstand zwischen den Kerzen und ihre Eigenschaften wichtig, aber es gibt noch eine weitere Nuance. Neben der Entfernung ist auch die Richtung entscheidend. Nur unidirektionale Preisbewegungen bilden Trends und entwickeln sich zu Markttendenzen.

Der zweite Aspekt betrifft die Größe der analysierten Sequenz. Die Anzahl der Atome in einem Molekül ist oft auf eine relativ geringe Anzahl beschränkt. In diesem Fall können wir für jedes Atompaar einen Abweichungsvektor berechnen. In unserem Fall kann das Volumen der zu analysierenden historischen Daten jedoch recht groß sein. Folglich kann die Berechnung und Speicherung einzelner Abweichungsvektoren für jedes Paar analysierter Kerzen zu einer sehr ressourcenintensiven Aufgabe werden.

Daher haben wir uns entschieden, den von den Autoren vorgeschlagenen Ansatz der Berechnung von Abweichungen zwischen einzelnen Sequenzelementen nicht zu verwenden. Auf der Suche nach einem alternativen Mechanismus haben wir uns für eine recht einfache Lösung entschieden: die Multiplikation der Matrix der Eingabedaten mit ihrer transponierten Kopie. Aus mathematischer Sicht ist das Punktprodukt zweier Vektoren gleich dem Produkt aus ihren Beträgen und dem Kosinus des Winkels zwischen ihnen. Daher ist das Produkt der senkrechten Vektoren gleich Null. Vektoren, die in dieselbe Richtung zeigen, ergeben einen positiven Wert, Vektoren, die in entgegengesetzte Richtungen zeigen, einen negativen Wert. Vergleicht man also einen Vektor mit mehreren anderen, so steigt der Wert des Vektorprodukts, wenn der Winkel zwischen den Vektoren kleiner und die Länge des zweiten Vektors größer wird.    

Nachdem wir nun die Methodik festgelegt haben, können wir mit der Konstruktion unseres neuen Objekts fortfahren, dessen Struktur im Folgenden dargestellt wird.

class CNeuronRelativeSelfAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                    iWindow;
   uint                    iWindowKey;
   uint                    iHeads;
   uint                    iUnits;
   int                     iScore;
   //---
   CNeuronConvOCL          cQuery;
   CNeuronConvOCL          cKey;
   CNeuronConvOCL          cValue;
   CNeuronTransposeOCL     cTranspose;
   CNeuronBaseOCL          cDistance;
   CLayer                  cBKey;
   CLayer                  cBValue;
   CLayer                  cGlobalContentBias;
   CLayer                  cGlobalPositionalBias;
   CLayer                  cMHAttentionPooling;
   CLayer                  cScale;
   CBufferFloat            cTemp;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionGraadient(void);

   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRelativeSelfAttention(void) : iScore(-1) {};
                    ~CNeuronRelativeSelfAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRelativeSelfAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Wie wir sehen können, enthält die Struktur der neuen Klasse eine ganze Reihe interner Objekte. Wir werden uns mit ihrer Funktionalität vertraut machen, wenn wir die Methoden der Klasse implementieren. Wichtig ist jetzt, dass alle Objekte als statisch deklariert werden. Das bedeutet, dass wir den Konstruktor und den Destruktor der Klasse leer lassen können. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt. Die Parameter dieser Methode enthalten Konstanten, die es uns ermöglichen, die Architektur des erstellten Objekts genau zu definieren. Alle Parameter der Methode werden direkt und ohne Änderungen aus der Implementierung der einfachen mehrköpfigen Selbstaufmerksamkeit übernommen. Der einzige Parameter, der auf dem Weg verloren gegangen ist, ist derjenige, der die Anzahl der internen Ebenen angibt. Dies ist eine bewusste Entscheidung, da bei dieser Implementierung die Anzahl der Ebenen durch das übergeordnete Objekt bestimmt wird, indem die erforderliche Anzahl interner Objekte erstellt wird.

bool CNeuronRelativeSelfAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                        uint window, uint window_key, uint units_count, uint heads, 
                                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Innerhalb des Methodenkörpers rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf und übergeben ihr einen Teil der erhaltenen Parameter. Wie Sie wissen, implementiert die Methode der Elternklasse bereits Algorithmen für eine minimale Validierung der empfangenen Parameter und die Initialisierung der geerbten Objekte. Wir überprüfen einfach das logische Ergebnis dieser Operationen.

Anschließend speichern wir die erhaltenen Konstanten in den internen Variablen der Klasse zur späteren Verwendung.

   iWindow = window;
   iWindowKey = window_key;
   iUnits = units_count;
   iHeads = heads;

Als Nächstes wird die Initialisierung der deklarierten internen Objekte durchgeführt. Zunächst initialisieren wir die internen Schichten, indem wir die Gleichheit von Query, Key und Value in den entsprechenden internen Objekten erzeugen. Wir verwenden identische Parameter für alle drei Schichten.

   int idx = 0;
   if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;

Als Nächstes müssen wir Objekte vorbereiten, um unsere Abstandsmatrix zu berechnen. Zu diesem Zweck erstellen wir zunächst ein Transpositionsobjekt für die Eingabedaten.

   idx++;
   if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

Und dann erstellen wir ein Objekt, um die Ausgabe aufzuzeichnen. Die Matrixmultiplikation ist bereits in der übergeordneten Klasse implementiert.

   idx++;
   if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnits, optimization, iBatch))
      return false;

Als Nächstes müssen wir den Prozess der Erzeugung der Tensoren BK und BV organisieren. Wie im theoretischen Teil beschrieben, werden sie mit Hilfe eines MLP erzeugt, der aus zwei Schichten besteht. Die erste Schicht wird von allen Aufmerksamkeitsköpfen gemeinsam genutzt, während die zweite Schicht individuelle Token für jeden Aufmerksamkeitskopf erzeugt. In unserer Implementierung verwenden wir zwei sequentielle Faltungsschichten für jede Entität. Wenden wir die Funktion des hyperbolischen Tangens (tanh) an, um Nichtlinearität zwischen den Schichten einzuführen.

   idx++;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;

Darüber hinaus benötigen wir lernfähige Vektoren für globale inhaltliche Verzerrungen und Positionsverzerrungen. Um diese zu erstellen, werden wir den Ansatz aus unserer früheren Arbeit verwenden. Ich beziehe mich auf den Aufbau eines MLP mit zwei Schichten. Eine davon ist eine statische Schicht, die „1“ enthält, und die zweite ist eine lernfähige Schicht, die den erforderlichen Tensor erzeugt. Wir werden Zeiger auf diese Objekte in den Arrays cGlobalContentBias und cGlobalPositionalBias speichern.

   idx++;
   CNeuronBaseOCL *neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;
   idx++;
   CBufferFloat *buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;
   idx++;
   buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;

An dieser Stelle haben wir alle notwendigen Objekte vorbereitet, um die Eingabedaten für unser Modul für relative Aufmerksamkeit korrekt einzurichten. In der nächsten Phase gehen wir zu den Komponenten über, die die Aufmerksamkeitsausgabe verarbeiten. Zunächst erstellen wir ein Objekt zum Speichern der Ergebnisse von Multi-Head-Attention und fügen seinen Zeiger dem Array cMHAttentionPooling hinzu.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(neuron)
     )
      return false;

Als Nächstes fügen wir die Pooling-Operationen MLP hinzu.

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, 
                                                                       optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;

Wir fügen am Ausgang eine Softmax-Schicht hinzu.

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   softmax.SetHeads(iUnits);

Beachten Sie, dass wir am Ausgang des Pooling MLP normalisierte Gewichtungskoeffizienten für jeden Aufmerksamkeitskopf für jedes Element in der Sequenz erhalten. Jetzt müssen wir nur noch die resultierenden Vektoren mit den entsprechenden Ausgaben des mehrköpfigen Aufmerksamkeits-Blocks multiplizieren, um die endgültigen Ergebnisse zu erhalten. Die Größe des Repräsentationsvektors für jedes Element der Sequenz ist jedoch gleich unserer internen Dimensionalität. Daher fügen wir auch Skalierungsobjekte hinzu, um die Ergebnisse an das Niveau der ursprünglichen Eingabedaten anzupassen.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iUnits, optimization, iBatch) ||
      !cScale.Add(neuron)
     )
      return false;
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(LReLU);
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(None);

Nun müssen wir die Datenpuffer ersetzen, um unnötige Kopiervorgänge zu vermeiden, und das logische Ergebnis der Methodenoperationen an das aufrufende Programm zurückgeben.

//---
   if(!SetGradient(conv.getGradient(), true))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Beachten Sie, dass wir in diesem Fall nur den Zeiger des Gradientenpuffers austauschen. Dies wird durch die Schaffung von Residuen-Verbindungen innerhalb des Aufmerksamkeitsblocks verursacht. Aber wir werden diesen Teil bei der Implementierung der Methode feedForward besprechen.

In den Parametern von Feedforward erhalten wir einen Zeiger auf das Quelldatenobjekt, den wir sofort an die gleichnamige Methode der internen Objekte zur Erzeugung der Entitäten Query, Key und Value übergeben.

bool CNeuronRelativeSelfAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL) ||
      !cKey.FeedForward(NeuronOCL) ||
      !cValue.FeedForward(NeuronOCL)
     )
      return false;

Die Relevanz des vom externen Programm erhaltenen Zeigers auf das Quelldatenobjekt wird nicht überprüft. Denn dieser Vorgang ist bereits in den Methoden der internen Objekte implementiert. Daher ist ein solcher Kontrollpunkt in diesem Fall nicht erforderlich.

Als Nächstes gehen wir dazu über, Entitäten für die Bestimmung von Entfernungen zwischen analysierten Objekten zu erzeugen. Wir transponieren den ursprünglichen Datentensor.

   if(!cTranspose.FeedForward(NeuronOCL) ||
      !MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnits, iWindow, iUnits, 1)
     )
      return false;

Dann führen wir sofort eine Matrixmultiplikation des ursprünglichen Datentensors mit seiner transponierten Kopie durch. Wir verwenden das Ergebnis der Operation, um die Entitäten BK und BV zu erzeugen. Zu diesem Zweck organisieren wir Schleifen durch die Schichten der entsprechenden internen Modelle.

   if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) ||
      !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject())
     )
      return false;
   for(int i = 1; i < cBKey.Total(); i++)
      if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1]))
         return false;
   for(int i = 1; i < cBValue.Total(); i++)
      if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1]))
         return false;

Dann führen wir Schleifen durch, die globale Bias-Entitäten erzeugen.

   for(int i = 1; i < cGlobalContentBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1]))
         return false;
   for(int i = 1; i < cGlobalPositionalBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1]))
         return false;

Damit ist die vorbereitende Arbeitsphase abgeschlossen. Wir rufen die Wrapper-Methode des obigen Vorwärtsdurchlaufs-Kernel der relativen Aufmerksamkeit.

   if(!AttentionOut())
      return false;

Danach fahren wir mit der Verarbeitung der Ergebnisse fort. Zunächst verwenden wir einen pooling MLP zur Erzeugung des Einflusstensors der Aufmerksamkeitsköpfe.

   for(int i = 1; i < cMHAttentionPooling.Total(); i++)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1]))
         return false;

Dann multiplizieren wir die resultierenden Vektoren mit den Ergebnissen der mehrköpfigen Aufmerksamkeit.

   if(!MatMul(((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).getOutput(),
              ((CNeuronBaseOCL*)cMHAttentionPooling[0]).getOutput(),
              ((CNeuronBaseOCL*)cScale[0]).getOutput(),
              1, iHeads, iWindowKey, iUnits)
     )
      return false;

Als Nächstes müssen wir die erhaltenen Werte nur noch mit Hilfe einer Skalierungs-MLP skalieren.

   for(int i = 1; i < cScale.Total(); i++)
      if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1]))
         return false;

Wir summieren die erhaltenen Ergebnisse mit den ursprünglichen Daten und schreiben das Ergebnis in den von der übergeordneten Klasse geerbten Ergebnispuffer der obersten Ebene. Um diese Operation durchzuführen, mussten wir den Zeiger auf den Ergebnispuffer unsubstituiert lassen.

   if(!SumAndNormilize(NeuronOCL.getOutput(), 
                       ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), 
                       Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Nach der Implementierung der Vorwärtsdurchlauf-Methode werden normalerweise die Rückwärtsdurchlaufs-Algorithmen erstellt, die in den Methoden calcInputGradients und updateInputWeights organisiert sind. Bei der ersten Methode werden die Fehlergradienten auf alle Modellelemente entsprechend ihrem Einfluss auf das Endergebnis verteilt. Bei der zweiten Methode werden die Modellparameter angepasst, um den Gesamtfehler zu verringern. Weitere Einzelheiten entnehmen Sie bitte den beigefügten Codes. Dort finden Sie den vollständigen Code für diese Klasse und alle ihre Methoden. Kommen wir nun zur nächsten Phase unserer Arbeit - der Konstruktion des Top-Level-Objekts zur Implementierung des Rahmens von R-MAT.

2.2 Implementierung des R-MAT-Rahmens

Um den High-Level-Algorithmus des R-MAT-Rahmens zu organisieren, werden wir eine neue Klasse namens CNeuronRMAT erstellen. Seine Struktur wird im Folgenden dargestellt.

class CNeuronRMAT :  public CNeuronBaseOCL
  {
protected:
   CLayer               cLayers;
   //---
   virtual bool         feedForward(CNeuronBaseOCL *NeuronOCL)
   override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRMAT(void) {};
                    ~CNeuronRMAT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRMAT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Anders als die vorherige Klasse enthält diese Klasse nur ein einziges verschachteltes dynamisches Array-Objekt. Auf den ersten Blick mag dies unzureichend erscheinen, um eine derart komplexe Architektur zu realisieren. Wir haben jedoch ein dynamisches Array deklariert, um Zeiger auf die für die Erstellung des Algorithmus erforderlichen Objekte zu speichern.

Das dynamische Array wird als statisch deklariert, was es uns ermöglicht, den Konstruktor und den Destruktor der Klasse leer zu lassen. Die Initialisierung von internen und geerbten Objekten wird in der Methode Init durchgeführt.

bool CNeuronRMAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint window_key, uint units_count, uint heads, 
                       uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Die Parameter der Initialisierungsmethode enthalten Konstanten, die die Anforderungen des Nutzers an das zu erstellende Objekt eindeutig interpretieren. Hier finden wir die bekannten Parameter des Aufmerksamkeitsblocks, einschließlich der Anzahl der internen Schichten.

Die erste Operation, die wir durchführen, ist der inzwischen übliche Aufruf der gleichnamigen Methode der übergeordneten Klasse. Als Nächstes bereiten wir die lokalen Variablen vor.

   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CResidualConv *conv = NULL;

Als Nächstes fügen wir eine Schleife mit einer Anzahl von Iterationen hinzu, die der Anzahl der internen Schichten entspricht.

   for(uint i = 0; i < layers; i++)
     {
      attention = new CNeuronRelativeSelfAttention();
      if(!attention ||
         !attention.Init(0, i * 2, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
         !cLayers.Add(attention)
        )
        {
         delete attention;
         return false;
        }

Innerhalb des Schleifenkörpers wird zunächst eine neue Instanz des zuvor implementierten relativen Aufmerksamkeitsobjekts erstellt und durch Übergabe der vom externen Programm erhaltenen Konstanten initialisiert.

Wie Sie sich vielleicht erinnern, organisiert die Vorwärtsdurchlauf-Methode der Klasse der relativen Aufmerksamkeit den Strom der Residuen-Verbindungen. Daher können wir diesen Vorgang auf dieser Ebene überspringen und weitermachen.

Der nächste Schritt ist die Erstellung eines FeedForward-Blocks, ähnlich dem einfachen Transformer. Um jedoch ein einfacher aussehendes High-Level-Objekt zu schaffen, haben wir beschlossen, die Architektur dieses Blocks leicht zu ändern. Stattdessen initialisieren wir einen Faltungsblock mit Restverbindungen CResidualConv. Wie der Name schon sagt, enthält dieser Block auch Restverbindungen, sodass diese nicht mehr in der Oberstufe implementiert werden müssen.

      conv = new CResidualConv();
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window, window, units_count, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
     }

Wir müssen also nur zwei Objekte erstellen, um eine Ebene der relativen Aufmerksamkeit zu konstruieren. Wir fügen die Zeiger auf die erstellten Objekte in der Reihenfolge ihres nachfolgenden Aufrufs in unser dynamisches Array ein und fahren mit der nächsten Iteration der internen Schleife zur Erzeugung der Aufmerksamkeitsebene fort.

Nach erfolgreichem Abschluss aller Schleifeniterationen ersetzen wir die Datenpufferzeiger aus unserer letzten internen Schicht durch die entsprechenden Puffer der oberen Ebene.

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

Anschließend geben wir das logische Ergebnis der Operationen an das aufrufende Programm zurück und beenden die Methode.

Wie Sie sehen, konnten wir durch die Aufteilung des Algorithmus von R-MAT in einzelne Blöcke ein recht übersichtliches High-Level-Objekt konstruieren.

Es ist anzumerken, dass sich diese Prägnanz auch in anderen Methoden der Klasse wiederfindet. Nehmen wir zum Beispiel die Methode feedForward. Die Methode erhält einen Zeiger auf das Eingangsdatenobjekt als Parameter.

bool CNeuronRMAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *neuron = cLayers[0];
   if(!neuron.FeedForward(NeuronOCL))
      return false;

Innerhalb des Methodenkörpers rufen wir zunächst die gleichnamige Methode des ersten verschachtelten Objekts auf. Dann organisieren wir eine Schleife, um nacheinander alle verschachtelten Objekte zu durchlaufen und ihre jeweiligen Methoden aufzurufen. Bei jedem Aufruf übergeben wir den Zeiger auf die Ausgabe des vorherigen Objekts als Eingabe.

   for(int i = 1; i < cLayers.Total(); i++)
     {
      neuron = cLayers[i];
      if(!neuron.FeedForward(cLayers[i - 1]))
         return false;
     }
//---
   return true;
  }

Nach Abschluss aller Schleifeniterationen brauchen wir die Daten nicht einmal zu kopieren, da wir zuvor eine Pufferzeigersubstitution organisiert haben. Daher schließen wir die Methode einfach ab, indem wir das logische Ergebnis der Operationen an das aufrufende Programm zurückgeben.

Ein ähnlicher Ansatz wird bei den Methoden der Rückwärtsdurchläufe angewandt, die ich Ihnen empfehle, unabhängig davon zu prüfen. Damit schließen wir unsere Untersuchung der Implementierungsalgorithmen von R-MAT mit MQL5 ab. Den vollständigen Code für die in diesem Artikel vorgestellten Klassen und alle ihre Methoden finden Sie in den Anhängen.

Dort finden Sie auch den vollständigen Code für die Programme zur Interaktion mit der Umgebung und zum Modelltraining. Diese wurden vollständig und ohne Änderungen aus früheren Projekten übernommen. Was die Modellarchitekturen betrifft, so wurden nur geringfügige Anpassungen vorgenommen, indem eine einzige Schicht im Umweltzustandscodierer ersetzt wurde.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRMAT;
   descr.window=BarDescr;
   descr.count=HistoryBars;
   descr.window_out = EmbeddingSize/2;                // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Eine vollständige Beschreibung der Architektur der trainierten Modelle finden Sie im Anhang.

3. Tests

Wir haben viel Arbeit in die Implementierung von R-MAT mit MQL5 gesteckt. Nun gehen wir zur letzten Phase unserer Arbeit über - dem Training der Modelle und dem Testen der daraus resultierenden Politik. In diesem Projekt halten wir uns an den zuvor beschriebenen Algorithmus zum Modelltraining. In diesem Fall trainieren wir alle drei Modelle gleichzeitig: den Zustands-Encoder, den Akteur und den Kritiker. Das erste Modell leistet die vorbereitende Arbeit der Interpretation der Marktsituation. Der Akteur trifft seine Handelsentscheidungen auf der Grundlage der erlernten Strategie. Der Kritiker bewertet das Handeln des Akteurs und gibt die Richtung für politische Anpassungen vor.

Wie zuvor werden die Modelle auf realen historischen Daten für EURUSD, Zeitrahmen H1, für das gesamte Jahr 2023 trainiert. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.

Die Modelle werden iterativ trainiert, wobei der Trainingsdatensatz in regelmäßigen Abständen aktualisiert wird.

Die Wirksamkeit der geschulten Politik wird anhand historischer Daten vom Januar 2024 überprüft. Die Testergebnisse sind wie folgt:

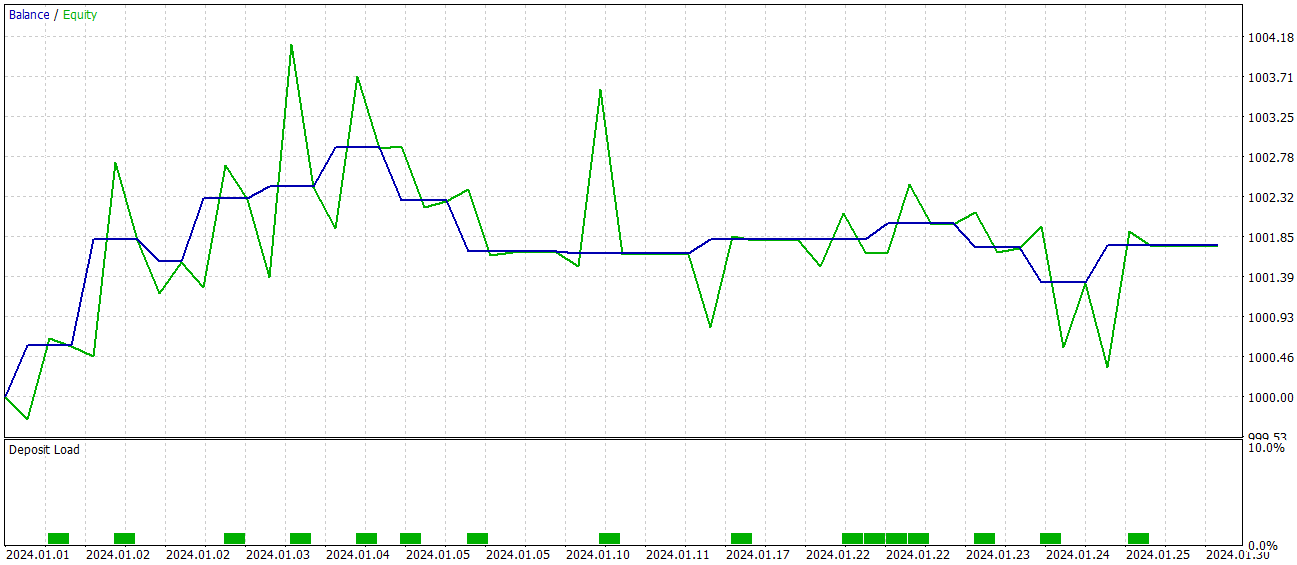
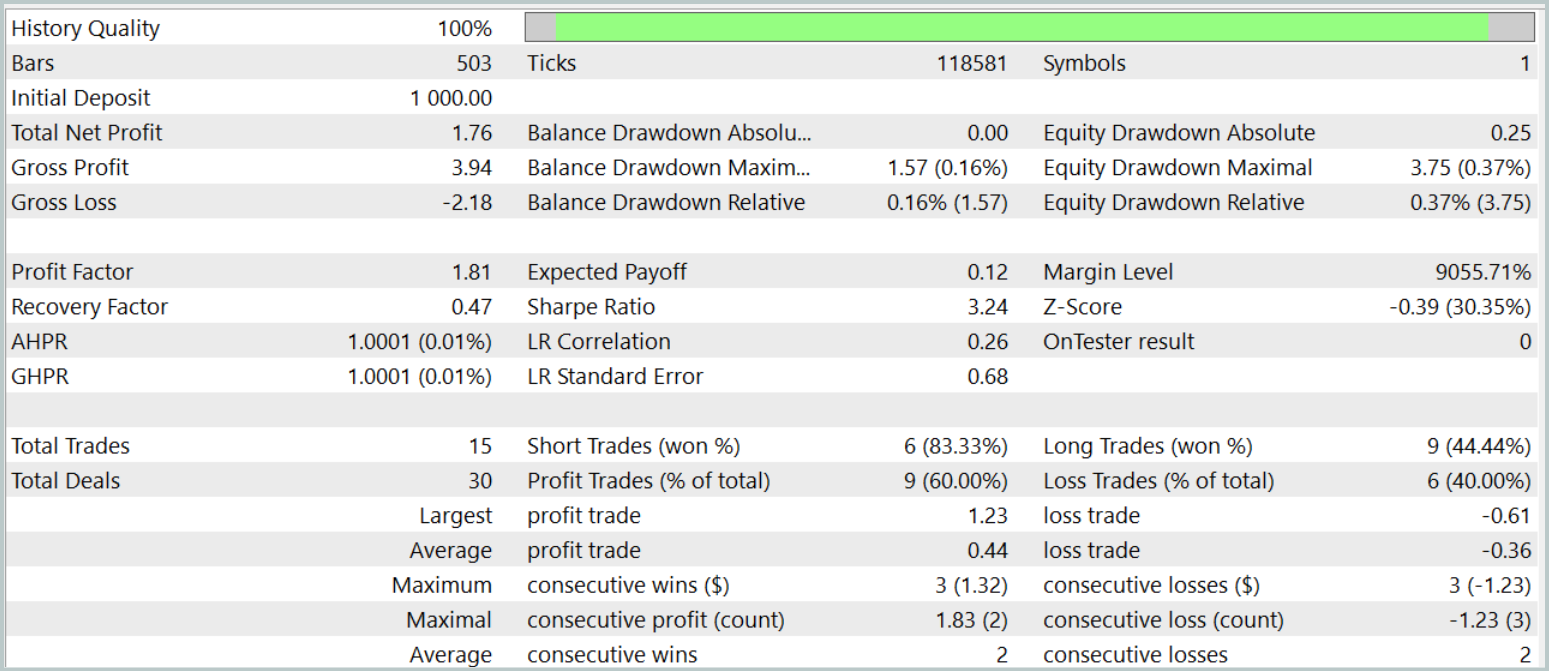
Während der Testphase erreichte das Modell eine Quote von 60 % profitablen Handelsgeschäften. Außerdem übertrafen sowohl der durchschnittliche als auch der maximale Gewinn pro Position die entsprechenden Verlustkennzahlen.

Allerdings gibt es einen Haken an der Sache. Während des Testzeitraums führte das Modell nur 15 Handelsgeschäfte aus. Die Saldenkurve zeigt, dass die größten Gewinne zu Beginn des Monats erzielt wurden. Und dann flacht sie ab. Daher können wir in diesem Fall nur über das Potenzial des Modells sprechen; um es für den längerfristigen Handel nutzbar zu machen, ist eine weitere Entwicklung erforderlich.

Schlussfolgerung

Der Relative Aufmerksamkeits-Transformer der Moleküle (R-MAT) stellt einen bedeutenden Fortschritt auf dem Gebiet der Vorhersage komplexer Eigenschaften dar. Im Zusammenhang mit dem Handel kann R-MAT als ein leistungsfähiges Instrument zur Analyse komplexer Beziehungen zwischen verschiedenen Marktfaktoren betrachtet werden, wobei sowohl ihre relativen Abstände als auch ihre zeitlichen Abhängigkeiten berücksichtigt werden.

Im praktischen Teil haben wir unsere eigene Interpretation der vorgeschlagenen Ansätze mit MQL5 implementiert und die resultierenden Modelle auf realen Daten trainiert. Die Testergebnisse zeigen das Potenzial der vorgeschlagenen Lösung. Das Modell muss jedoch noch weiter verfeinert werden, bevor es in realen Handelsszenarien eingesetzt werden kann.

Referenzen

• Relative Molecule Self-Attention Transformer
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	EA zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek