Neuronale Netze im Handel: Marktanalyse mit Hilfe eines Muster-Transformers

MetaTrader 5 — Handelssysteme | 25 Juli 2025, 07:58

Einführung

In den letzten zehn Jahren hat das Deep Learning (DL) in verschiedenen Bereichen erhebliche Fortschritte erzielt, die auch die Aufmerksamkeit der Finanzmarktforscher auf sich gezogen haben. Angeregt durch den Erfolg von DLs wollen viele sie für die Vorhersage von Markttrends und die Analyse komplexer Datenzusammenhänge einsetzen. Ein Schlüsselaspekt einer solchen Analyse ist das Darstellungsformat der Rohdaten, das die inhärenten Beziehungen und die Struktur der analysierten Instrumente bewahren sollte. Die meisten bestehenden Modelle arbeiten mit homogenen Graphen, was ihre Fähigkeit einschränkt, die umfangreichen semantischen Informationen zu erfassen, die mit Marktmustern verbunden sind. Ähnlich wie bei der Verwendung von N-Grammen in der natürlichen Sprachverarbeitung können häufig auftretende Marktmuster genutzt werden, um Zusammenhänge genauer zu erkennen und Trends vorherzusagen.

Um dieses Problem zu lösen, haben wir beschlossen, bestimmte Ansätze aus dem Bereich der chemischen Elementanalyse zu übernehmen. Ähnlich wie bei Marktmustern treten Motive (aussagekräftige Teilgraphen) häufig in molekularen Strukturen auf und können dazu verwendet werden, molekulare Eigenschaften aufzudecken. Sehen wir uns das System Molformer an, der in dem Artikel „Molformer: Motif-based Transformer on 3D Heterogeneous Molecular Graphs" vorgestellt wurde.

Die Autoren der Methode Molformer definieren einen neuartigen heterogenen molekularen Graphen (HMG) als Input für das Modell, der Knoten sowohl auf atomarer als auch auf motivischer Ebene enthält. Dieses Design bietet eine saubere Schnittstelle für die Integration von Knoten verschiedener Ebenen und verhindert die Ausbreitung von Fehlern, die durch eine unsachgemäße semantische Segmentierung von Atomen verursacht werden. Bei den Motiven wenden die Autoren unterschiedliche Strategien für verschiedene Molekültypen an. Bei kleinen Molekülen wird das Motivvokabular durch funktionelle Gruppen bestimmt, die auf chemischem Fachwissen beruhen. Für Proteine, die aus aufeinanderfolgenden Aminosäuren bestehen, wird eine auf Reinforcement Learning (RL) basierende Methode zur intelligenten Motivsuche eingeführt, um die wichtigsten Aminosäure-Untersequenzen zu identifizieren.

Um sich effektiv an die HMG anzupassen, führt Molformer ein äquivariantes geometrisches Modell ein, das auf der Transformer-Architektur aufbaut. Molformer unterscheidet sich von den bisher betrachteten Transformer-basierten Modellen in zwei wesentlichen Aspekten. Erstens nutzt es die heterogene Selbstbeobachtung (HSA), um Interaktionen zwischen Knoten verschiedener Ebenen zu erfassen. Zweitens wird einAFPS-Algorithmus (Attentive Farthest Point Sampling) eingeführt, um Knotenmerkmale zu aggregieren und eine umfassende Darstellung des gesamten Moleküls zu erhalten.

Die Autoren präsentieren experimentelle Ergebnisse, die die Wirksamkeit dieses Ansatzes bei der Bewältigung von Herausforderungen in der chemischen Industrie belegen. Lassen Sie uns das Potenzial dieser Methoden zur Lösung von Trendvorhersageaufgaben auf den Finanzmärkten bewerten.

1. Der Molformer-Algorithmus

Motive stellen häufig vorkommende substrukturelle Muster dar und dienen als Bausteine komplexer molekularer Strukturen. Sie verkörpern eine Fülle biochemischer Eigenschaften ganzer Moleküle. In der chemischen Gemeinschaft wurde eine Reihe von Standardkriterien entwickelt, um Motive mit bedeutenden funktionellen Fähigkeiten in kleinen Molekülen zu identifizieren. In großen Proteinmolekülen entsprechen Motive lokalen Regionen dreidimensionaler Strukturen oder Aminosäuresequenzen, die den Proteinen gemeinsam sind und ihre Funktion beeinflussen. Jedes Motiv besteht in der Regel aus nur wenigen Elementen und kann die Verbindungen zwischen sekundären Strukturelementen beschreiben. Auf der Grundlage dieser Eigenschaft haben die Autoren des System Molformer einen heuristischen Ansatz zur Entdeckung von Proteinmotiven mit Hilfe von Verstärkungslernen (Reinforcement Learning, RL) entwickelt. In ihrer Arbeit schlagen sie vor, sich auf Motive zu konzentrieren, die aus vier Aminosäuren bestehen, die die kleinsten Polypeptide bilden und unterschiedliche funktionelle Eigenschaften in Proteinen besitzen. In diesem Stadium besteht das Hauptziel darin, das wirksamste Lexikon 𝓥 unter den K biquadratische Aminosäurematrizen zu ermitteln. Da das Ziel darin besteht, ein optimales Lexikon für eine bestimmte Aufgabe zu finden, ist es praktisch machbar, nur die vorhandenen Quartette aus nachgelagerten Datensätzen zu berücksichtigen und nicht alle möglichen Kombinationen.

Das gelernte Lexikon 𝓥 wird als Vorlage für die Motivextraktion und für die Konstruktion von HMGs in nachgelagerten Aufgaben verwendet. Auf der Grundlage dieser HMGs wird dann Molformer ausgebildet. Ihre Effektivität wird als Belohnung r für die Aktualisierung der Parameter θ über Politik-Gradienten behandelt. So kann der Agent das für die jeweilige Aufgabe optimale Lexikon der biquadratische Motive auswählen.

Das vorgeschlagene Verfahren zur Motivsuche ist ein einstufiges Spiel, da das Politiknetzwerk πθ das Lexikon 𝓥 nur einmal pro Iteration erzeugt. Die Trajektorie besteht also nur aus einer Aktion, und das Ergebnis des Molformers, das auf dem gewählten Lexikon 𝓥 basiert, ist Teil der Gesamtbelohnung.

Die Autoren des Systems trennen Motive und Atome und behandeln Motive als neue Knoten für die Bildung der HMG. Dadurch werden die Darstellungen auf Motiv- und Atomebene voneinander getrennt, was dem Modell die Aufgabe erleichtert, semantische Bedeutungen auf der Motivebene genau zu extrahieren.

Ähnlich wie die Beziehungen zwischen Phrasen und einzelnen Wörtern in der natürlichen Sprache tragen Motive in Molekülen semantische Bedeutungen auf höherer Ebene als Atome. Daher spielen sie eine entscheidende Rolle bei der Festlegung der funktionellen Fähigkeiten ihrer atomaren Bestandteile. Die Autoren von Molformer behandeln jede Motivkategorie als einen neuen Knotentyp und konstruieren das HMG als Eingabe des Modells, sodass HMG sowohl Knoten auf Motiv- als auch auf Atomebene enthält. Die Positionen der einzelnen Motive werden durch eine gewichtete Summe der 3D-Koordinaten der sie bildenden Elemente dargestellt. Ähnlich wie bei der Wortsegmentierung verhindern HMGs, die aus mehrstufigen Knoten bestehen, eine Fehlerfortpflanzung aufgrund einer unsachgemäßen semantischen Segmentierung, indem sie atomare Informationen nutzen, um das Lernen der molekularen Repräsentation zu steuern.

Molformer modifiziert die Transformer-Architektur mit mehreren neuen Komponenten, die speziell für 3D HMG entwickelt wurden. Jeder Encoder-Block besteht aus HSA, einem FeedForward-Netzwerk (FFN) und einer zweistufigen Normalisierung. Anschließend wird durch aufmerksames Farthest-Point-Sampling (AFPS) adaptiv eine Moleküldarstellung erstellt, die dann in einen vollständig vernetzten Prädiktor für die Vorhersage von Eigenschaften für eine Vielzahl von nachgelagerten Aufgaben eingespeist wird.

Nach der Formulierung von HMG mit N+M Knoten auf der Atom- bzw. Motivebene ist es wichtig, das Modell mit der Fähigkeit auszustatten, Wechselwirkungen zwischen Knoten mehrerer Ordnung zu unterscheiden. Um dies zu erreichen, führen die Autoren eine Funktion φ(i,j)→Z ein, die Beziehungen zwischen zwei beliebigen Knoten in drei Arten definiert: Atom-Atom, Atom-Motiv und Motiv-Motiv. Dann wird ein lernfähiger Skalar bφ(i,j) eingeführt, um alle Knoten entsprechend ihrer hierarchischen Beziehungen innerhalb der HMG adaptiv zu behandeln.

Außerdem ziehen die Autoren die Verwendung der dreidimensionalen Molekulargeometrie in Betracht. Da die Robustheit gegenüber globalen Veränderungen wie 3D-Translationen und -Drehungen ein grundlegendes Prinzip des Lernens von Moleküldarstellungen ist, zielen sie darauf ab, durch Anwendung einer Faltungsoperation auf die paarweise Distanzmatrix 𝑫 roto-translationale Invarianz sicherzustellen.

Darüber hinaus hat sich die Nutzung des lokalen Kontexts in spärlichen 3D-Räumen als wichtig erwiesen. Es wurde jedoch festgestellt, dass die Selbstbeobachtung zwar globale Datenmuster erfasst, aber den lokalen Kontext tendenziell außer Acht lässt. Auf der Grundlage dieser Beobachtung wenden die Autoren eine distanzbasierte Einschränkung der Selbstaufmerksamkeit an, um mehrskalige Muster sowohl aus lokalen als auch aus globalen Zusammenhängen zu extrahieren. Zu diesem Zweck wurde eine mehrskalige Methode entwickelt, mit der Details zuverlässig erfasst werden können. Konkret werden Knoten außerhalb einer bestimmten Entfernungsschwelle τs bei jeder Skala s ausgeblendet. Anschließend werden die in verschiedenen Maßstäben extrahierten Merkmale zu einer mehrskaligen Darstellung kombiniert und in das FFN eingespeist.

Die Originalvisualisierung des Systems Molformer finden Sie unten.

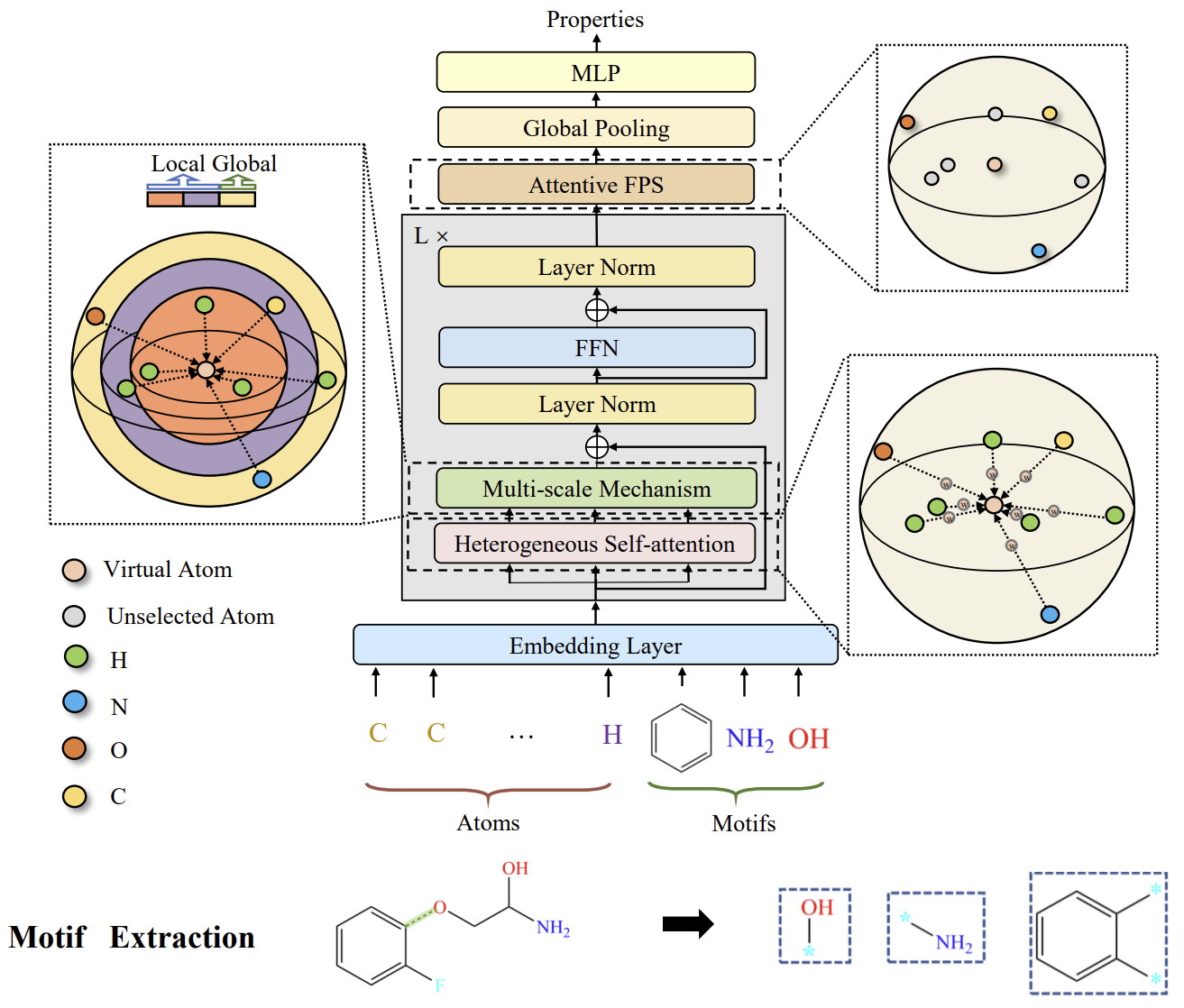
2. Die Implementation in MQL5

Nachdem wir die theoretischen Aspekte der Methode Molformer erläutert haben, gehen wir nun zum praktischen Teil des Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen. Wie in unserer früheren Arbeit werden wir den gesamten Prozess der Implementierung des Systems in separate Module aufteilen, die wiederkehrende Operationen durchführen.

2.1 Bündelung der Aufmerksamkeit

Zunächst werden wir den von den Autoren der Methode R-MAT vorgeschlagenen abhängigkeitsbasierten Pooling-Algorithmus in eine eigenständige Klasse isolieren.

Seien Sie nicht überrascht, dass wir mit der Implementierung von Molformer beginnen, indem wir einen Ansatz aus der Methode R-MAT einbeziehen. Beide Methoden wurden vorgeschlagen, um ähnliche Probleme in der chemischen Industrie zu lösen. Unserer Ansicht nach gibt es einige Überschneidungen zwischen ihnen, die wir nutzen werden. Der abhängigkeitsbasierte Pooling-Algorithmus ist eine dieser Überschneidungen.

Wir werden die Prozesse dieses Algorithmus in der Klasse CNeuronMHAttentionPooling organisieren, deren Struktur im Folgenden vorgestellt wird.

class CNeuronMHAttentionPooling  :  public   CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iHeads;
   uint              iUnits;
   CLayer            cNeurons;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHAttentionPooling(void) {};
                    ~CNeuronMHAttentionPooling(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMHAttentionPooling; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

In dieser Klasse deklarieren wir drei interne Variablen und ein dynamisches Array, in dem wir Zeiger auf interne Objekte in der Reihenfolge ihres Aufrufs speichern werden. Das Array selbst wird statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung aller geerbten und neu deklarierten Objekte erfolgt in der Methode Init, die als Parameter Konstanten erhält, die die Architektur des erstellten Objekts eindeutig definieren.

bool CNeuronMHAttentionPooling::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint units_count, uint heads,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Im Körper der Objektinitialisierungsmethode rufen wir zunächst die gleichnamige Methode der Elternklasse auf, in der ein Teil der erforderlichen Steuerelemente und der Initialisierungsalgorithmus für geerbte Objekte bereits implementiert sind. Anschließend speichern wir die vom externen Programm erhaltenen Konstanten in den internen Variablen.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;

Wir bereiten unser dynamisches Array vor.

   cNeurons.Clear();
   cNeurons.SetOpenCL(OpenCL);

Und dann beginnen wir mit der Erstellung einer Struktur von verschachtelten Objekten. Hier erstellen wir einen zweischichtigen MLP, bei dem wir die hyperbolische Tangente verwenden, um Nichtlinearität zwischen den neuronalen Schichten zu erzeugen.

   int idx = 0;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow*iHeads, iWindow*iHeads, 4*iWindow, iUnits, 1, optimization, iBatch) ||
      !cNeurons.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4*iWindow, 4*iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cNeurons.Add(conv)
     )
      return false;

Die Ausgabe des MLP wird durch die Funktion Softmax in Bezug auf die einzelnen Elemente der Sequenz normalisiert.

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cNeurons.Add(softmax)
     )
      return false;
   softmax.SetHeads(iUnits);
//---
   return true;
  }

Wir schließen die Methode ab, indem wir ein boolesches Ergebnis, das den Erfolg der Operationen anzeigt, an das aufrufende Programm zurückgeben.

Es ist wichtig zu beachten, dass wir in diesem Fall keine Zeigersubstitution für Datenpuffer durchführen. Das liegt daran, dass die von uns erstellten Objekte nur Zwischendaten erzeugen. Das eigentliche Ergebnis des erstellten Objekts wird durch Multiplikation der normalisierten Ausgänge des erstellten MLP mit dem Eingabedatentensor gebildet. Die Ergebnisse dieser Operation werden dann in dem entsprechenden Puffer gespeichert, der von der übergeordneten Klasse geerbt wurde. Ein ähnlicher Ansatz gilt für den Fehlergradientenpuffer.

Sobald die Initialisierungsmethode der Klasse abgeschlossen ist, gehen wir zur Konstruktion des Vorwärtsdurchlauf-Algorithmus in der Methode feedForward über.

bool CNeuronMHAttentionPooling::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *current = NULL;
   CObject *prev = NeuronOCL;

In den Methodenparametern erhalten wir einen Zeiger auf das Quelldatenobjekt. Im Hauptteil der Methode deklarieren wir zwei lokale Variablen für die temporäre Speicherung von Zeigern auf Objekte. Wir übergeben einen Zeiger auf das Quelldatenobjekt an einen von ihnen.

Als Nächstes organisieren wir eine Schleife durch die internen MLP-Objekte mit einem sequentiellen Aufruf der gleichnamigen Methoden des internen Modells.

   for(int i = 0; i < cNeurons.Total(); i++)
     {
      current = cNeurons[i];
      if(!current ||
         !current.FeedForward(prev)
        )
         return false;
      prev = current;;
     }

Nach Abschluss aller Iterationen der Schleife erhalten wir die Einflusskoeffizienten des Aufmerksamkeitskopfes für jedes einzelne Element der Sequenz. Nun müssen wir, wie bereits erwähnt, den gewichteten Durchschnitt der Aufmerksamkeitsköpfe in den Eingabedaten berechnen, indem wir die erhaltenen Koeffizienten mit dem Tensor der Eingabedaten multiplizieren. Das Ergebnis dieser Tensormultiplikation wird im Ergebnispuffer unseres Objekts gespeichert.

   if(!MatMul(current.getOutput(), NeuronOCL.getOutput(), Output,
                                      1, iHeads, iWindow, iUnits))
      return false;
//---
   return true;
  }

Schließlich geben wir das boolesche Ergebnis der Operationen an das aufrufende Programm zurück und schließen damit die Methode ab.

Ich schlage vor, die Backpropagation-Methoden dieses Kurses im Selbststudium zu erlernen. Der vollständige Code dieser Klasse und alle ihre Methoden sind im Anhang zu finden.

2.2 Extraktion von Mustern

In der nächsten Phase unserer Arbeit werden wir das Objekt zur Musterextraktion erstellen. Wie im theoretischen Teil erwähnt, werden die Mustereinbettungen dem Eingabedatentensor hinzugefügt, bevor sie an das Modell weitergegeben werden. Wir werden dies jedoch anders angehen: Wir füttern das Modell mit einem Standarddatensatz als Eingabe, und die Musterextraktion und die Verkettung ihrer Einbettungen mit dem Eingabedatentensor werden innerhalb des Modells selbst durchgeführt.

Es ist wichtig zu beachten, dass jedes zu den Eingabedaten hinzugefügte Muster die Dimensionalität eines einzelnen Sequenzelements haben muss und im selben Unterraum liegen muss Das erste Problem wird durch architektonische Entscheidungen gelöst. Das zweite Problem werden wir versuchen, während des Trainings der Mustereinbettungen zu lösen.

Um diese Aufgaben zu erfüllen, werden wir eine neue Klasse CNeuronMotifs erstellen. Seine Struktur wird im Folgenden dargestellt.

class CNeuronMotifs    :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL    cMotifs;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMotifs(void) {};
                    ~CNeuronMotifs(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint dimension, uint window, uint step, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMotifs; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override;
  };

In dieser Klasse wird nur eine interne Faltungsschicht deklariert, die für die Durchführung der Mustereinbettungsfunktionalität verantwortlich sein wird. Es ist jedoch erwähnenswert, dass wir die Methode zur Festlegung der Aktivierungsfunktion außer Kraft setzen. Interessanterweise wurde diese Methode in keiner unserer früheren Implementierungen außer Kraft gesetzt. In diesem Fall wird die Aktivierungsfunktion der internen Schicht mit derjenigen des Objekts selbst synchronisiert.

void CNeuronMotifs::SetActivationFunction(ENUM_ACTIVATION value)
  {
   CNeuronBaseOCL::SetActivationFunction(value);
   cMotifs.SetActivationFunction(activation);
  }

Wir initialisieren die deklarierte Faltungsschicht sowie alle geerbten Objekte in der Methode Init. In den Parametern dieser Methode übergeben wir Konstanten, die es uns ermöglichen, die Architektur des zu erstellenden Objekts eindeutig zu bestimmen.

bool CNeuronMotifs::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint dimension, uint window, uint step, uint units_count,
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   uint inputs = (units_count * step + (window - step)) * dimension;
   uint motifs = units_count * dimension;

Im Gegensatz zu ähnlichen Methoden, die wir früher betrachtet haben, verfügen wir in diesem Fall jedoch nicht über genügend Daten, um die gleichnamige Methode der übergeordneten Klasse direkt aufzurufen. Dies ist in erster Linie auf die Größe des Ergebnispuffers zurückzuführen. Wie oben erwähnt, ist die erwartete Ausgabe ein verketteter Tensor aus den Eingabedaten und den Mustereinbettungen. Daher werden wir zunächst die Größen des Eingabedatentensensors und des Mustereinbettungstensors auf der Grundlage der verfügbaren Daten bestimmen und erst dann die Initialisierungsmethode der übergeordneten Klasse aufrufen und die Summe der ermittelten Größen übergeben.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs + motifs, optimization_type, batch))
      return false;

Der nächste Schritt ist die Initialisierung der internen Mustereinbettungs-Faltungsschicht entsprechend den vom externen Programm erhaltenen Parametern.

   if(!cMotifs.Init(0, 0, OpenCL, dimension * window, dimension * step, dimension, units_count,
                                                                           1, optimization, iBatch))
      return false;

Beachten Sie, dass die Größe der zurückgegebenen Einbettungen gleich der Dimension der Eingabedaten ist.

Wir heben die Aktivierungsfunktion zwangsweise auf, indem wir die oben beschriebene Methode anwenden.

   SetActivationFunction(None);
//---
   return true;
  }

Danach schließen wir die Methode ab, indem wir das boolsche Ergebnis der Operationen an das aufrufende Programm übergeben.

Auf die Initialisierung des Objekts folgt die Konstruktion von Vorlaufprozessen, die wir in der Methode feedForward implementieren. Hier ist alles ganz unkompliziert.

bool CNeuronMotifs::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Sie nimmt als Parameter einen Zeiger auf das Eingabedatenobjekt entgegen, und der erste Schritt besteht darin, die Gültigkeit dieses Zeigers zu überprüfen. Danach synchronisieren wir die Aktivierungsfunktionen der Eingabedatenschicht und des aktuellen Objekts.

   if(NeuronOCL.Activation() != activation)
      SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation());

Dieser Vorgang ermöglicht es uns, den Ausgabebereich der Einbettungsschicht mit den Eingabedaten zu synchronisieren.

Und erst nach der Durchführung der vorbereitenden Arbeiten führen wir eine Vorwärtsbewegung der inneren Schicht durch.

   if(!cMotifs.FeedForward(NeuronOCL))
      return false;

Dann verketten wir den Tensor der erhaltenen Einbettungen mit den Eingabedaten.

   if(!Concat(NeuronOCL.getOutput(), cMotifs.getOutput(), Output, NeuronOCL.Neurons(), cMotifs.Neurons(), 1))
      return false;
//---
   return true;
  }

Wir schreiben den verketteten Tensor in den von der übergeordneten Klasse geerbten Ergebnispuffer und schließen die Methode ab, indem wir ein boolesches Ergebnis, das den Erfolg der Operationen anzeigt, an das aufrufende Programm zurückgeben.

Als Nächstes befassen wir uns mit Backpropagation-Verfahren. Und wie Sie vielleicht schon vermutet haben, ist ihr Algorithmus genauso einfach. In der Methode calcInputGradients zur Verteilung von Fehlergradienten führen wir beispielsweise nur eine Operation zur Dekonkatenation des von der übergeordneten Klasse geerbten Puffers für Fehlergradienten durch und verteilen die Werte zwischen dem Eingabedatenobjekt und der internen Schicht.

bool CNeuronMotifs::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(!DeConcat(NeuronOCL.getGradient(),cMotifs.getGradient(),Gradient,NeuronOCL.Neurons(),cMotifs.Neurons(),1))
      return false;
//---
   return true;
  }

Diese scheinbare Einfachheit erfordert jedoch einige Klarstellungen. Erstens passen wir den Fehlergradienten, der an die Eingabedaten und die interne Schicht weitergegeben wird, nicht durch die Ableitung der Aktivierungsfunktion der entsprechenden Objekte an. In diesem Fall ist ein solcher Vorgang überflüssig. Dies wird durch die Synchronisierung des Aktivierungsfunktionszeigers unseres Objekts, der internen Schicht und der Eingabedaten erreicht, die wir bei der Entwicklung der Feedforward-Pass-Methode festgelegt haben. Dieser einfache Vorgang ermöglichte es uns, den Fehlergradienten, der bereits durch die Ableitung der richtigen Aktivierungsfunktion angepasst wurde, auf der Ebene der Objektergebnisse zu erhalten. Daher führen wir die Dekonkatenation am bereits angepassten Fehlergradienten durch.

Der zweite Punkt, der zu beachten ist, ist, dass wir den Fehlergradienten nicht von der internen Musterextraktionsschicht an die Eingabedaten weitergeben. Interessanterweise liegt der Grund dafür in der Art unserer Aufgabe: Musterextraktion aus Eingabedaten. Unser Ziel ist es, die signifikanten Muster zu identifizieren und nicht, die Eingabedaten an die gewünschten Muster „anzupassen“. Wie jedoch leicht zu erkennen ist, erhalten die Eingabedaten durch den direkten Datenfluss immer noch ihren eigenen Fehlergradienten.

Der vollständige Code dieser Klasse und alle ihre Methoden sind im Anhang zu finden.

2.3 Mehrskalige Aufmerksamkeit

Ein weiterer „Baustein“, den wir erstellen müssen, ist das Mehrskalige-Aufmerksamkeitsobjekt. Ich muss sagen, dass wir hier vielleicht die größte Abweichung vom ursprünglichen Algorithmus Molformer vorgenommen haben. Die Autoren des Systems haben einen Maskierungsmechanismus implementiert, der Objekte ausschließt, die sich in einer bestimmten Entfernung vom Ziel befinden. Dabei richteten sie ihre Aufmerksamkeit nur auf einen bestimmten Bereich.

Bei unserer Umsetzung haben wir jedoch einen anderen Ansatz gewählt. Erstens haben wir anstelle des vorgeschlagenen Aufmerksamkeitsmechanismus die Relative Selbstaufmerksamkeit Methode verwendet, die nicht nur Positionsabweichungen, sondern auch kontextuelle Informationen analysiert. Zweitens erhöhen wir zur Anpassung der Aufmerksamkeitsskala die Größe eines einzelnen analysierten Elements, um zwei, drei und vier Elemente der ursprünglichen Sequenz abzudecken. Dies kann mit der Analyse eines Charts mit höherem Zeitrahmen verglichen werden. Die Implementierung unserer Lösung wird in der Klasse CNeuronMultiScaleAttention vorgestellt. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronMultiScaleAttention :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   //---
   CNeuronBaseOCL    cWideInputs;
   CNeuronRelativeSelfAttention  cAttentions[4];
   CNeuronBaseOCL    cConcatAttentions;
   CNeuronMHAttentionPooling cPooling;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMultiScaleAttention(void) {};
                    ~CNeuronMultiScaleAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Hier legen wir die Anzahl der Skalen explizit fest, indem wir ein festes Array von Objekten der relativen Aufmerksamkeit deklarieren. Darüber hinaus werden in der Klassenstruktur 3 weitere Objekte deklariert, mit deren Zweck wir uns bei der Implementierung der Klassenmethoden vertraut machen werden.

Wir deklarieren alle internen Objekte als statisch und können daher den Konstruktor und Destruktor der Klasse leer lassen. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.

bool CNeuronMultiScaleAttention::Init(uint numOutputs, uint myIndex,
                                      COpenCLMy *open_cl, uint window,
                                      uint window_key, uint units_count,
                                      uint heads,
                                      ENUM_OPTIMIZATION optimization_type,
                                      uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

In den Methodenparametern erhalten wir, wie üblich, Konstanten, die die Architektur des erstellten Objekts eindeutig definieren. Im Körper der Methode rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf. Ich glaube, es ist unnötig zu wiederholen, dass diese Methode bereits die notwendigen Prüfungen und Initialisierungsalgorithmen für geerbte Objekte enthält.

Nach der erfolgreichen Ausführung der Methode der übergeordneten Klasse speichern wir einige Konstanten in internen Variablen.

   iWindow = window;
   iUnits = units_count;

Vor der Initialisierung der neu deklarierten Objekte ist es wichtig zu beachten, dass wir in diesem Stadium die Größe des Eingabedatentensensors nicht kennen. Außerdem wissen wir nicht, ob seine Dimensionen mit unseren Analyseskalen kompatibel sind. Tatsächlich ist der Eingangstensor, den wir erhalten, vielleicht nicht einmal ein Vielfaches unserer Skalen. Allerdings müssen die Tensoren, die in die großen Aufmerksamkeitsobjekte eingespeist werden, die richtige Größe haben. Um diese Anforderung zu erfüllen, werden wir ein internes Objekt erstellen, in das wir die Eingabedaten kopieren und Nullwerte hinzufügen, um fehlende Elemente zu ergänzen. Aber zunächst werden wir die erforderliche Puffergröße als das Maximum der nächstgrößeren Vielfachen unserer Skalen bestimmen.

   uint units1 = (iUnits + 1) / 2;
   uint units2 = (iUnits + 2) / 3;
   uint units3 = (iUnits + 3) / 4;
   uint wide = MathMax(MathMax(iUnits, units1 * 2), MathMax(units2 * 3, units3 * 4));

Dann initialisieren wir das Objekt, um die Eingabedaten in der erforderlichen Größe zu kopieren.

   int idx = 0;
   if(!cWideInputs.Init(0, idx, OpenCL, wide * iWindow, optimization, iBatch))
      return false;
   CBufferFloat *temp = cWideInputs.getOutput();
   if(!temp || !temp.Fill(0))
      return false;

Wir füllen den Ergebnispuffer dieser Ebene mit Nullwerten.

Im nächsten Schritt initialisieren wir interne Aufmerksamkeitsobjekte verschiedener Größenordnungen unter Beibehaltung anderer Parameter.

   idx++;
   if(!cAttentions[0].Init(0, idx, OpenCL, iWindow, window_key, iUnits, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[1].Init(0, idx, OpenCL, 2 * iWindow, window_key, units1, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[2].Init(0, idx, OpenCL, 3 * iWindow, window_key, units2, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[3].Init(0, idx, OpenCL, 4 * iWindow, window_key, units3, heads, optimization, iBatch))
      return false;

An dieser Stelle sei angemerkt, dass wir trotz der unterschiedlichen Skalen der Objekte der Aufmerksamkeit erwarten, am Ausgang Tensoren vergleichbarer Größe zu erhalten. Dies liegt daran, dass sie im Wesentlichen alle eine einzige Quelle von Ausgangsdaten verwenden. Um die Aufmerksamkeitsergebnisse zu verknüpfen, wird das Objekt daher als viermal so groß wie die ursprünglichen Daten deklariert.

   idx++;
   if(!cConcatAttentions.Init(0, idx, OpenCL, 4 * iWindow * iUnits, optimization, iBatch))
      return false;

Um den Durchschnitt der Aufmerksamkeitsergebnisse zu ermitteln, wird die oben erstellte abhängigkeitsbasierte Poolingklasse verwendet.

   idx++;
   if(!cPooling.Init(0, idx, OpenCL, iWindow, iUnits, 4, optimization, iBatch))
      return false;

Dann ersetzen wir die Zeiger der Ergebnispuffer und Fehlergradienten des erstellten Objekts durch die Zeiger der entsprechenden Puffer der Pooling-Ebene.

   SetActivationFunction(None);
   if(!SetOutput(cPooling.getOutput()) ||
      !SetGradient(cPooling.getGradient()))
      return false;
//---
   return true;
  }

Am Ende der Methode übergeben wir die Ergebnisse der Operation an das aufrufende Programm.

Beachten Sie, dass wir in dieser Klasse keine Objekte zur Implementierung der Restverbindungen organisiert haben, die wir in den zuvor besprochenen Aufmerksamkeitsblöcken verwendet haben. Das liegt daran, dass die internen relativen Aufmerksamkeitsblöcke, die wir verwenden, bereits Restverbindungen enthalten. Folglich werden diese Restverbindungen bereits bei der Mittelung der Aufmerksamkeitsergebnisse berücksichtigt. Die Hinzufügung weiterer Operationen wäre überflüssig.

Nach der Initialisierung des Objekts gehen wir dazu über, die Prozesse der Vorwärtsdurchläufe zu konstruieren, die wir in der Methode feedForward implementieren werden.

bool CNeuronMultiScaleAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Attention
   if(!cAttentions[0].FeedForward(NeuronOCL))
      return false;

In den Parametern der Methode feedForward erhalten wir wie üblich einen Zeiger auf das Eingabedatenobjekt, den wir sofort an die gleichnamige Methode in der internen einskaligen Aufmerksamkeitsschicht weitergeben. In der Methode des internen Objekts wird zusätzlich zu den Kernoperationen auch die Gültigkeit des empfangenen Zeigers überprüft. Folglich können wir nach der erfolgreichen Ausführung der klasseninternen Methodenoperationen den vom externen Programm erhaltenen Zeiger sicher verwenden. Im nächsten Schritt übertragen wir die Eingangsdaten in den Puffer der entsprechenden internen Schicht. Danach synchronisieren wir die Aktivierungsfunktionen.

   if(!Concat(NeuronOCL.getOutput(), NeuronOCL.getOutput(), cWideInputs.getOutput(), iWindow, 0, iUnits))
      return false;
   if(cWideInputs.Activation() != NeuronOCL.Activation())
      cWideInputs.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation());

Es ist wichtig zu beachten, dass wir in diesem Fall eine Verkettungsmethode zum Kopieren der Eingabedaten verwenden, bei der wir den Zeiger auf den Ergebnispuffer des Eingabedatenobjekts zweimal angeben. Für den ersten Puffer geben wir die Fenstergröße der Eingabedaten an, und für den zweiten ist es „0“. Es ist klar, dass wir mit diesen Parametereinstellungen eine Kopie der Eingabedaten im angegebenen Ergebnispuffer erhalten. Gleichzeitig wird keine explizite Operation des Hinzufügens von Nullwerten für fehlende Daten durchgeführt, die wir bei der Objektinitialisierung diskutiert haben.

Die Addition von Nullwerten erfolgt jedoch implizit. Bei der Initialisierung des internen Eingangsdatenobjekts haben wir dessen Ergebnispuffer mit Nullwerten gefüllt. Während des Trainings und des Betriebs erwarten wir, dass wir Eingabedatentensoren der gleichen Größe erhalten. Folglich werden bei jedem Kopieren der Eingabedaten dieselben Elemente überschrieben, während die verbleibenden Einsen mit Nullen gefüllt bleiben.

Nach der Bildung des erweiterten Eingabedatenobjekts organisieren wir eine Schleife, um Aufmerksamkeitsoperationen auf mehreren Ebenen durchzuführen. In dieser Schleife rufen wir nacheinander die Methoden der Vorwärtsdurchläufe der größeren Aufmerksamkeitsobjekte auf und übergeben ihnen den Zeiger auf das erweiterte Eingabedatenobjekt.

//--- Multi scale attentions
   for(int i = 1; i < 4; i++)
      if(!cAttentions[i].FeedForward(cWideInputs.AsObject()))
         return false;

Wir fügen die Ergebnisse der Aufmerksamkeit auf allen Skalen zu einem einzigen Tensor zusammen. Trotz des unterschiedlichen Maßstabs der analysierten Daten ergibt die Ausgabe vergleichbare Tensoren, und jedes Element der ursprünglichen Sequenz bleibt an seinem Platz. Daher führen wir die Verkettung von Tensoren im Zusammenhang mit den Elementen der ursprünglichen Sequenz durch.

//--- Concatenate Multi-Scale Attentions
   if(!Concat(cAttentions[0].getOutput(), cAttentions[1].getOutput(), cAttentions[2].getOutput(),
              cAttentions[3].getOutput(), cConcatAttentions.getOutput(), 
              iWindow, iWindow, iWindow, iWindow, iUnits))
      return false;

Und dann führen wir auf die gleiche Weise, bezogen auf die Elemente der ursprünglichen Sequenz, ein gewichtetes Pooling der Ergebnisse der mehrskalige Aufmerksamkeit durch, wobei die Abhängigkeiten berücksichtigt werden.

//--- Attention pooling
   if(!cPooling.FeedForward(cConcatAttentions.AsObject()))
      return false;
//---
   return true;
  }

Bevor wir die Methode beenden, geben wir dem Aufrufer einen booleschen Wert zurück, der den Erfolg oder Misserfolg der Initialisierung anzeigt.

Zur Erinnerung: Während der Initialisierungsphase des Objekts haben wir die Zeiger auf die Ergebnispuffer und die Puffer für die Fehlergradienten ersetzt. Daher werden die Pooling-Ergebnisse direkt in den Puffern abgelegt, die für die Kommunikation zwischen den neuronalen Netzschichten des Modells verwendet werden. Folglich verzichten wir auf das redundante Kopieren von Daten.

Ich schlage vor, die Backpropagation-Methoden dieses Kurses im Selbststudium zu erlernen. Der vollständige Code für diese Klasse und alle ihre Methoden sind in den beigefügten Dateien enthalten.

2.4 Aufbau des Systems Molformer

Für den Aufbau der einzelnen Komponenten von Molformer wurde bereits ein erheblicher Teil der Arbeit geleistet. Nun ist es an der Zeit, diese einzelnen Komponenten zu einer vollständigen Architektur des Systems zusammenzufügen. Zu diesem Zweck werden wir eine neue Klasse CNeuronMolformer erstellen. In diesem Fall werden wir CNeuronRMAT als übergeordnete Klasse verwenden, die den Mechanismus des einfachsten linearen Modells implementiert. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronMolformer  :  public CNeuronRMAT
  {
public:
                     CNeuronMolformer(void) {};
                    ~CNeuronMolformer(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          uint motif_window, uint motif_step,
                          ENUM_OPTIMIZATION optimization_type, uint batch); //Molformer
   //---
   virtual int       Type(void) override   const   {  return defNeuronMolformer; }
  };

Beachten Sie, dass wir im Gegensatz zu den zuvor implementierten Komponenten hier nur die Initialisierungsmethode der neuen Klasse Init außer Kraft setzen. Möglich wurde dies durch die lineare Struktur, die in der übergeordneten Klasse organisiert ist. Jetzt genügt es, das dynamische Array, das von der übergeordneten Klasse geerbt wurde, mit der gewünschten Folge von Objekten zu füllen. Der gesamte Interaktionsalgorithmus zwischen diesen Komponenten ist bereits in den Methoden der übergeordneten Klasse angelegt.

In den Parametern dieser einzigen überschriebenen Methode erhalten wir eine Reihe von Konstanten, die es uns ermöglichen, die Architektur des erstellten Objekts eindeutig im Sinne des Nutzers zu interpretieren.

bool CNeuronMolformer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_key, uint units_count,
                            uint heads, uint layers,
                            uint motif_window, uint motif_step,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Im Hauptteil der Methode rufen wir sofort die Methode der Basisklasse der vollständig verbundenen neuronalen Schicht auf.

Es ist wichtig zu beachten, dass wir die Methode der Basisklasse der neuronalen Schicht aufrufen und nicht die des direkten übergeordneten Objekts. Im Hauptteil der Methode müssen wir eine völlig neue Architektur erstellen. Wir werden also nicht die architektonischen Lösungen der übergeordneten Klasse nachbilden.

Der nächste Schritt besteht darin, ein dynamisches Array vorzubereiten, in dem wir Zeiger auf die zu erstellenden Objekte speichern werden.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);

Gehen wir nun zu den Vorgängen im Zusammenhang mit der Erstellung und Initialisierung der erforderlichen Objekte über. Hier erstellen und initialisieren wir zunächst das Objekt zur Musterextraktion. Einem dynamischen Array fügen wir einen Zeiger auf das neue Objekt hinzu.

   int idx = 0;
   CNeuronMotifs *motif = new CNeuronMotifs();
   uint motif_units = units_count - MathMax(motif_window - motif_step, 0);
   motif_units = (motif_units + motif_step - 1) / motif_step;
   if(!motif ||
      !motif.Init(0, idx, OpenCL, window, motif_window, motif_step, motif_units, optimization, iBatch) ||
      !cLayers.Add(motif)
     )
      return false;

Dann erstellen wir lokale Variablen für die temporäre Speicherung von Zeigern auf Objekte und führen eine Schleife aus, die interne Schichten des Encoders erstellt. Die Anzahl der internen Schichten wird durch eine Konstante in den Methodenparametern festgelegt.

   idx++;
   CNeuronMultiScaleAttention *msat = NULL;
   CResidualConv *ff = NULL;
   uint units_total = units_count + motif_units;
   for(uint i = 0; i < layers; i++)
     {
      //--- Attention
      msat = new CNeuronMultiScaleAttention();
      if(!msat ||
         !msat.Init(0, idx, OpenCL, window, window_key, units_total, heads, optimization, iBatch) ||
         !cLayers.Add(msat)
        )
         return false;
      idx++;

Im Schleifenkörper wird zunächst das Objekt „Multiskalige Aufmerksamkeit“ erstellt und initialisiert. Und dann fügen wir einen Faltungsblock mit Restverbindung hinzu.

      //--- FeedForward
      ff = new CResidualConv();
      if(!ff ||
         !ff.Init(0, idx, OpenCL, window, window, units_total, optimization, iBatch) ||
         !cLayers.Add(ff)
        )
         return false;
      idx++;
     }

Wir fügen Zeiger auf die erstellten Objekte zum dynamischen Array der internen Objekte hinzu.

Als Nächstes ist zu beachten, dass wir am Ausgang des mehrskaligen Aufmerksamkeitsblocks einen verketteten Tensor der Eingabedaten und Mustereinbettungen erhalten, der mit Informationen über interne Abhängigkeiten angereichert ist. Am Ausgang der Klasse müssen wir jedoch einen Tensor mit angereicherten Eingabedaten zurückgeben. Anstatt die Mustereinbettungen einfach zu „verwerfen“, werden wir eine Skalierungsfunktion für die Daten innerhalb einzelner Einheitssequenzen verwenden. Dazu transponieren wir zunächst die Ergebnisse der vorherigen Ebene.

//--- Out
   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, idx, OpenCL, units_total, window, optimization, iBatch) ||
      !cLayers.Add(transp)
     )
      return false;
   idx++;

Dann fügen wir eine Faltungsschicht hinzu, die die Funktion der Skalierung einzelner unitärer Sequenzen übernimmt.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, units_total, units_total, units_count, window, 1, optimization, iBatch) ||
      !cLayers.Add(conv)
     )
      return false;
   idx++;

Setzen Sie die Ausgabe auf die ursprüngliche Datendarstellung zurück.

   idx++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) ||
      !cLayers.Add(transp)
     )
      return false;

Danach müssen wir nur noch die Zeiger auf die Datenpuffer ersetzen und das logische Ergebnis der Operationen an das aufrufende Programm zurückgeben.

   if(!SetOutput(transp.getOutput()) ||
      !SetGradient(transp.getGradient()))
     return false;
//---
   return true;
  }

Damit schließen wir unsere Diskussion über die Klasse des Systems Molder ab. Den vollständigen Quellcode für alle vorgestellten Klassen und ihre Methoden finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme. Bitte beachten Sie, dass wir auf Interaktions- und Schulungsprogramme aus früheren Artikeln zurückgreifen. Es wurden einige kleinere Änderungen an der Architektur des Environment State Encoders vorgenommen, die ich Ihnen ans Herz lege, selbst zu erkunden. Eine vollständige Beschreibung der Architektur der trainierbaren Modelle finden Sie im Anhang. Wir gehen nun zur letzten Phase unserer Arbeit über - dem Training der Modelle und dem Testen der Ergebnisse.

3. Tests

In diesem Artikel haben wir das System Molformer in MQL5 implementiert und gehen nun zur letzten Phase über - dem Training der Modelle und der Bewertung der trainierten Actor-Verhaltenspolitik. Wir folgen dem in früheren Arbeiten beschriebenen Trainingsalgorithmus und trainieren gleichzeitig drei Modelle: den State Encoder (Zustand-Encoder), den Actor (Akteur) und den Critic (Kritiker). Der Encoder analysiert die Marktsituation, der Akteur führt Handelsgeschäfte auf der Grundlage der erlernten Strategie aus, und der Kritiker bewertet die Aktionen des Akteurs und gibt Hinweise zur Verfeinerung der Verhaltenspolitik.

Das Training wird mit realen historischen EURUSD-Daten auf dem H1-Zeitrahmen für das gesamte Jahr 2023 durchgeführt, mit Standardparametern für die analysierten Indikatoren.

Der Trainingsprozess ist iterativ. Es beinhaltet regelmäßige Aktualisierungen der Trainingsdaten.

Um die Wirksamkeit der trainierten Politik zu überprüfen, verwenden wir historische Daten für Januar 2024. Die Testergebnisse werden im Folgenden vorgestellt.

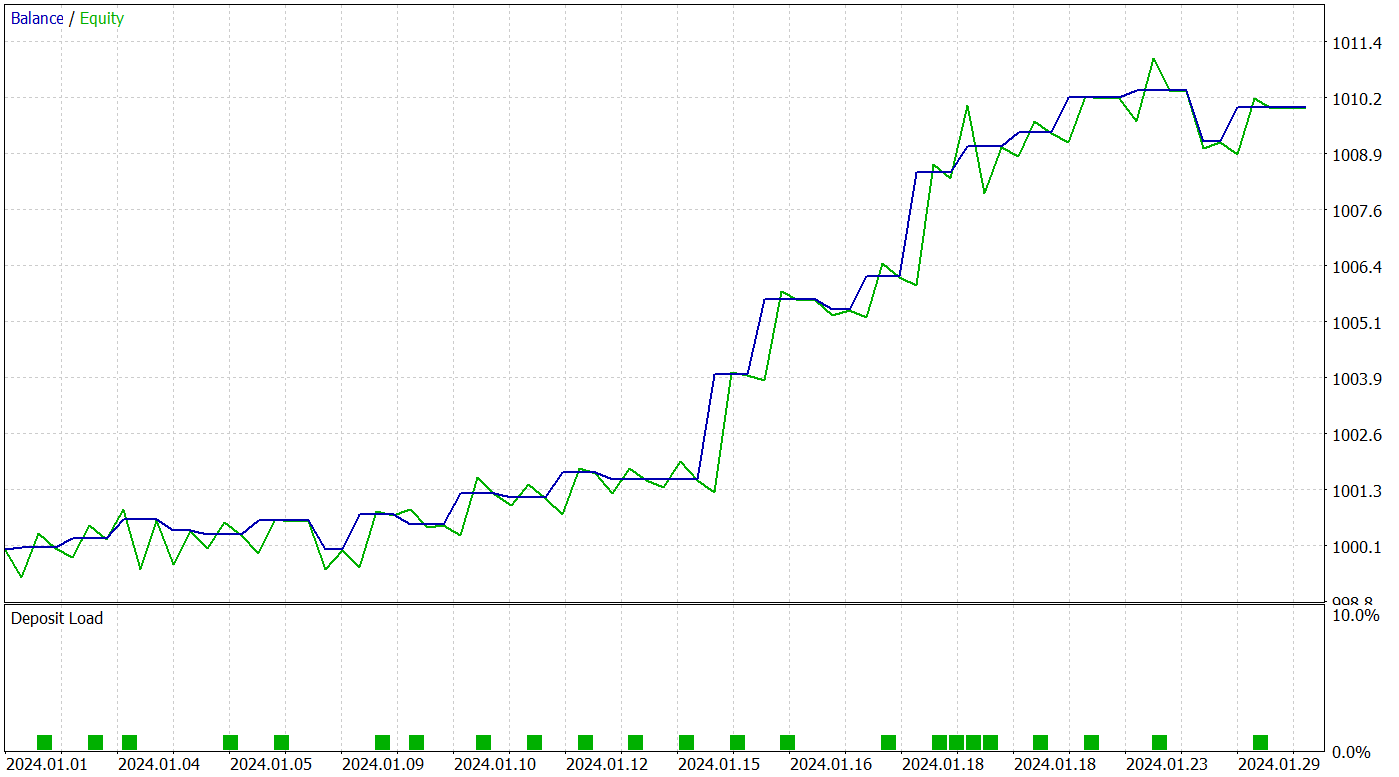
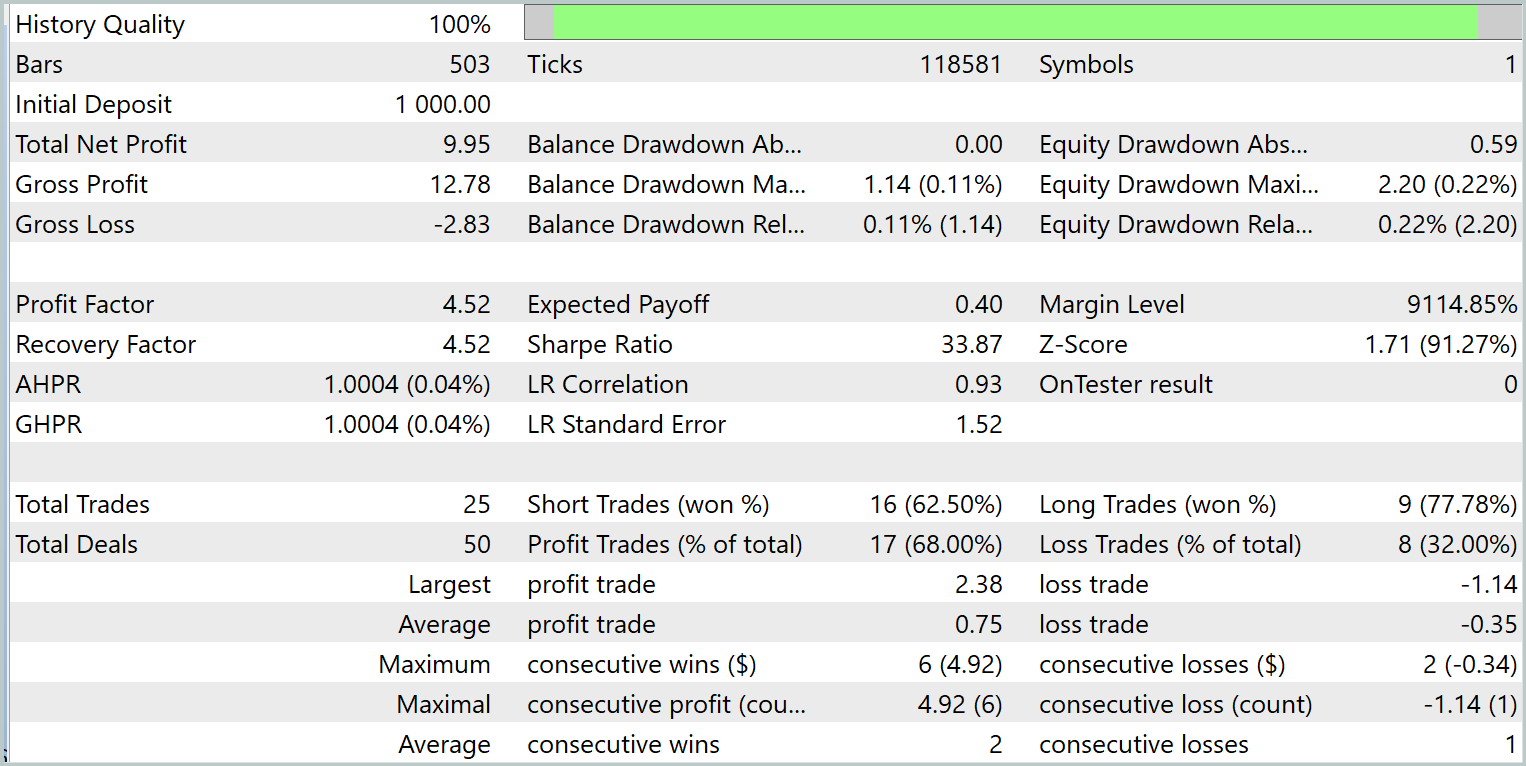
Das trainierte Modell führte während des Testzeitraums 25 Handelsgeschäfte aus, von denen 17 mit Gewinn abgeschlossen wurden. Dies entspricht 68 % der Gesamtzahl. Außerdem sind die durchschnittlichen und maximalen Gewinne doppelt so hoch wie die entsprechenden Verluste.

Das Potenzial des vorgeschlagenen Modells wird auch durch die Aktienkurve bestätigt, die einen deutlichen Aufwärtstrend aufweist. Aufgrund des kurzen Testzeitraums und der begrenzten Anzahl von Handelsgeschäften deutet dieses Ergebnis jedoch nur auf ein Potenzial hin.

Schlussfolgerung

Die Methode Molformer stellt einen bedeutenden Fortschritt auf dem Gebiet der Marktdatenanalyse und -prognose dar. Durch die Verwendung heterogener Marktgraphen, die sowohl einzelne Vermögenswerte als auch deren Kombinationen in Form von Marktmustern umfassen, ist das Modell in der Lage, komplexere Beziehungen und Datenstrukturen zu berücksichtigen, was die Genauigkeit der Vorhersage künftiger Preisbewegungen erheblich verbessert.

Im praktischen Teil des Artikels haben wir unsere Vision der Molformer-Ansätze mit MQL5 umgesetzt. Wir haben die vorgeschlagenen Lösungen in das Modell integriert und es mit realen historischen Daten trainiert. Als Ergebnis haben wir ein Modell geschaffen, das in der Lage ist, das erworbene Wissen auf neue Marktsituationen zu verallgemeinern und Gewinne zu erzielen. Dies wird durch die Testergebnisse bestätigt. Wir sind davon überzeugt, dass der vorgeschlagene Ansatz die Grundlage für weitere Forschungen und Anwendungen im Bereich der Finanzanalyse bilden kann, indem er Händlern und Analysten neue Instrumente für fundierte Entscheidungen unter unsicheren Bedingungen an die Hand gibt.

Referenzen

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	EA zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16130

Beigefügte Dateien |

ZIP herunterladen

MQL5.zip (2001.44 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Letzte Kommentare | Zur Diskussion im Händlerforum (1)

Rezus666 | 22 Okt. 2024 in 12:41

Guten Tag, ich kann keine Orders vom test.mq5 Expert Advisor erhalten.

if(temp[0] >= temp[3])
     {
      temp[0] -= temp[3];
      temp[3] = 0;
     }
   else
     {
      temp[3] -= temp[0];
      temp[0] = 0;
     }
//--- Kontrolle kaufen
   if(temp[0] < min_lot || (temp[1] * MaxTP * Symb.Point()) <= 2 * stops || (temp[2] * MaxSL * Symb.Point()) <= stops)
     {
     ...
     }
   else
     {
      ...
     }
//--- Kontrolle verkaufen
   if(temp[3] < min_lot || (temp[4] * MaxTP * Symb.Point()) <= 2 * stops || (temp[5] * MaxSL * Symb.Point()) <= stops)
     {
...
     }
   else...

Die Sache ist, dass die Array-Elemente temp[0] und temp[3] sind immer kleiner als min_lot, wo kann mein Fehler sein?

Von der Grundstufe bis zur Mittelstufe: Array (III)

In diesem Artikel werden wir uns ansehen, wie man mit Arrays in MQL5 arbeitet, einschließlich der Übergabe von Informationen zwischen Funktionen und Prozeduren unter Verwendung von Arrays. Der Zweck ist, Sie auf das vorzubereiten, was in den zukünftigen Materialien der Reihe gezeigt und erklärt werden wird. Daher empfehle ich Ihnen dringend, die in diesem Artikel enthaltenen Informationen sorgfältig zu studieren.

Entwicklung eines Replay-Systems (Teil 70): Das richtige Bestimmen der Zeit (III)

In diesem Artikel erfahren Sie, wie Sie die Funktion CustomBookAdd richtig und effektiv nutzen können. Trotz ihrer scheinbaren Einfachheit hat sie viele Nuancen. So können Sie dem Mauszeiger beispielsweise mitteilen, ob ein nutzerdefiniertes Symbol gerade versteigert oder gehandelt wird oder ob der Markt geschlossen ist. Der hier dargestellte Inhalt ist ausschließlich für Bildungszwecke bestimmt. Die Anwendung sollte unter keinen Umständen zu einem anderen Zweck als zum Erlernen und Beherrschen der vorgestellten Konzepte verwendet werden.

Entwicklung eines Replay-Systems (Teil 71): Das richtige Bestimmen der Zeit (IV)

In diesem Artikel werden wir uns ansehen, wie man das, was im vorigen Artikel über unseren Wiedergabe-/Simulationsdienst gezeigt wurde, implementiert. Wie bei vielen anderen Dingen im Leben sind auch hier Probleme vorprogrammiert. Und dieser Fall war keine Ausnahme. In diesem Artikel werden wir die Dinge weiter verbessern. Der hier dargestellte Inhalt ist ausschließlich für Bildungszwecke bestimmt. Die Anwendung sollte unter keinen Umständen zu einem anderen Zweck als zum Erlernen und Beherrschen der vorgestellten Konzepte verwendet werden.

Von der Grundstufe bis zur Mittelstufe: Array (II)

In diesem Artikel werden wir uns ansehen, was ein dynamisches Array und ein statisches Array sind. Gibt es einen Unterschied zwischen der Verwendung des einen oder des anderen? Oder ist es doch dasselbe? Wann sollten Sie den einen und wann den anderen Typ verwenden? Und was ist mit konstanten Arrays? Wir werden versuchen zu verstehen, wofür sie gedacht sind, und die Risiken berücksichtigen, die entstehen, wenn nicht alle Werte im Array initialisiert werden.