Эконометрический подход к поиску рыночных закономерностей: автокорреляция, тепловые карты и диаграммы рассеяния
Краткий обзор предыдущего материала и предпосылки создания новой модели
В первой статье мы познакомились с понятием "память рынка", которая определяется как долгосрочная зависимость ценовых приращений некоторого порядка. Дальше было разобрано понятие " сезонных закономерностей", которые, в том или ином виде, присутствуют на рынках. До текущего момента два этих понятия существовали как бы по отдельности и нигде не пересекались. Целью текущей статьи является показать, что "память рынка" имеет сезонный характер, который выражается через максимизацию корреляции приращений произвольного порядка для близких временных интервалов — и минимизацию корреляции для отдаленных друг от друга временных интервалов, соответственно.
Давайте выдвинем гипотезу, которая будет звучать, примерно, следующим образом:
Корреляция ценовых приращений происходит от наличия сезонных закономерностей, а также от кластеризации близлежащих приращений.
Смелая гипотеза, давайте пройдем через все этапы её подтверждения либо опровержения в свободном интуитивном и немного математическом стиле.
Классический эконометрический подход к выявлению закономерностей в ценовых приращениях это автокорреляция
Классический подход предполагает, что отсутствие закономерностей в приращениях цен определяется через отсутствие серийной корреляции. В случае отсутствия автокорреляции ряд приращений полагается случайным, а дальнейший поиск закономерностей неэффективным.
Проиллюстрируем это на примере визуального анализа автокорреляционной функции приращений валютной пары EURUSD. Для экспериментов будем использовать IPython.
def standard_autocorrelation(symbol, lag):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
standard_autocorrelation('EURUSD', 50)
Данная функция преобразует часовые цены закрытия в их разницы, с заданным периодом (используем лаг 50) и отображает график автокорреляции.
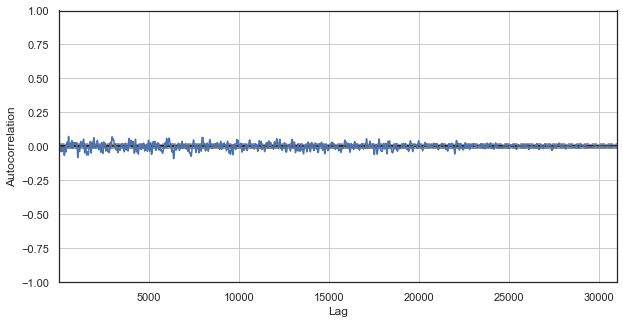
Рис. 1. классическая коррелограмма ценовых приращений
График автокорреляции не выявляет никаких закономерностей в ценовых приращениях. Корреляции между соседними приращениями колеблются вокруг нуля, что подразумевает случайность временного ряда. На этом эконометрический анализ мог бы закончиться и мы гордо могли бы заметить, что рынок случаен. Однако, я предлагаю взглянуть на АКФ под другим углом — в контексте сезонных закономерностей.
Поскольку я предположил, что корреляция ценовых приращений генерируется наличием сезонных закономерностей, то для чистоты эксперимента давайте исключим из ряда все часы, кроме конкретного. Таким образом, мы создадим новый временной ряд, который будет обладать своими особыми свойствами. Построим для него АКФ:
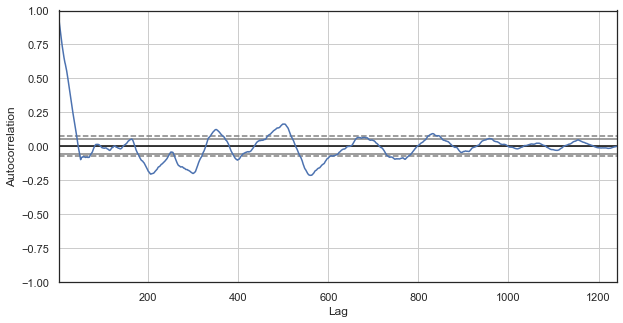
Рис. 2. коррелограмма ценовых приращений с исключенными часами (оставлен только 1-й час для каждых суток)
Для нового ряда коррелограмма выглядит более интересно. Наблюдается сильная зависимость текущих приращений от предыдущих, которая спадает с увеличением временной дельты между приращениями. Таким образом, приращения первого часа текущего дня сильно коррелирует с приращением первого часа предыдущего дня и так далее, по убывающей. Это очень важная информация, которая говорит о существовании сезонных закономерностей — приращения явно имеют память.
Кастомный подход к выявлению закономерностей в ценовых приращениях это сезонная автокорреляция
Я должен был достаточно убедить вас в наличии сезонных закономерностей, а именно в корреляции приращений первого часа текущего дня и первого часа предыдущих дней, которая уменьшается при увеличении дельты (расстояния в днях). Теперь давайте посмотрим, существует ли зависимость между рядом стоящими часами, для этого немного модифицируем код:
def seasonal_autocorrelation(symbol, lag, hour1, hour2):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
seasonal_autocorrelation('EURUSD', 50, 1, 2)
Здесь мы удалим из котировок все часы, кроме первого и второго, а затем получим разницы для нового ряда и построим АКФ:
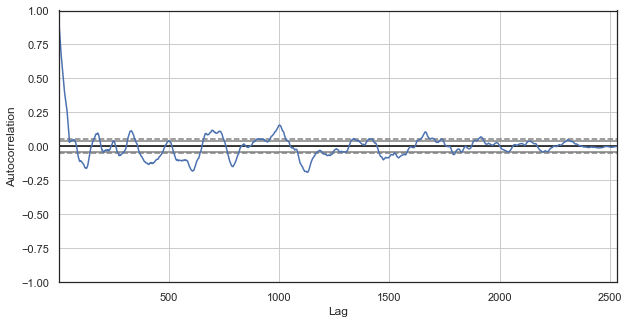
Рис. 3. коррелограмма ценовых приращений с исключенными часами (оставлены только 1 и 2 часы для каждых суток)
Очевидно, что высокая корреляция наблюдается также и для ряда, составленного из ближайших часов, что говорит об их зависимости и взаимовлиянии. Но что, если мы хотим получить достоверную относительную оценку для всех пар часов, а не только для выбранных? Для этого воспользуемся техникой, которая будет изложена ниже.
Тепловая карта сезонных корреляций для всех часов
Продолжаем исследовать рынок в надежде подтвердить изначальную гипотезу. Давайте посмотрим на полную картину. Представленная ниже функция последовательно удаляет часы из временного ряда, оставляя только один час, строит разницу цен для этого ряда и определяет корреляцию с рядами, построенными для других часов:
#calculate correlation heatmap between all hours def correlation_heatmap(symbol, lag, corrthresh): out = pd.DataFrame() rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') for i in range(24): ratesH = None ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna() out[str(i)] = ratesH['close'].reset_index(drop=True) plt.figure(figsize=(10, 10)) corr = out.corr() # Generate a mask for the upper triangle mask = np.zeros_like(corr, dtype=np.bool) mask[np.triu_indices_from(mask)] = True sns.heatmap(corr[corr >= corrthresh], mask=mask) return out out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)
Функция принимает порядок приращений (временной лаг), а также порог корреляции для отсева часов с низкой корреляцией. Посмотрим что получается:

Рис. 4. Тепловая карта корреляций между приращениями для разных часов за период 2015-20гг.
Хорошо заметны кластеры 0-5 и 10-14 часов, где корреляция максимальна. Вспомним, что в предыдущей статье была построена торговая система именно по первому кластеру, который был обнаружен другим способом (при помощи ящиков с усами), а теперь закономерности видны и на тепловой карте. Давайте теперь возьмем второй интересный кластер и дальнейшие манипуляции будем проводить с ним. Например, можно посмотреть сводную статистику по кластеру:
out[['10','11','12','13','14']].describe()
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 |
| mean | -0.001016 | -0.001015 | -0.001005 | -0.000992 | -0.000999 |
| std | 0.024613 | 0.024640 | 0.024578 | 0.024578 | 0.024511 |
| min | -0.082850 | -0.084550 | -0.086880 | -0.087510 | -0.087350 |
| 25% | -0.014970 | -0.015160 | -0.014660 | -0.014850 | -0.014820 |
| 50% | -0.000900 | -0.000860 | -0.001210 | -0.001350 | -0.001280 |
| 75% | 0.013460 | 0.013690 | 0.013760 | 0.014030 | 0.013690 |
| max | 0.082550 | 0.082920 | 0.085830 | 0.089030 | 0.086260 |
Параметры для всех часов кластера довольно близкие, но, что интересно, для исследуемой выборки их среднее отрицательно (в районе 100 пятизначных пунктов). Смещение среднего приращений говорит о большей вероятности снижения рынка в эти часы, нежели роста. Дополнительно стоит отметить, что увеличение лага приращений приводит к большей корреляции между часами из-за появления трендовой составляющей, тогда как уменьшение лага приводит к занижению показателей. Относительное расположение кластеров при этом остается практически неизменным.
Например, для единичного лага приращения 12, 13 и 14 часов по-прежнему сильно коррелируют:
plt.figure(figsize=(10,5)) plt.plot(out[['12','13','14']]) plt.legend(out[['12','13','14']]) plt.show()
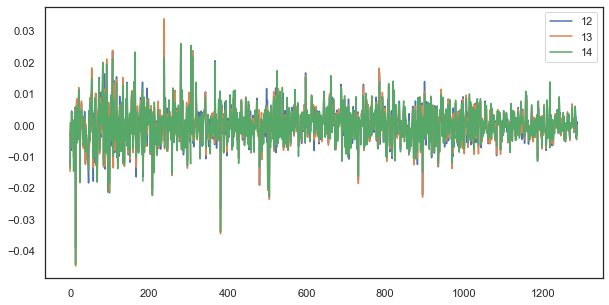
Рис. 5. Визуальное сходство рядов приращений с единичным лагом, составленных из разных часов суток
Формула закономерности: просто и со вкусом
Вспомним нашу гипотезу:
Корреляция ценовых приращений происходит от наличия сезонных закономерностей, а также от кластеризации близлежащих приращений.
На диаграмме АКФ и на тепловой карте я показал, что существует зависимость почасовых приращений как от их прошлых значений, так и от значений приращений близлежащих часов. Первое явление происходит от повторяемости событий в определенные часы суток, второе от кластеризации волатильности в некоторые периоды времени. Оба этих явления следует рассмотреть отдельно и, по возможности объединить. В данной статье мы проведем дополнительное исследование зависимости приращений конкретного часа (с удалением всех остальных часов из временного ряда) от их предыдущих значений, а самое "вкусное" оставим для следующей статьи.
# calculate joinplot between real an predicted returns def hourly_signals_statistics(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') # price differenсes for every hour series H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna() H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna() # current returns for both hours HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True) # previous returns for both hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1]) # or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) predicted = HF-(HF2-HL2) real = HL # correlation joinplot between two series outcorr = pd.DataFrame() outcorr['Hour ' + str(hour)] = H['close'] outcorr['Hour ' + str(hour2)] = H2['close'] # real VS predicted prices out = pd.DataFrame() out['real'] = real['close'] out['predicted'] = predicted['close'] out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))] # plptting results from scipy import stats sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)
Следует пояснить манипуляции с данными из предложенного выше листинга. Берется два ряда, сформированных прореживанием (отсеиванием лишних часов) и строятся приращения цен (их разницы). Часы для рядов определяются в параметрах "hour" и "hour2". Затем получаем последовательности с лагом 1 для каждого часа, иными словами, " HF" ряд опережает "HL" ряд на одно значение, что нужно для расчета фактического приращения и прогнозируемого приращения, а также их разницы. Сначала построим диаграмму рассеяния для приращений первого и второго часов:
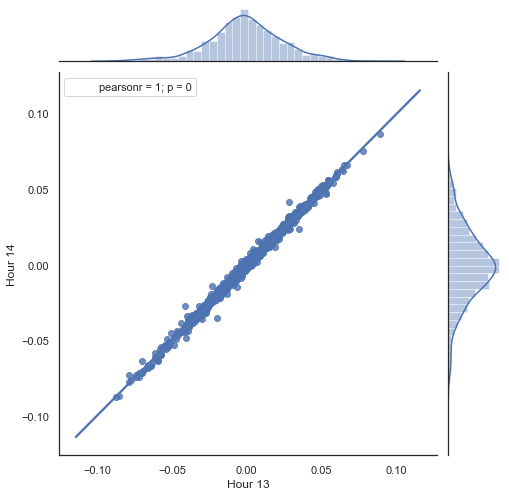
Рис. 5. диаграмма рассеяния для приращений 13 и 14 часов за период 2015-20гг.
Как и ожидалось, приращения сильно коррелируют. Теперь попробуем спрогнозировать следующее приращение на основе предыдущего. Для этого выведем простую формулу, которая будет прогнозировать следующее приращение:
Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1]))
Поясню полученную формулу. Для предсказания будущего приращения мы находимся на нулевом баре, соответственно, предсказываем значение следующего приращения ret[-1]. Для этого необходимо вычесть из текущего приращения разницу предыдущего (с отступом lag) и следующего за ним (lag-1) приращений. При условии, что корреляция приращений между двумя соседними часами высока, можно ожидать, что прогнозируемое приращение будет описываться данным уравнением. Ниже просто раскрытие уравнения для цен закрытия. В итоге в прогнозе будущего приращения участвуют всего 3 приращения. Вторая часть кода из предложенного листинга как раз прогнозирует будущие приращения по формуле и сравнивает их с фактическими. Проиллюстрируем на диаграмме:
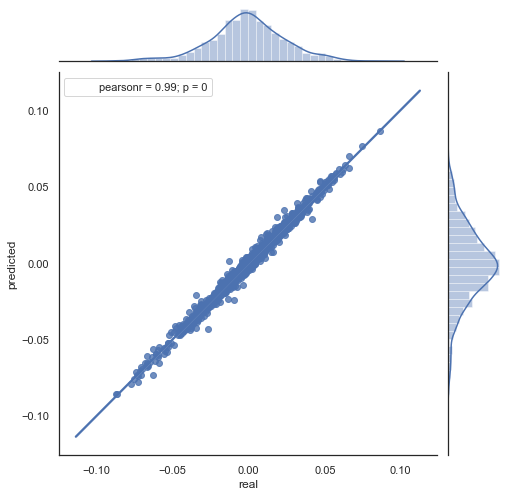
Рис. 6. диаграмма рассеяния для фактических и предсказанных приращений за период 2015-20гг.
Хорошо видно, что графики на рис. 5,6 похожи. Это говорит о том, что метод определения закономерностей через корреляцию прошел проверку и является адекватным. В то же время на диаграмме виден разброс значений, они не лежат на одной линии. Это является ошибками прогноза, которые будут негативно влиять на прогноз и с ними следует работать отдельно (что выходит за рамки данной статьи). Кроме того, прогноз в окрестностях нуля нам мало интересен, поскольку если прогноз приращения следующей цены равен текущей, то на этом заработать нельзя. Можно отфильтровать прогнозы при помощи параметра rfilter.
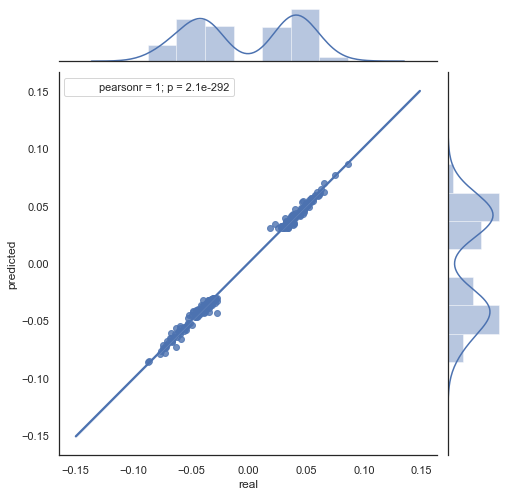
Рис. 7. диаграмма рассеяния для фактических и предсказанных приращений c rfilter = 0.03 за период 2015-20гг.
Стоит отметить, что приведенная тепловая карта строилась за период с 2015 года по сей день. Давайте отмотаем на 15 лет назад и посмотрим кусок с 2000 года по текущий момент:
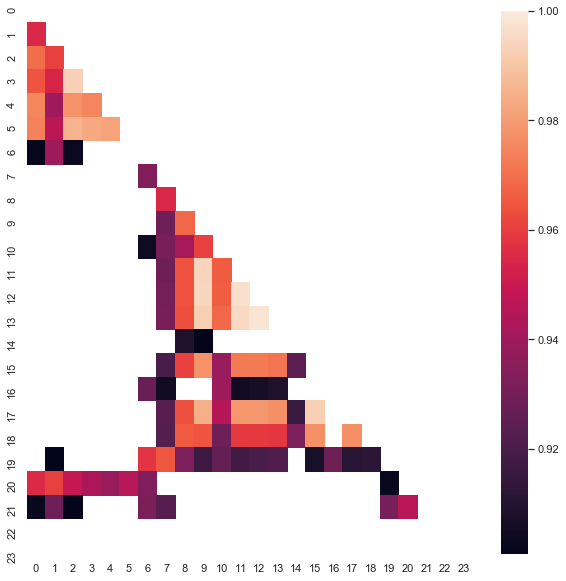
Рис. 8. Тепловая карта корреляций между приращениями для разных часов с 2000 по 2020гг.
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 |
| mean | 0.000470 | 0.000470 | 0.000472 | 0.000472 | 0.000478 |
| std | 0.037784 | 0.037774 | 0.037732 | 0.037693 | 0.037699 |
| min | -0.221500 | -0.227600 | -0.222600 | -0.221100 | -0.216100 |
| 25% | -0.020500 | -0.020705 | -0.020800 | -0.020655 | -0.020600 |
| 50% | 0.000100 | 0.000100 | 0.000150 | 0.000100 | 0.000250 |
| 75% | 0.023500 | 0.023215 | 0.023500 | 0.023570 | 0.023420 |
| max | 0.213700 | 0.212200 | 0.210700 | 0.212600 | 0.208800 |
Видно, что тепловая карта несколько поредела, зависимость между 13 и 14 часами снизилась. В то же время среднее приращений стало положительным, что, вообще-то, дает приоритет покупкам вместо продаж. Смещение среднего не позволит эффективно торговать на обоих временных промежутках, придется выбирать.
Посмотрим на получившуюся диаграмму рассеяния за этот период (я ограничусь только графиком факт\прогноз):

Рис. 9. диаграмма рассеяния для фактических и предсказанных приращений c rfilter = 0.03 за период 2000 - 2020гг.
Разброс значений увеличился, что говорит не в пользу положительного результата на таком длительном периоде.
Таким образом, получена формула и примерное представление о распределении фактических и предсказанных приращений для конкретных часов. Для большей наглядности, можно визуализировать зависимости в 3D.
# calculate joinplot between real an predicted returns def hourly_signals_statistics3D(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') rates = pd.DataFrame(rates['close'].diff(lag)).dropna() out = pd.DataFrame(); for i in range(hour, hour2): H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None; H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True) H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True) HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True); # current hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # last day hours predicted = HF-(HF2-HL2) real = HL out3D = pd.DataFrame() out3D['real'] = real['close'] out3D['predicted'] = predicted['close'] out3D['predictedABS'] = predicted['close'].abs() out3D['hour'] = i out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))] out = out.append(out3D) import plotly.express as px fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000) fig.show() hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)
В данной функции для расчета прогнозируемого и фактического значений используется уже известная формула. Каждая отдельная диаграмма рассеяния показывает зависимость факт\прогноз для каждого часа, если бы сигнал брался с приращения десятого часа предыдущего дня. Для примера, я взял все часы с 10.00 до 23.00. Видно, что корреляция с ближайшими часами максимальна, а с отдаленными снижается (диаграммы рассеяния становятся больше похожи на окружности). Начиная с 16 часа следующие часы текущего дня уже мало зависят от 10-го часа предыдущего дня. В приложении к статье вы можете поворачивать 3D объект и выделять интересующие фрагменты, для получения более подробной информации.
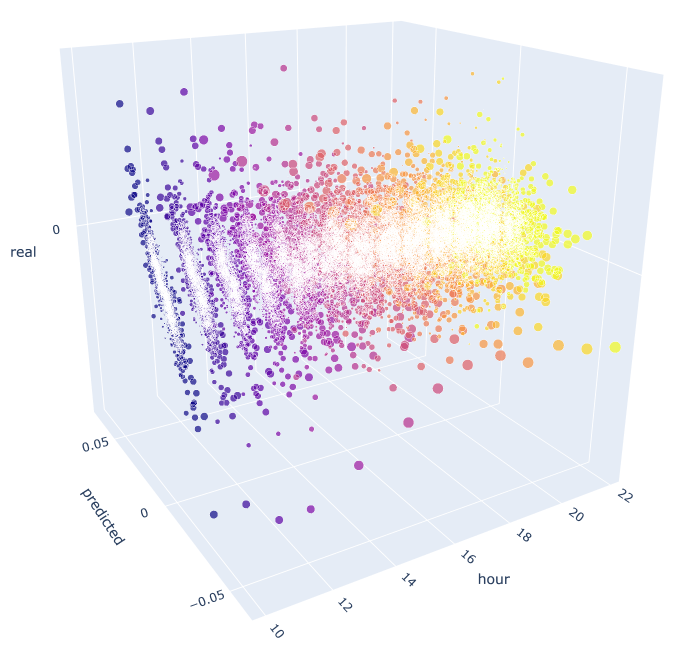
Рис. 10. 3D диаграмма рассеяния для фактических и предсказанных приращений c 2015 по 2020гг.
Осталось написать эксперта и посмотреть как это работает.
Пример эксперта, который торгует найденные сезонные зависимости
По аналогии с примером из предыдущей статьи, данный робот будет торговать сезонную закономерность, основанную только на статистической взаимосвязи текущего и предыдущего приращений по одному конкретному часу. Отличаться он будет тем, что торгуются другие часы и по другому принципу — на основе предложенной формулы.
Предлагаю рассмотреть пример использования полученной формулы для торговли, на основе проведенного статистического исследования:
input int OpenThreshold = 30; //Open threshold input int OpenThreshold1 = 30; //Open threshold 1 input int OpenThreshold2 = 30; //Open threshold 2 input int OpenThreshold3 = 30; //Open threshold 3 input int OpenThreshold4 = 30; //Open threshold 4 input int Lag = 10; input int stoploss = 150; //Stop loss input int OrderMagic = 666; //Orders magic input double MaximumRisk=0.01; //Maximum risk input double CustomLot=0; //Custom lot
Поскольку был определен интервал с закономерностями {10, 11, 12, 13, 14} часов включительно, можно задать параметр "Open threshold" для каждого часа отдельно. Эти параметры эквивалентны параметру "rfilter" на рис. 9. В переменной "Lag" содержится значение лага для приращений (вспомним, что, по умолчанию, мы анализировали лаг 25, т.е. почти сутки для часового таймфрейма). Можно было бы задать лаги для каждого часа отдельно, но для простоты изложения материала оставим его одинаковым для всех часов. Размер стоплосса я оставлю одинаковым для всех позиций. Все эти параметры можно оптимизировать, чем и займемся далее.
Сама торговая логика будет выглядеть следующим образом:
void OnTick() { //--- if(!isNewBar()) return; CopyClose(NULL, 0, 0, Lag*2+1, prArr); ArraySetAsSeries(prArr, true); const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1])); TimeToStruct(TimeCurrent(), hours); if(hours.hour >=10 && hours.hour <=14) { //if(countOrders(0)==0) // if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) // OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN); if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) { if(pr <= -signal && hours.hour==10) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic); if(pr <= -signal1 && hours.hour==11) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic); if(pr <= -signal2 && hours.hour==12) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic); if(pr <= -signal3 && hours.hour==13) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic); if(pr <= -signal4 && hours.hour==14) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic); } } }
Константа "pr" вычисляется по формуле, указанной выше. Эта формула прогнозирует приращение цены на следующем баре. Далее проверяется условие для каждого часа, и если приращение удовлетворяет минимальному порогу для конкретного часа, то открывается сделка на продажу. Хочу напомнить, что смещение среднего приращений в отрицательную зону делают неэффективными покупки на интервале с 2015 по 2020 год, вы можете самостоятельно это проверить.
Запустим генетическую оптимизацию с параметрами, указанными на рис. 11 и посмотрим на результат:
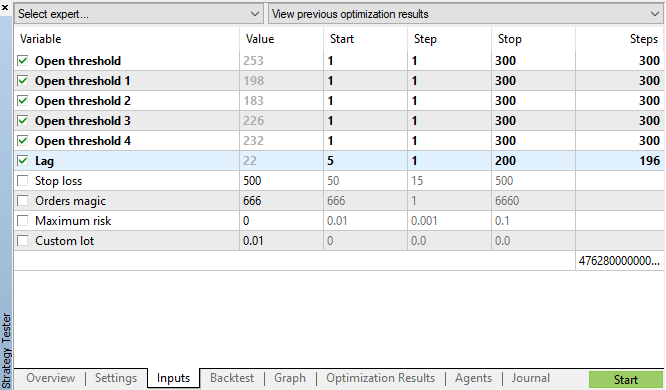
Рис. 11. таблица параметров генетической оптимизации
Посмотрим на график оптимизации. На оптимизируемом интервале наиболее эффективные значения "Lag" расположены на интервале 17-30 часов, что очень близко к нашему предположению о зависимости приращений конкретного часа текущего дня от того же часа предыдущего дня:
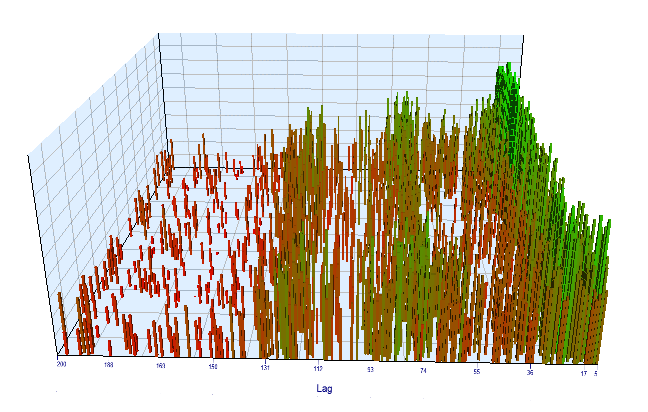
Рис 12. отношение переменной "Lag" к переменной "Order threshold" на оптимизируемом интервале
На форварде график выглядит аналогичным образом:
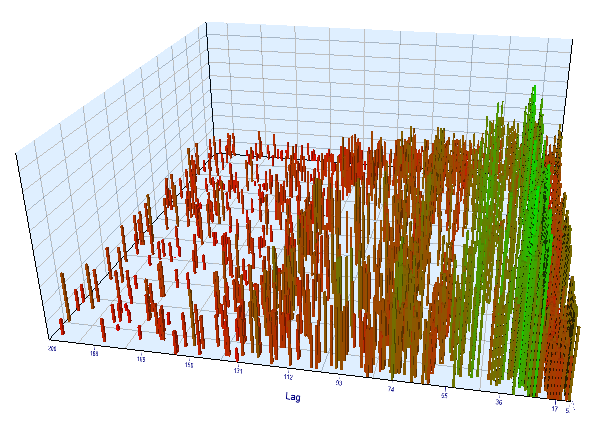
Рис 13. отношение переменной "Lag" к переменной "Order threshold" на форвард интервале
Давайте посмотрим на лучшие результаты из таблиц оптимизации бэктест и форвард:
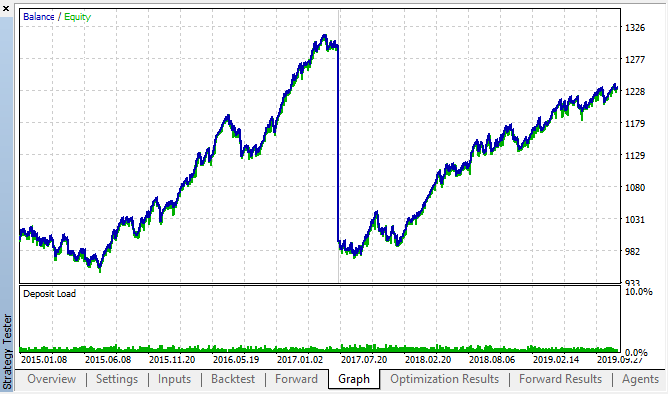
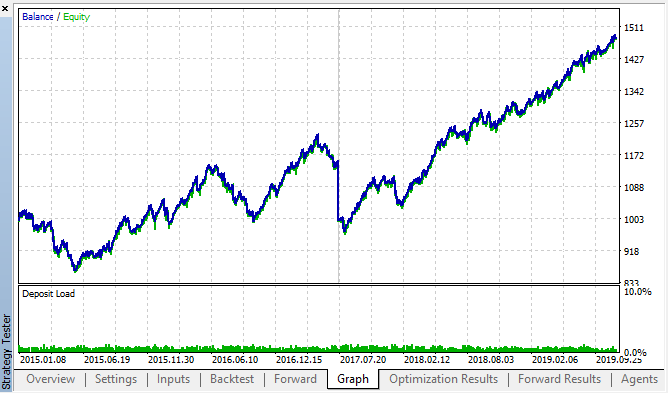
Рис 14, 15. графики бэктест и форвард оптимизаций.
Видно, что закономерность сохраняется на всем интервале 2015-2020гг. Можно считать, что наш эконометрический подход сработал на отлично. Мы увидели, что существуют зависимости между приращениями одних и тех же часов для ближайших дней недели, с некоторой кластеризацией (зависимость может быть не с тем же часом, но с близким к нему). Как использовать вторую закономерность вы узнаете в следующей статье.
Проверка периода приращений на другом таймфрейме
Давайте проведем дополнительную проверку на М15 таймфрейме. Предположим, что мы ищем всю ту же взаимосвязь текущего часа от того же часа предыдущего дня. В этом случае эффективный лаг должен быть в 4 раза больше и составлять, примерно, 24*4 = 96, поскольку в каждом часе 4 15-и минутки. Я оптимизировал советника с теми же настройками, изменив таймфрейм на М15.
На оптимизируемом участке эффективный лаг приращений получился <60, что странно. Вероятно, оптимизатор уловил другую закономерность, либо произошла переоптимизация.
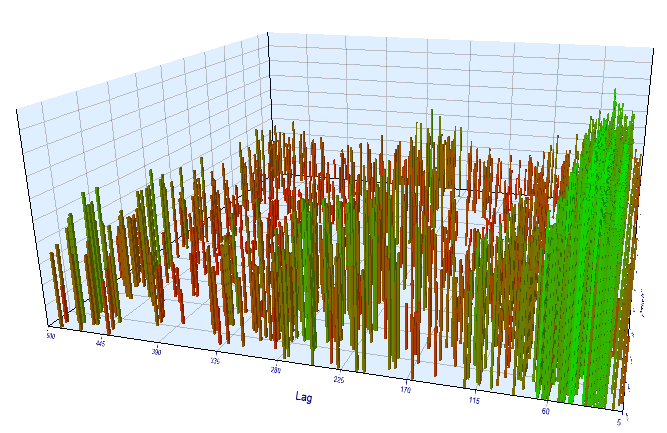
Рис 16. отношение переменной "Lag" к переменной "Order threshold" на оптимизируемом интервале
Давайте посмотрим результаты на форварде. Любопытно, что здесь все в порядке, эффективный лаг примерно соответствует 100, что подтверждает закономерность.
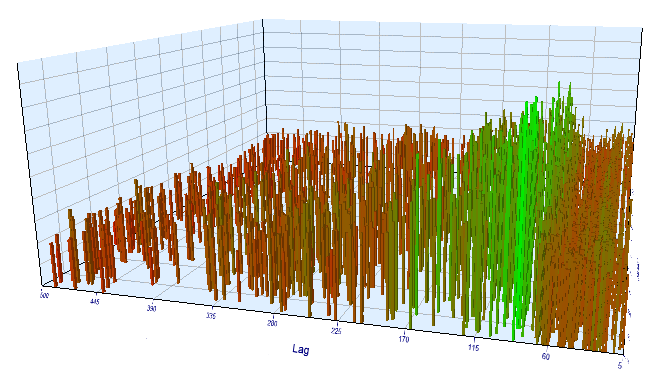
Рис 17. отношение переменной "Lag" к переменной "Order threshold" на форвард интервале
Посмотрим на лучшие бэк\форвард результаты:
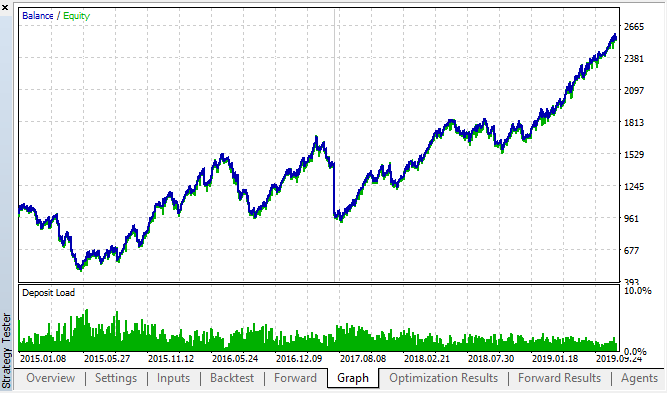
Рис 18. бэктест и форвард, лучший форвард проход
Кривая получилась похожей на кривую с H1 графика, при значительном увеличении количества сделок. Стоит полагать, что данную стратегию можно оптимизировать и для более "мелких" таймфреймов.
Заключение
В данной статье мы выдвинули следующую гипотезу:
Корреляция ценовых приращений происходит от наличия сезонных закономерностей, а также от кластеризации близлежащих приращений.
Мы полностью подтвердили первую часть, а именно: существуют зависимости между часовыми приращениями, взятыми за разные дни недели. Также мы неявно подтвердили второе утверждение: зависимость имеет кластеризацию и значения приращений текущих часов зависят еще и от значений приращений соседних часов.
Стоит заметить, что предложенный советник ни в коем случае не является единственно возможным вариантом торговли по найденным зависимостям. Предложенная логика отражает взгляд автора на зависимости, а оптимизация советника проводилась только для дополнительного подтверждения закономерностей, найденных посредством статистического исследования.
Поскольку вторая часть доказательства требует дополнительных существенных исследований, то в следующей статье мы применим простую модель машинного обучения для окончательного подтверждения либо опровержения второй части гипотезы.
В приложении находится готовый фреймворк в формате Jupyter notebook для самостоятельного исследования других финансовых инструментов, результаты исследований можно перепроверить приложенным тестовым советником.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети - это просто
Нейросети - это просто
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Большое спасибо за передачу такой ценной информации.
Читая такие статьи, хочется экспериментировать.
Спасибо за ваш отзыв.
Я советую вам читать его с оригинальной статьи, если вы хотите, чтобы вас читали. Не беспокойтесь о языке, инструмент перевода сделает свое дело.
https://www.mql5.com/ru/forum/330111
Спасибо.
Добрый день! Поясните, пожалуйста, про построение тепловой карты:
Мы берем приращения от часа одного дня до часа другого дня таким образом:
Если потом функция вызывается со значением лага 25, то мы в rateH получаем разницу не соседних суток, а 25 дней между сутками, потому что до этого мы выкинули все часы, не совпадающие с i, и получили ряд вида 2020-01-01 00:00:00|90, 2020-01-02 00:00:00|87, 2020-01-03 00:00:00|88, и потом если применить на него лаг 25 и посчитать дифф, а потом выкинуть na - получим ряд 2020-01-25 00:00:00|1, 2020-01-26 00:00:00|3, 2020-01-27 00:00:00|-2 - и так для каждого часа. В итоге что за тепловую карту мы построили?
Возможно, я где-то запуталась, помогите распутаться, пожалуйста.
Oi
Vi que você entende bem de cointegração
Хочу спросить, знаете ли вы, существует ли этот индикатор в mql5, или кто создал базу для него.
att
Cássio