Исследование сезонных характеристик финансовых временных рядов при помощи диаграмм Boxplot

Попытка опровержения гипотезы эффективного рынка и доказательства наличия рыночных циклов

В 2013 году Юджин Фама, разработавший гипотезу эффективного рынка, стал лауреатом Нобелевской премии по экономике. Его гипотеза подразумевает, что вся существенная информация сразу и полностью отражается на рынках ценных бумаг. В этом случае ни один из участников рынка не имеет преимуществ над другими. 

Впрочем, эта гипотеза имеет некоторые оговорки, а эффективность может принимать три степени:

• слабая, если стоимость рыночного актива полностью отражает прошлую информацию, касающуюся этого актива;
• средняя, отражает не только прошлую, но и текущую публичную информацию;
• сильная, отражает также не публичную инсайдерскую информацию.

В зависимости от степени эффективности рынки обладают различной степенью предсказуемости. Для технического аналитика это означает, что на рынке могут присутствовать циклические сезонные компоненты различной природы.

Например, активность рынка может изменяться от года к году, от месяца к месяцу, от торговой сессии к торговой сессии, от часа к часу и так далее. Более того, эти циклы, например, могут представлять из себя некоторые прогнозируемые последовательности, внутри и между которыми трейдер может найти свою альфу. Также, циклы могут накладываться друг на друга, создавая различные композиции паттернов, которые необходимо исследовать. 

Поиск сезонных закономерностей в ценовых приращениях

Мы можем исследовать как регулярные, так и составные циклы. Давайте рассмотрим пример анализа месячных колебаний какого-нибудь финансового инструмента. Для этого, используем язык IPython в связке с терминалом MetaTrader5.

Для того, что бы легко импортировать котировки прямо из терминала, используем следующий код:

from MetaTrader5 import *
from datetime import datetime
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
%matplotlib inline
import seaborn; seaborn.set()
# Initializing MT5 connection 
MT5Initialize("C:\\Program Files\\MetaTrader 5\\terminal64.exe")
MT5WaitForTerminal()

print(MT5TerminalInfo())
print(MT5Version())

Здесь необходимо указать путь до вашего терминала, потому что он может отличаться от моего.

Наберем еще несколько строк, чтобы сразу же окунуться в анализ данных:

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)

Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))

Переменная rates принимает pandas-датафрейм с ценами за указанный интервал времени (например, 10 лет, как в данном примере). Допустим, нас интересуют только цены закрытия (для простоты интерпретации), поэтому удалим лишние столбцы данных при помощи метода rates.drop().

Поскольку цены имеют смещение среднего во времени и образуют тренды, статистический анализ неприменим к таким сырым рядам. В эконометрике используются процентные изменения цен (ценовые приращения) для того, чтобы все они лежали примерно в одном диапазоне значений. Получим процентные изменения через метод  pd.DataFrame(rates['close'].pct_change(1)).

Нас интересуют средние диапазоны цен по месяцам. Сгруппируем таблицу таким образом, что бы получить среднее месячных приращений по годам и отобразим на графике boxplot (ящиков с усами).

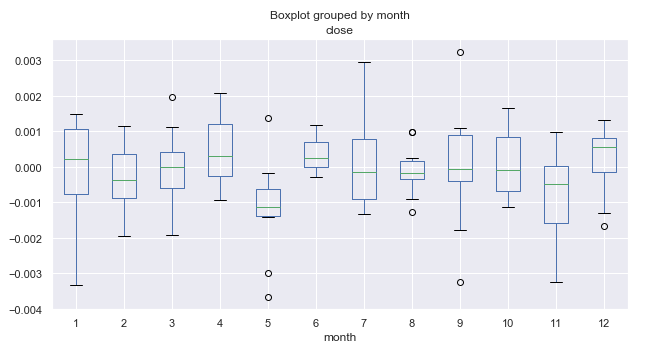
Рис. 1. Средние диапазоны ценовых приращений по месяцам, за десять лет.

Что такое boxplots (ящики с усами), и как их правильно интерпретировать

Нам необходимо иметь информацию об изменчивости или разбросе ценовых данных за какой-то период. Каждый отдельный ящик с усами дает хорошее представление о том, как распределены значения в наборе данных. Boxplots не следует путать с графиком японских свечей, хотя они визуально похожи. В отличие от свечей, это стандартизированный способ отображения распределения данных на основе пяти показаний.

1. Медиана, Q2 или 50-й перцентиль — показывает среднее значение набора данных. На графике отмечен зелеными горизонтальными линиями внутри ящиков.
2. Первый квартиль Q1 (или 25-й перцентиль) представляет собой медиану между Q2 и наименьшим значением выборки, попавшим в 99% доверительный интервал. На графике обозначен нижней границей "тела" ящика.
3. Третий квартиль Q3 (или 75-й перцентиль) является медианой между Q2 и максимальным значением, показан как верхняя граница "тела" ящика.
4. Тело ящика образует межквартильный размах (между 25 и 75 перцентилями), также называемый IQR.
5. Усы ящиков дополняют распределение, охватывая 99% дисперсии всей выборки, а точки сверху и снизу обозначают выбросы за 99% интервал значений.

Этой информации достаточно для того, что бы оценить диапазон колебаний, а также разброс значений внутри диапазона.

Продолжаем анализ сезонных закономерностей

Теперь рассмотрим рисунок 1 более внимательно. Мы видим, что медиана приращений за пятый месяц (май) смещена вниз относительно нуля, и имеется один существенный выброс, который превысил ноль. В среднем в мае рынок снижался относительно марта, о чем говорит статистика, собранная за 10 лет. И был только один год, когда рынок существенно рос за этот период. Это интересная информация, которая соответствует поговорке трейдеров "Sell in may and go away!".

Посмотрим на 6 месяц (июнь), следующий за маем. Практически всегда (за исключением одного года) рынок рос в июне относительно мая, что является несомненной закономерностью, повторяющейся из года в год. Размах июньских колебаний достаточно небольшой, без выбросов (в отличие от мая), что говорит о хорошей сезонной устойчивости.

Обратим внимание на 11-й месяц (ноябрь), вероятность снижения рынка в этот период высока, после чего в декабре рынок, как правило, снова рос. Январь (1-й месяц) отметился высокой волатильностью и тенденцией к снижению относительно декабря.

Полученные данные могут оказаться полезными в качестве обзорной картины для принятия торговых решений. Также, вероятности можно инкорпорировать в торговую систему, допустим, чтобы она совершала больше покупок или продаж в те или иные месяцы.

Информация о месячных циклах весьма интересна, но мы можем посмотреть на более короткие, дневные циклы.

Посмотрим на распределения ценовых приращений за каждый отдельный день недели, за те же 10 лет:

Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()

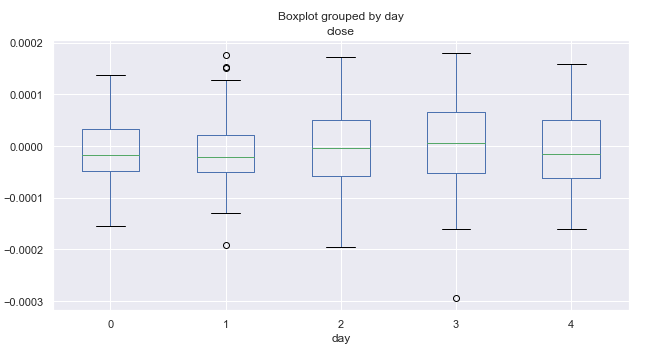
Рис. 2. Средние диапазоны ценовых приращений по торговым дням, за десять лет.

Здесь ноль соответствует понедельнику, а четверка пятнице. Судя по ценовому размаху, волатильность по дням остается почти постоянной, то есть нельзя утверждать, что в какой-то конкретный день недели торги происходят более активно, а в другой более спокойно. В среднем, в понедельник и в пятницу рынок склонен больше снижаться чем расти. Возможно, в какие-то отдельные месяцы распределения по дням имеют другой вид. Давайте проведем и такой анализ.

# leave only one month "returns.index[~returns.index.month.isin([1])"
returns = returns.drop(returns.index[~returns.index.month.isin([1])])

В приведенном листинге, единица соответствует январю месяцу. Меняя это значение, можно получить выборочную статистику по дням для любого месяца, в нашем случае за 10 лет.

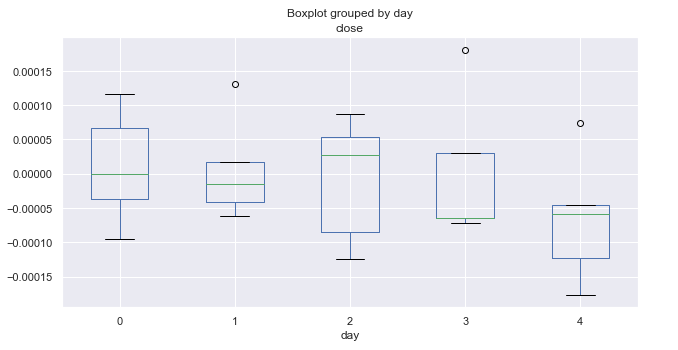
Рис. 3. Средние диапазоны ценовых приращений по торговым дням, за десять лет (январь).

На диаграмме выше представлены распределения приращений по дням для января месяца. Диаграмма стала более информативной, по сравнению со сводной статистикой по всем месяцам. Хорошо просматривается склонность рынка снижаться в пятницу, и только один раз валютная пара "EURUSD" не снижалась (выброс выше нуля в виде точки).

Посмотрим такую же статистику за март месяц:

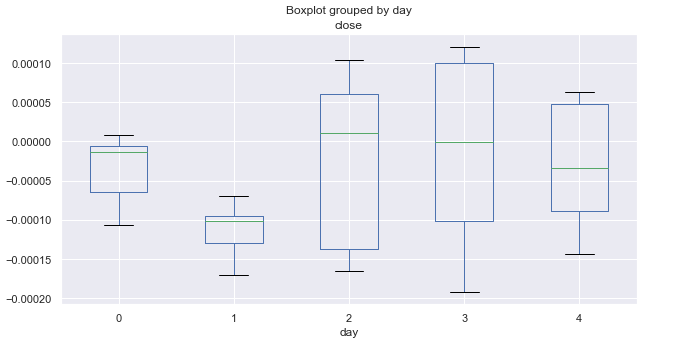
 Рис. 4. Средние диапазоны ценовых приращений по торговым дням, за десять лет (март).

Статистика за март совершенно отличается от январской. Понедельник и вторник (особенно вторник) демонстрируют медвежью тенденцию. Все вторники закрывались значительным снижением, тогда как остальные дни колеблются около нуля (в среднем). 

Проанализируем октябрь месяц таким же способом:

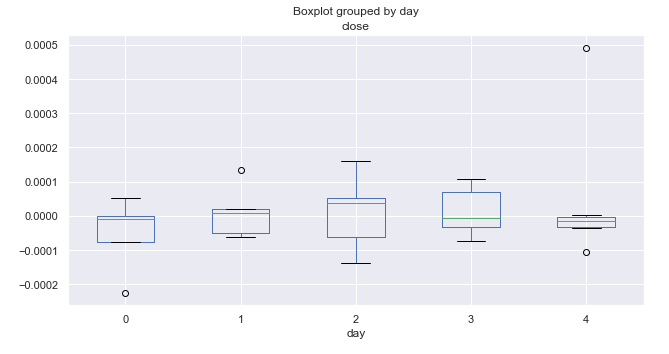
Рис. 5. Средние диапазоны ценовых приращений по торговым дням, за десять лет (октябрь).

Анализ распределений приращений по дням недели в октябре не выявляет каких-то выдающихся закономерностей. Можно лишь выделить среду, имеющую наибольший размах и потенциал движения цены, в остальном движения вверх и вниз равновероятны, с некоторыми выбросами.

Анализ сезонных закономерностей внутри дня

Часто, для построения торговых систем, необходимо учитывать распределения внутри дня, допустим, почасовые, в дополнение к месячным и дневным. Это легко сделать, давайте проанализируем.

Посмотрим на распределения ценовых приращений за каждый час:

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]

Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))

Как и в первом случае, мы получили котировки за 10 лет, но уже с 15-минутного таймфрейма. Второе отличие состоит в том, что данные были сгруппированы по дням и часам, чтобы получить медианную почасовую статистику для всех дней в подвыборке.

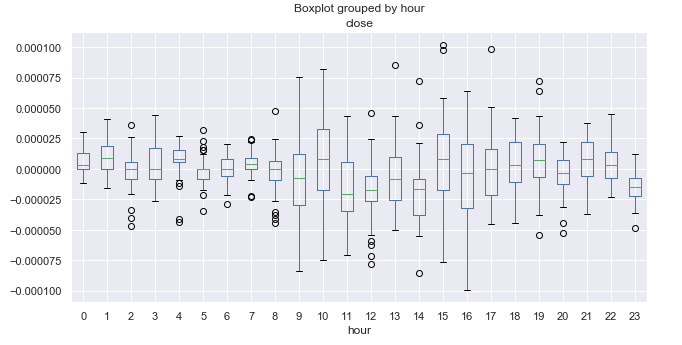
Рис. 6. Средние диапазоны ценовых приращений по часам, за десять лет.

Для того чтобы ориентироваться в выведенной статистике, необходимо знать часовой пояс вашего терминала. В моем случае это UTC + 2. Для ориентира, напишем время начала и окончания основных торговых сессий FOREX в UTC + 2 формате.

Сессия	Начало	Конец
Тихоокеанская	21.00	08.00
Азиатская	01.00	11.00
Европейская	08.00	18.00
Американская	14.00	00.00

Тихоокеанская сессия известна своими спокойными торгами. Если посмотреть на размах ящиков с усами, то легко заметить, что в диапазоне 21.00-08.00 размах минимален, что соответствует размеренной торговле. После начала Европейской и Американской сессий размах увеличивается, после чего постепенно уменьшается. На первый взгляд, отсутствуют явные периодичности, которые наблюдались ранее на дневном таймфрейме. Среднее приращений колеблется вокруг ноля в основном, не выявляя явно растущих или явно падающих часов.

Интересен 23.00 период (конец Американской сессии), за который цены, в среднем, снижаются относительно 22.00. Это может быть признаком некоторой коррекции в конце торгов. В то же время, в 00.00 цены растут относительно 23.00, т.е., в среднем, наблюдается некоторая периодичность. Какие-то более ярко выраженные циклы выделить сложно, зато мы имеем полную картину по ценовым размахам и знаем, чего можно ожидать в тот или иной момент времени.

Детренд по приращениям с единичным лагом может скрывать некоторые закономерности, поэтому, резонным будет посмотреть на детренд по скользящей средней, с произвольным периодом.

Поиск сезонных закономерностей с детрендом по скользящему среднему

Правильное выделение трендовой составляющей является почти искусством. Иногда можно слишком сгладить временной ряд и получать мало сигналов для торговли. Если период сглаживания уменьшать, то, напротив, высокая частота сделок может не покрыть спред и комиссию. Модифицируем код, что бы сделать детренд по скользящему среднему:

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]

plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)

Установим период скользящего среднего равным 25. Этот параметр можно менять, так же как и период получаемых цен закрытия. Здесь я взял 15-минутный таймфрейм, в результате усреднения по которому мы получим среднее отклонение цен закрытия от скользящего среднего по 15-минутному таймфрейму для каждого часа. Отобразим полученный временной ряд:

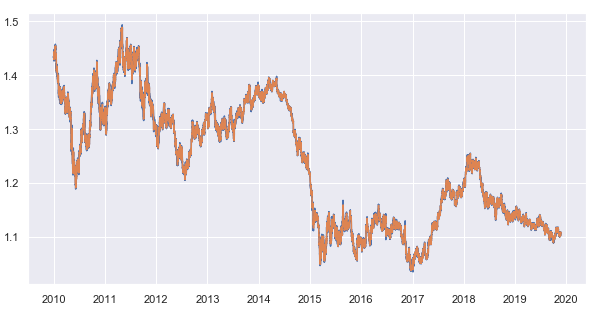
Рис. 7. Цены закрытия 15-минутного тайм-фрейма и скользящее среднее с периодом 25

Вычтем скользящее среднее из цен закрытия и получим детрендированный временной ряд (остатки):

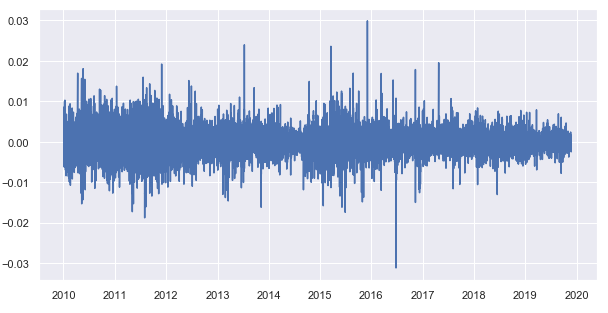
Рис. 8. остатки от вычитания скользящего среднего из цен закрытия

Осталось получить почасовую статистику распределений остатков по каждому торговому часу:

Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))

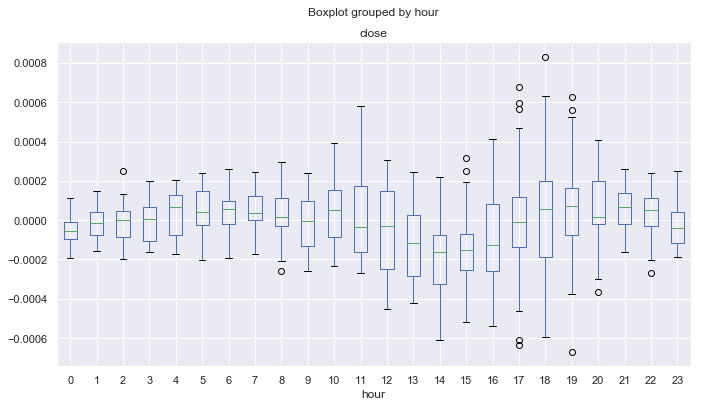
Рис. 9. Средние диапазоны ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет.

В отличие от диаграммы на рисунке 6, которая была построена по ценовым приращениям с единичным лагом, данная диаграмма демонстрирует меньше выбросов, а также выявляет больше циклических закономерностей. Например, теперь видно, что начиная с 0.00 и до 08.00 (тихоокеанская сессия) цены, в среднем, плавно растут относительно скользящего среднего. С 12.00 до 14.00 прослеживается тенденция к снижению, после чего, уже на американской сессии, в среднем цены растут. С начала тихоокеанской сессии цены снижаются на протяжении 4-х часов, начиная с 21.00.

Естественным образом возникает желание посмотреть на моменты распределений под "микроскопом", для более точных статистических оценок. Например, можно вывести стандартные отклонения для полученного детрендированного ряда в виде ящиков с усами:

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()

                                                                                       

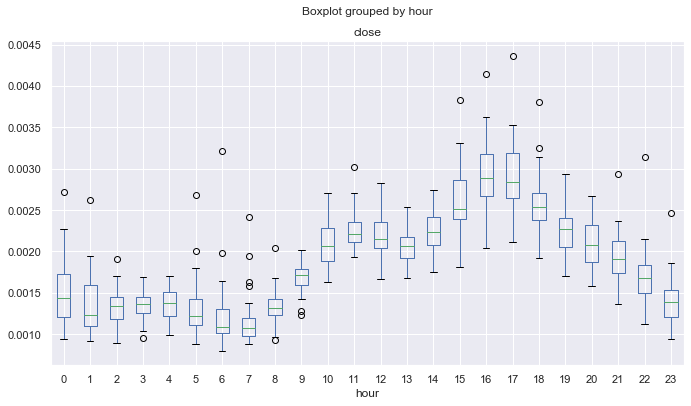
Рис. 10. Средние стандартные отклонения ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет.

На рис. 10 можно увидеть, в какие часы наблюдается более устойчивое поведение цены в плане его стандартного отклонения от матожидания. Например, 4, 13, 14, 19 часы обладают устойчивой дисперсией изо дня в день и могут быть более привлекательными для mean reversion стратегий. Другие же часы могут иметь выбросы и длинные усы, что говорит о более изменчивой почасовой волатильности ото дня ко дню.

Другим интересным моментом является коэффициент асимметрии, давайте выведем и его:

Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

 

Рис. 11. Средние коэффициенты асимметрии ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет.

Близость к нулю и небольшой разброс свидетельствуют о более "стандартном" распределении приращений. Здесь визуально диаграмма начинает приобретать вогнутый вид. Например, колебания в европейскую и американскую сессии хоть и имеют большой размах (рис. 9), но их распределения по часам более стабильны и наименее смещены, в отличие от тихоокеанской и азиатской сессий. Это может быть обусловлено большими перепадами активности у последних двух сессий, когда практически нулевая торговая активность сменяется внезапными движениями, вносящими большой вклад в перекос распределения.

Аналогичным образом проявляет себя статистика по эксцессам:

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)

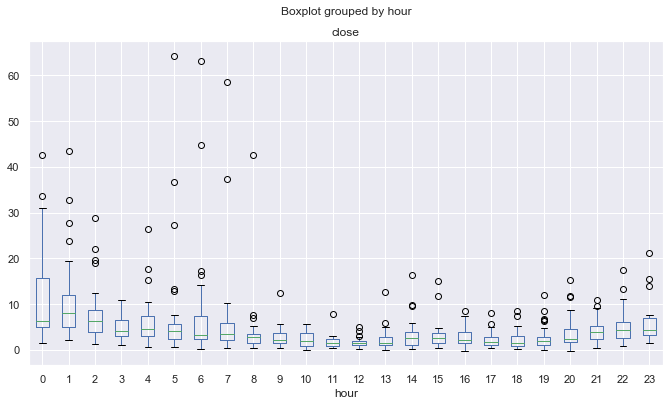
Рис. 12. Средние коэффициенты эксцессов ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет.

Из-за эффекта, описанного выше (предположительно), распределения менее островершинные и более "нормальные" для более волатильных торговых сессий и более "ненормальные" для спокойных торговых сессий. Вот такой вот парадокс.

Поиск сезонных закономерностей с детрендом по скользящему среднему за определенный месяц или день недели

Мы можем посмотреть на распределение часовых цен за вычетом тренда для каждого месяца отдельно, а также для любого дня недели. Весь код предложен в конце статьи, здесь лишь приведу сравнение между мартом и ноябрем.

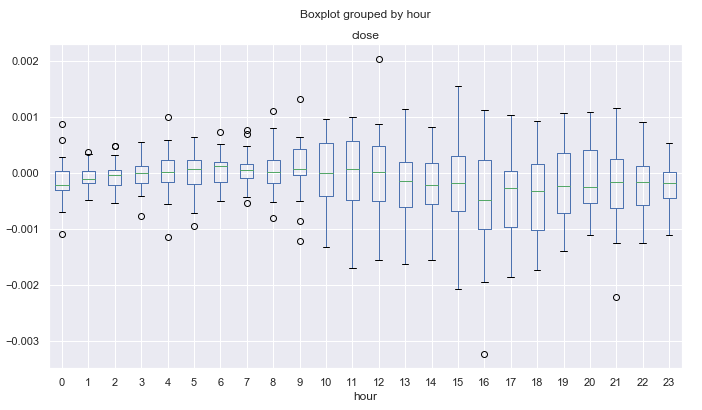
Рис. 13. Средние диапазоны ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет по месяцу "март".

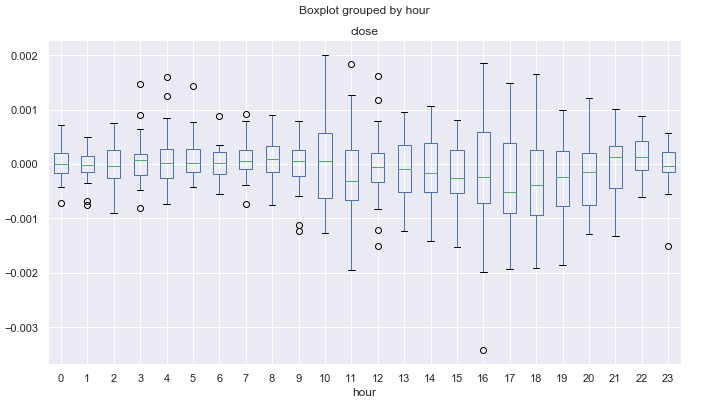
Рис. 14. Средние диапазоны ценовых приращений по часам по детренду по 25-периодичному МА, за десять лет по месяцу "ноябрь".

Можно искать и более мелкие внутридневные циклы, в том числе и в тиковых данных, но я решил ограничиться базовыми сезонными закономерностями, которые, по мнению трейдеров, присутствуют в финансовых временных рядах. Данную информацию можно использовать для разработки собственных торговых систем, учитывая сезонные "особенности" того или иного финансового инструмента.  

Проверка закономерностей торговой логикой

Напишем простого торгового эксперта, который будет эксплуатировать найденную закономерность на рис. 9. А именно предположение о том, что с 0.00 до 04.00 часов по GMT+2 цены на пару EURUSD растут относительно своего среднего, на протяжении всех четырех часов.

//+------------------------------------------------------------------+
//|                                              Seasonal trader.mq5 |
//|                                  Copyright 2020, Max Dmitrievsky |
//|                        https://www.mql5.com/ru/users/dmitrievsky |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, Max Dmitrievsky"
#property link      "https://www.mql5.com/ru/users/dmitrievsky"
#property version   "1.00"

#include <MT4Orders.mqh>
#include <Trade\AccountInfo.mqh>
#include <Math\Stat\Math.mqh>

input int OrderMagic = 666;
input double   MaximumRisk=0.01;
input double   CustomLot=0;

int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE);
MqlDateTime hours;
double maArr[], prArr[];

void OnTick()
  {
//---
      CopyBuffer(hnd, 0, 0, 1, maArr);
      CopyClose(NULL, 0, 0, 1, prArr);
      double pr = prArr[0] - maArr[0];
      
      TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=4)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >=0)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }
         
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int countOrders(int a) {
   int result=0;
   for(int k=0; k<OrdersTotal(); k++) {
      if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true)
         if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++;
   }
   return(result);
}

Здесь мы используем такое же скользящее среднее, как и для статистической оценки, с периодом 25. Далее, вычитаем из последней известной цены среднее и производим проверку, что текущее время торгов находится в диапазоне от нуля до четырех часов, включительно. Из диаграммы на рис. 9 понятно, что максимальная разница между ценами закрытия и скользящим средним, за этот период, составляет -0.0002 пункта, а среднее находится выше нуля. Соответственно, наша торговая логика заключается в открытии сделки на покупку при достижении этой разницы, а закрывать позицию следует при ее схлопывании до нуля. Данный проверочный бот не имеет стопов и других проверок, а предназначен только для проверки наличия закономерности. Проведем тестирование с 2015 по 2019 год на 15-минутном таймфрейме (скользящее среднее в исследовании строилось именно по этому периоду), по всем тикам:

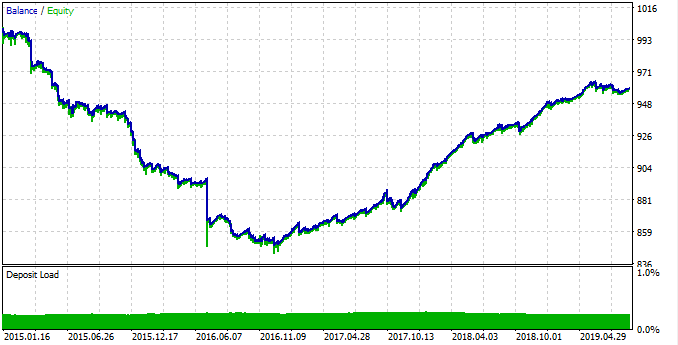
Рис. 15. Тестирование найденной закономерности.

С 2015 по 2017 год закономерность работала плохо и график значительно просел, тогда как с 2017 по 2019 год наблюдается устойчивый рост. Давайте посмотрим, почему так произошло. Для этого, посмотрим отдельные статистики для каждого временного интервала.

Для начала проанализируем прибыльный интервал торговли:

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])

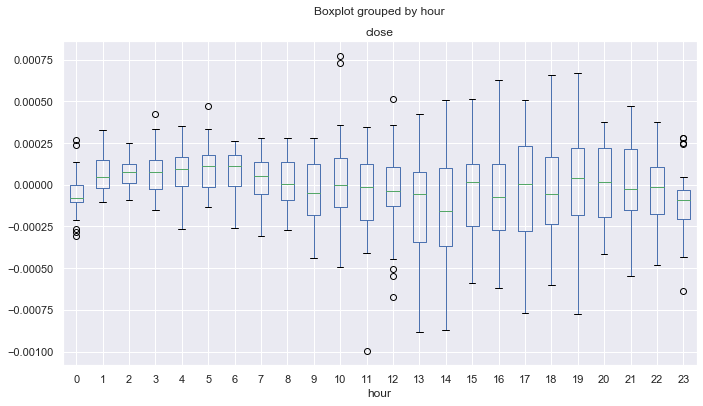
Рис. 16. статистика за 2017-19 годы.

Хорошо видно, что все часы (кроме нулевого) имеют среднее выше нуля, относительно скользящего среднего. Таким образом, статистически альфа на стороне нашей торговой системы и, в среднем система остается в прибыли. Теперь посмотрим на распределение за 2015-17 годы.

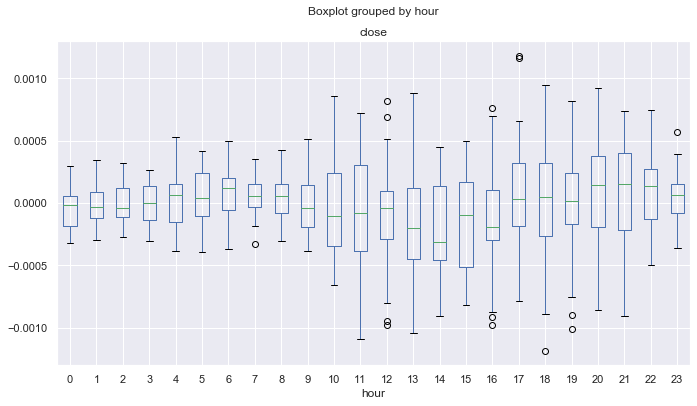
Рис. 17. статистика за 2015-19 годы.

В данном случае распределения имеют смещение среднего (медианы) ниже нуля или равны нолю для всех часов, кроме четвертого, что означает более низкую вероятность получения прибыли. Кроме того, ящики с усами имеют значительно больший средний размах, по сравнению с другим временным интервалом, за который минимальное значение не ниже -0.00025, здесь же оно достигает почти -0.0005. Другим недостатком является оценка распределений только по ценам закрытия, из-за чего выбросы в ценах не учитываются. Это можно исправить путем анализа потиковых данных, что выходит за рамки данный статьи.  Разница понятна, можно попробовать подстроить систему, чтобы выровнять результаты по всем годам.

Разрешим открывать сделки только в 0-1 часы, с предположением о том, что в последующие несколько часов сделка все равно будет закрыта в прибыль, поскольку отклонение от среднего стремиться выйти в положительную сторону. Также увеличим порог закрытия сделок с 0.0 до 0.0003, позволив роботу брать потенциально больше прибыли. Изменения предложены в следующем листинге:

TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=1)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >= 0.0003)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }

Протестируем робота, чтобы сделать окончательные выводы:

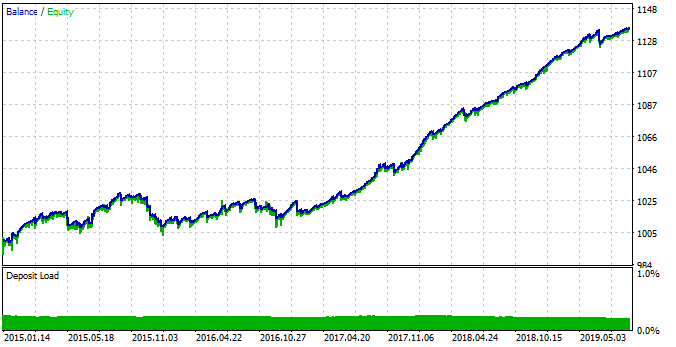
Рис. 18. Тестирование найденной закономерности, с измененными параметрами ТС.

Видно, что система стала более стабильной на интервале 2015-17 годов. Однако, изменившаяся сезонная закономерность не позволила ей торговать так же эффективно, как в 2017-19 годы. Данное поведение объясняется фундаментальными изменениями на рынке, которые легко описываются с помощью диаграмм boxplot.

Конечно, осталось еще много неисследованных закономерностей, но этот базовый пример должен дать понимание новых интересных возможностей, открывающихся при использовании такой техники.

Заключение

В данной статье был предложен статистический метод поиска сезонных закономерностей в финансовых временных рядах. Было показано, что на рынке могут присутствовать как месячные сезонные циклы, так и внутридневные циклы, в зависимости от месяца. Почасовой анализ показал, что при выборе определенного периода сглаживания (например, скользящего среднего), можно найти определенные циклы как внутри сессий, так и при переходе от одной торговой сессии к другой.

Среди преимуществ подхода можно выделить работу с конкретными рыночными закономерностями и фактически отсутствие переоптимизации в плане перебора параметров, благодаря чему ТС может обладать высокой стабильностью.

Из недостатков отметим трудоемкость самого процесса майнинга сезонных закономерностей, перебор различных комбинаций циклов.

Весь анализ проводился по валютной паре EURUSD за 10-летний временной интервал. Исходники кодов на языке Python приложены в конце статьи в формате .ipynb (Jupyter notebook). Вы можете провести самостоятельный анализ любого интересующего Вас инструмента с помощью данной библиотеки для разработки собственной торговой системы или улучшения предложенной.