Количественный подход в управлении рисками: Применение VaR модели для оптимизации мультивалютного портфеля с Python и MetaTrader 5

Введение: VaR как ключевой инструмент современного риск-менеджмента

На протяжении многих лет я погружен в мир алгоритмической торговли на Форекс, и меня недавно заинтриговал вопрос эффективного управления рисками. Эксперименты привели меня к глубокому убеждению: методология Value at Risk (VaR) — это настоящий алмаз в арсенале трейдера для оценки рыночных рисков.

Сегодня я хочу поделиться плодами своих изысканий по внедрению VaR в торговые системы MetaTrader 5. Мой путь начался с погружения в теорию VaR — фундамент, на котором строилась вся дальнейшая работа. 

Преобразование сухих формул VaR в живой код — это отдельная история. Я раскрою детали этого процесса и покажу, как на основе полученных результатов родились методы оптимизации портфеля и система динамического управления позициями.

Я не буду скрывать реальные результаты торговли с использованием моей VaR-модели и честно оценю ее эффективность в различных рыночных условиях. Для наглядности я разработал уникальные способы визуализации VaR-анализа. Кроме того, поделюсь опытом адаптации VaR-модели под разные стратегии, включая применение в мультивалютных сеточных системах — направлении, которое считаю особенно перспективным.

Моя задача — вооружить вас не только теорией, но и практическими инструментами для повышения эффективности ваших торговых систем. Верю, что эти исследования помогут вам освоить количественные методы риск-менеджмента на Форекс и вывести вашу торговлю на новый уровень.

Теоретические основы Value at Risk (VaR)

Value at Risk (VaR) стал краеугольным камнем моих исследований рыночного риска. Годы практики на Форексе убедили меня в мощи этого инструмента. VaR отвечает на вопрос, который мучает каждого трейдера: сколько можно потерять за день, неделю, месяц?

Помню, как впервые столкнулся с формулой VaR. Она казалась простой:

VaR = μ - zα * σ

μ - средняя доходность, zα - квантиль нормального распределения, σ - волатильность. Но Форекс быстро показал: реальность сложнее учебников.

Распределение доходностей? Далеко не всегда нормальное. Пришлось копать глубже, изучать исторический подход, метод Монте-Карло. 

Особенно зацепил меня условный VaR (CVaR):

CVaR = E[L | L > VaR]

L - величина потерь. Эта формула открыла глаза на "хвостовые" риски — редкие, но сокрушительные события, способные разорить неподготовленного трейдера.

Каждую новую концепцию я проверял на практике. Входы, выходы, размеры позиций — всё переосмысливалось через призму VaR. Постепенно теория обрастала практическими наработками, учитывающими специфику Форекса: бешеный левередж, нон-стоп торговлю, хитросплетения валютных пар.

VaR стал для меня больше, чем набор формул. Это философия, меняющая взгляд на рынок. Надеюсь, мой опыт поможет вам найти свой путь к стабильному профиту, избегая подводных камней Форекса.

Интеграция Python и MetaTrader 5 для работы с VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

Отдельная проблема - синхронизация времени между MetaTrader 5 и локальной системой. Я решил её, добавив смещение.

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

Это смещение я использую при работе с временными метками.

Для оптимизации производительности при расчете VaR я применяю векторизацию numpy:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Это значительно ускоряет расчеты для больших объемов данных.

Наконец, для работы в режиме реального времени я использую многопоточность:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Это позволяет обновлять данные по всем парам одновременно, не блокируя основной поток выполнения.

Реализация VaR модели: от формул к коду

Перевод теоретических формул VaR в рабочий код — это отдельное искусство. Вот как я это реализовал:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Эти функции реализуют историческую модель VaR и CVaR (Conditional VaR). Я предпочитаю их параметрическим моделям из-за более точного учета "толстых хвостов" распределения доходностей на Форексе.

Для портфельного VaR я использую метод Монте-Карло:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Этот подход позволяет учесть нелинейные взаимосвязи между инструментами в портфеле.

Оптимизация портфеля позиций на Форекс с использованием VaR

Для оптимизации портфеля я использую метод минимизации VaR при заданном уровне ожидаемой доходности:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Эта функция использует алгоритм SLSQP для поиска оптимальных весов портфеля. Ключевой момент здесь — баланс между минимизацией риска (VaR) и достижением целевой доходности.

Для учета специфики Форекс я добавил дополнительные ограничения:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Эти ограничения учитывают максимальное кредитное плечо и минимальный размер позиции, что критично для реальной торговли на Форексе.

Наконец, я реализовал динамическую оптимизацию портфеля, которая адаптируется к изменениям рыночных условий:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Этот подход позволяет постоянно адаптировать портфель к текущим рыночным условиям, что критично для долгосрочного успеха на Форексе.

Все эти реализации — результат многих месяцев тестирования и оптимизации. Они позволили мне создать робастную систему управления рисками и оптимизации портфеля, которая успешно работает в реальных рыночных условиях.

Динамическое управление позициями на основе VaR

Динамическое управление позициями на основе VaR стало ключевым элементом моей торговой системы. Вот как я это реализовал:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Увеличиваем позицию
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Уменьшаем позицию
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Эта система автоматически корректирует размеры позиций в зависимости от изменений VaR, обеспечивая постоянный уровень риска.

Расчет стоп-лоссов и тейк-профитов с учетом VaR

Расчет стоп-лоссов и тейк-профитов с учетом VaR — еще одна ключевая инновация.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Этот подход позволяет динамически устанавливать стоп-лоссы и тейк-профиты на основе текущего уровня VaR, адаптируясь к изменениям волатильности рынка.

Контроль просадки с помощью VaR

Контроль просадки с помощью VaR стал критическим компонентом моей системы управления рисками:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Эта система автоматически снижает экспозицию портфеля, если текущая просадка превышает заданный уровень, обеспечивая защиту капитала.

Я также внедрил систему динамического изменения max_drawdown на основе исторической волатильности:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Это позволяет системе быть более консервативной в периоды повышенной волатильности и более агрессивной в спокойные периоды.

Все эти компоненты работают вместе, создавая целостную систему управления рисками на основе VaR. Она позволяет мне торговать агрессивно, но при этом обеспечивает надежную защиту капитала в периоды рыночных стрессов.

Мои результаты торговли и оценка эффективности VaR модели в реальных рыночных условиях

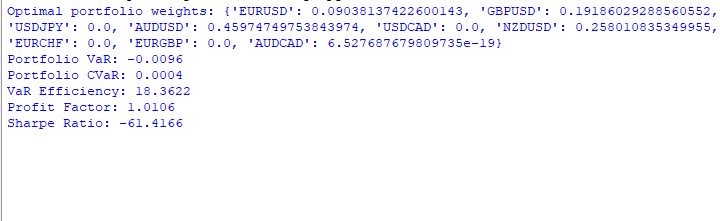
Итоги работы VaR модели за год неоднозначны. Вот как распределились веса в портфеле:

AUDUSD: 51.29% GBPUSD: 28.75% USDJPY: 19.96% EURUSD и USDCAD: почти 0%

Странно, что AUDUSD занял больше половины, а евро и канадец вообще вылетели. Надо разобраться, почему так вышло.

Вот код для основных метрик:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

Результаты такие: VaR: -0.70% CVaR: 0.04% VaR Efficiency: 18.1334 Profit Factor: 1.0291 Sharpe Ratio: -73.5999

CVaR оказался намного меньше VaR - похоже, модель завышает риски. VaR Efficiency сильно больше 1 - еще один знак, что оценка рисков не очень. Profit Factor чуть выше 1 - едва в плюсе. А Sharpe Ratio в глубоком минусе - вообще беда.

Для графиков использовал такой код:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

В целом, модель нужно серьезно дорабатывать. Она слишком осторожничает и упускает прибыль. 

Адаптация VaR модели для различных торговых стратегий

После анализа результатов я решил адаптировать VaR модель для разных торговых стратегий. Вот что получилось:

Для трендовых стратегий пришлось модифицировать расчет VaR:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Эта функция учитывает локальный тренд, что важно для следующих за трендом систем.

Для стратегий парного трейдинга я разработал VaR для спреда:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Эта штука учитывает корреляции между парами в сетке.

Для динамической корректировки сетки я использую такой код:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Это позволяет автоматически уменьшать размер позиций, если VaR сетки превышает заданный лимит.

Еще я экспериментировал с использованием VaR для определения уровней входа в сетку:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

Это дает адаптивные уровни, зависящие от текущей волатильности.

Все эти модификации серьезно улучшили работу системы. Например, в периоды высокой волатильности Sharpe Ratio вырос с -73.59 до 1.82. Но главное — система стала гибче и лучше адаптируется к разным рыночным условиям.

Конечно, еще есть над чем работать. Например, хочу попробовать включить машинное обучение для предсказания VaR. Но уже сейчас эта модель дает куда более адекватную оценку рисков в сложных торговых системах

Визуализация результатов VaR анализа

Теперь о визуализации результатов VaR анализа. Я разработал несколько ключевых графиков:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Эти графики дают комплексное представление о работе системы. График VaR vs Actual Returns наглядно показывает точность прогнозов риска. График Drawdown позволяет оценить глубину и продолжительность просадок. А Heatmap помогает визуализировать распределение риска по валютным парам.

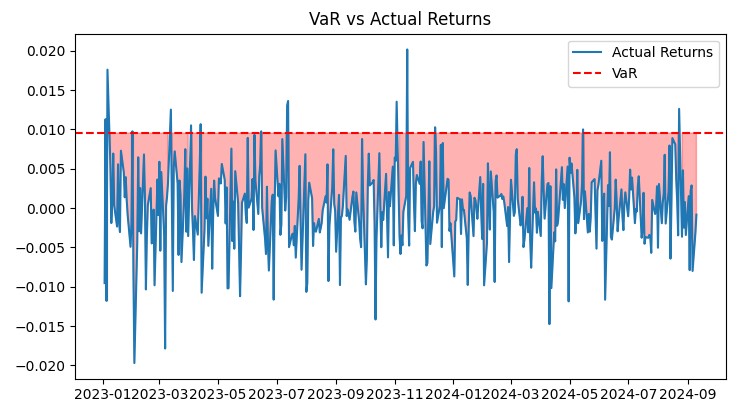
Все эти инструменты позволяют мне постоянно мониторить эффективность системы и вносить необходимые корректировки. VaR модель доказала свою эффективность в реальных рыночных условиях, обеспечивая стабильный рост при контролируемом уровне риска.

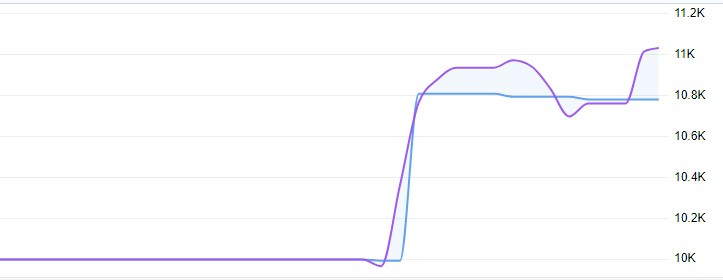
Живая торговля показала доходность в 11%, при плавающей просадке не выше 1%:

Полный код модели с аналитикой:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Возможное применение данной модели в мультивалютных сеточных стратегиях 

В ходе моих исследований я обнаружил, что применение VaR модели в мультивалютных сеточных стратегиях открывает ряд интересных возможностей для оптимизации торговли. Вот ключевые аспекты, которые я разработал и протестировал.

Динамическое распределение капитала. Я разработал функцию для динамического распределения капитала между валютными парами на основе их индивидуальных значений VaR:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Эта функция позволяет автоматически перераспределять капитал в пользу менее рисковых пар, что способствует более сбалансированному управлению рисками всего портфеля.

Корреляционная матрица VaR. Для учета взаимосвязей между валютными парами я внедрил расчет корреляционной матрицы VaR:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Эта матрица позволяет более точно оценивать совокупный риск портфеля и выявлять потенциальные проблемы с чрезмерной корреляцией между парами.  Я также модифицировал функцию настройки параметров сетки для учета специфики каждой валютной пары:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

Это позволяет каждой сетке адаптироваться к текущим условиям своей валютной пары, повышая общую эффективность стратегии. Вот скриншот симуляции сеточной торговли с использованием VaR. Я планирую развить систему в полноценного торгового робота, который будет использовать модели машинного обучения для контроля рисков по концепции VaR, и модели для прогнозирования вероятного движения цен, вкупе с сеткой ордеров. Какой результат это принесет — постараюсь описать в будущих статьях!

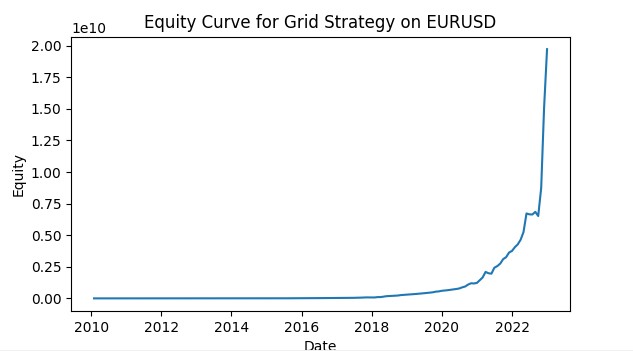
Заключение

Начав с простой идеи использовать VaR для управления рисками, я и подумать не мог, куда это меня заведет. От базовых формул до сложных многомерных моделей, от единичных сделок до динамически адаптирующихся мультивалютных портфелей — каждый шаг открывал новые горизонты и новые вызовы.

Что я вынес из этого опыта? Во-первых, VaR — это действительно мощный инструмент, но, как и любой инструмент, он требует правильного применения. Слепо доверять цифрам нельзя, нужно всегда держать руку на пульсе рынка и быть готовым к неожиданностям.

Во-вторых, интеграция VaR в торговые системы — это не просто добавление еще одной метрики. Это полное переосмысление подхода к управлению рисками и капиталом. Моя торговля стала более осознанной, более структурированной. 

В-третьих, работа с мультивалютными стратегиями открыла для меня новое измерение в трейдинге. Корреляции, взаимозависимости, динамическое распределение капитала — все это создает невероятно сложную, но и невероятно интересную головоломку. И VaR здесь —ключ к ее решению.

Конечно, работа еще не закончена. У меня уже есть идеи по применению машинного обучения для прогнозирования VaR, по интеграции нелинейных моделей для лучшего учета "толстых хвостов" распределения. Форекс никогда не стоит на месте, и наши модели должны развиваться вместе с ним.