Возможности Мастера MQL5, которые вам нужно знать (Часть 24): Скользящие средние

Введение

Мы продолжаем серию статей о Мастере MQL5. На этот раз мы рассмотрим индикатор скользящей средней и то, как его можно добавить в библиотеку уже доступных инструментов способами, о которых, возможно, знают не все трейдеры. Скользящая средняя имеет множество вариантов - в виде единого временного ряда, прикрепляемого к графику, осциллятора и даже конвертов.

Мы рассмотрим эти многочисленные приложения или варианты в рамках трех скользящих средних (Moving Averages, MA), называемых пифагоровыми средними. Это среднее арифметическое (Arithmetic Mean, AM), среднее геометрическое (Geometric Mean, GM) и среднее гармоническое (Harmonic Mean, HM). Среднее арифметическое — это то, что первым приходит на ум при упоминании MA. Это просто среднее значение любого количества значений в множестве. Википедия приводит очень интересное графическое представление всех этих трех средних:

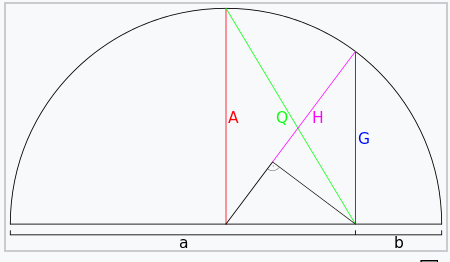
Выше представлен полукруг, диаметр которого неравномерно разделен на две величины - a и b. Среднее арифметическое этих двух значений обозначено на диаграмме как А красного цвета, что, как и следовало ожидать, эквивалентно радиусу полукруга. Для полноты картины формула для среднего арифметического приводится ниже:

где

• AM — среднее арифметическое
• x — значения в множестве, среднее значение которых вычисляется
• n — размер множества

Среднее геометрическое вычисляется по формуле:

где

• GM — геометрическое среднее
• x и n представляют то же самое, что и AM выше

Значение GM на полукруге выше эквивалентно по длине синей хорде, обозначенной буквой G, что делает его более склонным к меньшему значению b, чем к большему значению a. Также следует отметить, что GM всегда будет положительным, даже если все значения отрицательные! Это противоречие можно преодолеть, присвоив отрицательное значение вычисленному GM, если набор содержит только отрицательные числа, но в случае, если это смешанный набор отрицательных и положительных значений, то вычисление реального GM становится проблематичным.

Для гармонического среднего полукругом является линия, обозначенная буквой H, длина которой эквивалентна среднему значению a и b. Его формула имеет вид:

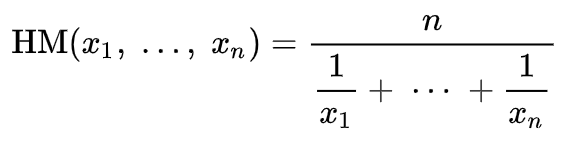
где

• HM — это, конечно, среднее гармоническое
• x и n представляют то же самое, что и выше

Если бы по какой-то причине значение b было равно нулю, как это видно из полукруговой диаграммы, то и геометрическое, и гармоническое средние были бы равны нулю. (Это несмотря на то, что при вычислении среднего гармонического значения мы получили "деление на ноль"). Интересно, что это будет верно независимо от количества (т. е. если их больше 2) чисел, средние значения которых вычисляются; если любое из этих чисел равно нулю, то среднее геометрическое и среднее гармоническое всех значений равны нулю.

По сути, это свойство измеряет степень близости наименьшего значения в наборе к нулю. Итак, что это означает для трейдеров? Это может означать ряд вещей, в зависимости от рассматриваемых данных скользящей средней.

Если это просто цена ценных бумаг, то скользящая средняя может служить хорошим индикатором поддержки. Почему? GM и HM придает большее значение низким ценам. Это может означать, например, что падение цены ниже этих средних значений будет иметь большее значение, чем падение ниже обычной скользящей средней. Таким образом, GM и HM могут быть полезны в обосновании большинства ценовых действий. А что насчет сопротивления? Мы можем получить зеркальный эквивалент GM и HM с помощью следующих формул:

HM’ = AM + (AM - HM)

GM’ = AM + (AM - GM)

где:

• HM’ - отраженное гармоническое среднее
• GM’ - среднее геометрическое отражение
• AM, GM и HM такие же, как указано выше.

Вводя зеркальные эквиваленты или отражения GM и HM, мы в некотором смысле добавляем баланс к средним значениям, поскольку веса этих отражений неизбежно склоняются в сторону больших значений в любом множестве, среднее значение которого вычисляется. Теперь мы можем использовать либо GM', либо HM' в качестве более высоких средневзвешенных значений цены, которые будут служить более эффективными индикаторами при определении уровня сопротивления.

Значение GM против HM для наших целей будет зависеть только от степени. Это связано с тем, что оба показателя имеют больший вес в сторону меньших значений, при этом основное различие заключается в том, что HM имеет больший вес в сторону нуля, чем GM.

Пользовательские реализации

Теперь рассмотрим, как эти простые средние можно использовать в MQL5, чтобы раскрыть их уникальные свойства. Во-первых, это обычное среднее арифметическое. Из трех разновидностей это самый простой способ, поскольку он использует самые основы средних значений без каких-либо изменений. Самый очевидный способ применения этого среднего значения — отслеживать пересечения цен. Существует множество вариантов применения скользящих средних при отслеживании ценовой структуры, и этот вариант, пожалуй, самый простой и распространенный. Среднее арифметическое представлено здесь в первую очередь для сравнения с другими, не столь распространенными средствами GM и HM, уже представленными выше.

Сравнительный анализ является неотъемлемой частью собранных Мастером MQL5 советников, особенно для классов сигналов, поскольку каждому выбранному классу сигналов в Мастере может быть назначен вес или возможность участия в определении условий на покупку и продажу торгуемой ценной бумаги. Благодаря векторным типам данных мы легко получаем буфер AM из следующей функции:

//+------------------------------------------------------------------+
//| Arithmetic Mean                                                  |
//+------------------------------------------------------------------+
double CSignalAM::AM(int Index, int Mask = 8)
{  vector _am;
   _am.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_fast);
   return(_am.Mean());
}

Кроме того, мы можем измерить текущий ценовой разрыв, который является ключевым в отслеживании пересечения скользящих средних, с помощью следующей функции:

   double            CrossOver(int Index)
   {                 m_close.Refresh(-1);
      return(AM(Index) - m_close.GetData(Index));
   }

Как правило, в случаях, когда торгуешь вручную, имеет смысл реализовать этот индикатор, а также GM и HM в виде пользовательского индикатора. Мы не торгуем вручную, поэтому функция, которая обращается к встроенным ценовым буферам класса, вполне подойдет.

Среднее значение HM, как и GM, смещено в сторону меньших значений, и, как мы видели выше, это можно зеркально отразить, чтобы создать другое среднее значение, HM', которое смещено в сторону более высоких значений. Таким образом, HM и HM', будучи средними, смещенными в сторону экстремумов, позволяют улавливать расхождения. Когда мы думаем о расхождениях, первое, что приходит на ум, — это разница в тренде между осциллятором и ценой его актива. Такие расхождения случаются в течение очень коротких промежутков времени, и нужно быть начеку, чтобы их заметить. Либо это может быть расхождение цен только одного актива, но на разных таймфреймах, например, падение цены на часовом таймфрейме, в то время как на недельном таймфрейме наблюдается сильный бычий тренд.

Однако, чтобы извлечь выгоду из "смещений" гармонического среднего, мы будем рассматривать расхождения в высоких и низких ценах. В частности, мы будем открывать позиции только тогда, когда изменение высоких цен отличается по направлению от изменения низких цен. Но здесь снова возникают альтернативы. Либо мы открываем позицию на падающих максимумах и растущих минимумах, либо - на растущих максимумах и падающих минимумах. В этой статье мы рассмотрим последний вариант. Все исходные данные приложены в конце статьи, поэтому читатель может настроить их и попытаться использовать более популярный вариант дивергенции поглощения (engulf divergence), который мы не рассматриваем.

Итак, для открытия позиций мы будем искать рост гармонического среднего максимумов, который совпадает с падением гармонического среднего минимумов. Можно настроить индикатор, который поможет открыть длинную или короткую позицию. Здесь же в качестве такого индикатора мы будем использовать просто изменение цены закрытия. Если цена закрытия растет после расхождения на предыдущем баре, то мы открываем длинную позицию и наоборот.

Код для реализации, как мы видели на примере AM, также состоит из двух частей. Во-первых, у нас есть функция HM и ее зеркало, представленное ниже:

//+------------------------------------------------------------------+
//| Harmonic Mean                                                    |
//+------------------------------------------------------------------+
double CSignalHM::HM(int Index, int Mask = 8)
{  vector _hm, _hm_i;
   _hm_i.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   _hm = (1.0 / _hm_i);
   return(m_slow / _hm.Sum());
}
//+------------------------------------------------------------------+
//| Inverse Harmonic Mean                                            |
//+------------------------------------------------------------------+
double CSignalHM::HM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _hm = HM(Index, Mask);
   return(_am + (_am - _hm));
}

Также у нас есть функция расхождения, которая выглядит следующим образом:

   double            Divergence(int Index)
   {                 return((HM_(Index, 2) - HM_(Index + 1, 2)) - (HM(Index, 4) - HM(Index + 1, 4)));
   }

При использовании векторов для копирования и загрузки данных индекс "маски цен" (rates mask) незаменим, так как он позволяет быстро переключаться между различными ценами (OHLC), а использование встроенных статистических функций векторного типа данных избавляет от необходимости писать много кода. Кроме того, наши тестовые функции для этих пифагоровых средних используют два периода скользящей средней - быстрый и медленный. Это обычная практика, особенно при использовании стратегии пересечения для определения точек входа и выхода. Для вычисления значений буферов как среднего гармонического, так и среднего геометрического мы полагаемся на медленный период. Быстрые периоды используются только для буфера среднего арифметического.

Конечно, такое поведение можно изменить для соответствия вашей стратегии. Мы придерживаемся его здесь исключительно в целях тестирования.

Наконец, рассмотрим среднее геометрическое, которое, как и гармоническое, будет применяться аналогично полосам Боллинджера. Как и гармоническое среднее, оно больше взвешено в сторону малых значений и в немного большей степени. Именно такой весовой коэффициент делает его идеальным для получения индикатора, подобного полосам Боллинджера, поскольку, как известно, полосы Боллинджера представляют собой скользящую среднюю плюс два стандартных отклонения. Однако прежде чем перейти к реализации, код для получения геометрического среднего и его зеркала (эквивалент с высоким взвешенным значением) будет выглядеть так, как показано ниже:

//+------------------------------------------------------------------+
//| Geometric Mean                                                   |
//+------------------------------------------------------------------+
double CSignalGM::GM(int Index, int Mask = 8)
{  vector _gm;
   _gm.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   return(pow(_gm.Prod(), 1.0 / m_slow));
}
//+------------------------------------------------------------------+
//| Inverse Geometric Mean                                           |
//+------------------------------------------------------------------+
double CSignalGM::GM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _gm = GM(Index, Mask);
   return(_am + (_am - _gm));
}

Мы снова используем векторные типы данных и их встроенные функции для ускорения кодирования. Буферов полос два - верхний и нижний. Они также извлекаются из двух функций, перечисленных ниже:

   double            BandsUp(int Index)
   {  vector _bu;
      _bu.CopyRates(m_symbol.Name(), m_period, 2, Index, m_slow);
      return(GM_(Index, 2) + (2.0 * _bu.Std()));
   }

   double            BandsDn(int Index)
   {  vector _bd;
      _bd.CopyRates(m_symbol.Name(), m_period, 4, Index, m_slow);
      return(GM(Index, 4) - (2.0 * _bd.Std()));
   }

Две функции просто возвращают цены верхнего и нижнего диапазонов для функций BandsUp и BandsDn соответственно. Эти возвращаемые значения можно легко преобразовать в параллельные буферы для анализа в различных формах. Мы просто используем их в стратегии пересечения, чтобы определить, есть ли у нас потенциальные возможности для длинных или коротких позиций. Для проверки наличия длинной позиции нам потребуется подтверждение того, что цена пересекла нижнюю полосу снизу, то есть она была ниже нижней полосы, но теперь находится выше нее. Аналогично, для проверки коротких позиций нам необходимо подтвердить пересечение ценой верхней полосы сверху, то есть цена была выше верхней полосы, но в последующем ценовом баре теперь находится ниже нее.

Пользовательские классы сигналов

Каждую из этих трех Пифагоровых МА можно объединить в один класс с дополнительным параметром, который позволяет выбрать одну из средних для использования в советнике. Однако мы реализуем их как отдельные классы сигналов, поскольку собираемся рассмотреть настройку веса классов сигналов, выполнив оптимизацию для идеального веса каждого среднего значения, чтобы получить представление о том, какой из этих сигналов и, соответственно, какая из средних более полезна для прогнозирования и размещения ордеров с помощью нашего советника.

Однако прежде чем получить представление об относительной важности, может быть полезно сначала провести независимые тесты каждого класса сигналов по отдельности, чтобы любые полученные в итоге относительные веса могли служить подтверждением (или опровержением) этих первых тестовых запусков. Итак, начнем с разработки советника для каждого из трех индексов и протестируем их по отдельности, чтобы оценить их собственную эффективность. Получив эти результаты, мы запустим тесты на советнике, объединяющем все три средних, которые мы оптимизируем для относительного веса каждого из них.

Чтобы разработать длинное и короткое условие для класса сигнала среднего арифметического, просто проверим изменение значения пересечения, возвращаемого функцией Crossover, код которой приведен выше. Наши длинный и короткий коды условий довольно короткие, и оба они приведены ниже:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAM::LongCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) > 0.0 && CrossOver(StartIndex()+1) < 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()) - CrossOver(StartIndex()+1))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAM::ShortCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) < 0.0 && CrossOver(StartIndex()+1) > 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()+1) - CrossOver(StartIndex()))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}

Как всегда, суть сводится к нормализации значения результата в случае наличия потенциального сигнала. Для AM мы используем текущее изменение значений пересечения, деленное на наибольшее по величине из его предыдущих значений. Очевидно, что это область, которую можно во многом настраивать, и читатель может реализовать ее по-своему, однако выбранный нами вариант, как правило, использует среднее арифметическое значение и поэтому мы используем его.

Гармоническое среднее условие на покупку и продажу, в свою очередь, будет использовать функции Divergence для сортировки потенциальных входов как на покупку, так и на продажу. У нас есть условия на покупку и продажу, указанные ниже:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) > m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) < m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}

Используя гармоническое среднее, мы ищем любую положительную дивергенцию, при которой максимумы растут, а минимумы падают, и за этим следует рост цены закрытия для открытия на покупку или падение цены закрытия для открытия на продажу. Эти два события происходят последовательно и не на одном и том же баре. Эта дивергенция во многом противоположна более популярной модели поглощения, которая обычно характеризуется падающими максимумами и растущими минимумами.

Как только у нас появится открытие на покупку или продажу, следующим вопросом станет определение целочисленного значения результата, которое всегда является выходом для длинных и коротких условий этих функций класса сигналов. Опять же, существует несколько подходов, которые можно использовать для количественной оценки результата, и некоторые из этих подходов могут быть связаны с другими показателями, помимо гармонического среднего. Однако для наших целей мы хотим еще больше опираться на гармоническое среднее при установлении величины результата, поэтому мы используем отношение текущего отклонения к величине предыдущих значений для получения целочисленного значения в диапазоне от 0 до 100.

Таким образом, этот результат просто означает, что чем больше текущее расхождение, тем более мы будем настроены на покупку или продажу. В знаменателе этого результирующего отношения (которое мы нормализуем к диапазону 0–100 через проценты) находятся текущие и предыдущие значения расхождения. Это приводит нас к применению среднего геометрического.

GM реализуется путем вычисления значений верхней и нижней полос Боллинджера на основе буферов GM, как описано выше. Чтобы превратить его в действенный сигнал, нужно проверить пересечение цен нижней и верхней полос для бычьих и медвежьих установок соответственно, как упоминалось выше. Реализация в коде выглядит следующим образом для условий на покупку и продажу:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalGM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) > m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) > BandsDn(StartIndex()) && m_close.GetData(StartIndex() + 1) < BandsDn(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalGM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) < m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) < BandsUp(StartIndex()) && m_close.GetData(StartIndex() + 1) > BandsUp(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()+1) - m_close.GetData(StartIndex()))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}

Величина результата, как мы уже убедились в случаях со средним арифметическим и средним гармоническим, также будет больше склоняться к среднему геометрическому и не будет использовать какой-либо другой показатель. Таким образом, при нашем использовании GM результатом является отношение изменения цены закрытия к разрыву между верхней и нижней полосами наших производных полос Боллинджера. Другими словами, этот результат означает, что большее движение цены относительно сжатия разрыва полос должно указывать на более сильный сигнал входа или закрытия. Мы говорим о сигнале закрытия, поскольку условия на покупку и продажу не только устанавливают пороги открытия, но и определяют порог, при котором закрываются их обратные позиции. Итак, в настройках входа у нас всегда есть порог открытия и порог закрытия. Последнее значение должно быть меньше первого, поскольку вам необходимо закрыть длинные позиции, прежде чем открывать короткие, и наоборот.

Кроме того, возможные альтернативные реализации полос Боллинджера, полученных с помощью GM, при установлении сигнала могли бы рассматривать варианты, отслеживающие размер разрыва между верхней и нижней полосами с наклоном базовой средней, а также несколько других итераций. Наша реализация — не единственный способ использования или изучения полос Боллинджера.

Тестирование стратегии и оценка эффективности

Итак, сначала мы выполним независимые тестовые прогоны с каждой пифагоровой скользящей средней по отдельности в советнике, и как только мы получим независимые результаты каждой из них, мы выполним тестовый прогон советника, собранного со всеми тремя сигналами пифагоровых средних, и оптимизируем его, чтобы найти относительный вес каждого из наших средних.

Для единообразия мы проведем тесты по одному символу EURJPY на 20-минутном таймфрейме для 2023 года. Для среднего арифметического мы получаем следующие результаты:

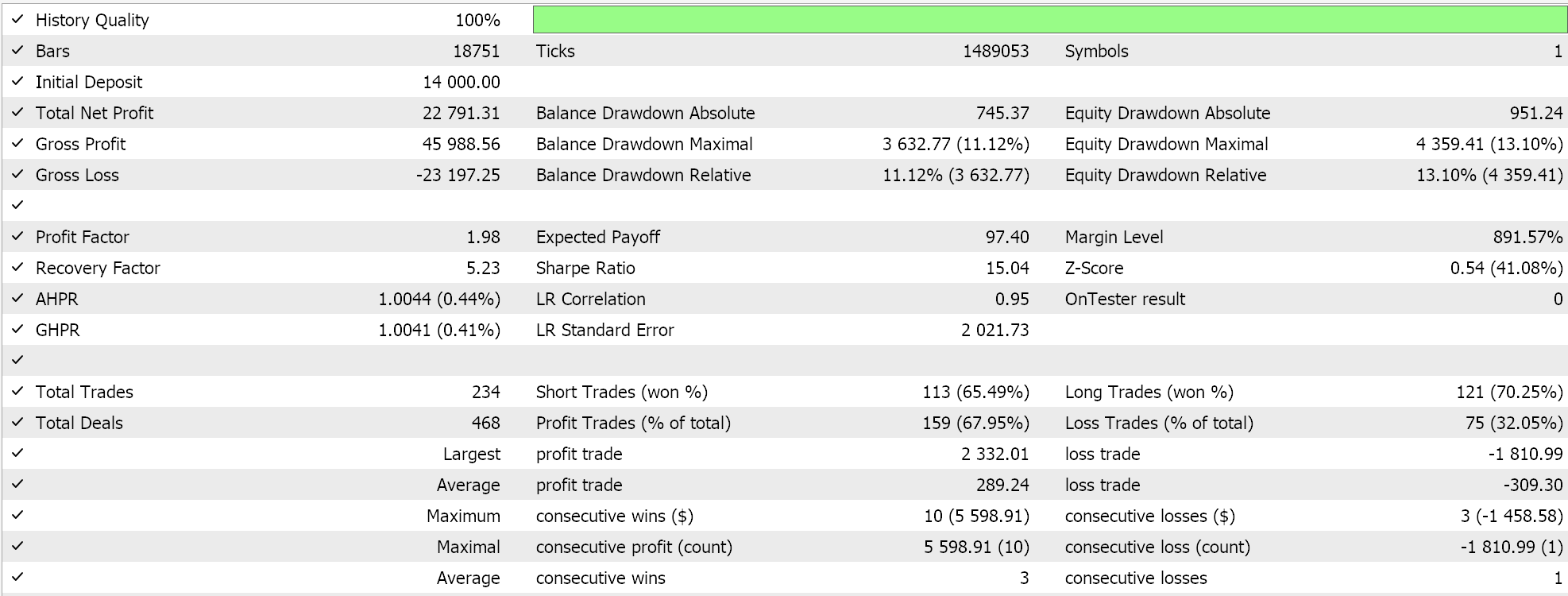
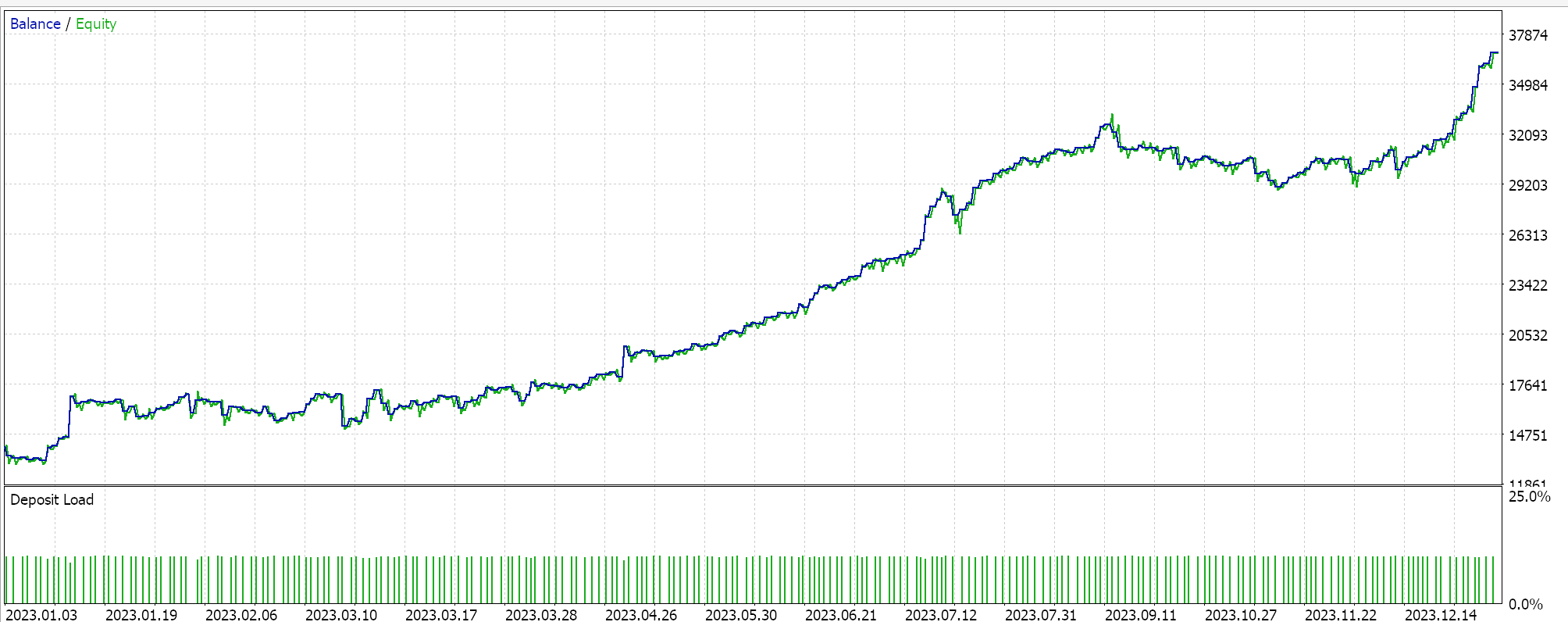
Для среднего гармонического получаем следующее:

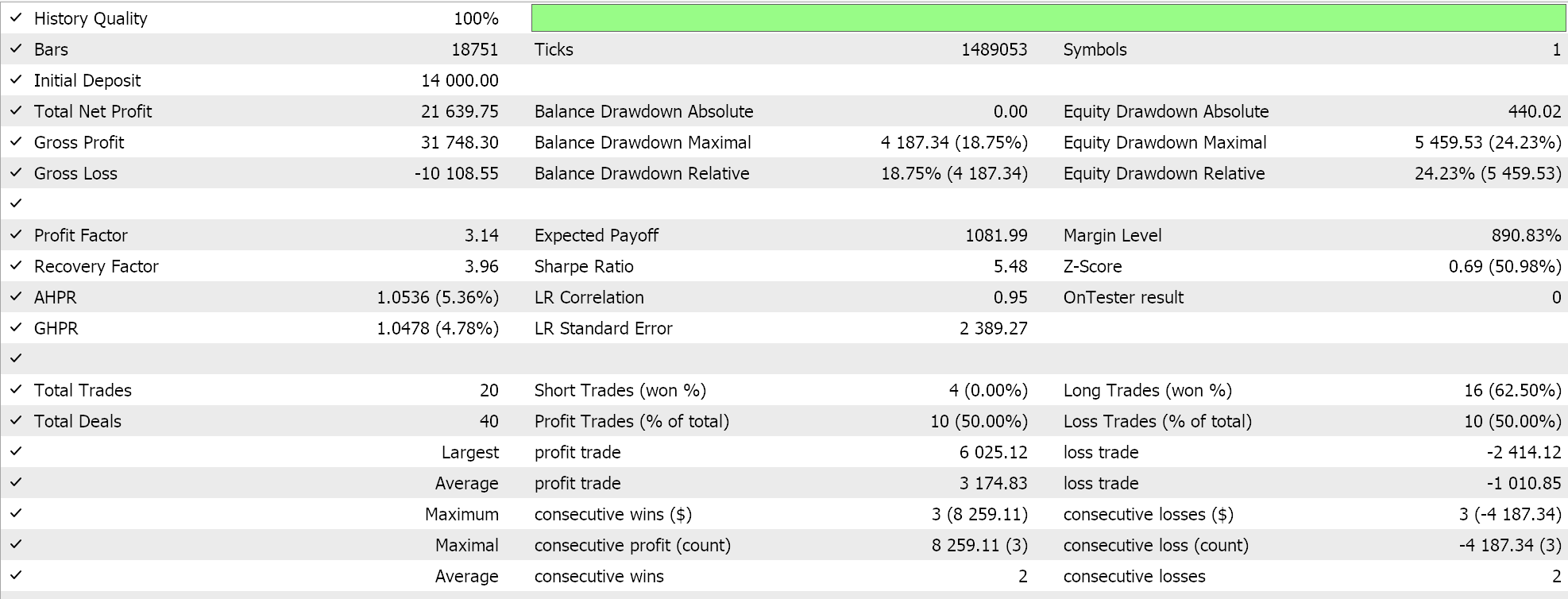
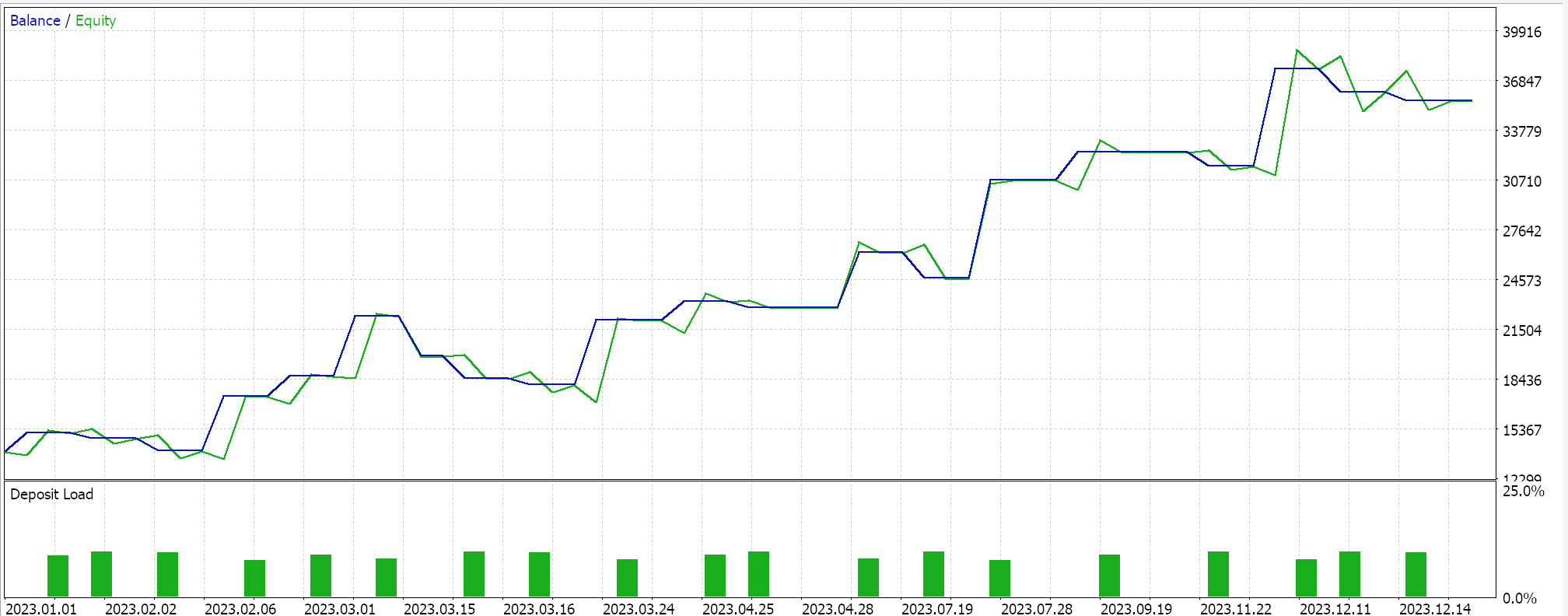
И наконец, для среднего геометрического имеем:

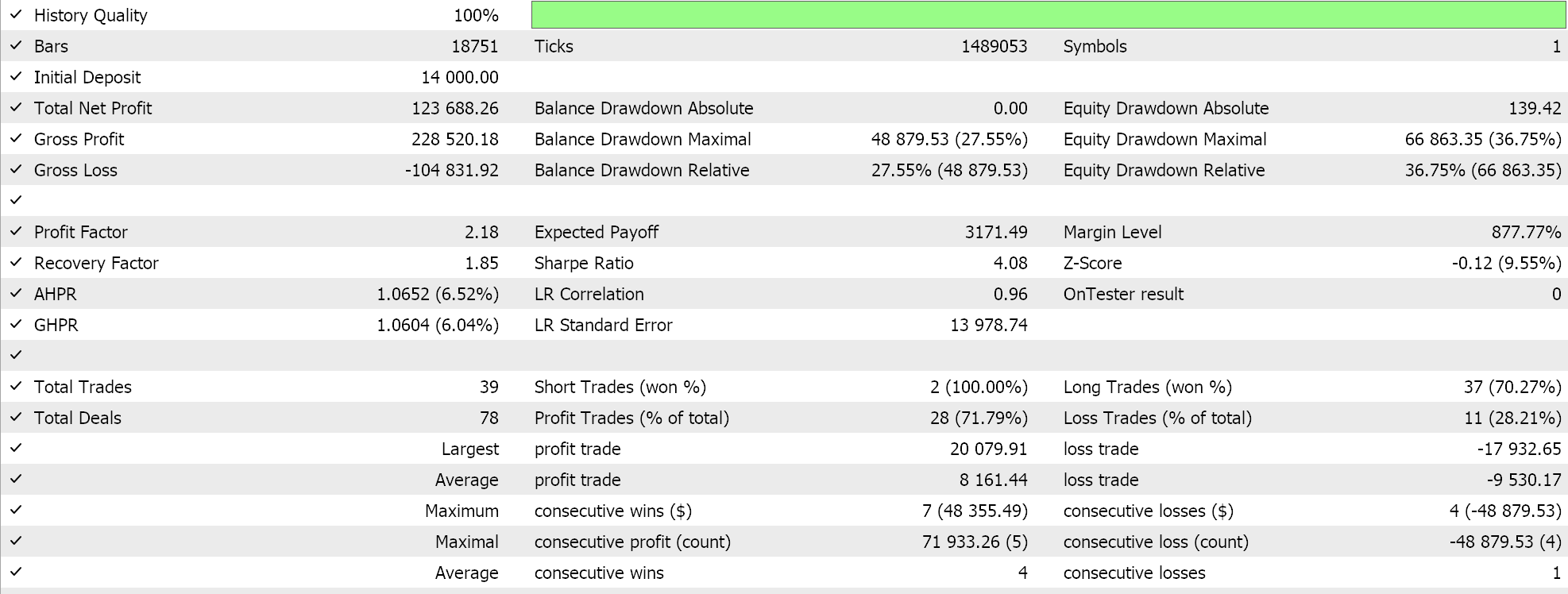
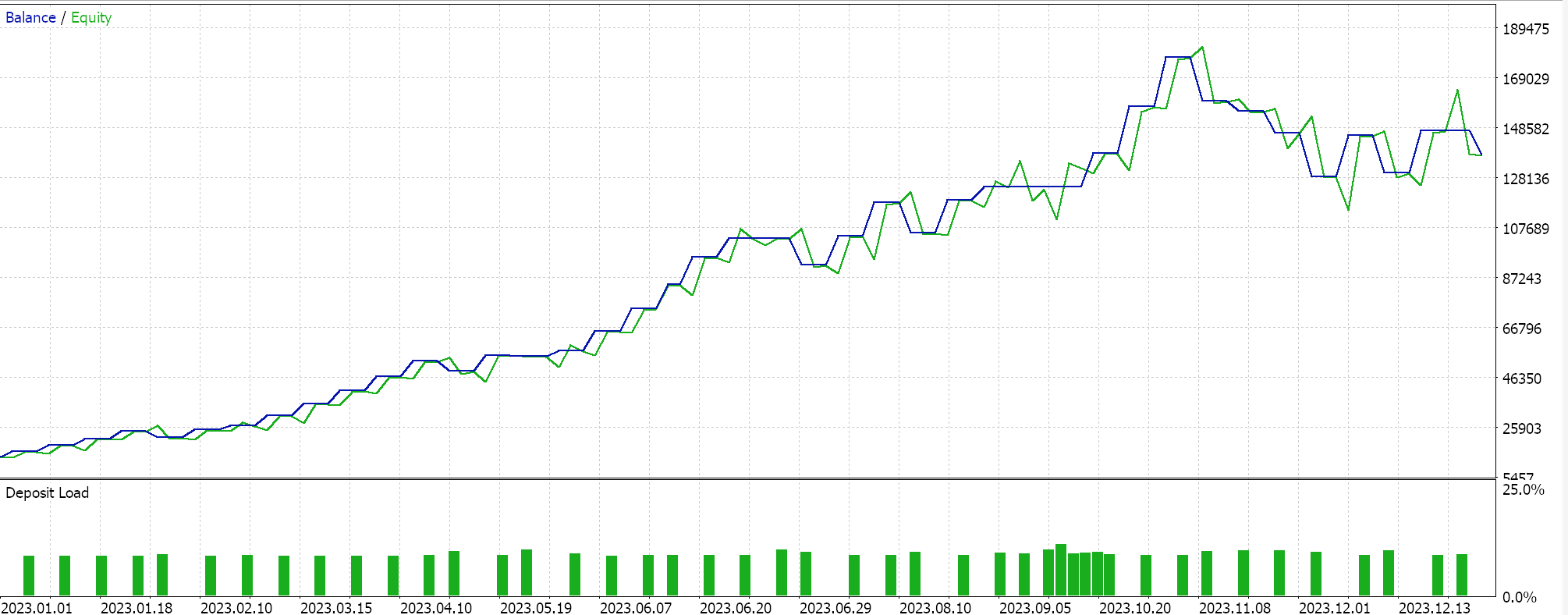
Судя по независимым показателям, среднее геометрическое оказывает большое влияние, за ним следует простое перекрестное среднее арифметическое, среднее гармоническое расхождение запаздывает. Конечно, на наши результаты влияет тот факт, что мы проводим тестирование в очень узком временном интервале и внесли определенные изменения в то, как мы интерпретируем и реализуем входные сигналы для каждого из средних. Очевидно, что для того, чтобы сделать выводы об относительной производительности, необходимо провести больше тестов, однако результаты указывают на относительно большую изменчивость производительности, что может быть многообещающим сигналом при предварительном тестировании.

Если теперь мы проведем тесты со всеми тремя средними значениями и попытаемся оптимизировать их для относительного взвешивания, то получим следующий результат как один из лучших:

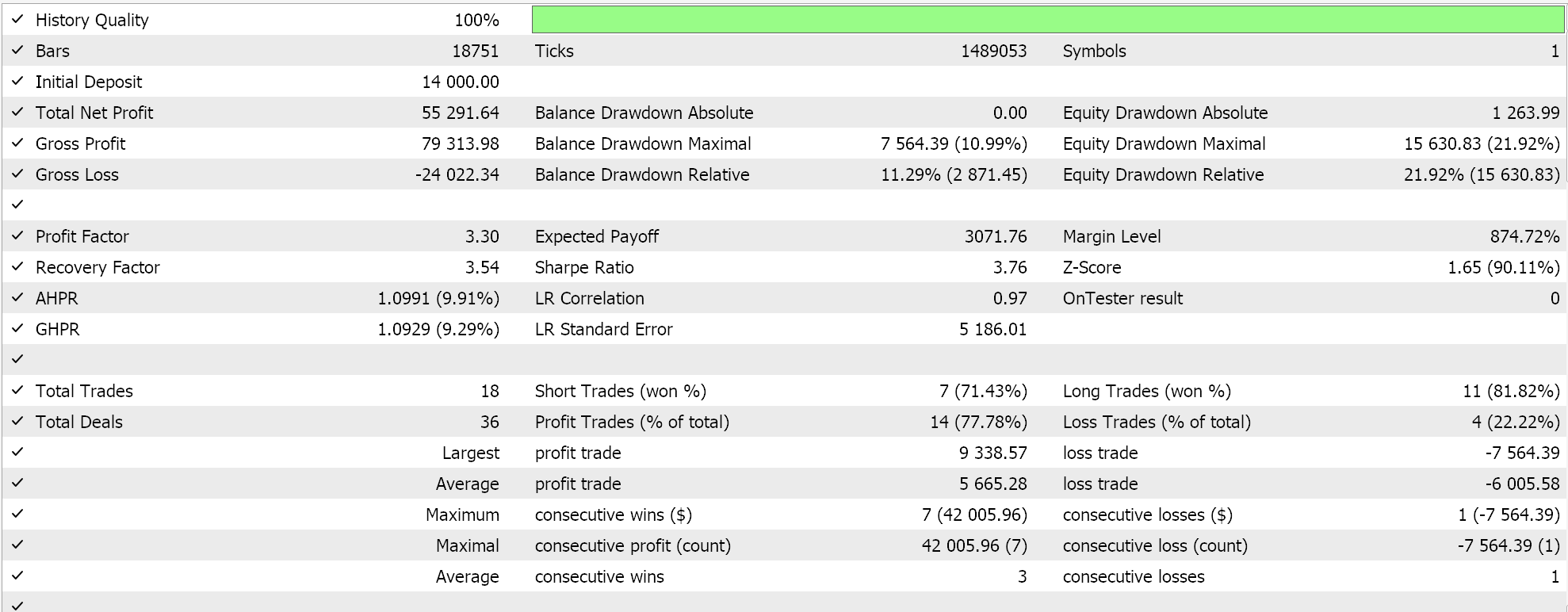
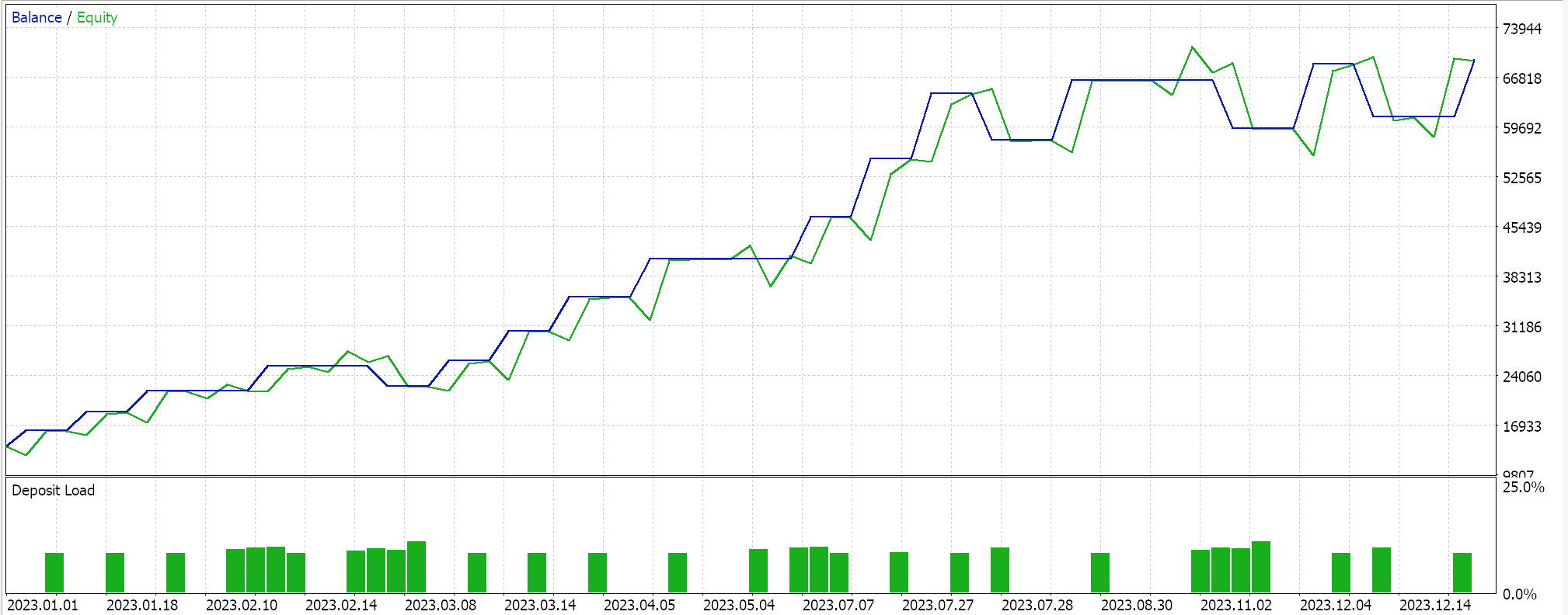
Очевидно, что независимые результаты среднего геометрического по-прежнему являются наиболее точными, конечно, при условии проверки на более длительных периодах. Ирония заключается в том, что для того, чтобы все три сигнала работали одновременно, лучшему среднему необходимо присвоить наименьший весовой коэффициент 0,4. Независимые отстающие показатели среднего гармонического и среднего арифметического получили более высокие веса 1,0 и 0,9, что может объяснить, почему общая производительность всех трех средних значений в совокупности не только ниже независимой производительности среднего геометрического, но и производительность GM все равно лучше, даже если сложить независимые производительности как среднего арифметического, так и среднего гармонического. Настройки для комбинированного советника приведены ниже:

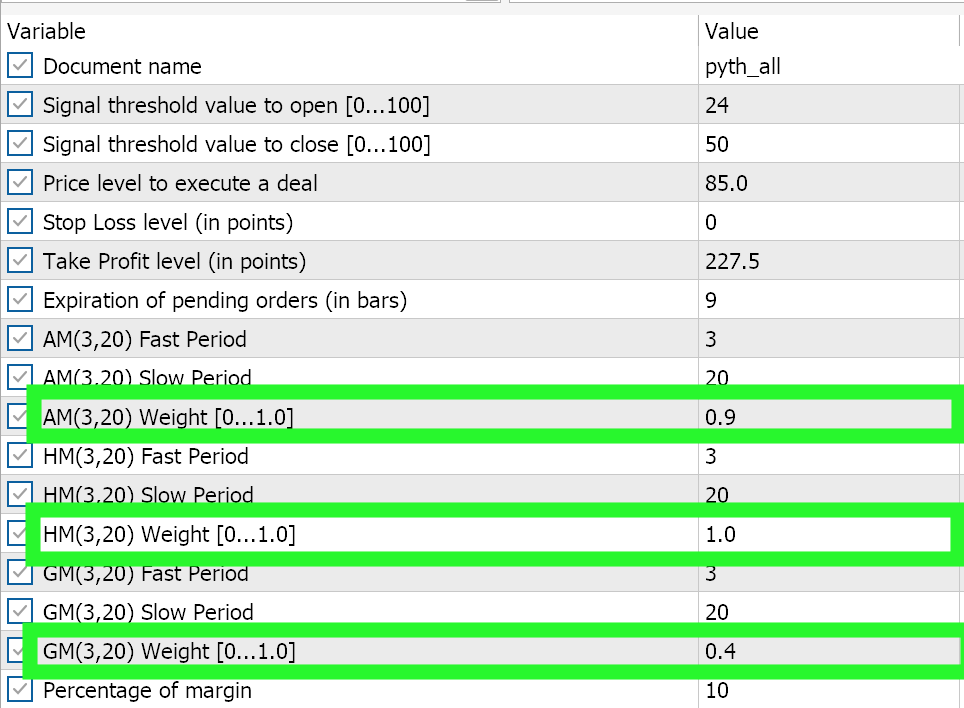
Заключение

Прошлые результаты не гарантируют будущих, и, как уже упоминалось, обширное тестирование, желательно на более длительных периодах, всегда оправдано. Это безопаснее, чем начать использовать советник в боевых условиях после небольшого тестирования, например, в течение одного года, как поступили мы. Как всегда, мы собираем прилагаемый код для этих сигналов, следуя рекомендациям, изложенным в статьях здесь и здесь. Геометрическое среднее, которое имеет наибольший вес в сторону меньших значений из трех средних, рассмотренных в этой статье, демонстрирует многообещающие результаты в условиях полос Боллинджера, однако мы не рассматривали гармоническое среднее в условиях аналогичных полос, чтобы сделать какие-либо более определенные выводы о его относительной эффективности. Кроме того, помимо полос Боллинджера, пересечения AM или расхождения HM существуют и другие реализации скользящих средних в форме осциллятора, такие как OSMA или TRIX, которые мы не рассматривали. Эти и другие методы можно учитывать при оценке относительного потенциала пифагоровых средних.