
在 MetaTrader 5 中使用自组织特征映射(Kohonen 映射)
简介
自组织特征映射 (SOM) 是一种人工神经网络,使用无监督学习方法来进行训练,从而形成训练样本输入空间的二维离散表示内容,称为映射。
这些映射类似于多维标度,适合用于实现高维数据低维表示的分类和可视化。该模型首先由芬兰教授 Teuvo Kohonen 作为人工神经网络提出,因此有时也被称为 Kohonen 映射。
有大量算法可供使用,我们将采用在 http://www.ai-junkie.com 中提出的代码。为了在 MetaTrader 5 客户端中实现数据可视化,我们将使用 cIntBMP - 一个用于创建 BMP 图像的库。在本文中,我们将讨论 Kohonen 映射的几个简单应用。
1. 自组织特征映射
自组织特征映射首先是由 Teuvo Kohonen 在 1982 年提出的。与众多神经网络相比,该映射无需在输入数据与目标输出数据之间存在一一对应关系。该神经网络使用无监督学习方法进行训练。
SOM 被正式描述为一个从高维输入数据到常规低维数组的元素的有序、平滑的非线性映射。就其基本形式而言,它生成了输入数据的一个相似性图形。
SOM 将高维数据之间的非线性统计关系转换为此类数据在常规两维网格节点上的图像点之间的简单几何关系。可使用 SOM 映射实现高维数据的分类和可视化。
1.1. 网络架构
简单的 16 节点网格 Kohonen 映射(4x4 排列,每个节点使用三维输入向量相连)如图 1 所示。
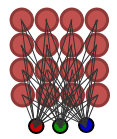
图 1. 简单 Kohonen 映射(16 个节点)
每个节点均具有以栅格和矢量表示的 (x,y) 坐标,以及带有分量的权重向量,这些都通过输入向量予以定义。
1.2. 学习算法
与很多其他类型的神经网络不同,SOM 无需指定目标输出值。与其相反,在节点权重与输入向量相匹配的位置,栅格区域被选择性地优化,从而为输入向量所属类更精确地模拟数据。
从随机权重的初始分布开始,经过多次迭代后,SOM 最终演变为稳定区域的映射。实际上每个区域都是一个特征分类器,因此您可以将图形输出视为一种输入空间的特征映射。
训练是通过几个步骤,并经由多次迭代进行的:
- 使用随机值对每个节点的权重进行初始化。
- 从培训数据集中随机选择一个向量。
- 检查每个节点以计算哪个节点的权重最接近输入向量。最接近的节点通常被称为最佳匹配单元 (BMU)。
- 计算 BMU 邻域的半径。最初,该值被设置为栅格的半径,但逐步减小。
- 对于 BMU 半径内的任何节点,调整该节点的权重以使其更类似于输入向量。节点越靠近 BMU,针对其权重变化的警告就越频繁。
- 重复第 2 步以进行 N 次迭代。
详细信息请参见 http://www.ai-junkie.com。
2. 案例研究
2.1. 示例 1. SOM 中的经典示例
Kohonen 映射的经典示例是颜色聚类问题。
假定我们有一组 8 种颜色,每种颜色都代表一个采用 RGB 颜色模型的三维向量。
-
 红色:(255,0,0);
红色:(255,0,0);  绿色:(0,128,0);
绿色:(0,128,0); 蓝色:(0,0,255);
蓝色:(0,0,255); 深绿色:(0,100,0);
深绿色:(0,100,0); 深蓝色:(0,0,139);
深蓝色:(0,0,139); 黄色:(255,255,0);
黄色:(255,255,0); 橙色:(255,165,0);
橙色:(255,165,0); 紫色:(128,0,128).
紫色:(128,0,128).
使用 MQL5 语言处理 Kohonen 映射时,我们将遵循面向对象范例。
我们需要两个类:用于常规网格节点的 CSOMNode 类和属于神经网络类的 CSOM。
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
可以在 som_ex1.mq5 中找到类方法的实现。代码中有大量注释,我们将着重于概念阐述。
CSOM 类的描述如下所示:
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
CSOM 类的使用相当简单:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
结果如图 2 所示。
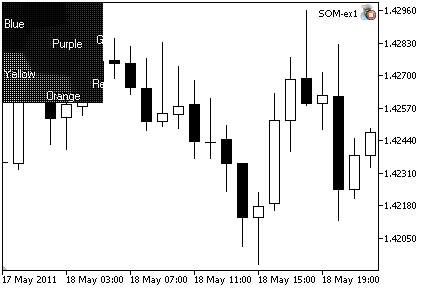
图 2. SOM_ex1.mq5 EA 交易的输出
Kohonen 映射的学习动态如图 3 所示(参见图片下面的步骤):
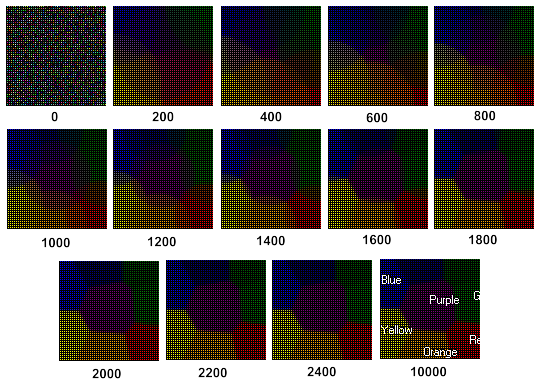
图 3. Kohonen 映射的学习动态
从图 3 可以看到,Kohonen 映射是在经过 2400 步以后形成的。
如果我们创建具有 300 个节点的栅格,并指定图像大小为 400x400:
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
我们将得到如图 4 所示的图像:
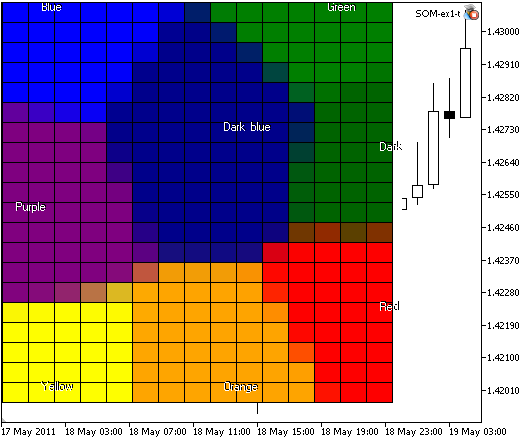
图 4. 含有 300 个节点,图像大小为 400x400 的 Kohonen 映射
如果您读过 Guido Deboeck 和 Teuvo Kohonen 合著的《Visual Explorations in Finance:with Self-Organizing Maps》(金融的视觉探索)一书,您会记得格栅节点也可表示为六边形单元格。通过修改 EA 交易的代码,我们可以实现其他方式的可视化。
SOM-ex1-hex.mq5 的结果如图 5 所示:
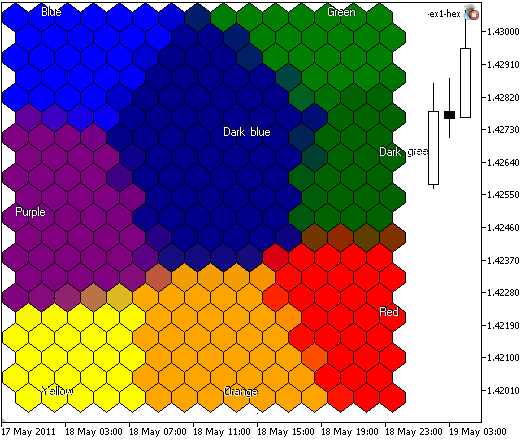
图 5. 含有 300 个节点,图像大小为 400x400,以六边形单元格表示节点的 Kohonen 映射
在这一版本中,我们可以通过使用输入参数来定义单元格边框的显示:
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
在某些情形下,我们不需要显示单元格边框,如果您指定 ShowBorders=false,则将获得以下图像(见图 6):
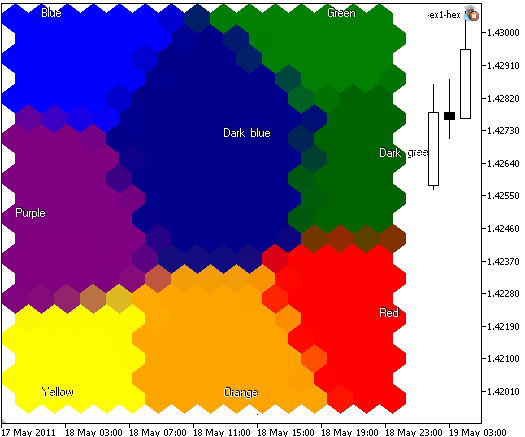
图 6. 含有 300 个节点,图像大小为 400x400,以六边形单元格描绘节点,不显示单元格边框的 Kohonen 映射
在第一个示例中,我们在具有指定颜色分量的训练集中使用了 8 种颜色。我们可以通过向 CSOM 类添加两个方法来扩展训练集并简化颜色分量的指定过程。
注意,在本例中,Kohonen 映射很简单,因为只有几种颜色在颜色空间中实现了分离。结果,我们得到了本地化后的聚类。
如果我们考虑使用颜色分量更为接近的更多颜色,就会出现问题。
2.2. 示例 2. 使用 Web 颜色作为训练样本
在 MQL5 语言中,Web 颜色是预定义的常量。
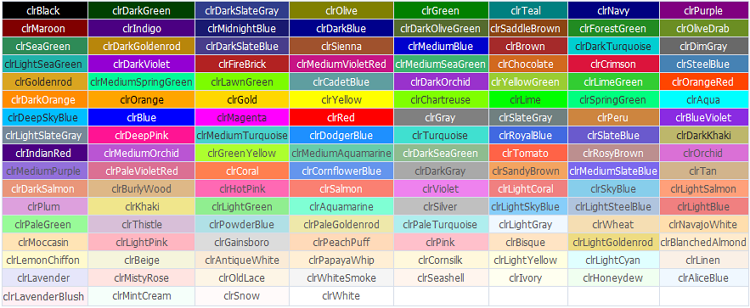
图 7. Web 颜色
如果我们将 Kohonen 算法应用到一组具有类似分量的向量,结果会怎么样?
我们可以从 CSOM 类中派生一个 CSOMWeb 类:
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
如您所见,为了简化颜色处理过程,我们添加了两种新方法,现在无需再明确指定颜色分量了。
类方法的实现如下所示:
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
所有 Web 颜色都可合并到数组 web_colors[]:
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
OnInit() 函数的形式很简单:
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
如果我们启动 som-ex2-hex.mq5,就将得到如图 8 所示的图片。
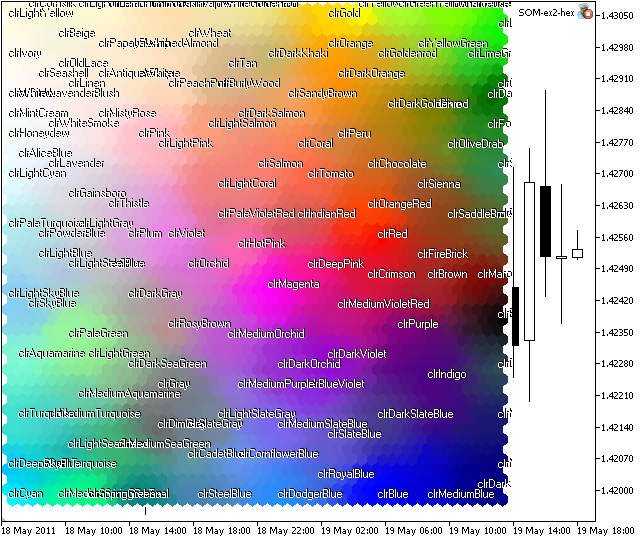
图 8. Web 颜色的 Kohonen 映射
如您所见,确实存在一些聚类,但是某些颜色(例如 xxxBlue)位于不同区域。
原因在于训练集的结构,其存在很多带有接近分量的向量。
2.3. 示例 3. 产品聚类
接下来我们将研究一个简单示例,尝试根据三个参数(即蛋白质、碳水化合物和脂肪),并根据其相似性对二十五种食物进行分组。
| 食物 | 蛋白质 | 碳水化合物 | 脂肪 | |
|---|---|---|---|---|
| 1 | 苹果 | 0.4 | 11.8 | 0.1 |
| 2 | 鳄梨 | 1.9 | 1.9 | 19.5 |
| 3 | 香蕉 | 1.2 | 23.2 | 0.3 |
| 4 | 牛排 | 20.9 | 0 | 7.9 |
| 5 | 巨无霸汉堡 | 13 | 19 | 11 |
| 6 | 巴西坚果 | 15.5 | 2.9 | 68.3 |
| 7 | 面包 | 10.5 | 37 | 3.2 |
| 8 | 黄油 | 1 | 0 | 81 |
| 9 | 奶酪 | 25 | 0.1 | 34.4 |
| 10 | 酪饼 | 6.4 | 28.2 | 22.7 |
| 11 | 饼干 | 5.7 | 58.7 | 29.3 |
| 12 | 玉米片 | 7 | 84 | 0.9 |
| 13 | 鸡蛋 | 12.5 | 0 | 10.8 |
| 14 | 炸鸡 | 17 | 7 | 20 |
| 15 | 炸薯条 | 3 | 36 | 13 |
| 16 | 热巧克力 | 3.8 | 19.4 | 10.2 |
| 17 | 意大利辣香肠 | 20.9 | 5.1 | 38.3 |
| 18 | 比萨饼 | 12.5 | 30 | 11 |
| 19 | 猪肉馅饼 | 10.1 | 27.3 | 24.2 |
| 20 | 土豆 | 1.7 | 16.1 | 0.3 |
| 21 | 大米 | 6.9 | 74 | 2.8 |
| 22 | 烤鸡 | 26.1 | 0.3 | 5.8 |
| 23 | 糖 | 0 | 95.1 | 0 |
| 24 | 金枪鱼排 | 25.6 | 0 | 0.5 |
| 25 | 水 | 0 | 0 | 0 |
表 1. 25 种食物所含的蛋白质、碳水化合物和脂肪。
这个问题很有趣,因为输入向量的值不同,且每个分量都有自己的取值范围。这对于可视化非常重要,因为我们使用的是分量范围介于 0 与 255 之间的 RGB 颜色模型。
幸好在本例中输入向量也是三维的,因此我们能够将 RGB 颜色模式用于实现 Kohonen 映射的可视化。
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
如您所见,我们添加了数组 m_max_values[] 和 m_min_values[] 以存储训练集的最大值和最小值。为了实现 RGB 颜色模型的可视化,需要进行“定标”,因此我们重载了 Train()、Render() 和 ShowPattern() 方法。
可使用 Train() 方法来查找最大值和最小值。
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
为了以 RGB 颜色模型显示分量,我们需要修改 Render() 方法:
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
som_ex3.mq5 的结果如图 9 所示。
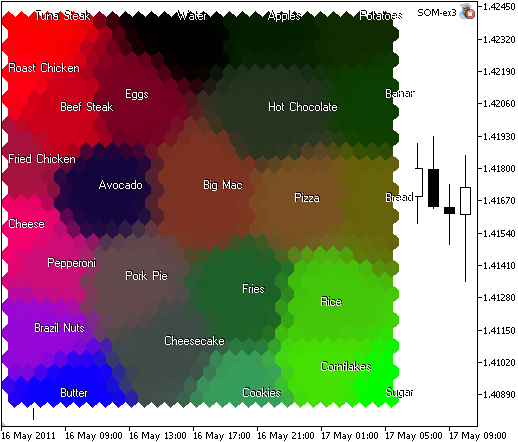
图 9. 根据蛋白质、碳水化合物和脂肪的含量按相似性分组的食物映射
分量分析。可以从映射看到,由于碳水化合物(第 2 个分量)的存在,糖、大米和玉米片是用绿色绘制的。黄油位于蓝色区域中,含有大量脂肪(第 3 个分量)。牛排、烧鸡和金枪鱼排含有大量蛋白质(第 1 个分量)。
如您所见,“纯”R、G、B 颜色所代表方向的问题得到了解决。对于其他含有相等(或几乎相等)分量的食物,结果又如何呢?我们将进一步研究分量平面,它非常有用,特别是在输入向量的维度大于 3 的情况下。
2.4. 示例 4. 4 维案例。Fisher 鸢尾花数据集。CMYK
对于三维向量,可视化方面没有任何问题。由于存在用于实现颜色分量可视化的 RGB 颜色模型,结果就很清楚了。
当处理高维数据时,我们需要找到实现其可视化的方法。简单的解决方案是用与向量长度成正比的颜色来绘制渐变图(例如黑/白渐变图)。另一种方式是使用其他颜色空间。在本例中,我们将研究 Fisher 鸢尾花数据集的 CMYK 颜色模型。有更好的解决方案可用,我们将进一步讨论它。
鸢尾花数据集也称为 Fisher 鸢尾花数据集,是 R. Fisher (1936) 作为判别式分析的示例提出的一个多元数据集。数据集由来自三种鸢尾花(山鸢尾、维吉尼亚鸢尾和变色鸢尾)的每种 50 个样本组成。
每个样本均测量了四个特征,分别为花萼和花瓣的长度和宽度,以厘米为单位。

图 10. 鸢尾花
每个样本均具有 4 个特征:
- 花萼长度;
- 花萼宽度;
- 花瓣长度;
- 花瓣宽度。
可以在 SOM_ex4.mq5 中找到鸢尾花数据集。
在本例中,我们将使用中间 CMYK 颜色空间进行绘图,即我们将节点的权重视为 CMYK 空间中的向量。为实现结果的可视化,将 CMYK 模式转成了 RGB 模式。向 CSOM 类添加了一个新方法 int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k),该方法用在了 CSOM::Render() 方法中。我们还得修改用于支持 4 维向量的类。
结果如图 11 所示。
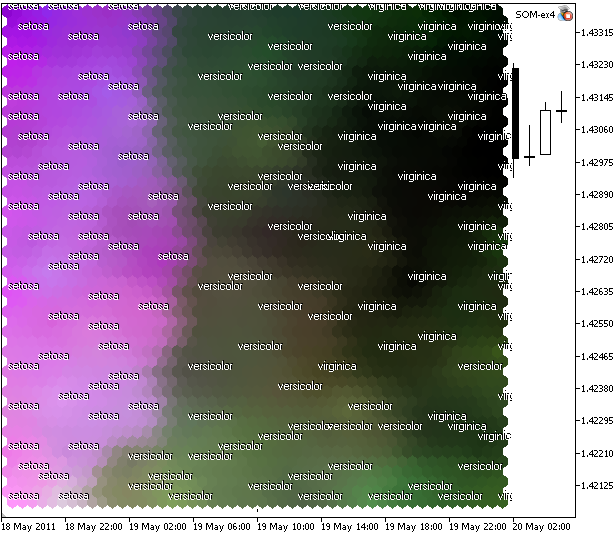
图 11. 以 CMYK 颜色模型绘制的鸢尾花数据集的 Kohonen 映射
我们看到什么了?我们没有得到完整的聚类(因为问题的特征),但是可以看到山鸢尾的线性分离。
山鸢尾线性分离的原因在于 CMYK 空间中存在较大的“洋红”分量(第 2 个分量)。
2.6. 分量平面分析
从以上示例(食物和鸢尾花数据聚类)可以看出,数据可视化存在一个问题。
例如,对于食物问题,我们使用特定颜色(红、绿、蓝)的相关信息来分析 Kohonen 映射。除基本聚类以外,还有含若干分量的某些食物。此外,如果分量几乎相等,则分析也会变得困难。
分量平面提供了查看每种食物相对强度的可能性。
我们需要将 CIntBMP 类的实例(数组 m_bmp[])添加到 CSOM 类并修改对应的呈现方法。我们还需要一个渐变图,对每个分量的强度进行可视化(值越小越偏蓝色,值越大越偏红色):
![]()
图 12. 渐变调色板
我们添加了 Palette[768] 数组、GetPalColor() 方法和 Blend() 方法。节点的绘制放在了 RenderCell() 方法中。
鸢尾花数据集
som-ex4-cpr.mq5 的结果如图 13 所示。
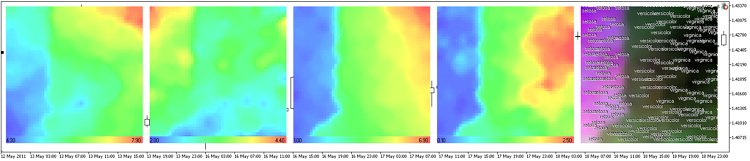
图 13. 鸢尾花数据集的分量平面表示法
在本例中,我们将使用含有 30x30 个节点、图像大小为 300x300 的网格。
分量平面在相关性检测中扮演了重要角色:通过比较这些平面,借由目视检查,甚至部分相关的变量也能被检测出来。如果重新组织分量平面,使相关平面挨在一起,则会更加方便。通过这种方式,就很容易选择感兴趣的分量组合以供进一步调查。
让我们研究下分量平面(图 14)。
渐变表中显示了最大分量和最小分量的值。
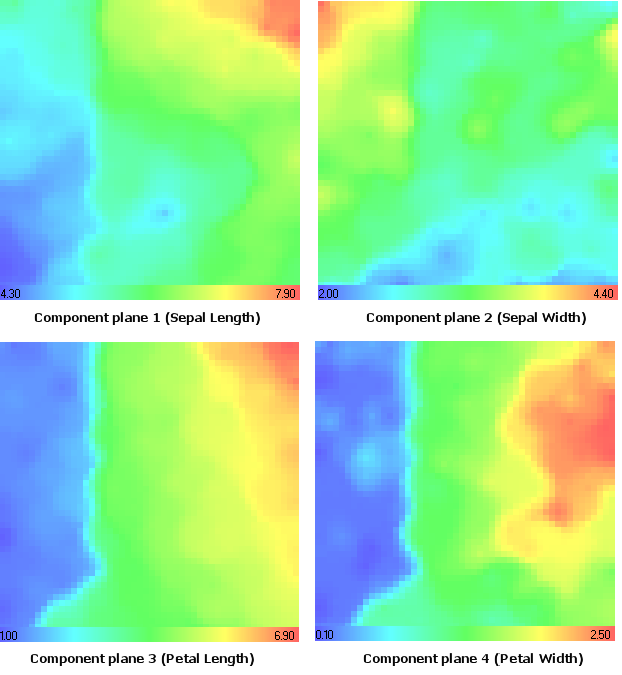
图 14. 鸢尾花数据集。分量平面
图 15 通过 CMYK 颜色模型显示了所有这些分量平面。

图 15. 鸢尾花数据集。以 CMYK 颜色模型表示的 Kohonen 映射
让我们回想一下山鸢尾类型。通过使用分量平面分析(图 14)可以看出,该类型在第 1(花萼长度)、第 3(花瓣长度)和第 4(花瓣宽度)分量平面中有最小值。
显然,该类型在第 2 分量平面(花萼宽度)中有最大值,与我们在 CMYK 颜色模型中得到的结果一致(图 15 中的洋红分量)。
食物聚类
现在,让我们使用分量平面分析法来研究下食物聚类问题 (som-ex3-cpr.mq5)。
结果如图 16 所示(30x30 个节点,图像大小 300x300,以无边框的六边形单元格表示)。
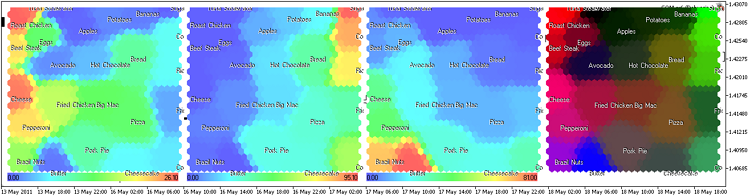
图 16. 使用分量平面表示法的食物 Kohonen 映射
我们在 CSOM 类的 ShowPattern() 方法中添加了显示标题的选项(输入参数 ShowTitles=true)。
分量平面(蛋白质、碳水化合物、脂肪)如下所示:
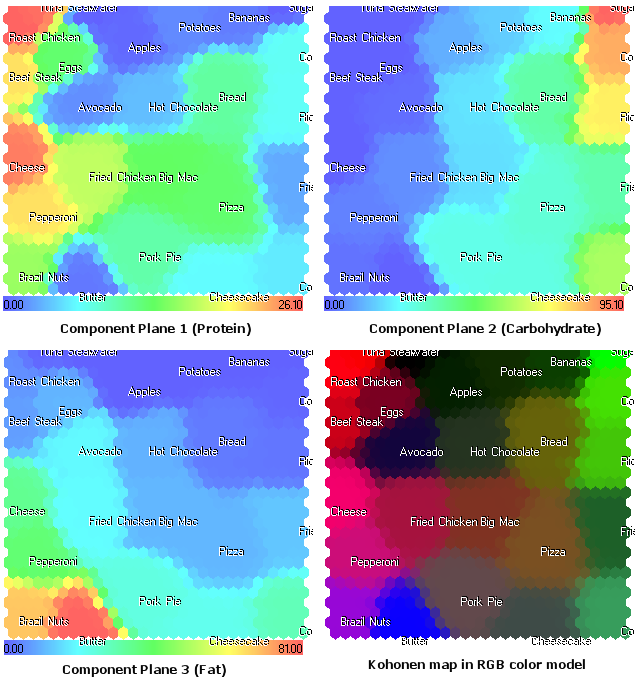
图 17. 食物的 Kohonen 映射。分量平面和 RGB 颜色模型
图 17 所示的分量平面表示法在食物分量结构方面提出了新观点。此外,它还提供了在如图 9 所示的 RGB 模式中看不到的其他信息。
例如,现在我们能够在第 1 分量平面(蛋白质)中看到奶酪。在 RGB 颜色模型中,由于包含了脂肪(第 2 分量),它以接近洋红的颜色显示。
2.5. 针对任意维度的分量平面的实现
我们研究过的示例具有一些特定功能,其维度是固定的,且可视化算法因表示方法(RGB 和 CMYK 颜色模型)不同而有所不同。
现在,我们能够针对任意维度生成算法,但在本例中我们将只实现分量平面的可视化。程序必须能够从 CSV 文件加载任意数据。
例如,food.csv 如下所示:
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
文件的第一行包含输入数据向量的名称(标题)。需要使用标题来区别分量平面,我们将在渐变面板中列出其名称。
样本的名称位于最后一列,在我们的示例中为食物的名称。
SOM.mq5 (OnInit function) 的代码很简单:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
含训练样本的文件的名称在 DataFileName 输入参数中进行了指定,在我们的示例中为 "food.csv"。
结果如图 18 所示。

图 18. 以黑/白渐变颜色方案表示的食物的 Kohonen 映射
我们还添加了 ColorScheme 输入参数以选择渐变方案。
目前有 4 个颜色方案可用(ColorScheme=0、1、2、4,分别表示黑-白、深蓝-蓝-绿-黄-红、红-黑-绿、红-白-绿)。

您可以将渐变添加到 CSOM::InitParameters() 方法中,从而轻松添加自己的方案。
可以从 EA 交易的输入参数中选择颜色方案:
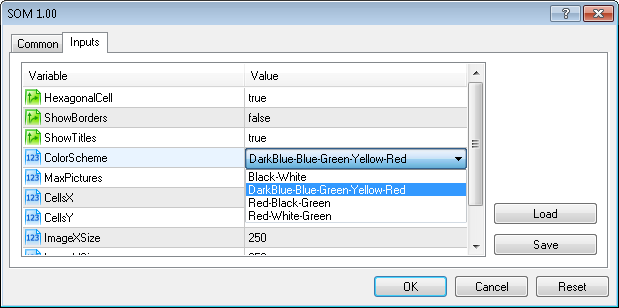
与此类似,我们也可以准备鸢尾花数据集 (iris-fisher.csv):
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
结果如图 19 所示。

图 19. 鸢尾花数据集。采用红-黑-绿颜色方案的分量平面(ColorScheme=2,iris-fisher.csv)
现在,我们拥有了可实际应用的工具。
2.6. 示例 5. 市场热度映射图
自组织特征映射可用于市场运行映射。有时需要市场架构图,市场热度映射图是一个很有用的工具。不同股票被组合在一起,具体视经济领域而定。
股票的当前颜色取决于当前增长率(以 % 为单位):

图 20. 标准普尔 500 指数股票的市场热度映射图
图 20 显示了标准普尔股票的每周市场热度映射图 (http://finviz.com)。颜色取决于增长率(以 % 为单位):
![]()
股票矩形的大小取决于市值大小。可以在 MetaTrader 5 客户端中使用 Kohonen 映射进行相同的分析。
这一想法是使用几个时间表的增长率(以 % 为单位)。我们具有可处理 Kohonen 映射的工具,因此只需要将数据保存到 .csv 文件中的脚本即可。
可以在 MetaQuotes Demo 服务器中找到有关美洲股票 CFD 价格的价格数据(#AA、#AIG、#AXP、#BA、#BAC、#C、#CAT、#CVX、#DD、#DIS、#EK、#GE、#HD、#HON、#HPQ、#IBM、#INTC、#IP、#JNJ、#JPM、#KFT、#KO、#MCD、#MMM、#MO、#MRK、#MSFT、#PFE、#PG、#T、#TRV、#UTX、#VZ、#WMT 和 #XOM)。
准备 dj.csv 文件的脚本非常简单:
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
必须下载历史数据,您可以使用 DownloadHistory 脚本来实现自动下载。
作为 dj.mq5 脚本的运行结果,我们将得到含有以下数据的 dj.csv 文件:
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
启动 som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv") 之后,我们将得到 8 个图片,每个对应的时间间隔为 30、60、90、120、150、180、210 和 240 分钟。
2011 年 5 月 23 日最后 4 小时交易进程的市场增长率数据(美洲股票)的 Kohonen 映射如图 21 所示。
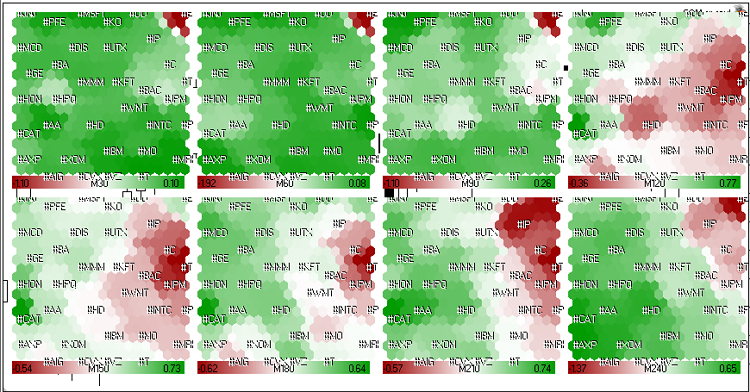
图 21. 美洲股票的 Kohonen 映射(2011 年 5 月 23 日最后 4 小时的交易进程)。
可以从图 21 看出,#C (Citigroup Inc.)、#T (AT&T Inc.)、#JPM (JPMorgan Chase & Co)、#BAC (Bank of America) 的动态比较相似。它们分组在一个长期的红色聚类中。
在最后 1.5 小时内(M30、M60、M90),其动态趋势变为绿色,但是整体而言 (M240),股票仍位于红色区域内。
使用 Kohonen 映射,我们能够实现股票相对动态的可视化,找出领先和落后的股票,以及其所在环境。具有类似数据形式的元素构成了聚类。
如图 21a 所示,花旗集团 (Citigroup Inc) 的股票价格下降最快。一般而言,所有金融公司的股票都在红色区域内。
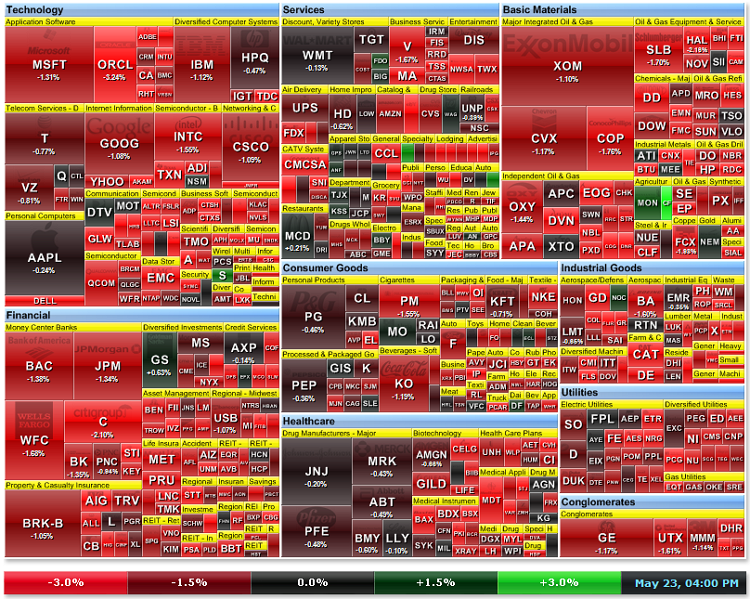
图 21a.2011 年 5 月 23 日的市场热度映射图(来源:http://finviz.com)
与此类似,我们也可以计算 FOREX 市场的 Kohonen 映射(图 22):
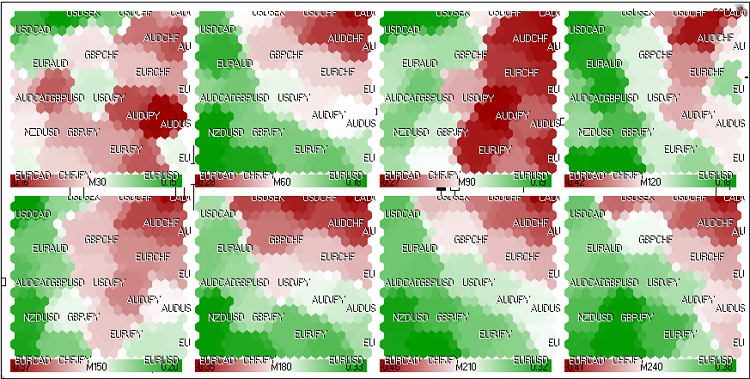
图 22. FOREX 市场的 Kohonen 映射(2011 年 5 月 24 日欧洲进程)
使用以下货币对:EURUSD、GBPUSD、USDCHF、USDJPY、USDCAD、AUDUSD、NZDUSD、USDSEK、AUDNZD、AUDCAD、AUDCHF、AUDJPY、CHFJPY、EURGBP、EURAUD、EURCHF、EURJPY、EURNZD、EURCAD、GBPCHF、GBPJPY、CADCHF。
使用 fx.mq5 脚本将增长率导出到 fx.csv 中。
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
除价格以外,还可以使用不同时间表的指标值。
2.6. 示例 6. 优化结果的分析
MetaTrader 5 客户端的策略测试程序让您有机会研究参数空间结构,以及查找找出最佳策略参数集。您还可以从 "Optimization Results"(优化结果)选项卡的上下文菜单中选择 "Export to XML (MS Office Excel)"(导出到 XML (MS Office Excel))选项来导出优化结果。
优化结果也包含了测试程序统计信息(41 列):
- 结果
- 盈利
- 毛利
- 毛损
- 提款
- 预计获利
- 盈利系数
- 回收系数
- 夏普比率
- 预付款水平
- 自定义
- 最少余额
- 余额亏损最大值
- 余额亏损最大值 (%)
- 余额亏损相对值
- 余额亏损相对值 (%)
- 最小资产净值
- 资产净值亏损最大值
- 资产净值亏损最大值 (%)
- 资产净值亏损相对值
- 资产净值亏损相对值 (%)
- 交易次数
- 成交笔数
- 短线交易次数
- 获利短线交易次数
- 长线交易次数
- 获利长线交易次数
- 获利交易次数
- 损失交易次数
- 最大获利交易
- 最大损失交易
- 最大连续获利次数
- 最大连续获利次数 ($)
- 最大连续收益
- 最大连续收益次数
- 最大连续亏损次数
- 最大连续亏损次数 ($)
- 最大连续损失金额
- 最大连续损失次数
- 平均连续获利次数
- 平均连续亏损次数
使用测试程序统计信息有助于对参数空间进行分析。显而易见,大量统计参数密切相关且取决于交易业绩。
例如,最佳交易结果就具有最大的获利、获利系数、回收系数和夏普比率参数值。这样便能够在结果分析中使用到这些参数。
MovingAverage.mq5 EA 交易的优化结果
在本章中,我们将考虑分析 MovingAverage.mq5 EA 交易的优化结果,该交易包含在 MetaTrader 5 客户端标准组件中。该 EA 交易基于价格和移动平均线指标的穿越。它有两个输入参数:MovingPeriod 和 MovingShift。这样我们便拥有了内含 43 列的 XML 文件。
我们将不考虑 43 维的参数空间。我们最感兴趣的是:
- 获利;
- 获利系数;
- 回收系数;
- 夏普比率;
- 交易次数;
- 获利交易次数百分比;
- 移动周期;
- 移动偏移;
注意,我们添加了参数 ProfitTrades (%)(获利交易次数百分比,它不在结果中),该参数表示获利交易的百分比,通过将获利交易次数 (28) 除以交易次数 (22),再乘以 100 得出。
让我们准备 optim.csv 文件,该文件有 9 列,包含 MetaTrader 5 策略测试程序的 400 组输入参数。
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
由于我们使用了 MovingPeriod(移动周期)的值作为一个标题列,它将用于在 Kohonen 映射上“标记”样本。
在策略测试程序中,我们已经通过以下参数优化了 MovingPeriod(移动周期)和 MovingShift(移动偏移)的值:
- 交易品种 - EURUSD,
- 周期 - H1,
- 价格变动生成模式 - "1 Minute OHLC",
- 测试区间 - 2011.01.01-2011.05.24,
- 优化 - 快速(遗传算法),
- 优化 - 最大余额
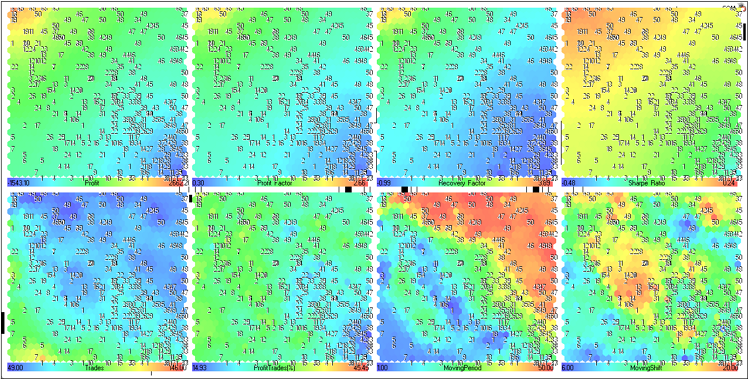
图 23. MovingAverage EA 交易优化结果的 Kohonen 映射(分量平面表示法)
让我们研究下上面一行的分量平面(获利、获利系数、回收系数和夏普比率)。
它们合并在了图 24 中。
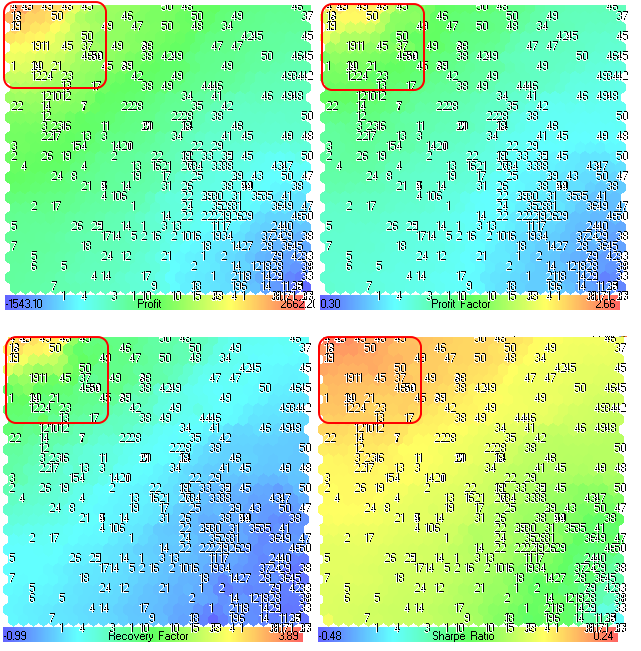
图 24. 获利、获利系数、回收系数和夏普比率参数的分量平面
首先,我们需要找出优化结果最佳的区域。
从图 24 可以看出,具有最大值的区域位于左上角。数字对应于移动平均线指标的平均周期(MovingPeriod 参数,我们将其用作标题)。对于所有分量平面而言,数字的位置都是相同的。每个分量平面都有自己的取值范围,其值列于渐变面板中。
由于最佳优化结果具有较大的获利、获利系数、回收系数和夏普比率值,因此我们便拥有了映射上各个区域的相关信息(如图 24 所述)。
图 25 显示了交易次数、获利交易次数百分比、移动周期和移动偏移的分量平面。
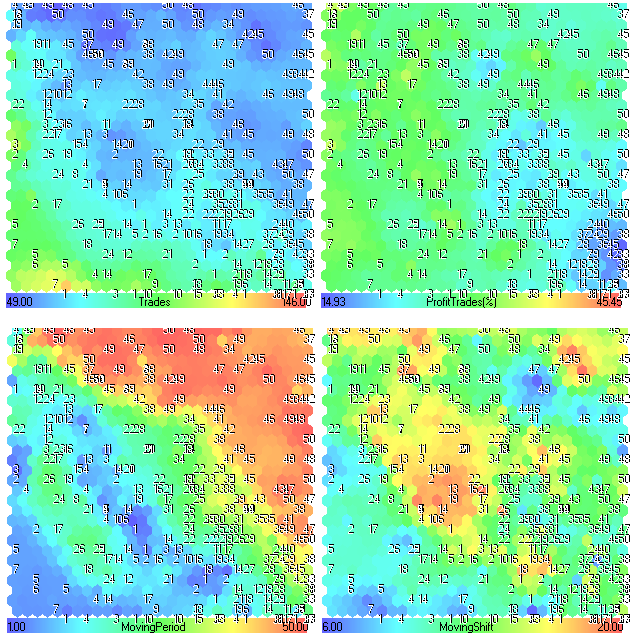
图 25. 交易次数、获利交易次数百分比、移动周期和移动偏移参数的分量平面
分量平面分析
乍看上去并没有任何有趣的信息。前 4 个分量平面(获利、获利系数、回收系数和夏普比率)看起来比较类似,因为它们直接取决于交易系统的性能。
从图 24 可以看出,左上角区域非常有趣(例如,如果我们将移动周期从 45 设为 50,则可能实现最佳结果)。
EA 交易是按 EURUSD 的一小时时间表测试的,其策略取决于趋势;我们可以将这些值视为一种“市场趋势”记忆内容。如果确实是这样,则 2011 年上半年的市场趋势记忆内容相当于 2 天。
让我们研究下其他分量平面。
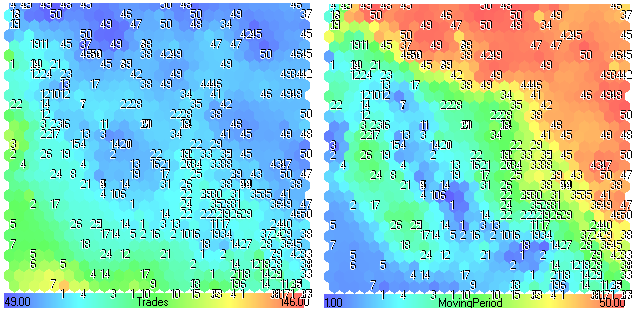
图 26. 交易次数-移动周期分量平面
从图 26 可以看到移动周期的较小值(蓝色区域)扩展到交易次数的较大值(黄-红区域)。如果移动平均线的周期较小,则会存在多次穿越(交易次数)。
我们也可以在交易次数分量平面(数字小于 20 的绿色区域)上看到这一情况。
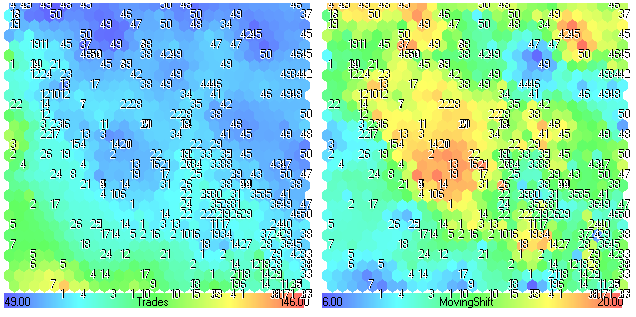
图 27. 交易次数-移动偏移分量平面
在移动偏移增加(黄-红区域)的地方交易次数就会下降(蓝色区域)。将移动偏移分量平面与图 24 比较,可以看出对于此交易策略的性能而言,移动偏移参数并不是非常重要。
获利交易次数百分比 ProfitTrades(%) 并不直接取决于移动周期或移动偏移,而是交易系统的一个整体特征。换言之,分析其与输入参数的相关性并没有意义。
可以用类似方法分析更加复杂的交易策略。您需要找出交易系统最重要的参数并将其用作标题。
总结
自组织特征映射的主要优势在于有机会生成高维数据的二维离散表示法。具有类似特征的数据会形成聚类,从而简化了相关性分析。
可以在 Guido Deboeck 与 Teuvo Kohonen 合写的著作《Visual Explorations in Finance:with Self-Organizing Maps》(金融的视觉探索)中找到详细信息和其他应用。
附录
在俄文版出版之后,Alex Sergeev 提出了改进型的类 (SOM_Alex-Sergeev_en.zip)。
变更清单:
1. 图像的显示出现改变:cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. 添加了打开含图像文件夹的功能:
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
在 CSOM 类中的变化:
- 添加了一个方法 CSOM::HideChart - 隐藏图表。
- 添加了类成员 m_chart、m_wnd、m_x0、m_y0 - (显示图片的图表、窗口和坐标)。
还添加了 m_sID - 对象名称前缀。前缀使用文件名,默认情况下使用 "SOM" 前缀。 - 所有映射都被保存到文件夹中,其名称含有 m_sID。
- bmp 文件按样本的列名称命名。
- 修改了 CSOM::ShowBMP 方法(映射保存在 \Files 文件夹而非 \Images 中,这样运行会更快)。
- CSOM::NetDeinit 更改为 CSOM::HideBMP。
- 修改了 CSOM::ReadCSVData 方法,第一列包含标题。
- 在 CSOM::Train(bool bShowProgress) 中添加了用于显示中间映射的标志。
- 在 CSOM::Train 中,每 2 秒钟显示一次中间映射(而非迭代),并通过注释将进度显示在图表中。
- 优化了某些按类别排列的变量和类方法的名称。
bmp 文件的绘制过程非常缓慢。如果不是确实需要,请不要每次都绘制它。
压缩档案包含了具有优化结果的 SOM 图像的示例。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/283
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
 创建 EA 交易优化的自定义标准
创建 EA 交易优化的自定义标准
 统计估计
统计估计
 使用带 ENCOG 机器学习框架的 MetaTrader 5 指标进行时间序列预测
使用带 ENCOG 机器学习框架的 MetaTrader 5 指标进行时间序列预测
人们总是看到自己想看到的东西。
这正是您在上面的帖子中所证实的--我一点也不想争论"科霍宁 的自组织地图"的正确翻译--这个翻译是否有任何余地:
我总是从根本上看问题,我知道如果科霍宁图不能预测,就不会有人称之为神经网络。
正如人们对讨论 "S.Osovsky "的名言 "的兴趣,实践证明--从英文资源转载作品的现象在 runet 中盛行,我不确定 Osovsky 是否写过自己的作品,我是在与论坛成员讨论,而不是与作者讨论?
我在链接中展示了我在runet上对这一主题的搜索,在权威的、我认为是BaseGroup Labs的网站上也没有确认.....
.... 好了,我说完了--我不想再重复了,只想预测一下 ))))。
所附更改列表:
1. 函数 cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, boolaFromImages=true)
中的小改动 2. 添加到了主脚本中
CSOM 类中的更改
1.已添加CSOM::HideChart 函数--该函数可在背景色下将图表、网格等调暗
2.添加了参数m_chart、m_wnd、m_x0、m_y0- 指示在哪个图表和窗口上显示地图。
+对象名称 的前缀m_sID。文件名 会自动使用该前缀,否则会指定为 "SOM"
3. 地图会被写入名为m_sID 的文件夹
4.
4. 更改了CSOM::ShowBMP 功能 - 地图不会复制到 Images文件夹 ,而是保留在 Files 文件夹中 (否则会非常耗时)
5.取代CSOM::NetDeinit 函数 - 现在有了CSOM::HideBMP 函数
7.重新配置了CSOM::ReadCSVData 函数,读取文件时第一列 为名称列
6.为CSOM::Train 函数添加了显示中间地图的标志CSOM::Train( boolbShowProgress)
8.在CSOM::Train 函数中,每 2 秒显示一次中间数据,而不是迭代,
,进度通知也从日志移到了注释
9.缩短了一些变量名,并对函数进行了分类。
Bmp 渲染会大大降低进程速度。因此最好不要不必要地使用它。
Kohonen 地图适用于对大量不同数据进行分类。例如,100 种不同的动物。在这种情况下,您必须根据一个参数(毛色)进行分类。这种方法的数学原理不允许将不同的参数组合在一起。
对于外汇交易决策来说,这种方法是最愚蠢的。试想一下,通过一个参数进行分类就可以做出 "购买 "或 "不购买 "的决定。那么你就可以在 Kohonen 地图上建立两个节点,这将非常有趣。当然,也有一些 "马斯达顿人 "会绘制出 1 万个节点,他们会津津有味地看着这张地图,说:"啊,它的颜色真漂亮。
下面是一个标准 MT5 智能交易系统的周期和移位示例--一个单独的 Kohonen 地图(网络?您可以坐下来思考如何处理它。
多层perseptron 是一个黑盒子,如果一切操作正确,您需要输入不同的参数,然后在输出端得到一个明确的答案--大于阈值(回答 "是")或小于阈值(回答 "否")。这比较适合我。
在阅读了几本关于机器学习的书籍后,我注意到有一个观点总是在重复:创建神经网络 没有单一的模板。每项任务都需要对数据进行极其个性化的研究、准备数据、找到网络结构并调整该网络。换句话说,有些选项并不适合外汇交易,也不适合做出 "买入 "或 "不买入 "的决定。我认为科霍宁的地图就不适合。
虽然我们这些有才能的人经常出错,但错误是人才的主要优势。
虽然我们这些人才经常犯错误,但错误正是人才的主要优势。
我差点吐了
Kohonen 地图适用于对大量不同数据进行分类。例如,100 种不同的动物。在这种情况下,您必须根据一个参数--毛色--进行分类。这种方法的数学原理不允许将不同的参数组合在一起。
对于外汇交易决策来说,这种方法是最愚蠢的。试想一下,用一个参数进行分类就可以做出 "买 "或 "不买 "的决定。那么你就可以在 Kohonen 地图上建立两个节点,这将非常有趣。当然,也有一些 "马斯达顿人 "会绘制 1 万个节点,他们会津津有味地看着这张地图,说:啊,它的颜色真漂亮。
下面是一个标准 MT5 智能交易系统的周期和移位示例--平滑周期有一个单独的 Kohonen 地图(网络?您可以坐下来思考如何处理它。
我认为 Kohonen 地图不适合做这个。
你就是不明白。
地图不一定要回答 "到哪里去 "的问题。
它可以突出历史中的类似模式,这样你就不必手动坐着找上半 年。
给猴子一个工具,它就有可能开始用尺子 敲 钉子。