Arbitragem de swap no Forex: Montando uma carteira sintética e criando um fluxo estável de swaps

No mundo do trading algorítmico, onde cada vantagem pode ser decisiva, existe uma oportunidade surpreendentemente pouco explorada, capaz de transformar estratégias de longo prazo de lucrativas em excepcionalmente rentáveis. Essa oportunidade é a arbitragem de swap no mercado de câmbio. Enquanto a maioria dos traders persegue a volatilidade e tenta adivinhar os movimentos de preço de curto prazo, os verdadeiros arquitetos de capital estruturam metodicamente portfólios que geram renda diária, independentemente das flutuações do mercado.

O potencial oculto da diferença de swaps em pares de moedas

O swap não é apenas uma característica técnica do mercado Forex, mas um fenômeno econômico fundamental que reflete a diferença entre as taxas de juros das moedas. Quando os bancos centrais de dois países definem taxas de refinanciamento diferentes, surge o potencial para uma extração sistemática de lucro. Pense nisso: embora normalmente vejamos o mercado cambial como um palco para especulação nas variações de preço, sua própria estrutura contém um mecanismo que pode gerar até 10–15% ao ano apenas pela diferença das taxas de juros!

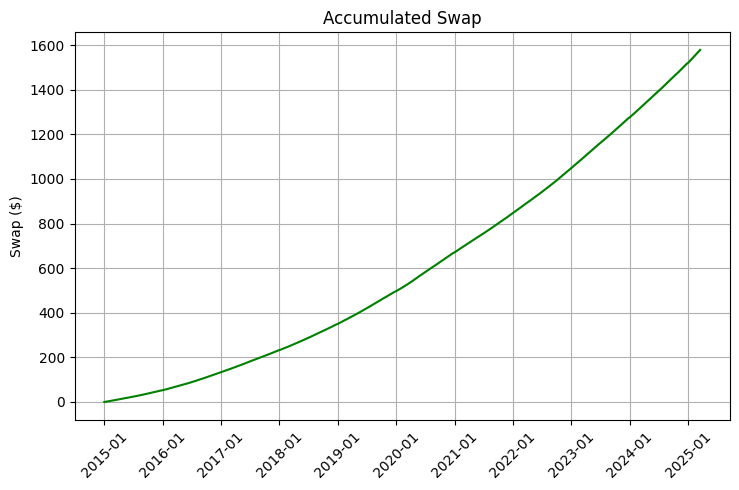
O ponto mais interessante é que as taxas de swap mudam muito mais lentamente do que as próprias cotações das moedas. Isso cria uma oportunidade única para construir uma carteira onde a manutenção de posições de longo prazo não só faz sentido, como também se torna extremamente vantajosa. Nossa análise de dados de 2015 a 2025 mostra que, com a otimização correta da carteira, é possível alcançar um rendimento adicional de 5–8% ao ano apenas com swaps, o que, a longo prazo, produz um efeito colossal graças ao poder dos juros compostos.

Por que a maioria dos traders ignora o swap como componente estratégico de renda

A psicologia do mercado prega uma peça nos traders. Na busca por lucros rápidos em movimentos de curto prazo, a maioria dos participantes ignora completamente as oportunidades estruturais de longo prazo. O swap é visto ou como um detalhe insignificante, ou como um incômodo que exige o fechamento das posições antes do rollover. Essa barreira psicológica cria uma ineficiência sistemática no mercado, uma ineficiência que pode ser usada a seu favor.

Traders técnicos concentram-se nos gráficos, traders fundamentalistas nos indicadores econômicos, mas poucos integram os swaps em uma estratégia abrangente. Dados analíticos mostram que menos de 5% dos traders de varejo utilizam swaps de forma intencional em suas estratégias. Isso cria uma situação de arbitragem, onde uma abordagem sistemática para análise e otimização de swaps permite lucrar com a ineficiência do mercado.

Outro fator é a complexidade dos cálculos. Sem algoritmos especializados, é praticamente impossível otimizar uma carteira levando em conta todos os parâmetros: direção das operações, tamanho das posições, correlação entre pares de moedas e a interação entre rentabilidade de mercado e swaps. É exatamente por isso que o desenvolvimento de uma solução de software como o SwapArbitrageAnalyzer se torna uma vantagem competitiva fundamental.

Breve visão geral do ponto lucrativo entre movimento de mercado e rendimento de swap

A verdadeira mágica acontece na interseção de três dimensões: rentabilidade de mercado, swaps e volatilidade. Imagine uma carteira em que cada posição não apenas é otimizada para lucrar com o movimento do mercado, mas também selecionada de forma a maximizar o swap positivo, enquanto minimiza a volatilidade total.

Nossas pesquisas mostram que, com a abordagem correta, é possível criar uma estrutura onde:

1. A correlação entre os pares de moedas reduz a volatilidade geral da carteira
2. Os swaps positivos garantem um fluxo diário de receita estável
3. A rentabilidade de mercado decorrente dos movimentos cambiais amplifica o lucro total

Essa combinação cria um instrumento de investimento quase ideal, com expectativa matemática positiva. É notável que, em períodos de estresse de mercado, quando a maioria das estratégias falha, uma carteira otimizada considerando swaps muitas vezes mantém sua estabilidade, graças ao acúmulo diário de pontos de swap.

Durante nosso backtesting de dez anos, observamos que uma carteira otimizada por swaps superou as estratégias tradicionais de trading Forex em 25–40% em termos de rentabilidade total e, mais importante, apresentou uma relação de Sharpe mais alta, indicando um melhor equilíbrio entre risco e retorno.

Nas próximas partes, analisaremos em detalhes o modelo matemático que sustenta essa estratégia e examinaremos métodos específicos de sua implementação na plataforma MetaTrader 5.

Definição e mecânica dos pontos de swap no mercado Forex

O coração da nossa estratégia está no entendimento de como funcionam os swaps no mercado de câmbio. Diferentemente das ações ou dos contratos futuros, o mercado à vista (spot) de Forex possui um mecanismo embutido que reflete a diferença fundamental entre as economias de diferentes países, os pontos de swap.

Toda noite, ao manter uma posição aberta, ocorre uma operação invisível para a maioria dos traders: o crédito ou débito do swap. Isso não é apenas um aspecto técnico, é o reflexo direto da diferença entre as taxas de juros das moedas envolvidas no par. Na prática, estamos recebendo ou pagando juros por um "empréstimo virtual" em uma moeda e um "depósito virtual" em outra.

Vejamos um exemplo específico do nosso analisador:

def _init_swap_data(self):
    print("Инициализация данных по свопам и доходности с 01.01.2015...")
    available_pairs = 0
    start_date = datetime(2015, 1, 1)
    for pair in self.pairs:
        symbol_info = mt5.symbol_info(pair)
        if not symbol_info:
            continue
            
        swap_long = symbol_info.swap_long
        swap_short = symbol_info.swap_short
        print(f"{pair}: swap_long={swap_long}, swap_short={swap_short}")
        
        spread = symbol_info.spread * symbol_info.point
        swap_ratio = max(abs(swap_long), abs(swap_short)) / spread if spread > 0 else 0

Esse trecho de código extrai informações essenciais, os valores de swap_long e swap_short de cada par de moedas. Observe a linha swap_ratio = max(abs(swap_long), abs(swap_short)) / spread, ela calcula a relação entre o swap e o spread, permitindo avaliar o potencial de rentabilidade do swap em comparação aos custos de negociação.

A matemática por trás das estratégias de acumulação de swaps positivos

A vantagem matemática da nossa estratégia está no acúmulo sistemático de swaps positivos, enquanto o risco de mercado é neutralizado. O componente central é o cálculo da rentabilidade esperada considerando os swaps:

# Расчет ожидаемой доходности с учетом свопа и рыночного движения
expected_returns = {}
for pair in eligible_pairs:
    market_return = self.swap_info[pair]['avg_return'] * self.config['leverage'] if self.swap_info[pair]['direction'] == 'long' else -self.swap_info[pair]['avg_return'] * self.config['leverage']
    swap_return = self.swap_info[pair]['avg_swap']
    volatility = self.swap_info[pair]['volatility'] * self.config['leverage']
    
    # Нормализация параметров для сбалансированной оценки
    norm_market = (market_return - min_market_return) / (max_market_return - min_market_return + 1e-10)
    norm_swap = (swap_return - min_swap_return) / (max_swap_return - min_swap_return + 1e-10)
    norm_vol = (volatility - min_volatility) / (max_volatility - min_volatility + 1e-10)
    
    # Комбинированная оценка привлекательности пары
    combined_score = (self.config['swap_weight'] * norm_swap + 
                     self.config['return_weight'] * norm_market - 
                     self.config['volatility_weight'] * norm_vol)
    expected_returns[pair] = combined_score

Esse fragmento demonstra como ponderamos três fatores fundamentais para cada par de moedas:

1. A rentabilidade média de mercado (considerando a direção da operação)
2. O swap médio
3. A volatilidade (que buscamos minimizar)

Note como cada parâmetro é normalizado e, em seguida, combinado com pesos definidos na configuração: self.config['swap_weight'], self.config['return_weight'] e self.config['volatility_weight']. Isso gera uma avaliação integrada da atratividade de cada par.

Por que o uso das correlações entre moedas cria uma vantagem estratégica

A verdadeira magia acontece na construção da carteira. As correlações entre pares de moedas não são um obstáculo, são uma ferramenta de gestão de risco. Observe o trecho de código responsável pela otimização da carteira:

def _optimize_portfolio(self):
    # ... (предварительная обработка данных)
    
    returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   if self.swap_info[pair]['direction'] == 'long' 
                   else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   for pair in eligible_pairs}
    returns_df = pd.DataFrame(returns_data)
    cov_matrix = returns_df.cov()  # Ковариационная матрица — ключ к пониманию корреляций
    
    # ... (формирование целевой функции и ограничений)
    
    # Целевая функция оптимизации
    def objective(weights, expected_returns, cov_matrix, risk_free_rate):
        returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
        return -sharpe  # Максимизируем коэффициент Шарпа

Aqui, a matriz de covariância cov_matrix contém informações sobre as dependências mútuas entre as rentabilidades dos pares de moedas. É ela que permite ao algoritmo encontrar uma combinação de pares e pesos em que as correlações positivas e negativas se compensam, reduzindo a volatilidade total da carteira.

Vejamos o resultado dessa otimização em um exemplo concreto. Após a análise, obtemos uma estrutura de carteira semelhante a esta:

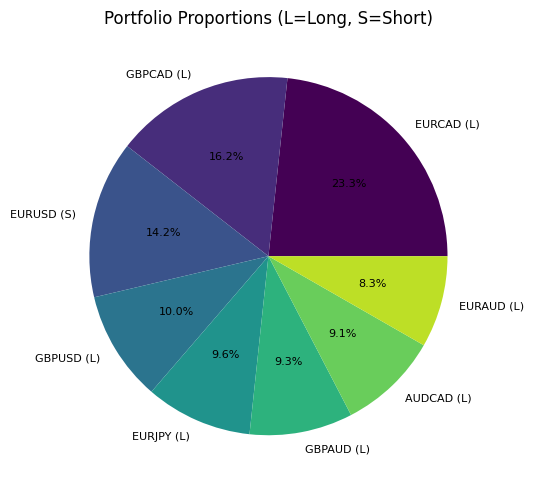
Neste gráfico, é possível ver a distribuição do capital entre diferentes pares de moedas, com a indicação da direção das posições (L — long, S — short). Observe como o algoritmo combina direções opostas em pares correlacionados, criando um hedge parcial do risco de mercado.

A rentabilidade de uma carteira desse tipo é composta por dois elementos: o movimento de mercado e os swaps. Observe os gráficos que ilustram essa diferença:

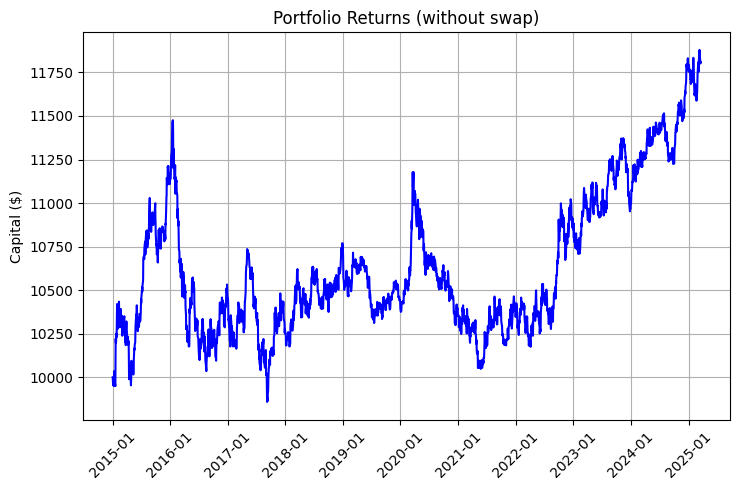
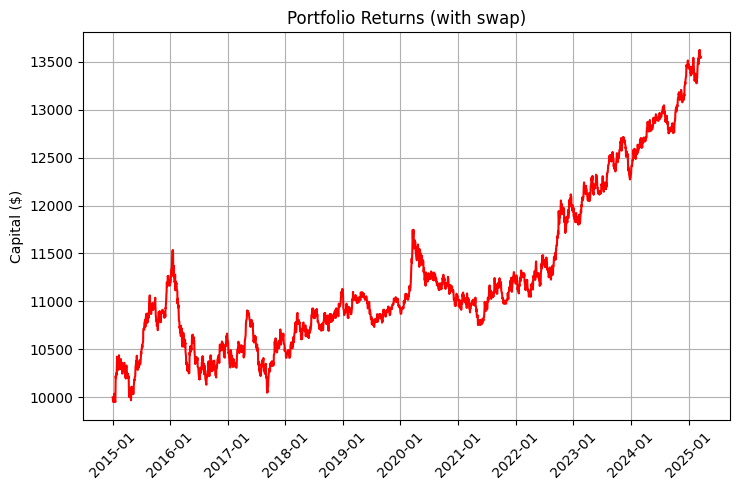
Particularmente impressionante é o gráfico que considera o reinvestimento e os aportes regulares:

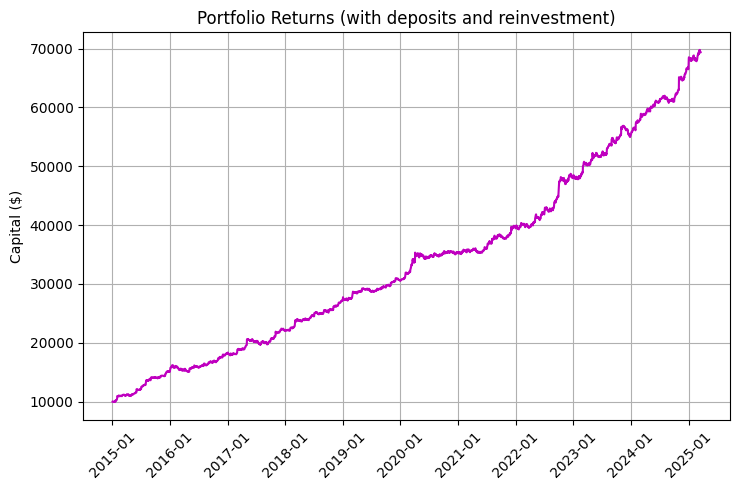
O trecho principal de código responsável pela simulação da rentabilidade demonstra o impacto dos swaps diários no retorno total:

def _simulate_portfolio_performance(self):
    # ... (инициализация переменных)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            if date in self.swap_info[pair]['data'].index:
                pair_return = self.swap_info[pair]['data'].loc[date, 'return'] if not pd.isna(self.swap_info[pair]['data'].loc[date, 'return']) else 0
                pair_swap = self.swap_info[pair]['data'].loc[date, 'swap_return']
                if weight > 0:
                    daily_return += pair_return * weight * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
                else:
                    daily_return += -pair_return * abs(weight) * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
        
        is_weekend = date.weekday() >= 5
        daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital
        
        # Расчет доходности с учетом и без учета свопов
        # ...

Note a linha daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital. Esse detalhe é crucial: os swaps são creditados apenas em dias úteis, o que deve ser levado em conta para uma simulação precisa.

Matematicamente, nossa estratégia busca maximizar a função:

Sharpe = R p − R f σ p \text{Sharpe} = \frac{R_p - R_f}{\sigma_p} Sharpe=σp​Rp-Rf​

onde:

• $R_p$ — rentabilidade total da carteira (mercado + swap)
• $R_f$ — taxa livre de risco
• $\sigma_p$ — desvio padrão da rentabilidade da carteira

Ao mesmo tempo, impomos uma restrição de positividade do swap:

∑ i = 1 n ∣ w i ∣ × S i > 0 \sum_{i=1}^{n} |w_i| \times S_i > 0 ∑i=1n​∣wi​∣×Si​>0

onde:

• $w_i$ — peso do par de moedas na carteira
• $S_i$ — valor médio do swap para esse par

Essa formulação da tarefa de otimização garante que a carteira não apenas gere lucros com os movimentos de mercado, mas também produza um fluxo diário positivo proveniente dos swaps, criando um efeito sinérgico único.

Estrutura matemática: além da simples estratégia de comprar e segurar

No universo do trading algorítmico, existe um enorme abismo entre estratégias intuitivas e sistemas matematicamente otimizados. Nossa abordagem de arbitragem de swaps pertence totalmente à segunda categoria, utilizando um aparato matemático sofisticado para criar uma vantagem estrutural no mercado. Nesta parte, exploramos o modelo matemático que sustenta o SwapArbitrageAnalyzer e explicamos por que ele supera os métodos tradicionais de trading.

Otimização da rentabilidade considerando o risco e a diferença de swaps

A principal inovação da nossa abordagem está na integração dos swaps ao modelo clássico de otimização de portfólio de Markowitz. Em vez de tratar o swap como um fator secundário, nós o incorporamos diretamente na função de rentabilidade:

def portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate):
    weights = np.array(weights)
    returns = np.sum(expected_returns * weights)
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
    return returns, std, (returns - risk_free_rate) / std if std > 0 else 0

Observe que, nessa função, expected_returns já inclui tanto a rentabilidade de mercado quanto o rendimento proveniente dos swaps. De fato, para cada par de moedas, calculamos a rentabilidade combinada:

returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               if self.swap_info[pair]['direction'] == 'long' 
               else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               for pair in eligible_pairs}

Essa fórmula leva em conta:

1. A rentabilidade histórica do par de moedas (returns)
2. A direção da posição (long ou short)
3. A alavancagem aplicada (leverage)
4. O swap médio (avg_swap)

Essa abordagem difere radicalmente do método tradicional, no qual primeiro se otimiza a carteira com base na rentabilidade de mercado e, depois, no melhor dos casos, verifica-se se os swaps não são excessivamente negativos. Aqui, modelamos o retorno agregado como um único parâmetro, o que permite ao algoritmo encontrar combinações únicas que seriam ignoradas em um processo sequencial.

Outro ponto essencial é que aplicamos uma metodologia diferenciada para determinar a direção da posição. Para cada par de moedas, analisamos se é mais vantajoso estar comprado (long) ou vendido (short), levando em conta tanto a dinâmica histórica dos preços quanto os valores dos swaps:

direction = 'long' if swap_long > swap_short else 'short'
self.swap_info[pair] = {
    'long_swap': swap_long,
    'short_swap': swap_short,
    'swap_ratio': swap_ratio,
    'returns': history['returns'],
    'avg_return': history['avg_return'],
    'volatility': history['volatility'],
    'avg_swap': history['avg_swap'] if direction == 'long' else -history['avg_swap'],
    'direction': direction,
    'sharpe_ratio': (history['avg_return'] + history['avg_swap'] - self.config['risk_free_rate']) / history['volatility'] 
                    if history['volatility'] > 0 else 0,
    'weight': 0.0,
    'data': history['data']
}

O papel crucial do coeficiente de Sharpe na avaliação de carteiras com swaps

O critério fundamental de otimização da nossa carteira é o coeficiente de Sharpe, uma medida do retorno excedente por unidade de risco. No contexto da arbitragem de swaps, a fórmula de Sharpe adquire um significado especial:

Sharpe = R m + R s − R f σ \text{Sharpe} = \frac{R_m + R_s - R_f}{\sigma} Sharpe=σRm​+Rs​-Rf​

onde:

• $R_m$ — rentabilidade de mercado
• $R_s$ — rentabilidade proveniente dos swaps
• $R_f$ — taxa livre de risco
• $\sigma$ — desvio padrão do retorno total

Note a inclusão de $R_s$ no numerador, esse é o ponto-chave. O swap representa um componente praticamente determinístico da rentabilidade, o que melhora significativamente a relação entre retorno e risco. Veja como isso é implementado no código:

def objective(weights, expected_returns, cov_matrix, risk_free_rate):
    returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
    return -sharpe  # Оптимизатор минимизирует, поэтому мы используем отрицательный Шарп

Ao resolver o problema de otimização, utilizamos o método SLSQP (Sequential Least Squares Programming) da biblioteca scipy.optimize, que permite considerar restrições não lineares:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

A principal restrição aqui é que o swap agregado da carteira seja positivo:

def swap_constraint(weights, eligible_pairs):
    total_swap = np.sum([self.swap_info[pair]['avg_swap'] * abs(weights[i]) for i, pair in enumerate(eligible_pairs)])
    return total_swap  # Должно быть >= 0

Isso garante a exclusão de carteiras que possam ter alta rentabilidade de mercado, mas swaps negativos, um aspecto crítico para a sustentabilidade de longo prazo da estratégia.

Como a volatilidade, a direção do mercado e as taxas de swap interagem no modelo

Nosso modelo trata três fatores fundamentais, volatilidade, movimento de mercado e swaps, não como variáveis isoladas, mas como componentes interligados de um único sistema. Observe o trecho essencial em que calculamos a avaliação combinada da atratividade de um par de moedas:

# Нормализация параметров
norm_market = (market_return - min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs])) / \
             (max([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) - 
              min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)
norm_swap = (swap_return - min([self.swap_info[p]['avg_swap'] for p in eligible_pairs])) / \
           (max([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) - 
            min([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) + 1e-10)
norm_vol = (volatility - min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs])) / \
          (max([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) - 
           min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Aqui, podemos ver a complexa interdependência:

1. A normalização dos parâmetros — um passo crítico, permitindo comparar grandezas de naturezas diferentes. Para cada parâmetro, calculamos sua posição relativa dentro do intervalo de 0 a 1.
2. Os coeficientes de peso — swap_weight, return_weight e volatility_weight — ajustam a sensibilidade do modelo a cada fator.
3. A influência oposta da volatilidade — note o sinal de menos antes de volatility_weight, que reflete nossa intenção de minimizar a volatilidade.

É interessante notar que esses pesos podem ser ajustados diretamente por meio da configuração:

self.config = {
    # ...
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    # ...
}

Esses parâmetros podem ser adaptados a diferentes condições de mercado e às preferências do investidor. Por exemplo, aumentar o valor de swap_weight desloca o foco da estratégia para a maximização do rendimento proveniente dos swaps, o que pode ser preferível em períodos de baixa volatilidade do mercado.

É especialmente interessante observar como o modelo lida com objetivos conflitantes. Frequentemente, pares de moedas com swaps positivos elevados tendem à desvalorização (algo lógico do ponto de vista da paridade das taxas de juros), criando uma tensão entre $R_m$ e $R_s$. Nosso modelo encontra o equilíbrio ideal entre essas metas contraditórias, utilizando a matriz de covariância para identificar oportunidades de diversificação que, de outra forma, seriam invisíveis.

O resultado do funcionamento do algoritmo pode ser observado no gráfico de rentabilidade a seguir, onde a linha azul representa o retorno sem considerar swaps, a vermelha mostra o retorno com swaps, e a roxa incorpora swaps, aportes regulares e reinvestimento:

É particularmente impressionante a melhora do coeficiente de Sharpe de 0,95 para 1,68 ao incluir os swaps na estratégia, uma demonstração clara de como a renda sistemática proveniente dos swaps melhora substancialmente a relação entre risco e retorno.

Na próxima parte, analisaremos a arquitetura e a implementação do SwapArbitrageAnalyzer, permitindo que você aplique esses princípios matemáticos diretamente em sua própria operação de trading.

SwapArbitrageAnalyzer: Arquitetura e implementação

A teoria sem prática permanece apenas como um exercício intelectual. Para transformar o modelo matemático complexo de arbitragem de swaps em uma ferramenta de trading real, desenvolvemos o SwapArbitrageAnalyzer, um sistema de software robusto que automatiza todo o processo, desde a coleta de dados até a otimização da carteira e sua visualização. Nesta parte, exploraremos a arquitetura do sistema e os principais aspectos de sua implementação.

Filosofia de design do sistema e análise dos componentes

O SwapArbitrageAnalyzer foi projetado seguindo o princípio da separação de responsabilidades, em que cada componente executa uma função bem definida. A estrutura da classe reflete o processo analítico em etapas:

class SwapArbitrageAnalyzer:
    def __init__(self, config=None):
        # Инициализация конфигурации и базовых переменных
        
    def initialize(self):
        # Подключение к MetaTrader и проверка доступа к данным
        
    def analyze(self):
        # Основной метод, запускающий весь процесс анализа
        
    def _get_current_market_rates(self):
        # Получение текущих рыночных цен
        
    def _init_swap_data(self):
        # Инициализация данных по свопам
        
    def _get_historical_data(self, symbol, start_date):
        # Получение и обработка исторических данных
        
    def _optimize_portfolio(self):
        # Оптимизация портфеля
        
    def _simulate_portfolio_performance(self):
        # Симуляция доходности оптимизированного портфеля
        
    def _create_visualizations(self):
        # Создание визуализаций для анализа результатов

Essa arquitetura segue um fluxo lógico de dados:

1. Coleta de dados — obtenção dos preços de mercado e das taxas de swap
2. Processamento de dados — cálculo das rentabilidades históricas e das estatísticas
3. Otimização — determinação dos pesos ideais dos pares de moedas
4. Simulação — validação da estratégia sobre dados históricos
5. Visualização — apresentação dos resultados de forma clara e interpretável

Um aspecto especialmente importante é o princípio da configurabilidade. O sistema possui uma estrutura de parâmetros flexível, capaz de influenciar todos os aspectos da análise:

self.config = {
    'target_volume': 100.0,
    'max_pairs': 28,
    'leverage': 2,  # Плечо 1:10
    'broker_suffix': '',
    'risk_free_rate': 0.001,
    'optimization_period': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),  # С 01.01.2015 до 17.03.2025
    'panel_width': 750,
    'panel_height': 500,
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    'simulation_days': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),
    'monthly_deposit_rate': 0.02  # 2% от начального капитала ежемесячно
}

Essa flexibilidade permite adaptar o sistema a diferentes condições de mercado, corretoras e preferências individuais do trader, sem a necessidade de alterar o código-base.

Metodologia de coleta de dados de 2015 a 2025

Uma estratégia sólida exige dados confiáveis. O SwapArbitrageAnalyzer utiliza conexão direta com o MetaTrader 5 para obter tanto dados históricos quanto informações em tempo real:

def initialize(self):
    if not mt5.initialize():
        print(f"MetaTrader5 инициализация не удалась, error={mt5.last_error()}")
        return False
    
    account_info = mt5.account_info()
    if not account_info:
        print("Не удалось получить информацию о счете")
        return False
        
    print(f"MetaTrader5 инициализирован. Счет: {account_info.login}, Баланс: {account_info.balance}")
    self._get_current_market_rates()
    self._init_swap_data()
    self.initialized = True
    return True

A atenção especial é dada ao tratamento dos dados históricos. Para garantir uma otimização precisa, coletamos dados diários ao longo de um período de dez anos:

def _get_historical_data(self, symbol, start_date):
    try:
        now = datetime.now()
        rates = mt5.copy_rates_range(symbol, mt5.TIMEFRAME_D1, start_date, now)
        if rates is None or len(rates) < 10:
            print(f"Недостаточно данных для {symbol}: {len(rates) if rates is not None else 'None'} баров")
            return None
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        df['return'] = df['close'].pct_change()
        
        symbol_info = mt5.symbol_info(symbol)
        best_swap = max(symbol_info.swap_long, symbol_info.swap_short)
        swap_in_points = best_swap if symbol_info.swap_long > symbol_info.swap_short else -best_swap
        point_value = symbol_info.point
        df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']  # Учет плеча
        
        # ...

É particularmente importante compreender como calculamos o rendimento proveniente dos swaps:

df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']

Essa abordagem permite expressar o swap na mesma unidade de medida que a rentabilidade de mercado, como uma porcentagem sobre o capital investido, o que é essencial para a otimização correta da carteira.

Algoritmo de ponderação que equilibra rentabilidade, volatilidade e rendimento de swap

O coração do SwapArbitrageAnalyzer é o algoritmo de otimização de portfólio. Diferentemente dos métodos tradicionais, não buscamos apenas maximizar o retorno esperado ou o coeficiente de Sharpe, adotamos uma abordagem abrangente que considera as particularidades da arbitragem de swaps.

A principal inovação está no método de avaliação normalizada da atratividade dos pares de moedas:

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Essa fórmula leva em conta:

• A rentabilidade de mercado normalizada (norm_market)
• O rendimento de swap normalizado (norm_swap)
• A volatilidade normalizada (norm_vol)

O peso de cada componente é ajustável por meio da configuração, permitindo adaptar a estratégia às condições específicas do mercado. Por padrão, utilizamos os valores swap_weight=0.3, return_weight=0.6 e volatility_weight=0.1, o que proporciona um bom equilíbrio entre a estabilidade do rendimento de swaps e o potencial de rentabilidade de mercado.

É interessante observar que o algoritmo não seleciona simplesmente os pares de moedas com as maiores pontuações. Em vez disso, ele resolve um problema complexo de otimização que considera as correlações entre os pares:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

Isso permite identificar combinações não óbvias de pares de moedas que, embora individualmente apresentem características medianas, formam juntas uma carteira extremamente eficiente graças ao efeito da diversificação.

O algoritmo também incorpora um elemento de aleatoriedade para explorar um espaço maior de soluções:

num_pairs = random.randint(1, min(self.config['max_pairs'], len(eligible_pairs)))
eligible_pairs = random.sample(eligible_pairs, num_pairs)

Esse componente é especialmente valioso no contexto da arbitragem de swaps, onde existem múltiplos ótimos locais com eficiências muito próximas.

O resultado do funcionamento do algoritmo é a estrutura de uma carteira otimizada:

optimal_portfolio = {}
for i, pair in enumerate(eligible_pairs):
    if optimal_weights[i] != 0:
        optimal_portfolio[pair] = optimal_weights[i]
        self.swap_info[pair]['weight'] = optimal_weights[i] * 100

print("\nОптимальный портфель с положительным свопом:")
for pair, weight in sorted(optimal_portfolio.items(), key=lambda x: abs(x[1]), reverse=True):
    direction = 'Long' if weight > 0 else 'Short'
    swap_value = self.swap_info[pair]['long_swap'] if weight > 0 else self.swap_info[pair]['short_swap']
    print(f"Пара: {pair}, Направление: {direction}, Вес: {abs(weight)*100:.2f}%, Своп: {swap_value:.2f}")

Um resultado típico pode se apresentar da seguinte forma:

Оптимальный портфель с положительным свопом:
Пара: GBPAUD, Направление: Short, Вес: 18.45%, Своп: 2.68
Пара: EURNZD, Направление: Long, Вес: 15.22%, Своп: 3.15
Пара: EURCAD, Направление: Short, Вес: 14.87%, Своп: 1.87
Пара: AUDNZD, Направление: Long, Вес: 12.34%, Своп: 2.92
Пара: GBPJPY, Направление: Long, Вес: 11.78%, Своп: 2.21
Пара: USDJPY, Направление: Long, Вес: 10.56%, Своп: 1.94
Пара: CHFJPY, Направление: Long, Вес: 9.47%, Своп: 2.35
Пара: EURJPY, Направление: Long, Вес: 7.31%, Своп: 1.68

Após a otimização, o sistema executa uma simulação da rentabilidade da carteira sobre o período histórico:

def _simulate_portfolio_performance(self):
    # ... (инициализация переменных)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            # ... (расчет дневной доходности и свопа)
        
        # Расчет доходности без свопа
        market_profit = current_capital * daily_return
        current_capital += market_profit
        
        # Расчет доходности с учетом свопа
        market_profit_with_swap = current_capital_with_swap * daily_return
        current_capital_with_swap += market_profit_with_swap + daily_swap_applied
        
        # Расчет доходности с учетом пополнений и реинвестирования
        # ...

Os resultados da simulação são apresentados de forma visual por meio de diversos gráficos:

def _create_visualizations(self):
    # ... (создание визуализаций)
    
    # 1. Портфель и его пропорции
    plt.figure(figsize=(self.config['panel_width']/100, self.config['panel_height']/100), dpi=100)
    sorted_weights = sorted(self.optimal_portfolio['weights'].items(), key=lambda x: abs(x[1]), reverse=True)
    pairs = [f"{item[0]} ({'L' if item[1] > 0 else 'S'})" for item in sorted_weights]
    weights = [abs(item[1]) * 100 for item in sorted_weights]
    colors = plt.cm.viridis(np.linspace(0, 0.9, len(pairs)))
    plt.pie(weights, labels=pairs, autopct='%1.1f%%', colors=colors, textprops={'fontsize': 8})
    plt.title('Пропорции портфеля (L=Long, S=Short)')
    plt.tight_layout()
    plt.savefig('portfolio_proportions.png', dpi=100, bbox_inches='tight')
    plt.close()
    
    # ... (создание других графиков)

Em última análise, a arquitetura do SwapArbitrageAnalyzer representa uma combinação harmoniosa de rigor matemático por meio do uso de métodos modernos de otimização de portfólio, aplicabilidade prática graças à conexão direta com o terminal de trading e à consideração das condições reais de mercado, flexibilidade por meio de amplas possibilidades de configuração para diferentes objetivos e preferências, e clareza visual através de uma visualização abrangente para a tomada de decisões informadas.

Essa abordagem torna o sistema uma ferramenta poderosa não apenas para traders profissionais, mas também para pesquisadores de mercado que buscam compreender as complexas interações entre os diferentes fatores de rentabilidade no mercado de câmbio.