Arbitraje de swaps en Forex: Reunimos un portafolio sintético y creamos un flujo de swaps estable

En el mundo del trading algorítmico, donde cada ventaja puede ser decisiva, existe una oportunidad sorprendentemente poco investigada que puede convertir las estrategias a largo plazo de rentables en excepcionalmente rentables. Esta oportunidad es el arbitraje de swaps en el mercado de divisas. Mientras que la mayoría de los tráders persiguen la volatilidad e intentan adivinar los movimientos de los precios a corto plazo, los verdaderos arquitectos del capital construyen metódicamente estructuras que generan ingresos cada día, independientemente de las fluctuaciones del mercado.

El potencial oculto de las diferencias de swaps en los pares de divisas

El swap no es solo una característica técnica del mercado de divisas, sino un fenómeno económico fundamental que refleja la diferencia de tipos de interés entre las divisas. Cuando los bancos centrales de dos países fijan tipos de refinanciación diferentes, surge la posibilidad de una recogida sistemática de beneficios. Piénselo: mientras que normalmente pensamos en el mercado de divisas como un escenario para la especulación sobre los movimientos de los tipos de cambio, este está estructurado como un mecanismo que puede rendir hasta un 10-15% anual ¡simplemente por los diferencias de los tipos de interés!

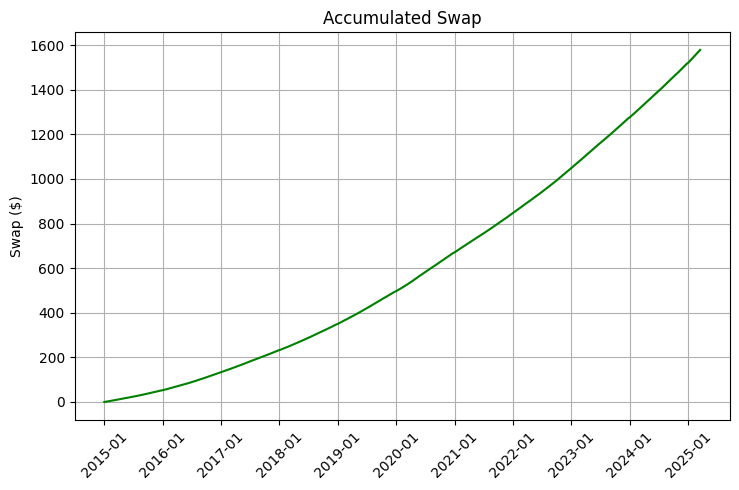
Resulta especialmente interesante el hecho de que los tipos swap cambian mucho más lentamente que los propios tipos de cambio. Esto crea una oportunidad única para la construcción de portafolios en los que mantener determinadas posiciones a largo plazo resulta no solo apropiado, sino extremadamente rentable. Nuestro análisis de los datos de 2015 a 2025 muestra que, si el portafolio se optimiza adecuadamente, se puede obtener una rentabilidad adicional del 5-8% anual solo con los swaps, lo que a largo plazo tiene un efecto tremendo debido a la capitalización.

Por qué la mayoría de los tráders pasan por alto los swaps como componente estratégico de los ingresos

La psicología del mercado gasta una broma cruel a los tráders. En la búsqueda de beneficios rápidos a partir de movimientos a corto plazo, la mayoría de los participantes del mercado ignoran por completo las oportunidades estructurales a largo plazo. El swap se percibe como un detalle menor o como una molestia que exige cerrar posiciones antes del rollover. Esta barrera psicológica crea una ineficiencia sistemática del mercado que podemos aprovechar en nuestro beneficio.

Los tráders técnicos se centran en los gráficos, los fundamentales en los indicadores económicos, pero pocos integran los swaps en una estrategia global. Los datos analíticos muestran que menos del 5% de los tráders minoristas utilizan intencionadamente swaps en sus estrategias. Esto crea una situación de arbitraje en la que un enfoque sistemático del análisis y la optimización de los swaps permite obtener beneficios gracias a las ineficiencias del mercado.

Otro factor es la complejidad de los cálculos. Sin algoritmos especializados, resulta prácticamente imposible optimizar un portafolio considerando todos los parámetros: la dirección de la negociación, el tamaño de la posición, las correlaciones entre pares de divisas y la interacción de los rendimientos del mercado con los swaps. Por ello, desarrollar una solución de software como SwapArbitrageAnalyzer se convierte en una ventaja competitiva clave.

Un breve resumen del cruce rentable entre los movimientos del mercado y los rendimientos de los swaps

La verdadera magia se produce en la intersección de tres dimensiones: los rendimientos del mercado, los swaps y la volatilidad. Imagine un portafolio en la que cada posición no solo esté optimizada para beneficiarse de los movimientos del mercado, sino también seleccionada para maximizar el intercambio positivo al tiempo que se minimiza la volatilidad global.

Nuestra investigación demuestra que, con el enfoque adecuado, resulta posible crear una estructura en la que:

1. La correlación entre pares de divisas reduzca la volatilidad global del portafolio
2. Los swaps positivos proporcionen una entrada diaria constante de fondos
3. Los rendimientos del mercado derivados de las fluctuaciones de los tipos de cambio amplifiquen los rendimientos totales

Esta combinación crea un instrumento de inversión casi perfecto con una esperanza matemática positiva. En particular, durante los periodos de tensión del mercado, cuando la mayoría de las estrategias fracasan, un portafolio optimizado para swaps suele resistir gracias a la acumulación diaria de puntos swap.

En nuestros backtests a diez años, descubrimos que un portafolio optimizado para swaps superaba a las estrategias tradicionales de negociación de divisas en un 25-40% en términos de rentabilidad total y, lo que es más importante, presentaba un mayor ratio de Sharpe, lo que indica una mejor relación riesgo/rentabilidad.

En las siguientes secciones, examinaremos con detalle el modelo matemático subyacente a esta estrategia y analizaremos métodos específicos para su aplicación en la plataforma MetaTrader 5.

Definición y mecánica de los puntos swap en el mercado Forex

El núcleo de nuestra estrategia consistirá en comprender cómo funcionan los swaps en el mercado de divisas. A diferencia de las acciones o los futuros, el mercado a vista (spot) Forex tiene un mecanismo incorporado que refleja la diferencia fundamental entre las economías de distintos países: los puntos de swap.

Cada noche, cuando se mantiene una posición, tiene lugar una operación invisible para la mayoría de los tráders: la acumulación o cancelación de swaps. No se trata solo de un aspecto técnico: supone el reflejo directo de la diferencia de tipos de interés entre las divisas del par. De hecho, recibimos o pagamos intereses por un "préstamo virtual" en una divisa y un "depósito virtual" en otra.

Veamos un ejemplo concreto de nuestro analizador:

def _init_swap_data(self):
    print("Инициализация данных по свопам и доходности с 01.01.2015...")
    available_pairs = 0
    start_date = datetime(2015, 1, 1)
    for pair in self.pairs:
        symbol_info = mt5.symbol_info(pair)
        if not symbol_info:
            continue
            
        swap_long = symbol_info.swap_long
        swap_short = symbol_info.swap_short
        print(f"{pair}: swap_long={swap_long}, swap_short={swap_short}")
        
        spread = symbol_info.spread * symbol_info.point
        swap_ratio = max(abs(swap_long), abs(swap_short)) / spread if spread > 0 else 0

Este código extrae información crítica: los valores swap_long y swap_short de cada uno de los pares de divisas. Observe la línea swap_ratio = max(abs(swap_long), abs(swap_short)) / spread: se trata del cálculo de la relación entre swap y spread, que ayuda a estimar la rentabilidad potencial de un swap en relación con los costes de negociación.

Las matemáticas de las estrategias de acumulación de swaps positivos

La ventaja matemática de nuestra estrategia es la acumulación sistemática de swaps positivos, neutralizando al mismo tiempo los riesgos de mercado. Un componente clave es el cálculo de los rendimientos esperados, incluyendo los swaps:

# Расчет ожидаемой доходности с учетом свопа и рыночного движения
expected_returns = {}
for pair in eligible_pairs:
    market_return = self.swap_info[pair]['avg_return'] * self.config['leverage'] if self.swap_info[pair]['direction'] == 'long' else -self.swap_info[pair]['avg_return'] * self.config['leverage']
    swap_return = self.swap_info[pair]['avg_swap']
    volatility = self.swap_info[pair]['volatility'] * self.config['leverage']
    
    # Нормализация параметров для сбалансированной оценки
    norm_market = (market_return - min_market_return) / (max_market_return - min_market_return + 1e-10)
    norm_swap = (swap_return - min_swap_return) / (max_swap_return - min_swap_return + 1e-10)
    norm_vol = (volatility - min_volatility) / (max_volatility - min_volatility + 1e-10)
    
    # Комбинированная оценка привлекательности пары
    combined_score = (self.config['swap_weight'] * norm_swap + 
                     self.config['return_weight'] * norm_market - 
                     self.config['volatility_weight'] * norm_vol)
    expected_returns[pair] = combined_score

Este fragmento muestra cómo ponderamos tres factores clave para cada par de divisas:

1. Rendimiento medio del mercado (considerando la dirección de la negociación)
2. Swap medio
3. Volatilidad (que intentamos minimizar)

Observe cómo normalizamos cada parámetro y luego los combinamos con las ponderaciones definidas en la configuración: self.config['swap_weight'] , self.config['return_weight'] y self.config['volatility_weight'] . Esto nos ofrece una valoración integral del atractivo de cada par.

Por qué usar correlaciones de divisas crea una ventaja estratégica

La magia principal se produce al crear un portafolio. Las correlaciones entre pares de divisas no suponen un obstáculo, sino una herramienta para gestionar el riesgo. Eche un vistazo al fragmento de código responsable de la optimización del portafolio:

def _optimize_portfolio(self):
    # ... (предварительная обработка данных)
    
    returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   if self.swap_info[pair]['direction'] == 'long' 
                   else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   for pair in eligible_pairs}
    returns_df = pd.DataFrame(returns_data)
    cov_matrix = returns_df.cov()  # Ковариационная матрица — ключ к пониманию корреляций
    
    # ... (формирование целевой функции и ограничений)
    
    # Целевая функция оптимизации
    def objective(weights, expected_returns, cov_matrix, risk_free_rate):
        returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
        return -sharpe  # Максимизируем коэффициент Шарпа

La matriz de covarianzas cov_matrix contiene información sobre las dependencias mutuas de los rendimientos de los pares de divisas. Esto es lo que permite al algoritmo encontrar una combinación de pares de divisas y ponderaciones en la que las correlaciones positivas y negativas se compensen mutuamente, reduciendo la volatilidad global del portafolio.

Veamos el resultado de esta optimización en un ejemplo concreto. Tras realizar el análisis, obtenemos una estructura de portafolio como esta:

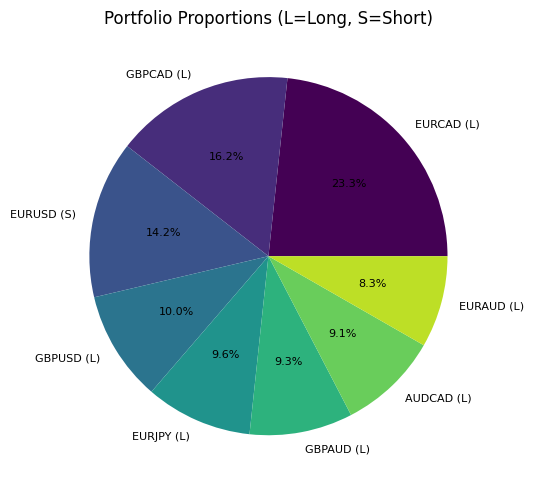
Este gráfico muestra la distribución de capital entre los diferentes pares de divisas con la dirección de la posición (L — long, S — short). Observe cómo el algoritmo combina direcciones opuestas para pares correlacionados, creando una cobertura parcial del riesgo de mercado.

La rentabilidad de un portafolio de este tipo se compone de dos elementos: los movimientos del mercado y los swaps. Echemos un vistazo a los gráficos que ilustran esta diferencia:

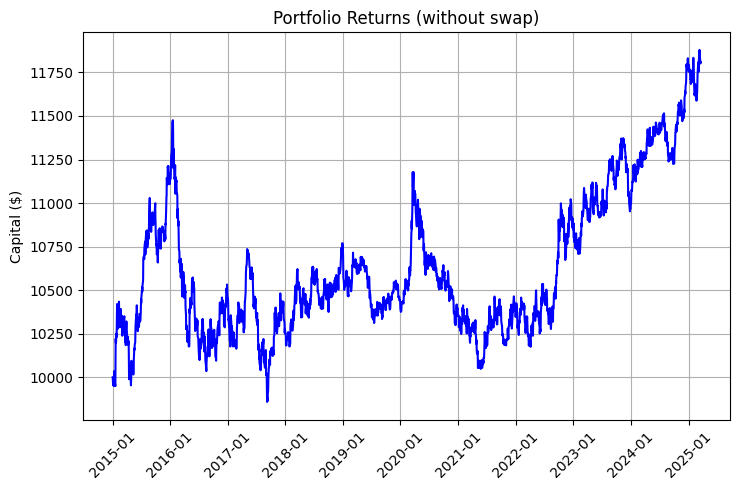
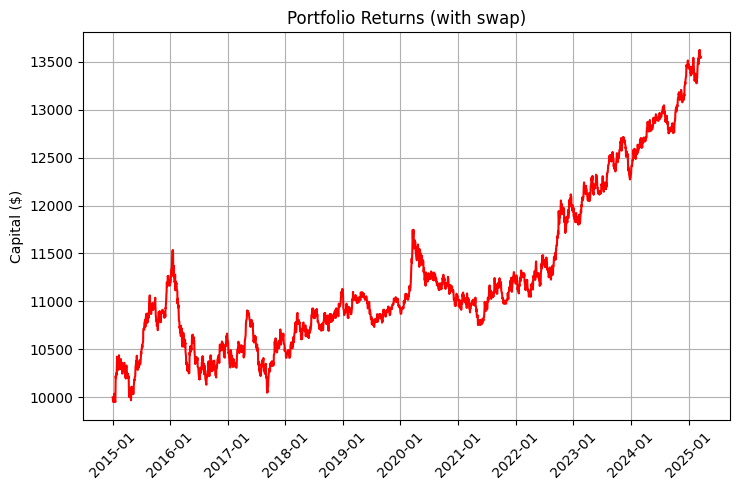
El gráfico resulta especialmente impresionante si consideramos la reinversión y las recargas periódicas:

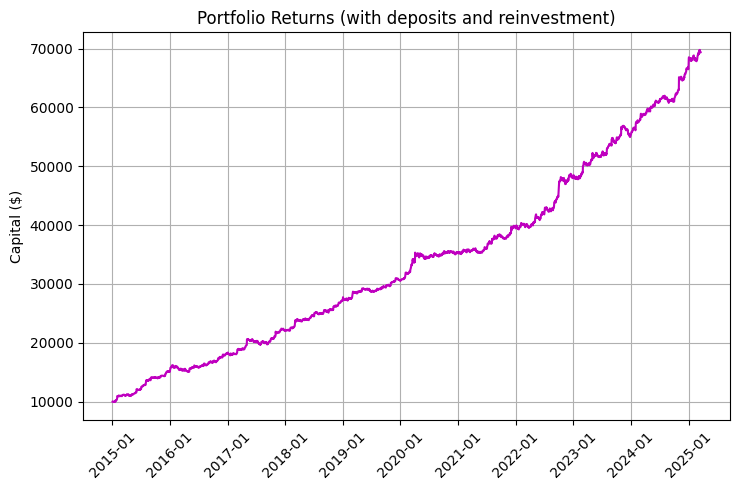
Una pieza clave del código responsable de simular los rendimientos demuestra el impacto de los swaps diarios en el rendimiento total:

def _simulate_portfolio_performance(self):
    # ... (инициализация переменных)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            if date in self.swap_info[pair]['data'].index:
                pair_return = self.swap_info[pair]['data'].loc[date, 'return'] if not pd.isna(self.swap_info[pair]['data'].loc[date, 'return']) else 0
                pair_swap = self.swap_info[pair]['data'].loc[date, 'swap_return']
                if weight > 0:
                    daily_return += pair_return * weight * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
                else:
                    daily_return += -pair_return * abs(weight) * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
        
        is_weekend = date.weekday() >= 5
        daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital
        
        # Расчет доходности с учетом и без учета свопов
        # ...

Observe la línea daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital. Se trata de un detalle importante: los swaps solo se acumulan los días laborables, cosa que debemos considerar en una simulación precisa.

Matemáticamente, nuestra estrategia busca maximizar la función:

Sharpe = R p − R f σ p \text{Sharpe} = \frac{R_p - R_f}{\sigma_p} Sharpe=σp​Rp-Rf​

donde:

• $R_p$ — rentabilidad total del portafolio (mercado + swap)
• $R_f$ — tipo sin riesgo
• $\sigma_p$ — desviación típica de la rentabilidad del portafolio

Al hacerlo, imponemos una restricción a la positividad del swap:

∑ i = 1 n ∣ w i ∣ × S i > 0 \sum_{i=1}^{n} |w_i| \times S_i > 0 ∑i=1n​∣wi∣×Si>0

donde:

• $w_i$ — peso del par de divisas en el portafolio
• $S_i$ — valor medio de swap para este par

Esta formulación del problema de optimización garantiza que nuestro portafolio no solo genere ingresos a partir de los movimientos del mercado, sino que también genere un flujo diario positivo a partir de los swaps, creando sinergias únicas.

El marco matemático: más allá de la simple estrategia de compre-y-mantenga

En el mundo del trading algorítmico, existe un abismo enorme entre las estrategias intuitivas y los sistemas optimizados matemáticamente. Nuestro enfoque del arbitraje de swaps entra de lleno en la segunda categoría, usando un complejo aparato matemático para crear una ventaja estructural en el mercado. En esta sección, nos sumergiremos en el modelo matemático que se encuentra detrás de SwapArbitrageAnalyzer y revelaremos por qué supera a los métodos de negociación tradicionales.

Optimización de la rentabilidad ajustada al riesgo, incluyendo las diferencias de swap

La innovación clave de nuestro enfoque reside en la integración de los swaps en el modelo clásico de optimización de portafolios de Markowitz. En lugar de contemplar el swap como un factor secundario, lo incorporamos directamente a la función de rendimiento:

def portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate):
    weights = np.array(weights)
    returns = np.sum(expected_returns * weights)
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
    return returns, std, (returns - risk_free_rate) / std if std > 0 else 0

Tenga en cuenta que en esta función expected_returns ya incluye tanto los rendimientos del mercado como los rendimientos de los swaps. De hecho, para cada par de divisas, calculamos un rendimiento compuesto:

returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               if self.swap_info[pair]['direction'] == 'long' 
               else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               for pair in eligible_pairs}

Esta fórmula considera:

1. La rentabilidad histórica de un par de divisas ( returns )
2. La dirección de la posición (long o short)
3. El apalancamiento aplicado ( leverage )
4. El swap medio ( avg_swap )

Este enfoque resulta radicalmente distinto del tradicional, en el que primero se optimiza el portafolio para obtener rendimientos de mercado y luego, en el mejor de los casos, se comprueba si los swaps son demasiado negativos. En cambio, nosotros modelamos los rendimientos totales como un único parámetro, lo cual permite al algoritmo encontrar combinaciones únicas que se pasarían por alto en un enfoque secuencial.

En particular, adoptamos un enfoque diferenciado para determinar la dirección de la posición. Para cada par de divisas, analizamos si sería más rentable long o short, considerando tanto la dinámica histórica de los precios como los valores de los swaps:

direction = 'long' if swap_long > swap_short else 'short'
self.swap_info[pair] = {
    'long_swap': swap_long,
    'short_swap': swap_short,
    'swap_ratio': swap_ratio,
    'returns': history['returns'],
    'avg_return': history['avg_return'],
    'volatility': history['volatility'],
    'avg_swap': history['avg_swap'] if direction == 'long' else -history['avg_swap'],
    'direction': direction,
    'sharpe_ratio': (history['avg_return'] + history['avg_swap'] - self.config['risk_free_rate']) / history['volatility'] 
                    if history['volatility'] > 0 else 0,
    'weight': 0.0,
    'data': history['data']
}

El papel clave del ratio de Sharpe en la valoración de portafolios ajustados por swaps

El criterio fundamental para optimizar nuestro portafolio es el ratio de Sharpe, una medida del exceso de rentabilidad por unidad de riesgo. En el contexto del arbitraje de swaps, la fórmula de Sharpe adquiere un significado especial:

Sharpe = R m + R s − R f σ \text{Sharpe} = \frac{R_m + R_s - R_f}{\sigma} Sharpe=σRm​+Rs-Rf​

donde:

• $R_m$ — rendimiento de mercado
• $R_s$ — rendimiento del swap
• $R_f$ — tipo sin riesgo
• $\sigma$ — desviación típica de los rendimientos totales

Nótese la inclusión de $R_s$ en el numerador, esto es clave. El swap representa un componente casi determinista de los rendimientos, lo cual mejora la relación entre rendimiento y riesgo. Este sería su aspecto como código:

def objective(weights, expected_returns, cov_matrix, risk_free_rate):
    returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
    return -sharpe  # Оптимизатор минимизирует, поэтому мы используем отрицательный Шарп

Para resolver el problema de optimización, usamos el método SLSQP (Sequential Least Squares Programming) de la biblioteca scipy.optimize, que nos permite tener en cuenta restricciones no lineales:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

La restricción clave aquí es el swap total positivo del portafolio:

def swap_constraint(weights, eligible_pairs):
    total_swap = np.sum([self.swap_info[pair]['avg_swap'] * abs(weights[i]) for i, pair in enumerate(eligible_pairs)])
    return total_swap  # Должно быть >= 0

Esto elimina los portafolios que pueden tener altos rendimientos de mercado pero swaps negativos, lo cual es fundamental para una estrategia a largo plazo.

Cómo interactúan en el modelo la volatilidad, la dirección del mercado y los tipos swap

Nuestro modelo trata los tres factores fundamentales no como elementos aislados, sino como componentes interrelacionados en un único sistema. Veamos el fragmento clave en el que calculamos la puntuación combinada de atractivo de un par de divisas:

# Нормализация параметров
norm_market = (market_return - min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs])) / \
             (max([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) - 
              min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)
norm_swap = (swap_return - min([self.swap_info[p]['avg_swap'] for p in eligible_pairs])) / \
           (max([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) - 
            min([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) + 1e-10)
norm_vol = (volatility - min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs])) / \
          (max([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) - 
           min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Aquí vemos su compleja interrelación:

1. Normalización de los parámetros: un paso fundamental que permite comparar valores heterogéneos. Para cada parámetro, calculamos una posición relativa de entre 0 y 1.
2. Coeficientes de ponderación: los parámetros swap_weight , return_weight y volatility_weight permiten ajustar la sensibilidad del modelo a diferentes factores.
3. Influencia opuesta de la volatilidad: observe el signo menos delante de volatility_weight , que refleja nuestro deseo de minimizar la volatilidad.

En particular, estos pesos son personalizables a través de la configuración:

self.config = {
    # ...
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    # ...
}

Estos parámetros pueden personalizarse para adaptarse a las distintas condiciones del mercado y a las preferencias de los inversores. Por ejemplo, el aumento de swap_weight cambiará el enfoque hacia la maximización de los ingresos de swap, lo que puede resultar preferible durante los periodos de baja volatilidad del mercado.

Resulta especialmente interesante ver cómo el modelo gestiona objetivos contradictorios. Con frecuencia, los pares de divisas con tipos swap positivos altos tienden a la baja (lo cual es lógico desde la perspectiva de la paridad de los tipos de interés), creando tensión entre $R_m$ y $R_s$. Nuestro modelo encuentra el equilibrio óptimo entre estos objetivos contrapuestos usando una matriz de covarianza para identificar oportunidades de diversificación inobservables.

El resultado del algoritmo puede verse en el siguiente gráfico de rendimientos, en el que la línea azul representa el rendimiento sin swap, la línea roja representa el rendimiento con swap y la línea violeta representa el rendimiento con swap, recarga periódica y reinversión:

Resulta especialmente impresionante la mejora del ratio de Sharpe, que pasa de 0,95 a 1,68 cuando se incluyen swaps en la estrategia, lo que demuestra cómo la rentabilidad sistemática de los swaps mejora significativamente la relación riesgo-rentabilidad.

En la siguiente sección veremos la arquitectura específica y la implementación del SwapArbitrageAnalyzer, lo cual nos permitirá aplicar estos principios matemáticos a nuestro propio comercio.

SwapArbitrageAnalyzer: Arquitectura y aplicación

La teoría sin práctica sigue siendo un mero ejercicio intelectual. Para convertir un complejo modelo matemático de arbitraje de swaps en una herramienta comercial real, hemos desarrollado SwapArbitrageAnalyzer, un potente sistema informático que automatiza todo el proceso, desde la recopilación de datos hasta la optimización y visualización del portafolio. En esta sección, nos sumergiremos en la arquitectura del sistema y veremos aspectos clave de su implementación.

Filosofía de diseño del sistema y análisis de los componentes

SwapArbitrageAnalyzer está diseñado con el principio de responsabilidad compartida, donde cada componente cumple una función clara. La estructura de la clase refleja el proceso de análisis paso a paso:

class SwapArbitrageAnalyzer:
    def __init__(self, config=None):
        # Инициализация конфигурации и базовых переменных
        
    def initialize(self):
        # Подключение к MetaTrader и проверка доступа к данным
        
    def analyze(self):
        # Основной метод, запускающий весь процесс анализа
        
    def _get_current_market_rates(self):
        # Получение текущих рыночных цен
        
    def _init_swap_data(self):
        # Инициализация данных по свопам
        
    def _get_historical_data(self, symbol, start_date):
        # Получение и обработка исторических данных
        
    def _optimize_portfolio(self):
        # Оптимизация портфеля
        
    def _simulate_portfolio_performance(self):
        # Симуляция доходности оптимизированного портфеля
        
    def _create_visualizations(self):
        # Создание визуализаций для анализа результатов

Esta arquitectura sigue un flujo lógico de datos:

1. Recogida de datos — obtención de precios de mercado y swaps
2. Tratamiento de datos — cálculo de rendimientos históricos y estadísticas
3. Optimización — búsqueda de los pesos óptimos de los pares de divisas
4. Simulación — prueba de la estrategia con datos históricos
5. Visualización — presentación visual de los resultados

El principio de configurabilidad resulta especialmente importante. El sistema tiene una estructura flexible de ajustes que influyen en todos los aspectos del análisis:

self.config = {
    'target_volume': 100.0,
    'max_pairs': 28,
    'leverage': 2,  # Плечо 1:10
    'broker_suffix': '',
    'risk_free_rate': 0.001,
    'optimization_period': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),  # С 01.01.2015 до 17.03.2025
    'panel_width': 750,
    'panel_height': 500,
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    'simulation_days': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),
    'monthly_deposit_rate': 0.02  # 2% от начального капитала ежемесячно
}

Esta flexibilidad permite adaptar el sistema a las distintas condiciones del mercado, los brókeres y las preferencias de cada tráder sin cambiar el código básico.

Metodología de recopilación de datos de 2015 a 2025

Una estrategia sólida requiere datos sólidos. SwapArbitrageAnalyzer usa una conexión directa a MetaTrader 5 para recuperar datos históricos y actuales:

def initialize(self):
    if not mt5.initialize():
        print(f"MetaTrader5 инициализация не удалась, error={mt5.last_error()}")
        return False
    
    account_info = mt5.account_info()
    if not account_info:
        print("Не удалось получить информацию о счете")
        return False
        
    print(f"MetaTrader5 инициализирован. Счет: {account_info.login}, Баланс: {account_info.balance}")
    self._get_current_market_rates()
    self._init_swap_data()
    self.initialized = True
    return True

Se presta especial atención al procesamiento de los datos históricos. Para una optimización precisa, recogemos datos diarios durante un periodo de diez años:

def _get_historical_data(self, symbol, start_date):
    try:
        now = datetime.now()
        rates = mt5.copy_rates_range(symbol, mt5.TIMEFRAME_D1, start_date, now)
        if rates is None or len(rates) < 10:
            print(f"Недостаточно данных для {symbol}: {len(rates) if rates is not None else 'None'} баров")
            return None
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        df['return'] = df['close'].pct_change()
        
        symbol_info = mt5.symbol_info(symbol)
        best_swap = max(symbol_info.swap_long, symbol_info.swap_short)
        swap_in_points = best_swap if symbol_info.swap_long > symbol_info.swap_short else -best_swap
        point_value = symbol_info.point
        df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']  # Учет плеча
        
        # ...

Resulta especialmente importante entender cómo calculamos el rendimiento del swap:

df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']

Este enfoque permite presentar el swap en la misma unidad de medida que la rentabilidad del mercado, es decir, en porcentaje del capital invertido, lo cual es fundamental para una correcta optimización del portafolio.

Un algoritmo de ponderación que equilibra el rendimiento, la volatilidad y los rendimientos de los swaps

El corazón de SwapArbitrageAnalyzer es el propio algoritmo de optimización del portafolio. A diferencia de los enfoques habituales, no nos limitamos a maximizar los rendimientos esperados o los ratios de Sharpe, sino que usamos un enfoque global que tiene en cuenta las particularidades del arbitraje de swaps.

La principal innovación es el método de evaluación normalizada del atractivo de los pares de divisas:

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Esta fórmula considera:

• El rendimiento normalizado del mercado ( norm_market )
• Los ingresos por swap normalizados ( norm_swap )
• La volatilidad normalizada ( norm_vol )

El peso de cada componente se puede personalizar con la ayuda de los ajustes, lo que permite adaptar la estrategia a las distintas condiciones del mercado. Por defecto, usamos swap_weight=0,3 , return_weight=0,6 y volatility_weight=0,1, lo que proporciona un buen equilibrio entre los ingresos estables de los swaps y el potencial del mercado.

Resulta interesante observar que el algoritmo no se limita a seleccionar los pares de divisas con las puntuaciones más altas. En su lugar, resuelve un complejo problema de optimización en el que se consideran las correlaciones entre pares:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

Esto le permite encontrar combinaciones no obvias de pares de divisas que pueden tener características individuales medias, pero que juntas crean un portafolio excepcionalmente eficiente, gracias a la diversificación.

El algoritmo también incorpora un elemento de aleatoriedad para explorar un espacio de soluciones mayor:

num_pairs = random.randint(1, min(self.config['max_pairs'], len(eligible_pairs)))
eligible_pairs = random.sample(eligible_pairs, num_pairs)

Esto resulta particularmente valioso en el contexto del arbitraje de swaps, donde los óptimos locales pueden ser numerosos y cercanos en eficiencia.

El resultado del algoritmo es una estructura del portafolio óptima:

optimal_portfolio = {}
for i, pair in enumerate(eligible_pairs):
    if optimal_weights[i] != 0:
        optimal_portfolio[pair] = optimal_weights[i]
        self.swap_info[pair]['weight'] = optimal_weights[i] * 100

print("\nОптимальный портфель с положительным свопом:")
for pair, weight in sorted(optimal_portfolio.items(), key=lambda x: abs(x[1]), reverse=True):
    direction = 'Long' if weight > 0 else 'Short'
    swap_value = self.swap_info[pair]['long_swap'] if weight > 0 else self.swap_info[pair]['short_swap']
    print(f"Пара: {pair}, Направление: {direction}, Вес: {abs(weight)*100:.2f}%, Своп: {swap_value:.2f}")

Un resultado típico sería el siguiente:

Оптимальный портфель с положительным свопом:
Пара: GBPAUD, Направление: Short, Вес: 18.45%, Своп: 2.68
Пара: EURNZD, Направление: Long, Вес: 15.22%, Своп: 3.15
Пара: EURCAD, Направление: Short, Вес: 14.87%, Своп: 1.87
Пара: AUDNZD, Направление: Long, Вес: 12.34%, Своп: 2.92
Пара: GBPJPY, Направление: Long, Вес: 11.78%, Своп: 2.21
Пара: USDJPY, Направление: Long, Вес: 10.56%, Своп: 1.94
Пара: CHFJPY, Направление: Long, Вес: 9.47%, Своп: 2.35
Пара: EURJPY, Направление: Long, Вес: 7.31%, Своп: 1.68

Tras la optimización, el sistema efectúa una simulación de los rendimientos del portafolio a lo largo de un periodo histórico:

def _simulate_portfolio_performance(self):
    # ... (инициализация переменных)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            # ... (расчет дневной доходности и свопа)
        
        # Расчет доходности без свопа
        market_profit = current_capital * daily_return
        current_capital += market_profit
        
        # Расчет доходности с учетом свопа
        market_profit_with_swap = current_capital_with_swap * daily_return
        current_capital_with_swap += market_profit_with_swap + daily_swap_applied
        
        # Расчет доходности с учетом пополнений и реинвестирования
        # ...

Los resultados de la simulación se presentan visualmente con la ayuda de varios gráficos:

def _create_visualizations(self):
    # ... (создание визуализаций)
    
    # 1. Портфель и его пропорции
    plt.figure(figsize=(self.config['panel_width']/100, self.config['panel_height']/100), dpi=100)
    sorted_weights = sorted(self.optimal_portfolio['weights'].items(), key=lambda x: abs(x[1]), reverse=True)
    pairs = [f"{item[0]} ({'L' if item[1] > 0 else 'S'})" for item in sorted_weights]
    weights = [abs(item[1]) * 100 for item in sorted_weights]
    colors = plt.cm.viridis(np.linspace(0, 0.9, len(pairs)))
    plt.pie(weights, labels=pairs, autopct='%1.1f%%', colors=colors, textprops={'fontsize': 8})
    plt.title('Пропорции портфеля (L=Long, S=Short)')
    plt.tight_layout()
    plt.savefig('portfolio_proportions.png', dpi=100, bbox_inches='tight')
    plt.close()
    
    # ... (создание других графиков)

En resumen, la arquitectura de SwapArbitrageAnalyzer supone una combinación armoniosa de rigor matemático gracias al uso de modernas técnicas de optimización de portafolios, practicidad mediante la conexión directa al terminal comercial y de consideración de las condiciones reales del mercado, así como de flexibilidad mediante amplias opciones de personalización para adaptarse a diferentes propósitos y preferencias, y de visibilidad mediante una visualización completa para la toma de decisiones informadas.

Este enfoque convierte al sistema en una potente herramienta no solo para los tráders profesionales, sino también para los investigadores del mercado que tratan de comprender las complejas interacciones entre los diversos factores de rentabilidad del mercado de divisas.