Se entendi corretamente, queremos encontrar o máximo da função Hill igual a 1.
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //máximo global + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //mínimo global. - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
Essa função tem apenas dois parâmetros.
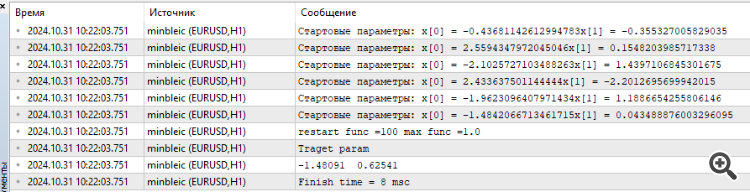
Conectei o MinBleic
Parece-me que não devemos contar o resultado médio fornecido pelo otimizador, mas o máximo. E, é claro, você pode ver o tempo, fenomenal 8 milissegundos.
1. Se entendi corretamente, queremos encontrar o máximo da função Hill igual a 1.
2. Essa função tem apenas dois parâmetros.
3. Conectado MinBleic
Parece-me que devemos contar não o resultado médio que o otimizador produz, mas o máximo. E, é claro, você pode ver o tempo, fenomenal 8 milissegundos.
Obrigado por seu comentário.
1. Sim, é isso mesmo. Todas as funções de teste são unificadas e seus valores estão no intervalo [0,0; 1,0].
2. Todas as funções de teste têm apenas dois parâmetros. Mas, ao testar algoritmos, usamos o espaço de pesquisa multidimensional (três tipos de testes, 5*2=10, 25*2=50, 500*2=1000 parâmetros para avaliar a capacidade de escala do AO) duplicando repetidamente uma função bidimensional.
3. O problema com dois parâmetros é simples demais para comparar adequadamente os algoritmos entre si; quase todos os algoritmos resolvem esse problema instantaneamente com 100% de convergência. Os algoritmos têm dificuldades com espaços multidimensionais.
Devemos considerar o resultado máximo? A questão é que a dispersão dos resultados em execuções separadas de algoritmos é importante. Em todos os algoritmos, na primeira iteração, os valores aleatórios dos pontos de semeadura, que podem ser completamente aleatórios e muito próximos do valor do extremo global, nesse caso, o algoritmo encontrará o melhor resultado com rapidez excessiva, portanto, o valor médio dos resultados das execuções reflete melhor a característica do algoritmo para excluir a dependência aleatória do "sucesso" do algoritmo.
Isso está relacionado à teoria da probabilidade. Não importa quão complexa seja a função-alvo, se houver apenas um parâmetro, mesmo depois de gerar 10 valores aleatórios, um deles estará muito próximo do extremo global. Os métodos ALGLIB (variações de descida de gradiente) são sensíveis à posição inicial dos pontos no espaço, assim como a natureza determinística desses métodos. À medida que a dimensionalidade do espaço de pesquisa aumenta, a complexidade do espaço aumenta exponencialmente, não há como chegar ao extremo global gerando números aleatórios.
A prova é a dificuldade desses métodos de convergir até mesmo em um paraboloide monótono, suave e unimodal se a dimensionalidade do problema aumentar.
Quanto mais estáveis forem os resultados mostrados pelo AO, independentemente dos valores iniciais no espaço de busca, mais esse método pode ser considerado confiável na solução de problemas. É por isso que, nos testes, escolhemos o valor médio de várias execuções do AO.
A realidade atual é tal que muitas tarefas exigem a otimização de milhões e até bilhões de parâmetros (IA, LLM, redes generativas, tarefas complexas de controle na produção e nos negócios), e não podemos falar em suavidade e unimodalidade das tarefas.
Obrigado por seu comentário.
1. Sim, correto. Todas as funções de teste são unificadas e seus valores estão no intervalo [0,0; 1,0].
2. Todas as funções de teste têm apenas dois parâmetros. Mas, ao testar algoritmos, usamos o espaço de pesquisa multidimensional (três tipos de testes, 5*2=10, 25*2=50, 500*2=1000 parâmetros para avaliar a capacidade de escala do AO) duplicando repetidamente uma função bidimensional.
3. O problema com dois parâmetros é simples demais para comparar adequadamente os algoritmos entre si; quase todos os algoritmos resolvem esse problema instantaneamente com 100% de convergência. Os algoritmos têm dificuldades com espaços multidimensionais.
Devemos considerar o resultado máximo? A questão é que a dispersão dos resultados em execuções separadas de algoritmos é importante. Em todos os algoritmos, na primeira iteração, os valores aleatórios dos pontos de semeadura podem ser completamente aleatórios e muito próximos do valor do extremo global; nesse caso, o algoritmo encontrará o melhor resultado com rapidez excessiva, portanto, o valor médio dos resultados das execuções reflete melhor a característica do algoritmo para excluir a dependência aleatória do "sucesso" do algoritmo.
Isso está relacionado à teoria da probabilidade. Não importa quão complexa seja a função-alvo, se houver apenas um parâmetro, mesmo depois de gerar 10 valores aleatórios, um deles estará muito próximo do extremo global. Os métodos ALGLIB (variações de descida de gradiente) são sensíveis à posição inicial dos pontos no espaço, assim como a natureza determinística desses métodos. À medida que a dimensionalidade do espaço de pesquisa aumenta, a complexidade do espaço aumenta exponencialmente, não há como chegar ao extremo global gerando números aleatórios.
A prova é a dificuldade desses métodos de convergir até mesmo em um paraboloide monótono, suave e unimodal se a dimensionalidade do problema aumentar.
Quanto mais estáveis forem os resultados mostrados pelo AO, independentemente dos valores iniciais no espaço de busca, mais esse método pode ser considerado confiável na solução de problemas. É por isso que, nos testes, escolhemos o valor médio de várias execuções do AO.
A realidade atual é tal que muitas tarefas exigem a otimização de milhões e até bilhões de parâmetros (IA, LLM, redes generativas, tarefas complexas de controle na produção e nos negócios), e não podemos falar em suavidade e unimodalidade das tarefas.
Você pegou uma função muito complexa por si só. À medida que o número de parâmetros aumenta, encontrar os parâmetros ideais para a soma de tais funções é de interesse puramente teórico, em minha opinião. Para negociação, um modelo matemático preditivo pode ter muitos parâmetros, mas a função de perda em si é muito simples, portanto, a pesquisa é muito mais fácil. E, certamente, não pode haver um bilhão de parâmetros, mas alguns modestos 10-100, se não estivermos interessados em kurvafitting, é claro, na minha opinião.
Se olharmos do ponto de vista do resultado. Estou interessado em parâmetros que encontrem o máximo da função, por que preciso de um resultado médio? Estou interessado no ótimo e no tempo para chegar a esse ótimo. Se esse tempo for aceitável, não me importa quanto esforço o computador despendeu para selecionar o vetor inicial de parâmetros, o principal é que obtive o resultado.
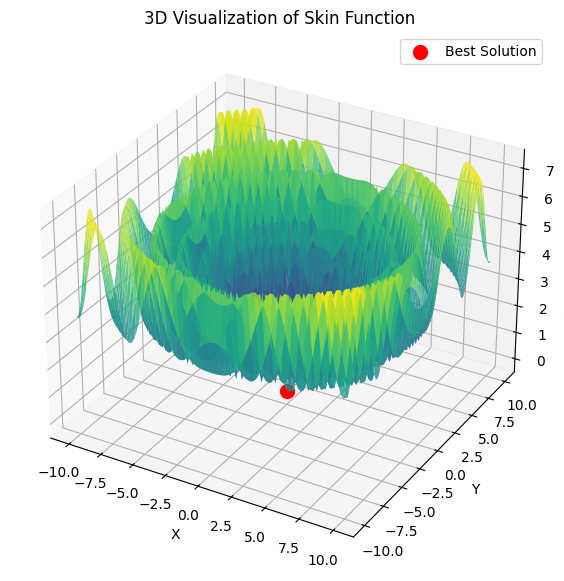
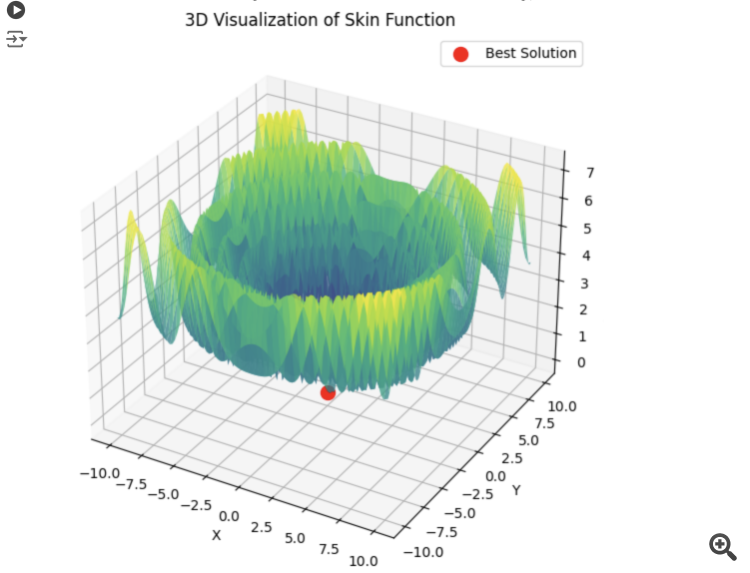
Aqui está um exemplo da soma de 5 funções Hilly
15 segundos de tempo e o resultado é 0,76. Nada mal, eu acho. Especialmente considerando o assunto de negociação, quando simplesmente não sabemos o que é o ótimo global e nunca o saberemos.
De qualquer forma, obrigado pelo artigo. Há muito o que se pensar aqui. Testarei os outros algoritmos um pouco mais tarde e publicarei os resultados.
1) Você pegou uma função muito complexa por si só. À medida que o número de parâmetros aumenta, encontrar os parâmetros ideais para a soma de tais funções é de interesse puramente teórico, em minha opinião.
2) Para negociação, um modelo matemático preditivo pode ter muitos parâmetros, mas a função de perda em si é muito simples, portanto, a busca é muito mais fácil. E certamente não pode haver um bilhão de parâmetros, mas alguns modestos 10-100, se não estivermos interessados em kurvafitting, é claro, na minha opinião.
3) Se olharmos do ponto de vista do resultado. Estou interessado em parâmetros que encontrem o máximo da função, por que preciso de um resultado médio? Estou interessado no ótimo e no tempo para atingir esse ótimo. Se esse tempo for aceitável, então não me importa quanto esforço o computador despendeu para selecionar o vetor inicial de parâmetros, o principal é que obtive o resultado.
4) Aqui está um exemplo para a soma de 5 funções Hilly
15 segundos de tempo e o resultado é 0,76. Nada mal, eu acho. Especialmente considerando o assunto de negociação, quando simplesmente não sabemos qual é o ótimo global e nunca o saberemos.
5) De qualquer forma, obrigado pelo artigo. Há muito o que se pensar aqui. Testarei o restante dos algoritmos um pouco mais tarde e publicarei os resultados.
1) Nos artigos, consideramos os OAs não isoladamente, como um cavalo no vácuo (exemplo: PSO, muito famoso e, portanto, popular, mas não poderoso, e o mesmo OAE - não conhecido por ninguém, mas que corta o espaço suave e discreto tão rápido quanto as fichas voam), mas, juntamente com a análise de sua lógica e dispositivo, consideramos suas habilidades de pesquisa em comparação umas com as outras. Isso nos permite entender profundamente suas potencialidades em tarefas práticas. E é com o aumento da dimensionalidade que as verdadeiras possibilidades podem ser reveladas, e isso ocorre na comparação dos algoritmos entre si. Na vida real, praticamente não há tarefas simples, a menos, é claro, que estejamos falando de tarefas que podem ser resolvidas analiticamente.
Expliquei acima por que é necessário usar o valor médio dos resultados finais ao comparar algoritmos - para excluir a influência do "sucesso aleatório" e revelar diretamente os recursos de pesquisa dos algoritmos.
E quando se trata da aplicação prática de AO (não para comparar AOs), sim, é recomendável usar várias execuções de otimizações para escolher o melhor resultado. Porém, se um algoritmo fraco tiver que ser reiniciado repetidamente, desperdiçando execuções preciosas da função de destino, outro algoritmo alcançará o mesmo resultado em muito menos execuções da função de destino. Por que pagar mais quando o resultado pode ser o mesmo? Algoritmos fracos ficarão presos, atolados no espaço de busca, exigindo várias reinicializações, e você nunca terá certeza de que não está preso elementarmente no início da otimização. Acho que ninguém está interessado em tal situação na prática.
2) Tente visualizar a função de perda em um problema prático com pelo menos dois parâmetros com algum Expert Advisor, a superfície acabará não sendo suave e nem unimodal. Devido à natureza discreta das tarefas de negociação, alvos simples e suaves simplesmente não existem. Portanto, os métodos que têm dificuldades até mesmo em um paraboloide suave serão ineficazes na negociação.
3) O resultado médio é usado para comparar os algoritmos entre si, não na prática (veja o ponto 1). Se você não se importa com o tempo e a energia gastos na busca, então faça uma busca completa, não há motivo para usar o AO. Mas, na prática, isso acontece muito raramente, pois estamos sempre limitados em termos de tempo e recursos computacionais.
4) Os resultados apresentados não contêm informações sobre o número de execuções da função-alvo necessárias para atingir o resultado especificado. Esse indicador é fundamental para avaliar a eficácia da AO. A escolha do AO deve se basear na maximização da eficiência (minimizando o número de execuções) e na minimização da probabilidade de ficar preso, especialmente em tarefas práticas de negociação.
5) Obrigado, fico feliz que os artigos estejam fundamentando o raciocínio. Seria ótimo se você pudesse fornecer o código dos testes que realizou, embora todo o código já tenha sido fornecido no artigo (aparentemente, você usa algum método de teste próprio). Vamos dar uma olhada e resolver o problema.
Estou trabalhando em um artigo separado sobre as questões levantadas nesta discussão.
Experimente algoritmos diferentes - consideramos muitos - e compare-os entre si. Os métodos Alglib são muito rápidos e acredito que sejam muito bons para resolver problemas formulados analiticamente (esse é um tópico separado), mas quando a fórmula analítica não é conhecida, há outras opções.
Para aqueles que precisam resolver problemas formulados analiticamente, os artigos também serão muito úteis, pois descrevem os princípios de trabalho com os métodos ALGLIB.
Não é correto comparar os solucionadores de metaevr. e gradiente dessa forma. Eles devem ser colocados em condições iguais.
O Metaevr. já tem pontos semeados, enquanto os solucionadores de gradiente começam a partir de um ponto.
Para criar condições iguais, precisamos fazer um lote para o último. Ou inicialização múltipla.
É por isso que os gradientes precisam ser avaliados pelo melhor resultado, não pelo resultado médio. E é por isso que eles são executados mais rapidamente. Isso proporciona um equilíbrio entre velocidade e precisão no treinamento de redes neurais.
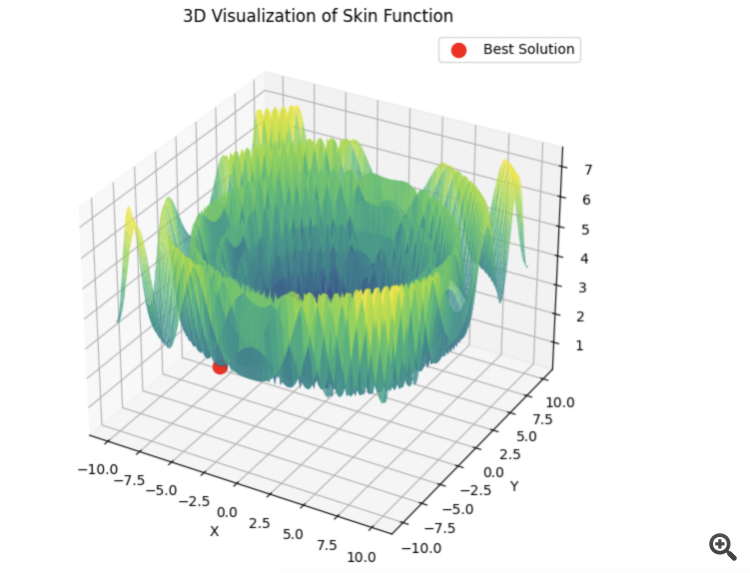
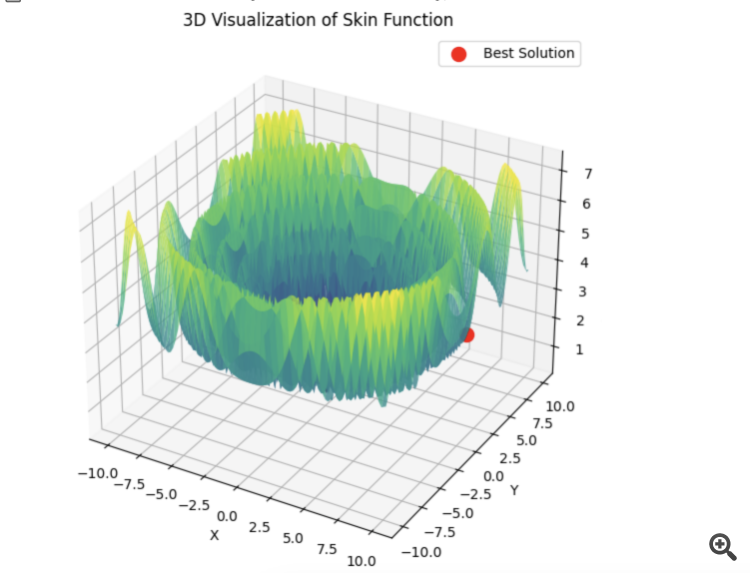
Se o PSO escolher o mínimo correto imediatamente:
Então, o lbfgs saltará de um local para outro, e esse é um comportamento normal para ele. Mas ele é rápido e pode saltar um número configurável de vezes, dividindo a função otimizada em lotes.
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso

Novo artigo Métodos de otimização da biblioteca Alglib (Parte II) foi publicado:
Na primeira parte do nosso estudo sobre os algoritmos de otimização da biblioteca ALGLIB incluídos na versão padrão do terminal MetaTrader 5, exploramos em detalhes os algoritmos: BLEIC (restrições lineares de igualdade/desigualdade e limites), L-BFGS (Broyden–Fletcher–Goldfarb–Shanno com memória limitada) e NS (Otimização não suave e não convexa com restrições do tipo caixa, lineares ou não lineares – Restrições não suaves). Não apenas discutimos suas bases teóricas, mas também explicamos uma forma simples de aplicá-los em problemas de otimização.
Neste artigo, daremos continuidade à análise dos métodos restantes do arsenal ALGLIB. A atenção estará voltada principalmente aos testes em funções complexas e multidimensionais, o que nos permitirá formar uma visão completa da eficácia de cada método. Ao final, faremos uma análise abrangente dos resultados obtidos e apresentaremos recomendações práticas para a escolha do algoritmo mais adequado para cada tipo específico de tarefa.
Autor: Andrey Dik