Redes neuronales: así de sencillo (Parte 95): Reducción del consumo de memoria en los modelos de transformadores
257
0
Introducción
La introducción de la arquitectura "Transformer" allá por 2017 propició la aparición de los Large Language Models (LLMs), que demuestran altos resultados en la resolución de problemas de procesamiento del lenguaje natural. Muy pronto, las ventajas de los enfoques de Autoatención han sido adoptadas por investigadores de prácticamente todos los ámbitos del aprendizaje automático.
Sin embargo, debido a su naturaleza autorregresiva, el decodificador Transformer está limitado por el ancho de banda de memoria utilizado para cargar y almacenar las entidades Key y Value en cada paso temporal (lo que se conoce como KV caching). Como esta caché se escala linealmente con el tamaño del modelo, el tamaño del lote y la longitud del contexto, puede incluso superar el uso de memoria de las ponderaciones del modelo.
Este problema no es nuevo. Hay distintos enfoques para resolverlo. Los métodos más utilizados implican la reducción directa de los cabezales KV utilizados. En 2019, los autores del artículo Fast Transformer Decoding: One Write-Head is All You Need propusieron el algoritmo Multi-Query Attention (MQA), que utiliza solo una proyección de Key y Value para todas las cabezas de atención a nivel de una capa. Esto reduce el consumo de memoria de la caché KV en 1/cabezales (heads). Esta importante reducción del consumo de recursos conlleva cierta degradación de la calidad y la estabilidad del modelo.
Los autores del método Grouped-Query Attention (GQA), descrito en el artículo GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints (2023), presentaron una solución intermedia para separar múltiples cabezales KV en varios grupos de atención. La eficiencia de reducción del tamaño de la caché KV cuando se utiliza GQA es igual a grupos/cabezas. Con un número razonable de cabezales, GQA puede alcanzar casi la paridad con el modelo base en varias pruebas. Sin embargo, la reducción del tamaño de la caché KV sigue limitada a 1/heads cuando se utiliza MQA. Esto puede no ser suficiente para algunas aplicaciones.
Para ir más allá de esta limitación, los autores del trabajo MLKV: Multi-Layer Key-Value Heads for Memory Efficient Transformer Decoding propusieron un algoritmo de compartición multinivel de Key y Value (MLKV). Llevan el uso compartido de KV un paso más allá. MLKV no sólo divide las cabezas KV entre las cabezas de atención de una capa, sino también entre las cabezas de atención de otros niveles. Los cabezales KV pueden utilizarse para grupos de cabezales de atención en una capa y/o para grupos de cabezales de atención en capas posteriores. En casos extremos, se puede utilizar un cabezal KV para todos los cabezales de atención de todas las capas. Los autores del método experimentan con varias configuraciones, que utilizan Query tanto en el mismo nivel como entre distintos niveles. Incluso con configuraciones en las que el número de cabezales KV es inferior al de capas. Los experimentos presentados en este artículo demuestran que estas configuraciones proporcionan un equilibrio razonable entre el rendimiento y el ahorro de memoria conseguido. La reducción práctica del uso de memoria a 2/capas del tamaño original de la caché KV no conlleva un deterioro significativo de la calidad del modelo.
1. Método MLKV
El método MLKV es una continuación lógica de los algoritmos MQA y GQA. En los métodos especificados, el tamaño de la caché KV se reduce debido a la reducción de cabezas KV, que son compartidas por un grupo de cabezas de atención dentro de una única capa de Autoatención. Un paso totalmente esperado es la compartición de entidades Key y Value entre capas de Autoatención. Este paso puede estar justificado por las recientes investigaciones sobre el papel del bloque FeedForward en el algoritmoTransformer. Se supone que el bloque especificado simula la memoria «Key-Value», procesando diferentes niveles de información. Sin embargo, lo más interesante para nosotros es la observación de que grupos de capas sucesivas computan cosas similares. Más concretamente, los niveles inferiores se ocupan de patrones superficiales, y los superiores de detalles más semánticos. Así, se puede concluir que la atención puede delegarse a grupos de capas manteniendo los cálculos necesarios en el bloque FeedForward. Intuitivamente, los cabezales KV pueden compartirse entre capas que tengan objetivos similares.
Desarrollando estas ideas, los autores del método MLKV proponen el intercambio de claves multinivel. MLKV no sólo comparte cabezas KV entre las cabezas de atención Query de la misma capa Self-Attention, sino también entre las cabezas de atención de otras capas. Esto permite reducir el número total de cabezales KV en el Transformer, permitiendo así una caché KV aún más pequeña.
MLKV puede escribirse de la siguiente manera:
A continuación se muestra la visualización del autor de la comparación de KV métodos de reducción de tamaño de caché.
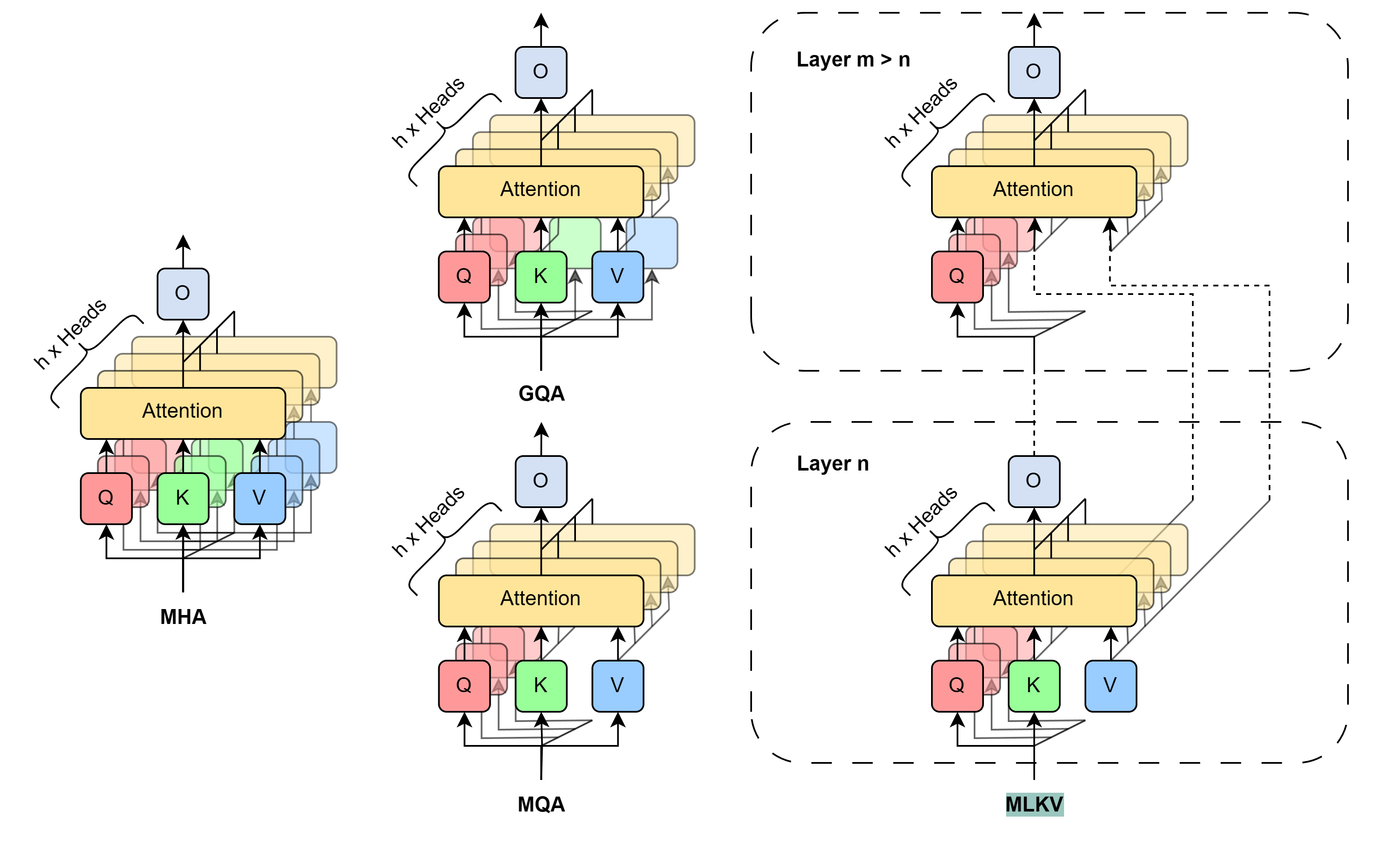
Los experimentos realizados por los autores del método demuestran un claro equilibrio entre memoria y precisión. Los diseñadores tienen que elegir qué sacrificar. Además, hay que tener en cuenta muchos factores. Para un número de cabezales KV superior o igual al número de capas, sigue siendo mejor utilizar GQA/MQA en lugar de MLKV. Los autores del método asumen que la presencia de múltiples cabezales KV en múltiples capas es más importante que tener múltiples cabezales KV en una capa. En otras palabras, debe sacrificar los cabezales KV a nivel de capa primero (GQA/MQA) y de capa cruzada después (MLKV).
Para situaciones más intensivas en memoria que requieran que el número de cabezales KV sea menor que el número de capas, la única forma es MLKV. Esta solución de diseño es viable. Los autores del método descubrieron que cuando las cabezas de atención se reducen a menos de la mitad del número de capas, MLKV funciona muy cerca de MQA. Esto significa que debería ser una solución relativamente sencilla si necesita que la caché KV tenga la mitad del tamaño que proporciona MQA.
Si se requiere un valor inferior, podemos utilizar un número de cabezales KV hasta 6 veces menor que el número de capas sin que se produzca un fuerte deterioro de la calidad. Cualquier cosa por debajo de eso se vuelve cuestionable.
2. Implementación en MQL5
Hemos examinado brevemente la descripción teórica de los enfoques propuestos. Ahora, podemos pasar a su aplicación práctica utilizando MQL5. Aquí implementaremos el método MLKV. En mi opinión, este es un enfoque más general, mientras que MQA y GQA pueden presentarse como casos especiales de MLKV.
El problema más agudo de la próxima aplicación es cómo transferir información entre las capas neuronales. En este caso, decidí no complicar el algoritmo existente de cómo se intercambian los datos entre los objetos de las capas neuronales. En su lugar, utilizaremos un bloque de secuencia multicapa, que ya hemos implementado muchas veces. Utilizaremos CNeuronMLMHAttentionOCL como clase padre para la próxima implementación.
2.1 Implementación en el lado OpenCL
Empecemos por preparar los núcleos en el lado del programa OpenCL. Nótese que en la clase padre seleccionada, utilizamos un tensor concatenado para la generación paralela de las entidades Query, Key y Value. Todo el mecanismo de atención se construyó sobre esto. Sin embargo, dado que utilizamos diferentes números de cabezas para Query y Key-Value, así como utilizamos Key-Value de otro nivel, deberíamos pensar en dividir dichas entidades en 2 tensores separados. Ya hemos hecho algo parecido al construir bloques de atención cruzada (cross-attention).
Esto significa que podemos aprovechar el código existente y ajustar ligeramente el algoritmo del núcleo de atención cruzada. Sólo tenemos que añadir otro parámetro del núcleo que indique el número de KVcabezas (resaltado en rojo en el código).
__kernel void MH2AttentionOut(__global float *q, ///<[in] Matrix of Querys __global float *kv, ///<[in] Matrix of Keys __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention int dimension, ///< Dimension of Key int heads_kv )
En el cuerpo del núcleo, para determinar la cabeza KV que se está analizando, necesitamos tomar el resto de dividir la cabeza de atención actual entre el número total de cabezas KV.
const int h_kv = h % heads_kv;
Añade un ajuste de desplazamiento en el búfer del tensor Key-Value.
const int shift_k = 2 * dimension * (k + h_kv); const int shift_v = 2 * dimension * (k + heads_kv + h_kv);
El resto del código del kernel permanece sin cambios. Se han realizado modificaciones similares en el código del núcleo de retropropagación MH2AttentionInsideGradients. El código completo de estos kernels está disponible en el archivo adjunto.
Con esto concluye nuestro trabajo sobre OpenCL. Pasemos a la parte del programa principal. Aquí primero tenemos que restaurar la funcionalidad del código creado anteriormente. Porque un parámetro adicional en los núcleos especificados anteriormente provocará errores al llamarlos. Así que vamos a encontrar todas las llamadas a estos núcleos y añadir la transferencia de datos a un nuevo parámetro.
Permítame recordarle que anteriormente utilizamos el mismo número de metas para Query y Key-Value.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_MH2AttentionInsideGradients, def_k_mh2aig_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
2.2 Creación de la clase MLKV
Continuemos con nuestro proyecto. En el siguiente paso, crearemos una clase de bloque de atención multicapa utilizando los enfoques MLKV: CNeuronMLMHAttentionMLKV. Como se ha mencionado anteriormente, la nueva clase será hija directa de la clase CNeuronMLMHAttentionOCL. A continuación se muestra la estructura de la nueva clase.
class CNeuronMLMHAttentionMLKV : public CNeuronMLMHAttentionOCL { protected: uint iLayersToOneKV; uint iHeadsKV; CCollection KV_Tensors; CCollection KV_Weights; CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronMLMHAttentionMLKV(void) {}; ~CNeuronMLMHAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLMHAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Como se puede observar, en la estructura de clases presentada hemos introducido 2 variables para almacenar el número de KV cabezas (iHeadsKV) y la frecuencia de actualización del tensor Key-Value (iLayersToOneKV).
También hemos añadido colecciones de almacenamiento de tensores Key-Value y matrices de pesos para su formación (KV_Tensors y KV_Weights respectivamente).
Además, hemos añadido un búfer Temp para registrar los valores intermedios de los gradientes de error.
El conjunto de métodos de la clase es bastante estándar y creo que ya entiendes su propósito. Las estudiaremos con más detalle durante el proceso de aplicación.
Declaramos todos los objetos internos como estáticos y así podemos dejar el constructor y el destructor de la clase vacíos. La inicialización de todos los objetos y variables anidados se realiza en el método Init. Como es habitual, los parámetros de este método contienen toda la información necesaria para crear el objeto requerido.
bool CNeuronMLMHAttentionMLKV::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En el cuerpo del método, llamamos inmediatamente al método relevante de la clase base de todas las capas neuronales CNeuronBaseOCL.
Tenga en cuenta que estamos accediendo al objeto de la clase base, no a la clase padre directa. Esto está relacionado con la separación de las entidades Query, Key y Value en 2 tensores, lo que provoca un cambio en los tamaños de algunos búferes de datos. Sin embargo, este enfoque nos obliga a inicializar no sólo los objetos nuevos, sino también los heredados de la clase padre.
Después de ejecutar con éxito el método de inicialización de la clase base, guardamos los parámetros recibidos de la clase en variables internas.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1);
El siguiente paso consiste en calcular los tamaños de todos los búferes que se van a crear.
uint num_q = iWindowKey * iHeads * iUnits; //Size of Q tensor uint num_kv = 2 * iWindowKey * iHeadsKV * iUnits; //Size of KV tensor uint q_weights = (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of Q tenzor uint kv_weights = 2 * (iWindow + 1) * iWindowKey * iHeadsKV; //Size of weights' matrix of KV tenzor uint scores = iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = iWindow * iUnits; //Size of out tensore uint w0 = (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
A continuación, añadimos un bucle con un número de iteraciones igual al número de capas internas del bloque de atención que se está creando.
for(uint i = 0; i < iLayers; i++) {
En el cuerpo del bucle, creamos otro bucle anidado en el que primero creamos buffers para almacenar datos. En la segunda iteración del bucle anidado, crearemos buffers para registrar los gradientes de error correspondientes.
CBufferFloat *temp = NULL; for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Aquí creamos primero los tensores de entidad de consulta. A continuación, creamos los tensores pertinentes para registrar las entidades Key-Value. Sin embargo, este último debe crearse una vez por cada iteración iLayersToOneKV del bucle.
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
A continuación, siguiendo el algoritmo Transformer, creamos buffers para almacenar los tensores de la matriz de coeficientes de dependencia, la atención multicabezal y su representación comprimida.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
A continuación, añadimos los búferes del bloque FeedForward.
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
//--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Tenga en cuenta que al crear buffers para almacenar las salidas y los gradientes de error de la 2ª capa del bloque FeedForward, primero comprobamos el número de capa. Como no crearemos nuevos buffers para la última capa, guardaremos punteros a los buffers ya creados de resultados y gradientes de error de nuestra clase CNeuronMLMHAttentionMLKV. Así evitamos la copia innecesaria de datos al intercambiarlos con la capa siguiente.
Después de crear buffers para almacenar los resultados intermedios y los gradientes de error correspondientes, crearemos buffers para las matrices de los parámetros entrenables de nuestra clase. Debo decir que aquí también hay bastantes. En primer lugar, creamos e inicializamos una matriz de pesos con parámetros aleatorios para generar la entidad Query.
//--- Initialize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Generamos los parámetros de generación del tensor Key-Value de forma similar. De nuevo, se crean una vez por cada iLayersToOneKV de capas internas.
//--- Initialize KV weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
A continuación, generamos parámetros de compresión para los resultados de la atención multicabezal.
//--- Initialize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Y por último están los parámetros del bloque FeedForward.
//--- Initialize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Durante el proceso de entrenamiento del modelo, necesitaremos buffers para registrar los momentos de todos los parámetros anteriores. Crearemos estos búferes en un bucle anidado, cuyo número de iteraciones depende del método de optimización elegido.
//--- for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(q_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(kv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
//--- Initialize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Después de crear todas las colecciones de nuestros buffers de bloque de atención, inicializamos otro buffer auxiliar que utilizaremos para escribir valores intermedios.
if(!Temp.BufferInit(MathMax(num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
En cada paso, asegúrese de controlar el progreso de las operaciones. Y al final del método, devolvemos el resultado lógico de las operaciones a la instancia que realiza la llamada.
Los métodos AttentionOut y AttentionInsideGradients colocan los núcleos que hemos ajustado en la cola de ejecución. Sin embargo, no vamos a discutir sus algoritmos en detalle ahora. El algoritmo para colocar cualquier núcleo en la cola de ejecución permanece inalterado:
- Definición del espacio de tareas.
- Pasar todos los parámetros necesarios al núcleo.
- Colocación del núcleo en la cola de ejecución.
El código de este algoritmo ya se ha descrito varias veces en esta serie de artículos. Los métodos para poner en cola la versión original de los núcleos que hemos modificado se describieron en el artículo dedicado al método ADAPT. Por tanto, estudie los códigos adjuntos para más detalles.
Ahora pasamos a considerar el algoritmo del método de paso hacia delante feedForward. En los parámetros del método, recibimos un puntero al objeto de la capa anterior, que en este caso proporciona las entradas.
bool CNeuronMLMHAttentionMLKV::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
En el cuerpo del método, primero comprobamos la relevancia del puntero recibido. Después declaramos un puntero local al búfer del tensor Key-Value y ejecutamos un bucle a través de todas las capas internas de nuestro bloque.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
En el cuerpo del bucle, primero generamos el tensor de entidades Query. Y luego generamos el tensor Key-Value. Nótese que generamos esta última no en cada iteración sobre las capas internas, sino sólo cada capa iLayersToOneKV. Matemáticamente, el control de esta condición es bastante sencillo: asegurarse de que el índice de la capa actual es divisible sin resto por el número de capas de un tensor Key-Value. Cabe señalar que para la primera capa con índice «0» el resto de la división también está ausente.
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; }
Guardamos el puntero al buffer de entidades generadas en la variable local que declaramos anteriormente. De esta forma, podemos acceder fácilmente a ellos en iteraciones posteriores del bucle.
Una vez generadas todas las entidades necesarias, realizamos operaciones de atención cruzada feed-forward. Sus resultados se escriben en el búfer de salida de la atención multicabezal.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
A continuación, comprimimos los datos resultantes hasta el tamaño de los datos originales.
//--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false;
Tras lo cual, siguiendo el algoritmo Transformer, resumimos los resultados de la operación del bloque Self-Attention con los datos de entrada y normalizamos los valores obtenidos.
//--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
A continuación pasamos los datos a través del bloque FeedForward.
//--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false;
A continuación, volvemos a sumar los datos de los 2 hilos y los normalizamos.
//--- Sum and normalize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- return true; }
Después de completar con éxito todas las iteraciones de nuestro bucle a través de las capas neuronales internas, devolvemos el resultado lógico de las operaciones a la persona que llama.
La implementación de métodos de paso feed-forward va seguida de la construcción de algoritmos de retropropagación. Aquí es donde realizamos la optimización de los parámetros del modelo para encontrar la función máxima verdadera en el conjunto de datos de entrenamiento. Como sabes, el algoritmo de retropropagación se construye en 2 etapas. En primer lugar, propagamos el gradiente de error a todos los elementos del modelo, teniendo en cuenta su impacto en el resultado global. Esta funcionalidad se implementa en el método calcInputGradients. En la segunda etapa (método updateInputWeights), realizamos una optimización directa de los parámetros hacia el antigradiente.
Comenzaremos nuestro trabajo implementando el algoritmo de retropropagación con el método de propagación de gradiente de error calcInputGradients. En parámetros, este método recibe un puntero al objeto de la capa neuronal anterior. Durante el paso feed-forward, interpretó el papel de los datos de entrada. En esta etapa, escribiremos el resultado de las operaciones del método en el buffer de gradiente de error del objeto obtenido.
bool CNeuronMLMHAttentionMLKV::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false;
En el cuerpo del método, comprobamos la relevancia del puntero recibido. Después de eso, creamos 2 variables locales para almacenar punteros a los búferes de datos pasados entre las capas internas.
CBufferFloat *out_grad = Gradient;
CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);
Tras realizar un pequeño trabajo preparatorio, creamos un bucle inverso sobre capas neuronales internas.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1);
En este bucle, primero determinamos la necesidad de cambiar el búfer de gradiente de error de las entidades Key-Value.
Como hemos visto, el método MLKV implica que un tensor de entidades Key-Value se utilizará para múltiples bloques Self-Attention. Al organizar el pase de avance, aplicamos los mecanismos correspondientes. Ahora tenemos que organizar la propagación del gradiente de error al nivel Key-Value apropiado. Y, por supuesto, sumaremos los gradientes de error de los distintos niveles.
La construcción posterior del algoritmo se aproxima mucho a la propagación del gradiente de error en los objetos de atención cruzada. En primer lugar, propagamos el gradiente de error obtenido de la capa posterior a través del bloque FeedForward.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None)) return false; CBufferFloat *temp = FF_Tensors.At(i * 6 + 3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), FF_Tensors.At(i * 6), temp, iWindow, 4 * iWindow, LReLU)) return false;
Sumamos los datos de 2 hilos en el paso de avance. Entonces, ahora sumamos el gradiente de error sobre los mismos hilos de datos en el pase de retropropagación.
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false)) return false; out_grad = temp;
En el siguiente paso, dividimos el gradiente de error obtenido en las cabezas de atención.
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None)) return false;
A continuación, propagamos el gradiente de error a las entidades Query, Key y Value. Aquí organizaremos una pequeña ramificación del algoritmo. Porque necesitamos sumar el gradiente de error del tensor Key-Value de varias capas internas. Al ejecutar el método de distribución del gradiente de error, borraremos cada vez los datos recogidos anteriormente y los sobrescribiremos con datos nuevos. Por lo tanto, escribimos directamente el gradiente de error en el búfer del tensor Key-Value sólo durante la primera llamada.
//--- Passing gradient to query, key and value if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; }
En otros casos, escribimos primero el gradiente de error en un búfer auxiliar. A continuación, sumamos los valores obtenidos a los recogidos anteriormente.
else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
A continuación, tenemos que pasar el gradiente de error al nivel de la capa anterior. Aquí «capa anterior» significa principalmente la capa anterior interna. Sin embargo, al procesar el nivel más bajo, pasaremos el gradiente de error al buffer del objeto recibido en los parámetros del método.
En primer lugar, definimos un puntero al objeto receptor del gradiente de error.
CBufferFloat *inp = NULL; if(i == 0) { inp = prevLayer.getOutput(); temp = prevLayer.getGradient(); } else { temp = FF_Tensors.At(i * 6 - 1); inp = FF_Tensors.At(i * 6 - 4); }
Después, descendemos el gradiente de error desde la entidad Query.
if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), inp, temp, iWindow, iWindowKey * iHeads, None)) return false;
Sumamos el gradiente de error sobre 2 tramos de datos (Query + «a través»).
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
Lo único que falta en el algoritmo descrito anteriormente es el gradiente de error de las entidades Key y Value. Como recordarás, estas entidades no se forman a partir de cada capa interna. En consecuencia, transferiremos el gradiente de error sólo a los datos que se utilizaron en su formación. Pero hay un punto. Anteriormente ya hemos escrito el error de la entidad Query y el hilo de paso al buffer de gradiente de los datos de entrada. Por lo tanto, primero escribimos el gradiente de error en un búfer auxiliar y luego lo añadimos a los datos recogidos anteriormente.
//--- if((i % iLayersToOneKV) == 0) { if(IsStopped() || !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; }
Al final de las iteraciones del bucle, pasamos un puntero al buffer del gradiente de error para realizar las operaciones de la siguiente iteración del bucle.
if(i > 0) out_grad = temp; } //--- return true; }
En cada paso, comprobamos el resultado de las operaciones. Y después de completar con éxito todas las iteraciones del bucle, pasamos el resultado lógico de las operaciones del método al programa llamador.
Hemos propagado el gradiente de error a todos los objetos internos y a la capa anterior. El siguiente paso consiste en ajustar los parámetros del modelo. Esta funcionalidad se implementa en el método updateInputWeights. Al igual que en los dos métodos comentados anteriormente, en los parámetros recibimos un puntero al objeto de la capa anterior.
bool CNeuronMLMHAttentionMLKV::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false; CBufferFloat *inputs = NeuronOCL.getOutput();
En el cuerpo del método, comprobamos la relevancia del puntero recibido y guardamos inmediatamente el puntero al búfer de resultados del objeto recibido en una variable local.
A continuación, creamos un bucle a través de todas las capas internas y actualizamos los parámetros del modelo.
for(uint l = 0; l < iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(l * 2 + 1), inputs, (optimization == SGD ? QKV_Weights.At(l * 2 + 1) : QKV_Weights.At(l * 3 + 1)), (optimization == SGD ? NULL : QKV_Weights.At(l * 3 + 2)), iWindow, iWindowKey * iHeads)) return false;
De forma similar al método de paso de avance, primero ajustamos los parámetros de generación del tensor Query.
A continuación, actualizamos los parámetros de generación del tensor Key-Value. Una vez más, tenga en cuenta que estos parámetros no se ajustan en cada iteración del bucle. Sin embargo, el ajuste de los parámetros del tensor Key-Value en el bucle general facilita la sincronización con el búfer de entrada correcto y hace que el código sea más claro.
if(l % iLayersToOneKV == 0) { uint l_kv = l / iLayersToOneKV; if(IsStopped() || !ConvolutuionUpdateWeights(KV_Weights.At(l_kv * (optimization == SGD ? 2 : 3)), KV_Tensors.At(l_kv * 2 + 1), inputs, (optimization == SGD ? KV_Weights.At(l_kv*2 + 1) : KV_Weights.At(l_kv*3 + 1)), (optimization == SGD ? NULL : KV_Weights.At(l_kv * 3 + 2)), iWindow, 2 * iWindowKey * iHeadsKV)) return false; }
El bloque Self-Attention no contiene parámetros entrenables. Sin embargo, los parámetros aparecen en la capa en la que comprimimos los resultados de la atención multicabezal hasta el tamaño de los datos de entrada. En el siguiente paso, ajustamos estos parámetros.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9)), FF_Tensors.At(l * 6 + 3), AO_Tensors.At(l * 2), (optimization == SGD ? FF_Weights.At(l * 6 + 3) : FF_Weights.At(l * 9 + 3)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 6)), iWindowKey * iHeads, iWindow)) return false;
Después de eso sólo tenemos que ajustar los parámetros del bloque FeedForward.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(l * 6 + 4), FF_Tensors.At(l * 6), (optimization == SGD ? FF_Weights.At(l * 6 + 4) : FF_Weights.At(l * 9 + 4)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 7)), iWindow, 4 * iWindow)) return false; //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 2), FF_Tensors.At(l * 6 + 5), FF_Tensors.At(l * 6 + 1), (optimization == SGD ? FF_Weights.At(l * 6 + 5) : FF_Weights.At(l * 9 + 5)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 8)), 4 * iWindow, iWindow)) return false;
Pasamos un puntero al búfer de entrada para el bucle neuronal interno posterior y pasamos a la siguiente iteración del bucle.
inputs = FF_Tensors.At(l * 6 + 2); } //--- return true; }
Una vez completadas con éxito todas las iteraciones del bucle, devolvemos al llamante el resultado lógico de las operaciones realizadas.
Con esto concluye la descripción de los métodos de nuestra nueva clase de bloque de atención que incluye los enfoques propuestos por los autores del método MLKV. El código completo de esta clase y todos sus métodos está disponible en el archivo adjunto.
Como ya se ha dicho, los mencionados métodos MQA y GQA son casos especiales de MLKV. Se pueden implementar fácilmente utilizando la clase creada, especificando en los parámetros del método de inicialización de la clase «layers_to_one_kv=1». Si el valor del parámetro cabezas_kv es igual al número de cabezas de atención de la entidad Query, obtenemos el transformador Transformer. Si es menor, entonces obtenemos GQA. Si heads_kv es igual a «1», tenemos la implementación MQA.
Mientras preparaba este artículo, también he creado una clase de atención cruzada utilizando los planteamientos de MLKV - CNeuronMLCrossAttentionMLKV. A continuación se presenta su estructura.
class CNeuronMLCrossAttentionMLKV : public CNeuronMLMHAttentionMLKV { protected: uint iWindowKV; uint iUnitsKV; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); public: CNeuronMLCrossAttentionMLKV(void) {}; ~CNeuronMLCrossAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key,uint heads, uint window_kw, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLCrossAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
Esta clase se construye como sucesora de la clase CNeuronMLMHAttentionMLKV descrita anteriormente. Sólo tuve que hacer pequeñas correcciones en sus métodos, que encontrará en el archivo adjunto.
2.3 Arquitectura de los modelos
Hemos implementado los enfoques propuestos por los autores del método MLKV en MQL5. Ahora podemos pasar a describir la arquitectura de los modelos de aprendizaje. Cabe señalar que, a diferencia de varios artículos recientes, hoy no vamos a ajustar las arquitecturas del codificador de estado de entorno. Añadiremos nuevos objetos a la arquitectura de los modelos Actor y Critic. La arquitectura de estos modelos se especifica en el método CreateDescriptions.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
En los parámetros, el método recibe punteros a 2 matrices dinámicas para registrar la arquitectura secuencial de los modelos. En el cuerpo del método, comprobamos los punteros recibidos y, si es necesario, creamos nuevas instancias de objetos.
En primer lugar, describimos la arquitectura del Actor. Alimentamos el modelo con una descripción del estado de la cuenta y las posiciones abiertas.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Los datos recibidos son preprocesados por una capa totalmente conectada.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
entonces AÑADIMOS una nueva capa de atención cruzada multinivel utilizando enfoques MLKV.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); }
Esta capa comparará el estado actual de la cuenta con la previsión del próximo movimiento de precios obtenida del codificador de estado del entorno.
Aquí utilizamos 8 cabezas de atención para Query y sólo 2 para el tensor Key-Value.
{
int temp[] = {8, 2};
ArrayCopy(descr.heads, temp);
}
En total, creamos 9 capas anidadas en nuestro bloque. Se genera un nuevo tensor Key-Value cada 3 capas.
descr.layers = 9; descr.step = 3;
Para optimizar los parámetros del modelo, utilizamos el método Adam.
descr.window_out = 32; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Tras el bloque de atención, los datos son procesados por 2 capas totalmente conectadas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A la salida del modelo, creamos una política estocástica del Actor, que permite acciones en un cierto rango de valores óptimos.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Además, utilizamos los planteamientos del método FreDF para coordinar las acciones en el ámbito de la frecuencia.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Del mismo modo, construimos un modelo Critic. Aquí, en lugar del estado de la cuenta, alimentamos el modelo con un vector de acciones generadas por la política del Actor.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Estos datos también son preprocesados por una capa totalmente conectada.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Le sigue un bloque de atención cruzada.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); } { int temp[] = {8, 2}; ArrayCopy(descr.heads, temp); } descr.window_out = 32; descr.step = 3; descr.layers = 9; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Los resultados del procesamiento de datos en el bloque de atención cruzada pasan por 3 capas totalmente conectadas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
A la salida del modelo, se forma un vector de recompensas esperadas.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
También añadimos una capa FreDF para la coherencia de la recompensa en el ámbito de la frecuencia.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Los Asesores Expertos para recoger los datos y entrenar los modelos no han cambiado. Puede ver su código completo en el archivo adjunto. El archivo adjunto también contiene el código completo de todos los programas utilizados en el artículo.
3. Pruebas
Hemos aplicado los métodos propuestos. Pasemos ahora a la fase final de nuestro trabajo: probar los enfoques propuestos con datos reales.
Como siempre, para entrenar los modelos utilizamos datos históricos reales del instrumento EURUSD, con el marco temporal H1, para todo el año 2023. Recopilamos datos para el conjunto de datos de entrenamiento ejecutando EAs de interacción ambiental en el probador de estrategias de MetaTrader 5.
Durante el primer lanzamiento, nuestros modelos se inicializan con parámetros aleatorios. Como resultado, obtenemos pases de políticas completamente aleatorios que distan mucho de ser óptimos. Para añadir ejecuciones rentables al conjunto de datos de entrenamiento, recomiendo utilizar los enfoques del método Real-ORL al recopilar los datos de origen.
Tras recopilar el conjunto de datos de entrenamiento inicial, primero entrenamos el codificador de estado de entorno ejecutando el «.../MLKV/StudyEncoder.mq5» en tiempo real en un gráfico del terminal MetaTrader 5. Este EA trabaja sólo con el conjunto de datos de entrenamiento, analizando las dependencias en los datos históricos de movimiento de precios. De hecho, basta con una sola pasada para entrenarla, independientemente de los resultados comerciales. Por lo tanto, entrenamos el codificador de estado hasta que el error de predicción deja de disminuir sin actualizar el conjunto de datos de entrenamiento.
Cabe señalar aquí que los modelos Actor y Critic que se entrenan a continuación utilizan las predicciones obtenidas de forma indirecta. Para lograr los máximos resultados, necesitamos extraer las tendencias actuales del estado del entorno y su fuerza en el estado oculto del codificador, al que luego acceden los modelos Actor y Critic.
Una vez obtenido el resultado deseado en el proceso de entrenamiento del Codificador del Estado del Entorno, pasamos a entrenar la política del Actor y la precisión de la evaluación de la acción de Critic. La segunda fase del entrenamiento del modelo es iterativa. La cuestión es que la variabilidad del entorno del mercado financiero analizado es muy alta. No podemos recoger todas las variantes posibles de interacción entre el Agente y el entorno. Por lo tanto, tras varias iteraciones de entrenamiento de los modelos Actor y Critic, realizamos una iteración adicional de recogida de datos de entrenamiento. Este proceso debe complementar el conjunto de datos de entrenamiento recogidos previamente con datos sobre la interacción con el entorno en un área determinada de la política actual del Actor, lo que permitirá perfeccionarla y optimizarla.
Así, varias iteraciones de entrenamiento de los modelos Actor y Critic se alternan con operaciones de actualización del conjunto de datos de entrenamiento. Este proceso se repite varias veces hasta obtener la política de Actor deseada.
Para probar el modelo entrenado, utilizamos datos históricos de enero de 2023, que no están incluidos en el conjunto de datos de entrenamiento. Los demás parámetros se utilizan tal cual a partir de las iteraciones de recogida del conjunto de datos de entrenamiento.
Debo admitir que en el proceso de entrenamiento de los modelos para este artículo, no conseguí obtener una política capaz de generar beneficios en el conjunto de datos de prueba. Obviamente, se trata de la influencia del proceso de degradación del modelo, que se indicaba en el documento original de los autores.
A continuación se presentan los resultados de las pruebas.
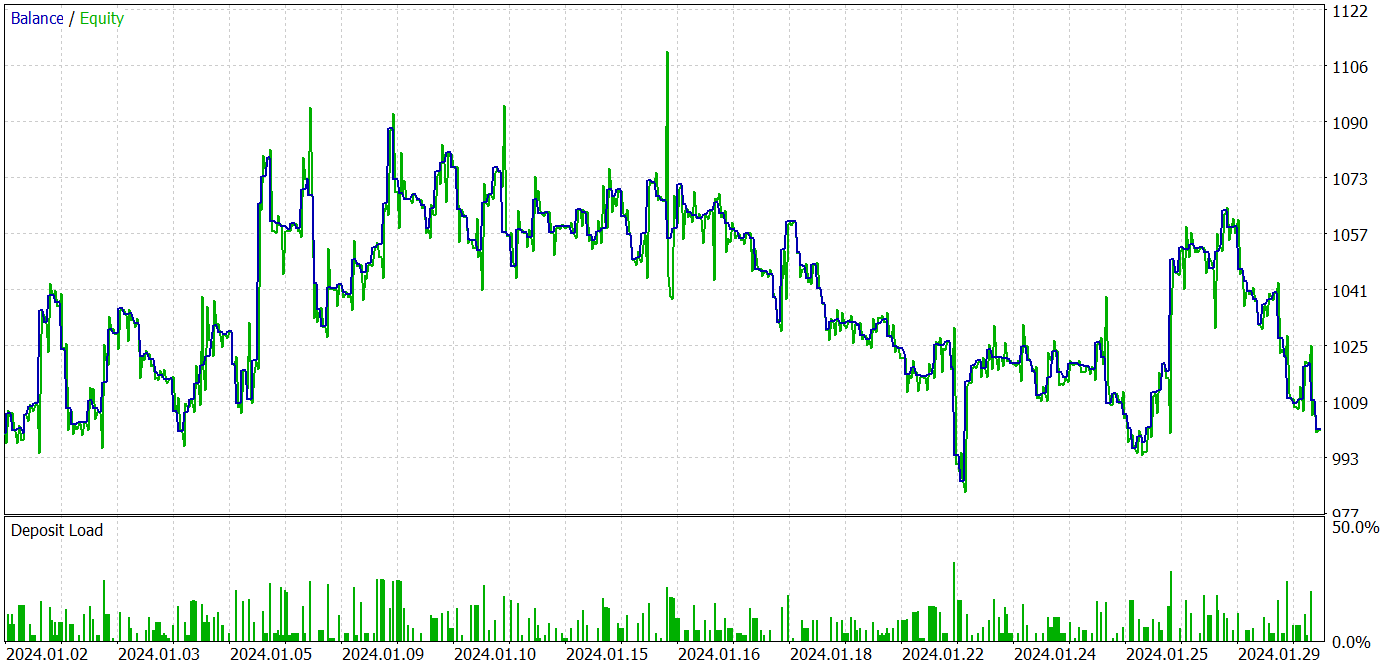
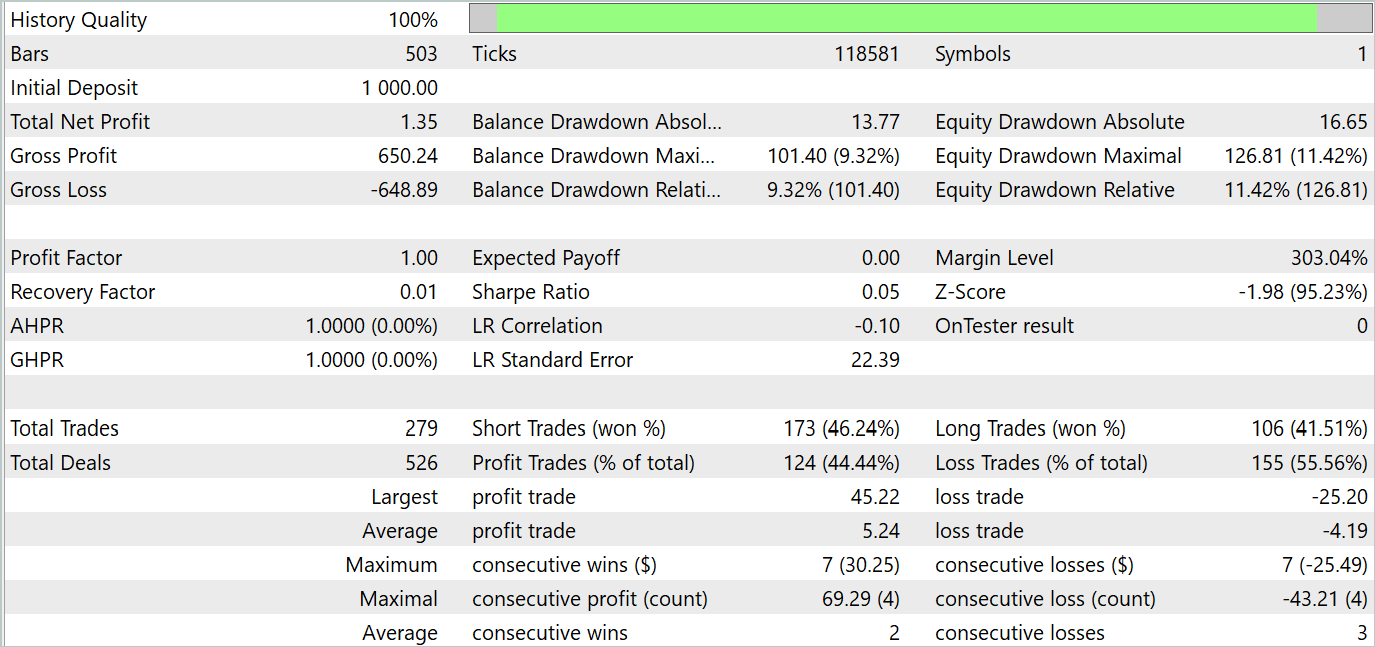
Según los resultados de las pruebas, observamos fluctuaciones de la rentabilidad en los nuevos datos cercanos a «0». En general, los beneficios máximos y medios son superiores a los indicadores de pérdidas similares. Sin embargo, la tasa de operaciones ganadoras del 44,4% no permitió obtener ningún beneficio durante el periodo de prueba.
Conclusión
En este artículo nos familiarizamos con un nuevo método MLKV (Multi-Layer Key-Value), que es un enfoque innovador para un uso más eficiente de la memoria en los Transformers. La idea principal es extender la caché KV a múltiples capas, lo que puede reducir significativamente el uso de memoria.
En la parte práctica del artículo, implementamos los enfoques propuestos utilizando MQL5. Entrenamos y probamos modelos con datos reales. Nuestras pruebas han demostrado que los enfoques propuestos pueden reducir significativamente los costos de entrenamiento y operación del modelo. Sin embargo, esto se produce a costa del rendimiento del modelo. Como conclusión, debemos adoptar un enfoque equilibrado para encontrar un compromiso entre los costos y el rendimiento del modelo.
Referencias
- MLKV: Multi-Layer Key-Value Heads for Memory Efficient Transformer Decoding
- Otros artículos de esta serie
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor experto | Colección de ejemplos |
| 2 | ResearchRealORL.mq5 | Asesor experto | EA para la recolección de ejemplos utilizando el método Real-ORL |
| 3 | Study.mq5 | Asesor experto | EA para el entrenamiento del modelo |
| 4 | StudyEncoder.mq5 | Asesor experto | EA de entrenamiento del codificador |
| 5 | Test.mq5 | Asesor experto | EA de prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Código base | Biblioteca OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15117
Desarrollamos un asesor experto multidivisa (Parte 18): Automatización de la selección de grupos considerando el periodo forward
Desarrollamos un asesor experto multidivisa (Parte 17): preparación adicional para el trading real
Desarrollo de un Asesor Experto (EA) en MQL5 basado en la estrategia de ruptura del rango de consolidación
Algoritmo de optimización de reacciones químicas (CRO) (Parte II): Ensamblaje y resultados
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso