
Redes neuronales en el trading: Red neuronal espacio-temporal (STNN)
Introducción
La previsión de series temporales desempeña un papel importante en diversos campos, incluidas las finanzas, y nos hemos acostumbrado al hecho de que muchos sistemas del mundo real nos permiten medir datos multimensionales que contienen información diversa sobre la dinámica de la variable objetivo. No obstante, el análisis y la previsión eficaces de las series temporales multimensionales se enfrentan al problema de la "maldición de la dimensionalidad". Y entonces la cuestión de la selección de la ventana de datos históricos analizados adquiere gran importancia. De hecho, muy a menudo, cuando usamos una ventana de datos analizados de tamaño insuficiente, el modelo de predicción demuestra un rendimiento insatisfactorio y fracasa.
Para investigar la información multidimensional, se ha desarrollado una ecuación de transformación espacio-temporal de la información (STI) basada en el teorema de la incorporación con retardo. El STI convierte la información espacial de las variables multimensionales en información temporal futura de la variable objetivo, lo que equivale a aumentar el tamaño de la muestra y resuelve el problema de los datos a corto plazo.
Los modelos ya conocidos basados en la arquitectura del Transformer procesan una secuencia de datos y aprenden información utilizando el mecanismo de Self-Attention, modelando la relación entre variables sin considerar la distancia entre ellas. Los mecanismos de atención pueden captar información global y centrarse en el contenido importante, lo cual ayuda a mitigar la maldición de la dimensionalidad.
Para resolver problemas de previsión de series temporales, en el artículo "Spatiotemporal Transformer Neural Network for Time-Series Forecasting" se propuso un modelo de Transformer espacio-temporal (STNN) para la previsión eficiente en varias etapas de series temporales multimensionales a corto plazo aprovechando la ecuación STI y la estructura el Transformer.
Los autores del método destacan las siguientes ventajas de los planteamientos propuestos:
- El STNN utiliza la ecuación STI para convertir la información espacial de las variables multimensionales en información sobre la evolución temporal de la variable objetivo, lo cual equivale a aumentar el tamaño de la muestra.
- Así, se propone un mecanismo de atención continua para mejorar la precisión de la predicción numérica.
- La estructura espacial de Self-Attention de STNN recoge información espacial efectiva de variables multimensionales; la estructura temporal de Self-Attention se utiliza para recopilar información de la evolución temporal, mientras que la estructura del Transformer combina información espacial y temporal.
- El modelo STNN puede reconstruir el espacio de fases de un sistema dinámico para pronosticar series temporales.
1. Algoritmo STNN
El objetivo del modelo STNN es resolver de forma eficiente la ecuación de transformación no lineal STI entrenando al Transformer.
![]()
El modelo STNN explota la ecuación de transformación STI e incluye 2 módulos de atención especial para efectuar previsiones anticipadas de varios pasos. Como podemos observar en la ecuación anterior, los datos de origen de dimensión D en el tiempo t (Xt) se suministran a la entrada del Codificador, que extrae la información espacial efectiva de las variables de origen.
A continuación, la información espacial efectiva pasa al Decodificador, que introduce una serie temporal de longitud L-1 de la variable objetivo Y (𝐘t). El Decodificador extrae información sobre la evolución temporal de la variable objetivo. A continuación, predice los valores futuros de la variable objetivo combinando la información espacial de las variables originales (𝐗t) y la información temporal de la variable objetivo (𝐘t).
Obsérvese que la variable objetivo es una de las variables de los datos de entrada multimensionales X.
La transformación no lineal STI se resuelve mediante el par Codificador-Decodificador. El Codificador consta de 2 capas. La primera es una capa totalmente conectada y la segunda es una capa de Self-Attention espacial continua. Los autores del método STNN usan la capa espacial continua de Self-Attention para extraer información espacial efectiva de los datos de entrada multidimensionales 𝐗t.
La capa totalmente conectada se usa para suavizar los datos originales de la serie temporal multimensional 𝐗t y filtrar el ruido. Las neuronas de esta capa se describen usando la siguiente ecuación.
![]()
donde WFFN es la matriz de coeficientes,
bFFN es el desplazamiento,
ELU es la función de activación.
La capa de Self-Attention espacial continua toma 𝐗t,FFN como datos de entrada. Como la capa de Self-Attention adopta una serie temporal multidimensional, el Codificador puede extraer información espacial de los datos de origen. Para obtener una información espacial eficaz (SSAt), se propone un mecanismo de atención continua de la capa espacial de Self-Attention, cuyo funcionamiento puede describirse del siguiente modo.
En primer lugar, se generan 3 matrices de parámetros entrenados (WQE, WKE y WVE) que se utilizan en la capa de Self-Attention espacial continua.
A continuación, multiplicando los datos originales 𝐗t,FFN por las matrices de pesos anteriores, se generan las entidades Query, Key y Value de la capa de Self-Attention espacial continua.
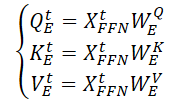
Realizando el producto escalar matricial, obtenemos la expresión de la información espacial clave (SSAt) para los datos de origen 𝐗t.
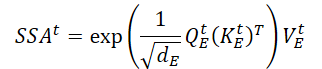
donde dE es la dimensionalidad de las matrices Query, Key y Value
Los autores del método STNN destacan que, a diferencia del mecanismo de atención probabilística discreta clásico, el mecanismo de atención continua propuesto puede garantizar la transmisión fluida de los datos del Codificador.
A la salida del Codificador, sumamos el tensor de información espacial clave con los datos de origen suavizados, seguido de una normalización de los datos, lo cual evita la rápida desaparición del gradiente y acelera la velocidad de convergencia del modelo.
![]()
El Decodificador combina eficazmente la información espacial y la variable objetivo temporal evolutiva. En su arquitectura, incluye 2 capas totalmente conectadas, una capa de Self-Attention temporal continua y una capa de atención a la transformación.
A la entrada del Decodificador se suministran los datos de origen históricos de la secuencia de la variable objetivo. Al igual que sucede con el Codificador, obtenemos una representación eficiente de los datos originales (𝐘t,FFN) tras filtrar el ruido con una capa totalmente conectada.
A continuación, los datos adquiridos se envían a la capa de Self-Attention temporal continua, que se centra en la información histórica sobre la evolución temporal entre distintos pasos temporales de la variable objetivo. Como el efecto del tiempo es irreversible, determinamos el estado actual de la serie temporal utilizando información histórica, pero no información futura. Así, la capa de atención temporal continua usa el mecanismo de atención enmascarada para filtrar la información futura. Veamos más de cerca esta operación.
Primero generamos 3 matrices de parámetros entrenados (WQD, WKD y WVD), para la capa espacio-temporal de Self-Attention. Y a continuación calculamos las matrices correspondientes de las entidades Query, Key y Value.
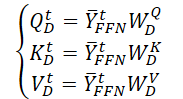
Y ejecutamos el producto escalar matricial para obtener información sobre la evolución temporal de la variable objetivo en el segmento analizado de la historia.
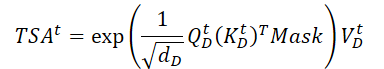
A diferencia del Codificador, aquí se añade una máscara que redefine la influencia de los elementos posteriores de los datos analizados. Así, no permitimos que el modelo "mire hacia el futuro" al construir la función de evolución temporal de la variable objetivo.
A continuación, utilizamos la conjunción residual y normalizamos la información sobre la evolución temporal de la variable objetivo.
![]()
La capa de atención de transformación continua para predecir los valores futuros de la variable objetivo combina la información de dependencia espacial (SSAt) con la evolución temporal de la variable objetivo (TSAt).
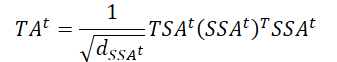
También se usan aquí las relaciones residuales y la normalización de los datos.
![]()
A la salida del Decodificador, los autores del método usan una segunda capa completamente conectada para predecir los valores de la variable objetivo
![]()
Para entrenar el modelo STNN, los autores del método usaron el MSE como función de pérdida y la regularización L2 de los parámetros.
A continuación le presentamos la visualización del método por parte del autor.
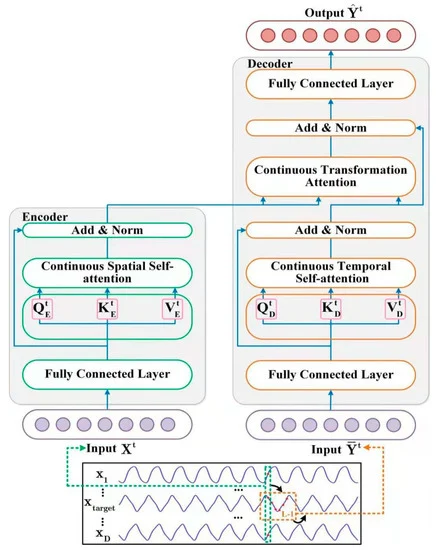
2. Implementación con MQL5
Tras considerar los aspectos teóricos del método STNN, pasaremos a la parte práctica de nuestro artículo, donde consideraremos una de las opciones para implementar los enfoques propuestos utilizando herramientas MQL5.
Como es habitual, en este artículo presentaremos nuestra propia la opinión sobre la aplicación, que puede diferir de la aplicación del método por parte del autor. Además, en esta aplicación hemos intentado aprovechar al máximo nuestros desarrollos, lo cual nos ha alejado un poco del método del autor. Hablaremos de ello durante la aplicación de los planteamientos propuestos.
Como ya hemos visto en la descripción teórica anterior del algoritmo STNN, este incluye 2 bloques principales: El Codificador y el Decodificador. También dividiremos nuestro trabajo en la implementación de las 2 clases correspondientes. Y comenzaremos nuestro trabajo con la implementación del Codificador.
2.1 Codificador STNN
Implementaremos los algoritmos del Codificador dentro de la clase CNeuronSTNNEncoder. Los autores del método hicieron algunos ajustes en el algoritmo de Self-Attention. No obstante, sigue resultando bastante reconocible e incorpora los componentes básicos del enfoque clásico. Por ello, para implementar la nueva clase, utilizaremos nuestro trabajo existente y heredaremos la funcionalidad básica del algoritmo básico de Self-Attention de la clase CNeuronMLMHAttentionMLKV. La estructura general de la nueva clase será la siguiente.
class CNeuronSTNNEncoder : public CNeuronMLMHAttentionMLKV { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSTNNEncoder(void) {}; ~CNeuronSTNNEncoder(void) {}; //--- virtual int Type(void) override const { return defNeuronSTNNEncoder; } };
Como podemos ver, no existe una declaración de las nuevas variables y objetos dentro de la nueva clase. Además, en la estructura presentada ni siquiera hay una redefinición de los métodos de inicialización de objetos. Y hay razones para ello. Como ya hemos dicho, aprovecharemos al máximo nuestra experiencia.
Primero veremos las diferencias entre los planteamientos propuestos y los que hemos aplicado anteriormente. En primer lugar, los autores del método STNN colocaron la capa de enlace completo delante del bloque de Self-Attention. Técnicamente, no se trata de un problema de declaración de objetos, sino de un simple problema de implementación de los algoritmos de pasada directa e inversa. Así que la aplicación de este punto no se refleja en el algoritmo del método de inicialización.
El segundo punto consiste en que los autores del método STNN solo proporcionaron una capa totalmente conectada. En el enfoque clásico, se crea un bloque de 2 capas totalmente conectadas. Mi opinión personal es que usar un bloque de 2 capas totalmente conectadas aumenta sin duda el coste de los recursos computacionales, pero no reduce la calidad del rendimiento del modelo. Y como experimento para conservar al máximo las construcciones existentes, podemos utilizar 2 capas en lugar de 1.
Además, los autores del método descartaron la función SoftMax para normalizar los coeficientes de atención. En su lugar, se aplicará un simple exponente del producto de las matrices Query y Key. En mi opinión, la única diferencia con SoftMax es la normalización de los datos y el cálculo más complejo. Y en nuestra implementación nos arriesgaremos a utilizar el enfoque ya implementado con SoftMax.
A continuación, procederemos a aplicar los algoritmos de la pasada directa. Y aquí hemos notado que los autores del método implementaron el enmascaramiento de los elementos posteriores solo en el Decodificador. Al hacerlo, deberemos recordar que la variable objetivo puede formar parte del conjunto de datos de entrada del Codificador. Y aquí hay cierta ilógica. Pero todo "encaja" tras un examen minucioso de la visualización del método por parte del autor.
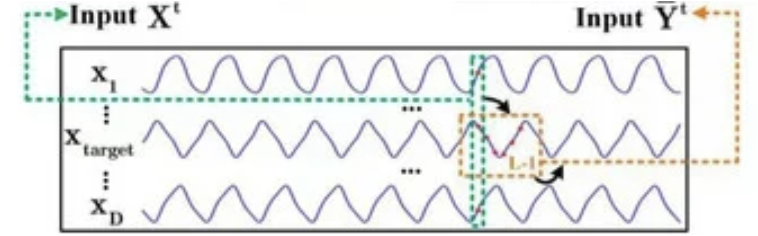
Los datos de origen del Codificador estarán a cierta distancia del estado analizado. No podemos juzgar las razones por las que los autores del método eligieron esta aplicación. Pero mi opinión personal es que usar toda la información disponible en el momento del análisis de los datos nos dará más información y mejorará potencialmente la calidad de nuestras previsiones. Por lo tanto, en nuestra implementación, desplazaremos los datos de origen del Codificador al momento actual y añadiremos una máscara de datos de origen que solo permitirá analizar las dependencias con datos anteriores.
Para implementar el enmascaramiento de datos, tendremos que hacer cambios en el programa OpenCL. Y aquí realizaremos solo pequeñas modificaciones en el kernel MH2AttentionOut. No usaremos un búfer de enmascaramiento adicional. Haremos esto de forma mucho más fácil: añadiremos solo 1 constante que determinará si se debe aplicar la máscara. Y organizaremos el enmascaramiento directamente en el algoritmo del kernel.
__kernel void MH2AttentionOut(__global float *q, __global float *kv, __global float *score, __global float *out, int dimension, int heads_kv, int mask ///< 1 - calc only previous units, 0 - calc all ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2); const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension); if(koef < 1) koef = 1; __local float temp[LOCAL_ARRAY_SIZE];
En el cuerpo del kernel, solo realizaremos ediciones puntuales en el cálculo de la suma de exponentes.
//--- sum of exp uint count = 0; if(k < ls) { temp[k] = 0; do { if(mask == 0 || q_id <= (count * ls + k)) if((count * ls) < (kunits - k)) { float sum = 0; int sh_k = 2 * dimension * heads_kv * count * ls; for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d + sh_k]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; temp[k] = temp[k] + sum; } count++; } while((count * ls + k) < kunits); } barrier(CLK_LOCAL_MEM_FENCE); count = min(ls, (uint)kunits);
Aquí añadiremos las condiciones necesarias y calcularemos los exponentes solo para los elementos anteriores. Y aquí deberemos considerar que, al crear los datos iniciales para el modelo, los formaremos a partir de las series temporales de los datos históricos de los movimientos de precio e indicadores. Y en ellas, la barra actual tendrá el índice "0". Por ello, para enmascarar los elementos de la cronología histórica, pondremos a cero los coeficientes de dependencia de todos los elementos cuyo índice sea inferior al Query analizado. Lo veremos al calcular la suma de los exponentes y las relaciones de dependencia (en el código lo hemos subrayado).
//--- do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- score float sum = temp[0]; float sc = 0; if(mask == 0 || q_id >= (count * ls + k)) if(sum != 0) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
De lo contrario, el código del kernel permanecerá inalterado.
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE); //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
Obsérvese que, con esta implementación, nos limitaremos a reducir a cero los coeficientes de dependencia de los elementos subsiguientes. Esto nos ha permitido organizar el enmascaramiento realizando las mínimas ediciones directas del kernel. Y además, este enfoque no requerirá de ajustes en los kernels de pasada inversa, puesto que un "0" en el coeficiente de dependencia simplemente pondrá a cero el gradiente de error en dichos elementos de la secuencia.
Debemos decir que con esto concluiremos nuestro trabajo en el lado del programa OpenCL de esta implementación y pasaremos a trabajar en nuestra clase en el programa principal.
Aquí organizaremos primero la llamada al kernel corregido anteriormente en el método CNeuronSTNNEncoder::AttentionOut. El algoritmo para el método que permite poner el kernel en la cola de ejecución seguirá siendo el mismo, por lo que no veo necesario repetirlo en cada artículo. Podrá familiarizarse con su código en el archivo adjunto. Solo querríamos señalar que, para realizar el enmascaramiento de datos, deberemos indicar "1" en el parámetro def_k_mh2ao_mask .
La siguiente etapa consistirá en implementar el método de pasada directa de nuestra nueva clase. Y aquí tendremos que redefinir el método para colocar el bloque FeedForward antes de Self-Attention. También deberemos señalar que, a diferencia del Transformer clásico, el bloque FeedForward carece de enlaces residuales y de normalización de datos.
Antes de empezar a implementar el algoritmo, deberemos recordar también que para evitar el copiado innecesario de datos en el método de inicialización de la clase padre, sustituiremos los punteros de los búferes de resultados y los gradientes de error de nuestra capa por búferes similares de la última capa FeedForward. Y aquí aprovecharemos una propiedad interesante: los tamaños de los búferes de resultados del bloque de atención y FeedForward tienen tamaños similares. Por lo tanto, simplemente cambiaremos la numeración al acceder a los búferes de datos correspondientes.
Veamos ahora nuestra implementación. Al igual que antes, en los parámetros del método obtendremos el puntero al objeto de la capa anterior que nos transmite los datos de origen.
bool CNeuronSTNNEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
E inmediatamente en el cuerpo del método comprobaremos la relevancia del puntero recibido. Después pasaremos directamente a la construcción del algoritmo de pasada directa. Merece la pena señalar aquí otra diferencia en nuestra aplicación. Los autores del método STNN no especifican en su trabajo el número de capas del Codificador ni el número de cabezas de atención. Basándonos en la visualización anterior y en la descripción del método, podemos suponer que solo hay una cabeza de atención en una capa del Codificador. En nuestra implementación, sin embargo, abandonaremos el enfoque clásico con el uso de atención multicabeza en una arquitectura multicapa. Y luego organizaremos un ciclo de iteración de las capas anidadas del Codificador.
En el cuerpo del ciclo, como ya hemos mencionado, los datos sin procesar pasarán primero por el bloque FeedForward, donde se suavizarán y filtrarán.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Feed Forward CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; inputs = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, inputs, 4 * iWindow, iWindow, None)) return false;
Después definiremos las matrices de las entidades Query, Key y Value.
//--- Calculate Queries, Keys, Values CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false; if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; }
Nótese que en este caso utilizaremos las aproximaciones del método MLKV heredado de la clase padre, que nos permitirá utilizar un único búfer Key-Value para múltiples cabezas de atención y capas de Self-Attention.
A partir de las entidades obtenidas, determinamos los coeficientes de dependencia considerando el enmascaramiento de los datos.
//--- Score calculation and Multi-heads attention calculation temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Y calcularemos el resultado de la capa de atención teniendo en cuenta las relaciones residuales y la normalización de los datos.
//--- Attention out calculation temp = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false; //--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false; } //--- return true; }
Después pasaremos a la siguiente capa anidada. Y cuando se agoten, finalizaremos el método.
De forma similar, pero en orden inverso, construiremos el algoritmo para el método de distribución de gradientes de error CNeuronSTNNEncoder::calcInputGradients. En los parámetros, el método también recibirá el puntero al objeto de la capa anterior, solo que esta vez tendremos que transmitirle el gradiente de error correspondiente a la influencia de los datos iniciales en el resultado final del modelo.
bool CNeuronSTNNEncoder::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false; //--- CBufferFloat *out_grad = Gradient; CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);
En el cuerpo del método comprobaremos, como antes, que el puntero recibido sea correcto. Y declararemos las variables locales para almacenar temporalmente punteros a los objetos de los búferes de datos de trabajo.
A continuación, declararemos un ciclo para iterar las capas anidadas del Codificador.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1); //--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None)) return false;
En el cuerpo del ciclo, primero distribuiremos el gradiente de error obtenido de la capa posterior entre las cabezas de atención. Después de eso, determinaremos el error a nivel de las entidades Query, Key y Value.
//--- Passing gradient to query, key and value if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; } else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
Observe la ramificación del algoritmo, que se debe a los distintos enfoques de distribución del gradiente de error al tensor Key-Value según la capa actual.
A continuación, transmitiremos el gradiente de error de la entidad Query al bloque FeedForward, teniendo en cuenta los enlaces residuales.
CBufferFloat *inp = FF_Tensors.At(i * 6); CBufferFloat *temp = FF_Tensors.At(i * 6 + 3); if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), inp, temp, iWindow, iWindowKey * iHeads, None)) return false; //--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
Y de ser necesario, añadiremos la influencia del margen de error a las entidades Key y Value.
if((i % iLayersToOneKV) == 0) { if(IsStopped() || !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; }
Y bajaremos el gradiente de error a través del bloque FeedForward.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None)) return false; inp = (i > 0 ? FF_Tensors.At(i * 6 - 4) : prevLayer.getOutput()); temp = (i > 0 ? FF_Tensors.At(i * 6 - 1) : prevLayer.getGradient()); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), inp, temp, iWindow, 4 * iWindow, LReLU)) return false; out_grad = temp; } //--- return true; }
Las iteraciones del ciclo se repetirán hasta que todas las capas anidadas hayan sido iteradas por completo y finalicen las transmisiones del gradiente de error al nivel de la capa precedente.
Una vez distribuido el gradiente de error, nos quedará optimizar los parámetros del modelo para minimizar el error global de predicción. Estas operaciones se implementarán en el método CNeuronSTNNEncoder::updateInputWeights. Su algoritmo repetirá completamente el método análogo de la clase padre. La única diferencia será la especificación de los búferes de datos. Por lo tanto, no nos detendremos ahora en su análisis detallado. Podrá leerlo por sí mismo en el archivo adjunto. Allí también encontrará el código completo de la clase del Codificador y todos sus métodos.
2.2 Decodificador STNN
Después de implementar el Codificador, pasaremos a la segunda parte de nuestro trabajo donde implementaremos el algoritmo del Decodificador del método STNN. Una vez más, seguiremos los mismos principios que usamos para construir el Codificador. En particular, como parte de esta aplicación, maximizaremos el uso de los desarrollos anteriores.
Y procediendo a implementar los algoritmos de nuestro Decodificador deberemos prestar atención a que, a diferencia del Codificador, heredaremos la nueva clase de objetos de atención cruzada. Al fin y al cabo, en esta capa tendremos información espacial y temporal para comparar. La estructura completa de la nueva clase será la siguiente.
class CNeuronSTNNDecoder : public CNeuronMLCrossAttentionMLKV { protected: CNeuronSTNNEncoder cEncoder; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override; public: CNeuronSTNNDecoder(void) {}; ~CNeuronSTNNDecoder(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSTNNDecoder; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Nótese que en esta clase declararemos un objeto anidado por encima del Codificador creado. Sin embargo, debemos decir de entrada que en este caso llevará una carga semántica algo diferente.
Si nos remitimos a la descripción teórica del método presentada en la primera parte de este artículo, podremos observar similitudes entre los bloques de identificación de relaciones espaciales y temporales. Las únicas diferencias radicarán en los datos de origen analizados. El bloque de relaciones espaciales analizará un gran número de parámetros en un pequeño intervalo de tiempo. En el bloque de dependencias intertemporales, la variable objetivo se analizará en un intervalo histórico independiente. Sin embargo, los algoritmos resultarán bastante similares. Por lo tanto, en este caso, utilizaremos el Codificador anidado para detectar las dependencias intertemporales de la variable objetivo.
Pero volvamos a la descripción de los algoritmos de nuestros métodos. La declaración de un objeto anidado adicional, aunque sea estático, requerirá que redefinamos el método de inicialización de la clase Init. No obstante, nuestro empeño por aprovechar al máximo los avances anteriores está dando sus frutos. El nuevo método de inicialización será lo más sencillo posible.
bool CNeuronSTNNDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!cEncoder.Init(0, 0, open_cl, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, optimization_type, batch)) return false; if(!CNeuronMLCrossAttentionMLKV::Init(numOutputs, myIndex, open_cl, window, window_key, heads, window_kv, heads_kv, units_count, units_count_kv, layers, layers_to_one_kv, optimization_type, batch)) return false; //--- return true; }
Aquí simplemente llamaremos a los métodos homónimos del Codificador anidado y de la clase padre usando los mismos valores para los parámetros homónimos. Solo tendremos que comprobar el resultado de las operaciones y retornar el valor lógico obtenido al programa que realiza la llamada.
Un planteamiento similar se observará en los métodos de pasada directa e inversa. Por ejemplo, en el método de pasada directa, primero llamaremos al método del Codificador homónimo para descubrir dependencias intertemporales entre los valores de la variable objetivo. Y luego compararemos las dependencias intertemporales obtenidas con las dependencias interespaciales obtenidas del Codificador del modelo STNN en los parámetros contextuales de este método. Esta operación se realizará usando los recursos de pasada directa heredados de la clase padre.
bool CNeuronSTNNDecoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) { if(!cEncoder.FeedForward(NeuronOCL, Context)) return false; if(!CNeuronMLCrossAttentionMLKV::feedForward(cEncoder.AsObject(), Context)) return false; //--- return true; }
Aquí debemos señalar algunos puntos en los que nos hemos desviado del algoritmo propuesto por los autores del método STNN. Hemos conservado el concepto propuesto en general, pero hemos dado un "gran paso al lado" en los recursos de aplicación de los planteamientos propuestos.
Así, hemos mantenido:
- La identificación de las dependencias intertemporales;
- La comparación de las relaciones intertemporales e interespaciales con el fin de predecir los valores de la variable objetivo.
No obstante, al igual que en el caso del Codificador, utilizaremos un bloque FeedForward de 2 capas totalmente conectadas en lugar de la capa 1, como proponen los autores del método. Esto se aplica tanto al filtrado de los datos antes de identificar las dependencias intertemporales como a la predicción de los valores de la variable objetivo a la salida del Decodificador.
Además, utilizaremos una pasada directa de la clase padre para implementar la atención cruzada, que implementará el algoritmo clásico de atención cruzada multicapa con conexiones residuales de bloques de atención y FeedForward. Y esto resultará diferente del algoritmo de atención cruzada propuesto por los autores del método STNN.
Sin embargo, en mi opinión, una aplicación de este tipo tiene cabida, sobre todo considerando nuestro experimento, que intenta aprovechar al máximo los desarrollos creados previamente.
También nos gustaría llamar la atención sobre el hecho de que, a pesar del uso de una estructura multicapa en los bloques de detección de dependencias intertemporales y atención cruzada, la arquitectura general del Decodificador adquiere un carácter monocapa. En otras palabras, primero identificaremos las dependencias intertemporales en el Codificador multicapa anidado. A continuación, la unidad de atención cruzada multicapa comparará las dependencias intertemporales e interespaciales antes de predecir los valores de la variable objetivo.
Los métodos de pasada inversa también se construyen de forma similar, pero no nos detendremos en ellos ahora. Le recomiendo que los revise por usted mismo en el archivo adjunto.
Con esto concluirá nuestro análisis de la arquitectura y los algoritmos de los nuevos objetos. Podrá revisar su código completo en el archivo adjunto a este artículo.
2.3 Arquitectura del modelo
Tras repasar los algoritmos para implementar los enfoques del método STNN propuestos, pasaremos a su aplicación práctica en los modelos entrenados. Y aquí deberemos señalar que el Codificador y Decodificador en el algoritmo propuesto trabajan con diferentes datos de entrada. Esto nos ha llevado a separarlos en modelos independientes, cuya arquitectura se presentará en el método CreateStateDescriptions.
En los parámetros del método especificado transmitiremos 2 punteros de array dinámicos, para registrar la arquitectura de los modelos correspondientes.
bool CreateStateDescriptions(CArrayObj *&encoder, CArrayObj *&decoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- if(!decoder) { decoder = new CArrayObj(); if(!decoder) return false; }
En el cuerpo del método comprobaremos los punteros obtenidos y, si es necesario, crearemos nuevas instancias del array.
A la entrada del Codificador suministraremos el conjunto de datos sin procesar que ya conocemos,
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
y cuyo procesamiento primario se implementa en la capa de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Después añadiremos la capa del Codificador STNN.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSTNNEncoder; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = 32; descr.layers = 4; descr.step = 2; { int ar[] = {8, 4}; if(ArrayCopy(descr.heads, ar) < (int)ar.Size()) return false; } descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Aquí utilizaremos 4 capas de Codificador anidadas, cada una de las cuales utilizará 8 cabezas de atención de entidades Query y 4 para el tensor Key-Value. Además, utilizaremos un tensor Key-Value para las 2 capas del Codificador anidadas.
Y con esto concluirá la arquitectura del modelo del Codificador. Luego utilizaremos los resultados de su trabajo en el Decodificador.
Y suministraremos a la entrada del Decodificador valores históricos de la variable objetivo, cuya profundidad de la historia analizada se corresponderá con nuestro horizonte de planificación.
//--- Decoder decoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (NForecast * ForecastBarDescr); descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Aquí también utilizaremos los datos de origen suministrados a la capa de normalización de datos por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Y a continuación seguirá la capa del Decodificador STNN, cuya arquitectura también cuenta con 4 capas anidadas de atención intertemporal y cruzada.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSTNNDecoder; { int ar[] = {NForecast, HistoryBars}; if(ArrayCopy(descr.units, ar) < (int)ar.Size()) return false; } { int ar[] = {ForecastBarDescr, BarDescr}; if(ArrayCopy(descr.windows, ar) < (int)ar.Size()) return false; } { int ar[] = {8, 4}; if(ArrayCopy(descr.heads, ar) < (int)ar.Size()) return false; } descr.window_out = 32; descr.layers = 4; descr.step = 2; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
A la salida del Decodificador, esperamos obtener los valores predichos de la variable objetivo. A ellos se añadirán las métricas estadísticas extraídas en la capa de normalización por lotes.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = ForecastBarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!decoder.Add(descr)) { delete descr; return false; }
Y acordaremos las características de frecuencia de las series temporales predictivas.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = ForecastBarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- return true; }
La arquitectura de los modelos del Actor y el Crítico se ha transferido sin cambios desde los artículos anteriores y está representada por el método CreateDescriptions, que encontrará en el archivo adjunto a este artículo (archivo "...\Experts\STNN\Trajectory.mqh").
2.4 Programas de entrenamiento de modelos
La separación del Codificador del entorno en 2 modelos ha requerido también de cambios en los programas de entrenamiento de modelos. Y debemos decir que, además de la división del algoritmo en 2 modelos, existen cambios en el bloque de preparación de datos iniciales y valores objetivo. Consideraremos los ajustes realizados en el ejemplo del asesor de entrenamiento del codificador del entorno "...\Experts\STNN\StudyEncoder.mq5".
Permítanme recordarles que en el marco de este asesor experto entrenaremos un modelo de previsión del próximo movimiento del precio para algún horizonte de planificación suficiente para tomar una decisión comercial en un momento determinado.
En el marco del presente artículo no nos detendremos en todos los procedimientos del programa, solo consideraremos el método de entrenamiento de los modelos Train. En primer lugar, determinaremos las probabilidades de seleccionar las trayectorias del búfer de reproducción de experiencias según su rendimiento real con datos históricos reales.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target, state; matrix<float> mstate = matrix<float>::Zeros(1, NForecast * ForecastBarDescr); bool Stop = false;
Y declararemos el mínimo requerido de variables locales. A continuación, organizaremos un ciclo de entrenamiento directo de modelos. El número de iteraciones del ciclo lo definirá el usuario en los parámetros externos del asesor experto.
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(i <= 0) { iter--; continue; } state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter--; continue; }
En el cuerpo del ciclo, muestrearemos la trayectoria y el estado en ella para realizar iteraciones de la optimización del modelo. Primero efectuaremos la detección de las dependencias interdimensionales entre las variables analizadas llamando al método de pasada inversa de nuestro Codificador.
bStateE.AssignArray(state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bStateE), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
A continuación, prepararemos los datos de origen para el Decodificador. En general, supondremos que el horizonte de planificación es menor que la profundidad de la historia analizada. Por lo tanto, primero transferiremos los datos históricos de del estado del entorno analizado a la matriz. Luego cambiaremos su tamaño para que cada fila de la matriz represente los datos de una barra de datos históricos. Y cortaremos la matriz. El número de filas de la matriz resultante deberá corresponderse con el horizonte de planificación. Y el número de columnas será la variable objetivo.
mstate.Assign(state); mstate.Reshape(HistoryBars, BarDescr); mstate.Resize(NForecast, ForecastBarDescr); bStateD.AssignArray(mstate);
Cabe señalar que al preparar la muestra de entrenamiento para cada barra, primero registraremos los parámetros del movimiento del precio. Eso es lo que vamos a planificar. Así que tomaremos las primeras columnas de la matriz.
Luego transferiremos los valores de la matriz obtenida al búfer de datos y realizaremos una pasada directa del Decodificador.
if(!Decoder.feedForward((CBufferFloat*)GetPointer(bStateD), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Tras realizar la pasada directa, tendremos que llevar a cabo la optimización de los parámetros del modelo. Para ello necesitaremos preparar los valores objetivo de las variables pronosticadas. Realizaremos esta operación de forma similar a la preparación de los datos iniciales del Decodificador, solo que realizaremos las operaciones con valores históricos posteriores.
//--- Collect target data mstate.Assign(Buffer[tr].States[i + NForecast].state); mstate.Reshape(HistoryBars, BarDescr); mstate.Resize(NForecast, ForecastBarDescr); if(!Result.AssignArray(mstate)) continue;
Y efectuaremos una pasada inversa del Decodificador. Aquí optimizaremos los parámetros del Decodificador y transmitiremos el gradiente de error al Codificador.
if(!Decoder.backProp(Result, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Después optimizaremos los parámetros del Codificador.
if(!Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Y ahora solo nos quedará informar al usuario del progreso del proceso de entrenamiento y pasar a la siguiente iteración del ciclo de entrenamiento.
if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Decoder", percent, Decoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Una vez completadas con éxito todas las iteraciones del entrenamiento, registraremos los resultados del entrenamiento del modelo e inicializaremos el proceso de finalización del programa.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError()); ExpertRemove(); //--- }
Con esto concluirá nuestro análisis de los algoritmos de entrenamiento de modelos. Encontrará el código completo de todos los programas utilizados en la elaboración de este artículo en el archivo adjunto.
3. Simulación
En este artículo, nos hemos familiarizado con un nuevo método de previsión de series temporales basado en la información espacio-temporal, el STNN. Asimismo, hemos implementado nuestra visión de los enfoques propuestos utilizando herramientas MQL5. Ahora es el momento de evaluar los resultados de nuestro trabajo.
Como de costumbre, para entrenar nuestros modelos usaremos los datos históricos del instrumento EURUSD en el marco temporal H1 para todo el año 2023. Después, probaremos los modelos entrenados en el simulador de estrategias de MetaTrader 5 con los datos de enero de 2024. No resulta difícil ver que el periodo de pruebas seguirá inmediatamente al periodo de análisis. Este enfoque nos acercará lo más posible a las condiciones reales de funcionamiento de los modelos.
Para entrenar un modelo de predicción del movimiento posterior de los precios, utilizaremos la muestra de entrenamiento recogida en los artículos anteriores de esta serie. Como ya sabrá, este modelo se entrena solo en el análisis de los datos históricos de los movimientos de precios y las métricas de los indicadores analizados. Las acciones del Agente no tienen ningún efecto sobre los datos analizados, lo cual permitirá entrenar el modelo del Codificador del estado del entorno sin actualizar periódicamente la muestra de entrenamiento.
Continuaremos el proceso de entrenamiento del modelo hasta que el error de predicción se estabilice. Desgraciadamente, en esta fase nos hemos topado con un desagradable imprevisto. Nuestro modelo no ha podido ofrecer la previsión deseada del próximo movimiento de los precios, indicando únicamente la dirección general de la tendencia.
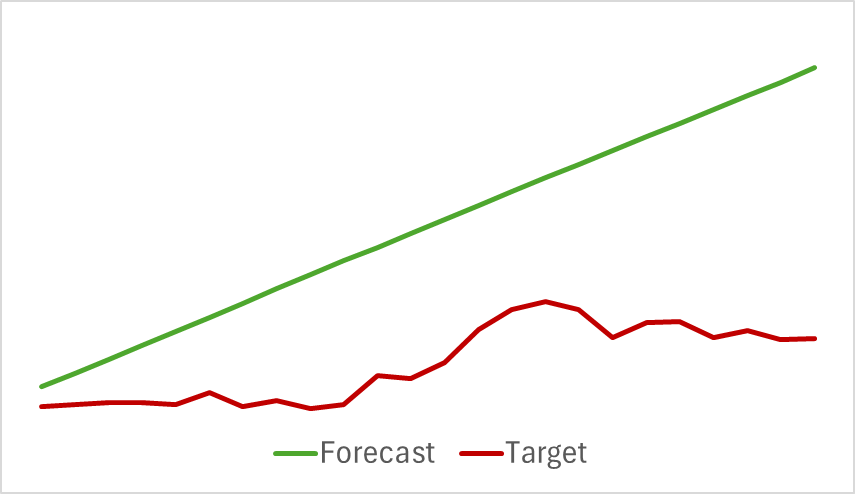
Obviamente, a pesar de la aparente rectitud del movimiento previsto, existen fluctuaciones en los valores cifrados. Pero son tan insignificantes que no se visualizarán en el gráfico. Lo cual nos lleva a preguntarnos: ¿son suficientes para que nuestro Actor construya una estrategia rentable?
Entrenaremos los modelos del Actor y el Crítico de forma iterativa con actualizaciones periódicas de la muestra de entrenamiento. Como ya sabrá, necesitamos actualizar periódicamente la muestra de entrenamiento para estimar con mayor precisión las acciones del Actor cuando su política cambia durante el proceso de aprendizaje.
Lamentablemente, no hemos podido formar una política del Actor capaz de generar beneficios sostenibles en la muestra de prueba.
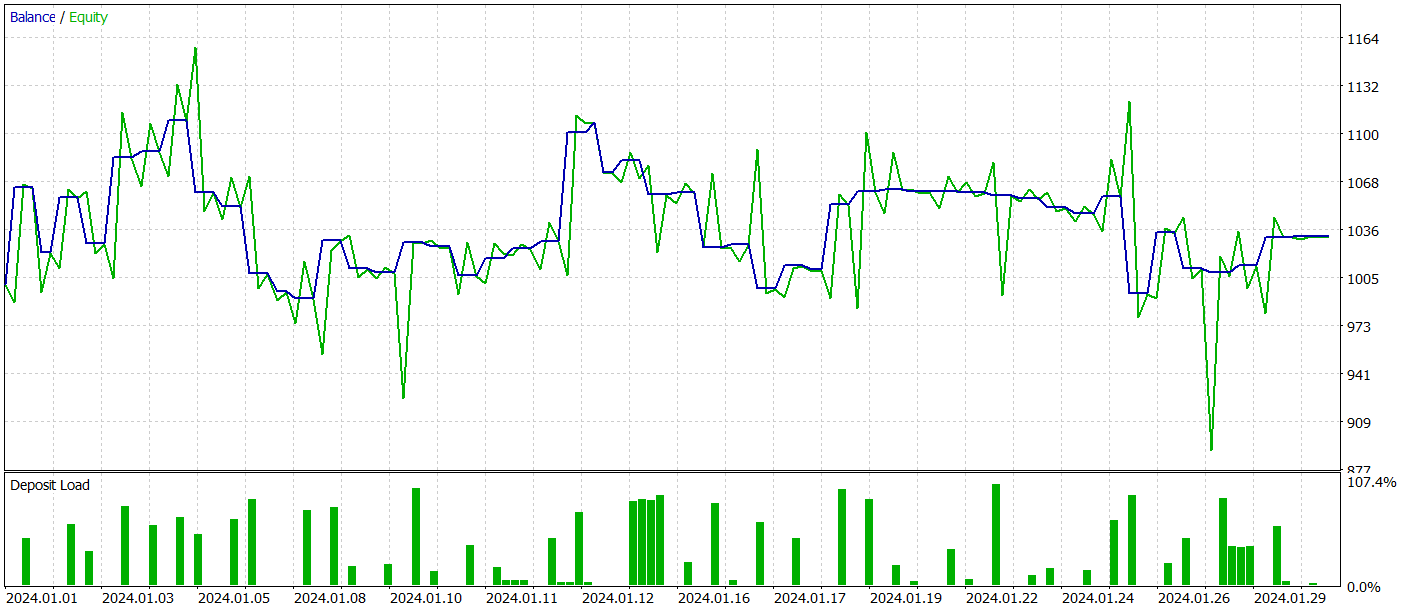
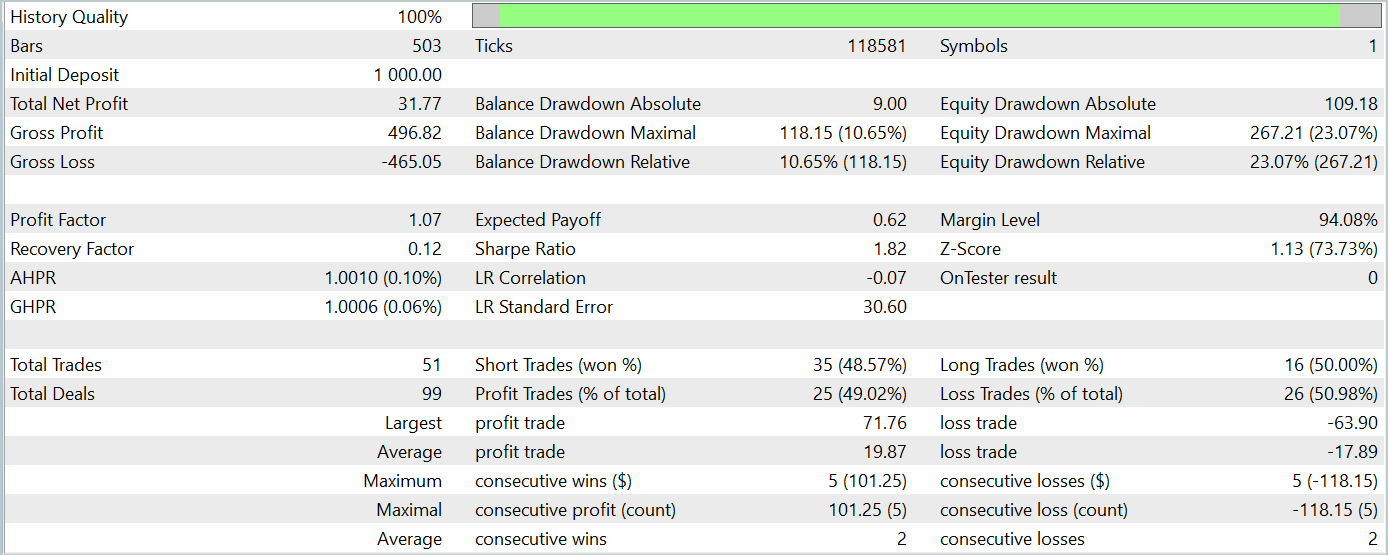
Y, por supuesto, reconocemos que han existido desviaciones significativas con respecto a la aplicación del método por parte del autor. Y esto puede haber afectado a los resultados obtenidos.
Conclusión
En este artículo se presenta otro enfoque de la previsión de series temporales, basado en la red neuronal del Transformer espacio-temporal (STNN). Este modelo combina las ventajas de la ecuación de transformación espacio-temporal (STI) y el marco del Transformer para una previsión eficaz en varias etapas de series temporales a corto plazo.
STNN utiliza la ecuación STI, que convierte la información espacial de las variables multimensionales en información temporal de la variable objetivo, lo cual equivale a aumentar el tamaño de la muestra y ayuda a resolver el problema de la insuficiencia de datos a corto plazo.
Para mejorar la precisión de la predicción numérica en el STNN, hemos propuesto un mecanismo de atención continua que permite al modelo tener más en cuenta aspectos importantes de los datos.
En la parte práctica del artículo, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Sin embargo, en nuestra aplicación hemos introducido desviaciones significativas con respecto al algoritmo del autor, lo cual puede haber afectado a los resultados experimentales obtenidos.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15290
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales en el trading: Reducción del consumo de memoria con el método de optimización Adam (Adam-mini)
Redes neuronales en el trading: Reducción del consumo de memoria con el método de optimización Adam (Adam-mini)
 Reimaginando las estrategias clásicas (Parte II): Ruptura de las Bandas de Bollinger
Reimaginando las estrategias clásicas (Parte II): Ruptura de las Bandas de Bollinger
 Construya Asesores Expertos Auto-Optimizables con MQL5 y Python
Construya Asesores Expertos Auto-Optimizables con MQL5 y Python
 Del básico al intermedio: Array (I)
Del básico al intermedio: Array (I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso