Redes neurais em trading: Transformer vetorial hierárquico (HiVT)

Introdução

Os desafios enfrentados na área de condução autônoma são muito semelhantes aos encontrados no trading. A navegação em condições dinâmicas com manobras seguras é uma tarefa crítica para esses veículos. Para alcançar esse objetivo, esses veículos precisam compreender o ambiente ao redor e prever eventos futuros na estrada. No entanto, prever com precisão as manobras dos participantes do tráfego, como carros, bicicletas e pedestres, é uma tarefa complexa, especialmente quando suas metas ou intenções são desconhecidas. Em cenários de tráfego com múltiplos agentes, o comportamento de cada um deles é influenciado por interações complexas com os demais, o que se torna ainda mais complicado devido às regras de trânsito dependentes do mapa. Isso torna extremamente difícil compreender a diversidade de comportamentos dos vários agentes na cena.

Pesquisas recentes utilizam uma abordagem vetorial para representar cenas de maneira mais compacta, extraindo um conjunto de vetores ou pontos a partir das trajetórias e elementos do mapa. No entanto, as abordagens vetorizadas existentes enfrentam dificuldades ao realizar previsões de movimento em tempo real em condições de tráfego em rápida mudança, pois esses métodos geralmente são instáveis em relação a alterações na posição e na orientação do sistema de coordenadas. Para mitigar esse problema, as cenas são normalizadas para que fiquem centralizadas no agente-alvo e alinhadas com a direção de seu movimento. No entanto, esse método se torna problemático quando é preciso prever o movimento de um grande número de agentes na cena, devido ao alto custo computacional da renormalização constante da cena e do recálculo das características para cada agente-alvo. Além disso, os trabalhos existentes modelam as interações entre todos os elementos em todas as dimensões de espaço e tempo para capturar detalhadamente as interações entre os elementos vetorizados, o que inevitavelmente leva a um aumento excessivo do custo computacional à medida que o número de elementos aumenta. Como previsões precisas em tempo real são críticas para a segurança da condução autônoma, muitos pesquisadores buscam elevar esse processo a um novo patamar, desenvolvendo uma estrutura inovadora que permita prever de forma mais rápida e precisa os movimentos de múltiplos agentes.

Um desses métodos foi apresentado no artigo "HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction". Ele utiliza simetrias e uma estrutura hierárquica para a tarefa de previsão do movimento de múltiplos agentes. Os autores do HiVT abordam o problema da previsão de movimento em várias etapas, modelando hierarquicamente as interações entre os elementos por meio de um Transformer.

Na primeira etapa, o modelo evita o alto custo computacional de modelar as interações entre todos os elementos simultaneamente, extraindo, em vez disso, características contextuais de forma local. Toda a cena é dividida em um conjunto de regiões locais, cada uma centralizada no agente em questão. A partir dos elementos vetorizados locais contidos nessas regiões centradas em um agente, são extraídas características contextuais que contêm informações ricas e relevantes para o agente central.

Na segunda etapa, para compensar as limitações dos campos de visão locais e capturar dependências de longo alcance na cena, é realizada uma transmissão global de informações entre as diferentes regiões locais centradas nos agentes. Para isso, os autores do método utilizam um Transformer equipado com conexões geométricas entre os sistemas de referência locais.

As representações locais e globais obtidas permitem que o decodificador preveja as trajetórias futuras de todos os agentes em uma única propagação para frente do modelo. Além disso, para aproveitar melhor as simetrias do problema, os autores introduzem uma representação da cena que é invariante a deslocamentos da referência no sistema de coordenadas global, na qual todos os elementos vetorizados são caracterizados por posições relativas. A partir dessa representação, são introduzidos módulos de atenção cruzada invariantes à rotação para o aprendizado espacial, de modo que o modelo possa capturar representações locais e globais sem depender da orientação da cena.

1. Algoritmo HiVT

O algoritmo do método HiVT começa com a representação da cena viária como um conjunto de elementos vetorizados. Com base nessa representação, o modelo agrega hierarquicamente as informações espaço-temporais da cena. A cena viária é composta por agentes e informações do mapa. Para estruturar essa representação da cena, primeiro extraímos os elementos vetorizados, incluindo segmentos das trajetórias dos agentes no tráfego e segmentos das faixas nos dados do mapa.

O elemento vetorizado é associado a atributos semânticos e geométricos. Ao contrário de métodos vetorizados anteriores, nos quais os atributos geométricos dos agentes ou faixas incluem posições absolutas de pontos, os autores do método evitam o uso de posições absolutas e propõem descrever os atributos geométricos por meio de posições relativas. Isso transforma toda a cena em um conjunto de vetores. Em particular, a trajetória do agente i é representada como "pt,i — pt-1,i", onde pt,i é a posição do agente i no instante de tempo t.

Para um segmento de faixa xi, o atributo geométrico é definido como p1,xi — p0,xi, onde p0,xi e p1,xi são as coordenadas inicial e final de xi, respectivamente. Ao converter o conjunto de pontos em um conjunto de vetores, essa representação garante, naturalmente, a invariança à translação. No entanto, a informação sobre as posições relativas entre os elementos também pode se perder. Para preservar as relações espaciais, introduzimos vetores de posição relativa pares agente-agente e agente-faixa. Por exemplo, o vetor de posição do agente j em relação ao agente i no instante de tempo t é dado por ptj — pti, o que descreve completamente a relação espacial entre os dois agentes e também é invariante à translação. Sem perda de informação, essa representação da cena garante que quaisquer funções aprendidas aplicadas a ela respeitem a invariança à translação.

Para prever com precisão as trajetórias futuras dos agentes em um ambiente altamente dinâmico, o modelo precisa aprender de maneira eficiente as dependências espaço-temporais entre um grande número de elementos vetorizados. O Transformer demonstrou potencial para capturar dependências de longo alcance entre elementos em diversas tarefas. No entanto, a aplicação direta de Transformers a elementos espaço-temporais enfrenta uma complexidade de O((NT + L)²), onde N, T e L representam, respectivamente, o número de agentes, os passos temporais históricos e os segmentos de faixa. Para extrair informações de maneira eficiente de um grande número de elementos, os autores do HiVT propõem a fatoração das dimensões espaciais e temporais, estudando as relações espaciais apenas localmente em cada passo temporal. Em particular, eles dividem o espaço em N regiões locais, cada uma centrada em um agente na cena. Dentro de cada região, são incluídos segmentos de trajetória e o ambiente local do agente central, onde as informações ambientais englobam segmentos das trajetórias de agentes vizinhos e segmentos locais de faixas que cercam o agente central. Para cada região local, as informações locais são agregadas em um único vetor de características, modelando sequencialmente as interações agente-agente em cada passo temporal, as dependências temporais para cada agente e as interações agente-faixa no passo temporal atual. Após a agregação, o vetor de características contém informações ricas relacionadas ao agente central. Ao mesmo tempo, a complexidade computacional é reduzida de O((NT + L)²) para O(NT² + TN² + NL) devido à fatoração das dimensões espaciais e temporais, e é ainda mais reduzida para O(NT² + TNk + Nl) ao limitar o raio das regiões locais, onde k < N e l < L.

Embora o codificador local consiga extrair representações ricas, a quantidade de informação capturada é limitada pelo alcance das regiões locais. Para evitar perdas na qualidade das previsões, os autores do método utilizam um módulo global de interação adicional, que compensa os campos receptivos locais reduzidos e captura a dinâmica em nível de cena, permitindo a troca de informações entre as regiões locais. Esse módulo global de interação melhora significativamente a expressividade do modelo, com um custo computacional de O(N²), que é relativamente leve em comparação com o codificador local.

O problema da previsão de movimento de múltiplos agentes apresenta simetrias de translação e rotação. Os métodos existentes renormalizam todos os elementos vetorizados em relação a cada agente e fazem previsões para um único agente várias vezes, a fim de garantir a invariança. Essa abordagem é linearmente escalável com o número de agentes. Em contraste, o modelo HiVT consegue fazer previsões para todos os agentes em um único processo de propagação para frente, sem perda de invariança, graças à sua representação invariante da cena e aos robustos módulos de aprendizado espacial à rotação.

O módulo de interação Agente-Agente foi projetado para estudar as relações entre o agente central e os agentes vizinhos dentro de cada região local, em cada passo temporal. Para explorar as simetrias do problema, os autores do método propõem um bloco robusto de atenção cruzada à rotação, que permite agregar informações espaciais. Em particular, eles adotam o último segmento da trajetória do agente central pT,i — pT-1,i como o vetor de referência da região local e rotacionam todos os vetores locais de acordo com a orientação desse vetor de referência ʘi. Os vetores rotacionados e seus atributos semânticos associados são processados por um Perceptron Multicamadas (MLP) para obter a incorporação (embedding) do agente central zti e a incorporação de qualquer agente vizinho ztij em qualquer instante de tempo t.

Como todos os atributos geométricos são normalizados em relação ao agente central antes de serem alimentados no MLP, essas incorporações tornam-se independentes da rotação do sistema de coordenadas global. Além dos segmentos de trajetória, os dados brutos da função фnbr(•) também contêm vetores de posição dos agentes vizinhos em relação ao agente central, tornando as incorporações dos vizinhos espacialmente sensíveis. A incorporação do agente central é então transformada em um vetor Query, enquanto as incorporações dos agentes vizinhos são usadas para calcular as entidades Key e Value. As entidades resultantes são utilizadas no bloco de atenção.

Diferentemente do Transformer clássico, os autores do HiVT propõem o uso de uma função de controle para a fusão das características do ambiente com as características do agente central zti. Isso permite que o bloco de atenção tenha um controle mais refinado sobre a atualização das características. Assim como na arquitetura original do Transformer, o bloco de atenção proposto pode ser estendido para múltiplas cabeças de atenção. Os resultados do bloco de atenção multicabeça passam por um bloco MLP para obter a incorporação espacial sti do agente i no instante de tempo t.

Além disso, os autores do método aplicam a normalização de camada antes de cada bloco e a conexão residual após cada bloco. Na prática, esse módulo pode ser implementado com operações eficientes de paralelismo de aprendizado, abrangendo todas as regiões locais e passos temporais.

A captura adicional da informação temporal de cada região é realizada por meio de um codificador Transformer temporal, que sucede o módulo de interação Agente-Agente. Para qualquer agente central i, a sequência de entrada desse módulo é composta pelas incorporações sti obtidas a partir do módulo de interação Agente-Agente nos diferentes passos temporais. Os autores do método adicionam um token treinável sT+1 ao final da sequência original. Em seguida, adicionam uma codificação posicional treinável a todos os tokens e os organizam em uma matriz Si, que é alimentada no bloco de atenção temporal.

O módulo de aprendizado temporal também consiste em blocos alternados de atenção multicabeça e blocos MLP.

A estrutura local do mapa pode indicar as intenções futuras do agente central. Por esse motivo, a informação do mapa local é adicionada à incorporação do agente central. Para isso, primeiramente, os segmentos locais da estrada e os vetores de posição relativa agente-estrada no instante de tempo T são rotacionados. Os vetores rotacionados são então codificados utilizando um MLP. Utilizando as características espaço-temporais do agente central como Query e as características dos segmentos da estrada, codificadas pelo MLP, como vetores Key-Value, a atenção cruzada Agente-Estrada é realizada de maneira semelhante às abordagens descritas anteriormente.

Os autores do método aplicam adicionalmente um bloco MLP para obter a incorporação local final hi do agente central i. Após a modelagem sequencial das interações Agente-Agente, das dependências temporais e das interações Agente-Estrada, a incorporação resultante contém informações enriquecidas associadas aos agentes centrais das regiões locais.

Na próxima etapa do algoritmo HiVT, as incorporações locais são processadas no módulo de interação global para capturar dependências de longo alcance na cena. Como as características locais são extraídas em sistemas de coordenadas orientados para cada agente, o módulo de interação global deve levar em consideração as relações geométricas entre diferentes quadros ao trocar informações entre as regiões locais. Para isso, os autores do método expandem o codificador Transformer para considerar as diferenças entre os sistemas de coordenadas locais. Durante a transmissão de mensagens do agente j para o agente i, os autores utilizam um MLP para obter uma incorporação de pares, que é então incluída na transformação dos vetores.

Para capturar interações par-a-par globalmente, é utilizado o mesmo mecanismo de atenção espacial empregado no codificador local, seguido por um bloco MLP, que produz uma representação global para qualquer agente.

Os movimentos previstos dos agentes de tráfego são, por natureza, multimodais. Por isso, os autores do método propõem parametrizar a distribuição das trajetórias futuras como uma mistura de modelos, em que cada componente segue uma distribuição de Laplace. As previsões são feitas para todos os agentes em uma única passagem. Para cada agente i e cada componente f, o MLP recebe as representações locais e globais como entrada e retorna a posição prevista e sua incerteza associada para cada passo de tempo futuro no sistema de coordenadas local. O tensor de saída da cabeça de regressão tem a dimensionalidade [F, N, H, 4], onde F é o número de componentes da mistura, N é o número de agentes na cena e H é o horizonte de previsão em passos temporais futuros. Aqui, também é utilizado um MLP, seguido por uma função SoftMax, que permite calcular os coeficientes da mistura do modelo para cada agente.

A visualização do método HiVT proposta pelos autores é apresentada a seguir.

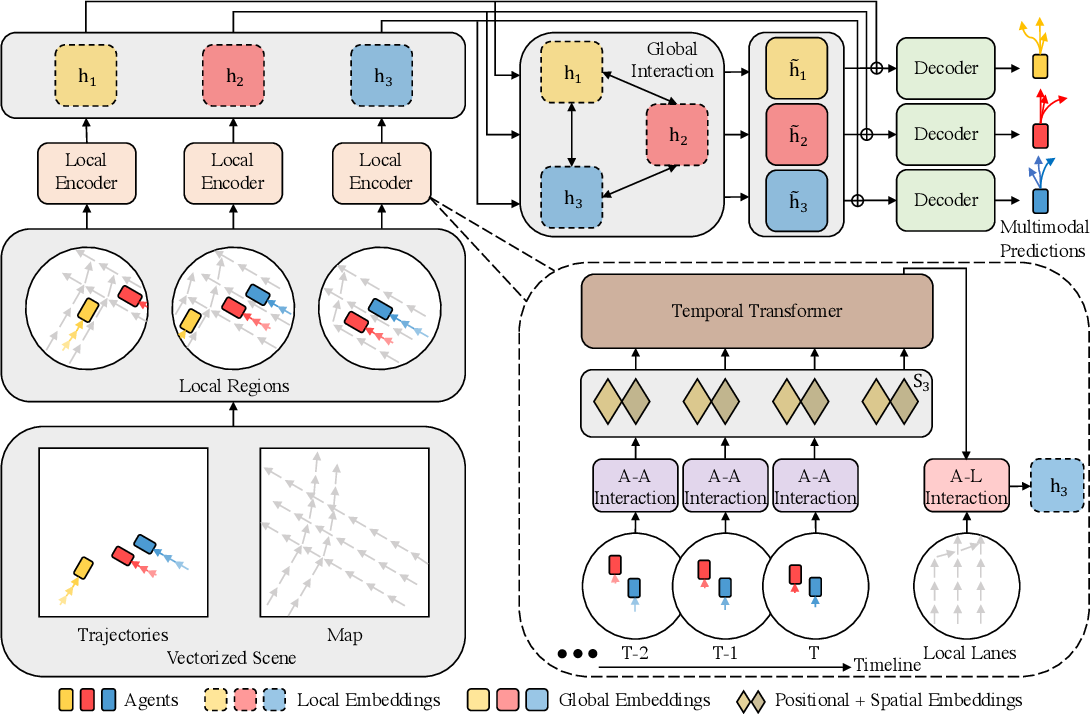
2. Implementação em MQL5

Acima, analisamos uma descrição bastante detalhada do complexo algoritmo proposto pelos autores do HiVT. Agora, chegou o momento de passar para a parte prática do nosso trabalho, na qual implementaremos nossa interpretação dos métodos sugeridos utilizando MQL5.

Vale ressaltar que as abordagens propostas pelos autores do método diferem significativamente dos mecanismos que utilizamos anteriormente. Portanto, temos um grande volume de trabalho pela frente.

2.1 Vetorização do estado inicial

Iniciamos o trabalho com o processo de vetorização do estado. Claro, já analisamos vários algoritmos de vetorização do estado inicial anteriormente. Entre eles, podemos destacar a representação segmentada linear de séries temporais, a segmentação de dados e diversas abordagens de incorporação. No entanto, neste caso, os autores do método propuseram uma abordagem completamente diferente, que implementaremos no kernel HiVTPrepare do OpenCL.

__kernel void HiVTPrepare(__global const float *data,
                          __global float2 *output
                         )
  {
   const size_t t = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t total_v = get_global_size(1);

Nos parâmetros do kernel, utilizamos apenas dois ponteiros para buffers globais de dados: os valores de entrada e os resultados das operações.

Vale destacar que, diferentemente dos dados de entrada, utilizamos o tipo vetorial float2 para o buffer de resultados. Já o utilizamos anteriormente para representar grandezas complexas. Porém, neste caso, não aplicaremos matemática de números complexos. O uso desse tipo de dado está relacionado à rotação da cena no espaço bidimensional. Em um vetor de dois elementos, será mais conveniente armazenar coordenadas e deslocamentos no plano.

Como deve ter notado, não passamos constantes que definam a dimensionalidade dos tensores de entrada e saída nos parâmetros do kernel. Pretendemos obter essas informações a partir do espaço bidimensional da tarefa. O primeiro eixo representará a profundidade do histórico analisado, enquanto o segundo indicará o número de séries temporais unitárias na sequência multimodal analisada.

Partimos do pressuposto de que nossa sequência multimodal é uma composição de séries temporais unitárias unidimensionais.

No corpo do kernel, identificamos o fluxo atual em todas as dimensões do espaço da tarefa. Em seguida, determinamos as constantes de deslocamento nos buffers globais de dados.

   const int shift_data = t * total_v;
   const int shift_out = shift_data * total_v;

Para esclarecer a questão do deslocamento no buffer de resultados, é necessário descrever brevemente o algoritmo que planejamos implementar nesse kernel.

Conforme discutido na parte teórica, os autores do método HiVT propuseram substituir valores absolutos por valores relativos, aplicando uma rotação da cena em torno do agente central.

Seguindo essa lógica, primeiramente determinamos o deslocamento de cada agente em um determinado passo de tempo.

   float value = data[shift_data + v + total_v] - data[shift_data + v];

Depois, calculamos o ângulo de inclinação do deslocamento obtido. Naturalmente, para obter esse ângulo no plano, são necessárias duas coordenadas de deslocamento. No entanto, os dados de entrada possuem apenas um parâmetro. Porém, como estamos lidando com uma série temporal, podemos considerar "1" como o deslocamento ao longo do eixo do tempo, equivalente a um passo temporal.

   const float theta = atan(value);

Agora podemos calcular o seno e o cosseno do ângulo para construir a matriz de rotação.

   const float cos_theta = cos(theta);
   const float sin_theta = sin(theta);

Em seguida, realizamos a rotação do vetor de deslocamento do agente central.

   const float2 main = Rotate(value, cos_theta, sin_theta);

Como a rotação precisa ser aplicada a todos os agentes, movi essa operação para uma função separada.

Vale destacar que, como resultado da rotação, obtemos deslocamentos em duas coordenadas. Para armazenar esses dados, utilizamos a variável vetorial float2.

Em seguida, criamos um laço que percorre todos os agentes presentes no momento atual.

   for(int a = 0; a < total_v; a++)
     {
      float2 o = main;
      if(a != v)
         o -= Rotate(data[shift_data + a + total_v] - data[shift_data + a], cos_theta, sin_theta);
      output[shift_out + a] = o;
     }
  }

Dentro do laço, armazenamos o deslocamento do agente central, enquanto calculamos o deslocamento relativo deste para os demais agentes. Para isso, primeiro determinamos o deslocamento de cada agente, aplicamos a rotação de acordo com a matriz de rotação do agente central e subtraímos o deslocamento resultante do vetor de movimento deste.

Dessa forma, para cada agente em cada instante de tempo, obtemos um tensor que descreve a cena com duas colunas (coordenadas no plano) e um número de linhas correspondente ao número de séries unitárias analisadas.

Aqui, vale mencionar que os autores do método limitaram o número de agentes pelo raio do segmento local. No entanto, optamos por não aplicar essa restrição, pois a divergência dos valores dos indicadores muitas vezes gera sinais de negociação bastante úteis.

2.2 Atenção dentro de um único passo temporal

O próximo desafio enfrentado durante a implementação das abordagens propostas foi a organização dos mecanismos de atenção entre agentes dentro de um único passo temporal.

Anteriormente, já implementamos mecanismos de atenção no contexto de variáveis individuais. No entanto, isso pode ser considerado uma análise "vertical". Neste caso, precisamos de uma análise "horizontal". Poderíamos resolver essa questão criando uma nova classe de "atenção horizontal", mas essa abordagem seria bastante trabalhosa.

Existe, porém, uma solução mais eficiente. Poderíamos simplesmente transpor os dados de entrada e utilizar os mecanismos de "atenção vertical" já existentes. No entanto, há um detalhe: o algoritmo atual de transposição de matrizes bidimensionais não é adequado para essa situação. Assim, precisaremos criar um algoritmo de transposição para um tensor tridimensional. Durante essa transposição, trocamos a primeira e a segunda dimensão, mantendo a terceira inalterada.

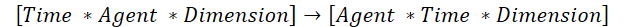
Isso é exatamente o que precisamos para utilizar os algoritmos existentes de "atenção vertical".

Para estruturar esse processo, criamos o kernel TransposeRCD.

__kernel void TransposeRCD(__global const float *matrix_in, ///<[in] Input matrix
                           __global float *matrix_out ///<[out] Output matrix
                          )
  {
   const int r = get_global_id(0);
   const int c = get_global_id(1);
   const int d = get_global_id(2);
   const int rows = get_global_size(0);
   const int cols = get_global_size(1);
   const int dimension = get_global_size(2);
//---
   matrix_out[(c * rows + r)*dimension + d] = matrix_in[(r * cols + c) * dimension + d];
  }

O algoritmo do kernel é quase idêntico ao do kernel de transposição de uma matriz bidimensional. A única diferença é a adição de uma dimensão extra ao espaço da tarefa, exigindo um ajuste correspondente nos deslocamentos nos buffers de dados para levar essa nova dimensão em consideração.

O mesmo pode ser dito sobre a estrutura da classe CNeuronTransposeRCDOCL. Aqui, utilizamos deliberadamente a classe de transposição de matriz bidimensional CNeuronTransposeOCL como classe pai. 

class CNeuronTransposeRCDOCL  :  public CNeuronTransposeOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTransposeRCDOCL(void){};
                    ~CNeuronTransposeRCDOCL(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint count, uint window, uint dimension, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) const { return defNeuronTransposeRCDOCL; }
  };

Vale destacar que não declaramos variáveis ou objetos adicionais no corpo da classe. Para que o processo seja bem-sucedido, as funcionalidades herdadas são suficientes. Isso nos permite apenas redefinir os métodos de chamada do kernel, enquanto toda a funcionalidade restante é coberta pelos métodos da classe pai. Portanto, não entraremos em detalhes sobre os algoritmos dos métodos dessa classe neste momento. Recomendo que você os analise pessoalmente. O código completo desta classe e de todos os seus métodos está disponível no anexo.

#2.3 Bloco de atenção agente-agente

Agora passamos para a implementação do bloco de atenção Agente-Agente. Vale lembrar que, nesse bloco, a atenção entre as incorporações locais dos agentes dentro de um único passo temporal é construída. A classe de transposição do tensor tridimensional, que criamos anteriormente, simplificou significativamente esse trabalho. No entanto, o mecanismo de controle da fusão de características proposto pelos autores do método requer ajustes no algoritmo.

Para estruturar os processos desse bloco de atenção, criaremos uma nova classe chamada CNeuronHiVTAAEncoder. Neste caso, utilizaremos a camada de atenção de variáveis independentes CNeuronMVMHAttentionMLKV como classe pai.

class CNeuronHiVTAAEncoder : public CNeuronMVMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronHiVTAAEncoder(void){};
                    ~CNeuronHiVTAAEncoder(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint heads_kv, 
                          uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMVMHAttentionMLKV;   }
  };

Como se pode notar, também não declaramos variáveis ou objetos adicionais na estrutura dessa classe. Mais uma vez, isso se deve à estrutura eficiente da classe pai. Vale lembrar que a classe CNeuronMVMHAttentionMLKV utiliza coleções dinâmicas de buffers de dados, que são manipuladas pelos métodos da classe. Podemos simplesmente adicionar a quantidade necessária de buffers às coleções existentes.

A inicialização de uma nova instância do nosso objeto ocorre no método Init.

bool CNeuronHiVTAAEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                uint window, uint window_key, uint heads, uint heads_kv, 
                                uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, 
                                                                   optimization_type, batch))
      return false;

Nos parâmetros desse método, recebemos as principais constantes que nos permitem definir corretamente a arquitetura do objeto conforme especificado pelo usuário. No corpo do método, seguindo a prática usual, chamamos o método homônimo da classe base da camada neural.

Vale destacar que chamamos o método não da classe pai direta, mas da classe base, pois mais adiante ainda precisaremos redefinir alguns buffers de dados.

Após a execução bem-sucedida do método da classe pai, armazenamos internamente as constantes recebidas do programa externo que definem a arquitetura do objeto.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   iLayers = fmax(layers, 1);
   iHeadsKV = fmax(heads_kv, 1);
   iLayersToOneKV = fmax(layers_to_one_kv, 1);
   iVariables = variables;

Em seguida, calculamos imediatamente as constantes que determinam o tamanho dos objetos internos.

   uint num_q = iWindowKey * iHeads * iUnits * iVariables;      //Size of Q tensor
   uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables;   //Size of KV tensor
   uint q_weights = (iWindow * iHeads + 1) * iWindowKey;        //Size of weights' matrix of Q tenzor
   uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey;     //Size of weights' matrix of KV tenzor
   uint scores = iUnits * iUnits * iHeads * iVariables;         //Size of Score tensor
   uint mh_out = iWindowKey * iHeads * iUnits * iVariables;     //Size of multi-heads self-attention
   uint out = iWindow * iUnits * iVariables;                    //Size of attention out tensore
   uint w0 = (iWindowKey * iHeads + 1) * iWindow;               //Size W0 weights matrix
   uint gate = (2 * iWindow + 1) * iWindow;                     //Size of weights' matrix gate layer
   uint self = (iWindow + 1) * iWindow;                         //Size of weights' matrix self layer

O algoritmo, em sua essência, foi herdado da classe pai, com apenas alguns ajustes pontuais.

Após a conclusão da fase preparatória, criamos um laço com um número de iterações correspondente à quantidade especificada de camadas aninhadas. Dentro desse laço, criamos os objetos necessários para executar a funcionalidade de cada camada aninhada individualmente a cada iteração.

   for(uint i = 0; i < iLayers; i++)
     {
      CBufferFloat *temp = NULL;
      for(int d = 0; d < 2; d++)
        {
         //--- Initilize Q tensor
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(num_q, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Tensors.Add(temp))
            return false;

Primeiramente, criamos buffers para armazenar os dados intermediários e os resultados dos blocos individuais, além dos buffers necessários para registrar os gradientes de erro correspondentes.

Vale destacar que o buffer de dados e o buffer de gradientes do erro têm o mesmo tamanho. Para reduzir o esforço manual, criamos um laço aninhado de duas iterações. Na primeira iteração, criamos os buffers de dados, e na segunda, os buffers dos gradientes do erro correspondentes.

O primeiro buffer que criamos é para armazenar as entidades Query. Em seguida, criamos os buffers para Key e Value.

         //--- Initilize KV tensor
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(2 * num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!KV_Tensors.Add(temp))
               return false;
           }

Os algoritmos de criação e inicialização dos buffers de dados são idênticos. No entanto, nosso algoritmo permite o uso de um único tensor Key-Value para várias camadas aninhadas. Por isso, antes de criar os buffers, verificamos se essa operação é necessária para a camada atual.

Depois, inicializamos o buffer dos coeficientes de dependência entre os objetos.

         //--- Initialize scores
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(scores, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!S_Tensors.Add(temp))
            return false;

E, em seguida, o buffer para os resultados da atenção multicabeça.

         //--- Initialize multi-heads attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(mh_out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!AO_Tensors.Add(temp))
            return false;

De acordo com o algoritmo de Multi-Head Self-Attention, os resultados da atenção multicabeça são reduzidos ao nível dos dados originais por meio de uma camada de projeção. Criamos um buffer para armazenar essa projeção resultante.

         //--- Initialize attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Até este ponto, o algoritmo descrito segue quase integralmente o método da classe pai. No entanto, a seguir, aplicamos modificações para organizar o mecanismo de controle da fusão de características. De acordo com o algoritmo proposto, primeiro concatenamos os dados originais com os resultados do bloco de atenção.

         //--- Initialize Concatenate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(2 * out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Com base nessa concatenação, calculamos os coeficientes de controle.

         //--- Initialize Gate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Depois, realizamos a projeção dos dados originais.

         //--- Initialize Self
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

E, ao final do laço aninhado, criamos o buffer dos resultados da camada aninhada atual.

         //--- Initialize Out
         if(i == iLayers - 1)
           {
            if(!FF_Tensors.Add(d == 0 ? Output : Gradient))
               return false;
            continue;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;
        }

Vale destacar que os buffers de resultados e de gradientes são criados apenas para as camadas internas intermediárias. Para a última camada aninhada, simplesmente copiamos os ponteiros para os buffers correspondentes da nossa classe.

Após criar os buffers dos resultados intermediários e dos gradientes do erro, inicializamos as matrizes dos parâmetros treináveis. Teremos várias delas. A primeira é a matriz de geração da entidade Query.

      //--- Initilize Q weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(q_weights))
         return false;
      float k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < q_weights; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!QKV_Weights.Add(temp))
         return false;

Aqui, primeiro criamos o buffer e, em seguida, o preenchemos com parâmetros aleatórios. Esses parâmetros serão otimizados durante o treinamento do modelo.

Da mesma forma, criamos os parâmetros para a geração das entidades Key e Value. No entanto, essas matrizes não são geradas para cada camada aninhada.

      //--- Initilize K weights
      if(i % iLayersToOneKV == 0)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!K_Weights.Add(temp))
            return false;
         //---
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!V_Weights.Add(temp))
            return false;
        }

Além disso, precisamos de uma matriz de projeção dos resultados da atenção multicabeça.

      //--- Initilize Weights0
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(w0))
         return false;
      for(uint w = 0; w < w0; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Aqui também adicionamos os parâmetros para o bloco de controle da fusão de características.

      //--- Initilize Gate Weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(gate))
         return false;
      k = (float)(1 / sqrt(2 * iWindow + 1));
      for(uint w = 0; w < gate; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

E as projeções dos dados originais.

      //--- Self
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(self))
         return false;
      k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < self; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Em seguida, adicionamos os buffers de dados para armazenar os momentos no nível da matriz de pesos, que serão utilizados no processo de otimização dos parâmetros.

      //---
      for(int d = 0; d < (optimization == SGD ? 1 : 2); d++)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Weights.Add(temp))
            return false;
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Weights.Add(temp))
               return false;
            //---
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Weights.Add(temp))
               return false;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Gate Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? gate : 2 * iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Self Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? self : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
        }
     }

Após a inicialização bem-sucedida dos objetos das camadas aninhadas, criamos um buffer adicional que será usado para armazenar temporariamente os resultados intermediários.

   if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Por fim, finalizamos o método, retornando à função chamadora um valor lógico indicando o sucesso da execução das operações do método.

O próximo passo, após a inicialização do objeto, é a construção do algoritmo de propagação para frente (feedForward), implementado no método feedForward.

bool CNeuronHiVTAAEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

Nos parâmetros desse método, recebemos um ponteiro para o objeto contendo os dados de entrada e verificamos imediatamente se o ponteiro recebido é válido. Se essa verificação for bem-sucedida, criamos um laço no qual executamos sequencialmente as operações de cada camada aninhada.

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(10 * i - 6));
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
         !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                       iWindow, iWindowKey * iHeads, None))
         return false;

Primeiro, geramos as entidades Query. Em seguida, quando necessário, formamos o tensor Key-Value.

      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         CBufferFloat *k = K_Tensors.At(i_kv * 2);
         CBufferFloat *v = V_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, 
                                                        iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, 
                                                         iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits))
            return false;
        }

Após a formação dos tensores das entidades necessárias, calculamos os resultados da atenção multicabeça.

      //--- Score calculation and Multi-heads attention calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

E os reduzimos à dimensionalidade dos dados originais.

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 10);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                       iWindowKey * iHeads, iWindow, None))
         return false;

Para calcular os coeficientes de controle, primeiro concatenamos os resultados do bloco de atenção com os dados originais.

      //--- Concat
      out = FF_Tensors.At(i * 10 + 1);
      if(IsStopped() || !Concat(temp, inputs, out, iWindow, iWindow, iUnits))
         return false;

Depois, calculamos os coeficientes de controle.

      //--- Gate
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), out, 
                                 FF_Tensors.At(i * 10 + 2), 2 * iWindow, iWindow, SIGMOID))
         return false;

Resta apenas realizar a projeção dos dados originais.

      //--- Self
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), inputs, 
                                         FF_Tensors.At(i * 10 + 3), iWindow, iWindow, None))
         return false;

Em seguida, combinamos a projeção obtida com os resultados do bloco de atenção, levando em conta os coeficientes de controle.

      //--- Out
      if(IsStopped() || 
        !GateElementMult(FF_Tensors.At(i * 10 + 3), temp, FF_Tensors.At(i * 10 + 2), 
                                                          FF_Tensors.At(i * 10 + 4)))
         return false; 
     }
//---
   return true;
  }

E passamos para a próxima camada aninhada na nova iteração do laço.

Após a execução bem-sucedida das operações de todas as camadas aninhadas, finalizamos o método e retornamos à função chamadora um valor lógico indicando o sucesso da execução do método.

Com isso, concluímos o trabalho com os métodos de propagação para frente. Quanto aos algoritmos dos métodos de propagação reversa, recomendo que você os analise pessoalmente. Lembro que o código completo desta classe e de seus métodos, assim como de todos os programas utilizados na preparação deste artigo, pode ser encontrado no anexo.

Considerações finais

Neste artigo, exploramos um método bastante interessante e promissor, o Transformer Vetorial Hierárquico (HiVT), proposto para a previsão do movimento de múltiplos agentes. Esse método oferece uma abordagem eficiente para a solução do problema de previsão, decompondo a tarefa em etapas de extração local de contexto e modelagem global das interações.

Os autores do método adotaram uma abordagem abrangente para resolver o problema proposto e sugeriram uma série de estratégias para aumentar a eficiência do modelo apresentado. Infelizmente, o volume de trabalho necessário para implementar todas essas abordagens ultrapassa o escopo deste artigo. Nesta publicação, conseguimos apenas realizar a preparação necessária. O trabalho iniciado será concluído no próximo artigo, quando também serão apresentados os resultados dos testes dos métodos propostos com dados históricos reais.

Referências

HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction

Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de Modelos
4	StudyEncoder.mq5	Expert Advisor	EA para treinamento do Codificador
5	Test.mq5	Expert Advisor	EA para testar o modelo
6	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
8	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL