Datenwissenschaft und ML (Teil 27): Convolutional Neural Networks (CNNs) in MetaTrader 5 Trading Bots — funktioniert das?
134
0
Die Pooling-Operation, die in einem faltenden neuronalen Netzwerk verwendet wird, ist ein großer Fehler, und die Tatsache, dass sie so gut funktioniert, ist eine Katastrophe.
Geoffrey Hinton
Inhalt
- Was sind faltende neuronale Netzwerke (Convolutional Neural Networks, CNNS)?
- Faltungsschichten
- Aktivierungsfunktionen
- Pooling-Schichten
- Vollständig verbundene Schichten
- Dropout-Schichten - Warum sollte man faltende neuronale Netzwerke (Convolutional Neural Networks, CNNs) für Finanzanalysen und Handelsanwendungen verwenden?
- Erstellung eines faltendes neuronales Netzwerks (CNN) in Python
- Erstellung eines Handelsroboters auf der Grundlage eines faltendes neuronales Netzwerks (CNN)
- Die Quintessenz
Ein grundlegendes Verständnis der Programmiersprache Python, künstlicher neuronaler Netze, maschinellem Lernen und ONNX in MQL5 ist erforderlich, um den Inhalt dieses Artikels vollständig zu verstehen.
Was sind faltende neuronale Netzwerke (Convolutional Neural Networks, CNNS)?
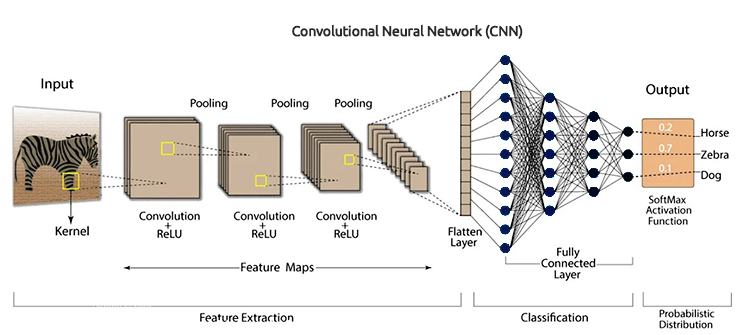
Die faltende neuronale Netzwerke (Convolutional Neural Networks, CNNs) sind eine Klasse von Deep-Learning-Algorithmen, die speziell für die Verarbeitung strukturierter gitterartiger Daten wie Bilder, Audiospektrogramme und Zeitreihendaten entwickelt wurden. Sie eignen sich besonders gut für visuelle Datenaufgaben, da sie automatisch und adaptiv räumliche Hierarchien von Merkmalen aus den Eingabedaten lernen können.
CNNs sind die erweiterte Version der künstlichen neuronalen Netze (ANN). Sie werden in erster Linie zur Extraktion der Merkmale aus dem gitterartigen Matrixdatensatz verwendet. Zum Beispiel visuelle Datensätze wie Bilder oder Videos, bei denen Datenmuster eine große Rolle spielen.
Die faltende neuronale Netzwerke haben mehrere Schlüsselkomponenten wie Faltungsschichten, Aktivierungsfunktionen, Pooling-Schichten, vollständig verbundene Schichten und Dropout-Schichten. Um CNNs im Detail zu verstehen, müssen wir die einzelnen Komponenten auseinander nehmen und sehen, worum es geht.
Faltungsschichten
Dies sind die Kernbausteine von CNNs, hier findet der Großteil der Berechnungen statt. Faltungsschichten sind für die Erkennung lokaler Muster in den Eingabedaten zuständig, wie z. B. Kanten in Bildern. Dies kann durch den Einsatz von Filtern (oder Kerneln) erreicht werden, die über die Eingabedaten gleiten, um Merkmalskarten zu erstellen.
Eine Faltungsschicht ist eine verborgene Schicht, die mehrere Faltungseinheiten in einem faltendes neuronales Netzwerk enthält, das zur Merkmalsextraktion verwendet wird.
from tensorflow.keras.layers import Conv1D
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) Filter/Kerne
Filter (oder Kernel) sind kleine lernfähige quadratische Matrizen (in der Regel der Größe 3x3, 5x5 usw.), die über die Eingabedaten gleiten, um lokale Muster zu erkennen.
Wie funktionieren sie?
Sie arbeiten, indem sie sich über die Eingabedaten bewegen und dann eine elementweise Multiplikation zwischen den Filterwerten und den Eingabewerten innerhalb des aktuellen Empfangsfeldes des Filters durchführen, gefolgt von der Summierung der Ergebnisse. Dieser Vorgang wird als Faltung bezeichnet.
Während des Trainings lernt das Netz die optimalen Werte der Filter. In den ersten Schichten lernen die Filter in der Regel, einfache Merkmale wie Kanten und Texturen zu erkennen, während die Filter in den tieferen Schichten komplexere Muster wie Formen und Objekte erkennen können.
Nehmen wir einen einfachen 3x3-Filter und ein 5x5-Eingabebild. Der Filter gleitet über das Bild und berechnet die Faltungsoperation, um eine Merkmalskarte zu erstellen.
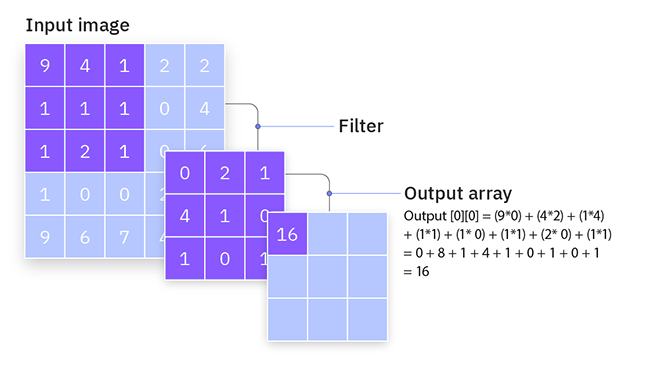
Stride
Dies ist ein weiteres Merkmal, das in der Faltungsschicht zu finden ist. Der Stride ist die Schrittweite, mit der sich der Filter über die Eingabedaten bewegt. Er bestimmt, wie stark der Filter bei jedem Schritt während des Faltungsprozesses verschoben wird.
Wie funktionieren das?
Schrittweite von 1, Der Filter bewegt sich jeweils um eine Einheit, was zu einer stark überlappenden und detaillierten Merkmalskarte führt. Dies führt zu einer größeren Ausgabekarte.
Stride von 2 oder mehr, Der Filter überspringt Einheiten, was zu einer weniger detaillierten, aber kleineren Ausgabe-Merkmalskarte führt. Dadurch werden die räumlichen Dimensionen der Ausgabe reduziert und die Eingabe effektiv heruntergetastet.
Wenn Sie z. B. einen 3x3-Filter und ein 5x5-Eingabebild mit einer Schrittweite von 1 haben, bewegt sich der Filter jeweils um ein Pixel und erzeugt eine 3x3-Ausgabe-Merkmalskarte. Mit einer Schrittweite von 2 verschiebt der Filter jeweils zwei Pixel, wodurch eine 2x2-Ausgabe-Merkmalskarte entsteht.
Padding
Beim Auffüllen (Padding) werden zusätzliche Pixel (in der Regel Nullen) am Rand der Eingabedaten hinzugefügt. Dadurch wird sichergestellt, dass der Filter richtig passt und die räumlichen Dimensionen der ausgegebenen Merkmalskarte kontrolliert werden.
Arten des Padding
Laut Keras gibt es drei Arten von Paddings (Groß- und Kleinschreibung beachten).
- valid - es wird keine Padding vorgenommen,
- same - füllt die Eingabe auf, sodass die Ausgabegröße der Eingabegröße entspricht, wenn strides=1.
- causal - wird für zeitliche Daten verwendet, um sicherzustellen, dass die Ausgabe im Zeitschritt 𝑡 nicht von zukünftigen Eingaben abhängt.
Das Padding hilft dabei, die räumlichen Dimensionen der Eingabedaten zu erhalten. Ohne Padding schrumpft die Ausgabekarte mit jeder Faltungsschicht, was zum Verlust wichtiger Kanteninformationen führen kann.
Durch das Hinzufügen eines Paddings kann das Netz Kantenmerkmale effektiv lernen und die räumliche Auflösung der Eingabe beibehalten.
Nehmen wir einen 3x3-Filter und ein 5x5-Eingabebild. Bei einem gültigen Padding (kein Padding) ist die ausgegebene Merkmalskarte 3x3. Mit dem gleichen Padding könnten Sie einen Rahmen aus Nullen um die Eingabe hinzufügen, sodass sie 7x7 wird. Die ausgegebene Merkmalskarte ist dann 5x5, wobei die Eingabedimensionen erhalten bleiben.
Nachfolgend finden Sie den Code für eine Faltungsschicht in Python.
from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Conv1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', strides=2, padding='causal', input_shape=(window_size, X_train.shape[2]) ) )
Aktivierungsfunktionen
Wie im Artikel Entmystifizierte Feed Forward Neurale Netzwerke beschrieben, ist eine Aktivierungsfunktion eine mathematische Funktion, die eine Eingabe annimmt und eine Ausgabe verarbeitet.
Die Aktivierungsfunktion wird elementweise angewendet, um Nichtlinearität in das Modell einzuführen. Zu den häufig verwendeten Aktivierungsfunktionen in CNNs gehören ReLU (Rectified Linear Unit), Sigmoid und TanH.
Pooling-Schichten
Diese auch als Desample-Schichten bezeichneten Schichten sind ein wesentlicher Bestandteil von CNNs, da sie für die Reduzierung der räumlichen Dimension der Eingabedaten in Bezug auf Breite und Höhe verantwortlich sind, während die wichtigsten Informationen erhalten bleiben.
Wie funktionieren sie?
Zunächst werden die Eingabedaten in sich überschneidende Regionen oder Fenster unterteilt, dann wird eine Aggregationsfunktion wie Max-Pooling oder Average-Pooling auf jedes Fenster angewendet, um einen einzigen Wert zu erhalten.
Beim Max-Pooling wird der maximale Wert aus einer Reihe von Werten innerhalb eines Filterbereichs ermittelt. Sie reduziert die räumliche Ausdehnung der Daten, was zu einer Verringerung des Rechenaufwands und der Anzahl der Parameter führt.
Python
from tensorflow.keras.layers import Conv1D, MaxPooling1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) model.add(MaxPooling1D(pool_size=2))
MaxPooling1D(pool_size=2) Diese Ebene nimmt den Maximalwert aus jedem 2-Elemente-Fenster.
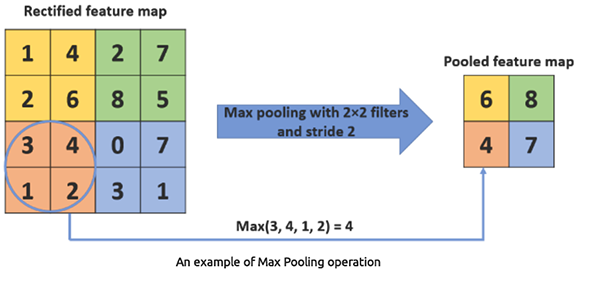
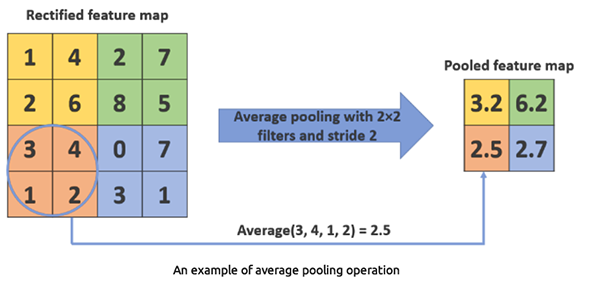
Beim Durchschnitts-Pooling wird der Durchschnittswert aus einer Reihe von Werten innerhalb eines Filterbereichs ermittelt. Wird weniger häufig verwendet als Max-Pooling.
Python
from tensorflow.keras.layers import Conv1D, AveragePooling1D model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2]))) model.add(AveragePooling1D(pool_size=2))
AveragePooling1D(pool_size=2) Diese Ebene nimmt den Durchschnittswert aus jedem 2-Elemente-Fenster.
Warum eine 1D-Faltungsschicht?
Es gibt Conv1D-, Conv2D- und Conv3D-Schichten für CNNs. Die 1D-Faltungsschicht ist für diese Art von Problem geeignet, da sie für eindimensionale Daten konzipiert ist und sich daher für sequentielle Daten oder Zeitreihen eignet. Andere Faltungsschichten wie die Conv2D und die Conv3D sind für diese Art von Problem zu komplex.
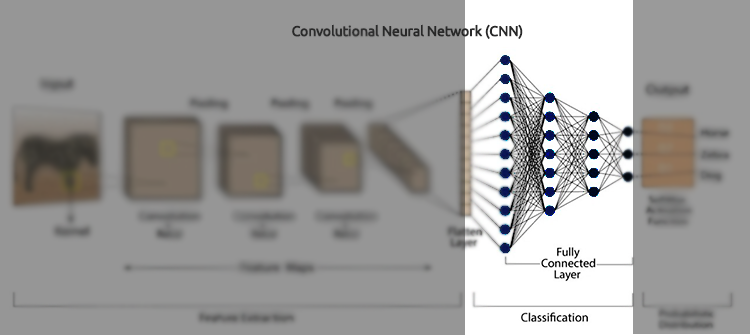
Vollständig verbundene Schichten
Neuronen in einer vollständig verbundenen Schicht haben Verbindungen zu allen Aktivierungen in der vorherigen Schicht. Diese Schichten werden in der Regel gegen Ende des Netzes verwendet, um eine Klassifizierung oder Regression auf der Grundlage der von den Faltungsschichten und Pooling-Schichten extrahierten Merkmale durchzuführen.
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid')) # For binary classification (e.g., buy/sell signal)
model.summary() Der Flatten-Layer wandelt die 1D-Pool-Merkmalskarte in einen 1D-Vektor um, sodass sie in die vollständig verknüpften (dichten) Schichten eingespeist werden kann.
Dichte Schichten (Dense) sind vollständig verknüpfte Schichten, die dazu dienen, endgültige Entscheidungen auf der Grundlage der von den Faltungsschichten und Pooling-Schichten extrahierten Merkmale zu treffen. Dichte Schichten sind im Wesentlichen der Kernbestandteil herkömmlicher künstlicher neuronaler Netze (ANN).
Dropout-Schichten
Die Dropout-Schicht wirkt wie eine Maske, die die Beiträge einiger Neuronen zur nachfolgenden Schicht eliminiert, während die Funktionalität aller anderen Neuronen erhalten bleibt. Wenn wir eine Dropout-Schicht auf den Eingabevektor anwenden, werden einige seiner Merkmale eliminiert; wenn wir sie jedoch auf eine versteckte Schicht anwenden, werden einige versteckte Neuronen eliminiert.
Da sie eine Überanpassung der Trainingsdaten verhindern, sind Dropout-Schichten für das Training von CNNs entscheidend. Fehlen sie, hat der erste Satz von Trainingsmustern einen übermäßig großen Einfluss auf das Lernen. Dies hätte zur Folge, dass Merkmale, die erst in späteren Proben oder Chargen auftreten, nicht gelernt würden.
from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid')) # For binary classification (e.g., buy/sell signal)
model.summary() Warum sollte man faltende neuronale Netzwerke (Convolutional Neural Networks, CNNs) für Finanzanalysen und Handelsanwendungen verwenden?
CNNs sind in der Bild- und Videoverarbeitung weit verbreitet, da sie für diesen Zweck entwickelt wurden. Wenn Sie sich die obigen Erklärungen ansehen, werden Sie vielleicht feststellen, dass ich mich auf die Verwendung von CNNs beziehe, wenn ich mit Bildklassifizierungen und ähnlichem arbeite.
Die Verwendung von faltenden neuronalen Netzwerks (CNNs) für tabellarische Daten, wie z. B. Finanzanalysen, mag im Vergleich zur Verwendung anderer faltendes neuronales Netzwerkypen wie Feed Forward Neural Networks (FFNN), Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTMs) und Gated Recurrent Units (GRUs) unkonventionell erscheinen. Es gibt jedoch mehrere Gründe und potenzielle Vorteile, die im Folgenden für den Einsatz von CNNs in diesem Zusammenhang genannt werden.
01. CNNs sind hervorragend in der Lage, automatisch lokale Muster aus Daten zu extrahieren
03. Sie können robust gegenüber Rauschen und redundanten Merkmalen sein.
04: CNNs können multivariate Zeitreihen gut verarbeiten
Da wir nun stichhaltige Gründe für den Einsatz von CNNs in Handelsanwendungen haben, wollen wir ein CNN erstellen und trainieren und dann sehen, wie wir ein CNN in einem Meta Trader 5 Expert Advisor (EA) verwenden können.
Erstellung eines faltendes neuronales Netzwerks (CNN) in Python
Dies umfasst mehrere Schritte, nämlich.
- Sammeln der Daten
- Aufbereitung der Daten für ein CNN-Modell
- Training eines CNN-Modells
- Speichern eines CNN-Modells im ONNX-Format
01: Erfassen der Daten
Wir verwenden die Daten für die Zeitreihenprognose, die wir in den vorherigen Artikeln verwendet haben.
Da wir nun wissen, dass faltende neuronale Netzwerke (CNNs) gut darin sind, Muster in hochdimensionalen Daten zu erkennen, können wir, ohne das Modell zu verkomplizieren, einige der Merkmale auswählen, von denen ich glaube, dass sie viele Muster enthalten, die das CNN-Modell erkennen kann.
Python-Code
open_price = df['TARGET_OPEN'] close_price = df['TARGET_CLOSE'] # making the target variable target_var = [] for i in range(len(open_price)): if close_price[i] > open_price[i]: # if the price closed above where it opened target_var.append(1) # bullish signal else: target_var.append(0) # bearish signal new_df = pd.DataFrame({ 'OPEN': df['OPEN'], 'HIGH': df['HIGH'], 'LOW': df['LOW'], 'CLOSE': df['CLOSE'], 'TARGET_VAR': target_var }) print(new_df.shape)
Kurz nach der Vorbereitung der Zielvariablen auf der Grundlage von TARGET_OPEN und TARGET_CLOSE, die jeweils Eröffnungs- und Schließwerte sind, wird ein Balken vorwärts gesammelt. Wir haben eine Mini-Datensatzversion mit dem Namen new_df erstellt, die nur 4 unabhängige Variablen mit den Werten OPEN, HIGH und LOW und eine abhängige Variable mit dem Namen TARGET_VAR enthält.
02: Aufbereitung der Daten für ein CNN-Modell
Zunächst müssen wir die Eingabedaten vorverarbeiten, indem wir sie zu Fenstern umformen und ausrichten. Dies ist bei der Arbeit mit tabellarischen Daten in CNNs sehr wichtig, und zwar aus folgenden Gründen.
Da es sich bei den Handelsdaten um sequenzielle Daten handelt, ergeben sich die Muster oft über eine Reihe von Zeitschritten und nicht zu einem einzigen Zeitpunkt. Indem wir überlappende Datenfenster erstellen, können wir zeitliche Abhängigkeiten erfassen und dem CNN-Modell einen Kontext geben.
Außerdem erwarten CNNs, dass die Eingabedaten eine bestimmte Form haben. Für 1D-Faltungsschichten sollte die Eingabestruktur in der Regel über (Anzahl der Fenster, Fenstergröße, Anzahl der Merkmale) verfügen. Diese Form ähnelt derjenigen, die wir in der Zeitreihenanalyse mit rekurrenten neuronalen Netzen (RNNs) im vorherigen Artikel verwendet haben. Das nun folgende Vorverarbeitungsverfahren stellt sicher, dass die Daten in diesem Format vorliegen, sodass sie für die Eingabe in ein CNN-Modell geeignet sind.
# Example data preprocessing function def preprocess_data(df, window_size): X, y = [], [] for i in range(len(df) - window_size): X.append(df.iloc[i:i+window_size, :-1].values) y.append(df.iloc[i+window_size, -1]) return np.array(X), np.array(y) window_size = 10 X, y = preprocess_data(new_df, window_size) print(f"x_shape = {X.shape}\ny_shape = {y.shape}")
Ausgabe
x_shape = (990, 10, 4) y_shape = (990,)
Da unsere Daten in einem täglichen Zeitrahmen gesammelt wurden, zeigt die Fenstergröße von 10 an, dass wir das CNN-Modell trainieren werden, um Muster innerhalb von 10 Tagen zu verstehen.
Dann müssen wir die Daten in Trainings- und Testproben aufteilen.
# Split data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False) # Standardize the data scaler = StandardScaler() X_train = scaler.fit_transform(X_train.reshape(-1, X_train.shape[-1])).reshape(X_train.shape) X_test = scaler.transform(X_test.reshape(-1, X_test.shape[-1])).reshape(X_test.shape) print(f"x_train\n{X_train.shape}\nx_test\n{X_test.shape}\n\ny_train {y_train.shape} y_test {y_test.shape}")
Ausgabe
x_train (792, 10, 4) x_test (198, 10, 4) y_train (792,) y_test (198,)
Schließlich müssen wir die Zielvariable für diese Klassifizierungsaufgabe einmalig kodieren.
from tensorflow.keras.utils import to_categorical
y_train_encoded = to_categorical(y_train)
y_test_encoded = to_categorical(y_test)
print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}") Ausgabe
One hot encoded y_train (792, 2) y_test (198, 2)
03: Training eines CNN-Modells
Hier wird die meiste Arbeit erledigt.
# Defining the CNN model model = Sequential() model.add(Conv1D(filters=64, kernel_size=3, activation='relu', strides=2, padding='causal', input_shape=(window_size, X_train.shape[2]) ) ) model.add(MaxPooling1D(pool_size=2)) model.add(Flatten()) model.add(Dense(100, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(units=len(np.unique(y)), activation='softmax')) # For binary classification (buy/sell signal) model.summary() # Compiling the model optimizer = Adam(learning_rate=0.001) model.compile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy']) # Training the model early_stopping = EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True) history = model.fit(X_train, y_train_encoded, epochs=100, batch_size=16, validation_split=0.2, callbacks=[early_stopping]) plt.figure(figsize=(7.5, 6)) plt.plot(history.history['loss'], label='Training Loss') plt.plot(history.history['val_loss'], label='Validation Loss') plt.xlabel('Epochs') plt.ylabel('Loss') plt.title('Training Loss Curve') plt.legend() plt.savefig("training loss cuver-cnn-clf.png") plt.show()
Ausgabe
Model: "sequential_2" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ conv1d_2 (Conv1D) │ (None, 5, 64) │ 832 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ max_pooling1d_2 (MaxPooling1D) │ (None, 2, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ flatten_2 (Flatten) │ (None, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_4 (Dense) │ (None, 100) │ 12,900 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dropout_2 (Dropout) │ (None, 100) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_5 (Dense) │ (None, 2) │ 202 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Das Training wurde bei der 34. Epoche beendet.
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5105 - loss: 0.6875 - val_accuracy: 0.4843 - val_loss: 0.6955 Epoch 32/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5099 - loss: 0.6888 - val_accuracy: 0.5283 - val_loss: 0.6933 Epoch 33/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.4636 - loss: 0.6933 - val_accuracy: 0.5283 - val_loss: 0.6926 Epoch 34/100 40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5070 - loss: 0.6876 - val_accuracy: 0.5346 - val_loss: 0.6963
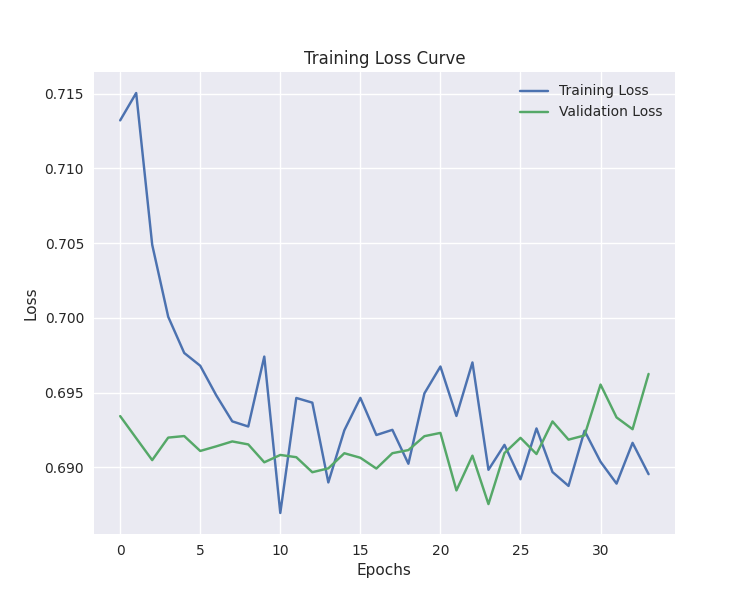
Das Modell war in etwa 57 % der Fälle bei Vorhersagen außerhalb der Stichprobe genau.
y_pred = model.predict(X_test)
classes_in_y = np.unique(y)
y_pred_binary = classes_in_y[np.argmax(y_pred, axis=1)]
# Confusion Matrix
cm = confusion_matrix(y_test, y_pred_binary)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.title("Confusion Matrix")
plt.savefig("confusion-matrix CNN") # Display the heatmap
print("Classification Report\n",
classification_report(y_test, y_pred_binary)) Ausgabe
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step Classification Report precision recall f1-score support 0 0.53 0.24 0.33 88 1 0.58 0.83 0.68 110 accuracy 0.57 198 macro avg 0.55 0.53 0.50 198 weighted avg 0.55 0.57 0.52 198
Unser CNN-Modell ist gut genug für einen Expert Advisor. Bevor wir jedoch mit der Kodierung eines EA beginnen können, müssen wir das trainierte CNN-Modell im ONNX-Format speichern.
04: Speichern eines CNN-Modells im ONNX-Format.
Das Verfahren ist recht einfach. Wir müssen das CNN-Modell im .onnx-Format und die Parameter der Skalierungstechnik in Binärdateien speichern.
import tf2onnx
onnx_file_name = "cnn.EURUSD.D1.onnx"
spec = (tf.TensorSpec((None, window_size, X_train.shape[2]), tf.float16, name="input"),)
model.output_names = ['outputs']
onnx_model, _ = tf2onnx.convert.from_keras(model, input_signature=spec, opset=13)
# Save the ONNX model to a file
with open(onnx_file_name, "wb") as f:
f.write(onnx_model.SerializeToString())
# Save the mean and scale parameters to binary files
scaler.mean_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_mean.bin")
scaler.scale_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_scale.bin") Erstellung eines Handelsroboters auf der Grundlage eines faltendes neuronales Netzwerks (CNN)
Innerhalb eines Expert Advisors müssen wir zunächst das ONNX-formatierte Modell und die Binärdateien des Standard Skalierer als Ressourcen einbinden.
MQL5 | ConvNet EA.mq5
#resource "\\Files\\cnn.EURUSD.D1.onnx" as uchar onnx_model[] #resource "\\Files\\cnn.EURUSD.D1.standard_scaler_scale.bin" as double scaler_stddev[] #resource "\\Files\\cnn.EURUSD.D1.standard_scaler_mean.bin" as double scaler_mean[]
Wir müssen sie beide initialisieren, den Skalierer und das Onnx-Modell.
#include <MALE5\Convolutioal Neural Networks(CNNs)\Convnet.mqh> #include <MALE5\preprocessing.mqh> CConvNet cnn; StandardizationScaler scaler; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ input group "cnn"; input uint cnn_data_window = 10; //this value must be the same as the one used during training in a python script vector classes_in_y = {0,1}; //we have to assign the classes manually | it is essential that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if (!cnn.Init(onnx_model)) //Initialize the ONNX model return INIT_FAILED; //--- Initializing the scaler with values loaded from binary files scaler = new StandardizationScaler(scaler_mean, scaler_stddev); //load the scaler return(INIT_SUCCEEDED); }
Das reicht aus, um das Modell zum Laufen zu bringen. Die Funktion zum Extrahieren von Daten soll so gestaltet werden, wie die unabhängigen Variablen beim Training verwendet wurden. Wir verwendeten vier Variablen OHLC-Werte von dem vorherigen geschlossenen Balken zu 10 Balken vorher, die die Fenstergröße und der Zeitrahmen muss beibehalten werden (der tägliche Zeitrahmen).
input group "cnn"; input uint cnn_data_window = 10; //this value must be the same as the one used during training in a python script input ENUM_TIMEFRAMES timeframe = PERIOD_D1; input int magic_number = 1945; input int slippage = 50;
matrix GetXVars(int bars, int start_bar=1) { vector open(bars), high(bars), low(bars), close(bars); //--- Getting OHLC values open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars); high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars); low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars); close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars); //--- matrix data(bars, 4); //we have 10 inputs from cnn | this value is fixed //--- adding the features into a data matrix data.Col(open, 0); data.Col(high, 1); data.Col(low, 2); data.Col(close, 3); return data; }
Da wir nun eine Funktion zur Erfassung der unabhängigen Variablen haben, können wir unsere Handelsstrategie fertigstellen.
void OnTick() { //--- if (NewBar()) //Trade at the opening of a new candle { matrix input_data_matrix = GetXVars(cnn_data_window); //get data for the past 10 days(default) input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data int signal = cnn.predict_bin(input_data_matrix, classes_in_y); //getting trade signal from the RNN model Comment("Signal==",signal); //--- MqlTick ticks; SymbolInfoTick(Symbol(), ticks); if (signal==1) //if the signal is bullish { if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions { if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, 0, 0)) //Open a buy trade printf("Failed to open a buy position err=%d",GetLastError()); ClosePosition(POSITION_TYPE_SELL); //close opposite trade } } else if (signal==0) //Bearish signal { if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, 0, 0)) //open a sell trade printf("Failed to open a sell position err=%d",GetLastError()); ClosePosition(POSITION_TYPE_BUY); } else //There was an error return; } }
Die Strategie ist einfach. Wenn wir ein bestimmtes Signal erhalten, z. B. ein Kaufsignal, eröffnen wir eine Kaufposition ohne Stop-Loss- und Take-Profit-Werte und schließen dann das entgegengesetzte Signal und umgekehrt für ein Verkaufssignal.
Schließlich habe ich diese Strategie auf einem Symbol getestet, auf dem sie trainiert wurde, nämlich EURUSD, und zwar zehn Jahre lang. Vom 01.01.2014 bis zum 27.05.2024 auf einem 4-Stunden-Chart auf den Eröffnungskursen eines jeden Balkens.
Die Ergebnisse der Strategietester waren hervorragend.
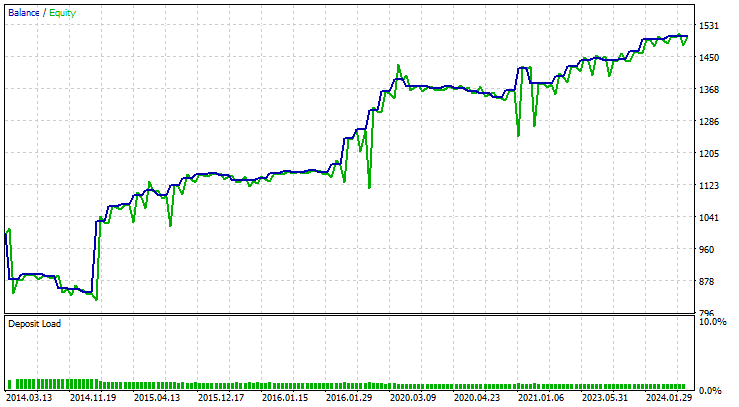
Der EA traf in 58 % aller Fälle die richtigen Vorhersagen, sodass der auf CNN basierende EA einen Nettogewinn von 503 Dollar erzielte.
Die Quintessenz
Obwohl es speziell für die Bild- und Videoverarbeitung entwickelt wurde, kann es auch für die Verarbeitung von Tabellendaten, wie z. B. die von uns zur Verfügung gestellten Devisendaten, eingesetzt werden. Faltende neuronale Netzwerke (CNN) sind in der Lage, Muster zu erkennen und sie für Vorhersagen auf dem Devisenmarkt zu nutzen.
Das geht aus dem Bericht des Strategietesters hervor. Ich wette, dass viele traditionelle Modelle, die für Tabellendaten entwickelt wurden, wie z. B. lineare Regression, Support Vector Machine, Naive Bayes usw., diese Vorhersagegenauigkeit nicht erreichen können, wenn man bedenkt, dass dem CNN-Modell nur 4 unabhängige Variablen (OHLC) gegeben wurden. Meiner Erfahrung nach können nicht viele Modelle so gut werden, wenn man ein paar Variablen beachtet.
Mit freundlichen Grüßen.
Verfolgen Sie die Entwicklung von Modellen für maschinelles Lernen und vieles mehr in dieser Artikelserie auf GitHub repo.
Tabelle der Anhänge
| Dateiname | Dateityp | Beschreibung und Verwendung |
|---|---|---|
| ConvNet EA.mq5 | Expert Advisor | Handelsroboter zum Laden des CNN-Modells im ONNX-Format und Testen der endgültigen Handelsstrategie im MetaTrader 5. |
| cnn.EURUSD.D1.onnx | ONNX | CNN-Modell im ONNX-Format. |
| cnn.EURUSD.D1.standard_scaler_mean.bin cnn.EURUSD.D1.standard_scaler_scale.bin | Binärdateien | Binärdateien für den Normierungsscaler |
| preprocessing.mqh | Eine Include-Datei | Eine Bibliothek, die aus dem Standardskalierer besteht |
| ConvNet.mqh | Eine Include-Datei | Eine Bibliothek zum Laden und Bereitstellen von CNN-Modellen im ONNX-Format |
| cnn-for-trading-applications-tutorial.ipynb | Python-Skript/Jupyter-Notebook | Besteht aus dem gesamten Python-Code, der in diesem Artikel besprochen wird |
Quellen und Referenzen
- Convolutional Neural Network-based a novel Deep Trend Following Strategy for Stock Market Trading (https://ceur-ws.org/Vol-3052/paper2.pdf)
- What are Convolutional Neural Networks (CNNs)? (https://youtu.be/QzY57FaENXg)
- Konvertierung von Tabellendaten in Bilder für Deep Learning mit faltendes neuronales Netzwerk (https://www.nature.com/articles/s41598-021-90923-y)
- Bildkerne (https://setosa.io/ev/image-kernels/)
- Pooling-Methoden in tiefen neuronalen Netzen, ein Überblick (https://arxiv.org/pdf/2009.07485)
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15259
MQL5 Handels-Toolkit (Teil 2): Erweiterung und Implementierung der Positionsmanagement EX5-Bibliothek
Selbstoptimierende Expert Advisors mit MQL5 und Python erstellen
Klassische Strategien neu interpretieren (Teil II): Bollinger-Bänder Ausbrüche
Aufbau des Kerzenmodells Trend-Constraint (Teil 7): Verfeinerung unseres Modells für die EA-Entwicklung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.