Técnicas do MQL5 Wizard que você deve conhecer (Parte 28): GANs revisitados com uma introdução às taxas de aprendizado

Introdução

Revisitamos um tipo de rede neural que já consideramos em um artigo anterior, concentrando-nos em um hiperparâmetro específico. A taxa de aprendizado. A Rede Generativa Adversária é uma rede neural que opera em pares, onde uma rede é treinada tradicionalmente para discernir a verdade, enquanto a outra é treinada para distinguir as projeções da primeira em relação a ocorrências reais. Essa dualidade implica que a rede treinada tradicionalmente (a primeira) tenta enganar a segunda, e isso é verdade. No entanto, as duas redes estão na "mesma equipe" e o treinamento simultâneo de ambas torna, em última instância, a rede geradora mais útil para o trader. Neste artigo, focamos no processo de treinamento, concentrando-nos na taxa de aprendizado.

Como sempre nesses artigos, o objetivo é apresentar classes de sinal, classes de trailing ou classes de gerenciamento de dinheiro que não estão pré-instaladas na biblioteca e, ainda assim, podem ser compatíveis, de alguma forma, com as estratégias existentes de um trader. O MQL5 Wizard, em particular, permite que a montagem e os testes dessas classes sejam feitos de maneira integrada, com requisitos mínimos de codificação para as funções de negociação comuns de um Expert Advisor. O que se pode extrair daqui é uma classe personalizada que pode ser testada independentemente como um Expert Advisor montado ou em paralelo com outras classes do wizard, pois a montagem do wizard permite isso facilmente. Para quem é novo no processo de montagem do wizard, esses artigos aqui e aqui fornecem introduções úteis ao assunto.

Neste artigo, dentro de uma Rede Generativa Adversária (GAN) simples, examinaremos a importância, se houver, das taxas de aprendizado no desempenho. O termo "desempenho" é bastante subjetivo e, estritamente falando, os testes deveriam ser realizados ao longo de períodos muito mais longos do que consideramos nesses artigos. Portanto, para nossos propósitos, "desempenho" será simplesmente o lucro total, levando em conta o fator de recuperação. Há vários tipos de taxas de aprendizado (ou cronogramas) que iremos considerar, e um esforço será feito para realizar testes exaustivos em todos eles, especialmente se forem claramente distintos entre si.

O formato deste artigo será um pouco diferente do que estamos acostumados em artigos anteriores. Ao apresentar cada formato de taxa de aprendizado, seus relatórios de teste de estratégia o acompanharão. Isso contrasta ligeiramente com o que fizemos antes, onde os relatórios geralmente vinham todos ao final do artigo, antes da conclusão. Portanto, este é um formato exploratório que mantém a mente aberta quanto ao impacto das taxas de aprendizado no desempenho de algoritmos de aprendizado de máquina, mais especificamente dos GANs. Como estamos analisando vários tipos e formatos de taxas de aprendizado, é importante ter métricas de teste uniformes. Por isso, usaremos um único símbolo, período de tempo e período de teste para todos os tipos de taxa de aprendizado.

Com base nisso, nosso símbolo será EURJPY, o período de tempo será diário e o período de teste será o ano de 2023. Estamos testando em uma GAN, e sua arquitetura padrão certamente é um fator a considerar. Sempre há o argumento de que um design mais elaborado, em termos do número e do tamanho de cada camada, é fundamental. No entanto, embora essas sejam considerações importantes, nosso foco aqui é a taxa de aprendizado. Para esse fim, nossas GANs serão relativamente simples, com apenas 3 camadas, incluindo uma camada oculta. O tamanho geral de cada camada será de 5-8-1, da entrada para a saída. As configurações dessas camadas estão indicadas no código anexado e podem ser facilmente modificadas pelo leitor caso deseje usar uma configuração alternativa.

Para gerar as condições de compra e venda, estamos implementando todos os diferentes formatos de taxa de aprendizado da mesma maneira que fizemos no artigo mencionado anteriormente, que explorou o uso de GANs como uma classe de sinal personalizada no MQL5. Esse código-fonte, como sempre, está anexado, mas também é apresentado abaixo para maior completude:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalCGAN::LongCondition(void)
{  int result = 0;
   double _gen_out = 0.0;
   bool _dis_out = false;
   GetOutput(_gen_out, _dis_out);
   _gen_out *= 100.0;
   if(_dis_out && _gen_out > 50.0)
   {  result = int(_gen_out);
   }
   //printf(__FUNCSIG__ + " generator output is: %.5f, which is backed by discriminator as: %s", _gen_out, string(_dis_out));return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalCGAN::ShortCondition(void)
{  int result = 0;
   double _gen_out = 0.0;
   bool _dis_out = false;
   GetOutput(_gen_out, _dis_out);
   _gen_out *= 100.0;
   if(_dis_out && _gen_out < 50.0)
   {  result = int(fabs(_gen_out));
   }
   //printf(__FUNCSIG__ + " generator output is: %.5f, which is backed by discriminator as: %s", _gen_out, string(_dis_out));return(0);
   return(result);
}

Taxa de Aprendizado Fixa

Para começar, a taxa de aprendizado fixa é provavelmente a que a maioria dos novos usuários de algoritmos de aprendizado de máquina utiliza, pois é a mais simples. Uma medida padrão pela qual os pesos e vieses de um algoritmo são ajustados a cada iteração de aprendizado, ela não muda ao longo das diferentes épocas de treinamento.

As vantagens de uma taxa fixa decorrem de sua simplicidade. É muito fácil de implementar, pois você tem apenas um valor de ponto flutuante para usar ao longo de todas as épocas, o que também torna a dinâmica do treinamento mais previsível. Isso ajuda a entender melhor todo o processo, além de facilitar a depuração. Além disso, isso gera reprodutibilidade. Em muitas redes neurais, especialmente aquelas inicializadas com pesos aleatórios, os resultados de um teste não são necessariamente reprodutíveis. No nosso caso, ao longo de todos os diferentes formatos de taxa de aprendizado, estamos utilizando um peso inicial padrão de 0,1 e um viés inicial de 0,01. Ao manter esses valores fixos, estamos melhor posicionados para reproduzir os resultados dos nossos testes.

Além disso, uma taxa de aprendizado fixa traz estabilidade no processo inicial de treinamento, pois a taxa não diminui nem se reduz nas fases posteriores, como ocorre com a maioria dos outros formatos de taxa de aprendizado. Os dados encontrados mais tarde nos testes são considerados com o mesmo grau de importância que os dados mais antigos. Isso facilita a comparação e a avaliação quando se está ajustando uma rede para outro hiperparâmetro que não seja a taxa de aprendizado. Isso pode ser, por exemplo, o peso inicial usado pela rede neural. Ao ter uma taxa de aprendizado fixa, uma busca por otimização pode chegar a um resultado significativo mais rapidamente.

O principal problema de uma taxa de aprendizado fixa é a convergência subótima. Há uma preocupação de que, durante o treinamento, o gradiente descendente possa ficar preso em mínimos locais e não convergir de forma ideal. Isso é particularmente importante antes de se estabelecer a taxa de aprendizado fixa ideal. Além disso, há o argumento da baixa adaptação, que segue o consenso geral de que, à medida que as épocas sucessivas de treinamento ocorrem, a necessidade de "aprender" não permanece a mesma. A visão geral é que essa necessidade diminui.

Com essas vantagens e desvantagens, temos o seguinte cenário ao realizar um teste para o ano de 2023 para o par EURJPY no período diário:

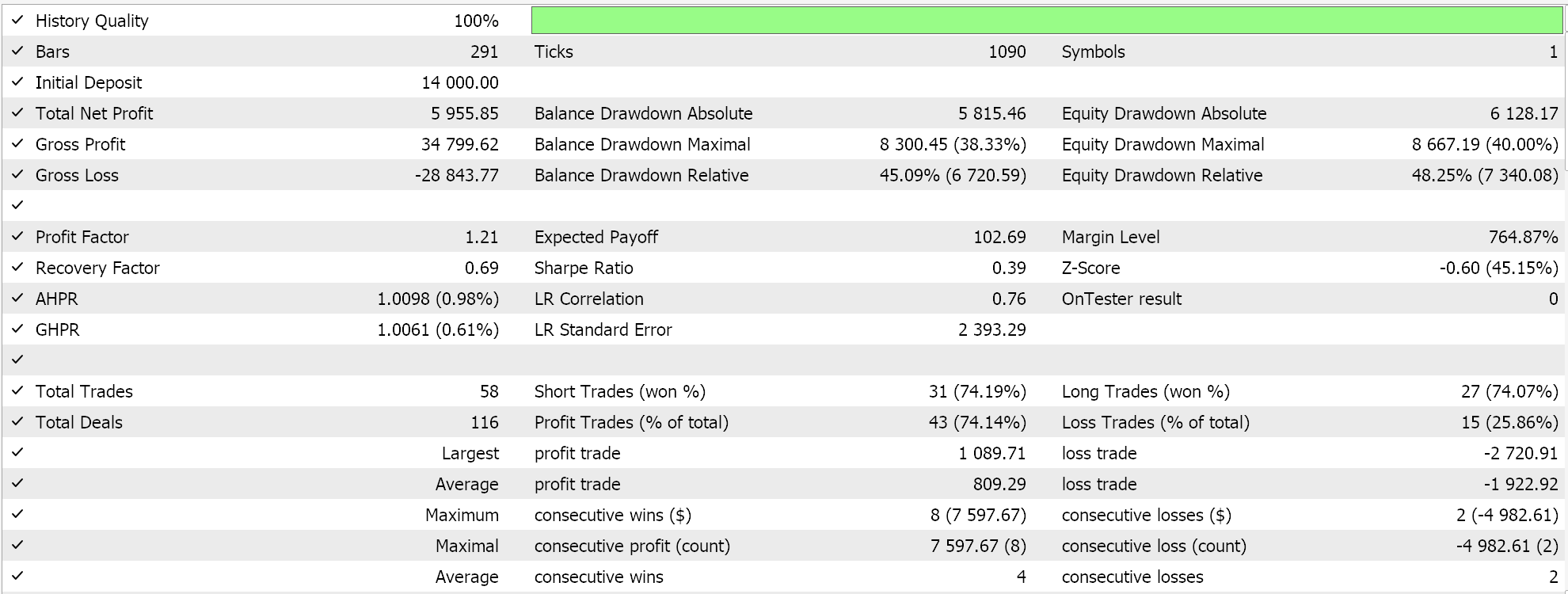
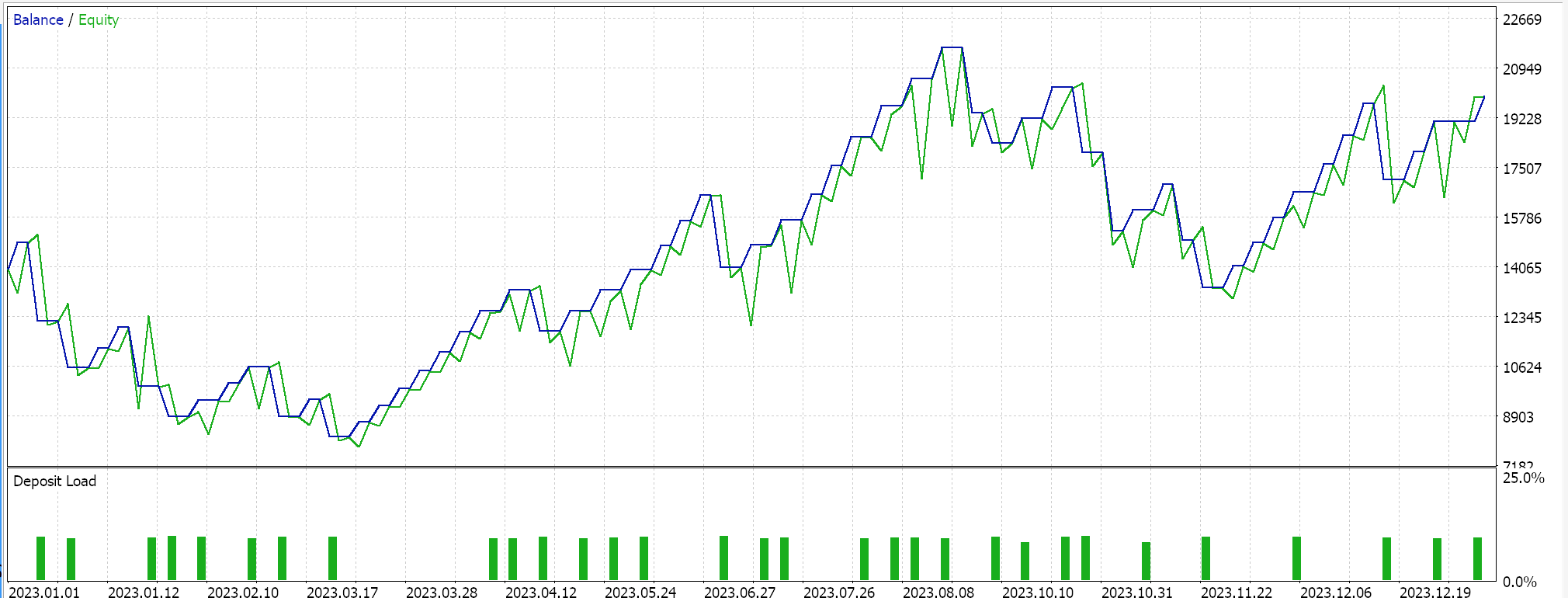
Decaimento em Etapas

A seguir, temos a taxa de aprendizado com decaimento em etapas, que na verdade é uma taxa de aprendizado fixa com dois parâmetros extras que determinam como a taxa inicial fixa será reduzida a cada época subsequente. Isso é implementado da seguinte forma no MQL5:

      if(m_learning_type == LEARNING_STEP_DECAY)
      {  int _epoch_index = int(MathFloor((m_epochs - i) / m_decay_epoch_steps));
         _learning_rate = m_learning_rate * pow(m_decay_rate, _epoch_index);
      }

Então, determinar a taxa de aprendizado em cada época é um processo de duas etapas. Primeiro, precisamos obter o índice da época. Este é simplesmente um índice que mede o quão avançado estamos nas épocas durante uma sessão de treinamento. Seu valor é fortemente influenciado por um segundo parâmetro de entrada, o ‘m_decay_epoch_steps’. Nosso loop for está contando para trás, e não para frente, como normalmente acontece. Portanto, subtraímos o valor atual de i do número total de épocas e, em seguida, realizamos uma divisão de piso (Math-Floor) em relação a esse segundo parâmetro de entrada. O resultado inteiro arredondado serve como um índice de época, que usamos para quantificar o quanto precisamos reduzir a taxa de aprendizado inicial na época atual. Se nosso tamanho de passo (segundo valor de entrada ^nd) for 5, então sempre esperamos e apenas reduzimos a taxa de aprendizado após cada 5 épocas. Se o tamanho do passo for 10, então a redução ocorre após 10 épocas, e assim por diante.

A estratégia geral do decaimento em etapas é reduzir gradualmente a taxa de aprendizado para evitar ‘ultrapassar’ o mínimo e chegar de forma eficiente à solução ideal. O método se destaca por fornecer um equilíbrio entre aprendizado rápido no início e ajuste fino posteriormente. Ele pode ajudar a evitar mínimos locais e pontos de sela na paisagem de perda e muitas vezes leva a uma melhor generalização por meio da redução da taxa de aprendizado (ao contrário da taxa fixa), o que pode ajudar a evitar o overfitting.

Se realizarmos testes como os anteriores para EURJPY no período diário ao longo do ano de 2023, obtemos o seguinte:

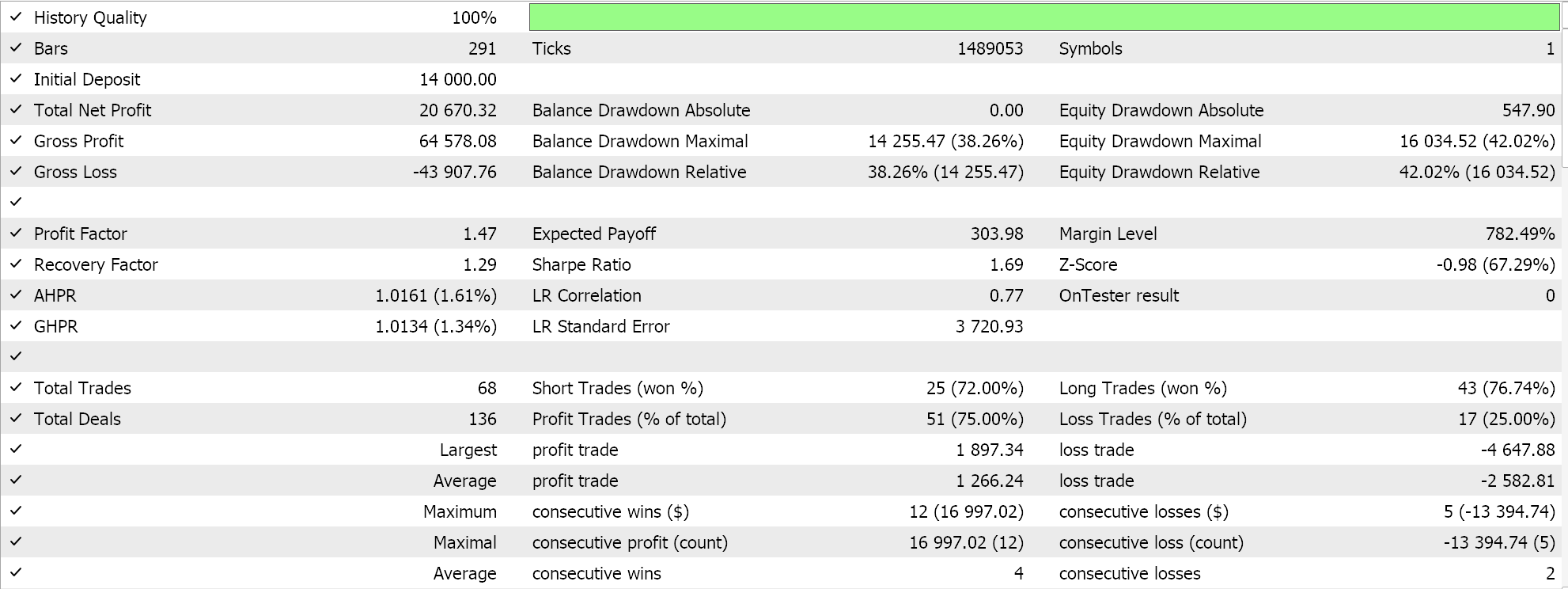
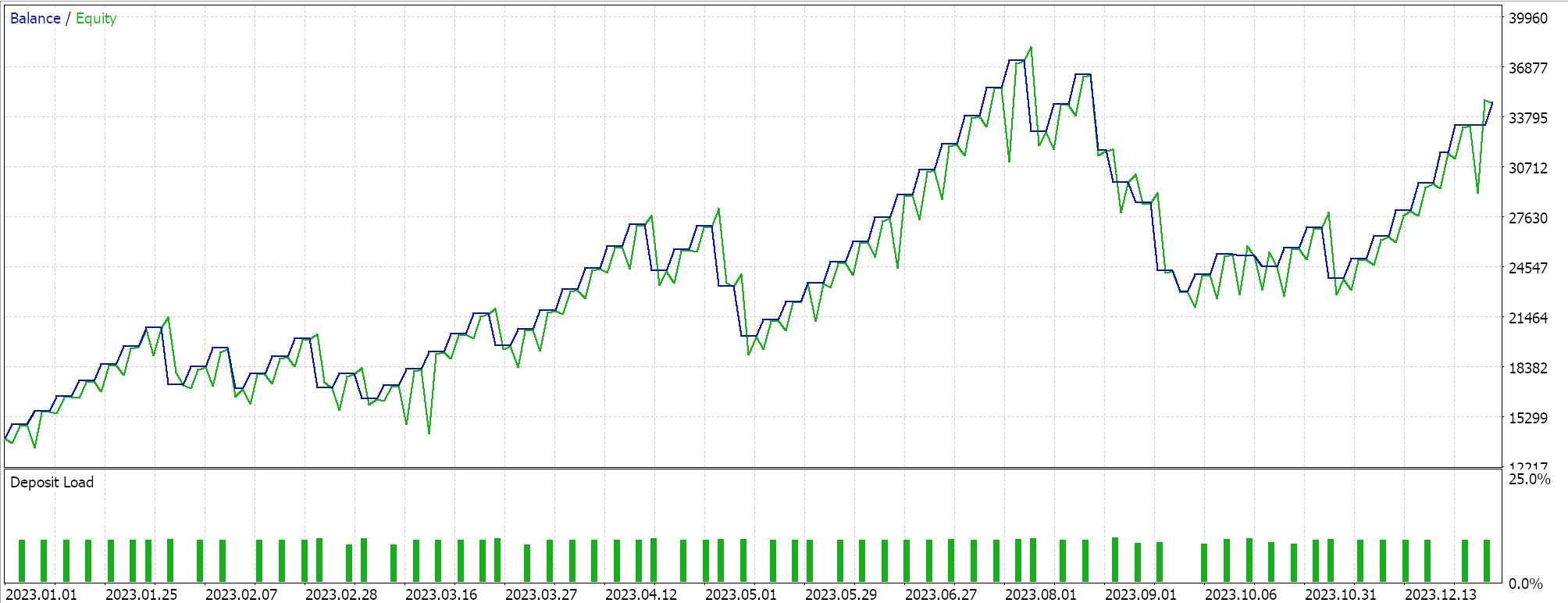
Decaimento Exponencial

A taxa de aprendizado com decaimento exponencial, ao contrário do decaimento em etapas, reduz a taxa de aprendizado de forma mais suave. Lembre-se de que vimos anteriormente como a taxa de aprendizado com decaimento em etapas só é reduzida quando o índice da época aumenta ou após um número pré-definido de passos de época. Com o decaimento exponencial, a redução da taxa de aprendizado ocorre continuamente a cada nova época. Isso é representado pela seguinte fórmula:

Onde

• lr é a taxa de aprendizado
• initial_lr é a taxa de aprendizado inicial
• e é a constante de Euler
• decay_rate e epoch representam seus respectivos valores

Isso seria implementado em MQL5 da seguinte forma:

      else if(m_learning_type == LEARNING_EXPONENTIAL_DECAY)
      {  _learning_rate = m_learning_rate * exp(-1.0 * m_decay_rate * (m_epochs - i + 1));
      }

O decaimento exponencial consegue reduzir a taxa de aprendizado multiplicando-a por um fator de decaimento a cada nova época. Isso garante uma redução mais gradual na taxa de aprendizado quando comparado à abordagem em etapas. As vantagens dessa abordagem gradual estão mais alinhadas com estratégias gerais para reduzir a taxa de aprendizado. Essas vantagens já foram discutidas anteriormente com o método de decaimento em etapas. O que o decaimento exponencial pode fornecer e que falta ao decaimento em etapas é a evitação de quedas súbitas na taxa de aprendizado, que podem desestabilizar o processo de treinamento.

Se realizarmos testes como os anteriores para EURJPY no período diário ao longo do ano de 2023, obtemos os seguintes resultados:

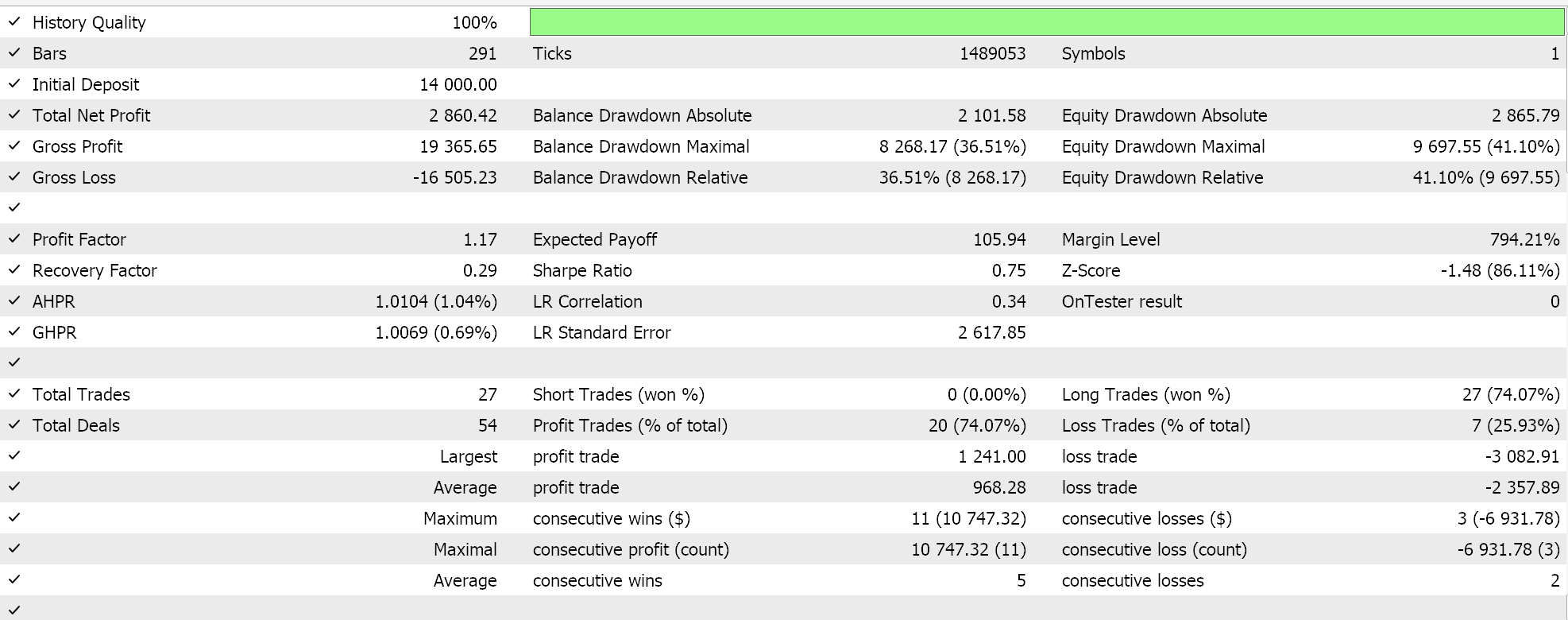
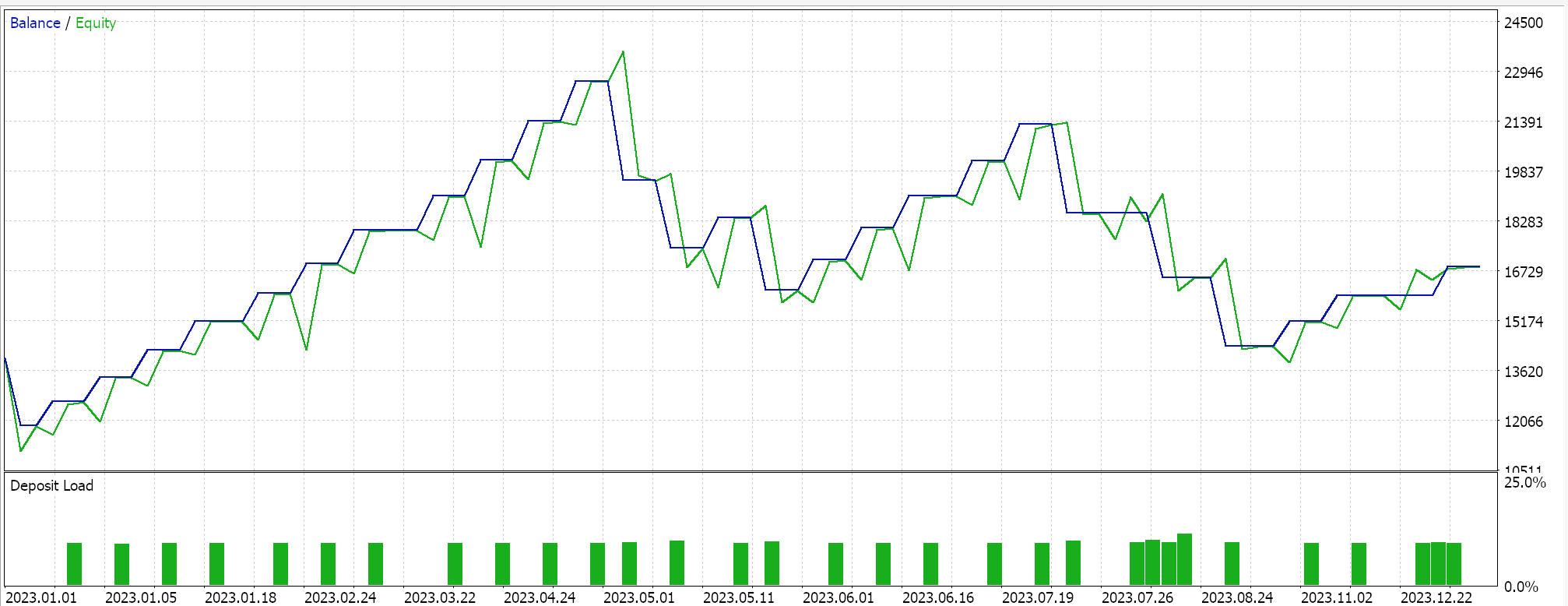
Embora o decaimento exponencial permita uma redução mais suave e gradual na taxa de aprendizado ao revisá-la a cada época, nem todas as reduções ocorrem no mesmo ritmo. No início do treinamento, as reduções na taxa de aprendizado são significativamente maiores, e esses valores diminuem à medida que o treinamento avança para as últimas épocas.

Decaimento Polinomial

Assim como o decaimento exponencial, o decaimento polinomial também reduz a taxa de aprendizado à medida que o treinamento avança. A principal diferença em relação ao decaimento exponencial é que o decaimento polinomial começa reduzindo a taxa de aprendizado lentamente. A taxa de redução aumenta conforme o treinamento se aproxima das últimas épocas do processo. Isso pode ser representado pela seguinte equação:

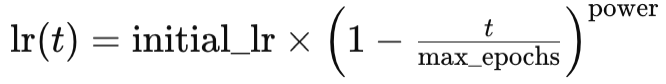
Onde

• lr(t) é a taxa de aprendizado na época t
• initial_lr é a taxa de aprendizado inicial
• t é o índice da época
• max_epochs e power representam seus respectivos valores

A implementação seria a seguinte:

      else if(m_learning_type == LEARNING_POLYNOMIAL_DECAY)
      {  _learning_rate = m_learning_rate * pow(1.0 - ((m_epochs - i) / m_epochs), m_polynomial_power);
      }

O decaimento polinomial introduz o parâmetro de entrada ‘power’ para nossa classe de sinal. Todos os formatos de taxa de aprendizado estão sendo combinados em um único arquivo de classe de sinal, onde os parâmetros de entrada permitem a seleção de uma taxa de aprendizado específica. Esse arquivo de código está anexado no final do artigo. O parâmetro de entrada power do decaimento polinomial é um expoente constante de um fator que usamos para reduzir a taxa de aprendizado com base na época, conforme mostrado na fórmula acima.

O decaimento polinomial, assim como o decaimento exponencial e o decaimento em etapas, reduz suas taxas de aprendizado. O que pode diferenciar o decaimento polinomial desse grupo é, conforme mencionado anteriormente, a rápida redução na taxa de aprendizado ao final do treinamento. Essa redução acelerada no final tende a permitir um ‘ajuste fino’ do processo de treinamento, pois a taxa de aprendizado é mantida o mais alta possível pelo maior tempo possível, sendo reduzida apenas quando as épocas estão se esgotando. Esse ‘ajuste fino’ é alcançado determinando a potência polinomial ideal em vários ciclos de treinamento e, uma vez definida, um processo de aprendizado mais eficiente pode ser esperado.

As vantagens do decaimento polinomial são semelhantes às mencionadas acima para os outros formatos de taxa de aprendizado, concentrando-se principalmente na redução gradual, que proporciona um processo mais suave no geral. O ajuste fino da taxa de aprendizado, além de determinar as taxas ideais ao longo das épocas, também permite o controle do tempo que o processo de treinamento leva. Uma potência polinomial maior pode acelerar o treinamento, enquanto uma potência menor deve desacelerá-lo.

Os testes no par EURJPY no período diário ao longo de 2023 nos fornecem os seguintes resultados:

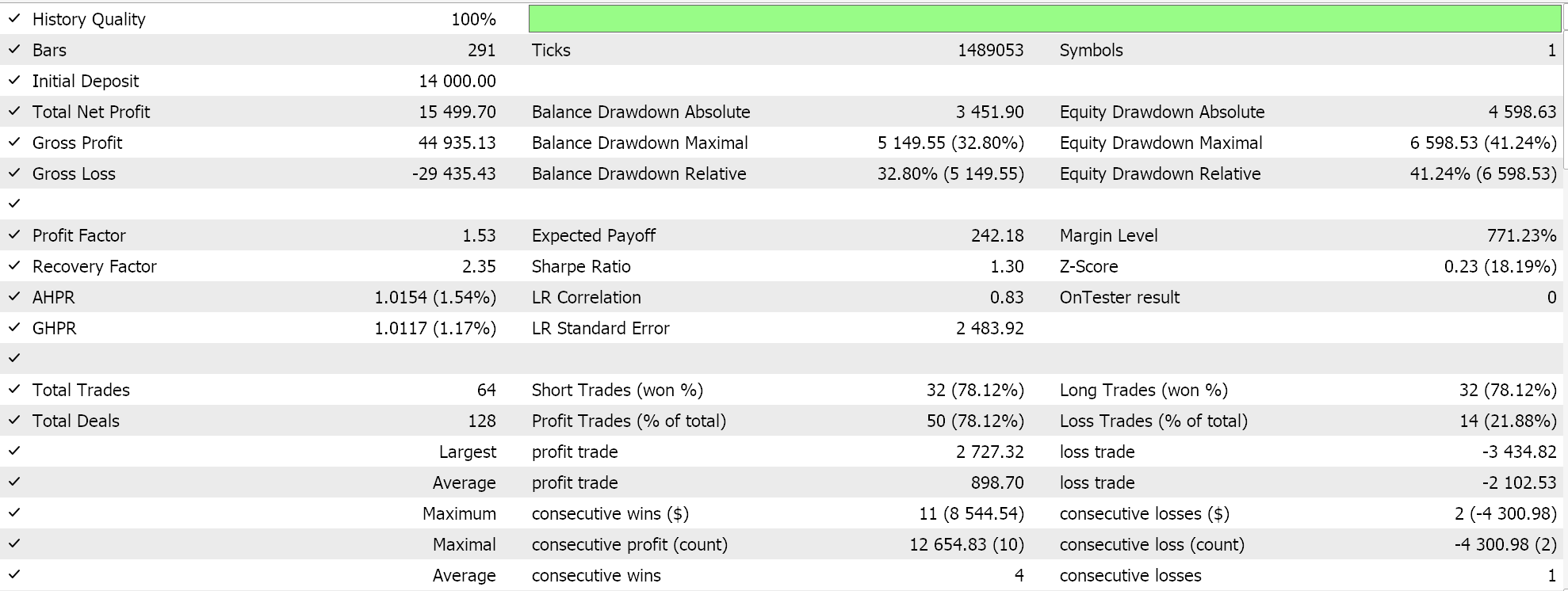
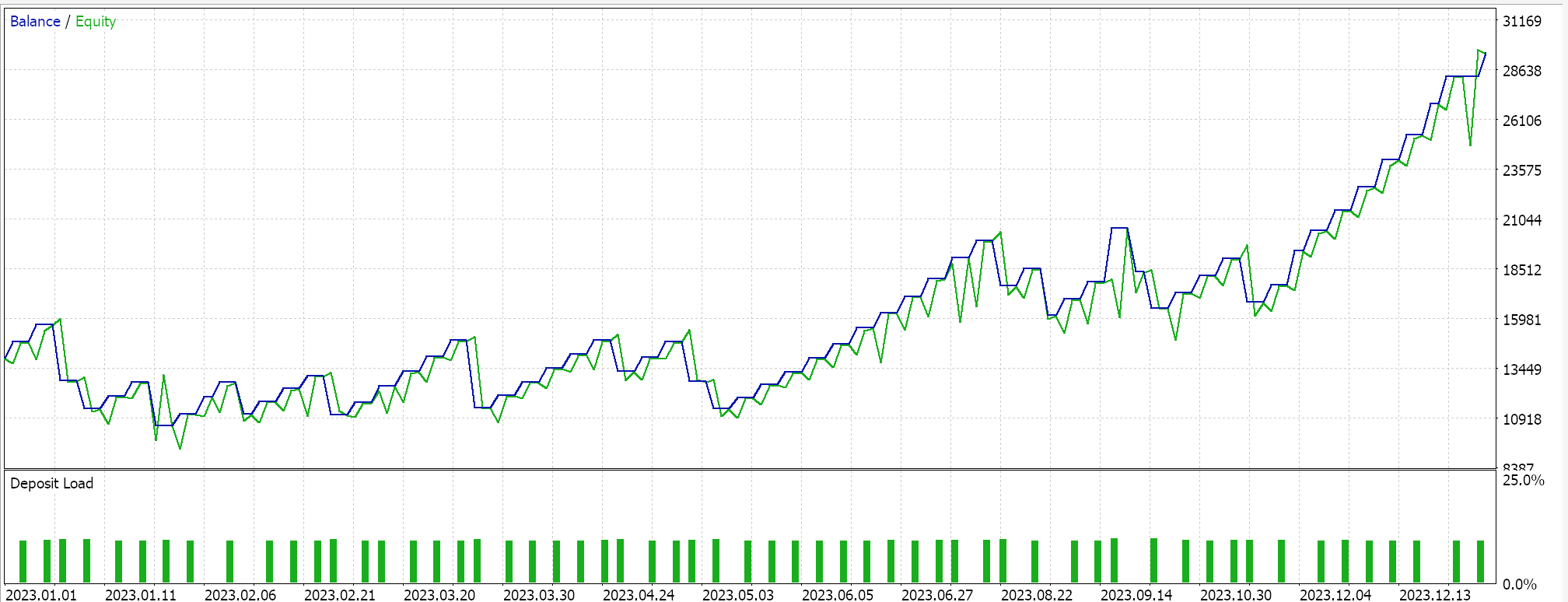
Decaimento Inverso no Tempo

O decaimento inverso no tempo também reduz a taxa de aprendizado em uma base por época através do que é chamado de decaimento temporal. Enquanto acima consideramos uma rápida redução inicial da taxa de aprendizado com o decaimento exponencial, versus uma redução mais lenta com o decaimento polinomial, o decaimento temporal permite uma redução ainda mais lenta da taxa de aprendizado, tornando-o mais adequado que o decaimento polinomial para lidar com grandes conjuntos de dados de treinamento.

A fórmula para o decaimento inverso no tempo é:

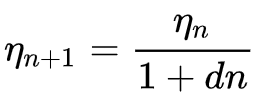
Onde

• ηn+1 é a taxa de aprendizado na época n + 1
• ηn é a taxa de aprendizado anterior na época n
• d é a taxa de decaimento
• e n é o índice da época.

Implementamos isso no MQL5 da seguinte forma:

      else if(m_learning_type == LEARNING_INVERSE_TIME_DECAY)
      {  _learning_rate = m_prior_learning_rate / (1.0 + (m_decay_rate * (m_epochs - i)));
         m_prior_learning_rate = _learning_rate;
      }

Esse algoritmo é ideal para conjuntos de dados de treinamento muito grandes, dada a forma como desacelera a redução da taxa de aprendizado. Ele compartilha a maioria das vantagens mencionadas anteriormente com os outros formatos de taxa de aprendizado. Está incluído aqui como um estudo para compará-lo com as outras taxas de aprendizado quando testado no mesmo símbolo, período de tempo e período de teste. O código-fonte completo está anexado, permitindo que o usuário faça alterações para realizar testes mais elaborados. Se realizarmos um teste seguindo as configurações usadas até agora, obtemos os seguintes resultados:

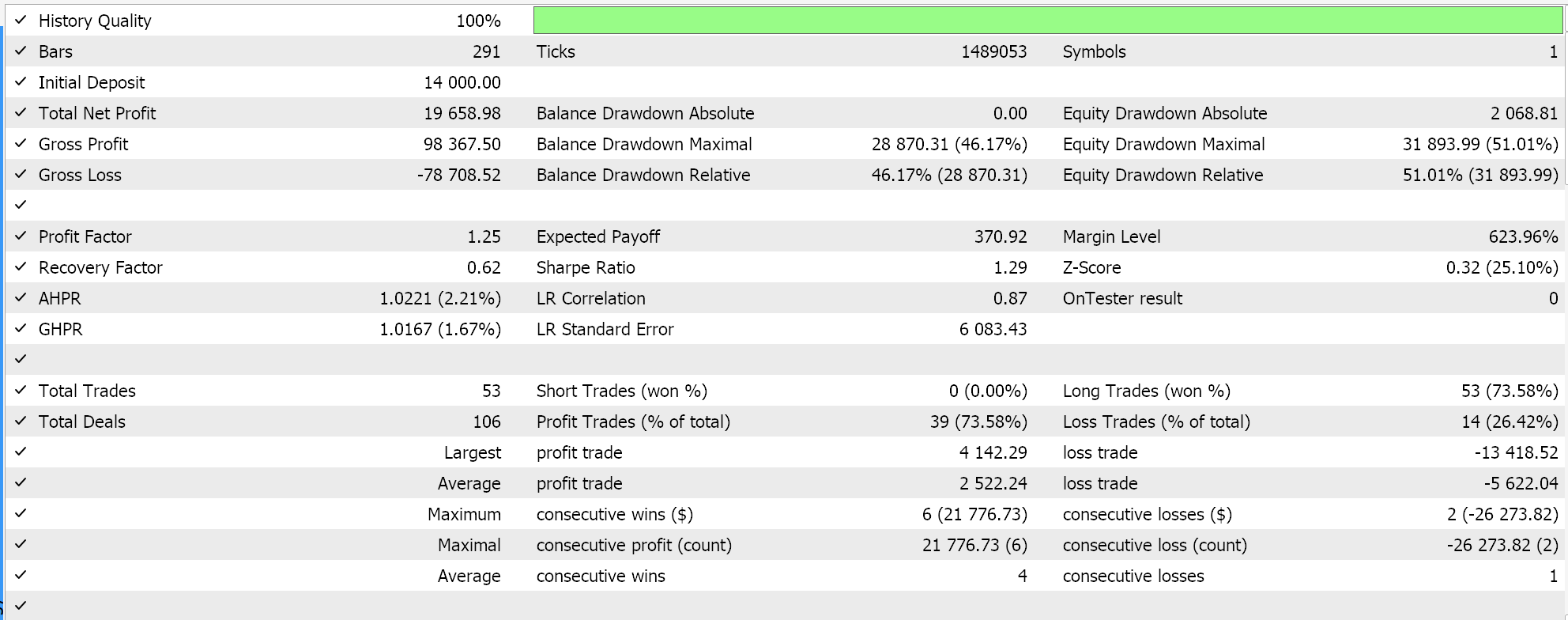
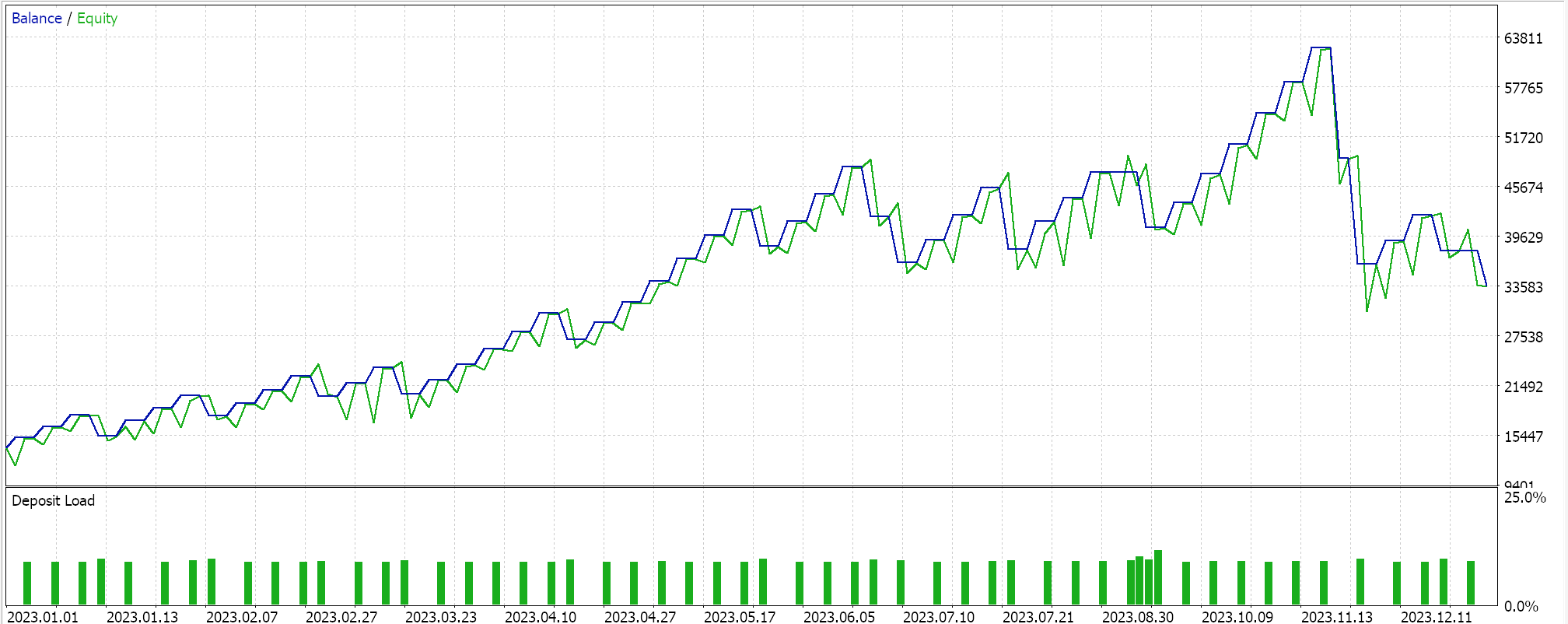
Ajuste Coseno

O agendador de taxa de aprendizado por ajuste coseno também reduz a taxa de aprendizado gradualmente até um mínimo predefinido, seguindo uma função cosseno. O objetivo da redução da taxa de aprendizado é semelhante aos formatos mencionados acima. No entanto, no ajuste coseno, há um mínimo-alvo, e o processo continua sendo reiniciado sempre que a taxa de aprendizado mínima é atingida, até que todas as épocas sejam concluídas.

A fórmula para isso pode ser representada da seguinte forma:

Onde

• lr(t) é a taxa de aprendizado na época t
• initial_lr é a taxa de aprendizado inicial
• t é o índice da época
• T é o número total de épocas
• min_lr é a taxa de aprendizado mínima

A implementação disso em MQL5 pode ser a seguinte:

      else if(m_learning_type == LEARNING_COSINE_ANNEALING)
      {  _learning_rate = m_min_learning_rate + (0.5 * (m_learning_rate - m_min_learning_rate) * (1.0 + MathCos(((m_epochs - i) * M_PI) / m_epochs)));
      }

O ajuste coseno é mais adequado para grandes conjuntos de dados, ainda mais do que o decaimento inverso no tempo. Isso ocorre porque, enquanto o decaimento inverso no tempo posterga quedas significativas na taxa de aprendizado até as últimas épocas, o ajuste coseno permite um ‘reset’ da taxa de aprendizado, restaurando-a ao valor inicial assim que um mínimo predefinido for atingido. Isso é semelhante, mas diferente de outra técnica chamada ‘warm restarts’ (reinícios aquecidos), na qual, em um ciclo de treinamento predefinido, a taxa de aprendizado é restaurada ao seu valor inicial.

Os warm restarts seriam adequados para cenários de treinamento muito grandes, nos quais lotes/ciclos são usados de forma que cada lote seja dividido em épocas, em oposição à abordagem de lote único que temos considerado até agora em todos os formatos de taxa de aprendizado. Quando lotes são usados, o reset ou a restauração da taxa de aprendizado para seu valor original seria realizado automaticamente no final de um determinado lote.

Os resultados dos testes com o formato de lote único para o ajuste coseno nos fornecem o seguinte relatório:

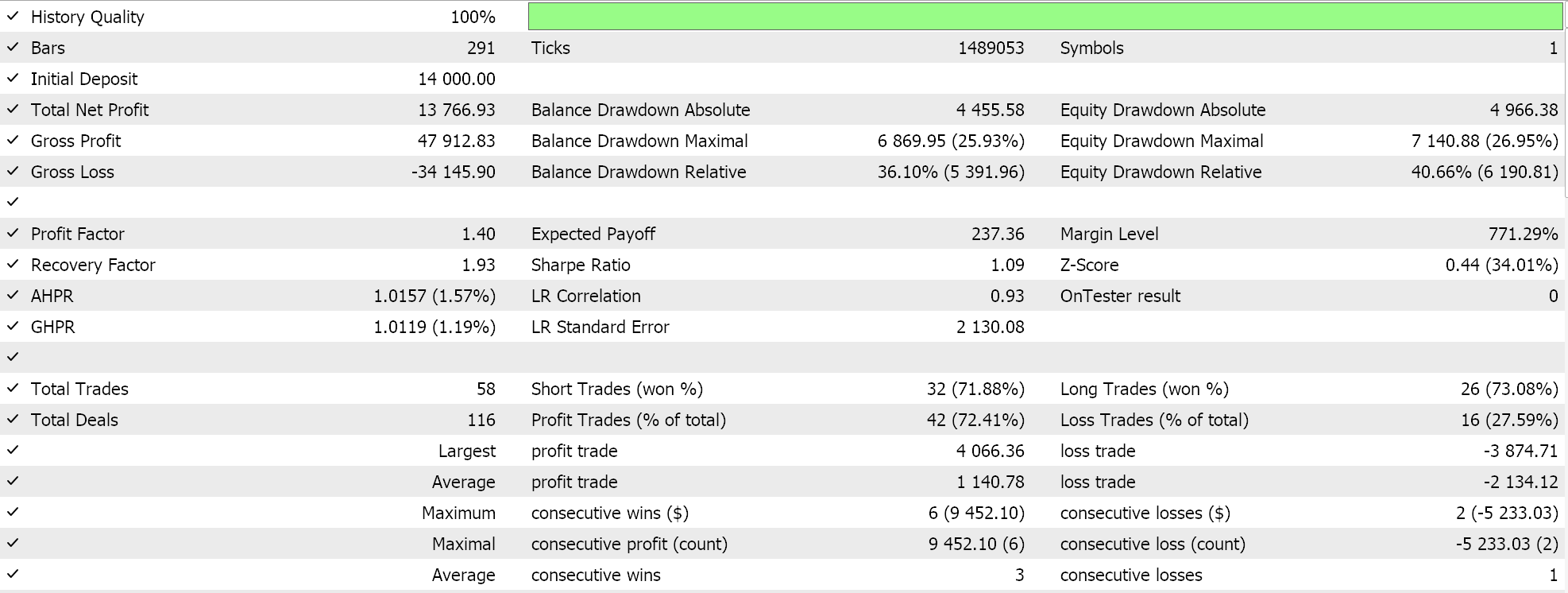
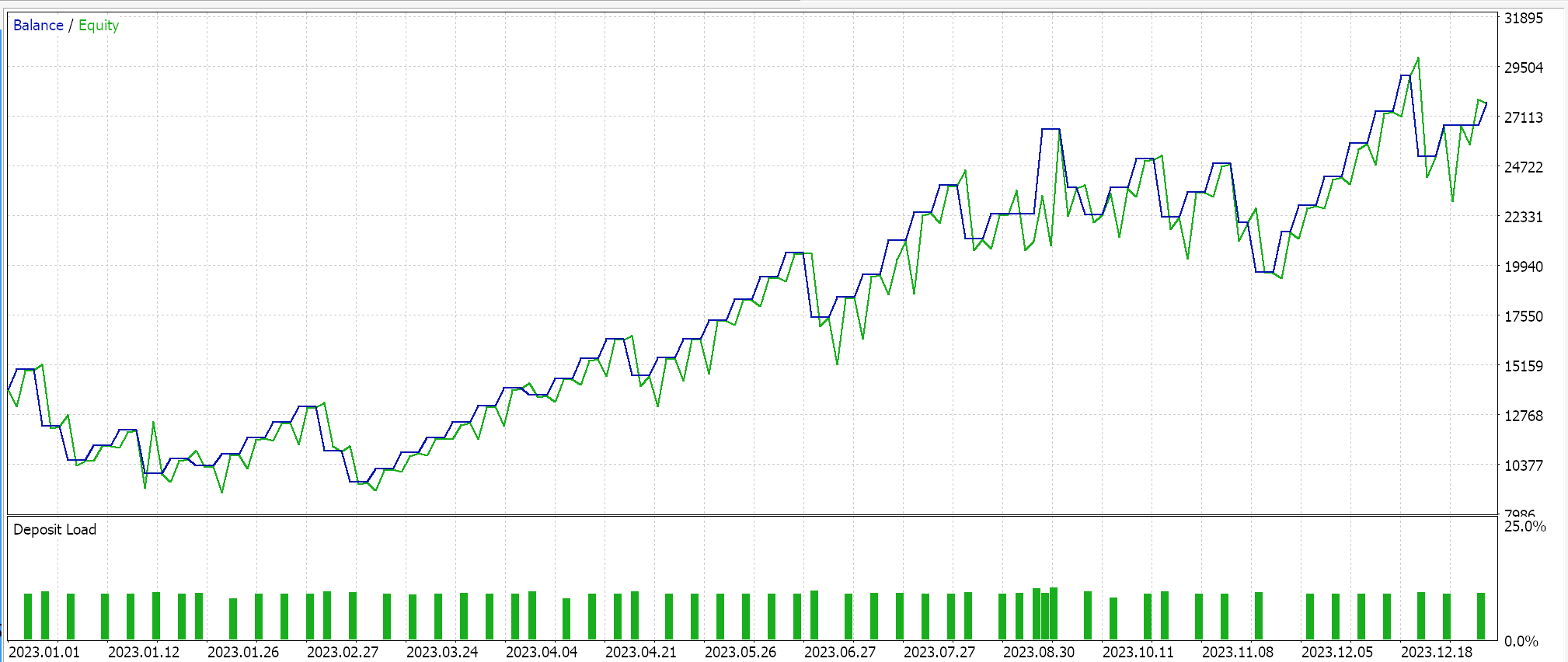
Além disso, o ajuste fino também é possível com o ajuste coseno, pois temos um parâmetro de entrada adicional para a taxa de aprendizado mínima. Dependendo do valor atribuído a essa taxa, não apenas podemos controlar a qualidade/exaustividade do processo de treinamento, mas também determinar quanto tempo o treinamento levará ao longo de todas as épocas. Portanto, dependendo do tamanho dos dados de treinamento enfrentados, isso pode ser altamente significativo.

Nesse sentido, é frequentemente argumentado que o ajuste coseno proporciona um equilíbrio entre exploração e exploração. Exploração refere-se à busca da taxa de aprendizado ideal, especialmente por meio do ajuste fino da taxa mínima de aprendizado; enquanto exploração se refere à obtenção dos melhores pesos e vieses da rede, utilizando as melhores taxas de aprendizado conhecidas. Isso tende a levar a uma melhor generalização do modelo, dada a otimização em duas frentes.

Taxa de Aprendizado Cíclica

A taxa de aprendizado cíclica, diferentemente dos formatos que analisamos até agora, começa aumentando a taxa de aprendizado antes de eventualmente reduzi-la novamente ao mínimo. Isso ocorre em um padrão cíclico. O treinamento, portanto, sempre começa com a taxa de aprendizado mínima em cada ciclo. Ela é guiada pela seguinte fórmula:

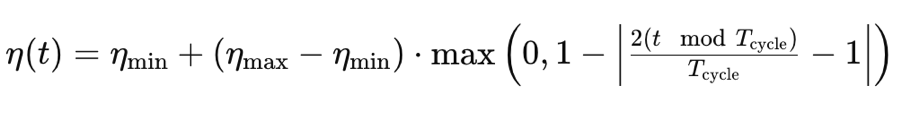
Onde

• η(t) é a taxa de aprendizado na época t
• ηmin é a taxa de aprendizado mínima
• ηmax é a taxa de aprendizado máxima
• Tcycle é o número total de épocas em um determinado lote ou ciclo (estamos testando apenas ciclos únicos)
• (t modTcycle) é o restante da divisão do número de épocas em um ciclo pelo índice da época. Multiplicamos esse valor por 2.

Implementamos isso no MQL5 da seguinte forma:

      else if(m_learning_type == LEARNING_CYCLICAL)
      {  double _x = fabs(((2.0 * fmod(m_epochs - i, m_epochs))/m_epochs) - 1.0);
         _learning_rate = m_min_learning_rate + ((m_learning_rate - m_min_learning_rate) * fmax(0.0, (1.0 - _x)));
      }

Executar testes com essa taxa de aprendizado, mantendo o mesmo símbolo, período de tempo e configurações de período de teste que usamos anteriormente, nos fornece os seguintes resultados:

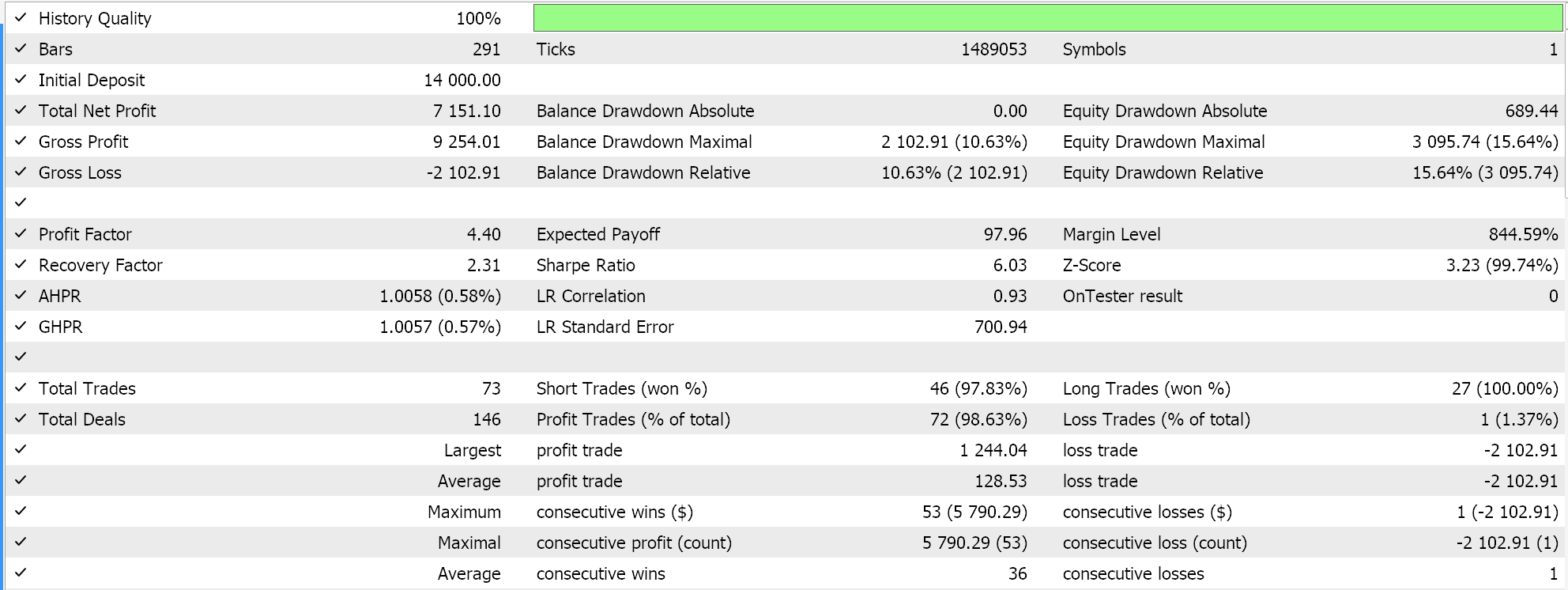
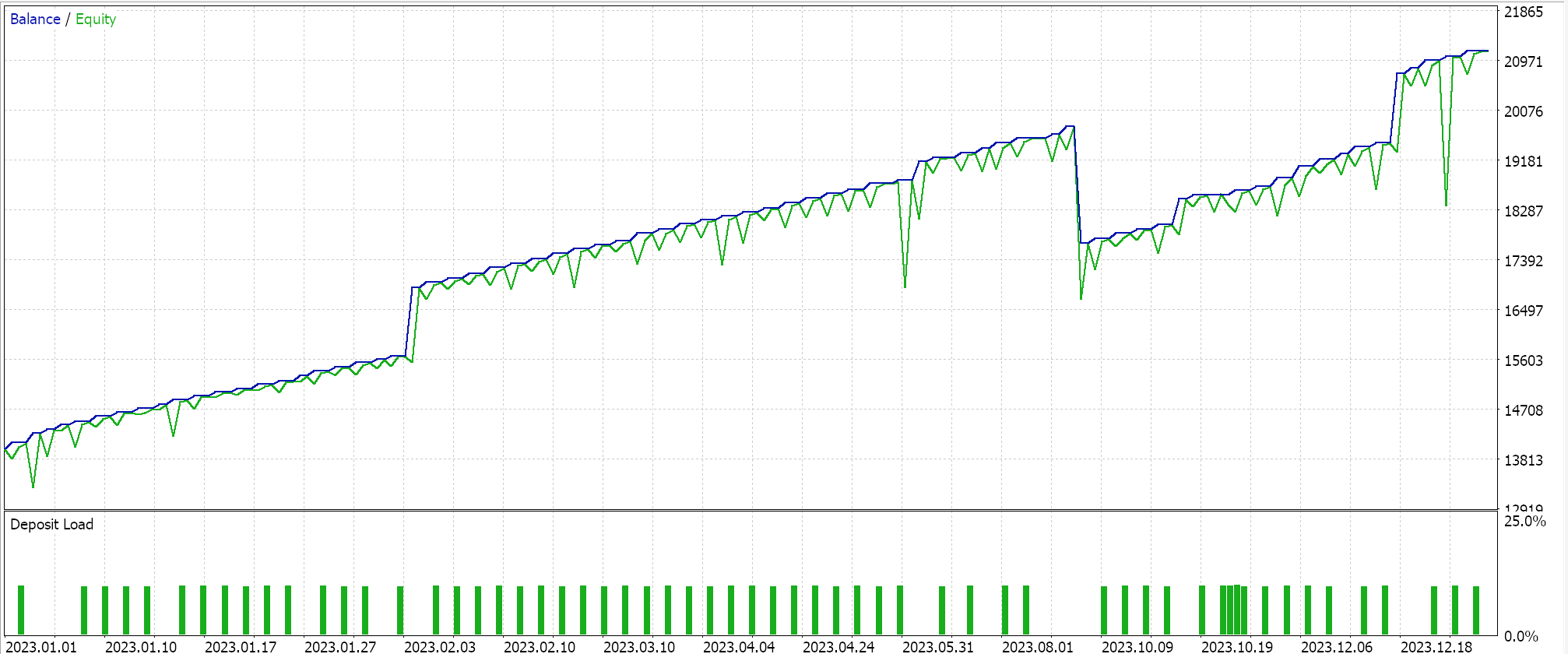
Há outra implementação da taxa de aprendizado cíclica chamada ‘triangular-2’, na qual, mais uma vez, a taxa de aprendizado é inicialmente aumentada antes de ser reduzida ao mínimo. A diferença aqui, no entanto, em relação ao que vimos acima, é que o valor máximo da taxa de aprendizado para o qual a taxa é aumentada continua sendo reduzido a cada ciclo.

Consideraremos esse formato de taxa de aprendizado, bem como formatos adicionais que incluem a taxa de aprendizado adaptativa (que, por si só, é relativamente ampla, pois apresenta diferentes variações), warm restarts e taxas de ciclo único no próximo artigo.

Conclusão

Para concluir, vimos como a alteração apenas da taxa de aprendizado dentro de um algoritmo de aprendizado de máquina, como redes generativas adversárias, pode gerar uma infinidade de resultados diferentes. Fica claro que a taxa de aprendizado é um hiperparâmetro muito sensível. O principal objetivo de algo que pode parecer trivial como uma taxa de aprendizado é chegar aos pesos e vieses da rede mais concretos e desejados. No entanto, fica evidente que o caminho escolhido para chegar a esses pesos e vieses pode variar significativamente, dependendo da taxa de aprendizado utilizada, quando se testa dentro de um tempo e recursos fixos.