Neuronale Netze leicht gemacht (Teil 93): Adaptive Vorhersage im Frequenz- und Zeitbereich (letzter Teil)
222
0
Einführung
Im vorangegangenen Artikel haben wir den ATFNet-Algorithmus kennengelernt, bei dem es sich um ein Ensemble von 2 Zeitreihenprognosemodellen handelt. Eine davon arbeitet im Zeitbereich und konstruiert Vorhersagewerte der untersuchten Zeitreihen auf der Grundlage der Analyse der Signalamplituden. Das zweite Modell arbeitet mit den Frequenzmerkmalen der analysierten Zeitreihe und erfasst deren globale Abhängigkeiten, ihre Periodizität und ihr Spektrum. Die adaptive Zusammenführung zweier unabhängiger Prognosen führt nach Angaben des Autors der Methode zu beeindruckenden Ergebnissen.
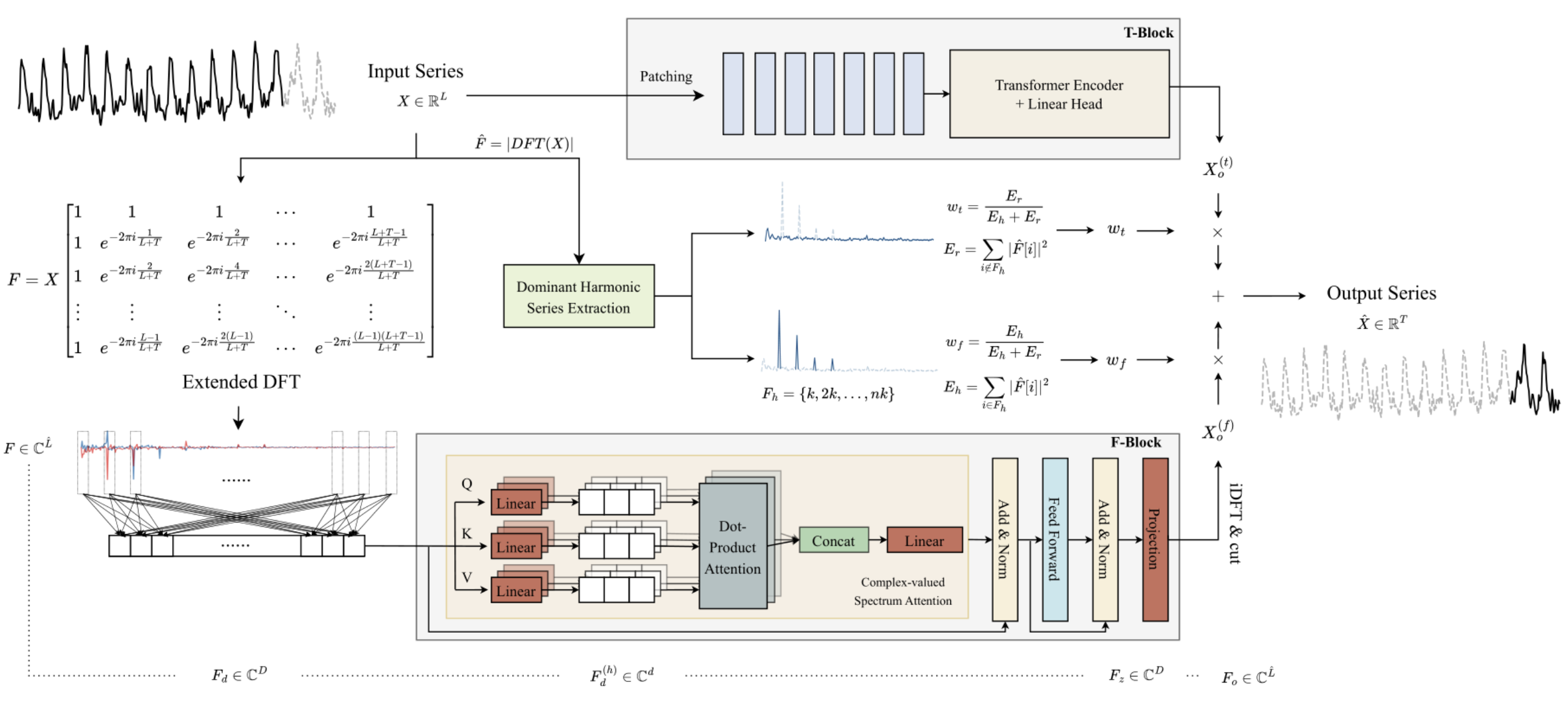
Das Hauptmerkmal des Frequenz-F-Blocks ist eine vollständige Konstruktion des Algorithmus unter Verwendung der Mathematik der komplexen Zahlen. Um diese Anforderung zu erfüllen, haben wir im vorherigen Artikel die Klasse CNeuronComplexMLMHAttention erstellt. Es wiederholt vollständig die mehrschichtigen Transformator Encoder-Algorithmen mit Elementen der mehrköpfigen Selbstbeobachtung. Die integrierte Aufmerksamkeitsklasse, die wir aufgebaut haben, ist die Grundlage des Blocks F. In diesem Artikel werden wir die von den Autoren in der Studie ATFNet vorgeschlagene Konzepte implementieren.
1. Erstellen der Klasse ATFNet
Nachdem wir die Grundlage des Frequenz-Blocks F, die komplexe Aufmerksamkeitsklasse CNeuronComplexMLMHAttention, implementiert haben, gehen wir eine Ebene höher und erstellen die Klasse CNeuronATFNetOCL, in der wir den gesamten ATFNet-Algorithmus implementieren werden.
Ich muss zugeben, dass die Implementierung eines so komplexen Algorithmus wie ATFNet innerhalb einer einzigen neuronalen Schichtklasse vielleicht nicht die optimalste Lösung ist. Aber das sequenzielle neuronale Netzmodell, das wir früher aufgebaut haben, sieht nicht die Möglichkeit vor, die Arbeit mehrerer verschiedener paralleler Prozesse zu organisieren, was genau unser Fall ist: Wir verwenden die Blöcke T und F. Die Implementierung einer solchen Funktionalität wird weitere globale Änderungen erfordern. Daher beschloss ich, eine Lösung mit minimalen Kosten zu schaffen, d.h. den gesamten Algorithmus als eine neuronale Schichtklasse zu implementieren. Die Struktur der Klasse CNeuronATFNetOCL ist unten dargestellt.
class CNeuronATFNetOCL : public CNeuronBaseOCL { protected: uint iHistory; uint iForecast; uint iVariables; uint iFFT; //--- T-Block CNeuronBatchNormOCL cNorm; CNeuronTransposeOCL cTranspose; CNeuronPositionEncoder cPositionEncoder; CNeuronPatching cPatching; CLayer caAttention; CLayer caProjection; CNeuronRevINDenormOCL cRevIN; //--- F-Block CBufferFloat *cInputs; CBufferFloat cInputFreqRe; CBufferFloat cInputFreqIm; CNeuronBaseOCL cInputFreqComplex; CBufferFloat cMainFreqWeights; CNeuronBaseOCL cNormFreqComplex; CBufferFloat cMeans; CBufferFloat cVariances; CNeuronComplexMLMHAttention cFreqAtteention; CNeuronBaseOCL cUnNormFreqComplex; CBufferFloat cOutputFreqRe; CBufferFloat cOutputFreqIm; CBufferFloat cOutputTimeSeriasRe; CBufferFloat cOutputTimeSeriasIm; CBufferFloat cOutputTimeSeriasReGrad; CBufferFloat cReconstructInput; CBufferFloat cForecast; CBufferFloat cReconstructInputGrad; CBufferFloat cForecastGrad; CBufferFloat cZero; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool ComplexNormalize(void); virtual bool ComplexUnNormalize(void); virtual bool ComplexNormalizeGradient(void); virtual bool ComplexUnNormalizeGradient(void); virtual bool MainFreqWeights(void); virtual bool WeightedSum(void); virtual bool WeightedSumGradient(void); virtual bool calcReconstructGradient(void); public: CNeuronATFNetOCL(void) {}; ~CNeuronATFNetOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronATFNetOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *net, float tau); virtual void SetOpenCL(COpenCLMy *obj); virtual CBufferFloat *getWeights(void); };
In der vorgestellten Klassenstruktur CNeuronATFNetOCL sind die vier internen Variablen zu beachten:
- iHistory: die Tiefe der analysierten Geschichte;
- iForecast: Planungshorizont;
- iVariablen: die Anzahl der analysierten Variablen (unitäre Zeitreihen);
- iFFT: die Größe des schnellen Fourier-Zerlegungstensors (DFT).
Wie wir bereits gesehen haben, erfordert der Algorithmus DFT, dass die Größe des anfänglichen Datenvektors gleich einer der Potenzen von „2" ist. Daher erweitern wir den ursprünglichen Datentensor mit Nullwerten auf die erforderliche Größe.
Die internen Objekte der Methode sind in zwei Blöcke unterteilt, je nachdem, zu welchem Block des ATFNet-Algorithmus sie gehören. Wir werden bei der Implementierung des Algorithmus ihren Zweck und die Funktionalität der Klassenmethoden berücksichtigen.
Alle internen Objekte werden statisch deklariert, und daher können wir den Konstruktor und Destruktor der Klasse CNeuronATFNetOCL leer lassen.
1.1 Initialisierung von Objekten
Die Initialisierung der internen Objekte unserer neuen Klasse wird in der Methode Init durchgeführt. Hier treffen wir auf die erste Konsequenz unserer Entscheidung, den gesamten ATFNet-Algorithmus in einer Klasse zu implementieren: Wir müssen eine große Anzahl von Parametern vom Aufrufer übergeben.
Innerhalb der Klasse CNeuronATFNetOCL müssen wir zwei parallele mehrschichtige Modelle erstellen, die Aufmerksamkeitsmechanismen sowohl im Zeit-Block T als auch im Frequenz-Block F verwenden. Für jedes der Modelle müssen wir die Architektur festlegen.
Um dieses Problem zu lösen, haben wir beschlossen, wenn immer möglich „universelle" Parameter zu verwenden, d.h. Parameter, die von beiden Modellen gleichermaßen verwendet werden können. Nun, wir haben Parameter zur Beschreibung des Eingangs- und Ausgangstensors: die Tiefe der analysierten Historie, die Anzahl der einheitlichen Zeitreihen und den Planungshorizont. Diese Parameter werden gleichermaßen in den Blöcken T und F verwendet.
Außerdem sind beide Modelle um den Encoder des Transformators herum aufgebaut und nutzen die mehrköpfige Self-Attention-Architektur mit mehreren Schichten. Wir haben uns entschieden, in beiden Blöcken die gleiche Anzahl von Aufmerksamkeitsköpfen und Encoder-Ebenen zu verwenden.
Wir müssen jedoch zusätzliche Parameter für die Datensegmentierungsschicht übergeben, die im Block Tverwendet wird und keine Entsprechung im Block F hat. Um die Anzahl der Methodenparameter nicht zu sehr zu erhöhen, habe ich mich für ein Array mit 3 Elementen entschieden. Das erste Element dieses Arrays enthält die Fenstergröße eines Segments, und das zweite Element enthält den Schritt dieses Fensters im Quelldatenpuffer. In das letzte Element des Arrays schreiben wir die Größe eines Patches am Ausgang der Datensegmentierungsschicht.
bool CNeuronATFNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
Im Methodenkörper rufen wir wie üblich die gleichnamige Initialisierungsmethode der übergeordneten Klasse auf. Bitte beachten Sie, dass wir bei der Parent-Class-Methode die Schichtgröße als das Produkt aus der Anzahl der analysierten Variablen (unitäre Zeitreihen) und dem Planungshorizont festlegen. Mit anderen Worten, wir erwarten, dass die Ausgabe der Schicht CNeuronATFNetOCL ein fertiges Ergebnis der vorhergesagten Fortsetzung der analysierten Zeitreihe sein wird.
Nach erfolgreicher Initialisierung der abgeleiteten Objekte speichern wir wichtige Architekturparameter in Variablen.
iHistory = MathMax(history, 1); iForecast = forecast; iVariables = variables;
Dann berechnen wir die Größe des Tensors für die schnelle Fourier-Zerlegung. Die Autoren von ATFNet schlagen eine erweiterte Fourier-Zerlegung vor, die die Frequenzmerkmale der vollständigen Zeitreihe anhand von historischen und prognostizierten Daten bestimmt.
uint size = iHistory + iForecast; int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) < size) power++; iFFT = uint(MathPow(2, power));
Der nächste Schritt besteht darin, die internen Objekte unserer Klasse zu initialisieren. Beginnen wir mit der erwarteten Darstellung der Ausgangsdaten. Da unser Modell von der Analyse einheitlicher Zeitreihen im Zeit- und Frequenzbereich ausgeht, erwarten wir eine Matrix einheitlicher Zeitreihen als Eingabe für unsere Schicht. CNeuronATFNetOCL liefert am Ausgang eine ähnliche Karte mit vorhergesagten Werten.
Ein weiterer Punkt ist die Normalisierung der Daten. Beide Blöcke des Modells verwenden eine Normalisierung der Eingabedaten. Der Unterschied besteht darin, dass der Block T die Normalisierung im Zeitbereich und der Block F im Frequenzbereich vornimmt. Daher habe ich mich bei dieser Implementierung dafür entschieden, nicht normalisierte Daten in die Ebene einzuspeisen. Die Normalisierung und umgekehrte Addition der stochastischen Merkmale erfolgt innerhalb der einzelnen Blöcke entsprechend den entsprechenden Dimensionen.
Um die Lesbarkeit und Transparenz des Codes zu erhöhen, werden wir die internen Objekte nach Blöcken ihrer Verwendung und in der Reihenfolge des konstruierten Algorithmus initialisieren. Beginnen wir mit dem Block T.
Wie bereits erwähnt, werden nicht normalisierte Daten in die Ebene eingegeben. Daher müssen wir die gewonnenen Daten zunächst in eine vergleichbare Form bringen.
//--- T-Block if(!cNorm.Init(0, 0, OpenCL, iHistory * iVariables, batch, optimization)) return false;
Die Autoren der Methode ATFNet verwenden keine Positionsdatenkodierung im Frequenzbereich, sondern verwenden sie bei der Analyse von Daten im Zeitbereich. Fügen wir eine Ebene der Positionskodierung hinzu.
if(!cPositionEncoder.Init(0, 1, OpenCL, iVariables, iHistory, optimization, batch)) return false;
Beim Aufbau einer Datensegmentierungsschicht haben wir eine Art Datentransposition in den Algorithmus eingebaut. Nun müssen wir die Eingabe vorbereiten, bevor wir sie an die Schicht CNeuronPatching weiterleiten. Um diese Operation durchzuführen, fügen wir eine Datenumsetzungsschicht hinzu.
if(!cTranspose.Init(0, 2, OpenCL, iHistory, iVariables, optimization, batch)) return false; cTranspose.SetActivationFunction(None);
Als Nächstes müssen wir die Anzahl der Felder am Ausgang der Segmentierungsschicht auf der Grundlage der Fenstergröße eines Segments und seines Schritts berechnen, die wir in den Methodenparametern aus dem externen Programm erhalten.
uint count = (iHistory - patch[0] + 2 * patch[1] - 1) / patch[1];
Nach der Durchführung der notwendigen Vorbereitungsarbeiten wird die Datensegmentierungsschicht initialisiert.
if(!cPatching.Init(0, 3, OpenCL, patch[0], patch[1], patch[2], count, iVariables, optimization, batch)) return false;
Bei der Konstruktion der Methode PatchTST haben wir den Conformer als einen Aufmerksamkeitsblock. Hier werden wir die gleiche Lösung verwenden. Im nächsten Schritt erstellen wir die erforderliche Anzahl von verschachteltenCNeuronConformer-Schichten.
caAttention.SetOpenCL(OpenCL); for(uint l = 0; l < layers; l++) { CNeuronConformer *temp = new CNeuronConformer(); if(!temp) return false; if(!temp.Init(0, 4 + l, OpenCL, patch[2], 32, heads, iVariables, count, optimization, batch)) { delete temp; return false; } if(!caAttention.Add(temp)) { delete temp; return false; } }
Auf den Aufmerksamkeitsblock, der die Eingangszeitreihen analysiert, folgt ein Block aus 3 Faltungsschichten, der die Vorhersage nachfolgender Daten in der gesamten Planungstiefe im Kontext einzelner einheitlicher Zeitreihen vornimmt.
int total = 3; caProjection.SetOpenCL(OpenCL); uint window = patch[2] * count; for(int l = 0; l < total; l++) { CNeuronConvOCL *temp = new CNeuronConvOCL(); if(!temp) return false; if(!temp.Init(0, 4+layers+l, OpenCL, window, window, (total-l)*iForecast, iVariables, optimization, batch)) { delete temp; return false; } temp.SetActivationFunction(TANH); if(!caProjection.Add(temp)) { delete temp; return false; } window = (total - l) * iForecast; }
Beachten Sie, dass wir in jeder Schicht die gleiche Anzahl von Sequenzelementen angeben, die der Anzahl der einheitlichen Zeitreihen in den analysierten Zeitreihen entspricht. In jeder nachfolgenden Schicht nimmt die Anzahl der Filter am Ausgang der neuronalen Schicht ab und entspricht der angegebenen Vorhersagetiefe in der letzten Schicht.
Am Ausgang des Blocks T ergänzen wir die Prognosewerte um statistische Parameter der Eingangszeitreihe unter Verwendung der Schicht CNeuronRevINDenormOCL.
if(!cRevIN.Init(0, 4 + layers + total, OpenCL, iForecast * iVariables, 1, cNorm.AsObject())) return false;
Zu diesem Zeitpunkt haben wir alle internen Objekte, die mit dem Block Tzusammenhängen, mit der Zeitbereichsvorhersage initialisiert. Nun gehen wir zur Arbeit mit Objekten der Frequenz F-Block über.
Nach dem ATFNet-Algorithmus werden die in den F-Block eingespeisten Eingangsdaten mithilfe der schnellen Fourier-Zerlegung (DFT) in den Frequenzbereich umgewandelt. Wie Sie sich erinnern, schreibt die Implementierung des DFT-Algorithmus, die wir zuvor erstellt haben, das Frequenzspektrum in zwei Datenpuffer. Eine für den realen Teil des Spektrums, die zweite für den imaginären Teil.
//--- F-Block if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL)) return false; if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL)) return false;
Um die weitere Verarbeitung zu erleichtern, werden wir die Spektrumsinformationen in einem Puffer zusammenfassen.
if(!cInputFreqComplex.Init(0, 0, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
Wir müssen auch einen Puffer vorbereiten, um den Anteil der dominanten Frequenz zu schreiben. Dabei ist zu beachten, dass wir die dominante Frequenz für jede unitäre Zeitreihe separat bestimmen.
if(!cMainFreqWeights.BufferInit(iVariables, 0) || !cMainFreqWeights.BufferCreate(OpenCL)) return false;
Der Input für unsere Schicht sind Rohdaten, die ganz unterschiedliche Spektren von uniformen Zeitreihen erzeugen. Um die Spektren vor der Weiterverarbeitung in eine vergleichbare Form zu bringen, empfehlen die Autoren der Methode eine Normierung der Frequenzverläufe. Die normalisierten Daten werden in Puffern der Schichten cNormFreqComplex gespeichert.
if(!cNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
In diesem Fall speichern wir die statistischen Merkmale des ursprünglichen Spektrums in den entsprechenden Datenpuffern.
if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL)) return false; if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL)) return false;
Wir werden die Frequenzcharakteristiken der vorbereiteten Eingangsdaten mit Hilfe des komplexen Aufmerksamkeitsblocks verarbeiten. Im vorherigen Artikel haben wir eine große Implementierung der Klasse CNeuronComplexMLMHAttention durchgeführt. Jetzt müssen wir nur noch das interne Objekt der angegebenen Klasse initialisieren.
if(!cFreqAtteention.Init(0, 2, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch)) return false;
Gemäß dem Algorithmus müssen wir nach der Verarbeitung des Eingangsspektrums im komplexen Aufmerksamkeitsblock inverse Verfahren durchführen. Zunächst fügen wir dem verarbeiteten Spektrum statistische Indikatoren der Eingangsfrequenzmerkmale hinzu.
if(!cUnNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
Trennen wir den realen und den imaginären Teil des Spektrums.
if(!cOutputFreqRe.BufferInit(iFFT*iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL)) return false; if(!cOutputFreqIm.BufferInit(iFFT*iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL)) return false;
Dann geben wir die Daten an den temporären Bereich zurück.
if(!cOutputTimeSeriasRe.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasRe.BufferCreate(OpenCL)) return false; if(!cOutputTimeSeriasIm.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasIm.BufferCreate(OpenCL)) return false;
Für den Backpropagation-Durchgang erstellen wir einen Gradientenpuffer für den realen Teil der Zeitreihe.
if(!cOutputTimeSeriasReGrad.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasReGrad.BufferCreate(OpenCL)) return false;
Bitte beachten Sie, dass wir keinen Gradientenpuffer für den imaginären Teil der Zeitreihe erstellen. Der Punkt ist, dass für eine Zeitreihe die Zielwerte des Imaginärteils „0" sind. Daher ist der Fehlergradient des Imaginärteils gleich den Werten des Imaginärteils mit umgekehrtem Vorzeichen. Im Backpropagation-Durchgang können wir die Ergebnisse des Feedforward-Durchgangs als Puffer für den Imaginärteil der verarbeiteten Zeitreihe verwenden.
Bitte beachten Sie, dass wir nach der inversen DFT (iDFT) eine verarbeitete vollständige Zeitreihe erhalten wollen, die aus einer Rekonstruktion der Eingangsdaten und Prognosewerten für einen bestimmten Planungshorizont besteht. Um den benötigten Teil der Prognosewerte zu extrahieren, unterteilen wir die vollständige Zeitreihe in zwei Puffer: rekonstruierte Daten und Prognosewerte.
if(!cReconstructInput.BufferInit(iHistory*iVariables, 0) || !cReconstructInput.BufferCreate(OpenCL)) return false; if(!cForecast.BufferInit(iForecast*iVariables, 0) || !cForecast.BufferCreate(OpenCL)) return false;
Hinzufügen von Puffern für die entsprechenden Fehlergradienten.
if(!cReconstructInputGrad.BufferInit(iHistory*iVariables, 0) || !cReconstructInputGrad.BufferCreate(OpenCL)) return false; if(!cForecastGrad.BufferInit(iForecast*iVariables, 0) || !cForecastGrad.BufferCreate(OpenCL)) return false;
Bitte beachten Sie, dass die Autoren von den ATFNe vorgeschlagene Methode keine Analyse der Abweichungen der rekonstruierten Daten von den Eingangswerten der analysierten Zeitreihen vorsieht. Wir fügen diese Funktion hinzu, um eine feinere Abstimmung des komplexen Aufmerksamkeitsblocks zu erreichen. Ein besseres Verständnis der zu analysierenden Daten kann die Vorhersagequalität des Modells verbessern.
Zusätzlich wird ein Puffer mit Nullwerten angelegt, der zum Auffüllen fehlender Werte in den Eingabedaten und Fehlergradienten verwendet wird.
if(!cZero.BufferInit(iFFT*iVariables, 0) || !cZero.BufferCreate(OpenCL)) return false; //--- return true; }
Vergessen Sie nicht, die Arbeitsabläufe in jeder Phase zu überwachen. Nachdem die Initialisierung aller deklarierten Objekte abgeschlossen ist, geben wir den logischen Wert der Ausführung der Methodenoperationen an den Aufrufer zurück.
1.2 Vorwärtsdurchgang
Nachdem die Initialisierung der Klassenobjekte abgeschlossen ist, gehen wir zur Konstruktion des Vorwärtsdurchgangs-Algorithmus über. Beginnen wir mit der Erstellung zusätzlicher Kernel in OpenCL.
Denken Sie zunächst an die Normalisierung der Frequenzgang-Spektren von uniformen Zeitreihen. Wenn wir zuvor implementierte Algorithmen zur Normalisierung von Echtdaten verwenden, kann dies die Daten stark verzerren. Daher müssen wir die Datennormalisierung in einem komplexen Bereich implementieren. Wir implementieren diese Funktionsweise im Kernel von ComplexNormalize. In den Kernel-Parametern werden wir Zeiger auf 4 Datenpuffer und die Größe der unitären Sequenz übergeben. Wir werden diesen Kernel in einem eindimensionalen Problemraum im Zusammenhang mit unitären Zeitreihenspektren verwenden.
__kernel void ComplexNormalize(__global float2 *inputs, __global float2 *outputs, __global float2 *means, __global float *vars, int dimension) { if(dimension <= 0) return;
Beachten Sie die Angabe von Datenpuffern. Die Eingangs-, Ausgangs- und Mitteldatenpuffer sind vom Vektortyp float2. Wir haben uns entschieden, diese Art von Daten auf der Seite von OpenCL für die Arbeit mit komplexen Größen zu verwenden. Es gibt jedoch auch einen Dispersionspuffer, der mit einem realen Typ float deklariert ist. Streuungen zeigen die Standardabweichung eines Wertes vom Mittelwert. Der Abstand zwischen zwei Punkten ist eine reelle Größe.
Im Hauptteil der Methode überprüfen wir die erhaltene Dimension des normalisierten Vektors. Sie muss natürlich größer als „0" sein. Anschließend identifizieren wir den aktuellen Thread im Aufgabenraum, bestimmen den Offset in den Datenpuffern und erstellen eine komplexe Darstellung der Dimensionalität der zu analysierenden Sequenz.
size_t n = get_global_id(0); const int shift = n * dimension; const float2 dim = (float2)(dimension, 0);
Als Nächstes organisieren wir eine Schleife, in der wir den Durchschnittswert des analysierten Spektrums ermitteln.
float2 mean = 0; for(int i = 0; i < dimension; i++) { float2 val = inputs[shift + i]; if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) inputs[shift + i] = (float2)0; else mean += val; } means[n] = mean = ComplexDiv(mean, dim);
Das erhaltene Ergebnis wird sofort im entsprechenden Element des Durchschnittswertpuffers gespeichert.
In der nächsten Phase organisieren wir eine Schleife zur Bestimmung der Streuung der analysierten Sequenz.
float variance = 0; for(int i = 0; i < dimension; i++) variance += pow(ComplexAbs(inputs[shift + i] - mean), 2); vars[n] = variance = sqrt((isnan(variance) || isinf(variance) ? 1.0f : variance / dimension));
Hier sind zwei Punkte zu beachten. Erstens: Obwohl wir den Durchschnittswert im externen Datenpuffer speichern, verwenden wir bei der Durchführung von Operationen den Wert der lokalen Variablen, da der Zugriff auf ein Pufferelement im globalen Speicher des Kontexts viel langsamer ist als der Zugriff auf eine lokale Kernelvariable.
Der zweite Punkt ist methodisch: Bei der Berechnung der Varianz einer Folge komplexer Zahlen quadrieren wir im Gegensatz zu reellen Zahlen den Absolutwert der Abweichung eines Elements der komplexen Folge vom Mittelwert. Es ist der Absolutwert einer komplexen Größe, der den Abstand zwischen Punkten im 2-dimensionalen Raum der Real- und Imaginärteile angibt. Eine einfache Differenz komplexer Größen zeigt uns nur eine Verschiebung der Koordinaten.
In der letzten Phase der Kerneloperation organisieren wir die letzte Schleife, in der wir die Daten des Eingangsspektrums normalisieren. Wir schreiben die erhaltenen Werte in die entsprechenden Elemente des Ergebnispuffers.
float2 v=(float2)(variance, 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexDiv((inputs[shift + i] - mean), v); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; outputs[shift + i] = val; } }
Hier arbeiten wir auch mit lokalen Variablen wie Mittelwert und Standardabweichung.
Und wir werden sofort den umgekehrten Normalisierungskern ComplexUnNormalize erstellen, in dem wir die extrahierten statistischen Indikatoren des Eingangsspektrums zurückgeben.
__kernel void ComplexUnNormalize(__global float2 *inputs, __global float2 *outputs, __global float2 *means, __global float *vars, int dimension) { if(dimension <= 0) return;
Dieser Kernel erhält den gleichen Parametersatz von 4 Zeigern auf Datenpuffer und eine Variable. Wir planen auch, den Kernel in einem 1-dimensionalen Aufgabenraum für die Anzahl der uniformen Zeitreihen laufen zu lassen.
Im Hauptteil des Kernels identifizieren wir den Thread im Aufgabenbereich und definieren Offsets in den Datenpuffern.
size_t n = get_global_id(0); const int shift = n * dimension;
Wir laden die statistischen Variablen aus den Puffern und wandeln die Standardabweichung sofort in einen komplexen Wert um.
float v= vars[n]; float2 variance=(float2)((v > 0 ? v : 1.0f), 0) float2 mean = means[n];
Dann organisieren wir die einzige Datenumwandlungsschleife in diesem Kernel.
for(int i = 0; i < dimension; i++) { float2 val = ComplexMul(inputs[shift + i], variance) + mean; if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; outputs[shift + i] = val; } }
Die erhaltenen Werte werden in die entsprechenden Elemente des Ergebnispuffers geschrieben.
Um die oben erstellten Kernel auf der Seite des Hauptprogramms aufzurufen, verwenden wir die Methoden ComplexNormalize und ComplexUnNormalize. Der Algorithmus für ihre Konstruktion unterscheidet sich nicht von den zuvor betrachteten Methoden für das Enqueuing der Kernel des Programms OpenCL. Daher werden wir uns nicht mit diesen Methoden befassen. In jedem Fall sind sie im Anhang zu finden.
Um die Ergebnisse der Zeit- und Frequenzprognose adaptiv zu kombinieren, benötigen wir außerdem Einflusskoeffizienten. Die Autoren der Methode ATFNet schlagen vor, sie anhand des Anteils der dominanten Frequenz am Gesamtspektrum zu bestimmen. Dementsprechend werden wir auf der Seite von OpenCL zwei Kernel für das Programm erstellen:
- MainFreqWeight — bestimmt den Anteil der dominanten Frequenz;
- WeightedSum — Berechnung der gewichteten Summe der Vorhersagen im Frequenz- und Zeitbereich.
Wir planen beide Kernel in einem 1-dimensionalen Aufgabenraum entsprechend der Anzahl der analysierten uniformen Zeitreihen.
In den Kernelparametern von MainFreqWeight übergeben wir die Zeiger auf zwei Datenpuffer (Frequenzmerkmale und Ergebnisse) und die Dimension der analysierten Reihen.
__kernel void MainFreqWeight(__global float2 *freq, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
Im Kernelkörper identifizieren wir den aktuellen Thread im Aufgabenbereich und bestimmen die Offsets in den Datenpuffern. Danach bereiten wir lokale Variablen vor.
float max_f = 0; float total = 0; float energy;
Als Nächstes führen wir eine Schleife durch, um die Energie der dominanten Frequenz und des gesamten Spektrums zu bestimmen.
for(int i = 0; i < dimension; i++) { energy = ComplexAbs(freq[shift + i]); total += energy; max_f = fmax(max_f, energy); }
Um die Kernel-Operationen zu vervollständigen, dividieren wir die Energie der dominanten Frequenz durch die Gesamtenergie des Spektrums. Der resultierende Wert wird im entsprechenden Element des Ausgabepuffers gespeichert.
weight[n] = max_f / (total > 0 ? total : 1); }
Der Algorithmus des Kerns WeightedSum zur Bestimmung der gewichteten Summe von Zeit- und Frequenzbereichsprognosen ist recht einfach. In den Parametern erhält der Kernel 4 Zeiger auf Datenpuffer und die Dimension des Vektors einer Sequenz (in unserem Fall die Vorhersagetiefe).
__kernel void WeightedSum(__global float *inputs1, __global float *inputs2, __global float *outputs, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
Im Kernelkörper identifizieren wir den aktuellen Thread im eindimensionalen Aufgabenraum und bestimmen die Offsets in den Datenpuffern: Dann erstellen wir eine Schleife zur gewichteten Summierung der Elemente. Die Ergebnisse der Operationen werden in das entsprechende Element des Ergebnispuffers geschrieben.
float w = weight[n]; for(int i = 0; i < dimension; i++) outputs[shift + i] = inputs1[shift + i] * w + inputs2[shift + i] * (1 - w); }
Um die Kernel in die Ausführungswarteschlange auf der Seite des Hauptprogramms zu stellen, erstellen wir gleichnamige Methoden. Sie finden diese Codes in der Anlage.
Nach Abschluss der vorbereitenden Arbeiten gehen wir zur Konstruktion der Methode des Vorwärtsdurchgangs feedForward unserer Klasse CNeuronATFNetOCL über. In den Parametern dieser Methode, wie auch in der ähnlichen Methode der übergeordneten Klasse, erhalten wir einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, das in diesem Fall als Ausgangsdaten für die nachfolgenden Operationen dient.
bool CNeuronATFNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false;
Im Hauptteil der Methode wird zunächst die Relevanz des empfangenen Zeigers geprüft. Hier speichern wir auch einen Zeiger auf den Ergebnispuffer der erhaltenen neuronalen Schicht in der internen Variable des aktuellen Objekts.
if(cInputs != NeuronOCL.getOutput())
cInputs = NeuronOCL.getOutput();
Als Nächstes führen wir zunächst Vorhersageoperationen für die nachfolgenden Daten der analysierten Zeitreihen im Zeitbereich durch. Zunächst normalisieren wir die erhaltenen Daten.
//--- T-Block if(!cNorm.FeedForward(NeuronOCL)) return false;;
Dann fügen wir die Positionskodierung hinzu
if(!cPositionEncoder.FeedForward(cNorm.AsObject())) return false;
und transponieren den resultierenden Tensor und teilen die Daten in Felder auf.
if(!cTranspose.FeedForward(cPositionEncoder.AsObject())) return false; if(!cPatching.FeedForward(cTranspose.AsObject())) return false;
Die vorbereiteten Daten durchlaufen den Aufmerksamkeitsblock.
int total = caAttention.Total(); CNeuronBaseOCL *prev = cPatching.AsObject(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *att = caAttention.At(i); if(!att.FeedForward(prev)) return false; prev = att; }
Und es wird die Vorhersage der nachfolgenden Werte durchgeführt.
total = caProjection.Total(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj.FeedForward(prev)) return false; prev = proj; }
Am Ausgang des Blocks T werden die statistischen Werte der Eingangszeitreihen zu den Prognosewerten addiert.
if(!cRevIN.FeedForward(prev)) return false;
Nachdem wir die vorhergesagten Werte im Zeitbereich erhalten haben, gehen wir zur Arbeit mit dem Frequenzbereich über. Zunächst wandeln wir die erhaltenen Zeitreihen in ein Spektrum von Frequenzmerkmalen um. Hierfür verwenden wir den Algorithmus FFT.
//--- F-Block if(!FFT(cInputs, cInputs, GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), false)) return false;
Nachdem wir zwei Puffer für den Real- und den Imaginärteil des Frequenzspektrums erhalten haben, kombinieren wir sie zu einem einzigen Tensor.
if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(), 1, 1, iFFT * iVariables)) return false;
Beachten Sie, dass wir bei der Verkettung für beide Datenpuffer eine Fenstergröße von 1 Element verwenden. So erhält man einen Tensor, bei dem der Real- und der Imaginärteil der entsprechenden Frequenzcharakteristik eng beieinander liegen.
Wir normalisieren den resultierenden Tensor der Eingangsfrequenz,
if(!ComplexNormalize()) return false;
bestimmen den Anteil der dominanten Frequenz
if(!MainFreqWeights()) return false;
und leiten die vorbereiteten Frequenzdaten durch den Aufmerksamkeitsblock. Hier müssen wir nur die Feed-Forward-Pass-Methode der im vorigen Artikel erstellten mehrschichtigen komplexen Aufmerksamkeitsklasse aufrufen.
if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject())) return false;
Nach erfolgreicher Ausführung der Operationen des Aufmerksamkeitsblocks geben wir die statistischen Parameter der Eingangsreihenfrequenz an die verarbeiteten Daten zurück.
if(!ComplexUnNormalize()) return false;
Zerlegen wir den Frequenzspektrumstensor in seine reellen und imaginären Teile.
if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables)) return false;
Wir transformieren das Frequenzspektrum zurück in eine Zeitreihe.
if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), true)) return false;
Ich denke, wir sollten die oben genannten Vorgänge des Blocks F erklären. Auf den ersten Blick mag es seltsam erscheinen, eine große Anzahl von Transformationen einer Zeitreihe in Frequenzgänge vorzunehmen, diese zu normalisieren und dann inverse Operationen durchzuführen, die die Daten in dieselbe Zeitreihe zurückführen, nur um Aufmerksamkeitsoperationen durchzuführen. Außerdem haben alle diese Operationen, mit Ausnahme der Aufmerksamkeit, keine trainierbaren Parameter und sollten theoretisch die ursprüngliche Zeitreihe zurückgeben. Aber es geht nur um den Aufmerksamkeitsblock.
Ich möchte Sie daran erinnern, dass die Autoren der Methode vorgeschlagen haben, die erweiterte diskrete Fourier-Transformation zu verwenden. In der Praxis verwenden wir einfach eine komplexe Exponentialbasis für eine DFT einer vollständigen Zeitreihe. Bei der Umwandlung der ursprünglichen Zeitreihe in ihr Frequenzmerkmal haben wir jedoch keine vorhergesagten Werte und ersetzen sie einfach durch Nullwerte. Daher wird die Ausführung einer inversen DFT erwartungsgemäß Vorhersagewerte nahe „0" liefern, was nicht adäquat ist. Deshalb bringen wir die Spektren von uniformen Zeitreihen in eine vergleichbare Form, indem wir sie normalisieren. Indem wir sie im Aufmerksamkeitsblock miteinander vergleichen, versuchen wir, dem Modell beizubringen, die fehlenden Daten der analysierten Frequenzmerkmale wiederherzustellen.
So erwarten wir am Ausgang des komplexen Aufmerksamkeitsblocks modifizierte und gegenseitig konsistente Spektren von Frequenzmerkmalen einheitlicher vollständiger Zeitreihen mit wiederhergestellten fehlenden Daten. Durch die Wiederherstellung der Zeitreihen aus den modifizierten Spektren können wir Prognosewerte der analysierten Zeitreihen erhalten, die von Null abweichen.
Um die Vorwärtsdurchgangs-Operationen abzuschließen, müssen wir lediglich die vorhergesagten Werte aus der vollständigen Zeitreihe extrahieren
if(!DeConcat(GetPointer(cReconstructInput), GetPointer(cForecast), GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasRe), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables)) return false;
und die Vorhersagen im Zeit- und Frequenzbereich unter Berücksichtigung des Signifikanzkoeffizienten addieren.
//--- Output if(!WeightedSum()) return false; //--- return true; }
Vergessen wir dabei nicht, die Ergebnisse der Maßnahmen in jeder Phase zu überwachen. Nachdem die Operationen der Methode abgeschlossen sind, geben wir das logische Ergebnis aller Operationen an den Aufrufer zurück.
1.3 Fehlergradientenverteilung
Nach der Durchführung des Vorwärtsdurchgangs muss der Fehlergradient auf alle Trainingsparameter des Modells verteilt werden. In unserer neuen Klasse sind sie sowohl in den Blöcken T und auch F. Daher müssen wir einen Mechanismus zur Weitergabe des Fehlergradienten durch die Blöcke T und F implementieren. Dann müssen wir den Fehlergradienten aus den beiden Strömen kombinieren und den resultierenden Gradienten an die vorherige Schicht weitergeben.
Wie beim Vorbereitende müssen wir vor der Erstellung der Methode calcInputGradients einige vorbereitende Arbeiten durchführen. Während des Vorwärtsdurchgangs haben wir auf der Seite von OpenCL einen Kernel für die Normalisierung und die umgekehrte Rückgabe der statistischen Verteilungswerte erstellt: ComplexNormalize und ComplexUnNormalize. Im Rückwärtsdurchgang müssen wir durch die angegebenen Operationen ComplexNormalizeGradient bzw. ComplexUnNormalizeGradient die Kerne für die Fehlergradientenverteilung erstellen.
Im Kernel der Fehlergradientenverteilung wird durch den Frequenznormalisierungsblock lediglich der erhaltene Fehlergradient durch die Standardabweichung des entsprechenden Spektrums geteilt.
__kernel void ComplexNormalizeGradient(__global float2 *inputs_gr, __global float2 *outputs_gr, __global float *vars, int dimension) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension; //--- float v = vars[n]; float2 variance = (float2)((v > 0 ? v : 1.0f), 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexDiv(outputs_gr[shift + i], variance); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; inputs_gr[shift + i] = val; } }
Ich muss sagen, dass dies ein ziemlich vereinfachter Ansatz ist, um dieses Problem zu lösen. Hier nehmen wir den Mittelwert und die Standardabweichung als Konstanten. Sie sind in der Tat Funktionen, und nach den Regeln des Gradientenabstiegs müssen wir auch ihren Einfluss berücksichtigen und den Fehlergradienten auf die beeinflussenden Elemente des Modells übertragen. Wie die Praxis jedoch zeigt, ist der Einfluss dieser Elemente auf die Ausgangsdaten recht gering. Um die Kosten für die Modellschulung zu senken, lassen wir diese Operationen weg.
Der Kernel für die Gradientenverteilung durch Daten-Denormalisierungsoperationen ist ähnlich, mit dem einzigen Unterschied, dass wir hier den resultierenden Fehlergradienten mit der Standardabweichung multiplizieren.
__kernel void ComplexUnNormalizeGradient(__global float2 *inputs_gr, __global float2 *outputs_gr, __global float *vars, int dimension) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension; //--- float v = vars[n]; float2 variance = (float2)((v > 0 ? v : 1.0f), 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexMul(outputs_gr[shift + i], variance); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; inputs_gr[shift + i] = val; } }
Als Nächstes müssen wir einen Kernel implementieren, um den Gesamtfehlergradienten auf die Vorhersageblöcke im Zeit- und Frequenzbereich zu verteilen. Wir implementieren diese Funktionalität in den Kernl von WeightedSumGradient. In den Parametern erhält dieser Kernel Zeiger auf 4 Datenpuffer und 1 Parameter, ähnlich wie der entsprechende Kernel des Vorwärtsdurchgangs.
__kernel void WeightedSumGradient(__global float *inputs_gr1, __global float *inputs_gr2, __global float *outputs_gr, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
Im Hauptteil des Kernels identifizieren wir wie üblich den aktuellen Thread im eindimensionalen Aufgabenbereich und bestimmen den Offset in Datenpuffern. Danach werden wir lokale Gewichtungsvariablen für die Frequenz- und Zeitreihenprognosen vorbereiten.
float w = weight[n]; float w1 = 1 - weight[n];
Dann erstellen wir eine Schleife, um den Fehlergradienten in den entsprechenden Datenpuffern weiterzugeben.
for(int i = 0; i < dimension; i++) { float grad = outputs_gr[shift + i]; inputs_gr1[shift + i] = grad * w; inputs_gr2[shift + i] = grad * w1; } }
Die oben genannten Fehlergradientenausbreitungskerne werden in die Ausführungswarteschlange innerhalb der entsprechenden Methoden auf der Hauptprogrammseite gestellt. Sie können sich mit dem Code dieser Methoden im Anhang vertraut machen.
Ein weiterer Punkt, dem wir Aufmerksamkeit schenken sollten, ist die Berechnung des Fehlergradienten der rekonstruierten Zeitreihe historischer Werte. Wir werden diese Funktionalität in der Methode calcReconstructGradient implementieren.
Obwohl die Operationen auf der Kontextseite OpenCL durchgeführt werden, erstellen wir zur Durchführung der angegebenen Operationen keinen neuen Kernel. Stattdessen wird ein vorgefertigter Kernel verwendet, der den Fehlergradienten auf der Grundlage der Zielwerte bestimmt. Wir müssen nur eine Methode erstellen, um den Kernel in die Ausführungswarteschlange zu stellen, indem wir die Datenpuffer unseres Blocks F verwenden.
Der von uns verwendete Kernel läuft in einem eindimensionalen Aufgabenraum entsprechend der Anzahl der Elemente des Tensors. In unserem Fall ist die Größe des analysierten Vektors gleich dem Produkt aus der Tiefe der analysierten Geschichte und der Anzahl der einheitlichen Zeitreihen.
bool CNeuronATFNetOCL::calcReconstructGradient(void) { uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = iHistory * iVariables;
Unsere Zieldaten umfassen die Werte der ursprünglichen Daten, die wir während des Vorwärtsdurchgangs von der vorherigen neuronalen Schicht erhalten haben. Während des Vorwärtsdurchgangs haben wir einen Zeiger auf den benötigten Datenpuffer gespeichert.
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_t, cInputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Wir bestimmen den Fehlergradienten für die rekonstruierten Daten aus dem bearbeiteten Spektrum
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_o, cReconstructInput.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
und schreiben die Ergebnisse der Operationen in den Gradientenpuffer der wiederhergestellten Daten.
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_ig, cReconstructInputGrad.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Im Vorwärtsdurchlauf haben wir keine Aktivierungsfunktionen verwendet.
if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_activation, (int)None)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Wir stellen den Kernel in die Ausführungswarteschlange, prüfen das Ergebnis der Operationen und schließen die Methode ab, indem wir das logische Ergebnis der durchgeführten Operationen an den Aufrufer zurückgeben.
if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_error, 1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } ResetLastError(); if(!OpenCL.Execute(def_k_CalcOutputGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel CalcOutputGradient: %d", GetLastError()); return false; } //--- return true; }
Nach Abschluss der vorbereitenden Arbeiten gehen wir direkt zur Konstruktion der Methode der Fehlergradientenfortpflanzung calcInputGradients über.
In den Parametern dieser Methode erhalten wir, ähnlich wie bei der gleichen Methode der Elternklasse, einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, an die wir den Fehlergradienten weitergeben müssen.
bool CNeuronATFNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getGradient() || !cInputs) return false;
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Danach verteilen wir den von der nachfolgenden Schicht erhaltenen Fehlergradienten in 2 Datenströme zwischen den Vorhersageblöcken im Zeit- und Frequenzbereich.
//--- Output if(!WeightedSumGradient()) return false;
Zunächst propagieren wir den Fehlergradienten durch den Block T der Zeitbereichsvorhersage. Hier rufen wir in der umgekehrten Reihenfolge wie beim Vorwärtsdurchlauf die entsprechenden Methoden der verschachtelten Objekte auf.
//--- T-Block if(cRevIN.Activation() != None && !DeActivation(cRevIN.getOutput(), cRevIN.getGradient(), cRevIN.getGradient(), cRevIN.Activation())) return false; CNeuronBaseOCL *next = cRevIN.AsObject(); for(int i = caProjection.Total() - 1; i >= 0; i--) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj || !proj.calcHiddenGradients((CObject *)next)) return false; next = proj; } for(int i = caAttention.Total() - 1; i >= 0; i--) { CNeuronBaseOCL *att = caAttention.At(i); if(!att || !att.calcHiddenGradients((CObject *)next)) return false; next = att; } if(!cPatching.calcHiddenGradients((CObject*)next)) return false; if(!cTranspose.calcHiddenGradients(cPatching.AsObject())) return false; if(!cPositionEncoder.calcHiddenGradients(cTranspose.AsObject())) return false; if(!cNorm.calcHiddenGradients(cPositionEncoder.AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cNorm.AsObject())) return false;
Der Algorithmus der Gradientenfortpflanzung im Frequenzvorhersageblock ist etwas komplizierter. Hier definieren wir zunächst den Fehlergradienten für den Imaginärteil der rekonstruierten Zeitreihe. Wie bereits erwähnt, ist der Zielwert für den Imaginärteil der Zeitreihe 0. Um den Fehlergradienten zu bestimmen, ändern wir daher einfach das Vorzeichen der Ergebnisse des Vorwärtsdurchgangs.
//--- F-Block if(!CNeuronBaseOCL::SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), iFFT*iVariables, false, 0, 0, 0, -0.5)) return false;
Als Nächstes definieren wir den Gradienten des Fehlers bei der historischen Datenwiederherstellung.
if(!calcReconstructGradient()) return false;
Danach kombinieren wir die Gradiententensoren des Fehlers der historischen Datenwiederherstellung (definiert in der Methode calcReconstructGradient), den Gradienten des Vorhersagefehlers der Zeitreihe (erhalten durch Teilung des Gradienten des Fehlers der nachfolgenden Schicht in zwei Ströme) und ergänzen sie mit Nullwerten bis zur Größe des Spektrums der vollständigen Reihe.
if(!Concat(GetPointer(cReconstructInputGrad), GetPointer(cForecastGrad), GetPointer(cZero), GetPointer(cOutputTimeSeriasReGrad), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables)) return false;
Wir hängen Nullwerte an das Ende des Fehlergradiententensors der vollständigen Zeitreihe an, da wir keine Daten über Zielwerte jenseits des Planungshorizonts haben. Das bedeutet, dass wir sie einfach nicht korrigieren.
Der sich daraus ergebende Fehlergradient für die vollständige Zeitreihe, die unter Verwendung der Frequenzvorhersage-Blockdaten erstellt wurde, wird durch Anwendung der FFT in den Frequenzbereich übersetzt.
if(!FFT(GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), false)) return false;
Wir kombinieren die erhaltenen Daten der Real- und Imaginärteile des Frequenzspektrums des Fehlergradienten zu einem einzigen Tensor.
if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables)) return false;
Wir korrigieren den Fehlergradienten für die Ableitung der Daten-Denormalisierungsoperationen
if(!ComplexUnNormalizeGradient()) return false;
und übertragen den Fehlergradienten durch den komplexen Aufmerksamkeitsblock.
if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject())) return false;
Anschließend wird der Fehlergradient durch die Ableitung der Datennormalisierungsfunktion korrigiert
if(!ComplexNormalizeGradient()) return false;
und wir trennen den realen und den imaginären Teil des Spektrums.
if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables)) return false;
Es folgt die Rückführung des Fehlergradienten in den Zeitbereich mittels IFFT.
if(!FFT(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), false)) return false;
Beachten Sie, dass wir den Fehlergradienten für die gesamte Zeitreihe erhalten haben. Wir müssen jedoch nur den Gradienten des Fehlers der historischen Daten an die vorherige Schicht weitergeben. Daher wählen wir zunächst die Daten für den untersuchten historischen Horizont aus.
if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasRe), iHistory, iFFT-iHistory, iVariables)) return false;
Dann addieren wir die erhaltenen Werte zu den Ergebnissen der Fehlergradientenverteilung des Blocks T.
if(!CNeuronBaseOCL::SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cInputFreqRe), NeuronOCL.getGradient(), iHistory*iVariables, false, 0, 0, 0, 0.5)) return false; //--- return true; }
Wie immer kontrollieren wir bei jeder Iteration den Prozess der Durchführung von Operationen. Nach erfolgreichem Abschluss aller Operationen geben wir das logische Ergebnis der Methode an den Aufrufer zurück.
1.4 Aktualisierung der Modellparameter
Der Fehlergradient der einzelnen trainierten Parameter des Modells bestimmt seinen Einfluss auf das Gesamtergebnis. Im nächsten Schritt passen wir die Modellparameter an, um den Fehler zu minimieren. Diese Funktion wird in der Methode updateInputWeights ausgeführt. In der Implementierung unserer Klasse bedeutet die Aktualisierung der Parameter, dass die gleichnamigen Methoden der verschachtelten Objekte, die die zu trainierenden Parameter enthalten, aufgerufen werden. Im F-Block handelt es sich nur um eine komplexe Aufmerksamkeitsklasse.
bool CNeuronATFNetOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { //--- F-Block if(!cFreqAtteention.UpdateInputWeights(cNormFreqComplex.AsObject())) return false;
Der T-Block hat mehr solcher Objekte.
//--- T-Block if(!cPatching.UpdateInputWeights(cPositionEncoder.AsObject())) return false; int total = caAttention.Total(); CNeuronBaseOCL *prev = cPatching.AsObject(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *att = caAttention.At(i); if(!att.UpdateInputWeights(prev)) return false; prev = att; } total = caProjection.Total(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj.UpdateInputWeights(prev)) return false; prev = proj; } //--- return true; }
Damit ist unsere Betrachtung der Algorithmen zur Umsetzung der von den Autoren der Methode ATFNet vorgeschlagenen Ansätze abgeschlossen. Den vollständigen Code der Klasse CNeuronATFNetOCL finden Sie im Anhang.
2. Modell der Architektur
Wir haben unsere Klasse fertiggestellt, die die Ansätze der ATFNet-Methode implementiert. Kommen wir nun zum Aufbau der Architektur unserer Modelle. Wie Sie vielleicht schon erraten haben, werden wir eine neue neuronale Schicht in den Environment State Encoder implementieren. Natürlich ist es schwierig, die Klasse CNeuronATFNetOCL als neuronale Schicht zu bezeichnen. Es implementiert eine recht komplexe Architektur für den Aufbau eines umfassenden Modells.
Wir füttern unseren Encoder mit einer Reihe von Roheingaben, so wie wir es mit den zuvor konstruierten Modellen getan haben.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
In diesem Fall werden die erhaltenen Daten jedoch nicht normalisiert. Beide Böcke, sowohl Tals auch F, verfügen über eine Datennormalisierung in ihren Architekturen. Daher überspringen wir diesen Schritt. Unsere Eingaben werden jedoch anhand von Vektoren gebildet, die einzelne Zustände der Umwelt beschreiben. Vor der weiteren Verarbeitung transponieren wir die Eingaben, um eine Analyse in Form von unitären Zeitreihen zu ermöglichen.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
Als Nächstes verwenden wir unsere neue Klasse, um die nachfolgenden Daten der analysierten Zeitreihe vorherzusagen.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronATFNetOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.window_out = NForecast; descr.step = 8; descr.layers = 4; { int temp[] = {5, 1, 16}; ArrayCopy(descr.windows, temp); } descr.activation = None; descr.batch = 10000; if(!encoder.Add(descr)) { delete descr; return false; }
Eigentlich enthält diese Ebene unser gesamtes Modell. An seinem Ausgang erhalten wir die Prognosewerte, die wir für die gesamte Planungstiefe benötigen. Wir müssen sie nur in die gewünschte Dimension transponieren.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Für die Konsistenz des Spektrums der vorhergesagten Werte werden wir die Ansätze der Methode FreDF.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Wir lassen die Modelle von Akteur und Kritiker unverändert.
Die Trainings- und Testprogramme für die trainierten Modelle wurden ebenfalls aus den vorherigen Artikeln übernommen. Sie können den Code im Anhang selbst studieren.
3. Tests
Wir haben viel Arbeit investiert, um die von den Autoren der Methode ATFNet vorgeschlagenen Ansätze mit MQL5 umzusetzen. Der Umfang der geleisteten Arbeit würde sogar den Rahmen eines Artikels sprengen. Schließlich kommen wir zur letzten Phase unserer Arbeit: dem Training und Testen der Modelle.
Um die Modelle zu trainieren, verwenden wir den EA, den wir zuvor zum Trainieren der vorherigen Modelle erstellt haben. Daher können auch zuvor gesammelte Trainingsdaten verwendet werden.
Die Modelle werden auf den historischen Daten von EURUSD mit dem Zeitrahmen H1 über das gesamte Jahr 2023 trainiert.
In der ersten Phase trainieren wir das Encoder-Modell, um die nachfolgenden Zustände der Umgebung über einen Planungshorizont vorherzusagen, der durch die Konstante NForecast bestimmt wird.
Wie zuvor analysiert das Encoder-Modell nur die Preisbewegung, sodass wir in der ersten Phase des Trainings die Trainingsmenge nicht aktualisieren müssen.
In der zweiten Phase unseres Lernprozesses suchen wir nach der optimalen Handlungsstrategie des Akteurs. Hier führen wir ein iteratives Training der Modelle von Akteur und Kritiker durch, das sich mit der Aktualisierung des Trainingsdatensatzes abwechselt. Der Prozess der Aktualisierung des Trainingsdatensatzes ermöglicht es uns, die Belohnungen aus der Umgebung im Bereich der aktuellen Politik des Akteurs zu verfeinern, was uns wiederum eine Feinabstimmung der gewünschten Politik ermöglicht.
Während des Trainingsprozesses war es uns möglich, eine Akteurspolitik zu erhalten, die in der Lage war, sowohl in den Trainings- als auch in den Testdatensätzen Gewinne zu erzielen. Die Ergebnisse der Modellversuche sind nachstehend aufgeführt.
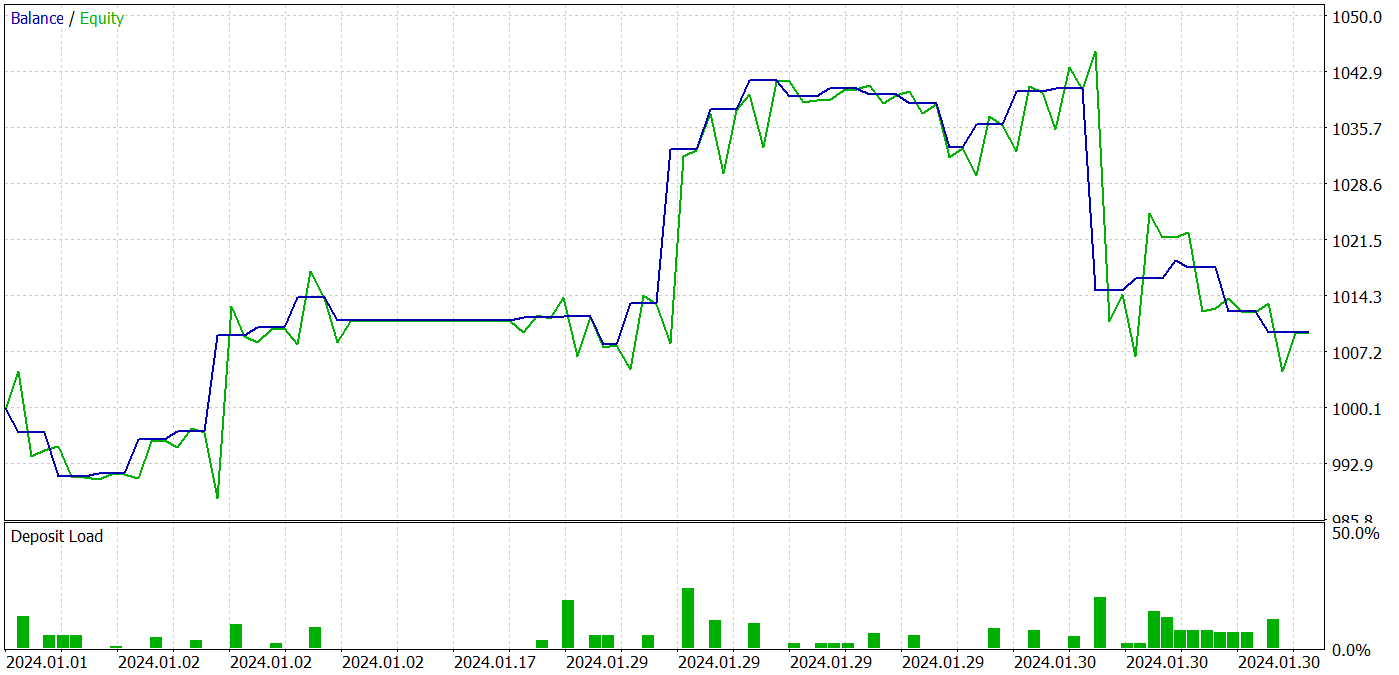
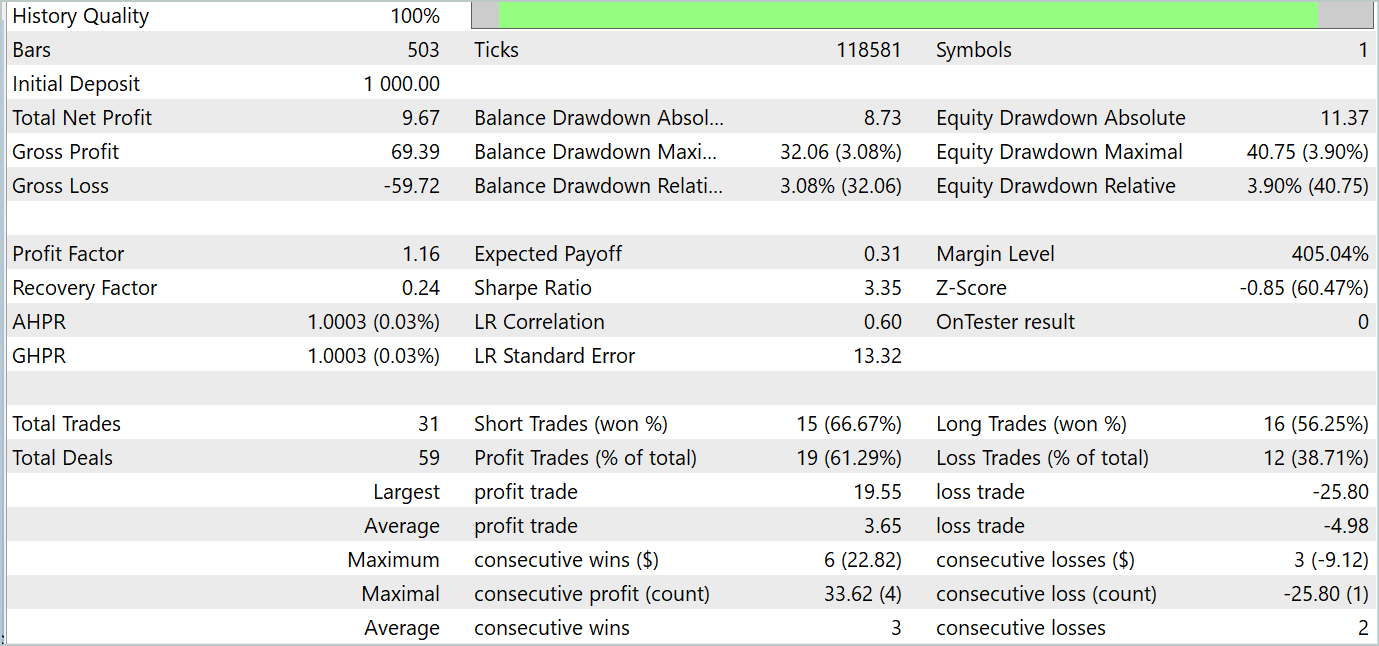
Während des Testzeitraums tätigte das Modell 31 Abschlüsse, von denen 19 mit Gewinn abgeschlossen wurden. Der Anteil der gewinnbringenden Handelsgeschäfte lag bei über 61 %. Bemerkenswert ist, dass das Modell fast die gleiche Anzahl von Kauf- und Verkaufs-Positionen aufwies (15 gegenüber 16).
Schlussfolgerung
Die letzten beiden Artikel waren der ATFNet-Methode gewidmet, die für die Vorhersage von multivariaten Zeitreihen vorgeschlagen und in dem Artikel „ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting" vorgestellt wurde. Das ATFNet-Modell kombiniert Zeit- und Frequenzbereich-Module zur Analyse von Abhängigkeiten in Zeitreihendaten. Es verwendet den T-Block zur Erfassung lokaler Abhängigkeiten im Zeitbereich und den F-Block zur Analyse der Zyklizität von Zeitreihen im Frequenzbereich.
ATFNet wendet die Energiegewichtung der dominanten harmonischen Reihe, die erweiterte Fourier-Transformation und die Beachtung des komplexen Spektrums an, um sich an die Periodizität und die Frequenzabweichungen in den Eingabezeitreihen anzupassen.
Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben Modelle mit echten Daten trainiert und getestet. Die Testergebnisse zeigen das Potenzial der vorgeschlagenen Ansätze für die Entwicklung profitabler Handelsstrategien.
Referenzen
- ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting
- Andere Artikel aus dieser Reihe
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15024
Vom Neuling zum Experten: Umfassende Fehlersuche in MQL5
Algorithmus einer chemischen Reaktionsoptimierung (CRO) (Teil I): Prozesschemie in der Optimierung
Aufbau des Kerzenmodells Trend-Constraint (Teil 9): Expert Advisor für mehrere Strategien (I)
Visualisierung der Handelsgeschäfte auf dem Chart (Teil 2): Grafische Anzeige der Daten
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.