Redes neurais de maneira fácil (Parte 91): previsão na área de frequência (FreDF)
172
0
Introdução
A previsão de séries temporais de preços futuros é de importância crítica em vários cenários no mercado financeiro. A maioria dos métodos atuais baseia-se na existência de autocorrelação nos dados. Em outras palavras, exploramos a dependência entre os passos temporais, tanto nos dados brutos quanto nos valores previstos.
Recentemente, modelos baseados na arquitetura Transformer, que utilizam mecanismos de Self-Attention para avaliar dinamicamente a autocorrelação, estão ganhando popularidade. Ao mesmo tempo, há um crescente interesse no uso da análise de frequência para previsões. Ao representar a sequência de dados brutos na área de frequência, é possível contornar a complexidade da descrição da autocorrelação, o que aumenta a eficiência dos diferentes modelos.
Outro aspecto importante é a autocorrelação nos valores previstos. É evidente que os valores previstos fazem parte de uma série temporal maior, que inclui tanto a sequência analisada quanto a prevista. Portanto, os valores previstos mantêm as dependências dos dados analisados. No entanto, esse fenômeno muitas vezes é ignorado nos métodos modernos de previsão. Em particular, os métodos atuais tendem a usar a abordagem de previsão direta (Direct Forecast — DF), que gera previsões de múltiplos passos simultaneamente. Isso implicitamente pressupõe a independência dos passos na sequência dos valores previstos. Essa discrepância entre as suposições do modelo e as características dos dados resulta em previsões de qualidade subótima.
Uma solução para esse problema foi proposta no artigo "FreDF: Learning to Forecast in Frequency Domain". Nele, os autores apresentam um método de previsão direta com aprimoramento de frequência (FreDF). Ele ajusta a abordagem DF, alinhando os valores previstos e a sequência de referência na área de frequência. Ao migrar para a área de frequência, onde as bases são ortogonais e independentes, a influência da autocorrelação é efetivamente reduzida. Dessa forma, FreDF evita a discrepância entre a suposição do DF e a existência de autocorrelação nas referências, mantendo as vantagens do DF.
Os autores testaram a eficácia do método em uma série de experimentos, que demonstraram uma melhoria significativa do desempenho em relação aos métodos atuais.
1. Algoritmo FreDF
A abordagem DF utiliza um modelo com múltiplas saídas ɡθ para gerar previsões em T passos Ŷ = ɡθ(X). Seja Yt o t-ésimo passo de Y, e Yt(n) a n-ésima observação amostral. Os parâmetros do modelo θ são otimizados, minimizando o erro quadrático médio (MSE):
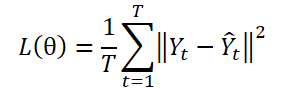
A abordagem DF calcula o erro de previsão em cada etapa de forma independente, tratando cada elemento da sequência como uma tarefa separada. No entanto, essa abordagem não leva em conta a autocorrelação presente em Y, o que contradiz a existência de autocorrelação nas etiquetas. Como resultado, isso leva a um viés no cálculo da verossimilhança e um desvio do princípio da máxima verossimilhança durante o treinamento do modelo.
Uma das estratégias para superar essa limitação é a representação da sequência de etiquetas em um domínio transformado, formado por bases ortogonais. Especificamente, isso pode ser realizado de maneira eficiente com a transformação de Fourier, que projeta a sequência em bases ortogonais associadas a diferentes frequências. Ao transformar a sequência de etiquetas para o domínio de frequência ortogonal, é possível reduzir eficazmente a dependência da autocorrelação das etiquetas.
Onde i é a unidade imaginária, definida como √(-1),
exp(•) é a base de Fourier associada à frequência k, sendo ortogonal para diferentes valores de k.
Devido à ortogonalidade da base, a representação da sequência de etiquetas no domínio de frequência contorna a dependência originada pela autocorrelação no domínio temporal. Isso destaca o potencial de aprendizado de previsão no domínio de frequência.
No uso clássico das abordagens DF, em um ponto temporal n, a sequência histórica Xn é inserida no modelo para gerar previsões de T passos, denotados como Ŷn = ɡθ(Xn). E o erro de previsão é calculado no domínio temporal Ltmp.
Além da abordagem canônica, os autores do método FreDF propõem transformar os valores previstos e as sequências de etiquetas para o domínio de frequência. Nesse caso, o erro de previsão no domínio de frequência é calculado pela fórmula:
Aqui, cada termo da soma representa uma matriz de números complexos A, e |A| denota a operação de cálculo e soma do módulo de cada elemento na matriz. O módulo de um número complexo a = ar + i ai é calculado como √(ar^2 + ai^2).
É importante notar que, devido às diferentes características numéricas da sequência de etiquetas no domínio de frequência, os autores do método FreDF não utilizam a forma quadrática de perda (MSE), como é típico no cálculo do erro de perda no domínio temporal. Em particular, diferentes componentes de frequência costumam ter magnitudes muito distintas: as frequências mais baixas possuem amplitudes muito maiores — em várias ordens de magnitude, comparadas às frequências mais altas, o que torna os métodos de perda quadrática instáveis.
Os erros de previsão nos domínios temporal e de frequência são combinados utilizando um coeficiente α no intervalo de valores [0,1], que controla a força relativa do alinhamento no domínio de frequência:
FreDF contorna o efeito de autocorrelação das etiquetas-alvo ao alinhar os valores previstos gerados e a sequência de etiquetas no domínio de frequência. Ao fazer isso, mantêm-se as vantagens do DF, como a inferência eficiente e a capacidade de multitarefa. Uma característica notável do FreDF é sua compatibilidade com vários modelos de previsão e transformações. Essa flexibilidade expande significativamente o potencial de aplicação do FreDF.
A visualização do método, feita pelos autores, está apresentada abaixo.
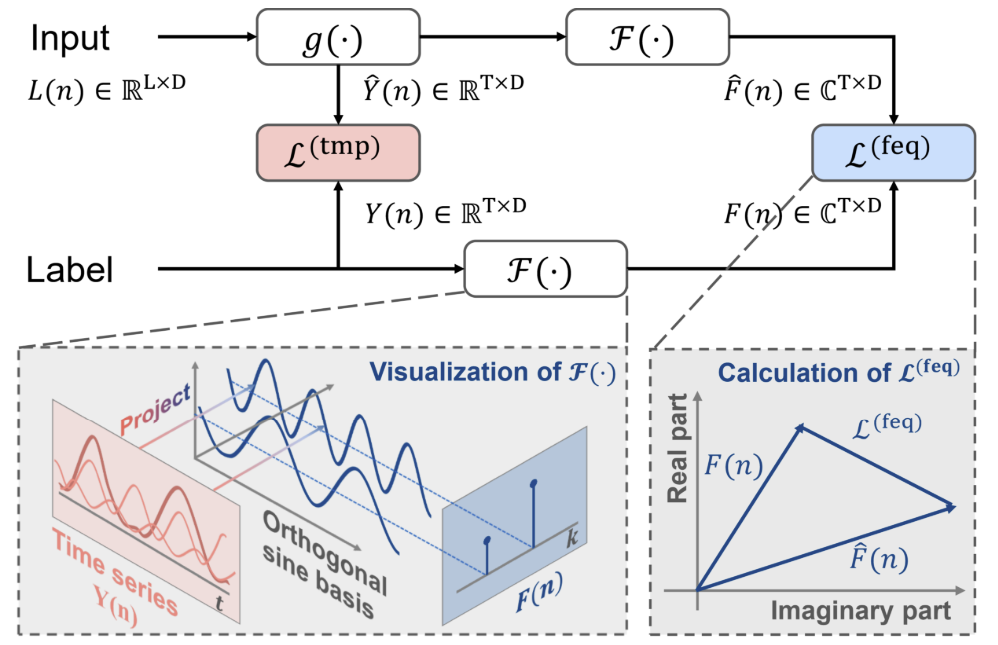
2. Implementação com MQL5
Depois de analisarmos os aspectos teóricos do método FreDF, nós passamos à parte prática do nosso artigo, na qual implementamos nossa visão sobre a abordagem sugerida. A partir da descrição teórica acima, podemos concluir que o método proposto essencialmente não introduz nenhuma característica construtiva na arquitetura do modelo. Além disso, ele não afeta o desempenho do modelo durante a execução. Seu impacto só é percebido durante o treinamento do modelo. Provavelmente, o método FreDF pode ser comparado a uma função de perda complexa, que utilizaremos para treinar o modelo, cujas etiquetas-alvo, de acordo com nosso conhecimento prévio, possuem dependências autocorrelacionadas.
Antes de construir um novo objeto para implementar as abordagens propostas, é importante destacar que, para transformar os dados da série temporal para o domínio de frequência, os autores do método utilizaram a Transformada de Fourier. Vale mencionar que o FreDF é bastante flexível. Ele funciona bem também com outros métodos de transformação de dados para um domínio ortogonal. Os autores do método realizaram uma série de experimentos e demonstraram sua eficácia ao usar outras transformações. Os resultados desses experimentos estão apresentados abaixo.
Como pode ser observado, os modelos que utilizam a Transformada de Fourier mostram melhores resultados.
Gostaria de chamar sua atenção para o coeficiente α. Seu valor em torno de 0,8 parece ser o ideal com base nos resultados dos experimentos realizados. Vale ressaltar que a previsão apenas no domínio de frequência (uso de α igual a 1) levou a uma queda na precisão do modelo, conforme os mesmos experimentos.
Disso, podemos concluir que, para obter um modelo de previsão ideal para séries temporais, é necessário considerar tanto o domínio temporal quanto o de frequência durante o treinamento. Diferentes representações permitem obter mais informações sobre o sinal e, como resultado, treinar um modelo mais eficiente.
Agora, voltando à nossa implementação. Com base nos experimentos dos autores, a Transformada de Fourier permite treinar modelos com menor erro de previsão. Vale lembrar que, em trabalhos anteriores, já implementamos a Transformada Rápida de Fourier (FFT) direta e inversa. E nesta implementação, podemos utilizar esses desenvolvimentos.
Para implementar as abordagens do FreDF, criaremos uma nova classe chamada CNeuronFreDFOCL, que herdará a funcionalidade principal da classe base de camadas neurais CNeuronBaseOCL. A estrutura da nova classe está apresentada abaixo.
class CNeuronFreDFOCL : public CNeuronBaseOCL { protected: uint iWindow; uint iCount; uint iFFTin; bool bTranspose; float fAlpha; //--- CBufferFloat cForecastFreRe; CBufferFloat cForecastFreIm; CBufferFloat cTargetFreRe; CBufferFloat cTargetFreIm; CBufferFloat cLossFreRe; CBufferFloat cLossFreIm; CBufferFloat cGradientFreRe; CBufferFloat cGradientFreIm; CBufferFloat cTranspose; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool Transpose(CBufferFloat *inputs, CBufferFloat *outputs, uint rows, uint cols); virtual bool FreqMSA(CBufferFloat *target, CBufferFloat *forecast, CBufferFloat *gradient); virtual bool CumulativeGradient(CBufferFloat *gradient1, CBufferFloat *gradient2, CBufferFloat *cummulative, float alpha); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFreDFOCL(void) {}; ~CNeuronFreDFOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1); virtual bool calcOutputGradients(CArrayFloat *Target, float &error); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFreDFOCL; } virtual void SetOpenCL(COpenCLMy *obj); };
Na estrutura apresentada da nova classe, podemos notar duas características:
- os objetos internos são representados apenas por buffers de dados e não há camadas internas;
- redefinição do método calcOutputGradients.
Além disso, há uma característica implícita: este objeto não contém parâmetros treináveis, o que é bastante raro. Todas as características mencionadas estão relacionadas ao propósito da classe — estamos criando uma classe de função de perda complexa, e não uma camada de rede neural treinável. E o método calcOutputGradients na nossa arquitetura de camadas de rede neural é responsável por calcular as diferenças entre os valores previstos e os valores-alvo. E quanto ao propósito dos objetos e variáveis internas, sugiro explorá-los no processo de implementação dos métodos da classe.
Todos os objetos internos foram declarados estaticamente, o que nos permite deixar o construtor e o destrutor da classe "vazios". A limpeza da memória será feita pelo próprio sistema.
A inicialização dos objetos da classe ocorre no método Init. Como de costume, nos parâmetros desse método, passamos as principais constantes que definem a arquitetura da classe. Aqui vemos:
- janela de descrição de um elemento dos dados de entrada (window),
- número de elementos na sequência (count),
- coeficiente de força de alinhamento entre as áreas de frequência e temporal (alpha),
- flag para indicar a necessidade de transpor os dados para a transformação de frequência (need_transpose).
A primeira coisa a se destacar: pretendemos usar este objeto na saída do modelo. Portanto, os valores de entrada serão previsões geradas pelo nosso modelo. Os dados devem estar em um formato compatível com os resultados esperados. Aqui, os parâmetros window e count correspondem tanto aos valores previstos quanto aos alvos. Ao mesmo tempo, oferecemos ao usuário a possibilidade de transformar os dados para o domínio de frequência em outro eixo. Para isso, introduzimos o flag need_transpose.
Aqui vale mencionar os resultados de outros experimentos realizados pelos autores do método. Eles testaram a eficácia dos modelos ao comparar as características de frequência em séries temporais unidimensionais de sequência multidimensional (T), em diferentes passos temporais (D) e para a sequência total (2D).
Os melhores resultados foram demonstrados pelo modelo que analisou as características de frequência da sequência total. Comparar as características de frequência de passos temporais separados teve o pior desempenho. A análise das características de frequência em séries temporais unidimensionais ficou em segundo lugar, com uma pequena diferença em relação ao líder.
Na nossa implementação, permitimos que o usuário escolha a dimensão para a transformação de frequência, indicando o valor apropriado do flag need_transpose. Para comparar as características de frequência 2D, basta definir o tamanho total da sequência no parâmetro window, e para os outros parâmetros, utilizar os seguintes valores:
- count: 1,
- need_transpose: false.
bool CNeuronFreDFOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float Alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch)) return false;
No corpo do método, primeiro chamamos o método homônimo da classe pai e verificamos o resultado da execução das operações. Lembro que na classe pai foi implementado um conjunto mínimo necessário de controles, incluindo o tamanho da camada neural criada. E como tamanho da camada, especificamos o produto das variáveis window e count. Obviamente, se uma delas tiver valor zero, o produto será "0" e o método da classe pai terminará com um erro.
Após a execução bem-sucedida do método da classe pai, armazenamos os valores obtidos em variáveis locais.
bTranspose = need_transpose; iWindow = window; iCount = count; fAlpha = MathMax(0, MathMin(Alpha, 1)); activation = None;
Vale lembrar que, para a Transformada Rápida de Fourier, precisamos de buffers cujo tamanho seja uma potência de 2. Vamos calcular os tamanhos dos buffers de dados:
//--- Calculate FFTsize uint size = (bTranspose ? count : window); int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) != size) power++; iFFTin = uint(MathPow(2, power));
O próximo passo é inicializar os buffers de dados internos. Primeiro, inicializamos os buffers das características de frequência dos valores previstos. Vamos usar uma estrutura com 2 buffers de dados. Um para armazenar a parte real e outro para a parte imaginária dos dados.
//--- uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false;
Em seguida, criamos buffers semelhantes para as características de frequência dos valores-alvo:
if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false;
O erro de previsão será registrado nos buffers cLossFreRe e cLossFreIm.
if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false;
Aqui, vale destacar a importância de comparar ambas as partes das características de frequência, pois, para a previsão correta de séries temporais, são importantes tanto as amplitudes quanto as fases das características de frequência da série temporal.
E, claro, vamos criar buffers para registrar os gradientes de erro no nível dos valores previstos da série temporal:
if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false;
Naturalmente, para economizar memória, podemos optar por não usar os buffers cGradientFreRe e cGradientFreIm. Eles podem ser facilmente substituídos, por exemplo, pelos buffers cForecastFreRe e cForecastFreIm. No entanto, sua presença torna o código mais legível. E a quantidade de memória que eles consomem, no nosso caso, não é crítica.
Por fim, criaremos um buffer temporário para armazenar os valores transpostos, caso isso seja necessário:
if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; //--- return true; }
Depois de inicializar os dados, normalmente criamos o método de propagação para frente. Já foi mencionado que o objeto dessa classe não realiza operações com os dados durante o uso. E, como você sabe, o método de propagação para frente descreve as operações do modo de uso do modelo. À primeira vista, poderíamos substituir o método de propagação para frente por um "placeholder", mas então surgiria a questão da transferência de dados. Ao mesmo tempo, gostaríamos de minimizar o processo de cópia de dados, pois o volume pode ser variado e isso adicionaria sobrecarga ao processo. Nesse contexto, criamos o método de propagação para frente o mais simples possível. Nele, verificamos apenas a correspondência dos ponteiros dos buffers de resultados no nível atual e no anterior. Quando necessário, substituímos o ponteiro do nível atual pelo buffer de resultados do nível anterior.
bool CNeuronFreDFOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false; if(NeuronOCL.getOutput() != Output) { Output.BufferFree(); delete Output; Output = NeuronOCL.getOutput(); } //--- return true; }
Dessa forma, a substituição do ponteiro de um buffer substitui o processo de transferência de dados, independentemente do seu volume. Observe que o controle é feito em cada passagem, e a substituição dos buffers ocorre apenas na primeira delas.
A principal funcionalidade da classe será implementada para a retropropagação. Inicialmente, faremos uma pequena preparação. Para implementar o funcionamento necessário, vamos criar dois pequenos kernels no lado do programa OpenCL.
Os autores do método FreDF recomendam o uso do MAE (Mean Absolute Error) como função de perda para avaliar as discrepâncias no domínio de frequência, observando que o uso do MSE (Mean Squared Error) reduz a estabilidade do treinamento. Vale lembrar que, na nossa camada neural base CNeuronBaseOCL, usamos o MSE para determinar o gradiente de erro. Portanto, precisamos criar um kernel para calcular o gradiente de erro dos valores previstos usando o MAE. Matematicamente, isso é bastante simples: basta subtrair o vetor de valores previstos do vetor de valores-alvo.
__kernel void GradientMSA(__global float *matrix_t, __global float *matrix_o, __global float *matrix_g ) { int i = get_global_id(0); matrix_g[i] = matrix_t[i] - matrix_o[i]; }
Após calcular o gradiente de erro nos domínios de frequência e temporal, é necessário combinar os gradientes de erro utilizando um coeficiente de temperatura. Essa funcionalidade será realizada no kernel CumulativeGradient, cujo algoritmo, acredito, não trará dificuldades para compreensão.
__kernel void CumulativeGradient(__global float *gradient_freq, __global float *gradient_tmp, __global float *gradient_out, float alpha ) { int i = get_global_id(0); gradient_out[i] = alpha * gradient_freq[i] + (1 - alpha) * gradient_tmp[i]; }
Lembro que, para converter dados entre os domínios temporal e de frequência, usaremos o algoritmo da Transformada Rápida de Fourier, que implementamos no artigo anterior. Lá, você também encontrará a descrição do algoritmo e do método de enfileiramento do kernel.
Neste artigo, não abordaremos os algoritmos de enfileiramento de kernels, pois todos seguem o mesmo esquema, já apresentado em artigos anteriores desta série, incluindo o anterior.
Vamos agora analisar o método CNeuronFreDFOCL::calcOutputGradients, onde está implementada a funcionalidade principal da nossa classe. Como você sabe, na estrutura dos nossos modelos, esse método é responsável por calcular o erro entre os valores previstos pelo modelo e os valores-alvo. Nos parâmetros do método, recebemos um ponteiro para o buffer dos valores-alvo. Após as operações do método, precisamos salvar o gradiente de erro no buffer correspondente da camada atual.
bool CNeuronFreDFOCL::calcOutputGradients(CArrayFloat *Target, float &error) { if(!Target) return false; if(Target.Total() < Output.Total()) return false;
No corpo do método, verificamos a validade do ponteiro recebido para o buffer de valores-alvo. Além disso, o tamanho desse buffer deve ser no mínimo o do tensor dos resultados da nossa modelo.
Como o buffer recebido pode não ter uma cópia no contexto do OpenCL, precisamos criá-la para realizar os cálculos subsequentes. No entanto, para usar os recursos do contexto OpenCL de forma mais eficiente, transferiremos os dados para um buffer de gradientes já criado.
if(Target.Total() == Output.Total()) { if(!Gradient.AssignArray(Target)) return false; } else { for(int i = 0; i < Output.Total(); i++) { if(!Gradient.Update(i, Target.At(i))) return false; } } if(!Gradient.BufferWrite()) return false;
Aqui, temos dois cenários possíveis. Se os tamanhos dos buffers de valores-alvo e previstos forem iguais, usamos o método existente de cópia. Caso contrário, utilizamos um laço para transferir a quantidade necessária de valores. Em ambos os casos, após a cópia, transferimos os dados para a memória do contexto OpenCL.
Os dados transferidos são então usados para calcular os desvios tanto no domínio temporal quanto no domínio de frequência. Aqui, vale observar que, ao calcular os desvios no domínio temporal, o buffer de gradientes de erro da nossa camada será sobrescrito pelos desvios calculados, resultando na perda total dos valores-alvo. Por isso, antes de calcular os desvios no domínio temporal, é necessário decompor a série temporal de valores-alvo em componentes de frequência.
Agora que mencionamos a possibilidade de decompor séries temporais em características de frequência em duas dimensões, o valor do flag bTranspose determina essa escolha. Se o flag for true, transpomos o buffer dos resultados do modelo antes de decompor em características de frequência:
if(bTranspose) { if(!Transpose(Output, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false;
Operações semelhantes são feitas para o tensor das etiquetas-alvo:
if(!Transpose(Gradient, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Se o valor do flag bTranspose for false, decompondo diretamente os valores de previsão e os alvos em suas respectivas características de frequência, sem transposição prévia:
else { if(!FFT(Output, NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false; if(!FFT(Gradient, NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Após determinar as características de frequência, podemos calcular os desvios tanto no domínio temporal quanto no de frequência, sem temer a perda dos valores-alvo.
if(!FreqMSA(GetPointer(cTargetFreRe), GetPointer(cForecastFreRe), GetPointer(cLossFreRe))) return false; if(!FreqMSA(GetPointer(cTargetFreIm), GetPointer(cForecastFreIm), GetPointer(cLossFreIm))) return false; if(!FreqMSA(Gradient, Output, Gradient)) return false;
É importante notar que, no domínio de frequência, calculamos desvios tanto para a parte real quanto para a imaginária das características de frequência, já que o deslocamento de fase é tão importante quanto a amplitude do sinal. No entanto, não podemos diretamente unir os gradientes de erro dos domínios temporal e de frequência, pois os dados são incompatíveis. Portanto, precisamos primeiro trazer os gradientes de erro das características de frequência de volta ao domínio temporal, usando a transformada inversa de Fourier.
if(!FFT(GetPointer(cLossFreRe), GetPointer(cLossFreIm), GetPointer(cGradientFreRe), GetPointer(cGradientFreIm), true)) return false;
Depois de tornar os gradientes de erro temporais e de frequência comparáveis, devemos lembrar que o dimensionamento da extração das características de frequência depende do valor do flag bTranspose. Logo, o gradiente de erro no domínio de frequência deve ser transformado de acordo com esse valor. Só então podemos calcular o gradiente de erro total do nosso modelo.
if(bTranspose) { if(!Transpose(GetPointer(cGradientFreRe), GetPointer(cTranspose), iCount, iWindow)) return false; if(!CumulativeGradient(GetPointer(cTranspose), Gradient, Gradient, fAlpha)) return false; } else if(!CumulativeGradient(GetPointer(cGradientFreRe), Gradient, Gradient, fAlpha)) return false; //--- return true; }
Devemos monitorar a execução das operações em cada etapa. E retornar o status dessas operações ao programa chamador.
Após calcular o gradiente de erro na saída do modelo, passamos o gradiente para a camada anterior, usando o método CNeuronFreDFOCL::calcInputGradients, que recebe um ponteiro para o objeto da camada anterior.
Vale lembrar que nossa camada não contém parâmetros treináveis. Durante o propagação para frente, substituímos o buffer de dados e exibimos os valores da camada anterior como resultados. Em que consiste a tarefa desse método? É muito simples. Precisamos apenas ajustar o gradiente total de erro calculado anteriormente à função de ativação da camada anterior.
bool CNeuronFreDFOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; //--- return DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), Gradient, NeuronOCL.Activation()); }
Como nossa classe não contém parâmetros treináveis, o método updateInputWeights é sobrescrito como uma função vazia.
A ausência de parâmetros treináveis também afeta os métodos de trabalho com arquivos, já que não há necessidade de salvar objetos internos cujos dados não têm valor. Portanto, ao salvar, apenas chamamos o método equivalente da classe pai.
bool CNeuronFreDFOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
E armazenamos os valores das variáveis que descrevem as características construtivas do objeto:
if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(bTranspose)) < INT_VALUE) return false; if(FileWriteFloat(file_handle, fAlpha) < sizeof(float)) return false; //--- return true; }
O algoritmo de restauração do objeto a partir de um arquivo de dados com o método Load é um pouco mais complexo. Primeiro, restauramos os elementos da classe pai:
bool CNeuronFreDFOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Em seguida, carregamos os dados das variáveis na ordem em que foram salvos, sempre verificando se chegamos ao fim do arquivo de dados:
if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; bTranspose = bool(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; fAlpha = FileReadFloat(file_handle);
Depois, iniciamos os objetos internos consoante os parâmetros de arquitetura carregados, de forma semelhante ao processo de inicialização de um novo objeto da classe:
uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false; if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false; if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false; if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false; if(bTranspose) { if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; } else { cTranspose.BufferFree(); cTranspose.Clear(); } //--- return true; }
Isso conclui a análise dos métodos da nova classe CNeuronFreDFOCL. O código completo está no anexo.
Após construir os métodos do novo classe, geralmente passamos para a descrição da arquitetura dos modelos treináveis. No entanto, neste artigo, criamos uma camada neural um tanto incomum. Na verdade, implementamos uma função de perda complexa como uma camada neural. E, essencialmente, podemos adicionar esse novo objeto a uma das nossas modelos previamente treinadas, re-treiná-la e observar como os resultados mudam. Para meus experimentos, escolhi o modelo FEDformer, cuja arquitetura é descrita aqui. E adicionei a nova camada.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- ........ ........ //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Devo dizer que, após alguma reflexão, decidi expandir o experimento. Afinal, os autores do método FreDF propuseram seu algoritmo para levar em consideração as dependências nos resultados previstos. Em grande parte, também existe uma dependência entre os diferentes parâmetros dos resultados do nosso Ator. Por exemplo, os volumes de negociações de compra e venda se excluem mutuamente, pois em qualquer momento temos uma posição aberta apenas em uma direção. Os parâmetros de stop-loss e take-profit determinam a força do movimento provável. Consequentemente, o take-profit de uma posição longa deve, em certo grau, correlacionar-se com o stop-loss de uma posição curta e vice-versa. Usando um raciocínio semelhante, podemos assumir dependências nos valores previstos do Crítico. Então, por que não expandir o experimento para incluir esses modelos? Dito e feito. Adicionamos uma nova camada nos modelos do Ator e Crítico:
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- Critic ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Observe que, neste caso, analisamos as características de frequência de toda a sequência de resultados, e não de séries unitárias separadas.
Nossa implementação dos métodos propostos pelo FreDF, não requer ajustes nos EAs de aprendizado das modelos e na interação com o ambiente. Isso significa que podemos usar os EAs e os dados de treinamento previamente coletados durante os testes dos resultados obtidos.
3. Testes
Realizamos um grande trabalho na implementação dos métodos propostos pelos autores do FreDF usando MQL5. Agora, estamos prontos para o estágio final de nossa pesquisa — o treinamento e teste dos modelos.
Como mencionado anteriormente, usaremos o EA criado anteriormente e os dados de treinamento previamente coletados para o treinamento das modelos. Vale lembrar que o treinamento dos modelos é feito com base nos dados históricos do ativo EURUSD, no time frame H1, durante todo o ano de 2023.
Primeiro, treinamos o modelo Codificador do estado do ambiente. O modelo é treinado para prever os estados futuros do ambiente para um horizonte de planejamento determinado pela constante NForecast. No meu experimento, isso corresponde a 12 velas subsequentes. A previsão abrange todos os parâmetros analisados que descrevem o estado do ambiente.
#define NForecast 12 //Number of forecast
Durante o treinamento do Codificador, é possível observar uma redução no erro de previsão em comparação com um modelo similar que não utiliza os métodos do FreDF. No entanto, não fizemos uma comparação gráfica dos resultados previstos, o que torna difícil avaliar a qualidade real das previsões. É importante destacar que nosso objetivo não é obter previsões precisas de todos os indicadores analisados. O ponto principal é que o Ator usa o espaço latente do Codificador para tomar decisões sobre as ações ideais. E o objetivo do primeiro estágio do treinamento é criar um espaço latente informativo no Codificador, no qual o movimento de preço provável esteja codificado.
Como antes, o modelo do Codificador analisa apenas o movimento dos preços, portanto, durante o primeiro estágio de treinamento, não há necessidade de atualizar o conjunto de dados de treinamento.
Na segunda fase, buscamos a política ideal de ações do nosso Ator. E aqui já realizamos o treinamento iterativo dos modelos do Ator e do Crítico, alternando com a atualização do conjunto de dados de treinamento.
Após várias iterações de treinamento da política do Ator, conseguimos um modelo capaz de gerar lucro. A eficácia da modelo treinada foi testada no tester de estratégias do MetaTrader 5, com dados históricos reais de janeiro de 2024. Os parâmetros de teste correspondiam totalmente aos do conjunto de dados de treinamento, incluindo o ativo, time frame e os indicadores analisados. Os resultados dos testes são mostrados nas capturas de tela abaixo.
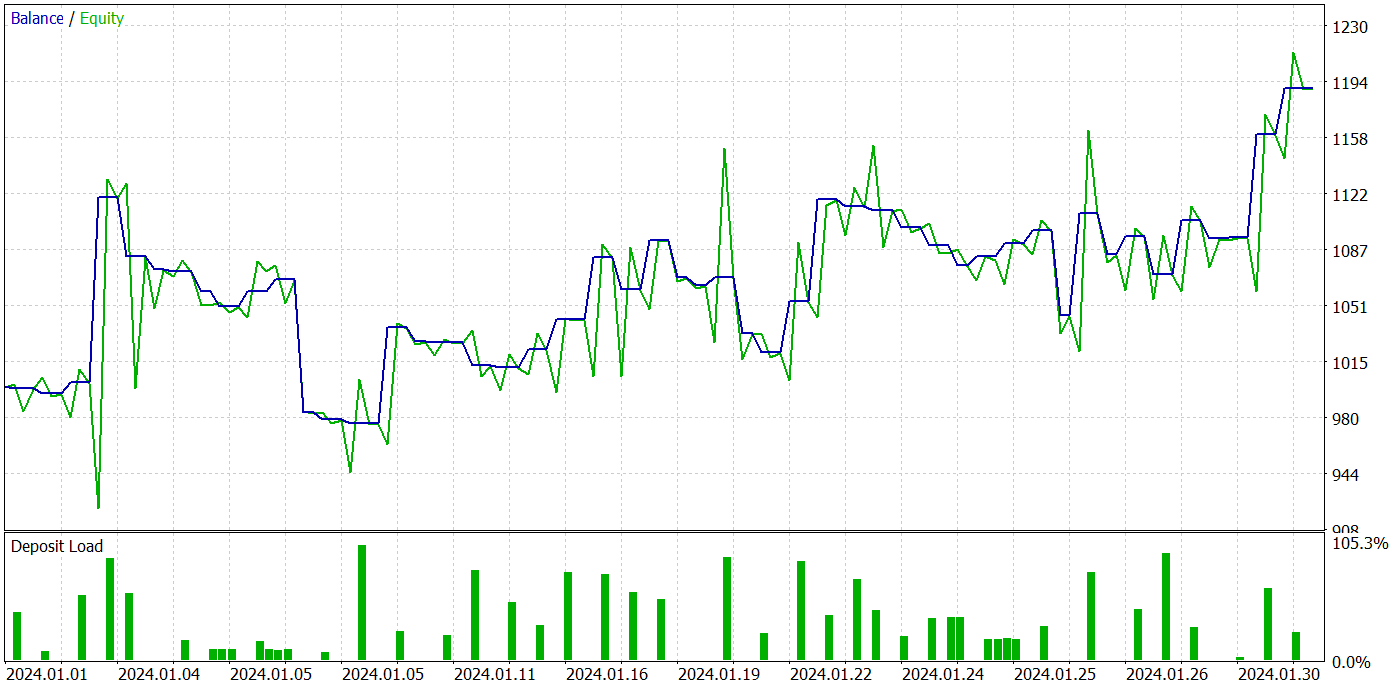
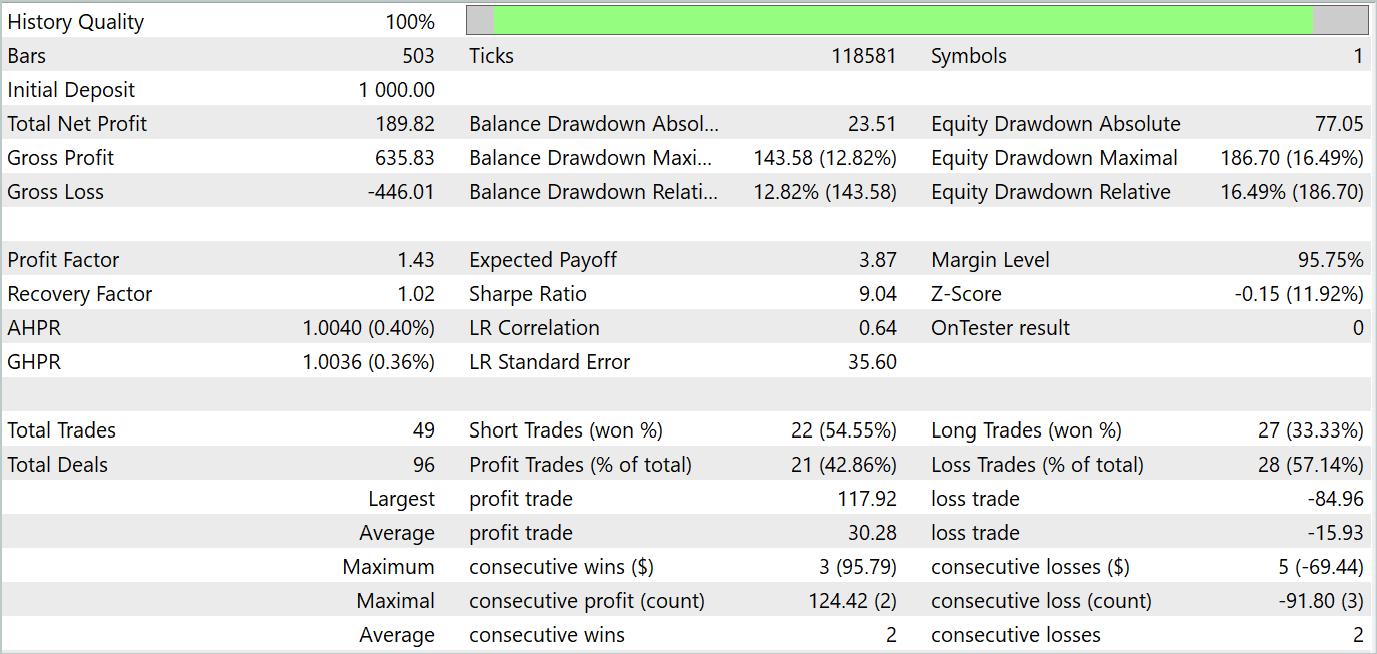
Com base nos testes, podemos notar uma tendência clara de crescimento do saldo da conta. Durante o período de teste, o modelo fez 49 negociações, das quais 21 foram lucrativas. Sim, menos da metade das posições foram lucrativas. No entanto, o lucro médio por operação foi quase o dobro da perda média. Como resultado, o profit factor da modelo na amostra de teste foi de 1,43, e o retorno total em um mês foi de aproximadamente 19%.
Conclusão
Neste trabalho, exploramos o método FreDF, que visa melhorar a previsão de séries temporais. Os autores do método demonstraram empiricamente que ignorar a autocorrelação nas sequências de rótulos resulta em um viés de verossimilhança e na redução da qualidade das previsões na atual abordagem DF. Eles apresentaram uma modificação simples, mas eficaz, da abordagem DF, que leva em consideração a autocorrelação, alinhando previsões e sequências de rótulos no domínio da frequência. O método FreDF é compatível com várias modelos de previsão e transformações, o que o torna flexível e universal.
Na parte prática, implementamos nossa visão dos métodos propostos utilizando MQL5. Incorporamos os métodos ao modelo FEDformer criado anteriormente e realizamos seu treinamento. Os resultados dos testes da modelo treinada indicam a eficácia dos métodos propostos, já que a adição do FreDF aumenta a eficiência do modelo em condições idênticas.
Vale destacar a flexibilidade do método FreDF, que permite sua aplicação eficaz em uma ampla gama de modelos existentes.
Referências
Programas utilizados na publicação:
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA de coleta de exemplos |
| 2 | ResearchRealORL.mq5 | EA | EA de coleta de exemplos com o método Real-ORL |
| 3 | Study.mq5 | EA | EA de treinamento de Modelos |
| 4 | StudyCodificador.mq5 | EA | EA de treinamento do Codificador |
| 5 | Test.mq5 | EA | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14944
Algoritmo de Fechadura Codificada (Code Lock Algorithm, CLA)
Desenvolvendo um EA multimoeda (Parte 11): Início da automação do processo de otimização
Desenvolvendo um EA multimoeda (Parte 12): Gerenciamento de Risco como em empresas de prop trading
Técnicas do MQL5 Wizard que você deve conhecer (Parte 22): GANs Condicionais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso