ニューラルネットワークが簡単に（第93回）：周波数領域と時間領域における適応予測（最終回）

MetaTrader 5 — トレーディングシステム | 6 12月 2024, 11:07

138

Dmitriy Gizlyk

はじめに

前回の記事では、2つの時系列予測モデルのアンサンブルであるATFNetアルゴリズムについて学びました。そのうちの1つは時間領域で動作し、信号振幅の分析に基づいて対象の時系列の予測値を構築します。2つ目は、対象の時系列の周波数特性を使用して動作し、その全体的な依存関係、周期性、およびスペクトルを記録します。この手法の提案者は、2つの独立した予測を適応的に統合することで、非常に優れた結果が得られると主張しています。

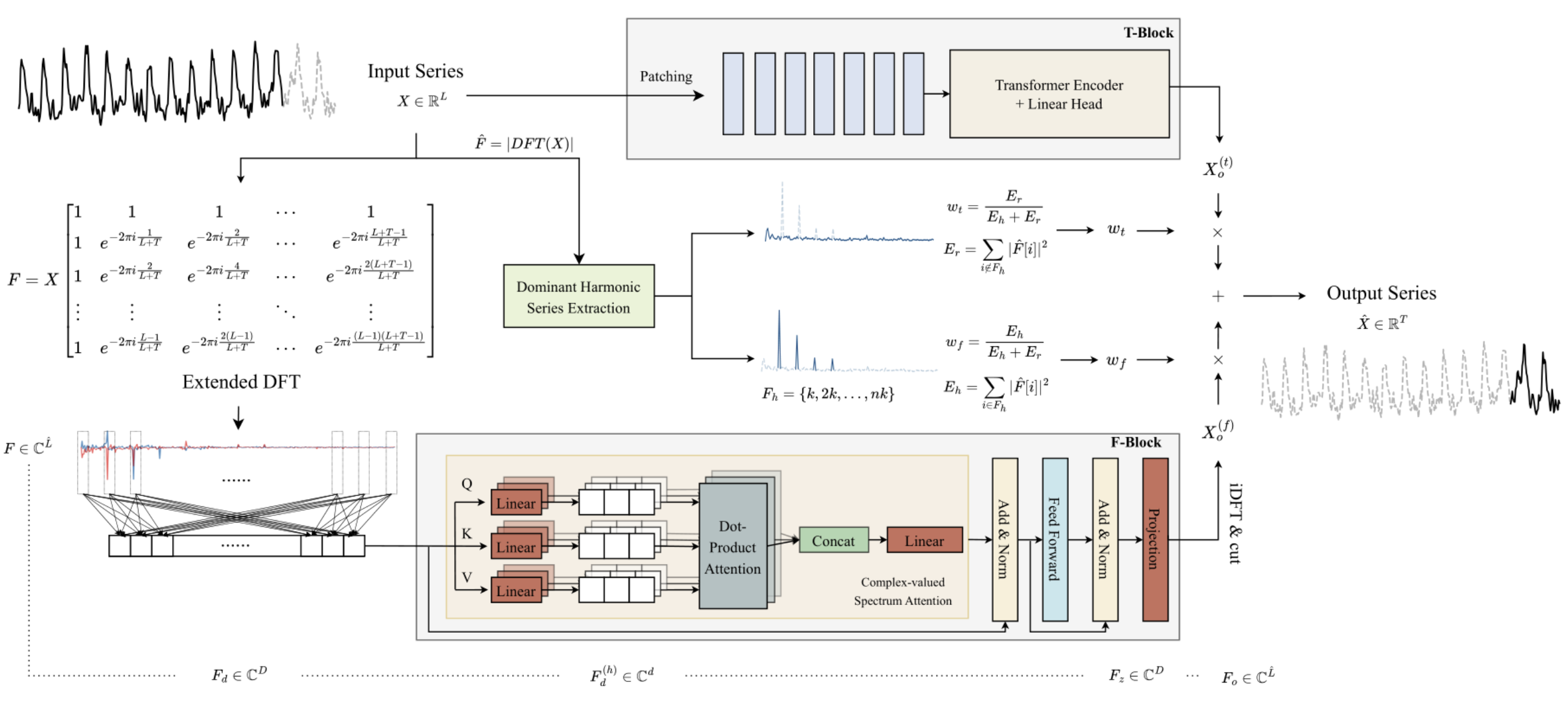
周波数Fブロックの主な特徴は、複素数の数学を使用してアルゴリズム全体を構築している点です。この要件を満たすために、前回の記事ではCNeuronComplexMLMHAttentionクラスを構築しました。このクラスは、マルチヘッド自己注意(Self-Attention)の要素を備えたTransformer型の多層エンコーダアルゴリズムを完全に再現しています。この統合注意クラスは、Fブロックの基礎となるものです。この記事では、ATFNet法の提案者が示したアプローチを引き続き実装します。

1. ATFNetクラスの作成

複雑な注意クラスCNeuronComplexMLMHAttentionである周波数Fブロックの基礎を実装した後、レベルを上げて、ATFNetアルゴリズム全体を実装するCNeuronATFNetOCLクラスを作成します。

ATFNetのような複雑なアルゴリズムを単一のニューラル層クラスに実装解決策は最適ではない可能性があることは、認めなければなりません。ただし、以前に構築したシーケンシャルニューラルネットワークモデルでは、複数の異なる並列プロセスの作業を整理することはできません。これはまさにここでのケースであり、TブロックとFブロックを使用します。このような機能の実装には、より全体的な変更が必要になります。そのため、最小限のコストで解決策を作成すること、つまり、アルゴリズム全体を1つのニューラル層クラスとして実装することにしました。CNeuronATFNetOCLのクラス構造体を以下に示します。

class CNeuronATFNetOCL  :  public CNeuronBaseOCL
  {
protected:
   uint              iHistory;
   uint              iForecast;
   uint              iVariables;
   uint              iFFT;
   //--- T-Block
   CNeuronBatchNormOCL  cNorm;
   CNeuronTransposeOCL  cTranspose;
   CNeuronPositionEncoder  cPositionEncoder;
   CNeuronPatching      cPatching;
   CLayer               caAttention;
   CLayer               caProjection;
   CNeuronRevINDenormOCL cRevIN;
   //--- F-Block
   CBufferFloat      *cInputs;
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CBufferFloat      cMainFreqWeights;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CBufferFloat      cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cOutputTimeSeriasReGrad;
   CBufferFloat      cReconstructInput;
   CBufferFloat      cForecast;
   CBufferFloat      cReconstructInputGrad;
   CBufferFloat      cForecastGrad;
   CBufferFloat      cZero;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, 
                         bool reverse = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   virtual bool      MainFreqWeights(void);
   virtual bool      WeightedSum(void);
   virtual bool      WeightedSumGradient(void);
   virtual bool      calcReconstructGradient(void);

public:
                     CNeuronATFNetOCL(void) {};
                    ~CNeuronATFNetOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronATFNetOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *net, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual CBufferFloat   *getWeights(void);
  };

提示されたCNeuronATFNetOCLのクラス構造体にある4つの内部変数に注目してください。

iHistory：分析された歴史の深さ
iForecast：計画期間
iVariables：分析変数（ユニタリ時系列）の数
iFFT：高速フーリエ分解テンソル(DFT)のサイズ

先に見たように、DFTアルゴリズムでは、初期データベクトルのサイズが2の累乗の1つに等しいことが必要です。そこで、初期データテンソルをゼロ値で補って必要なサイズにします。

メソッドの内部オブジェクトは、ATFNetアルゴリズムのどのブロックに属するかによって、2つのブロックに分けられます。アルゴリズムを実装しながら、クラスメソッドの機能だけでなく、その目的も考えていきます。

内部オブジェクトはすべて静的に宣言されるので、CNeuronATFNetOCLクラスのコンストラクタとデストラクタは空にしておくことができます。

1.1 オブジェクトの初期化

新しいクラスの内部オブジェクトの初期化はInitメソッドでおこないます。ここで、ATFNetアルゴリズム全体を1つのクラスで実装するという決断の最初の影響が発生します。つまり、呼び出し元から多数のパラメータを渡す必要があるということです。

実際には、CNeuronATFNetOCLクラスの中で、時間Tブロックと周波数Fブロックの両方で注意メカニズムを使用する2つの並列多層モデルを構築する必要があります。それぞれのモデルについて、アーキテクチャを指定する必要があります。

この問題を解決するために、可能な限り「普遍的な」パラメータ、つまりどちらのモデルでも同じように使えるパラメータを使うことにしました。さて、入出力テンソルを記述するためのパラメータとして、分析履歴の深さ、単位時系列の数、計画期間があります。これらのパラメータは、Tブロックと Fブロックで同じように使用されます。

さらに、どちらのモデルもTransformerのエンコーダーを中心に構築され、複数層を持つマルチヘッド自己注意アーキテクチャを利用しています。ここでは、両ブロックで同じ数の注意ヘッドとエンコーダー層を使うことにしました。

ただし、Tブロックでは使用され、Fブロックでは類似のものがないデータ分割層のために、追加のパラメータを渡す必要があります。メソッドのパラメータの数を大幅に増やさないために、3要素の配列を使うことにしました。この配列の最初の要素には1セグメント分のウィンドウサイズが格納され、2番目の要素にはソースデータバッファ内のこのウィンドウのステップが格納されます。配列の最後の要素には、データ分割層の出力における1パッチのサイズを書き入れます。

bool CNeuronATFNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[],
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch))
      return false;

メソッド本体では、いつものように、同じ名前の親クラスの初期化メソッドを呼び出します。親クラスメソッドでは、層のサイズを分析変数（単位時系列）の数と計画期間の積として指定することに注意してください。言い換えれば、CNeuronATFNetOCL層の出力は、分析された時系列の予測された継続の準備された結果となることが期待されます。

継承したオブジェクトの初期化に成功したら、主要なアーキテクチャーパラメータを変数に保存します。

   iHistory = MathMax(history, 1);
   iForecast = forecast;
   iVariables = variables;

次に、高速フーリエ分解のためのテンソルのサイズを計算します。ATFNetの著者は、過去のデータと予測データが与えられた場合に、全時系列の周波数特性を決定する拡張フーリエ分解を提案しています。

   uint size = iHistory + iForecast;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

次のステップは、クラスの内部オブジェクトを初期化することです。まずは、予想される初期データのプレゼンテーションから始めましょう。私たちのモデルは時間領域と周波数領域におけるユニタリ時系列の分析を想定しているため、ユニタリ時系列の行列を層の入力として受け取ることが期待されます。CNeuronATFNetOCLは、予測値の同様のマップを出力に返します。

もう1つのポイントは、データの正規化です。モデルの両ブロックは、入力データの正規化を使用します。違いは、Tブロックは時間領域での正規化を使い、Fブロックは周波数領域での正規化を使うことです。そこで、今回の実装では、正規化されていないデータを層に投入することにしました。確率的特性の正規化と逆追加は、対応する次元に従って個々のブロック内でおこなわれます。

読みやすさとコードの透明性のために、内部オブジェクトを使用するブロックごとに、構築されたアルゴリズムの順序で初期化します。まずはTブロックから始めます。

前述のように、正規化されていないデータが層に入力されます。したがって、まず得られたデータを比較可能な形に変換しなければなりません。

//--- T-Block
   if(!cNorm.Init(0, 0, OpenCL, iHistory * iVariables, batch, optimization))
      return false;

ATFNetmethodの著者は、周波数領域では位置データ符号化を使用しませんが、時間領域のデータを分析するときには使用します。位置エンコーディング層を追加ましょう。

   if(!cPositionEncoder.Init(0, 1, OpenCL, iVariables, iHistory, optimization, batch))
      return false;

データ分割層を構築する際、そのアルゴリズムに一種のデータ転置を組み込みました。ここで、CNeuronPatching層に入力する前に、入力を準備する必要があります。この操作をおこなうために、データ転置層を追加します。

   if(!cTranspose.Init(0, 2, OpenCL, iHistory, iVariables, optimization, batch))
      return false;
   cTranspose.SetActivationFunction(None);

次に、分割層の出力におけるパッチの数を、外部プログラムからのメソッドパラメータで得られた、1つのセグメントのウィンドウサイズとそのステップに基づいて計算する必要があります。

   uint count = (iHistory - patch[0] + 2 * patch[1] - 1) / patch[1];

必要な準備作業をおこなった後、データ分割層を初期化します。

   if(!cPatching.Init(0, 3, OpenCL, patch[0], patch[1], patch[2], count, iVariables, optimization, batch))
      return false;

PatchTSTメソッドを構築する際にConformerを注意ブロックとして使用しました。ここでは同じ解決策を使います。次のステップでは、必要な数のCNeuronConformerの入れ子層を作成します。

   caAttention.SetOpenCL(OpenCL);
   for(uint l = 0; l < layers; l++)
     {
      CNeuronConformer *temp = new CNeuronConformer();
      if(!temp)
         return false;
      if(!temp.Init(0, 4 + l, OpenCL, patch[2], 32, heads, iVariables, count, optimization, batch))
        {
         delete temp;
         return false;
        }
      if(!caAttention.Add(temp))
        {
         delete temp;
         return false;
        }
     }

入力時系列を分析する注意ブロックに続いて、3つの畳み込み層からなるブロックが、個々の単位時系列の文脈で、全計画深度における後続データの予測を実行します。

   int total = 3;
   caProjection.SetOpenCL(OpenCL);
   uint window = patch[2] * count;
   for(int l = 0; l < total; l++)
     {
      CNeuronConvOCL *temp = new CNeuronConvOCL();
      if(!temp)
         return false;
      if(!temp.Init(0, 4+layers+l, OpenCL, window, window, (total-l)*iForecast, iVariables, optimization, batch))
        {
         delete temp;
         return false;
        }
      temp.SetActivationFunction(TANH);
      if(!caProjection.Add(temp))
        {
         delete temp;
         return false;
        }
      window = (total - l) * iForecast;
     }

各層で、分析された時系列のユニタリ時系列の数と同じ数のシーケンス要素を指定します。後続の各層では、ニューラル層の出力におけるフィルタの数は減少し、最後の層で指定された予測深度に等しくなります。

Tブロックの出力では、CNeuronRevINDenormOCL層を使って、入力時系列の統計パラメータを予測値に追加します。

   if(!cRevIN.Init(0, 4 + layers + total, OpenCL, iForecast * iVariables, 1, cNorm.AsObject()))
      return false;

この時点で、Tブロックに関連するすべての内部オブジェクトを時間領域予測で初期化しました。次に、周波数Fブロックのオブジェクトを操作します。

ATFNetアルゴリズムによれば、Fブロックに入力された入力データは、高速フーリエ分解 (DFT)を用いて周波数領域に変換されます。覚えているように、先に構築したDFTアルゴリズムの実装では、周波数スペクトルを2つのデータバッファに書き込みます。1つはスペクトルの実数部用、もう1つは虚数部用です。

//--- F-Block
   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

その後の処理を容易にするため、スペクトル情報を1つのバッファにまとめます。

   if(!cInputFreqComplex.Init(0, 0, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

優位周波数の割合を書き込むためのバッファも用意する必要があります。ここで注意しなければならないのは、各ユニタリ時系列について個別に優位周波数を決定していることです。

   if(!cMainFreqWeights.BufferInit(iVariables, 0) || !cMainFreqWeights.BufferCreate(OpenCL))
      return false;

この層への入力は生データであり、ユニタリ時系列のまったく異なるスペクトルを生成します。後続の処理の前にスペクトルを比較可能な形式に変換するために、この方法の著者は周波数特性を正規化することを推奨しています。正規化したデータをcNormFreqComplex層バッファに保存します。

   if(!cNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

この場合、元のスペクトルの統計的特性を対応するデータバッファに保存します。

   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

用意された入力データの周波数特性を、コンプレックス注意ブロックを使って処理します。前回は、CNeuronComplexMLMHAttentionクラスの大規模な実装をおこないました。あとは、指定したクラスの内部オブジェクトを初期化するだけです。

   if(!cFreqAtteention.Init(0, 2, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

アルゴリズムによれば、複雑な注意ブロックで入力スペクトルを処理した後、逆プロシージャを実行する必要があります。まず、入力周波数特性の統計的指標を処理されたスペクトラムに加えます。

   if(!cUnNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

スペクトルの現実部分と虚数部分を分けてみましょう。

   if(!cOutputFreqRe.BufferInit(iFFT*iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT*iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

そしてデータを一時領域に戻します。

   if(!cOutputTimeSeriasRe.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

バックプロパゲーションのパスのために、時系列の実数部分の勾配バッファを作成します。

   if(!cOutputTimeSeriasReGrad.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasReGrad.BufferCreate(OpenCL))
      return false;

時系列の虚数部分については、勾配バッファを作成しないことに注意してください。ポイントは、時系列では虚数部の目標値は0であるということです。したがって、虚数部の誤差勾配は、逆符号の虚数部の値と等しくなります。バックプロパゲーションパスでは、処理された時系列の虚数部分に対してフィードフォワードパスの結果バッファを使用することができます。

逆DFT (iDFT)の後、入力データの再構築と所定の計画地平線の予測値からなる処理された全時系列を受け取る予定であることに注意してください。予測値の必要な部分を抽出するために、時系列全体を再構成データと予測値の2つのバッファに分割します。

   if(!cReconstructInput.BufferInit(iHistory*iVariables, 0) || !cReconstructInput.BufferCreate(OpenCL))
      return false;
   if(!cForecast.BufferInit(iForecast*iVariables, 0) || !cForecast.BufferCreate(OpenCL))
      return false;

対応するエラー勾配用のバッファを追加します。

   if(!cReconstructInputGrad.BufferInit(iHistory*iVariables, 0) || !cReconstructInputGrad.BufferCreate(OpenCL))
      return false;
   if(!cForecastGrad.BufferInit(iForecast*iVariables, 0) || !cForecastGrad.BufferCreate(OpenCL))
      return false;

ATFNetの著者が提案した方法では、分析された時系列の入力値からの再構成データの乖離の分析は行われていないことに注意してください。複雑な注意ブロックをより細かく調整するために、この機能を追加しました。分析対象のデータをより深く理解することで、モデルの予測品質が向上する可能性があります。

さらに、入力データとエラー勾配の欠損値を埋めるために使用されるゼロ値のバッファを作成します。

   if(!cZero.BufferInit(iFFT*iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

各段階での作動プロセスの監視を忘れないでください。宣言されたすべてのオブジェクトの初期化が完了したら、メソッド操作の実行の論理値を呼び出し元に返します。

1.2 フィードフォワードパス

クラスオブジェクトの初期化を終えたら、フィードフォワードアルゴリズムの構築に移ります。OpenCLプログラムで追加のカーネルをビルドすることから始めましょう。

まず、ユニタリ時系列の周波数応答スペクトルの正規化について考えてみましょう。以前に実装された実データの正規化アルゴリズムを使用すると、データが大きく歪む可能性があります。そのため、複雑な領域でデータの正規化を実施する必要があっります。この機能はComplexNormalizeカーネルに実装されています。カーネルパラメータには、4つのデータバッファへのポインタとユニタリシーケンスのサイズを渡します。このカーネルをユニタリ時系列スペクトルの文脈で1次元の問題空間で使用します。

__kernel void ComplexNormalize(__global float2 *inputs,
                               __global float2 *outputs,
                               __global float2 *means,
                               __global float *vars,
                               int dimension)
  {
   if(dimension <= 0)
      return;

データバッファの宣言に注目してください。入力、出力、平均データバッファはfloat2ベクトル型です。複雑な量を扱うために、OpenCL側でこの型のデータを使うことにしました。しかし、実数型floatで宣言される分散バッファもあります。分散は平均からの値の標準偏差を示します。2点間の距離は実数です。

メソッドの本体では、得られた正規化ベクトルの次元を確認します。明らかに「0」より大きくなければなりません。次に、タスク空間内の現在のスレッドを特定し、データバッファ内のオフセットを決定し、分析対象のシーケンスの次元の複雑な表現を作成します。

   size_t n = get_global_id(0);
   const int shift = n * dimension;
   const float2 dim = (float2)(dimension, 0);

次に、分析したスペクトルの平均値を決定するループを構成します。

   float2 mean = 0;
   for(int i = 0; i < dimension; i++)
     {
      float2 val = inputs[shift + i];
      if(isnan(val.x) || isinf(val.x) ||
         isnan(val.y) || isinf(val.y))
         inputs[shift + i] = (float2)0;
      else
         mean += val;
     }
   means[n] = mean = ComplexDiv(mean, dim);

得られた結果は直ちに平均値バッファの対応する要素に保存します。

次の段階では、分析した配列の分散を決定するためのループを編成します。

   float variance = 0;
   for(int i = 0; i < dimension; i++)
      variance += pow(ComplexAbs(inputs[shift + i] - mean), 2);
   vars[n] = variance = sqrt((isnan(variance) || isinf(variance) ? 1.0f : variance / dimension));

ここで注意すべき点が2つあります。まず、平均値を外部データバッファに保存しているにもかかわらず、コンテキストのグローバルメモリにあるバッファ要素にアクセスする方がローカルカーネル変数にアクセスするよりもはるかに遅いため、操作を実行するときにローカル変数の値を使用します。

2つ目のポイントは方法論的なものです。複素数列の分散を計算する場合、実数とは異なり、複素数列の要素の平均値からの偏差の絶対値を二乗します。複素数の絶対値は、実部と虚部の 2 次元空間内の点間の距離を示します。一方、複素数の単純な差は、座標のシフトのみを示します。実部と虚部の2次元空間における点間の距離を示す複素数の絶対値です。複雑な量の単純な差は、座標のずれを示すだけです。

カーネル操作の最後の段階で、最後のループを構成し、そこで入力スペクトルのデータを正規化します。得られた値を結果バッファの対応する要素に書き込みます。

   float2 v=(float2)(variance, 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexDiv((inputs[shift + i] - mean), v);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      outputs[shift + i] = val;
     }
  }

ここでは、平均と標準偏差のローカル変数も扱います。

そしてすぐに逆正規化カーネルComplexUnormalizeを作成し、入力スペクトルの抽出された統計指標を返します。

__kernel void ComplexUnNormalize(__global float2 *inputs,
                                 __global float2 *outputs,
                                 __global float2 *means,
                                 __global float *vars,
                                 int dimension)
  {
   if(dimension <= 0)
      return;

このカーネルは、データバッファへの4つのポインタと1つの変数という同じパラメータセットを受け取ります。また、ユニタリ時系列数の1次元タスク空間でカーネルを実行する予定です。

カーネル本体では、タスク空間でスレッドを識別し、データバッファのオフセットを定義します。

   size_t n = get_global_id(0);
   const int shift = n * dimension;

バッファから統計変数をロードし、直ちに標準偏差を複素数に変換します。

   float v= vars[n];
   float2 variance=(float2)((v > 0 ? v : 1.0f), 0)
   float2 mean = means[n];

そして、このカーネルで唯一のデータ変換ループを編成します。

   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexMul(inputs[shift + i], variance) + mean;
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      outputs[shift + i] = val;
     }
  }

得られた値は、結果バッファの対応する要素に書き込まれます。

上記で作成したカーネルをメインプログラム側で呼び出すには、ComplexNormalizeメソッドとComplexUnormalizeメソッドを使用します。その構築アルゴリズムは、以前に検討されたOpenCLプログラムのカーネルをエンキューイングする方法と変わりません。従って、これらの方法については触れないことにします。いずれにせよ、それらは添付ファイルに記載されています。

さらに、時間予測と周波数予測の結果を適応的に組み合わせるためには、影響係数が必要です。ATFNet法の著者は、スペクトル全体における優位周波数の割合によって決定することを提案しています。したがって、OpenCL側では、プログラム用に2つのカーネルを作成します。

MainFreqWeight：優位周波数の割合を決める
WeightedSum：周波数領域と時間領域における予測の加重和を計算する

解析されたユニタリ時系列の数に応じて、1次元のタスク空間で両カーネルを計画します。

MainFreqWeightカーネルパラメータでは、2つのデータバッファ（周波数特性と結果）へのポインタと、分析された系列の次元を渡します。

__kernel void MainFreqWeight(__global float2 *freq,
                             __global float *weight,
                             int dimension
                            )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

カーネル本体では、タスク空間で現在のスレッドを識別し、データバッファのオフセットを決定します。その後、ローカル変数を準備します。

   float max_f = 0;
   float total = 0;
   float energy;

次に、優位周波数とスペクトル全体のエネルギーを決定するループを実行します。

   for(int i = 0; i < dimension; i++)
     {
      energy = ComplexAbs(freq[shift + i]);
      total += energy;
      max_f = fmax(max_f, energy);
     }

カーネル演算を完了するために、優位周波数エネルギーを全スペクトルエネルギーで割ります。結果の値は、出力バッファの対応する要素に保存されます。

   weight[n] = max_f / (total > 0 ? total : 1);
  }

時間領域と周波数領域の予測値の加重和を決定するためのWeightedSumカーネルのアルゴリズムは非常に単純です。パラメータでは、カーネルはデータバッファへの4つのポインタと、1つのシーケンスのベクトルの次元（この場合は予測深度）を受け取ります。

__kernel void WeightedSum(__global float *inputs1,
                          __global float *inputs2,
                          __global float *outputs,
                          __global float *weight,
                          int dimension
                         )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

カーネル本体では、1次元のタスク空間で現在のスレッドを識別し、データバッファのオフセットを決定します。そして、要素の重み付き和のループを作ります。演算結果は、結果バッファの対応する要素に書き込まれますう。

   float w = weight[n];
   for(int i = 0; i < dimension; i++)
      outputs[shift + i] = inputs1[shift + i] * w + inputs2[shift + i] * (1 - w);
  }

メインプログラム側でカーネルを実行キューに入れるために、同じ名前のメソッドを作ります。これらのコードは添付ファイルにあります。

準備作業が終わったら、CNeuronATFNetOCLクラスのフィードフォワードパスメソッドfeedForwardの構築に移ります。このメソッドのパラメータでは、親クラスの同様のメソッドと同様に、前のニューラル層オブジェクトへのポインタを受け取ります。この場合、このポインタは後続の操作の初期データとして機能します。

bool CNeuronATFNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !NeuronOCL.getOutput())
      return false;

メソッド本体では、まず受け取ったポインタの妥当性を確認します。ここでは、得られたニューラル層の結果バッファへのポインタもカレントオブジェクトの内部変数に保存します。

   if(cInputs != NeuronOCL.getOutput())
      cInputs = NeuronOCL.getOutput();

次に、分析した時系列の後続データに対して、まず時間領域で予測演算をおこないます。得られたデータを正規化します。

//--- T-Block
   if(!cNorm.FeedForward(NeuronOCL))
      return false;;

その後、位置エンコーディングを追加します。

   if(!cPositionEncoder.FeedForward(cNorm.AsObject()))
      return false;

得られたテンソルを転置し、データをパッチに分割します。

   if(!cTranspose.FeedForward(cPositionEncoder.AsObject()))
      return false;
   if(!cPatching.FeedForward(cTranspose.AsObject()))
      return false;

準備されたデータは注意ブロックを通過します。

   int total = caAttention.Total();
   CNeuronBaseOCL *prev = cPatching.AsObject();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att.FeedForward(prev))
         return false;
      prev = att;
     }

その後の値は予測値です。

   total = caProjection.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj.FeedForward(prev))
         return false;
      prev = proj;
     }

Tブロックの出力では、予測値に入力時系列の統計値を加えます。

   if(!cRevIN.FeedForward(prev))
      return false;

時間領域で予測値を得た後、周波数領域での作業に移ります。まず、得られた時系列を周波数特性のスペクトルに変換します。これにはFFTアルゴリズムを使用します。

//--- F-Block
   if(!FFT(cInputs, cInputs, GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), false))
      return false;

周波数スペクトルの実数部と虚数部の2つのバッファを得た後、それらを1つのテンソルに結合します。

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(), 1, 1,
                                                                                     iFFT * iVariables))
      return false;

両データバッファの連結には、1要素のウィンドウサイズを使用します。これにより、対応する周波数特性の実数部と虚数部が近いテンソルが得られます。

得られた入力周波数のテンソルを正規化します。

   if(!ComplexNormalize())
      return false;

優位周波数の割合を決定します。

   if(!MainFreqWeights())
      return false;

用意された周波数データを注意ブロックに通します。ここでは、前回の記事で作成した多層複合注意クラスのフィードフォワードパスメソッドを呼び出すだけで済みます。

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

注意ブロックの操作が正常に実行された後、処理されたデータに入力系列周波数の統計パラメータを返します。

   if(!ComplexUnNormalize())
      return false;

周波数スペクトルテンソルを実部と虚部に分割します。

   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getOutput(), 1, 1,
                                                                                          iFFT * iVariables))
      return false;

周波数スペクトルを時系列に戻します。

   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm),

           GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;

上記のFブロックの運用について説明しなければならないと思います。一見すると、注意操作を実行するためだけに、時系列を周波数応答に大量に変換し、それらを正規化し、次にデータを同じ時系列に戻す逆操作を実行するのは奇妙に思えるかもしれません。さらに、注意を除くこれらの操作はすべて、訓練可能なパラメータを持たず、理論的には元の時系列を返す必要があります。しかし、それはすべて注意ブロックに関することです。

この手法の著者が拡張離散フーリエ変換の使用を提案したことを思い出してください。実際には、完全な時系列のDFTに複雑な指数基底を使用するだけです。ただし、元の時系列をその周波数特性に変換する際、予測値が存在しないため、単にゼロ値で置き換えます。このため、逆DFTを実行すると、当然ながら「0」に近い予測値が得られますが、これは望ましい結果ではありません。そのため、ユニタリ（正規化された）時系列のスペクトルを正規化し、比較可能な形式に整えます。そして、注意ブロック内でそれらを相互に比較することで、分析した周波数特性の欠損データを復元するようモデルに学習させるのです。

この結果として、複雑な注意ブロックの出力では、欠損データが復元されたユニタリな完全時系列の周波数特性が、一貫性を持った修正済みスペクトルとして得られることが期待されます。この修正済みスペクトルから時系列を復元することで、分析対象の時系列においてゼロではない予測値を得ることが可能になります。

フィードフォワードパス操作を完了するには、この完全な時系列から予測値を抽出するだけです。

   if(!DeConcat(GetPointer(cReconstructInput), GetPointer(cForecast), GetPointer(cOutputTimeSeriasReGrad),

                GetPointer(cOutputTimeSeriasRe), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables))
      return false;

そして、有意係数を考慮に入れて、時間領域と周波数領域でおこなわれた予測を合計します。

//--- Output
   if(!WeightedSum())
      return false;
//---
   return true;
  }

すべての段階で、操作の結果をモニターすることを忘れないでください。メソッドの操作が完了したら、すべての操作の論理結果を呼び出し元に返します。

1.3 誤差勾配分布

フィードフォワードパスを実行した後、誤差勾配をモデルのすべての学習パラメータに分配する必要があります。新しいクラスでは、TブロックとFブロックの両方にあります。したがって、TブロックとFブロックを介して誤差勾配を伝播するメカニズムを実装する必要があります。次に、2つのストリームからの誤差勾配を結合し、その結果の勾配を前の層に渡す必要があります。

フィードフォワードパスと同様に、calcInputGradientsメソッドを構築する前にはいくつかの準備作業が必要です。フィードフォワードパスの間、OpenCL側では、正規化と統計分布値の逆戻り用のカーネルを作成しました。ComplexNormalizeとComplexUnormalizeです。バックプロパゲーションのパスでは、それぞれComplexNormalizeGradientとComplexUnormalizeGradientの操作をおこない、誤差勾配分布カーネルを作成する必要があります。

誤差勾配分布カーネルでは、周波数正規化ブロックを通して、得られた誤差勾配を対応するスペクトルの標準偏差で割るだけです。

__kernel void ComplexNormalizeGradient(__global float2 *inputs_gr,
                                       __global float2 *outputs_gr,
                                       __global float *vars,
                                       int dimension)
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;
//---
   float v = vars[n];
   float2 variance = (float2)((v > 0 ? v : 1.0f), 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexDiv(outputs_gr[shift + i], variance);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      inputs_gr[shift + i] = val;
     }
  }

これは、この問題を解決するためのかなり単純化されたアプローチであると言わざるを得ません。ここでは、平均値と標準偏差を定数として取ります。実際、これらは関数であり、勾配降下法のルールに従って、それらの影響を調整し、モデルの影響要素にエラー勾配を伝播する必要もあります。しかし、実践が示すように、これらの要素が初期データに与える影響は非常に小さいです。したがって、モデルの訓練コストを削減するために、これらの操作を省略します。

データの非正規化操作による勾配分布のカーネルも同様ですが、唯一の違いは、ここでは結果の誤差勾配に標準偏差を掛ける点です。

__kernel void ComplexUnNormalizeGradient(__global float2 *inputs_gr,
      __global float2 *outputs_gr,
      __global float *vars,
      int dimension)
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;
//---
   float v = vars[n];
   float2 variance = (float2)((v > 0 ? v : 1.0f), 0);
   for(int i = 0; i < dimension; i++)
     {
      float2 val = ComplexMul(outputs_gr[shift + i], variance);
      if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y))
         val = (float2)0;
      inputs_gr[shift + i] = val;
     }
  }

次に、時間領域と周波数領域の予測ブロック間の合計エラー勾配を分散するカーネルを実装する必要があります。この機能をWeightedSumGradientカーネルに実装します。パラメータでは、このカーネルは対応するフィードフォワードカーネルと同様に、4つのデータバッファと1つのパラメータへのポインタを受け取ります。

__kernel void WeightedSumGradient(__global float *inputs_gr1,
                                  __global float *inputs_gr2,
                                  __global float *outputs_gr,
                                  __global float *weight,
                                  int dimension
                                 )
  {
   if(dimension <= 0)
      return;
//---
   size_t n = get_global_id(0);
   const int shift = n * dimension;

カーネル本体では、通常どおり、1次元タスク空間内の現在のスレッドを識別し、データバッファー内のオフセットを決定します。その後、頻度と時系列の予測のためのローカル重み変数を準備します。

   float w = weight[n];
   float w1 = 1 - weight[n];

次に、対応するデータバッファ全体に誤差勾配を伝播するループを作成します。

   for(int i = 0; i < dimension; i++)
     {
      float grad = outputs_gr[shift + i];
      inputs_gr1[shift + i] = grad * w;
      inputs_gr2[shift + i] = grad * w1;
     }
  }

上記の誤差勾配伝播カーネルは、メインプログラム側の関連メソッド内の実行キューに配置されます。添付ファイルでこれらのメソッドのコードを確認できます。

注意すべきもう1つの点は、履歴値の再構築された時系列の誤差勾配の計算です。この機能はcalcReconstructGradientメソッドに実装します。

操作はOpenCLコンテキスト側で実行されますが、指定された操作を実行するために新しいカーネルを作成する必要はありません。代わりに、ターゲット値に基づいてエラー勾配を決定する既製のカーネルを使用します。Fブロックのデータバッファーを使用してカーネルを実行キューに入れるメソッドを作成する必要があります。

私たちが使用するカーネルは、テンソルの要素数に応じて1次元のタスク空間で実行されます。この場合、分析されるベクトルのサイズは、分析される履歴の深さとユニタリ時系列の数の積に等しくなります。

bool CNeuronATFNetOCL::calcReconstructGradient(void)
  {
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = iHistory * iVariables;

ターゲットデータには、前のニューラル層からのフィードフォワードパス中に取得した元のデータの値が含まれます。フィードフォワードパス中に、必要なデータバッファへのポインターを保存しました。

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_t, cInputs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

処理されたスペクトルから再構成データの誤差勾配を求めます。

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_o, cReconstructInput.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

その演算結果を回収データの勾配バッファに書き込みます。

   if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_ig, cReconstructInputGrad.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

フォワードパスでは活性化関数は使いませんでした。

   if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_activation, (int)None))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

カーネルを実行キューに入れ、操作の結果をチェックしてメソッドを完了し、実行された操作の論理結果を呼び出し元に返します。

   if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_error, 1))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   ResetLastError();
   if(!OpenCL.Execute(def_k_CalcOutputGradient, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel CalcOutputGradient: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

準備作業が完了したら、誤差勾配伝播メソッドcalcInputGradientsの構築に直接進みます。

このメソッドのパラメータでは、親クラスの同じメソッドと同様に、誤差勾配を伝播する必要がある前のニューラル層のオブジェクトへのポインタを受け取ります。

bool CNeuronATFNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !NeuronOCL.getGradient() || !cInputs)
      return false;

メソッド本体では、受け取ったポインタの妥当性を即座に確認します。その後、後続の層から取得した誤差勾配を、時間領域と周波数領域の予測ブロック間の2つのストリームに分配します。

//--- Output
   if(!WeightedSumGradient())
      return false;

まず、時間領域の予測Tブロックを通して誤差勾配を伝播させます。ここでは、フィードフォワードパスと逆の順序で、ネストされたオブジェクトの関連メソッドを呼び出します。

//--- T-Block
   if(cRevIN.Activation() != None && 
     !DeActivation(cRevIN.getOutput(), cRevIN.getGradient(), cRevIN.getGradient(), cRevIN.Activation()))
      return false;
   CNeuronBaseOCL *next = cRevIN.AsObject();
   for(int i = caProjection.Total() - 1; i >= 0; i--)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj || !proj.calcHiddenGradients((CObject *)next))
         return false;
      next = proj;
     }
   for(int i = caAttention.Total() - 1; i >= 0; i--)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att || !att.calcHiddenGradients((CObject *)next))
         return false;
      next = att;
     }
   if(!cPatching.calcHiddenGradients((CObject*)next))
      return false;
   if(!cTranspose.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cPositionEncoder.calcHiddenGradients(cTranspose.AsObject()))
      return false;
   if(!cNorm.calcHiddenGradients(cPositionEncoder.AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(cNorm.AsObject()))
      return false;

周波数予測ブロックの勾配伝播アルゴリズムはもう少し複雑です。ここではまず、再構成された時系列の虚数部に対する誤差勾配を定義します。前述の通り、時系列の虚数部の目標値は0です。したがって、誤差勾配を決定するには、フィードフォワードパスの結果の符号を変えるだけで済みます。

//--- F-Block
   if(!CNeuronBaseOCL::SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), 
                                       GetPointer(cOutputTimeSeriasIm), iFFT*iVariables, false, 0, 0, 0, -0.5))
      return false;

次に、過去のデータ復元誤差の勾配を定義します。

   if(!calcReconstructGradient())
      return false;

その後、履歴データ復元誤差の勾配テンソル（calcReconstructGradientメソッドで定義）、時系列予測誤差の勾配（後続層の誤差の勾配を2つのストリームに分割して得られる）を組み合わせ、全系列のスペクトルのサイズまでゼロ値で補完します。

   if(!Concat(GetPointer(cReconstructInputGrad), GetPointer(cForecastGrad), GetPointer(cZero), 
              GetPointer(cOutputTimeSeriasReGrad), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables))
      return false;

計画地平線を超える目標値に関するデータがないため、全時系列の誤差勾配テンソルの末尾にゼロ値を追加します。つまり、単に修正しないだけです。

その結果、周波数予測ブロックデータを用いて構築された全時系列の誤差勾配は、FFTを適用することで周波数領域に変換されます。

   if(!FFT(GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasIm),





           GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), false))
      return false;

得られた誤差勾配の周波数スペクトルの実数部と虚数部のデータを1つのテンソルにまとめます。

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getGradient(),
                                                                              1, 1, iFFT * iVariables))
      return false;

データ非正規化操作の微分の誤差勾配を修正します。

   if(!ComplexUnNormalizeGradient())
      return false;

複合注意ブロックを通して誤差勾配を伝播させます。

   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;

次に、データ正規化関数の微分によって誤差勾配を補正します。

   if(!ComplexNormalizeGradient())
      return false;

スペクトルの実部と虚部を分けます。

   if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getGradient(),
                                                                             1, 1, iFFT * iVariables))
      return false;

IFFTを用いて誤差勾配を時間領域に戻します。

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm),



           GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), false))
      return false;

なお、誤差勾配は全時系列について求めましたが、過去のデータの誤差の勾配を前の層に伝搬させるだけも大丈夫です。そのため、まず分析対象の歴史的地平のデータを選択します。

   if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasRe), 
                                                                        iHistory, iFFT-iHistory, iVariables))
      return false;

そして、得られた値をTブロックの誤差勾配分布の結果に加えます。

   if(!CNeuronBaseOCL::SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cInputFreqRe), 
                                       NeuronOCL.getGradient(), iHistory*iVariables, false, 0, 0, 0, 0.5))
      return false;
//---
   return true;
  }

いつものように、各反復において、我々はオペレーションを実行するプロセスをコントロールします。すべての操作が成功したら、メソッドの論理結果を呼び出し元に返します。

1.4 モデルパラメータの更新

モデルの各訓練パラメータの誤差勾配は、全体的な結果に対する影響を決定します。次のステップでは、誤差を最小化するためにモデルのパラメータを調整します。この機能はupdateInputWeightsメソッドで実行されます。このクラスの実装では、パラメータの更新は、学習されるパラメータを含むネストされたオブジェクトの同名のメソッドを呼び出すことを意味します。Fブロックでは複雑な注意クラスでしかありません。

bool CNeuronATFNetOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
//--- F-Block
   if(!cFreqAtteention.UpdateInputWeights(cNormFreqComplex.AsObject()))
      return false;

Tブロックにはそのようなオブジェクトがもっとあります。

//--- T-Block
   if(!cPatching.UpdateInputWeights(cPositionEncoder.AsObject()))
      return false;
   int total = caAttention.Total();
   CNeuronBaseOCL *prev = cPatching.AsObject();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *att = caAttention.At(i);
      if(!att.UpdateInputWeights(prev))
         return false;
      prev = att;
     }
   total = caProjection.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *proj = caProjection.At(i);
      if(!proj.UpdateInputWeights(prev))
         return false;
      prev = proj;
     }
//---
   return true;
  }

以上で、ATFNet法の著者たちが提案したアプローチを実装するためのアルゴリズムについての考察を終えます。CNeuronATFNetOCLクラスの完全なコードは添付ファイルにあります。

2. モデルアーキテクチャ

ATFNet法のアプローチを実装したクラスが完成しました。モデルのアーキテクチャの構築に移りましょう。もうお分かりかもしれませんが、環境状態エンコーダーに新しいニューラル層を実装します。もちろん、CNeuronATFNetOCLクラスをニューラル層と呼ぶのは難しいです。包括的なモデルを構築するために、かなり複雑なアーキテクチャを実装しています。

先に構築したモデルと同じように、エンコーダーに生の入力セットを与えます。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

ただしこの場合、得られたデータを正規化することはしません。TブロックもFブロックも、そのアーキテクチャーにはデータの正規化があるため、このステップは省略します。しかし、入力は環境の個々の状態を表すベクトルに従って形成されます。さらに処理を進める前に、単位時系列で分析できるように入力を移項します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、分析した時系列の後続データを予測するために、新しいクラスを使用します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronATFNetOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.window_out = NForecast;
   descr.step = 8;
   descr.layers = 4;
     {
      int temp[] = {5, 1, 16};
      ArrayCopy(descr.windows, temp);
     }
   descr.activation = None;
   descr.batch = 10000;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

実は、この層にはモデル全体が含まれています。その出力で、計画深度全体に必要な予測値が得られます。必要な次元に移し替えるだけです。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

予測値のスペクトルの一貫性を保つために、FreDF法のアプローチを用います。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(false);
   descr.probability = 0.8f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ActorとCriticのモデルは変更しません。

訓練済みモデルの訓練プログラムとテストプログラムも、以前の記事からコピーしました。添付ファイルにあるコードをご自分で研究してください。

3.テスト

ATFNet法の著者が提案したアプローチをMQL5を使って実装するために、かなり多くの作業をおこないました。その仕事量は、1本の記事の範囲を超えています。最後に、作業の最終段階であるモデルの訓練とテストに移ります。

モデルを訓練するために、以前に作成したEAを使用します。したがって、以前に収集した訓練データも使用できます。

モデルは、2023年全体にわたるH1時間枠のEURUSDの履歴データで訓練されます。

最初の段階では、NForecast定数によって決定される計画期間にわたって、環境のその後の状態を予測するために、エンコーダーモデルを訓練します。

これまでと同様に、エンコーダモデルは価格変動のみを分析するため、訓練の最初の段階では訓練セットを更新する必要はありません。

学習プロセスの第2段階では、最適なActor行動方策を検索します。ここでは、ActorモデルとCriticモデルの反復訓練を実行し、訓練データセットの更新を交互におこないます。訓練データセットを更新する過程で、Actorの現在の方策の領域における環境報酬を洗練させることができ、その結果、望ましい方策を微調整できるようになります。

訓練の過程で、訓練データセットとテストデータセットの両方で利益を生み出すことができるアクター方策を得ることができました。モデルテストの結果を以下に示します。

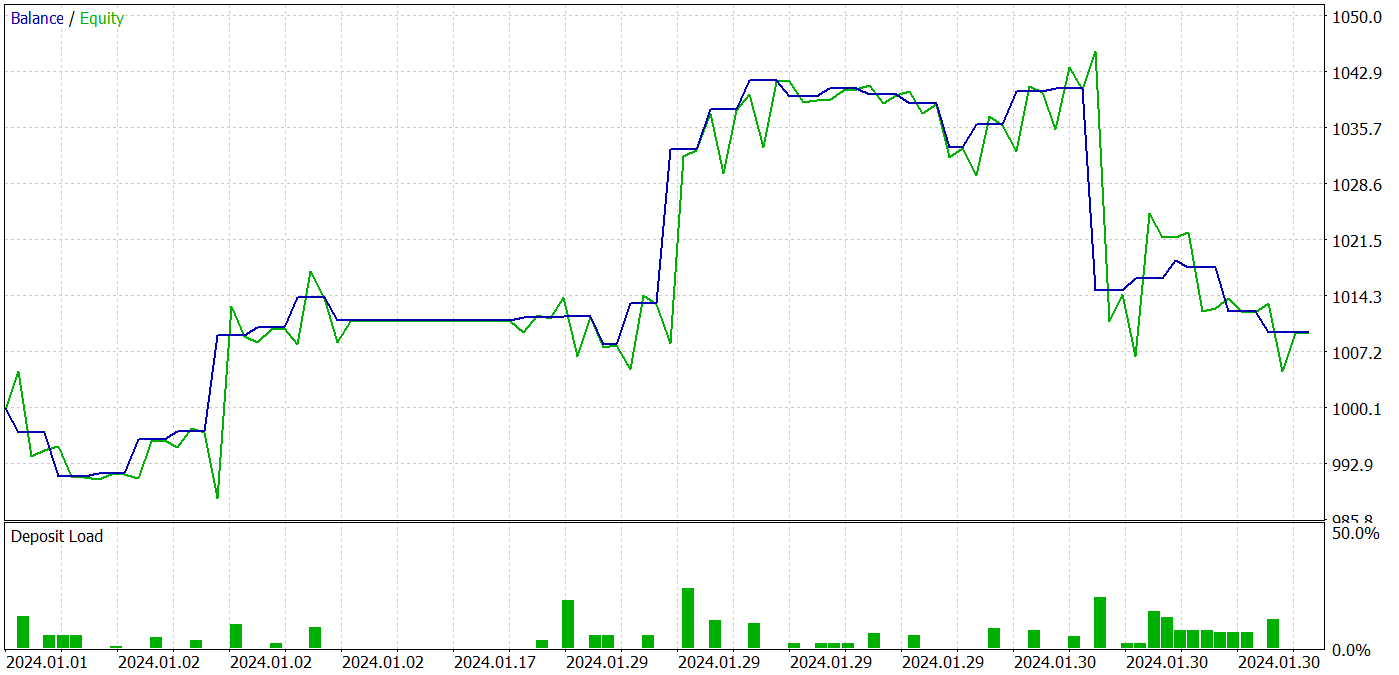
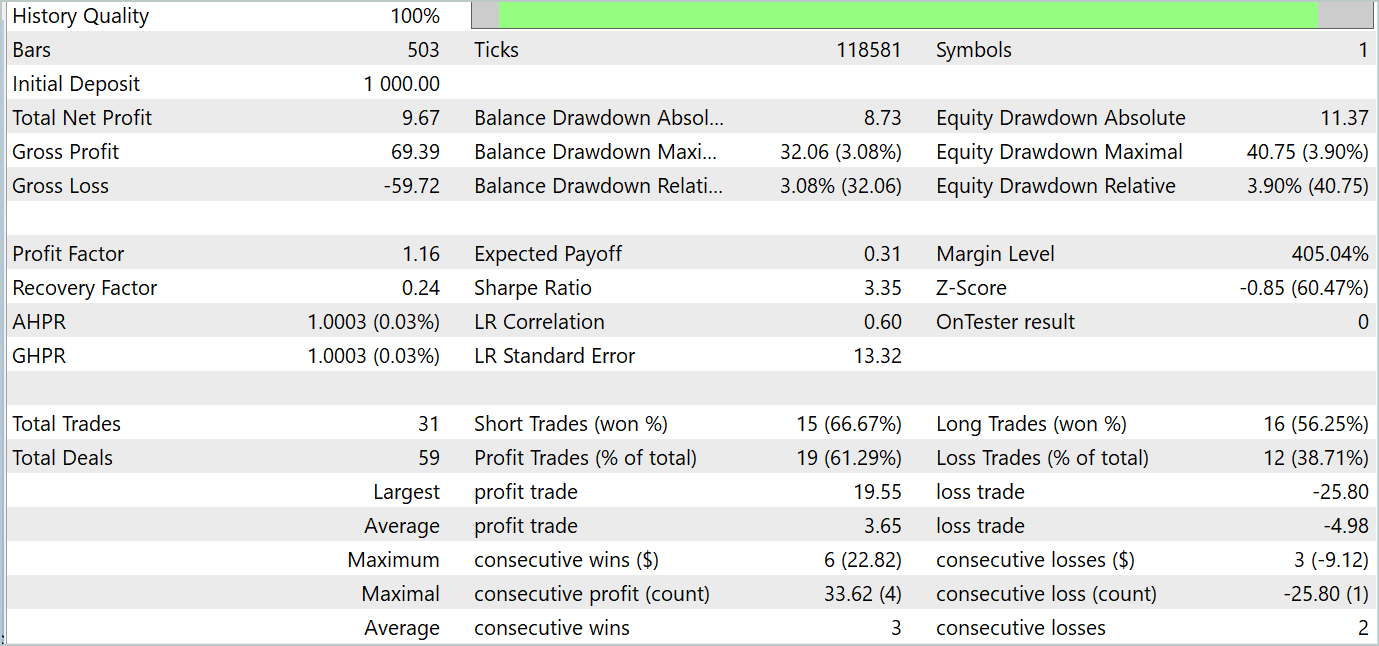
テスト期間中、このモデルは31回の取引を行い、うち19回は利益で決済しました。利益を上げた取引の割合は61％以上でした。注目すべきは、このモデルのロングポジションとショートポジションの数がほぼ同数（15対16）であったことです。

結論

最後の2つの記事は、多変量時系列の予測のために提案され、論文「ATFNet:Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting」で発表されたATFNet法に焦点を当てています。ATFNetモデルは、時間領域と周波数領域のモジュールを組み合わせて、時系列データの依存関係を分析します。Tブロックを使って時間領域での局所依存性をとらえ、Fブロックを使って周波数領域での時系列の周期性を分析します。

ATFNetは、入力時系列の周期性と周波数オフセットに適応するために、主要な高調波系列エネルギーの重み付け、拡張フーリエ変換、および複雑なスペクトルアテンションを適用します。

この記事の実践部分では、MQL5 を使用して提案されたアプローチのビジョンを実装しました。実際のデータを使用してモデルを訓練およびテストしました。テスト結果は、収益性の高い取引戦略の構築に使用できる提案されたアプローチの可能性を示しています。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコード訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15024

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1298.75 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

Candlestick Trend Constraintモデルの構築（第9回）：マルチ戦略エキスパートアドバイザー(I)

今日は、MQL5を使って複数の戦略をエキスパートアドバイザー(EA)に組み込む可能性を探ります。EAは、指標やスクリプトよりも幅広い機能を提供し、変化する市場環境に適応できる、より洗練された取引アプローチを可能にします。詳しくは、この記事のディスカッションをご覧ください。

初心者からエキスパートへ：MQL5での共同デバッグ

問題解決は、MQL5でのプログラミングのような複雑なスキルを習得するための簡潔なルーチンを確立することができます。このアプローチでは、問題解決に集中しながら、同時にスキルアップを図ることができます。問題に取り組めば取り組むほど、高度な専門知識が脳に伝達されます。個人的には、デバッグはプログラミングをマスターするための最も効果的な方法だと思っています。今日は、コードクリーニングのプロセスを紹介し、乱雑なプログラムをクリーンで機能的なものに変えるための最善のテクニックについて解説します。この記事を読んで、貴重な洞察を発見してください。

化学反応最適化(CRO)アルゴリズム（第1回）：最適化におけるプロセス化学

この記事の最初の部分では、化学反応の世界に飛び込み、最適化への新しいアプローチを発見します。化学反応最適化(CRO)は、熱力学の法則から導き出された原理を使用して効率的な結果をもたらします。この革新的な方法の基礎となった分解、合成、その他の化学プロセスの秘密を明らかにします。

チャート上で取引を視覚化する（第2回）：データのグラフ表示

ここでは、取引エントリを分析するために取引の印刷画面のアンロードを簡素化するスクリプトをゼロから開発します。単一の取引に関するすべての必要な情報は、異なる時間枠を描画する機能を備えた1つのチャートに便利に表示されます。