MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークが簡単に(第2回): ネットワークのトレーニングとテスト

ニューラルネットワークが簡単に(第2回): ネットワークのトレーニングとテスト

MetaTrader 5 — 例 | 4 12月 2020, 08:31
1 272 0
Dmitriy Gizlyk
Dmitriy Gizlyk

目次

イントロダクション

ニューラルネットワークと容易性（パーセプトロンニューラルネットワーク）と題した前回の記事では、MQL5を使って完全に接続されたニューラルネットワークを扱うためのCNetの構築原理を考えました。 この記事では、EAでこのクラスを使用して、実際の条件で評価する例を示します。


1. 問題の定義

EAの作成を始める前に、新しいニューラルネットワークに設定する目標と目的を定義する必要があります。 もちろん、金融相場におけるあらゆるEAの共通の目標は、利益を上げることです。 しかし、この目的は一般的なものです。 ニューラルネットワークに、より具体的なタスクを設定する必要があります。 さらに、ニューラルネットワークの未来の成果をどのように評価するかを理解する必要があります。

もう一つの重要な点は，先に作成したCNetクラスは教師付き学習の原理を用いているため，学習セットにラベル付きデータが必要であることです．

フラクタル

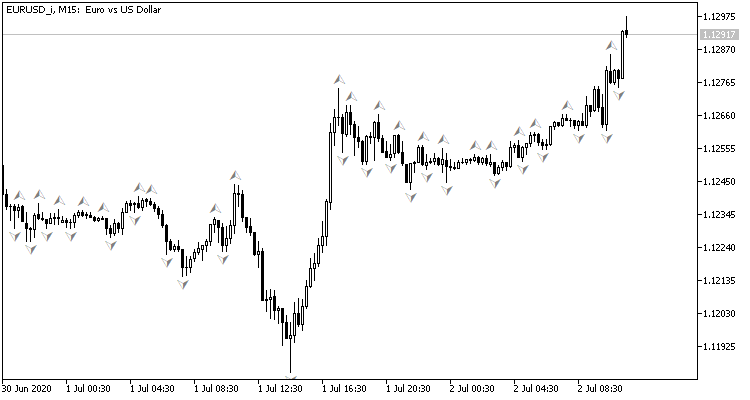
価格チャートを見ていると、価格の天井で売買操作を執行したいという欲求が自然と湧いてきますが、標準的なビル・ウィリアムズのフラクタルインジケータで示すことができます。 このインジケータの問題点は、3本のローソク足で天井を決定し、常に1本のローソク足で遅延したシグナルを出し、逆シグナルになってしまうことです。 3本目のローソク足が形成される前に、ニューラルネットワークでピボットポイントを決定するように設定したらどうでしょうか？ このアプローチでは、トレード方向の動きの少なくとも1つ前のローソク足を与えることになります。

トレーニングセットを参照します。

  • ダイレクトパスでは、現在の相場状況をニューラルネットワークにインプットし、最後にクローズしたローソク足のピック形成確率の推定値を出力します。
  • 逆パスについては、次のローソク足形成後、前のローソク足にフラクタルがあったかどうかを確認し、その結果をインプットしてウェイトを調整します。 

ネットワークの運用結果を評価するためには、２乗平均予測誤差、フラクタル予測が正しい割合、フラクタルが認識されていない割合を用いることができます。

さて、どのデータをニューラルネットワークにインプットするかを決定する必要があります。 チャートを元に相場の状況を見極めようとした時の行動を覚えているでしょうか？

まず、初心者トレーダーはチャートからトレンドの方向性を目視で判断することをお勧めします。 そのため、値動きの情報をデジタル化してニューラルネットワークにインプットする必要があります。 始値、終値、高値、安値の価格、出来高、形成時期などのデータをインプットすることを提案します。 

また、トレンドを見極める方法として人気があるのが、オシレータインジケータを利用する方法です。 インジケータは正規化されたデータを出力するので、このようなインジケータを使うと便利です。 実験に4つの標準的なインジケータを使用することにしました。RCI、CCI、ATR、MACD、すべて標準的なパラメータです。 インジケータとそのパラメータを選択するための追加分析はしていません。

すでにニューラルネットワークにインプットしているローソク足の価格データを再計算して作られているので、インジケータを使う意味がないという人もいるかもしれません。 しかし、これは完全に真ではありません。 インジケータ値は、複数のローソク足からデータを計算して決定されるため、分析サンプルをある程度拡張することができます。 ニューラルネットワークのトレーニングプロセスは、どのように結果に影響を与えるかを決定します。

相場の動きを評価できるように、一定の過去の期間の情報を全てニューラルネットワークにインプットします。

2. ニューラルネットワークモデルプロジェクト

2.1. インプット層のニューロン数の決定

ここでは、インプット層のニューロンの数を把握する必要があります。 そのためには、各ローソク足の初期情報を評価し、分析したヒストリーデプスを掛け合わせます。

インジケータデータは正規化されており、関連するインジケータバッファの数が分かっているので、インジケータデータを前処理する必要はありません（上記の4つのインジケータはすべて5つの値があります）。 したがって、インジケータをインプット層で受け取るためには、分析されたローソク足ごとに5つのニューロンを作成する必要があります。

ローソク足の価格データでは少し状況が異なります。 チャートから視覚的にトレンドの方向性や強さを判断する際には、まずローソク足の方向性や大きさを分析します。 その後、トレンドの方向性と可能性のあるピボットポイントを決定するために来るときだけ、分析されたシンボルの価格レベルに注意を払います。 そのため、ニューラルネットワークにインプットする前に、このデータを正規化する必要があります。 個人的には、記載されているローソク足の始値価格から、終値価格、高値価格、安値価格の差をインプットします。 このアプローチでは、最初のニューロンの符号がローソク足の方向を決定する3つのニューロンを記述するだけで十分です。

様々な時間的要因が通貨のボラティリティに与える影響を記述している記事はたくさんあります。 例えば、季節、週や日による力学の差、欧米やアジアのトレードセッションの差など、通貨レートには様々な影響があります。 このような要因を分析するには、ローソク足の形成月、時間、曜日をニューラルネットワークにインプットします。 よりニューラルネットワークが一般化し、依存関係を見つけることができるため、意図的にローソク足の形成日時をコンポーネントに分割します。

さらに、ボリュームについての情報も載せておきましょう。 ブローカーがリアルボリュームのデータを提供している場合は、ボリュームを表示し、そうでない場合はティックボリュームを指定します。

したがって、それぞれのローソク足を記述するためには12個のニューロンが必要になります。 この数値に分析されたヒストリーデプスを乗算することで、ニューラルネットワークのインプット層の大きさを得ることができます。

2.2. 隠しレイヤーの設計

次のステップは、ニューラルネットワークの隠れ層を準備することです。 ネットワーク構造（層数やニューロン数）の選択は、最も困難なタスクの一つです。 単層パーセプトロンは線形にクラスを分離するのに適します。 ２層ネットワークは非線形境界をたどることができます。 3層構造のネットワークにより、複雑に接続された複数の領域を記述することができます。 レイヤー数を増やすと、関数のクラスが拡大されますが、収束性が悪くなり、学習コストが増加します。 各層のニューロンの数は、期待される関数の変動性を満たさなければならない。 実際には、シンプルなネットワークでは、実際の条件で必要な精度で挙動をシミュレーションすることができず、複雑すぎるネットワークでは、目的関数だけでなくノイズも繰り返すようにトレーニングされてしまいます。

第1回目の記事では、「5つの理由」の方法について触れました。 この実験を続けて、4つの隠された層を持つネットワークを作ることを提案します。 第１の隠れのニューロンの数を１００００に等しく設定してみました。 ただし、分析期間の深さにある程度の依存性を設定することも可能です。 パレート則を用いることで、トレーリングの各層のニューロン数を70％削減します。 また、隠れ層のニューロン数は２０個以下であってはならないという制限を設けます。

2.3. 出力層のニューロン数の決定

出力層のニューロンの数は、タスクとその解決策へのアプローチに依存します。 回帰問題を解くには、期待値を出すニューロンが1つあれば十分です。 分類問題を解決するためには、期待されるクラスの数に等しい数のニューロンが必要です - 各ニューロンは、元のオブジェクトを各クラスに割り当てる確率を生成します。 実際には、オブジェクトのクラスは最大確率で決定されます。

今回のケースでは、2つのニューラルネットワーク亜種を作成し、実際に問題への適用性を評価することを提案します。 第１の場合、出力層は１個のニューロンを有することになります。 0.5...1.0の範囲の値は買いフラクタル、-0.5...-1.0は売りシグナルに対応し、-0.5...0.5の範囲の値はシグナルがないことを意味します。 この解では、双曲正接が活性化関数として使用され、-1.0から+1.0までの範囲で出力値を持つことができます。

2つ目の場合は、出力層に3つのニューロンが生成されます（買い、売り、シグナルなし）。 この亜種では、0.0 ... 1.0の範囲で結果を得るためにニューラルネットワークをトレーニングします ここで、この結果はフラクタルが出現する確率です。 シグナルは最大の確率に従って決定され、その方向は最も高い確率を持つニューロンのインデックスに従って決定されます。

3. プログラミング

3.1. 準備タスク

さて、いよいよプログラミングの時間です。 まず、必要なライブラリを追加します。

  • NeuroNet.mqh - 前回の記事のニューラルネットワークを作成するためのライブラリ
  • SymbolInfo.mqh - シンボルデータを受信するための標準ライブラリ
  • TimeSeries.mqh - 時系列を扱うための標準ライブラリ。
  • Volumes.mqh - ボリュームデータを受信するための標準ライブラリ。
  • Oscilators.mqh - オシレータクラスを含む標準ライブラリ

#include "NeuroNet.mqh"
#include <Trade\SymbolInfo.mqh>
#include <Indicators\TimeSeries.mqh>
#include <Indicators\Volumes.mqh>
#include <Indicators\Oscilators.mqh>

次のステップでは、ニューラルネットワークとインジケータのパラメータを設定するプログラムのパラメータを書きます。

//+------------------------------------------------------------------+
//|   input parameters                                               |
//+------------------------------------------------------------------+
input int                  StudyPeriod =  10;            //Study period, years
input uint                 HistoryBars =  20;            //Depth of history
ENUM_TIMEFRAMES            TimeFrame   =  PERIOD_CURRENT;
//---
input group                "----RSI----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod=  9;             //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price

次に、グローバル変数を宣言します。

CSymbolInfo         *Symb;
CiOpen              *Open;
CiClose             *Close;
CiHigh              *High;
CiLow               *Low;
CiVolumes           *Volumes;
CiTime              *Time;
CNet                *Net;
CArrayDouble        *TempData;
CiRSI               *RSI;
CiCCI               *CCI;
CiATR               *ATR;
CiMACD              *MACD;
//---
double               dError;
double               dUndefine;
double               dForecast;
double               dPrevSignal;
datetime             dtStudied;
bool                 bEventStudy;

これで準備タスクは終了です。 では、クラスの初期化に進みます。

3.2 クラスの初期化

クラスの初期化はOnInit関数で行います。 まず、シンボルを扱うためのCSymbolInfoクラスのインスタンスを作成し、チャートシンボルに関するデータを更新してみましょう。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Symb=new CSymbolInfo();
   if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();

そして、時系列インスタンスを作成します。 クラスインスタンスを作成するたびに、クラスインスタンスが正常に作成されたかどうかを確認し、初期化します。 エラーが発生した場合は、INIT_FAILED の結果で関数を終了します。

   Open=new CiOpen();
   if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Close=new CiClose();
   if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   High=new CiHigh();
   if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Low=new CiLow();
   if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;
//---
   Volumes=new CiVolumes();
   if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK))
      return INIT_FAILED;
//---
   Time=new CiTime();
   if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

この例では、ティックボリュームを使用します。 実際のボリュームを使用したい場合は、Volumes.Creareメソッドを呼び出す際に「VOLUME_TICK」を「VOLUME_REAL」に置き換えてください。

時系列を宣言した後、同様の方法でインジケータを扱うためのクラスのインスタンスを作成します。

   RSI=new CiRSI();      
   if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice))
      return INIT_FAILED;
//---
   CCI=new CiCCI();      
   if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice))
      return INIT_FAILED;
//---
   ATR=new CiATR();      
   if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod))
      return INIT_FAILED;
//---
   MACD=new CiMACD();      
   if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice))
      return INIT_FAILED;

これで、ニューラルネットワーククラスで直接タスクを進めることができるようになりました。 まず、クラスのインスタンスを作成します。 CNet クラスの初期化時には，コンストラクタのパラメータはネットワーク構造を指定した配列への参照を渡します． ネットワーク・トレーニング・プロセスは、計算リソースを消費し、多くの時間がかかることに注意してください。 したがって、ネットワークを新たに起動した後にトレーニングするのは正しくありません。 まず、構造を指定せずにネットワークインスタンスを宣言し、ローカルストレージ（#defineでファイル名を指定しています）から以前に学習したネットワークをアップロードしてみます。

#define FileName        Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea"
...
...
...
...
   Net=new CNet(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());

以前に学習したデータをロードできなかった場合は、エラー・コードを示すメッセージがログに出力され、新しい未学習ネットワークの作成が開始されます。 まず、CArrayIntクラスのインスタンスを宣言し、そこにニューラルネットワークの構造を指定します。 要素数はニューラルネットワークの層の数を示し、要素の値は対応する層のニューロンの数を示します。

      CArrayInt *Topology=new CArrayInt();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;

すでに述べたように、各ローソク足を記述するためには、インプット層に12個のニューロンが必要です。 したがって、１２の積を第１の配列要素に解析ヒストリーデプスで書き込む。

      if(!Topology.Add(HistoryBars*12))
         return INIT_FAILED;

続いて、隠れたレイヤーを説明します。 第1の隠れ層に1000個のニューロンを持つ4つの隠れ層があると判断しました。 そうすると、トレーリングの各層ではニューロンの数が７０％減少するが、各層は少なくとも２０個のニューロンを有することになります。 データはループで配列に追加されます。

      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         result=(Topology.Add(n) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }

回帰モデルを構築するための出力層に1を示します。

      if(!Topology.Add(1))
         return INIT_FAILED;

分類モデルを使う場合は、出力ニューロンに3を指定する必要があります。

次に，先に作成したCNetクラスのインスタンスを削除し，作成するニューラルネットワークの構造を示したクラスを新規に作成します。 新しいニューラルネットワークのインスタンスを作成した後、それ以上は使用しないので、ネットワーク構造のクラスを削除します。

      delete Net;
      Net=new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;

統計データを収集するための変数の初期値を設定します。

  • dError - 標準偏差（エラー)
  • dUndefine - 未定義フラクタルのパーセンテージ．
  • dForecast - 正しく予測されたフラクタルの割合
  • dtStudied - 直近のトレーニングローソク足の日付。

      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

ニューラルネットワークの構造を設定し、ニューラルネットワーククラスの新しいインスタンスを作成し、統計変数を初期化する必要があることを忘れないでください。
OnInit関数の最後に、ニューラルネットワークとのデータ交換に使用するCArrayDouble()クラスのインスタンスを作成し、ニューラルネットワークのトレーニング処理を開始します。

ここでもう一つ解決策をお伝えしたいと思います。 MQL5には非同期関数呼び出しがありません。 OnInit関数から明示的に学習関数を呼び出すと、ターミナルは学習が完了するまでプログラムの初期化処理が未完了とみなします。 そのため、関数を直接呼び出すのではなく、カスタムイベントを作成し、トレーニング関数はOnChartEvent関数から呼び出すようにします。 イベントを作成する際には、lparamパラメータにトレーニング開始日を指定します。 このアプローチにより、関数を呼び出してOnInit関数を完成させることができます。

   TempData=new CArrayDouble();
   if(CheckPointer(TempData)==POINTER_INVALID)
      return INIT_FAILED;
//---
   bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init");
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| ChartEvent function                                              |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,
                  const long &lparam,
                  const double &dparam,
                  const string &sparam)
  {
//---
   if(id==1001)
     {
      Train(lparam);
      bEventStudy=false;
      OnTick();
     }
  }

OnDeinit関数でメモリをクリアするのを忘れないようにしてください。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   if(CheckPointer(Symb)!=POINTER_INVALID)
      delete Symb;
//---
   if(CheckPointer(Open)!=POINTER_INVALID)
      delete Open;
//---
   if(CheckPointer(Close)!=POINTER_INVALID)
      delete Close;
//---
   if(CheckPointer(High)!=POINTER_INVALID)
      delete High;
//---
   if(CheckPointer(Low)!=POINTER_INVALID)
      delete Low;
//---
   if(CheckPointer(Time)!=POINTER_INVALID)
      delete Time;
//---
   if(CheckPointer(Volumes)!=POINTER_INVALID)
      delete Volumes;
//---
   if(CheckPointer(RSI)!=POINTER_INVALID)
      delete RSI;
//---
   if(CheckPointer(CCI)!=POINTER_INVALID)
      delete CCI;
//---
   if(CheckPointer(ATR)!=POINTER_INVALID)
      delete ATR;
//---
   if(CheckPointer(MACD)!=POINTER_INVALID)
      delete MACD;
//---
   if(CheckPointer(Net)!=POINTER_INVALID)
      delete Net;
   if(CheckPointer(TempData)!=POINTER_INVALID)
      delete TempData;
  }

3.3. ニューラルネットワークのトレーニング

ニューラルネットワークをトレーニングするには、Train関数を作成します。 トレーニング期間の開始日は、関数のパラメータに渡されます。

void Train(datetime StartTrainBar=0)

関数の先頭にローカル変数を宣言します。

  • count - 学習エポックを数える
  • prev_un - 以前のエポックで認識されなかったフラクタルの割合．
  • prev_for - 前のエポックにおけるフラクタルの「予測」が正しい割合
  • prev_er - 前のエポックエラー
  • bar_time - 再計算足の日付
  • stop - 強制的なプログラム終了の呼び出しを追跡するためのフラグ。

   int count=0;
   double prev_up=-1;
   double prev_for=-1;
   double prev_er=-1;
   datetime bar_time=0;
   bool stop=IsStopped();
   MqlDateTime sTime;

次に、関数パラメータで得られた日付が、初期に指定されたトレーニング期間を超えていないかどうかを確認します。

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year-=StudyPeriod;
   if(start_time.year<=0)
      start_time.year=1900;
   datetime st_time=StructToTime(start_time);
   dtStudied=MathMax(StartTrainBar,st_time);

ニューラルネットワークのトレーニングはdo-whileループで実施します。 ループの最初に、ニューラルネットワークをトレーニングするためのヒストリー足の数を再計算し、前回のパス統計量を保存します。

   do
     {
      int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame));
      prev_un=dUndefine;
      prev_for=dForecast;
      prev_er=dError;
      ENUM_SIGNAL bar=Undefine;

そして、バッファのサイズを調整し、必要なヒストリーデータをロードします。

      if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) ||
         !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars))
         break;
      Open.Refresh(OBJ_ALL_PERIODS);
      Close.Refresh(OBJ_ALL_PERIODS);
      High.Refresh(OBJ_ALL_PERIODS);
      Low.Refresh(OBJ_ALL_PERIODS);
      Volumes.Refresh(OBJ_ALL_PERIODS);
      Time.Refresh(OBJ_ALL_PERIODS);
      RSI.Refresh(OBJ_ALL_PERIODS);
      CCI.Refresh(OBJ_ALL_PERIODS);
      ATR.Refresh(OBJ_ALL_PERIODS);
      MACD.Refresh(OBJ_ALL_PERIODS);

強制プログラム終了を追跡するためのフラグを更新し、学習エポックが経過したことを示す新しいフラグを宣言します(add_loop)。

      stop=IsStopped();
      bool add_loop=false;

すべてのヒストリーデータを通して、ネストになったトレーニングサイクルを整理します。 サイクルの開始時に、ヒストリーデータの終了点に達しているかどうかを確認します。 必要に応じて add_loop フラグを変更します。 また、ニューラルネットワークトレーニングの現在の状態をコメントを用いてチャート上に表示します。 これより、トレーニングの過程を監視することができます。

      for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--)
        {
         if(i==0)
            add_loop=true;
         string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%% \nError %.2f\n%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal);
         Comment(s);

次に、予測されたシステム状態がサイクルの前のステップで計算されているかどうかを確認します。 ある場合は、正しい値の方向にウェイトを調整します。 これを行うには、TempData配列の内容をクリアし、フラクタルが前のローソク足に形成されたかどうかを確認し、TempData配列に正しい値を追加します（出力層に1つのニューロンを持つ回帰ニューラルネットワークのコードです）。 その後、パラメータとして TempData 配列への参照を渡してニューラルネットワークの backProp メソッドを呼び出します。 dForecast（正しく予測されたフラクタルの割合）とdUndefine（認識されていないフラクタルの割合）の統計データを更新しました。

         if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2)
           {
            TempData.Clear();
            bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1));
            bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1));
            TempData.Add(buy && !sell ? 1 : !Buy & sell ? -1 : 0);
            Net.backProp(TempData);
            if(DoubleToSignal(dPrevSignal)!=Undefine)
              {
               if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0)))
                  dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor;
               else
                  dForecast-=dForecast/Net.recentAverageSmoothingFactor;
               dUndefine-=dUndefine/Net.recentAverageSmoothingFactor;
              }
            else
              {
               if(sell || buy)
                  dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor;
              }
           }

ニューラルネットワークの加重係数を調整した後、現在のヒストリー足でフラクタルが形成される確率を計算します（ｉが０に等しい場合は、現在のヒストリー足でフラクタルが形成される確率を計算する）。 これを行うには、TempData 配列をクリアして、ニューラルネットワークインプット層の現在のデータを追加します。 データの追加に失敗した場合や、データが不足している場合はループを終了します。

         TempData.Clear();
         int r=i+(int)HistoryBars;
         if(r>bars)
            continue;
//---
         for(int b=0; b<(int)HistoryBars; b++)
           {
            int bar_t=r+b;
            double open=Open.GetData(bar_t);
            TimeToStruct(Time.GetData(bar_t),sTime);
            if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) ||
               !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) ||
               !TempData.Add(RSI.Main(bar_t)) ||
               !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t)))
                  break;
           }
         if(TempData.Total()<(int)HistoryBars*12)
            break;

初期データを用意したら、feedForwardメソッドを実行し、ニューラルネットワークの結果を変数dPrevSignalに書き込む。 下記は出力層に1つのニューロンを持つ回帰ニューラルネットワークのコードです。 出力層に３つのニューロンを持つ分類ニューラルネットワークのコードを以下に添付します。

         Net.feedForward(TempData);
         Net.getResults(TempData);
         dPrevSignal=TempData[0];

ニューラルネットワークの動作をチャート上で可視化するには、過去200本のロウソク足の予測フラクタルのラベルを表示します。

         bar_time=Time.GetData(i);
         if(i<200)
           {
            if(DoubleToSignal(dPrevSignal)==Undefine)
               DeleteObject(bar_time);
            else
               DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i));
           }

ヒストリーデータサイクルの終了時に、プログラム強制終了フラグを更新します。

         stop=IsStopped();
        }

ニューラルネットワークが利用可能なすべての過去のデータでトレーニングされたら、トレーニングエポックのカウンタを増やして、ニューラルネットワークの現在の状態をローカルファイルに保存します。 次回、ニューラルネットワークのデータを起動するときに使えるようになります。

      if(add_loop)
         count++;
      if(!stop)
        {
         dError=Net.getRecentAverageError();
         if(add_loop)
           {
            Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false);
            printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast);
           }
         }

最後に、トレーニングサイクルを終了する条件を指定します。 条件は次のようにすることができます：所定のレベル以上の目標に到達する確率を持つシグナルを受信した場合、目標誤差パラメータに到達した場合、またはトレーニングエポックの後、統計データが変化しないか、または取るに足らない変化をした場合（トレーニングは局所的な最小値でストップします）。 トレーニングを終了する際の条件を自分で定義することができます。 

     }
   while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);

トレーニング関数を終了する前に、直近のトレーニングローソク足の時間を保存します。

   if(count>0)
     {
      dtStudied=bar_time;
     }
  }

3.4. スロープ計算方法の改善

テストの過程で見つけた以下の点に注目していただきたいと思います。 ニューラルネットワークを学習する際に、隠れ層のニューロンの加重係数が制御できずに増加し、最大許容変数値を超えてしまい、結果的にニューラルネットワーク全体が麻痺してしまうケースがありました。 トレーリングの層のエラーが、活性化関数の可能な値の範囲を超えた値を出力するようにニューロンにリクエストしたときに起こりました。 見つけた解決策は、ニューロンの目標値を正規化することでしました。 スロープ計算法の修正コードは以下の通りです。

void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal;
   gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0);
  }

すべてのメソッドと関数のフルコードは添付ファイルにあります。

4. 検証

ニューラルネットワークのテストトレーニングは、H1タイムフレームのEURUSDペアで実施されました。 ローソク足20本のデータをニューラルネットワークにインプットしました。 過去2年間のトレーニングを実施しました。 結果を確認するために、同じターミナルの2つのチャート上で2つのExpert Advisorsを起動しました。1つのEAは回帰ニューラルネットワーク（Fractal - 出力層に1つのニューロンを持つ）と分類ニューラルネットワーク（Fractal_2 - 出力層に3つのニューロンを持つ）を持つEAです。

12432本の最初のトレーニングエポックは2時間20分でした。 両ＥＡともに命中率６％強と同様のパフォーマンスを示しました。

回帰ニューラルネットワーク（1出力ニューロン）の1回目の学習エポックの結果 分類ニューラルネットワークの1回目の学習エポックの結果（出力ニューロン3個)

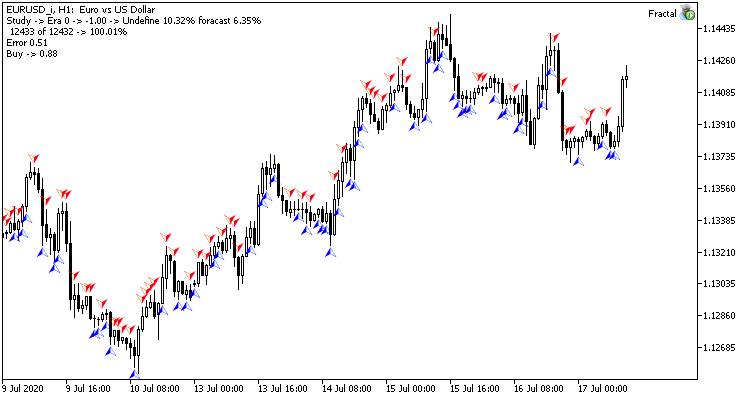
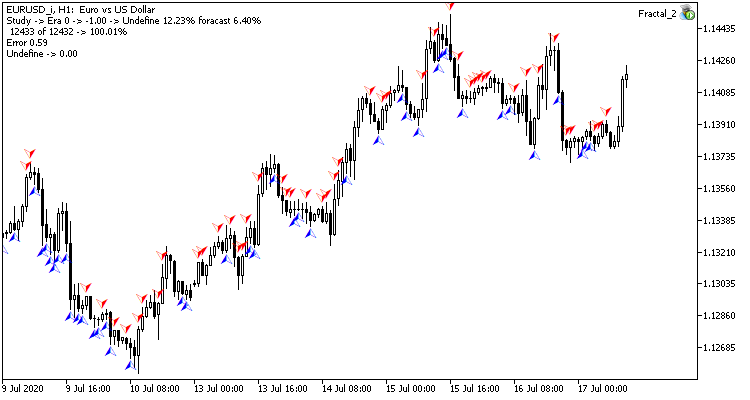
最初のエポックは、初期段階でランダムに選択されたニューラルネットワークの加重に強く依存します。

35エポックのトレーニングを行った後、統計量の差はわずかに増加した - 回帰ニューラルネットワークモデルはより良いパフォーマンスを示しました。

値 回帰ニューラルネットワーク 分類ニューラルネットワーク
ルート平均２乗誤差 0.68 0.78
ヒット率 12.68% 11.22%
未認識フラクタル 20.22% 24.65%

回帰ニューラルネットワーク（1出力ニューロン）の35回目の学習エポックの結果 分類ニューラルネットワークの35回目の学習エポックの結果（出力ニューロン3個)

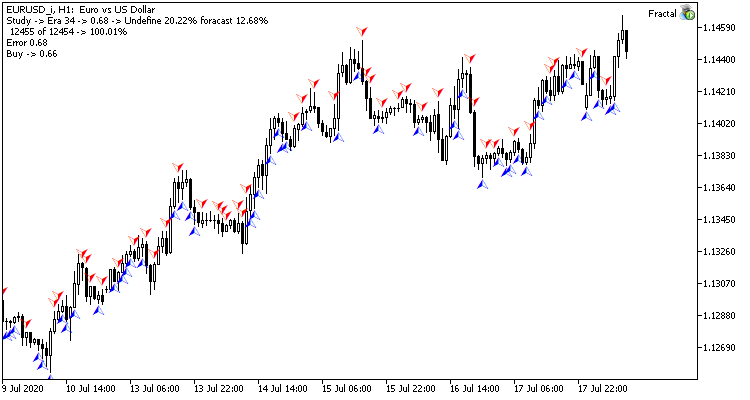
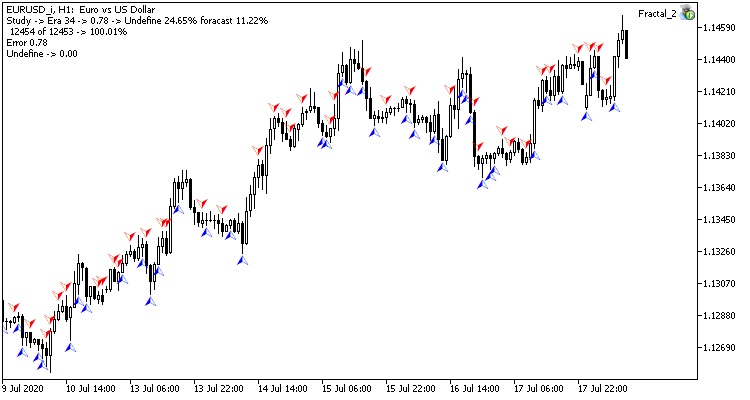
テストの結果、どちらのニューラルネットワーク組織亜種も、学習時間と予測精度の点で似たような結果が得られることがわかりました。 同時に、得られた結果から、ニューラルネットワークのトレーニングには追加の時間とリソースが必要であることが示されました。 ニューラルネットワークの学習ダイナミクスを解析したい場合は、添付ファイルの各学習エポックのスクリーンショットをご覧ください。

結論

今回は、ニューラルネットワークの作成からトレーニング、テストまでのプロセスを考えてみました。 得られた結果から、著書技術の利用の可能性があることを示します。 しかし、ニューラルネットワークのトレーニングプロセスは、多くの計算リソースを消費し、多くの時間を要します。

記事内で使用しているプログラム

# 発行 種類 詳細
Experts\NeuroNet_DNG\
1 Fractal.mq5   EA  回帰ニューラルネットワーク（出力層に1ニューロン）を持つEA
2 Fractal_2.mq5  EA  分類ニューラルネットワーク（出力層に3つのニューロン）を持つEA
3 NeuroNet.mqh クラスライブラリ ニューラルネットワーク（パーセプトロン）を作成するためのクラスのライブラリ
  Files\    
4  Fractal  Directory  回帰ニューラルネットワークのテストを示すスクリーンショットがあります。
5   Fractal_2  Directory  分類ニューラルネットワークのテストを示すスクリーンショットがあります。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8119

添付されたファイル |
ZIPをダウンロード
MQL5.zip (2005.76 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
カスタムシンボル。実用的な基礎 カスタムシンボル。実用的な基礎
この記事では、クオートを表示するための一般的な方法を示すために、カスタムシンボルプログラムの生成を行います。 派生したカスタムシンボルチャートから実際のシンボルをトレードするためのEAにおける提案された亜種についても説明します。 この記事にはMQLのソースコードが添付されています。
トレンドとは何か、相場の構造はトレンドかレンジかで決まるのか？ トレンドとは何か、相場の構造はトレンドかレンジかで決まるのか？
トレーダーはよくトレンドやレンジについて話しますが、トレンドやレンジとは何かを理解している人はほとんどおらず、概念を明確に説明できる人はさらにいません。 基本的な用語について考察することは、多くの場合、偏見や誤解の固まりに悩まされます。 しかし、利益を上げたいのであれば、概念の数学的・論理的な意味を理解する必要があります。 今回は、トレンドとレンジの本質に迫るとともに、相場の構造がトレンドなのか、レンジなのか、何か別のものなのかを定義してみたいと思います。 また、トレンド相場やレンジ相場で利益を出すための最適な戦略についても考えていきたいと思います。
DoEasyライブラリの時系列(第48部): 単一サブウィンドウでの単一バッファ複数銘柄・複数期間指標 DoEasyライブラリの時系列(第48部): 単一サブウィンドウでの単一バッファ複数銘柄・複数期間指標
本稿では、単一の指標バッファを使用して、指標サブウィンドウを構築および操作するための複数銘柄・複数期間標準指標の作成例について説明します。プログラムのメインウィンドウで動作し、データを表示するための複数のバッファを持つ標準指標を操作するためのライブラリクラスを準備します。
価格系列の離散化、ランダム成分とノイズ 価格系列の離散化、ランダム成分とノイズ
普段我々はローソク足や、価格シリーズを一定の間隔でスライスした足を使って相場を分析しています。 このような離散化手法は、相場の動きの本当の構造を歪めてしまうのではないでしょうか？ オーディオ信号は時間の経過とともに変化する関数であるため、オーディオ信号を一定の間隔で離散化することは、許容される解決策です。 信号自体は時間に依存する振幅です。 この信号特性は基本的なものです。