この記事の一節が私の目を引いた。この記事は非常によく書かれており、どのように設計され、考え抜かれたのかが詳細に述べられているにもかかわらず、である。この一節には、あなたの理解について微妙な点がある。おそらく、誰もがニューラルネットワークについて特定のことを言いたがるので、あなたは偏っているのでしょう。しかし、あなたの記事はよく書けているし、その詳細を説明している。私は今後見せるであろう何かを予想することにした。そのための記事はすでに書き終えているが、まずはリプレイ/シミュレーターの作り方について説明を終えたいと思う。次のことを理解してほしい:活性化関数は、方程式に非線形性を発生させるために使われるのではない。むしろ、活性化関数は、構築されるネットワーク内の層やパーセプトロンの数を減らすことを目的とした、一種のフィルターとして機能する。これにより、データを特定の方向に収束させるプロセスがスピードアップする。この過程で、分類や知識の保持を目指すことができる。最終的には、どちらか一方の結果は得られるが、両方が得られることはない。
私の記事、https://www.mql5.com/ja/articles/13745 では、このことを比較的簡単な方法で示している。そこでは、ニューラルネットワークを理解する方法を説明し始めたばかりですが。しかし、あなたの記事はよく書けており、多くの努力を払っているので、ヒントをあげよう。一見ランダムなデータをいくつか取り、パーセプトロンの活性化関数を削除する。その後、収束を試みてください。あまりうまくいかないことに気づくだろう。しかし、レイヤーを追加したり、パーセプトロンを増やしたりすれば、収束は時間とともに改善されるでしょう。なぜ活性化関数が必要なのか、これを見ればよくわかるでしょう。😁👍

- www.mql5.com
記事のこの一節が私の注意を引いた。この記事は非常によく書けており、どのように設計され、どのように考え出されたかが詳細に書かれているが。この一節には、あなたの理解には微妙なところがある。おそらく、誰もがニューラルネットワークについて特定のことを言いたがるので、あなたは偏っているのでしょう。しかし、あなたの記事はよく書けているし、詳細を説明してくれている。私は、将来見せるであろうものを予想することにした。そのための記事はすでに書いてありますが、まずはリプレイ/シミュレーターの作り方の説明を終えたいと思います。次のことを理解してほしい:アクティベーション関数は、方程式に非線形性を作り出すために使われるのではない。 むしろ、活性化関数は一種のフィルターとして機能し、その目的は構築されるネットワークのレイヤーやパーセプトロンの数を減らすことである。これによって、データが特定の方向に収束するプロセスがスピードアップする。この過程で、分類や知識の保持を目指すことができる。最終的にはどちらか一方の結果を得ることになるが、両方を得ることはない。
自動翻訳はおそらくあまり正確ではないが、ハイライトは正しくない。ネットワークの計算能力を向上させるのは非線形性であり、収束プロセスをスピードアップさせるだけでなく(これはあなた自身も別の文章で述べている)、非線形性を導入しなければ解決できない問題を根本的に解決できるようになる(レイヤーをどれだけ増やしても)。さらに、非線形性がなければ、どのような(同期)ニューラルネットワークも同等の単層ネットワークに「折り畳む」ことができる。
ネットワークの計算能力を向上させるのは非線形性であり、収束プロセスをスピードアップさせるだけでなく(これはあなた自身も別の文章で述べている)、非線形性を導入しなければ解けないような問題でも(どれだけ層を増やしても)根本的に解くことができるようになる。さらに、非線形性がなければ、どのような(同期)ニューラルネットワークも同等の単層ネットワークに「折りたたむ」ことができる。
+100500
よく言った。私が返事を書いている間に、すでに回答されていたようですね。
どんな非線形関数も、無限大に向かう数の線形区分関数で記述することができ、記述誤差はゼロになります。しかし、もし非線形活性化関数が問題の対象の記述を単純化するためだけに使われるのであれば、それはなぜでしょうか?
言いたかったことと、実際に文章にしたことに誤解があったようです。
今度からはもう少しはっきりさせるようにします。 物事を 画像、物体、図形、音、要するに確率が支配するもの。ニューラルネットワーク内の値が所定の範囲に収まるように制限する必要がある。この範囲は通常、-1から1の間であるが、ネットワークのヒット率や、ネットワークに接触させたい入力情報に対してどのような処理を行うか、また、物事の分類を作成するためにネットワークがどのように学習を行うのが最適かによって、0から1の間になることもある。 この場合 活性化関数だ。この場合、活性化関数が必要になる。最終的には、入力があるものであるか別のものであるかの確率で値を生成する手段を持つことになる。これは事実であり、私は否定しない。それだけに、入力データの正規化や標準化が必要になることも多い。
しかし、ニューラルネットワークは物事を分類するために使われるだけでなく、知識を保持するためにも使われる。この場合、活性化関数は多くの場合捨てなければならない。詳細:物事を制限する必要がある場合もある。しかし、それは非常に特殊なケースである。なぜなら、これらの機能はネットワークがその目的を果たすのを邪魔するからである。それはまさに知識を保持することなのだ。実際、私はスタニスラフ・コロツキーの コメントに一部同意しているのだが、このような場合、活性化関数を使わなければ、ネットワークは単層に相当するものに折りたたむことができる。というのも、いくつかの変数を持つ単一の多項式だけでは、知識を表現する、あるいは知識を保持するのに十分でない場合があるからだ。このような場合、結果を本当に再現できるようにするために余分なレイヤーを使う必要がある。あるいは新しいものを生成することもできる。適切なデモンストレーションなしにこのように説明するのは少しわかりにくい。しかし、うまくいく。
大きな問題は、今は何でも流行りだから、記憶が確かならここ10年くらいは人工知能やニューラルネットワークと結びついている。ビジネスが本格的に軌道に乗ったのはここ5年ほどだが。多くの人々は、人工知能が実際にどのようなものなのかまったく知らない。あるいは、実際にどのように機能するのかも。というのも、私が目にする誰もが、常に既製のフレームワークを使っているからだ。そしてそれは、ニューラルネットワークがどのように機能するかを理解するのにまったく役立たない。ニューラルネットワークは単なる多変数の方程式だ。学術界では何十年も研究されてきた。そして、学術界から出てきたときでさえ、これほど派手に発表されることはなかった。初期段階から長い間 活性化関数は使われなかった.しかし、当時はニューラルネットワークとさえ呼ばれていなかったネットワークの目的は異なっていた。しかし、3人の人々がそのネットワークから利益を得ようとしたため、私の意見では、やや間違った方法で公表された。少なくとも私に言わせれば、正しいのはきちんと説明することだ。多くの人々の心に混乱を生じさせないためにね。しかし、それでいいのだ。3人が大儲けしている一方で、国民は撤去用ローリーから落ちた犬よりも迷っているのだから。いずれにせよ、私はアンドレイ・ディクに 新しい記事を書く意欲を失わせたくない。私は、あなたが純粋なMQL5を使ってシステムを作ろうとしたのを見た。ところで、これはとてもいいことだ。あなたの記事がとてもよく書かれ、計画されていることに気づかされました。私はただ、その点に注目してもらい、もう少し考えてもらいたかっただけです。実際、このテーマはとても興味深く、ほとんどの人が知らないことがたくさんある。しかし、あなたはそれを研究した。
Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

- 2025.01.21
- MetaQuotes
- www.mql5.com
活性化関数としては何でも使用でき、コサインでも、結果は一般的なもののレベルである。 relu(バイアス0.1(ランダムウォーク初期化との併用は推奨さ れない) )を使用することを推奨する のは、シンプル(高速カウント)であり、より良い学習ができるからで ある:これらのブロックは線形ブロックと非常によく似ているため、最適化が容易である。唯一の違いは ,線形整流ブロックは その定義 領域の半分で0を出力することである. したがって,線形整流ブロックの導関数は, そのブロックがアクティブであればどこでも大きい ままである. 勾配が大きいだけでなく、 一貫性もある。整流操作の2次導関数はどこでも0であり、 1次導関数はブロックがアクティブであればどこでも1である。これは、 活性化関数が 2次の影響を受ける場合よりも 、 勾配の方向が はるかに学習に有用である ことを意味する ...。アフィン変換パラメータを初期化するとき、bのすべての 要素に小さな正の値を代入 することを推奨する。. そうすると,線形平行化ブロックは ,ほとんどの学習例で 最初の瞬間に アクティブに なる可能性が非常に高く なり, 導関数は0とは異なる値になる.
区分的線形ブロックとは 異なり、シグモイド・ブロックは 、その定義領域のほとんどにおいて 漸近線に 近く 、 zが無限大に なると高い値に 近づき 、 zがマイナス無限大になると 低い値になる 。ゼロ付近でのみ 高い感度を持つ。シグモイド・ブロックの飽和により、勾配 学習は著しく妨げられる。したがって、 シグモイド・ブロックを 順伝播ネットワークの 隠れブロックとして 使用することは 、現在では推奨されていない.シグモイド活性化関数を使う必要がある場合は、 ロジスティック・シグモイドの代わりに 双曲線タンジェントを使うのがよい。 σ(0)=1/2に対し 、tanh(0)=0という意味で 同一関数に 近い 。tanhは ゼロ近傍で恒等 関数に似ている ため 、ディープニューラルネットワークの トレーニングは、ネットワークの活性化信号を低く抑えることができれば、線形モデルのトレーニングに似ている 。この場合、活性化関数tanhを持つネットワークのトレーニングは 単純化される。
lstmの場合、シグモイドまたはアークタンジェントを使用する必要がある(忘却ベントのオフセットを1に設定することを推奨):シグモイド活性化関数は今でも使われているが、 フィードフォワードネットワークでは 使われていない 。 リカレントネットワーク、多くの確率モデル、 いくつかのオートエンコーダには、 区分的線形活性化関数を使用 できない追加要件があり、 飽和の問題があるにもかかわらず、シグモイドブロックの方が適している。
線形活性化とパラメータ削減:ネットワークの各レイヤーが 線形変換のみで 構成されている場合 、ネットワークは 全体として線形になる。しかし、いくつかのレイヤーは 純粋に線形で あっても構わない 。 n個の 入力と p個の 出力を持つニューラルネットワークの 層を考えてみよう 。この層は、 重み行列 Uを持つ 層と 重み行列 Vを持つ 層の 2層に置き換えることができる。 最初のレイヤーに活性化関数がない場合、 Wに基づいて元のレイヤーのウェイト行列を乗数に 分解したことに なります。 Uがq個の 出力を 生成する 場合 、 Uと Vを合わせても(n + p)q個の パラメータしか 含まれませんが、 Wには np個の パラメータが 含まれます 。 qが 小さい場合、 パラメータは大幅に 節約できる。 線形変換は 低ランクで なければ ならないが、低ランクのリンクで十分であることが多い。このように、 線形隠れブロックはネットワークのパラメータ数を削減する効率的な方法を提供する。
Reluはディープネットワークに適している:初期のモデルでは 整流が人気であったにもかかわらず、 1980年代にはほとんど例外なくシグモイドに取って代わられた 。
しかし、一般的にはシグモイドの方が優れている。小さなデータセットの場合 、非線形の整流を使うことは 隠れ層の重みを学習するよりもさらに重要である 。ランダムな重みは、線形整流によって有用な情報をネットワークに 伝搬させるのに十分であり、分類出力層が異なる特徴ベクトルをクラス識別子にマッピングするように学習できる。 より多くのデータが利用可能であれば、学習プロセスは多くの 有用な知識を 抽出し始め 、ランダムに選択されたパラメータを 凌駕する... 学習は、 活性化関数が曲率や双方向飽和によって特徴づけられるディープネットワークよりも、整流線形ネットワークの 方が はるかに簡単である 。
私が言いたかったことと、実際に文章にしたことの間に誤解があったようだ。
今回はもう少し分かりやすくしようと思う。 分類する 画像、物体、形、音、要するに確率が支配するようなもの。ニューラルネットワークの値が所定の範囲に収まるように制約する必要がある。しかし、ネットワークに学習させたい入力情報が、どのような速度で、どのような方法で処理され、どのように学習させれば物事の分類を作成するのに最適なのかによって、0から1の範囲になることもある。 この場合 活性化関数。値をその範囲内に保つためだ。最終的には、入力がどちらか一方である確率という観点から値を生成する手段に行き着くことになる。これは事実であり、否定はしない。それだけに、入力データを正規化したり標準化したりしなければならないことも多い。
しかし、ニューラルネットワークは分類に使われるだけでなく、知識の保持にも使われる。この場合、多くの場合、活性化関数は捨てるべきである。詳細:何かを制限する必要がある場合もある。しかし、これは非常に特殊なケースである。重要なのは、これらの機能がネットワークの目的を果たすのを妨げるということだ。それは知識を保存することだ。実際、活性化関数を使わなければ、このような場合のネットワークは単層に相当するものに縮小できるというスタニスラフ・コロツキーの コメントには部分的に同意する。というのも、いくつかの変数を持つ単一の多項式だけでは、知識を表現したり保存したりするのに十分でない場合があるからだ。この場合、結果を実際に再現できるように、追加のレイヤーを使わなければならない。あるいは、新しいものを生成することもできる。このように説明するのは、適切なデモンストレーションがないと少しわかりにくい。しかし、うまくいく。
大きな問題は、今は何でも流行りのため、私の記憶が正しければ、ここ10年ほどは人工知能とニューラルネットワークの話題で持ちきりだったということだ。このビジネスが本当に花開いたのはここ5年ほどのことだが。多くの人々は、これらのものが本当は何なのかをまったく知らない。そして、実際にどのように機能するのかも。というのも、私が目にする誰もが、いつも既製のフレームワークを使っているからだ。そしてそれは、ニューラルネットワークがどのように機能するかを理解するのにまったく役に立たない。いくつかの変数を使った方程式に過ぎない。ニューラルネットワークは何十年もの間、学術的に研究されてきた。そして、学問の域を超えたとしても、これほど華々しく発表されたことはない。当初、そして長い間 活性化関数は使われなかった.しかし、当時はニューラルネットワークとさえ呼ばれていなかったネットワークの目的は異なっていた。しかし、3人の人間がそれを利用しようとしたため、大げさに宣伝された。少なくとも私から見れば、正しいのはその本質をきちんと説明することだった。多くの人の心を混乱させないように。しかし、それでいいのだ。3人は大金を稼ぎ、人々はゴミ収集車から落ちた犬よりも迷っているのだから。とにかく、アンドリュー・ディックよ、私は君がもっと記事を書くのを止めるつもりはない。あなたが純粋なMQL5を使ってシステムを作ろうとしているのを見ました。ところで、それはとてもいいことだ。あなたの記事はとてもよく書かれていて、計画的であることに気づきました。私はただ、この点に注目してもらい、もう少し考えてもらいたかっただけです。このトピックは実に興味深く、あまり知られていない。しかし、あなたはそれを取り上げ、研究した。
そう、非直線性は活性化PHが持つ間接的な効果だ。Phsはもともと、例えば分類タスクのように、目標定義のある領域から別の領域へ変換するためのものです。「非直線性」は、例えば特徴の数を増やしたり、特徴を変換したり、特徴を変換するカーネルによって、さまざまな方法で達成することができます。
最も単純な例はロジスティック回帰で、これは最後に活性化関数があるにもかかわらず、線形のままである。
しかし多層ネットワークでは、活性化関数を持つ層の数によって、単にカーネル・タイプの変換の結果として、非線形性が得られます。歴史的背景
ロジスティック 回帰と初期のニューラルネットワークの基礎となる概念は、 現代のディープ・ニューラル・ネットワークよりも前に生まれたという のは正しい。
年表を見てみよう:
-
ロジスティック関数は 19世紀に開発されました。ロジスティック関数は19世紀に開発され、分類のための統計モデル(ロジスティック回帰)として使われるようになったのは20世紀半ば(およそ1940~50年代)です。
-
活性化関数を持つニューロンの最初の数学的モデル(McCulloch and Pittsモデル)は1943 年に登場した。このモデルは単純な閾値関数を使用していた。
-
パーセプトロンは単層ニューラルネットワークで、1958 年にフランク・ローゼンブラットによって開発された。パーセプトロンは閾値活性化関数を使用し、線形分離可能な問題しか解くことができなかった。
-
ディープラーニングと 多層ネットワークのブレークスルーは、1986 年にRumelhart、Hinton、Williamsによって普及したバックプロパゲーションアルゴリズムの 登場によって初めてもたらされた。
このアルゴリズムによって多層ニューラルネットワークの学習が実用的になり、閾値だけでなく微分可能な非線形活性化関数(シグモイドや後のReLUなど)が必要であることが示された。
結論
歴史的に見ると
-
最初に、本質的に1層モデルであるモデル(ロジスティック回帰、パーセプトロン)があった。
-
これらのモデルでは、活性化関数は、モデル全体が線形のままであったので、目的の領域への変換(線形和からバイナリ・クラスまたは確率への変換)として機能しました。
-
その後、多層ネットワークの出現により、活性化関数の新たな、基本的により重要な役割が 出現した-ネットワークが学習できるように、隠れ層に非線形性を導入することである。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
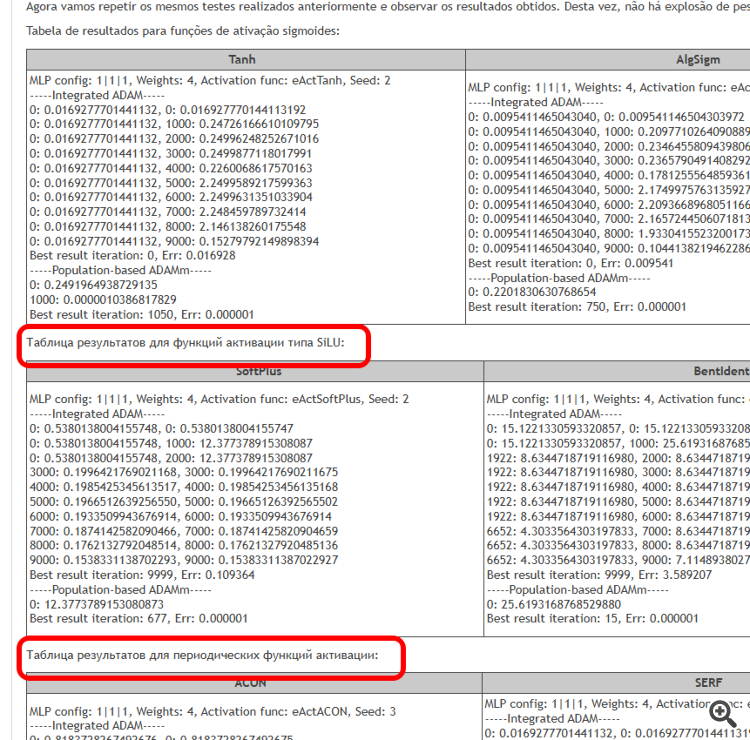
新しい記事「学習中にニューロンを活性化する関数:高速収束の鍵は?」はパブリッシュされました:
川を想像してください。多くの支流を持つその通常の状態では、水は自由に流れ、複雑な流れや渦を作り出します。しかし、水門や堰のシステムを作り始めたらどうなるでしょうか。水の流れを制御し、適切な方向に導き、流れの強さを調整できるようになります。ニューラルネットワークにおける活性化関数も同様の役割を果たします。どの信号を通すか、どの信号を遅らせるか、あるいは弱めるかを決定するのです。活性化関数がなければ、ニューラルネットワークは単なる線形変換の集合に過ぎません。
活性化関数はニューラルネットワークの動作に動的な性質を加え、データの微妙なニュアンスを捉えることを可能にします。たとえば顔認識タスクでは、活性化関数によって眉のアーチや顎の形状などの小さな特徴を検知できます。適切な活性化関数の選択は、ニューラルネットワークがさまざまなタスクでどのように機能するかに影響します。ある特徴量は学習初期の段階で明確で理解しやすい信号を提供します。別の特徴量はネットワークがより微細なパターンを学習する後期段階で有用です。また、不要な情報を抑制し、重要な特徴量のみを強調する役割を果たすものもあります。
活性化関数の特性を知らなければ、ニューラルネットワークは単純な課題でつまずいたり、重要な詳細を見落としたりし始める可能性があります。活性化関数の主な目的は、ニューラルネットワークに非線形性を導入し、出力値を正規化することです。
本記事の目的は、異なる活性化関数の使用に関連する問題点を明らかにし、誤差を最小化しつつ例点を補間する際のニューラルネットワークの精度に与える影響を検証することです。また、活性化関数が実際に収束速度に影響を与えるのか、それともこれは使用する最適化アルゴリズムの性質によるものなのかを明らかにします。参照アルゴリズムとして、確率的要素を用いた改良版集団ADAMmを使用し、MLPに組み込まれたADAM(従来の使用法)でテストをおこないます。後者は直感的には有利に思えます。なぜなら、活性化関数の導関数を通じて適合度関数の勾配に直接アクセスできるからです。一方、集団型の確率的ADAMmは導関数へのアクセスがなく、最適化問題の表面について全く情報を持たないためです。これらの結果を見て結論を導きます。
作者: Andrey Dik