MetaTrader 5 / トレーディングシステム
English
preview
データサイエンスとML（第42回）：PythonでARIMAを用いた外国為替時系列予測、知っておくべきことすべて

データサイエンスとML（第42回）：PythonでARIMAを用いた外国為替時系列予測、知っておくべきことすべて

MetaTrader 5 — トレーディングシステム |
46 0
Omega J Msigwa
Omega J Msigwa

内容


時系列予測とは何か

時系列予測とは、一連のデータポイントにおける将来の値を予測するために過去のデータを使用するプロセスです。このシーケンスは通常、時間順に並べられるため、時系列と呼ばれます。

時系列データの中核変数 

データにはいくらでも特徴量を持たせることができますが、時系列分析や予測のためのデータには、必ずこの2つの変数が必要です。

  1. 時間

     これは独立変数で、データポイントが観測された特定の時点を表します。

  2. 目標変数

    過去の観測値やその他の要因に基づいて予測したい値です（例：日次の株価終値、時間ごとの気温、1分ごとのWebサイトアクセス数など）。

時系列予測の目的は、データ内の過去のパターンとトレンドを活用して、将来の値について情報に基づいた予測をおこなうことです。

これまで、通常のAIモデルを使った時系列予測についても触れてきましたが、 この記事では、時系列問題専用に設計されたモデル「ARIMA」を使った予測について解説します。

時系列予測は2つのタイプに分けられます。

  1. 単変量時系列予測
    1つの予測変数（目標変数自身）を使って将来の値を予測する問題です（例：株価の現在の終値を使って将来の終値を予測する）。

    ARIMAモデルはこのタイプの予測に対応しています。
  2. 多変量時系列予測
    複数の予測変数を使って将来の目標変数を予測する問題です（例：過去の株価や出来高、経済指標を組み合わせて株価を予測する）。

    この記事でおこなったことと同様です。


ARIMAモデルの紹介

ARIMAとはAuto Regressive Integrated Moving Average（自己回帰和分移動平均）の略です。

これは、与えられた時系列をその過去の値、すなわちラグやラグに基づく予測誤差をもとに説明するモデルの一種です。

この方程式は将来の値を予測するために使用できます。季節性のない時系列で、パターンが存在し、完全なランダムな白色雑音でないものは、ARIMAモデルで表現することができます。

つまり、ARIMAは、時系列の過去の情報だけを使って将来の値を予測するという考え方に基づいた予測アルゴリズムです。

ARIMAモデルは3つの次数パラメータp、d、qによって指定されます。

ここで

  • pはAR項の次数
  • qはMA項の次数
  • dは時系列を定常化するために必要な差分の次数


ARIMAモデルにおけるp、d、qの意味

pの意味

pはAR（自己回帰、Auto Regressive）項の次数です。Yのラグをいくつ予測変数として使うかを表します。

dの意味

ARIMAの「Auto Regressive」とは、ラグ（過去の値）を予測変数として利用する線形回帰モデルを意味します。線形回帰モデルは、予測変数同士が相関しておらず独立しているときに最もよく機能します。そのため、時系列データを定常化する必要があります。

時系列を定常化する最も一般的な方法は「差分」を取ることです。つまり、現在の値から直前の値を引き算します。時系列の複雑さによっては、1回以上の差分が必要になる場合もあります。

したがって、dの値は系列を定常化するために必要な最小の差分回数を意味します。時系列がすでに定常である場合、d = 0になります。

qの意味

qはMA（移動平均、Moving Average）項の次数です。これは、ARIMAモデルに組み込む「ラグ付き予測誤差」の数を意味します。


ARIMAモデルの主要要素

ARIMAを理解するためには、その構成要素を分解する必要があります。要素を分けて考えることで、この時系列予測手法が全体としてどのように機能するのかが理解しやすくなります。

ARIMAという名前は、以下の3つの部分（AR, I, MA）に分けられます。

自己回帰（Auto Regressive、AR(p)）

自己回帰(AR)要素は、過去の値から現在の傾向を導き出す役割を持ちます。自己回帰の枠組みは、回帰モデルに似ており、時系列データ自身のラグ（過去の値）を説明変数として用いるモデルです。 

この部分は次の式で計算されます。

AR式

ここで

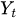  • は時刻tにおける現在の時系列の値
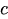  • は定数項
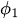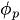  • ～は自己回帰係数（パラメータ）で、それぞれのラグが現在の値にどの程度寄与しているかを示す
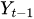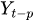  • ～は過去のラグ付き時系列の値
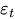  • は時刻tにおける誤差項

差分（Integrated、I(d)）

差分要素は、時系列を定常化するために差分を取ることに関係します。定常性とは、平均と分散が時間の経過に対して一定であることを意味します。

基本的には、ある観測値からその直前の観測値を引き算することで、トレンドや季節性を除去します。差分を取ることでデータを定常化し、モデルがノイズではなく本来のデータ構造に適合しやすくなります。

移動平均（Moving Average、MA(q)）

移動平均(MA)要素は、観測値と残差（誤差項）の関係に着目します。現在の観測値が過去の誤差とどのように関連しているかを見ることで、データ内の短期的な変動やランダムなショックに関する情報を引き出すことができます。 

残差をこうした誤差のひとつと考えることができ、移動平均モデルの考え方は、これらの誤差が最新の観測値に与える影響を推定するというものです。これは特に、データ内の短期的な変化やランダムなショックを捉えるのに有効です。MA成分を時系列に組み込むことで、その振る舞いに関する重要な情報を得ることができ、より高い精度での予測や予報につながります。

ここで

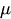  • は定数
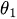  • はMAパラメータ
  • は以前の誤差
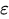  • 現在の誤差


PythonにおけるARIMAモデル

ARIMAモデルは、これまで説明してきた3つの構成要素（AR、I、MA）を組み合わせたものです。式で表すと次のようになります。

ここで、p、d、qの値を正しく決めることがARIMAモデルの大きな課題となります。これらの値がモデルの動作を左右するため、適切に選ぶ必要があります。


AR項(p)の次数を決める方法

AR項の必要な次数(p)を決定するには、偏自己相関(PACF: Partial Autocorrelation Function)プロットを用います。

偏自己相関は、系列とそのラグ（過去の値）との相関を、中間ラグの寄与を取り除いた上で測定したものとして説明できます。つまり、PACFは特定のラグと系列との「純粋な相関関係」を示すものです。これにより、そのラグをAR項に含める必要があるかどうかを判断することができます。

まず、コマンドプロンプト(CMD)で依存関係をすべてインストールしてください。必要なパッケージは本記事の末尾に添付しているrequirements.txtに記載されています。

pip install -r requirements.txt

Import文

# Importing required libraries
import pandas as pd
import numpy as np
import MetaTrader5 as mt5

# Use auto_arima to automatically select best ARIMA parameters

import seaborn as sns
import matplotlib.pyplot as plt
import warnings
import os

# Suppress warning messages for cleaner output
warnings.filterwarnings("ignore")

# Set seaborn plot style for better visualization
sns.set_style("darkgrid")

MetaTrader5からデータを取得します。

# Getting (EUR/USD OHLC data) from MetaTrader5

mt5_exe_file = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # Change this to your MetaTrader5 path
if not mt5.initialize(mt5_exe_file):
    print("Failed to initialize Metatrader5, error = ",mt5.last_error)
    exit()

# select a symbol into the market watch
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1

if not mt5.symbol_select(symbol, True):
    print(f"Failed to select {symbol}, error = {mt5.last_error}")
    mt5.shutdown()
    exit()

rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 1000) # Get 1000 bars historically
df = pd.DataFrame(rates)

print(df.head(5))
print(df.shape)

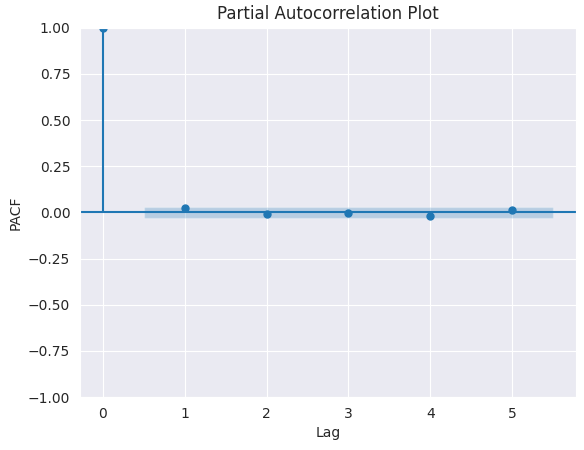
PACFプロットをおこないます。

from statsmodels.graphics.tsaplots import plot_pacf
import matplotlib.pyplot as plt

plt.figure(figsize=(6,4))
plot_pacf(series.diff().dropna(), lags=5)

plt.title("Partial Autocorrelation Plot")
plt.xlabel('Lag')  # X-axis label
plt.ylabel('PACF')  # Y-axis label

plt.savefig("pacf plot.png")
plt.show()

以下が出力です。

適切なpの値を決定するためには、PACFがカットオフするラグ、すなわち相関がゼロ付近まで落ちて以降有意でなくなる点を確認します。そのラグの値がpの候補となります。 

上記のグラフからは、適切なpの値は0です（0以降のすべてのラグは有意ではありません）。

ARIMAモデルにおける差分次数(d)の決定

前述のとおり、時系列を差分する目的は、系列を定常化することにあります。これはARIMAモデルが定常性を前提としているためです。ただし、階差の不足や過剰には注意する必要があります。

適切な差分次数は、系列を「ほぼ定常」と見なせる状態にするために必要最小限の階差です。具体的には、系列が一定の平均の周辺を推移し、自己相関関数(ACF)のプロットが比較的速やかにゼロへ収束することが目安となります

自己相関が多数のラグ（10以上）にわたって正の値を示す場合、その系列はさらなる階差が必要です。一方で、自己相関のラグ1が強く負の値を示す場合、その系列は過剰に階差が行われている可能性があります。

もし2つの差分次数のどちらを採用すべきか判断できない場合は、階差後の系列において標準偏差が最も小さくなる差分次数を選択します。

EURUSDの終値データを用いて、適切な差分次数を求めてみましょう。

まず、与えられた系列（この場合は終値）が定常であるかどうかを、Pythonのfrom the statsmodelsパッケージに含まれる拡張ディッキー＝フラー検定（ADF検定）を用いて確認する必要があります。定常性を確認するのは、差分次数を決定するのは非定常系列に対してのみ意味を持つためです。

ADF検定の帰無仮説(Ho)は「その時系列は非定常である」というものです。したがって、検定のp値が有意水準0.05未満であれば、帰無仮説を棄却し、その時系列が定常であると判断します。

このため、本ケースではp値が0.05より大きい場合に、適切な差分次数を求める作業に進みます。

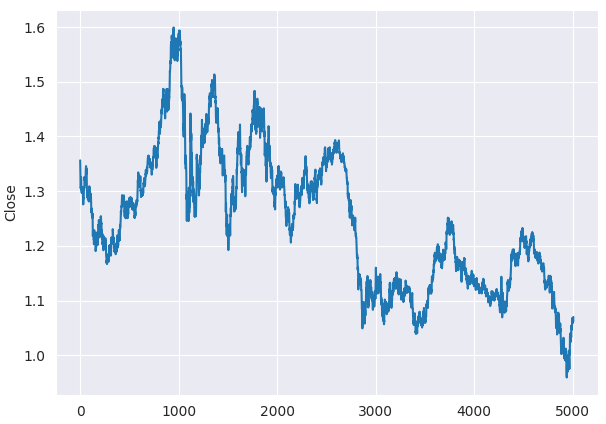
なお、ADF検定をおこなう前に、EURUSDの終値を折れ線グラフで確認するだけでも、その系列が定常ではないことが視覚的に分かります。

plt.figure(figsize=(7,5))
sns.lineplot(df, x=df.index, y="Close")
plt.savefig("close prices.png")

以下が出力です。

定常性を確認します。

from statsmodels.tsa.stattools import adfuller

series = df["Close"]
result = adfuller(series)

print(f'p-value: {result[1]}')

以下が出力です。

p-value: 0.3707268514544181

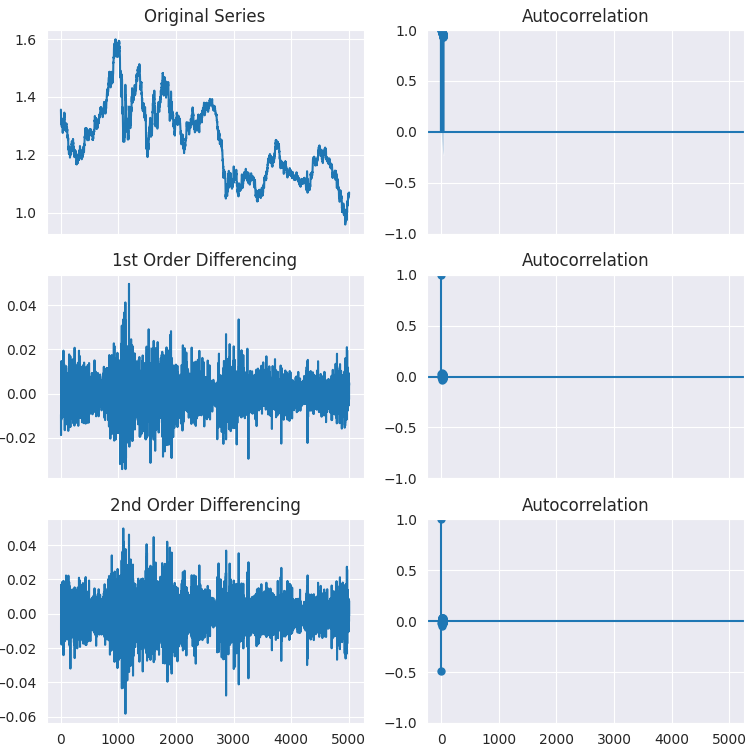
ご覧のとおり、p値は有意水準(0.05)を大きく上回っています。そこで、系列を1回階差し、さらに2回階差して、自己相関プロットがどのように変化するかを確認してみましょう。

# Original Series
fig, axes = plt.subplots(3, 2, sharex=True, figsize=(9, 9))

axes[0, 0].plot(series); axes[0, 0].set_title('Original Series')
plot_acf(series, ax=axes[0, 1])

# 1st Differencing
axes[1, 0].plot(series.diff().dropna()); axes[1, 0].set_title('1st Order Differencing')
plot_acf(series.diff().dropna(), ax=axes[1, 1])

# 2nd Differencing
axes[2, 0].plot(series.diff().diff()); axes[2, 0].set_title('2nd Order Differencing')
plot_acf(series.diff().diff().dropna(), ax=axes[2, 1])

plt.savefig("acf plots.png")
plt.show()

以下が出力です。

プロットから分かるように、1階差で十分であり、2階差においては定常性の結果に大きな違いは見られません。このことは、ADF検定によって改めて確認することができます。

result = adfuller(series.diff().dropna())
print(f'p-value d=1: {result[1]}')

result = adfuller(series.diff().diff().dropna())
print(f'p-value d=2: {result[1]}')

以下が出力です。

p-value d=1: 0.0
p-value d=2: 0.0

MA項の次数(q)の決定

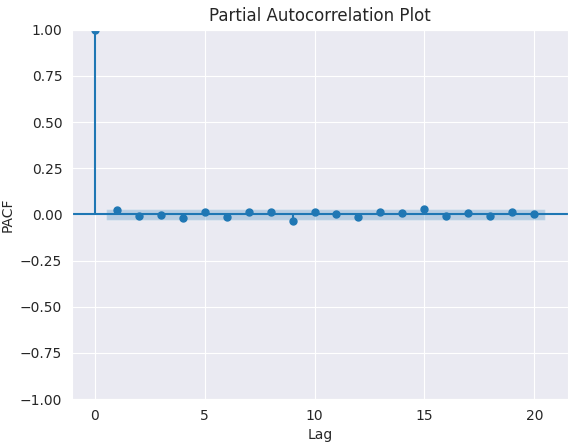
AR項の次数(d)を求める際にPACFプロットを確認したのと同様に、MA項の次数を求める際にはACFプロットを確認します。なお、MA項とは技術的にはラグ付き予測における誤差を意味します。

ACFプロットは、定常化された系列における自己相関を取り除くために必要なMA項の数を示してくれます。

plt.figure(figsize=(7,5))
plot_pacf(series.diff().dropna(), lags=20)

plt.title("Partial Autocorrelation Plot")
plt.xlabel('Lag')  # X-axis label
plt.ylabel('PACF')  # Y-axis label

plt.savefig("pacf plot finding q.png")
plt.show()

以下が出力です。

最適なqの値は0です。

ここまで説明してきたp、d、qの値を求める方法は、あくまで手作業による大まかな手法です。しかし、このプロセスはpmdarimaライブラリに含まれるauto_arimaというユーティリティ関数を使うことで、自動化して手間なくパラメータを求めることができます。

from pmdarima.arima import auto_arima

model = auto_arima(series, seasonal=False, trace=True)
print(model.summary())

以下が出力です。

Performing stepwise search to minimize aic
 ARIMA(2,1,2)(0,0,0)[0] intercept   : AIC=-35532.282, Time=3.21 sec
 ARIMA(0,1,0)(0,0,0)[0] intercept   : AIC=-35537.068, Time=0.49 sec
 ARIMA(1,1,0)(0,0,0)[0] intercept   : AIC=-35537.492, Time=0.59 sec
 ARIMA(0,1,1)(0,0,0)[0] intercept   : AIC=-35537.511, Time=0.74 sec
 ARIMA(0,1,0)(0,0,0)[0]             : AIC=-35538.731, Time=0.25 sec
 ARIMA(1,1,1)(0,0,0)[0] intercept   : AIC=-35535.683, Time=1.22 sec

Best model:  ARIMA(0,1,0)(0,0,0)[0]          
Total fit time: 6.521 seconds

このようにして、手作業で分析したときと同じパラメータを得ることができました。


EURUSDに対するARIMAモデルの構築

p、d、qの値が決定できたので、ARIMAモデルを適合（学習）させるために必要な準備が整いました。

from statsmodels.tsa.arima.model import ARIMA

arima_model = ARIMA(series, order=(0,1,0))
arima_model = arima_model.fit()
print(arima_model.summary())

以下が出力です。

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                  Close   No. Observations:                 4007
Model:                 ARIMA(0, 1, 0)   Log Likelihood               13987.647
Date:                Mon, 26 May 2025   AIC                         -27973.293
Time:                        16:59:38   BIC                         -27966.998
Sample:                             0   HQIC                        -27971.062
                               - 4007                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
sigma2      5.427e-05   7.78e-07     69.768      0.000    5.27e-05    5.58e-05
===================================================================================
Ljung-Box (L1) (Q):                   1.47   Jarque-Bera (JB):              1370.86
Prob(Q):                              0.22   Prob(JB):                         0.00
Heteroskedasticity (H):               0.49   Skew:                             0.09
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.86
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

それでは、このモデルをデータに学習させ、従来の機械学習モデルと同様に、アウトオブサンプルデータに対する予測に使用してみましょう。

まずは、データを学習用とテスト用に分割するところから始めます。

series = df["Close"]

train_size = int(len(series) * 0.8)
train, test = series[:train_size], series[train_size:]

モデルを学習用データに適合させます。

from statsmodels.tsa.arima.model import ARIMA

arima_model = ARIMA(train, order=(0,1,0))
arima_model = arima_model.fit()
print(arima_model.summary())

学習用データに基づいて予測をおこないます。

predicted = arima_model.predict(start=1, end=len(train))

結果を可視化します。

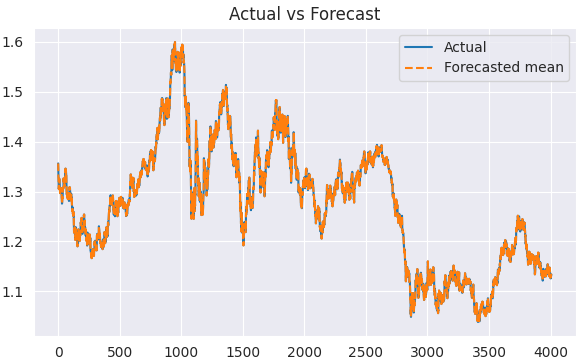
plt.figure(figsize=(7,4))
plt.plot(train.index, train, label='Actual')
plt.plot(train.index, predicted, label='Forecasted mean', linestyle='--')
plt.title('Actual vs Forecast')
plt.legend()
plt.show()

以下が出力です。

これで実際の値と予測値が揃ったので、任意の評価手法や損失関数を用いてモデルを評価することができます。

しかしその前に、アウトオブサンプルデータに対してこのARIMAモデルを用いて予測をおこなう方法を確認しておきましょう。


ARIMAを用いたアウトオブサンプル予測

従来の時系列予測モデルは、クラシックな機械学習アルゴリズムとは異なるアプローチで、未知の情報に対する予測をおこないます。

クラシックな機械学習フレームワークやPythonライブラリでは、predictというメソッドを呼び出し、データの配列を渡すと、次の（将来の）値を予測します。しかし、ARIMAモジュールのpredict関数は少し異なる役割を果たします。

ARIMAモデルにおけるこのメソッドは、必ずしも未来を予測するわけではなく、主にモデル内にすでに存在する情報（つまり学習データ）に基づいて予測をおこなう際に便利です。

これを理解するために、まず予測(predicting)と将来予測(forecasting)の違いについて説明します。

予測とは、モデルを用いて未知の値（将来の値である場合もあればそうでない場合もあります）を推定することを指します。一方で将来予測は、時系列データにおける時間的パターンや依存関係を利用して、将来の値を予測することを意味します。

予測は、たとえば市場の方向性を分類したり、次の終値を推定したりする問題に適用できます。一方、将来予測は、現在の値に基づいて次の株価を予測する場合に用いられます。

ARIMAモデルでは、predictメソッドは通常、モデルが学習した過去の値に対する予測（評価）に使用されます。そのため、開始インデックスと終了インデックスを指定する必要があります。また、過去のどのステップまで予測（評価）するかを指定することも可能です。

predicted = arima_model.predict(start=1, end=len(train))
print(arima_model.predict(steps=10))

将来の値を予測するには、forecast()というメソッドを使用する必要があります。 

前述のとおり、ARIMAのような従来の時系列モデルは、次の値を予測する際に前の値に依存します。これは、図03に示されている数式からも確認できます。

つまり、モデルを常に最新の情報で更新しておく必要があります。たとえば、EURUSDの翌日の終値をARIMAモデルで予測するには、本日の終値をモデルに入力する必要があります。同様に、翌日やその次の日の予測も、最新の値をモデルに反映させる必要があります。

これは、従来の機械学習でおこなう手法とは大きく異なります。

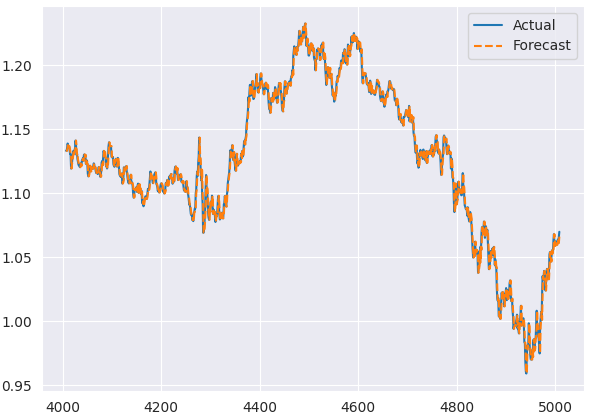
それでは、アウトオブサンプルデータに対する予測をおこなってみましょう。

# Fit initial model

model = ARIMA(train, order=(0, 1, 0)) 
results = model.fit()

# Initialize forecasts
forecasts = [results.forecast(steps=1).iloc[0]]  # First forecast

# Update with test data iteratively
for i in range(len(test)):
    # Append new observation without refitting
    results = results.append(test.iloc[i:i+1], refit=False)
    
    # Forecast next step
    forecasts.append(results.forecast(steps=1).iloc[0])

forecasts = forecasts[:-1] # remove the last element which is the predicted next value 

# Compare forecasts vs actual test data
plt.plot(test.index, test, label="Actual")
plt.plot(test.index, forecasts, label="Forecast", linestyle="--")
plt.legend()

appendメソッドは、新しい情報（最新のデータ）をモデルに追加する役割を果たします。この場合、EURUSDの現在の終値をモデルに追加することで、次の終値を予測することができます。 

refit=Falseは、モデルを再度学習させないことを保証します。これにより、ARIMAモデルを効率的に更新することが可能になります。

次に、ARIMAモデルの性能を評価するために使用できるいくつかの評価指標を組み込んだ関数を作成してみましょう。

import sklearn.metrics as metric
from statsmodels.tsa.stattools import acf
from scipy.stats import pearsonr

def forecast_accuracy(forecast, actual):
    # Convert to numpy arrays if they aren't already
    forecast = np.asarray(forecast)
    actual = np.asarray(actual)
    
    metrics = {
        'mape': metric.mean_absolute_percentage_error(actual, forecast),
        'me': np.mean(forecast - actual),  # Mean Error
        'mae': metric.mean_absolute_error(actual, forecast),
        'mpe': np.mean((forecast - actual) / actual),  # Mean Percentage Error
        'rmse': metric.mean_squared_error(actual, forecast, squared=False),
        'corr': pearsonr(forecast, actual)[0],  # Pearson correlation
        'minmax': 1 - np.mean(np.minimum(forecast, actual) / np.maximum(forecast, actual)),
        'acf1': acf(forecast - actual, nlags=1)[1],  # ACF of residuals at lag 1
        "r2_score": metric.r2_score(forecast, actual)
    }

    return metrics
forecast_accuracy(forecasts, test)

以下が出力です。

{'mape': 0.0034114761554881936,
 'me': 6.360279441117738e-05,
 'mae': 0.0037872155688622737,
 'mpe': 6.825424905960248e-05,
 'rmse': 0.005018824533752777,
 'corr': 0.99656297100796,
 'minmax': 0.0034008221524469695,
 'acf1': 0.04637470541528736,
 'r2_score': 0.9931220697334551}

MAPEの値が0.003であることは、モデルの精度が約99.996%であることを示しています。同様の精度は、r2_scoreでも確認できます。

以下は、テストサンプルにおける実際の値と予測値を比較したプロットです。


ARIMAモデルの残差プロット

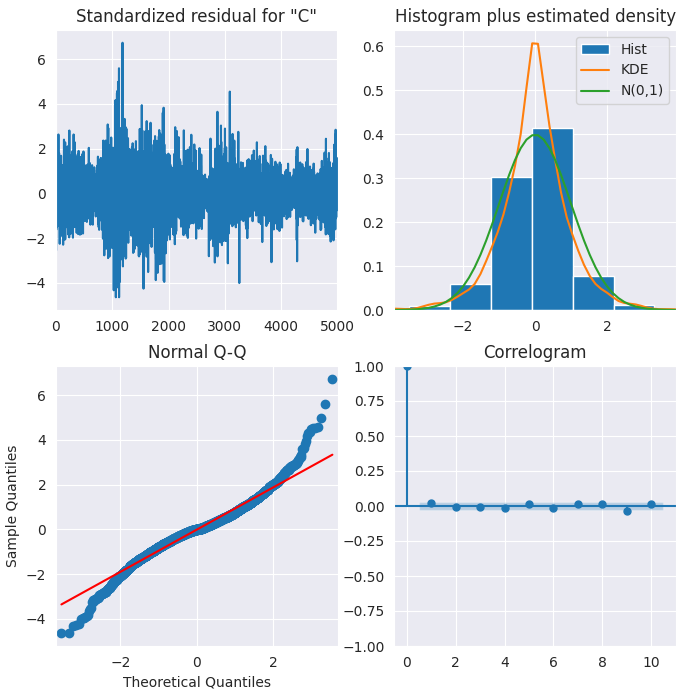
ARIMAには、モデルをより深く理解するために残差を可視化するためのメソッドが用意されています。

results.plot_diagnostics(figsize=(8,8))
plt.show()

以下が出力です。

標準化残差

残差誤差は平均ゼロの周りで変動しており、分散も均一に見えます。

ヒストグラム

密度プロットは、平均がやや右にずれた正規分布を示唆しています。

理論的分位数

ほとんどの点が赤い直線上にぴったり並んでいます。大きく逸脱する点がある場合は、分布が歪んでいることを意味します。

相関図

相関図（またはACFプロット）を見ると、残差誤差に自己相関は見られません。もしACFプロットにパターンが見られる場合、モデルで説明されていない残差誤差の傾向が存在することを意味し、その場合はモデルにさらに説明変数(X)を追加する必要があります。

全体として、このモデルは良好に適合しているといえます。


SARIMAモデル

通常のARIMAモデルには1つの問題があります。それは季節性に対応していないことです。

季節性とは、金融データにおいて一定の間隔（時間単位、日次、週次、月次、四半期、年次など）で繰り返されるパターンのことを指します。

多くの金融商品は特定の繰り返しパターンを示すことがあります。たとえば、小売株は第4四半期（ホリデーシーズン）に上昇しやすく、エネルギー株は季節的な気象パターンに従うことがあります。FXでは、特定の取引セッション中に市場のボラティリティが高まることが観察されます。

時系列データに観察可能な、あるいは明確に定義された季節性がある場合は、季節差分を利用するSARIMA(Seasonal ARIMA)モデルを使用すべきです。

SARIMAX(p, d, q)x(P, D, Q, S)モデルの要素

  • 自己回帰(AR)

    前述の通り、自己回帰は時系列の過去の値を参照して現在の値を予測します。

  • 移動平均(MA)

    移動平均は、過去の予測誤差をモデル化し続けます。

  • 差分要素(I)

    差分要素は時系列を定常化するために常に存在します。

  • 季節要素(S)

    季節要素は、定期的に繰り返される変動を捉えます。

季節差分は通常の差分と似ていますが、連続する項を引くのではなく、前の季節の値との差を計算します。

SARIMAXモデルを呼び出す前に、auto_arimaを用いて適切なパラメータを決定しましょう。

from pmdarima.arima import auto_arima

# Auto-fit SARIMA (automatically detects P, D, Q, S)

auto_model = auto_arima(
    series,
    seasonal=True,          # Enable seasonality
    m=5,                    # Weeky cycle (5 days) for daily data
    trace=True,             # Show search progress
    stepwise=True,          # Faster optimization
    suppress_warnings=True,
    error_action="ignore"
)

print(auto_model.summary())

以下が出力です。

Performing stepwise search to minimize aic
 ARIMA(2,1,2)(1,0,1)[5] intercept   : AIC=-35529.092, Time=3.81 sec
 ARIMA(0,1,0)(0,0,0)[5] intercept   : AIC=-35537.068, Time=0.29 sec
 ARIMA(1,1,0)(1,0,0)[5] intercept   : AIC=-35536.573, Time=0.97 sec
 ARIMA(0,1,1)(0,0,1)[5] intercept   : AIC=-35536.570, Time=4.38 sec
 ARIMA(0,1,0)(0,0,0)[5]             : AIC=-35538.731, Time=0.21 sec
 ARIMA(0,1,0)(1,0,0)[5] intercept   : AIC=-35536.048, Time=0.67 sec
 ARIMA(0,1,0)(0,0,1)[5] intercept   : AIC=-35536.024, Time=0.87 sec
 ARIMA(0,1,0)(1,0,1)[5] intercept   : AIC=-35534.248, Time=0.92 sec
 ARIMA(1,1,0)(0,0,0)[5] intercept   : AIC=-35537.492, Time=0.37 sec
 ARIMA(0,1,1)(0,0,0)[5] intercept   : AIC=-35537.511, Time=0.55 sec
 ARIMA(1,1,1)(0,0,0)[5] intercept   : AIC=-35535.683, Time=0.57 sec

Best model:  ARIMA(0,1,0)(0,0,0)[5]          
Total fit time: 13.656 seconds
                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                 5009
Model:               SARIMAX(0, 1, 0)   Log Likelihood               17770.365
Date:                Tue, 27 May 2025   AIC                         -35538.731
Time:                        11:16:40   BIC                         -35532.212
Sample:                             0   HQIC                        -35536.446
                               - 5009                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
sigma2      4.846e-05   6.06e-07     80.005      0.000    4.73e-05    4.96e-05
===================================================================================
Ljung-Box (L1) (Q):                   2.42   Jarque-Bera (JB):              2028.68
Prob(Q):                              0.12   Prob(JB):                         0.00
Heteroskedasticity (H):               0.34   Skew:                             0.08
Prob(H) (two-sided):                  0.00   Kurtosis:                         6.11
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

auto_arimaはSARIMAXモデルを返すため、手動で再学習させる必要はありませんが、SARIMAXモデルを手動で再学習させることで結果に対する制御がより効くようになります。そこで、もう一度手動で再学習させてみましょう。

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(
    train,
    order=auto_model.order,                  # Non-seasonal (p,d,q)
    seasonal_order=auto_model.order+(5,),      # Seasonal (P,D,Q,S)
    enforce_stationarity=False
)

results = model.fit()
print(results.summary())

以下が出力です。

                                     SARIMAX Results                                     
=========================================================================================
Dep. Variable:                             Close   No. Observations:                 4007
Model:             SARIMAX(0, 1, 0)x(0, 1, 0, 5)   Log Likelihood               12613.829
Date:                           Tue, 27 May 2025   AIC                         -25225.658
Time:                                   11:16:41   BIC                         -25219.364
Sample:                                        0   HQIC                        -25223.427
                                          - 4007                                         
Covariance Type:                             opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
sigma2         0.0001   1.68e-06     63.423      0.000       0.000       0.000
===================================================================================
Ljung-Box (L1) (Q):                   3.42   Jarque-Bera (JB):               676.61
Prob(Q):                              0.06   Prob(JB):                         0.00
Heteroskedasticity (H):               0.48   Skew:                            -0.01
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.01
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

季節値をtrueに設定しているにもかかわらず、 auto_arimaから返される次数はARIMA(p,d,q)の形式であり、季節性を有効にしていても同様です。そのため、SARIMAXモデルを宣言する際には、タプルに季節ウィンドウの値（ここでは5）を追加して、モデルが(p,d,q,s)となるようにする必要があります。

実際の値と予測値を可視化・分析する前に、配列の最初の要素（季節ウィンドウの長さに相当する値）を削除する必要があります。この値より前のデータは不完全であるためです。

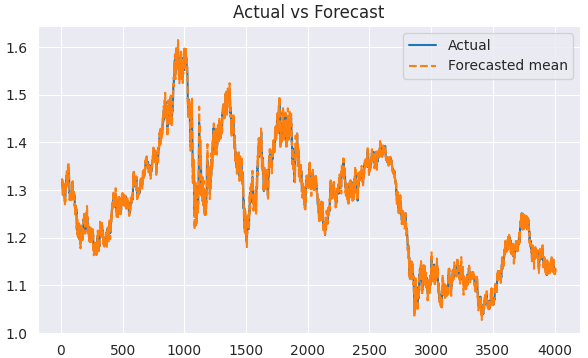
predicted = results.predict(start=1, end=len(train))

clean_train = train[5:]
clean_predicted = predicted[5:]

plt.figure(figsize=(7,4))
plt.plot(clean_train.index[5:], clean_train[5:], label='Actual')
plt.plot(clean_train.index[5:], clean_predicted[5:], label='Forecasted mean', linestyle='--')
plt.title('Actual vs Forecast')
plt.legend()
plt.savefig("sarimax train actual&forecast plot.png")
plt.show()

以下が出力です。

このモデルも、先ほどのARIMAモデルと同様の方法で評価することができます。

# Initialize forecasts
forecasts = [results.forecast(steps=1).iloc[0]]  # First forecast

# Update with test data iteratively
for i in range(len(test)):
    # Append new observation without refitting
    results = results.append(test.iloc[i:i+1], refit=False)
    
    # Forecast next step
    forecasts.append(results.forecast(steps=1).iloc[0])

clean_test = test[5:]
forecasts = forecasts[5:-1] # remove the last element which is the predicted next value and the first 5 items
forecast_accuracy(forecasts, clean_test)

以下が出力です。

{'mape': 0.004900183060803821,
 'me': -6.94082142749275e-06,
 'mae': 0.005432456867698095,
 'mpe': -7.226495372320155e-06,
 'rmse': 0.007127465498996785,
 'corr': 0.9931778828074744,
 'minmax': 0.004880027322298863,
 'acf1': 0.10724254539104018,
 'r2_score': 0.9864021833085908}

r2_scoreによると精度は98.6%で、まずまずの値です。

最後に、MetaTrader5から取得したデータに基づいて、ARIMAモデルを用いたリアルタイム予測をおこなうことができます。

まず、このモデルを日次データで学習させたため、1日後に予測を実行するのを助けるために、scheduleライブラリをインポートする必要があります。

import schedule
# Make realtime predictions based on the recent data from MetaTrader5

def predict_close():
    
    rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, 1) 
    if not rates:
        print(f"Failed to get recent OHLC values, error = {mt5.last_error}")
        time.sleep(60)
    
    rates_df = pd.DataFrame(rates)    
    
    global results # Get the variable globally, outside the function
    global forecasts
    
    # Append new observation to the model without refitting
    
    new_obs_value = rates_df["close"].iloc[-1]
    new_obs_index = results.data.endog.shape[0]  # continue integer index
    
    new_obs = pd.Series([new_obs_value], index=[new_obs_index]) # Its very important to continue making predictions where we ended on the training data
    results = results.append(new_obs, refit=False)
    
    # Forecast next step
    forecasts.append(results.forecast(steps=1).iloc[0])
    print(f"Current Close Price: {new_obs_value} Forecasted next day Close Price: {forecasts[-1]}")
    

予測を立ててスケジュールを立てます。

schedule.every(1).days.do(predict_close) # call the predict function after a given time

while True: 
    
    schedule.run_pending()    
    time.sleep(60)

mt5.shutdown()

以下が出力です。

Current Close Price: 1.1374900000000001 Forecasted next day Close Price: 1.1337899981049262
Current Close Price: 1.1372200000000001 Forecasted next day Close Price: 1.1447100065656721

これらの予測終値をもとに、取引戦略に応用し、MetaTrader5-Pythonを使って実際の取引操作をおこなうことも可能です。



最後に

ARIMAおよびSARIMAは、さまざまな分野や産業で利用されてきた伝統的な時系列モデルとして十分に有用です。しかし、それらの限界や欠点を理解しておくことが重要です。

  • 定常性の前提（階差後）

    これらのモデルは定常性を前提としています。実務では必ずしも定常データを扱うわけではなく、データをそのまま使いたい場合もあります。階差を取ることで、本来の自然な構造やトレンドが歪められる可能性があります。

  • 線形性の前提

    ARIMAは本質的に線形モデルであり、未来の値が過去のラグや誤差に線形に依存すると仮定しています。しかし、金融市場やFX市場では複雑なパターンが頻繁に見られるため、この仮定が当てはまらず、モデルが期待通りに機能しないことがあります。

  • 単変量モデル

    これらのモデルは基本的に1つの特徴量のみを扱います。金融市場は複雑であり、複数の特徴や視点から市場を分析する必要があります。単変量モデルでは1次元的にしか市場を見られないため、有用な情報を見逃す可能性があります。 

    SARIMAXモデルには外生変数(exogenous feature)を追加することもできますが、多くの場合それだけでは不十分です。

とはいえ、適切なパラメータや問題タイプ、利用可能な情報を組み合わせれば、シンプルなARIMAモデルがRNNのような複雑なモデルを上回る場合もあります。

ご一読、誠にありがとうございました。


情報源と参考文献


添付ファイルの表

ファイル名 説明と使用法
forex_ts_forecasting_using_arima.py 説明したすべてのPython言語での例を含むPythonスクリプト
requirements.txt  Pythonの依存関係とそのバージョン番号を含むテキストファイル


MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/18247

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動
EAのサンプル EAのサンプル
一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。
データサイエンスとML（第41回）：YOLOv8を用いた外国為替および株式市場のパターン検出 データサイエンスとML（第41回）：YOLOv8を用いた外国為替および株式市場のパターン検出
金融市場でパターンを検出するのは、チャート上の内容を確認する必要があるため困難ですが、これは画像の制限によりMQL5では実行が困難です。この記事では、最小限の労力でチャート上のパターンを検出するのに役立つ、Pythonで作成された適切なモデルについて説明します。
エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
MQL5 Algo Forgeへの移行（第1回）：メインリポジトリの作成 MQL5 Algo Forgeへの移行（第1回）：メインリポジトリの作成
MetaEditorでプロジェクトを進める際、開発者はしばしばコードのバージョンを管理する必要に直面します。MetaQuotesは最近、Gitへの移行と、コードのバージョン管理や共同作業を可能にするMQL5 Algo Forgeの立ち上げを発表しました。本記事では、新しく導入されたツールと既存のツールを、より効率的に活用する方法について解説します。