知っておくべきMQL5ウィザードのテクニック（第66回）：FrAMAのパターンとForce Indexを内積カーネルで使用する

はじめに

前回の記事では、これらのインジケーターのペアをエキスパートアドバイザー(EA)のエントリーシグナルパターンのソースとして紹介しましたが、フォワードウォークの結果はあまり有望ではありませんでした。その理由をいくつか提示するとともに、私たちのトレーニングおよび最適化は1年間のみを対象としているため、いかなるパターンに対してもできる限り膨大な履歴に基づいて徹底的にテストすることが不可欠であると注意しました。常にそうしているように、その記事の続きとして、フォワードウォークに成功したパターンを機械学習とともに検証します。

MQL5で機械学習アルゴリズムを適用する際、OpenCLは常に選択肢の一つですが、これはしばしばGPUハードウェアを必要とします。これは便利ですが、Pythonのコードライブラリは非常に充実しており、CPUだけでも多くの効率性を享受することができます。本連載ではその点を探求しており、今回も過去におこなったようにニューラルネットワークをPythonで実装しています。なぜなら、Pythonでの実装とトレーニングは非常に効率的だからです。 

前回の記事で最適化またはトレーニングした10個のパターンのうち、フォワードウォークに成功したのは2つだけでした。Pattern_6とPattern_9です。したがって、これらをニューラルネットワークでさらにテストします。過去の記事と同様ですが、違いは畳み込みニューラルネットワーク(CNN)を使用する点です。このCNNは内積カーネルを実装します。しかしまず、Pythonでの実装においては常にそうであるように、ネットワークにシグナルを供給するために必要なインジケーター関数を定義します。 

フラクタル適応移動平均(FrAMA)関数

FrAMAは動的な移動平均であり、価格変動のフラクタル次元に応じて平滑化を適応させます。これにより、大きな価格変動にはより敏感に反応し、ノイズにはあまり反応しなくなります。この関数をPythonで次のように実装します。

def FrAMA(df, period=14, price_col='close'):
    """
    Calculate Fractal Adaptive Moving Average (FrAMA) for a DataFrame with price data.
    
    Args:
        df: Pandas DataFrame with a price column (default 'close').
        period: Lookback period for fractal dimension (default 20).
        price_col: Name of the price column (default 'close').
        
    Returns:
        Pandas DataFrame with a single column 'main' containing FrAMA values.
    """
    prices = df[price_col]
    frama = pd.Series(index=prices.index, dtype=float)
    
    for t in range(period, len(prices)):
        # 1. High-Low range (volatility proxy)
        high = prices.iloc[t-period:t].max()
        low = prices.iloc[t-period:t].min()
        range_hl = high - low
        
        # 2. Fractal Dimension (simplified)
        fd = 1.0 + (np.log(range_hl + 1e-9) / np.log(period))  # Avoid log(0)
        
        # 3. Adaptive EMA smoothing factor
        alpha = 2.0 / (period * fd + 1)
        
        # 4. Update FrAMA (recursive EMA)
        frama.iloc[t] = alpha * prices.iloc[t] + (1 - alpha) * frama.iloc[t-1]
    
    return pd.DataFrame({'main': frama})

上記の関数は、pandasのデータフレームを入力として受け取り、価格列と期間パラメータをカスタマイズ可能であるため、柔軟性を提供します。この関数は、高値から安値の範囲をボラティリティの代理として使用し、市場のボラティリティを推定し、価格の複雑性を測定するために単純化したフラクタル次元を計算します。そして、この関数は再帰的なEMAを通じてFrAMAを更新します。

コードを確認すると、最初におこなうことは、入力データフレームから指定された価格列を抽出することです。この抽出により、ユーザーが指定した任意の価格列で関数が動作することを保証します。ハード実装を避け、互換性を維持します。使用する際には、入力の価格列がデータフレーム内に存在することを検証し、また価格データがNaNや欠損値を含まずクリーンであることを確認することで関数を改善するのが良いでしょう。FrAMAは価格入力に敏感であるためです。

次に、入力データフレームのインデックスに整合するように空のpandasシリーズを初期化します。これにより、FrAMAの値を格納するためのメモリが事前に確保され、効率的にイテレーティブな更新をおこなうことができます。FrAMAは計算にルックバックウィンドウを必要とするため、最初の値はNaNとなり、ゼロにするか適切に処理する必要があります。また、価格のインデックスが一貫していること、例えば価格と時間のペアリングが適切であることを確認し、ミスアラインメントを避けることも重要です。

この準備の後、forループに入り、ルックバック期間にわたる高値から安値の範囲を計算してボラティリティを推定します。各タイムステップtにおいて、t期間のウィンドウ内の最高値と最安値を取り、その差を計算します。この高値から安値の範囲は市場ボラティリティの代理として機能し、フラクタル次元を決定するために重要です。範囲が大きいほどボラティリティが高くなり、それによりFrAMAの適応性に影響します。実装においては、NaNを検出して処理するエラーハンドリング機構を導入することが、欠損データ対策に有効です。

次に、対数比を用いて単純化したフラクタル次元を計算します。ここで用いる1e-9のε相当値は、高値から安値の範囲がゼロの場合にゼロ除算やゼロの対数を避けるためのものです。フラクタル次元fdは価格の複雑性またはトレンド性を測定します。fdが2に近いほど、市場はノイズが多く不規則であり、1に近いほどトレンドが発生していることを示します。このパラメータがFrAMAの適応性を駆動します。1e9は数値安定性のためのトリックであり、結果を歪めない程度に小さい値としています。また、ここで使用しているフラクタル次元は単純化したバージョンであり、より複雑な形式ではボックスカウント法などを用いることも可能です。その後、平滑化係数αを計算します。

これはフラクタル次元と期間に基づいた指数移動平均の平滑化係数です。適応的なαはFrAMAが新しい価格にどれだけ反応するかを決定するため重要です。ノイズの多い市場で得られる高いfdはαを減少させ、EMAを遅くしてノイズを除去します。一方、トレンド市場で得られる低いfdはαを増加させ、FrAMAが価格変動により敏感に反応します。

この数式は応答性と平滑性のバランスを取ります。感度を制御するために期間を調整することも可能です。また、分母であるperiod*fd+1が正であることを確認し、除算エラーを避けることも重要です。

次のコード行では、時刻tにおけるFrAMAの値をEMAの公式で更新します。これは現在の価格と直前のFrAMA値の加重平均を取るものであり、FrAMAの核心となる再帰的EMA計算です。これにより、αを通じて市場環境に適応する平滑化移動平均が生成されます。この実装において改善できる点として、最初のFrAMA値をNaNとしないことや、FrAMAバッファのエッジケースもチェックすることが挙げられます。

FrAMA関数の最終行では、FrAMA値を単一の列「main」を持つpandasデータフレームとして返します。これにより、他のテクニカル分析ツールやプロットライブラリとの互換性のために出力フォーマットが標準化されます。単一バッファを持つインジケーターにおいて「main」という列名を用いるのは慣例です。異なる環境に統合する際にこの名前が呼び出しポイントとなる場合、「FrAMA」やその他の特定の名称にカスタマイズすることも可能です。また、返されるデータフレームが入力データフレームのインデックスと整合することを保証する必要もあります。

Force Indexオシレーター関数

このオシレーターは、価格変動の強さを、価格の変化と出来高の変化を組み合わせることで測定します。これにEMAで平滑化を施すことで、トレンドや反転を強調します。Pythonでの実装は次のとおりです。

def ForceIndex(df, period=14, price_col='close', volume_col='tick_volume'):
    """
    Calculate Force Index for a DataFrame with price and volume data.
    
    Args:
        df: Pandas DataFrame with columns for price and volume (default 'close' and 'volume').
        period: Smoothing window for EMA (default 13).
        price_col: Name of the price column (default 'close').
        volume_col: Name of the volume column (default 'volume').
        
    Returns:
        Pandas DataFrame with a single column 'main' containing Force Index values.
    """
    closes = df[price_col]
    volumes = df[volume_col]
    
    # 1. Raw Force Index = Price Delta * Volume
    price_delta = closes.diff()
    raw_force = price_delta * volumes
    
    # 2. Smooth with EMA
    alpha = 2.0 / (period + 1)
    force_index = pd.Series(index=closes.index, dtype=float)
    
    for t in range(1, len(raw_force)):
        if pd.isna(raw_force.iloc[t]):
            force_index.iloc[t] = np.nan
        else:
            force_index.iloc[t] = alpha * raw_force.iloc[t] + (1 - alpha) * force_index.iloc[t-1]
    
    return pd.DataFrame({'main': force_index})

上記の関数は、FrAMAと同様に、価格および出来高の列をカスタマイズ可能であるため、入力の柔軟性を提供します。この関数は、価格変化と出来高を組み合わせた生のForce計算を使用し、買い圧力および売り圧力を評価します。EMAによる平滑化をおこない、ノイズを低減し持続的な動きを強調します。また、NaNを処理します。最後に、データフレームを返すことで出力を標準化し、統合を容易にしています。

コードを順に確認すると、まずおこなうことは、pandasのデータフレームから終値と出来高を抽出することです。これは計算に必要なデータを分離するために重要であり、列名の柔軟性や効率的な処理を可能にします。ここでの改善点としては、price_colおよびvolume_colがデータフレーム内に存在することを確認してエラーを防ぐことや、出来高が負でないこと、価格データがクリーンであることを確認することです。Force Indexは両方のデータに依存するためです。

次に、価格差を終値の差として設定します。Pythonでは、連続する終値間の差を計算するバッファを返す方法を使用しています。これは価格変動を測定するために重要です。価格変化は、市場の出来高加重ドリフトの方向性と大きさを反映し、Force Indexの主要な構成要素となります。最初のインデックスに対するNaN値はゼロに変換する必要があり、欠損値も適切に処理する必要があります。

続いて、生のForce Index値を計算します。これは価格差と出来高の積として求めます。Pythonでは、バッファや配列をスカラー値のように掛け算できるため、実装が簡素化されます。この積は価格変動の強さを表し、価格モメンタムと出来高を組み合わせて買い圧力や売り圧力を定量化します。価格変動が大きく、かつ出来高も多い場合、通常は市場の意思決定が強いことを示します。このベクトル積をおこなう際には、価格差バッファと出来高バッファがインデックスで整列していることを確認すると誤計算を防げます。また、生のForce Indexはノイズを含みやすいため、後段で平滑化を適用することが望ましいです。

次にα値を設定します。これは指定された期間に基づくEMAの平滑化係数であり、標準EMA公式2/(N+1)を使用します。これは、新しいデータと過去データの重みを決定するため重要です。期間が大きいとαは小さくなり、結果として平滑化が強くなります。デフォルト期間は14で、これは一般的です。ただし、使用する時間軸に応じて調整が必要です。一般的に、短期間はデイトレードに適し、長期間は日足やそれ以上の時間軸に適します。期間値が正であることを確認して、ゼロ除算エラーを避けることも重要です。

次に、入力pandasデータフレームから実際のForce Indexバッファを初期化します。これは単に、価格データと同じインデックスで空のバッファを作成し、平滑化されたForce Index値を格納するものです。これはメモリの事前確保とインデックス整合を保証するもので、EMAの反復計算を容易にします。初期のNaN値は、最初のForce Indexが前値を必要とするため予想されます。

そのため、時刻tにおける生のForce IndexがNaNであるかを確認します。これにより、欠損データを明示的に処理し、無効なEMA計算を防ぐ堅牢性が確保されます。実際のデータはしばしばギャップを含むため、表面的には単純でも見落としてはいけません。デバッグ時にNaN値をログまたはフラグとして記録することも良い習慣です。

次に、EMAの公式を用いて各時刻tでForce Indexバッファを更新します。これは現在の生のForce Indexと前回の平滑化値を組み合わせるもので、ノイズを低減し、持続的なトレンドや反転を強調する核心的な平滑化ステップです。この段階では、force_index[t-1]が適切に初期化されていることを確認する必要があります。初期インデックスではNaNであることが多いため、バッファのエッジケースも適切に処理する必要があります。

この処理が完了したら、平滑化されたForce Index値を単一列「main」を持つpandasデータフレームとして返します。出力フォーマットの標準化により、ユーザーの要件に応じて二次フォーマットやツールへの統合・可視化が容易になります。「main」というタグはテクニカル分析の慣例に沿ったものです。データフレームのインデックスが入力と一致することを確認することも、統合時のスムーズさに重要です。

Pythonでインジケーター関数を定義した後は、前回の記事でフォワードウォークに成功した2つのシグナルパターンを確認します。Pattern_6とPattern_9です。これらは、ニューラルネットワークへの入力として機能する単純な2ビットベクトルとして実装します。この「ビット」は強気および弱気を示し、各インデックスの値は0または1です。具体的には、入力ベクトルのサイズは2で、最初のインデックスでは全ての強気条件が満たされていなければ0、満たされていれば1を記録します。次のインデックスも同様に、全ての弱気条件が満たされていなければ0、満たされていれば1を記録します。

以前は、強気・弱気シグナルの構成要素を分解し、より詳細な入力ベクトルをニューラルネットワークに提供するシナリオを検討しました。しかし、そこからのフォワードウォークはあまり有望ではなく、過去の記事で試した複数パターンを単一のEAに統合する方法に近い結果となりました。

ただし、この分析が必ずしも正確とは限りません。読者は添付のソースコードを使用・修正し、独自にテストをおこなって結論を導くことができます。添付コードはMQL5ウィザードで使用することを想定しており、使用方法についてのガイドも提供されています。

feature_6関数

PythonでのPattern_6関数の実装では、上記で説明したように0または1の二値シグナルの2次元配列を生成します。まず、特徴量出力用配列をゼロで初期化します。この出力はNumPyの2次元配列であり、2列の行列に相当します。この「行列」の行数は、入力データフレームの1つであるone_dfのサイズまたは長さに設定されます。この初期化により、強気シグナルと弱気シグナルを別々に格納するための出力構造が整います。ゼロによる初期化は、パターン条件が満たされない限りシグナルが生成されないことを意味し、いわば「白紙の状態」を提供します。

実装する際には、最初の入力であるpandasデータフレームの長さが、2番目のtwo_dfおよび価格データフレームprice_dfの長さと一致していることを確認することが重要です。これにより、インデックスのずれを回避できます。2次元構造は強気と弱気のシグナルを区別するための重要な要素であり、形状が期待通りであることを確認することも重要です。これを実装する方法は次のとおりです。

def feature_6(one_df, two_df, price_df):
    """
    Generate binary signals based on sustained price-FrAMA alignment and Force Index momentum.
    
    Args:
        one_df: DataFrame with FrAMA values ('main' column).
        two_df: DataFrame with Force Index values ('main' column).
        price_df: DataFrame with price data ('close' column).
    
    Returns:
        2D NumPy array with bullish (column 0) and bearish (column 1) signals.
    """
    feature = np.zeros((len(one_df), 2))
    
    feature[:, 0] = ((price_df['close'] > one_df['main']) &
                     (price_df['close'].shift(1) > one_df['main'].shift(1)) &
                     (price_df['close'].shift(2) > one_df['main'].shift(2)) &
                     (two_df['main'] > 0.0) &
                     (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int)
    feature[:, 1] = ((price_df['close'] < one_df['main']) &
                     (price_df['close'].shift(1) < one_df['main'].shift(1)) &
                     (price_df['close'].shift(2) < one_df['main'].shift(2)) &
                     (two_df['main'] < 0.0) &
                     (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

次に、各行の最初のインデックス値として強気の期待値を定義します。前回の記事を振り返ると、現在の価格がFrAMAより上にあること、前回の価格も直前のFrAMAより上にあること、2期間前も同じ条件であったこと、現在のForce Indexが正であること、さらに1期間前のForce Indexが現在より低く、かつ2期間前も同様であることの条件がすべて満たされる場合に強気のセットアップとなります。

この最初の列は強気のケースを表し、価格トレンドが適応型FrAMAの上に一貫してある場合にのみシグナルを発生させることを保証します。これにより上昇トレンドを示します。Force Indexは強い買い圧力を確認する役割を果たします。3期間のチェックにより堅牢性が増し、Force Indexの確認により弱い動きは除外されます。実装においては、すべての入力データフレームのインデックスが整合しており、有効なデータが含まれていることを確認することが重要です。shift()操作により初期の行にはNaNが生成されるため、インジケーター値を返す前にこれを処理する必要があります。 

次に、2列目では、現在の価格がFrAMAより下にあること、前回の価格もFrAMAより下にあること、2期間前も同様の条件であること、現在のForce Indexが負であること、さらに1期間前のForce Indexが現在より上で、2期間前も同様であることの条件に従って弱気シグナルを定義します。このForce Indexにおける逆U字型の形状は、ネガティブな出来高や市場心理の悪化を示しています。

このパターンは、売りの機会に対して強気パターンを鏡写ししたものです。持続的な下降トレンドと強い売り圧力を識別します。左右対称性により、両パターンで一貫したロジックが確保されます。強気パターンと同様に、データ整合の確認が重要です。また、このパターンの発生頻度が十分であることもテストすべきです。Force Indexのモメンタムチェック(shift(1) < shift(2))は、強気市場と弱気市場で異なる挙動を示す可能性があります。そのため、歴史的なパフォーマンスを分析し、信頼性を検証することが重要です。

次に、特徴量配列の最初の2行をゼロに設定します。これは、shift(1)およびshift(2)操作によってこれらの行がNaNとなり、条件が未定義になるためです。これにより、初期行での不正なシグナルを防ぎ、手動での後処理なしにクリーンで使用可能な出力が得られます。このチェックは堅牢性を確保するために不可欠です。また、このパターンは2以上のシフトを使用して実装可能であるため、使用する最大シフト数に基づいて最初の2行だけの設定で十分かを確認することが重要です。追加のシフトをおこなう場合は、この設定を適宜調整する必要があります。

Feature_6のまとめとして、強気パターンは、価格がFrAMAを上回るクロスオーバーが少なくとも3期間持続し、Force Indexが正で最近U字型の動きを示すことに焦点を当てています。これにより上昇トレンドが持続しているかを確認します。弱気パターンはその逆で、価格がFrAMAを下回るクロスオーバーが少なくとも3期間持続し、Force Indexが負で最近逆U字型の動きを示すことに焦点を当てます。これにより下降トレンドが維持されていることを確認します。

両者が対称的かつ逆向きであること以外の大きな違いは、Force Indexの市場心理チェック（または売買意欲チェック）が、直近の強さの増加を特有の条件としている点です。これは上昇局面と下降局面では非対称性により異なる挙動を示す可能性があります。たとえば、市場は上昇よりも下降の方が速く進む傾向があります。

feature_9関数

このPythonでのSignal_9の実装は、価格、FrAMA、およびForce Indexにおける単一期間の市場心理の整合に焦点を当てており、feature_6よりも短期的な変化に敏感です。まず、Feature_9と同様に、出力ターゲットをゼロで初期化します。これはFeature_6と同様の設定であり、出力2次元NumPy配列の初期サイズは、入力データフレームの1つであるone_dfの長さに合わせて設定します。  Pythonでの実装は次のとおりです。

def feature_9(one_df, two_df, price_df):
    """
    Generate binary signals based on single-period momentum alignment of price, FrAMA, and Force Index.
    
    Args:
        one_df: DataFrame with FrAMA values ('main' column).
        two_df: DataFrame with Force Index values ('main' column).
        price_df: DataFrame with price data ('close' column).
    
    Returns:
        2D NumPy array with bullish (column 0) and bearish (column 1) signals.
    """
    feature = np.zeros((len(one_df), 2))
    
    feature[:, 0] = ((price_df['close'] > price_df['close'].shift(1)) &
                     (one_df['main'] > one_df['main'].shift(1)) &
                     (two_df['main'] > two_df['main'].shift(1))).astype(int)
    feature[:, 1] = ((price_df['close'] < price_df['close'].shift(1)) &
                     (one_df['main'] < one_df['main'].shift(1)) &
                     (two_df['main'] < two_df['main'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

両方の特徴量関数において、one-dfはFrAMAのデータフレームを、two-dfはForce Indexのデータフレームを指します。したがって、Feature_6で述べたように、one-df、two-df、および価格データフレームが同じ長さであることを確認し、形状の不一致を避ける必要があります。この行列/2次元配列は強気パターンと弱気パターンを分離するため、行数が期待通りであることを確認することが重要です。

次に、このパターンで最初にチェックするのは強気条件です。その条件は、現在の価格が前回の終値より高いこと現在のFrAMAが前回のFrAMAより高いこと、現在のForce Indexが直前の値より高いことです。これは、価格、FrAMA、Force Indexのすべてが上昇している短期的な強気モメンタムを捉え、買い圧力が整合していることを示します。また、単一期間のみをチェックするため、Feature_6よりもやや感度が高くなっています。これにより、スキャルピングや短期取引に適している場合があります。

使用する際には、すべての入力データのインデックスが整合していることを確認し、ずれた比較を避けることが重要です。このパターンは単一期間の変化に敏感であるため、ノイズの多い市場では過剰取引を避けるためにシグナルの頻度をテストする必要があります。また、シグナルを価格チャート上で可視化し、それが想定される出来高による市場心理と一致しているかを確認することも有益です。

Feature_9の弱気パターンは、現在の価格が前回の価格より低いこと、現在のFrAMAが前回のFrAMAより低いこと、現在のForce Indexが前回のForce Indexより低いことの条件を満たす場合に設定します。これにより、価格、FrAMA、Force Indexの3つの指標すべてが下降している短期的な弱気な市場心理を捉え、売り圧力が整合していることを示します。単一期間に焦点を当てるため、即時の下降に対して敏感に反応します。

強気パターンと同様に、データ整合性の確認およびシグナル頻度のテストが不可欠です。弱気シグナルは変動の大きい市場ではより頻繁に発生する可能性があるため、戦略を微調整する際には過去のパフォーマンス分析が重要です。

最後に、上記で述べたshiftの使用により、出力配列の最初の行をゼロに設定し、その後、配列を関数の出力として返します。

内積カーネルを使用したCNN

FrAMAとForce Indexのパターンを拡張するために選択した機械学習アルゴリズムは、内積カーネルを使用する畳み込みニューラルネットワーク(CNN)です。これは、DotProductConv1Dクラスを通じて実現しています。このクラスはPyTorchのニューラルネットワークモジュールであり、1次元畳み込みとDot Product Attention（内積注意）機構を組み合わせたもので、Transformerアーキテクチャに触発されています。

入力データは形状[batch, channels, width]を処理し、各サンプルに対して[0, 1]の範囲で単一の値を出力します。0に近い場合は弱気の予測、1に近い場合は強気の予測となります。Dot Product Attention機構により、ネットワークは入力シーケンスの関連部分に注目でき、畳み込み層はAttention計算に適した空間にデータを射影します。

CNN内でこのカーネルを使用することには、いくつかの利点があります。まず、関連する特徴量に選択的に注目できる点です。Dot Product Attention機構は、QueryベクトルとKeyのベクトル間の類似度スコアを計算するため、ネットワークは重要なキーステップや特徴量をより重く評価できます。これは、特定の期間がより情報量を持つ時系列（たとえば、変動の大きい期間とそうでない期間）に有益です。次に、グローバルな文脈認識を導入できる点です。

従来のCNNが固定サイズのカーネルと局所受容野に依存するのに対し、Dot Product Attentionは各タイムステップがすべての他のタイムステップに注目できるため、カーネルサイズを増やすことなく長期依存関係を捉えることが可能です。さらに、Attentionスコアが入力に基づいて動的に計算されるため、モデルは異なる市場状況など、時系列データ内の変動するパターンに適応できます。 

最後に、CNNとの組み合わせによる相補的な強みがあります。CNNは局所的な特徴量抽出に優れ、内積カーネルはグローバルな関係性を捉えるのに適しています。Dot Product Attention機構は、中程度のシーケンス長では計算効率が良く、1次元CNNは入力の次元を削減するため、フルTransformerモデルと比べてモデル全体が軽量になります。このネットワーククラスのコードは以下の通りです。

class DotProductConv1D(nn.Module):
    def __init__(self, in_channels=1, out_channels=1, kernel_size=3):
        super().__init__()
        self.kernel_size = kernel_size
        self.padding = kernel_size // 2
        
        # Projections for dot product attention (1D convolution)
        self.query = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        self.key = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        self.value = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        
        # Output projection to produce a single value per sample
        self.proj = nn.Sequential(
            nn.Conv1d(out_channels, 1, kernel_size=1),
            nn.AdaptiveAvgPool1d(1),  # Reduce width to 1 (global average pooling)
            nn.Sigmoid()  # Ensures output in [0, 1]
        )

    def forward(self, x):
        B, C, W = x.shape  # [Batch, Channels, Width]
        
        # Compute Q/K/V (all [B, out_channels, W])
        q = self.query(x)
        k = self.key(x)
        v = self.value(x)
        
        # Dot product attention
        attn = torch.bmm(q.transpose(1, 2), k)  # [B, W, W]
        attn = F.softmax(attn / (W ** 0.5), dim=-1)  # Scaled softmax
        
        # Apply attention to values
        out = torch.bmm(v, attn.transpose(1, 2))  # [B, out_channels, W]
        
        # Project to [B, 1, 1] and squeeze to [B, 1]
        out = self.proj(out)  # [B, 1, 1]
        return out.squeeze(-1)  # [B, 1]

まず、上記ではクラスをPyTorchのnn.Moduleのサブクラスとして定義します。これにより、自動的なパラメータ管理やGPUサポートを備えたニューラルネットワークモジュールとして使用可能になります。次に、入力チャネル数、Attention機構の出力チャネル数、パディング計算用のカーネルサイズをパラメータとしてモジュールを初期化します。これらのパラメータは、ネットワークの容量や入力データとの互換性を定義します。次に、畳み込み後も入力シーケンスの長さを維持するために、整数除算を用いて対称パディングのサイズを計算します。

次に、入力をAttention機構用のQuery、Key、Valueテンソルに射影するための3つの1次元畳み込み層を定義します。それぞれカーネルサイズ1を持ち、各タイムステップごとの線形変換として機能します。その後、出力射影パイプラインを定義します。これはAttention出力のチャネル数を1に削減し、グローバル平均プーリングを適用して時間次元を単一の値に圧縮します。最終的に、出力を[0, 1]の範囲の単一スカラーに変換します。 

この「クラスヘッダー」を定義した後、forward関数の処理に進みます。forward関数内で最初におこなうことは、入力テンソルx（形状[B, C, W]）に対してQuery、Key、Valueの畳み込み層を適用し、3つのテンソル（形状[B, out_channels, W]）を生成することです。次に、Queryテンソルを転置した[B, W, out_channels]とKey[B, out_channels, W]の間でバッチ行列積(bmm)をおこない、形状[B, W, W] のAttention行列を算出してDot Product Attentionスコアを計算します。

その後、Attentionスコアに対してスケーリングされたソフトマックスを適用します。これはシーケンス長の平方根で割ることで勾配の安定化を図ります。最後に、最後の次元に沿って正規化し、合計が1になるAttention重みを生成します。forward関数の出力は、v（形状[B, out_channels, W]）と転置されたAttention行列（形状[B, W, W]）の間でバッチ行列積をおこない、出力形状[B, out_channels, W]を得ることによって定義されます。

次に、Attention出力を射影パイプライン（self.proj）に通して、形状 [B, 1, 1]のテンソルを生成します。その後、最後の次元を圧縮して、返される出力の形状を[B, 1]とします。

テスト実行

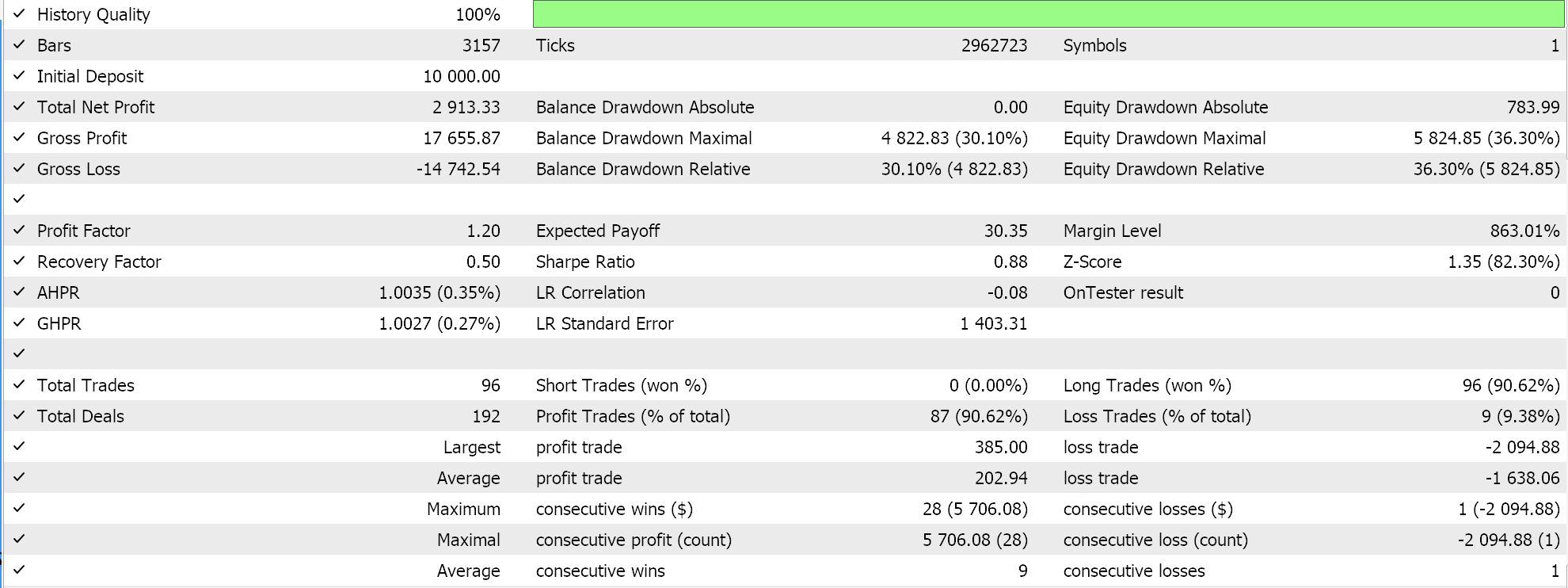
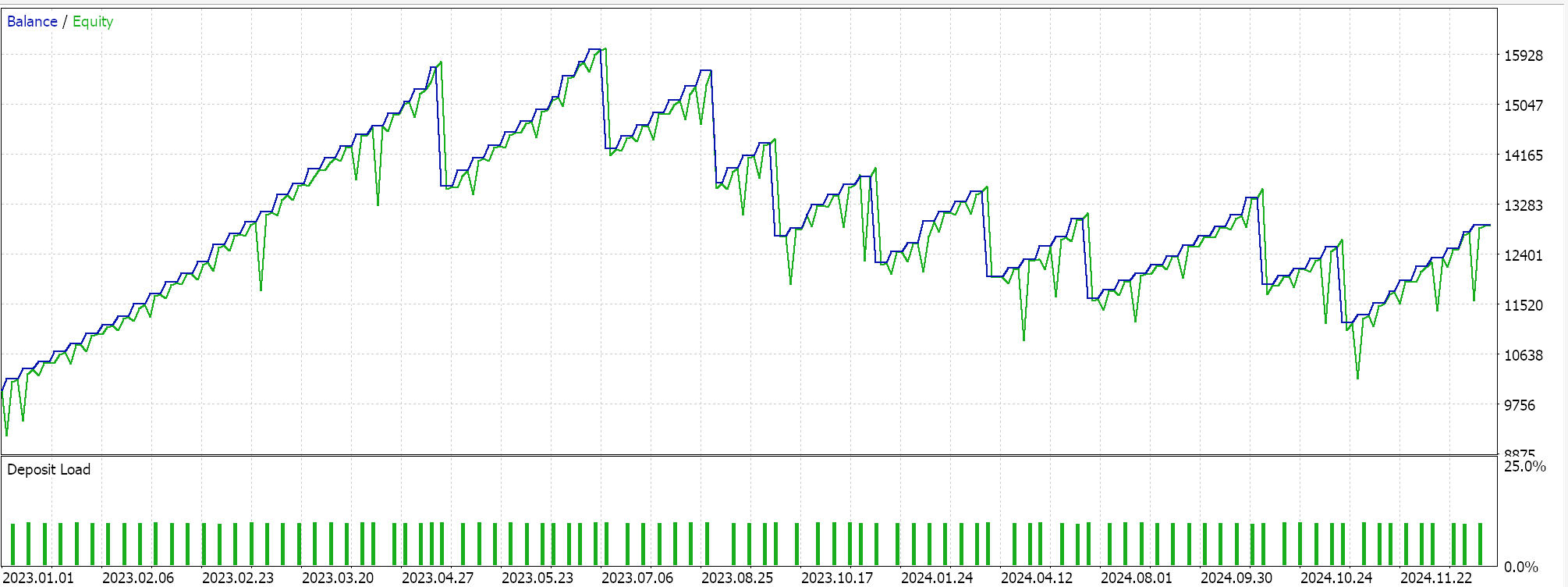
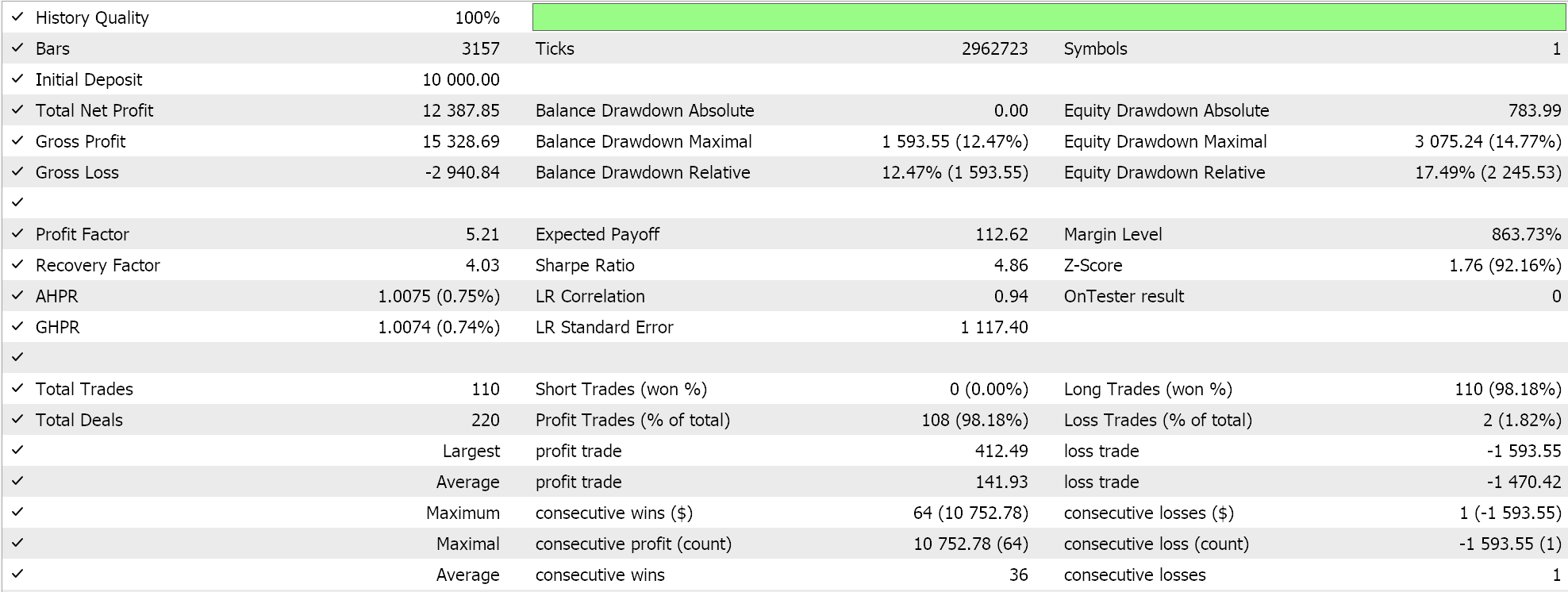
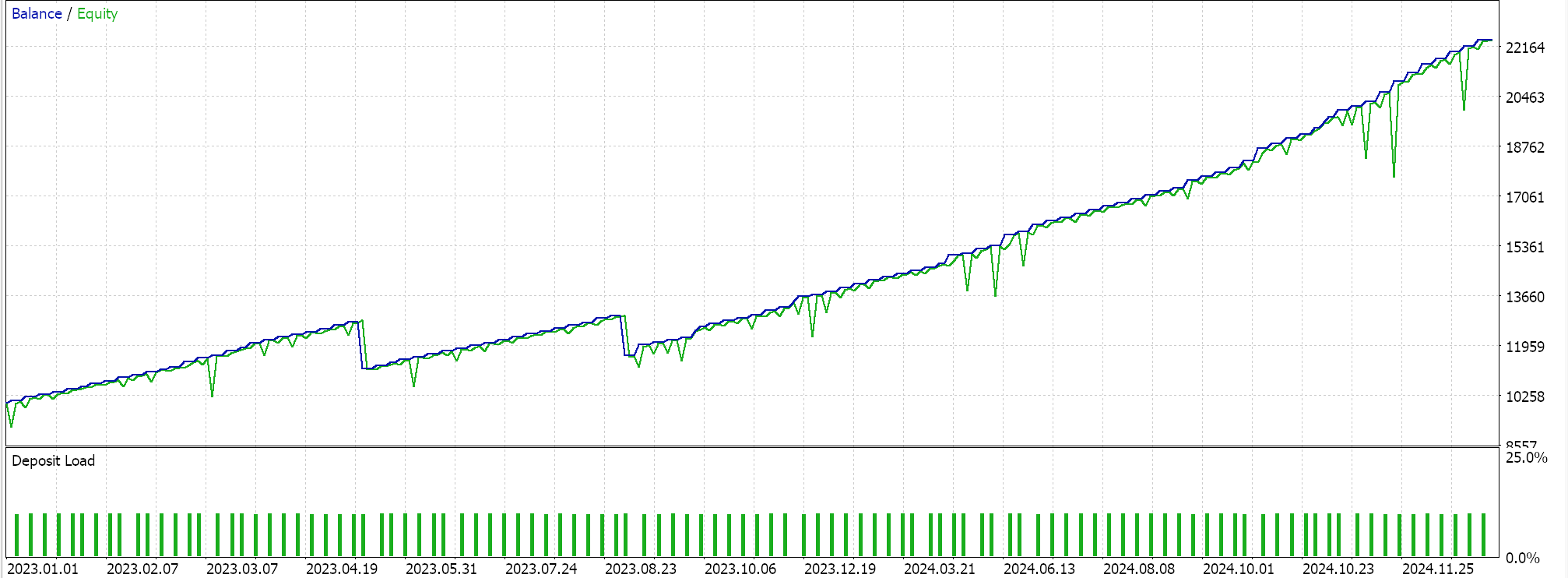
以下に、2つの特徴量パターン（Feature_6およびFeature_9）のテスト実行結果を示します。両方ともフォワードウォークが可能であるように見えますが、常に述べている通り、トレーニングは非常に限られたデータセットに基づいておこなわれているため、長期的な結論を導く前に、読者自身によるより慎重かつ広範なテストが常に必要です。

上記はPattern_6の場合です。

上記はPattern_9の場合です。

結論

内積カーネルを用いた機械学習により、FrAMAインジケーターとForce Indexオシレーターのシグナルから示唆される初期的な可能性を拡張し、活用する方法を示しました。今回テストしたのはPattern_6とPattern_9の2つのみであり、非常に限定的です。しかし、残りの8パターン以外にも、これら2つのインジケーターの組み合わせによるさまざまな実装が探索可能です。

名前	説明
wz_66.mq5	ヘッダにインクルードファイルを示すウィザード組み立てEA
SignalWZ_66.mqh	カスタムシグナルクラスファイル
66_6.0nnx	Pattern_6 ONNXファイル
66_9.onnx	Pattern_9 ONNXファイル