ニューラルネットワークが簡単に（第94回）：入力シーケンスの最適化

はじめに

時系列データを処理する際、時間ステップの元の並び順をそのまま保持することが一般的なアプローチです。これは、歴史的な順序が最適であると仮定されているからです。しかし、既存のモデルの多くには、時系列データ内の遠く離れたセグメント間の関係を調査するための明確なメカニズムが欠けています。それらのセグメント間には強い依存関係が存在する可能性があるにもかかわらずです。たとえば、畳み込みネットワーク(CNN)を用いた時系列学習モデルでは、限られた時間枠内のパターンしか捉えることができません。そのため、重要なパターンが長い時間枠にわたる時系列データを分析する際、こうしたモデルではその情報を効果的に捉えるのが難しくなります。ディープネットワークを使用することで受容野の範囲を広げ、この問題を部分的に解決することが可能です。しかし、シーケンス全体をカバーするために必要な畳み込み層の数が増えすぎると、モデルが過剰に大きくなり、勾配消失問題が発生するリスクがあります。

Transformerアーキテクチャを用いたモデルでは、長期的な依存関係を検出する有効性は、シーケンスの長さ、位置エンコーディングの戦略、データのトークン化など、さまざまな要因に大きく依存します。

こうした課題を背景に、論文「Segment, Shuffle, and Stitch:A Simple Mechanism for Improving Time-Series Representations」の著者は、履歴シーケンスの最適な使用というアイデアに達しました。手元のタスクを考慮すると、より効率的な表現学習を可能にする、より優れた時系列の構成はあるでしょうか。

この記事では、時系列データの表現を最適化するために設計された、Segment, Shuffle, Stitch (S3)と呼ばれるシンプルかつ即時利用可能なメカニズムを紹介します。その名前が示すように、S3は時系列データを複数の重複しないセグメントに分割し、それらを最適な順序にシャッフルしてから、新しいシーケンスとして結合する仕組みです。ここで重要な点は、セグメントのシャッフル順序がタスクごとに学習されるということです。

さらに、S3は元の時系列データをシャッフル後のバージョンと学習可能な加重和の演算によって統合し、元のシーケンスに含まれる重要な情報を保持します。

S3は、どのような時系列分析モデルともシームレスに統合できるモジュール型のメカニズムとして機能し、誤差を減らしつつスムーズな訓練手順を実現します。S3はバックボーンとなるネットワークと同時に学習されるため、シャッフルのパラメータが意図的に更新され、データの特性やモデル構造に適応して、時間的なダイナミクスをより正確に反映します。さらに、S3を複数重ねることで、より高い粒度の詳細なシャッフルを作成することも可能です。

提案されたアルゴリズムは調整すべきハイパーパラメータが少なく、追加の計算リソースもほとんど必要としません。

提案されたアプローチの有効性を評価するために、著者は、CNNやTransformerベースのモデルを含むさまざまなニューラルアーキテクチャにS3を統合しました。単変量および多変量の予測・分類問題における複数のデータセットでのパフォーマンス評価により、他の条件が同じ場合、S3を追加することでモデルの効率が大幅に向上することが確認されています。結果として、S3を最新手法に統合することで、分類タスクの性能は最大39.59%向上する可能性があります。さらに、1次元および多次元の時系列予測タスクにおいても、それぞれ68.71%と51.22%の効率向上が見込めると示されています。

1. S3アルゴリズム

提案されたS3手法について、さらに詳しく見ていきましょう。

この手法では、入力データとして、T個の時間ステップとC個のチャネルから成る多次元時系列データXを使用し、これをN個の互いに重ならないセグメントに分割します。

ここの手法は単変量時系列にも対応していますが、ここでは多変量時系列の一般的なケースについて説明します。実際には、チャネル数Cが1の場合、1次元時系列は多次元時系列の特別なケースとみなすことができます。

この手法の目的は、セグメントを最適に再配置して新しいシーケンスX'を構築し、時系列データ内の主要な時間的関係や依存関係をより効果的に捉えることです。このプロセスにより、対象タスクの理解が向上します。

S3手法の著者は、この課題を以下の3つの段階で解決することを提案しています。「セグメンテーション」、「ミキシング」、および「結合」です。

Segmentモジュールは、元のシーケンスXをN個の互いに重ならないセグメントに分割します。各セグメントにはτ個の時間ステップ(τ = T/N)が含まれます。セグメント集合は、S = {s1, s2, . . . , sn}.と表すことができます。

セグメントはShuffleモジュールに送られ、混合ベクトルP = {p1, p2, . . . , pn}を使用して最適な順序に並べ替えられます。ベクトルPの各シャッフルパラメータpjは、行列S内のセグメントsjに対応しています。基本的に、Pは並べ替えられたシーケンス内でのセグメントの位置と優先順位を制御する学習可能な重みの集合です。

シャッフルプロセスは非常に直感的で、 pjの値が高いほど、シャッフル後のシーケンスにおけるセグメントsjの優先順位が高くなります。シャッフルされたシーケンスSshuffledは次のように表されます。

しかし、このような順序Pに基づいてSを並べ替える操作は、離散的な操作を伴うためデフォルトでは微分不可能です。これに対して、ソフトソート手法は、各要素が他の要素と比較してどれだけ大きいかを反映する確率を割り当てることで順序を近似します。この近似は微分可能ですが、ノイズや不正確さを引き起こし、操作が直感的でなくなることがあります。従来の方法と同じくらい正確で直感的な微分可能な並び替えとシャッフルを実現するために、この手法の著者はいくつかの中間ステップを導入しました。これらのステップにより、勾配がシャッフルパラメータPを通過するパスが作成されます。

まず、σ = Argsort(P)を使用してPの要素をソートするインデックスを取得します。テンソルのリストS = {s1, s2, s3, ...sn}があり、これをインデックスのリストσ = {σ1, σ2, ..., σn}に基づいて微分可能な方法で並べ替えるとします。次に、サイズが(τ × C) × n × nのU行列を作成し、各siをN回繰り返します。

その後、サイズがn × nのΩ行列を形成します。この行列では、各行jの位置 k = σjに非ゼロ要素が1つ存在します。スケーリング係数を使用して、Ω行列を各非ゼロ要素を1にスケーリングするバイナリ行列に変換します。このプロセスにより、バックプロパゲーション中に勾配がPを通過できる経路を確立します。

その後、UとΩのアダマール積を実行し、各行jにおいて非ゼロ要素がskに等しいkが含まれる行列Vを得ます。最後に、この行列を次元ごとに合計し、転置することで最終的なシャッフルされた行列Sshuffledを生成します。

さらに、著者は多次元行列P'を使用して、より複雑な表現を捉える追加のパラメータを導入しました。これを実現するため、S3法の著者は、ハイパーパラメータλを設定し、P'の次元数を決定します。その後、最初のλ−1次元にわたってP'の合計を実行して1次元ベクトルPを取得します。このベクトルを用いて順列インデックスσ = Argsort(P)を計算します。

この手法により、シャッフルパラメータの数を増加させ、並び替え操作に影響を与えずに時系列データ内のより複雑な依存関係を捉えることが可能となります。

最後に、Stitchモジュールではでは、シャッフルされたセグメントSを連結し、新しいシャッフルされたシーケンスX'を作成します。

元の時系列データの順序に含まれる情報を保持するため、メインモデルの学習を通じて最適化されるパラメータw1およびw2を用いて、元のシーケンスとシャッフルされたシーケンスの加重和を計算します。

S3をモジュールレベルの構成要素とみなすと、これをニューラルアーキテクチャ内に積み重ねることが可能です。S3層の数を決定するハイパーパラメータをϕとし、簡略化のため、各S3層に個別のセグメント数を設定する代わりに、後続の層におけるセグメント数をスケーリングする係数θを定義します。

複数のS3層が積み重なる場合、各層ℓ（1からϕ）は、前の層の出力に基づいて入力データをセグメント化しシャッフルします。

S3の全学習可能パラメータはモデルのパラメータと同時に更新され、S3層に対して中間損失は導入されません。これにより、S3層が特定のタスクと目標に従って訓練されるようになります。

入力シーケンスXの長さがセグメント数Nで割り切れない場合は、入力シーケンスから最初のT mod N時間ステップを削除します。その後、最終的なS3層の出力に対して、削除したサンプルを先頭に追加することで、データの損失を防ぎ、入力と出力の形状を一致させます。

この方法の元の視覚化を以下に示します。

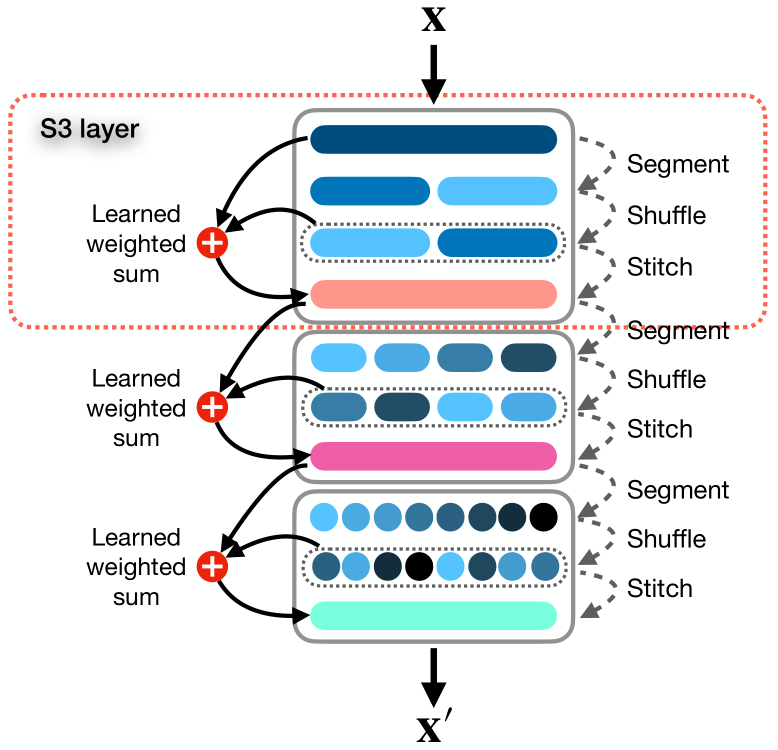
ここで付け加えておきたいのは、論文で紹介されている実験の結果に基づいて、訓練の初期段階で順列パラメータが調整され、その後は固定されるということです。

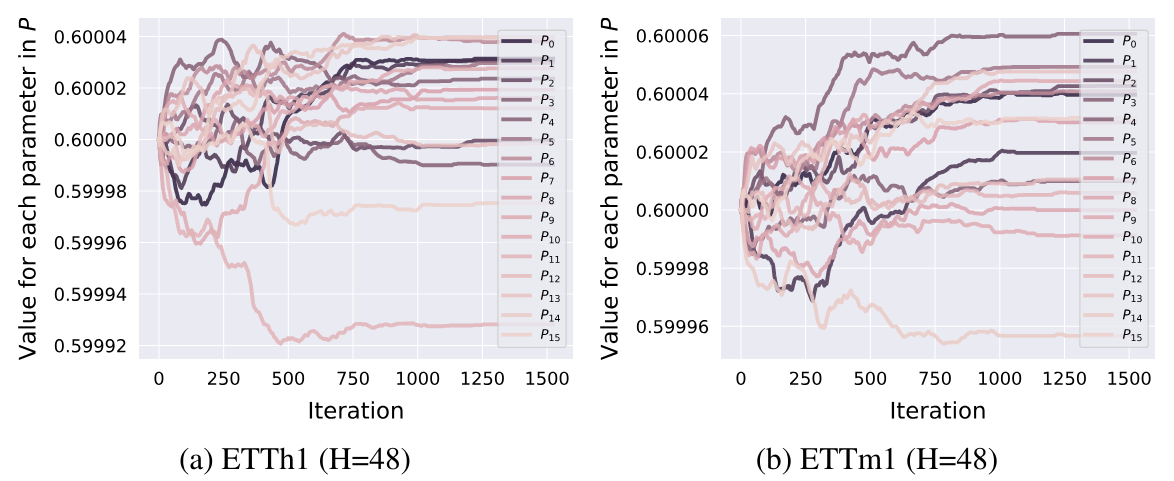
2. MQL5での実装

S3手法の理論的側面を検討した後、提案されたアプローチをMQL5で実装するこの記事の実践的な部分に進みます。しかし、コードを書き始める前に、既存の開発を踏まえて、提案されたアプローチのアーキテクチャについて考えてみましょう。

2.1 ソリューションアーキテクチャ

データのソート順序を決定するために、S3法の著者は学習可能なパラメータベクトルPを使用しています。私たちのライブラリでは、学習可能なパラメータはニューラル層にのみ存在します。そのため、ニューラル層を利用してセグメントの優先順位を生成できます。この場合、ニューラル層内で利用可能な既存の方法を用いてパラメータを学習することが可能です。しかし、一点注意が必要なのは、学習パラメータに基づかない入力をニューラル層に与える必要があることです。この状況は非常に単純で、ニューラル層に「1」で埋められた固定ベクトルを入力することで解決します。

このアプローチにより、多次元順列行列P'の問題を即座に解決できます。この行列の次元を変更するには（S3手法の著者がハイパーパラメータλとして定義）、元のデータベクトルのサイズを変更するだけで済みます。その他の機能は一切変更する必要がありません。各セグメントの個々のパラメータの合計は、ニューラル層内に既に実装されています。このようなニューラル層の出力サイズは、セグメント数と等しくなります。

セグメントの優先順位を確率値に変換するために、SoftMax関数を使用します。

元のシーケンスとシャッフルされたシーケンスの影響を重み付けするパラメータについても同様のアプローチを採用します。この場合、層の出力サイズは「2」に固定されます。この層の活性化関数として、シグモイド関数を使用します。

これが学習可能なパラメータに関する部分です。次に、セグメントを確率の昇順または降順にソートするアルゴリズムを実装する必要があります。

理論上は、個々のセグメントの優先順位を昇順または降順のどちらでソートするかは重要ではありません。なぜなら、セグメントの順列そのものを学習するからです。したがって、学習プロセスでは、モデルが指定されたソート順序に従って優先順位を適切に割り当てます。この際、学習時および推論時のソート順序が一貫していることが重要です。これにより、誤差の原因となるズレが回避されます。

S3手法の著者は、優先順位ベクトルPへの勾配誤差伝播を可能にするために、多次元配列を作成し入力を複製するという複雑なアルゴリズムを提案しました。しかし、この方法は計算コストとメモリ消費を増加させます。これをより効率的に実現する方法を提案します。

S3手法の著者が提案したプロセスを見て、アクションと結果を分析してみましょう。

最初に、元のデータを複製した行列Uが形成されます。このステップを省略すれば、大きな行列の保存に関連するメモリ消費を削減でき、データの複製に要する計算リソースも節約できます。

次に、行列Ωはゼロ以外の要素がほとんど存在しないバイナリ行列として構築されます。ゼロ以外の要素の数はセグメント数(N)に等しくなり、ゼロ要素の数はそのN - 1倍となります。この行列をスパース形式で実装すれば、メモリ消費と行列の乗算にかかる計算コストを削減することが可能です。

その後、S3アルゴリズムに従って、要素ごとの行列乗算、最後の次元に沿った加算、そして結果の行列の転置がおこなわれます。

しかし、これら一連の操作によって得られる結果は、単にシャッフルされた元のテンソルです。このテンソルの要素を直接シャッフルする操作に置き換えれば、必要なリソースを減らし、計算もより高速に実行できます。

著者がこのように複雑な順列アルゴリズムを開発したのは、優先順位ベクトルPに誤差勾配を伝播させる必要があったからです。これは部分的には、著者がアルゴリズムを構築する際に使用したPyTorchの自動微分機能による「制約」に起因しています。

私たちの手法では、フィードフォワードとバックプロパゲーションのアルゴリズムを独自に構築するため、初期コストが増加しますが、プロセスの柔軟性が大幅に向上します。これにより、フィードフォワードパスでは前述の複雑な操作をデータの直接シャッフルに置き換えることが可能になります。この方法はより効果的であり、リソース効率も向上します。

ここで、誤差勾配伝播の問題について考える必要があります。入力をシャッフルする際、各セグメントは出力テンソル内で一度だけ現れます。その結果、誤差勾配全体が対応するセグメントに伝播されます。入力データに誤差勾配を分配する際には、セグメントの逆順列を適用する必要があります。この逆順列は、誤差勾配テンソルに対して実行されます。

次に、優先順位ベクトルPに誤差勾配を伝播する方法について考えます。ここでのアルゴリズムはもう少し複雑です。フィードフォワードパスでは、各セグメントには単一の優先順位が割り当てられます。したがって、バックプロパゲーションでは、セグメント全体の誤差勾配を1つの優先順位に集約する必要があります。これを実現するために、該当するセグメントの入力ベクトルに誤差勾配テンソルの対応部分を乗算します。

さらに、バイナリ行列Ωの構築時に使用したスケーリング係数に基づいて、ゼロ以外の要素を1に変換しました。当然ですが、ゼロ以外の数を1に変換するには、同じ数で割るか、逆数を掛ける必要があります。このスケーリング係数は優先順位の逆数に相当します。そのため、上記で計算された誤差勾配の値は対応するセグメントの優先順位で割る必要があります。

ここで、セグメントの優先順位が「0」になってはならないことに注意してください。SoftMax関数を使用することで、この状況は排除されます。しかし、十分に小さい値が残る可能性があり、その値による除算が誤差勾配の極端な増大を引き起こす場合があります。

また、SoftMax関数を使用してセグメントの優先順位を確率値として生成すると、すべての値が(0, 1)の範囲内に収まります。優先順位が低いセグメントは、1未満の値で割ることによってより大きな誤差勾配を受け取ります。

これらがこのアルゴリズムにおける重要なポイントです。これを念頭に置いた上で、コードでの実装に進みます。まずはOpenCLコンテキスト側から実装を始めましょう。

2.2 OpenCLカーネルの構築

いつものように、フィードフォワードアルゴリズムの実装から始めます。OpenCLプログラム側では、まずFeedForwardS3カーネルを作成します。

ここで、セグメント分布確率の生成と、元のシーケンスとシャッフルされたシーケンスの加重合計を、ネストされたニューラル層で実装することを思い出してください。このため、このカーネルはパラメータの形式で既成のデータを受け取ります。

したがって、カーネルはパラメータで5つのデータバッファへのポインタと2つの定数を受け取ります。3つのバッファには、元のシーケンス、セグメントの確率、重みなどの入力が含まれます。さらに2つのバッファはカーネル出力を記録するために使用されます。そのうちの1つでは出力シーケンスを記述し、もう1つではバックプロパゲーション操作を実行するときに必要となるセグメントシャッフルインデックスを記述します。

定数では、1つのセグメントのウィンドウサイズとシーケンス内の要素の合計数を指定します。

2番目の定数では、セグメント数や時間ステップ数ではなく、入力ベクトルのサイズを指定することに注意してください。セグメントウィンドウサイズでは、時間ステップではなく配列要素の数も指定します。したがって、両方の定数は、1つの時間ステップのベクトルのサイズで余りなく割り切れる必要があります。

__kernel void FeedForwardS3(__global float* inputs,
                            __global float* probability,
                            __global float* weights,
                            __global float* outputs,
                            __global float* positions,
                            const int window,
                            const int total
                           )
  {
   int pos = get_global_id(0);
   int segments = get_global_size(0);

分析対象のシーケンス内のセグメントの数に基づいて、1次元のタスク空間でカーネルを起動する予定です。カーネル本体では、現在のフローを即座に識別し、実行中のタスクの数に基づいてセグメントの合計数も決定します。

合計入力サイズが1つのセグメントのウィンドウサイズの倍数でない場合は、セグメントの合計数を1減らします。

   if((segments * window) > total)
      segments--;

次のステップでは、セグメントの優先順位を並べ替えて順序を決定します。ただし、ソートアルゴリズムを純粋な形で整理することはしません。代わりに、シーケンス内の分析されたセグメントの位置を決定します。1つの要素の位置を決定するには、セグメント確率ベクトルを1回通過するだけで済みます。ただし、ベクトルをソートする場合、確率ベクトルを複数回通過し、計算スレッドを同期する必要があります。

ここでは、現在のスレッドのインデックスに応じて、アルゴリズムを2つのブランチに分割します。最初のブランチは一般的なケースであり、現在のスレッドインデックスがセグメント数より小さい場合に使用されます。最初のスレッドのインデックスが0に等しいことを考慮すると、条件の指定された定式化は奇妙に思えるかもしれません。以前、入力サイズがセグメントウィンドウのサイズの倍数ではないケースを検討するときに、セグメント数の変数の値を減らしました。この場合、最後のスレッドは、セグメントの位置を決定するアルゴリズムの2番目のブランチに従います。

一般に、現在の操作スレッドに対応するセグメントの位置を決定するには、その優先順位をローカル定数で固定します。最初のセグメントから現在のセグメントまでループを実行し、現在の優先順位以下の優先順位を持つ要素の数をカウントします。降順ソートの場合、現在のセグメント以上の優先順位を持つ要素の数を決定します。

次に、次のセグメントから最後のセグメントまでのループを構成し、その中で、優先順位が厳密に低い（降順で並べ替える場合は厳密に高い）要素の数を追加します。

両方のループの操作が完了すると、全体のシーケンスにおける現在のセグメントの位置が取得されます。

   int segment = 0;
   if(pos < segments)
     {
      const float prob = probability[pos];
      for(int i = 0; i < pos; i++)
        {
         if(probability[i] <= prob)
            segment++;
        }
      for(int i = pos + 1; i < segments; i++)
        {
         if(probability[i] < prob)
            segment++;
        }
     }

優先順位ベクトルのパスを2つのループに分割するのは、優先順位が同じ要素が2つ以上あるという特殊なケースのためです。この場合、元のシーケンス内の前の要素が優先されます。1つのループでアルゴリズムを構築することもできますが、この場合、優先順位を比較する前に、各反復でセグメントが元のシーケンス内の現在のセグメントの前か後かをチェックする必要があります。

特殊なケースのアルゴリズムの2番目のブランチでは、単にセグメント番号をシーケンス内の順序に割り当てます。上記の特殊なケースでは、すべての完全なセグメントが混合され、最後の（完全ではない）セグメントがそのまま残ります。

   else
      segment = pos;

シャッフルされたシーケンス内のセグメントの位置を決定したので、セグメントを移動できます。これおこなうには、入力バッファと出力バッファのオフセットを定義します。

   const int shift_in = segment * window;
   const int shift_out = pos * window;

特定の位置を対応するバッファにすぐ保存します。

   positions[pos] = (float)segment;

元のシーケンスと混合シーケンスの加重合計を忘れないようにしましょう。当然、結果バッファへのデータの不必要なコピーを避けるために、元のシーケンスと混合シーケンスからの2つのセグメントの加重合計をすぐに保存します。これをおこなうには、重み付けパラメータをローカル定数に保存します。

   const float w1 = weights[0];
   const float w2 = weights[1];

1つのセグメントのウィンドウサイズに等しい反復回数のループを作成し、重みを考慮して2つのシーケンスの要素を合計し、得られた値を結果バッファに保存します。

   for(int i = 0; i < window; i++)
     {
      if((shift_in + i) >= total || (shift_out + i) >= total)
         break;
      outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i];
     }
  }

フィードフォワードパスカーネルを構築した後、バックプロパゲーションパスの作業に移ります。ここで、InsideGradientS3カーネルの構築を開始します。このカーネルでは、誤差勾配を前の層のレベルとセグメントの優先順位に分散します。カーネルパラメータでは、対応する誤差勾配のバッファへのポインタが、以前に考慮されたバッファに追加されます。

__kernel void InsideGradientS3(__global float* inputs,
                               __global float* inputs_gr,
                               __global float* probability,
                               __global float* probability_gr,
                               __global float* weights,
                               __global float* outputs_gr,
                               __global float* positions,
                               const int window,
                               const int total
                              )
  {
   size_t pos = get_global_id(0);

カーネルは、分析されたシーケンス内のセグメントの数に応じて、1次元のタスク空間で起動されます。カーネル本体では、現在の操作スレッドをすぐに識別します。この場合、セグメントの合計数を決定する必要はありません。

次に、フィードフォワードパス中に決定された定数をデータバッファからロードします。

   int segment = (int)positions[pos];
   float prob = probability[pos];
   const float w1 = weights[0];
   const float w2 = weights[1];

その後、データバッファ内のオフセットを決定します。

   const int shift_in = segment * window;
   const int shift_out = pos * window;

そして、中間データ用のローカル変数を宣言します。

   float grad = 0;
   float temp = 0;

次のステップでは、セグメントウィンドウサイズに等しい反復回数のループを作成し、セグメント優先順位の誤差勾配を収集します。

   for(int i = 0; i < window; i++)
     {
      if((shift_out + i) >= total)
         break;
      temp = outputs_gr[shift_out + i] * w1;
      grad += temp * inputs[shift_in + i];

同時に、誤差勾配を前の層バッファに転送します。フィードフォワードパス中に、元のシーケンスとシャッフルされたシーケンスを合計しました。したがって、各入力要素は、対応する重みを持つ2つのスレッドから誤差勾配を受け取る必要があります。

      inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2;
     }

セグメント優先順位誤差勾配を対応するデータバッファに書き込む前に、出力値を現在のセグメントの確率で割ります。

   probability_gr[segment] = grad / prob;
  }

上で検討した勾配伝播カーネルには、元のシーケンスと混合シーケンスの重みに対する誤差勾配の伝播という点が1つ欠けています。この機能を実装するには、別のカーネルWeightGradientS3を作成します。

ここで1つの要素の誤差勾配が各個別のスレッドで収集されるときに使用する一般的なアプローチは、この場合はあまり効果的ではないと言わなければなりません。これは、重みベクトルの要素数が少ないためです。ご覧のとおり、ここには2つしかありません。ただし、モデルの訓練に費やす全体的な時間を短縮するには、並列スレッドを増やす方がよいでしょう。この効果を実現するために、スレッドのワーキンググループを2つ作成し、各グループでそのパラメータの誤差勾配を収集します。

__kernel void WeightGradientS3(__global float *inputs,
                               __global float *positions,
                               __global float *outputs_gr,
                               __global float *weights_gr,
                               const int window,
                               const int total
                              )
  {
   size_t l = get_local_id(0);
   size_t w = get_global_id(1);

したがって、カーネルは2次元のタスク空間で起動されます。最初の次元は、1つのグループ内の並列スレッドの数を定義します。2番目の次元は、誤差勾配が収集されるパラメータのインデックスを示します。

次に、グループの各スレッドが作業の一部を保存するローカル配列を宣言します。

   __local float temp[LOCAL_ARRAY_SIZE];

作業スレッドの数は宣言されたローカル配列のサイズより大きくすることはできないため、「主力」スレッドの数を制限する必要があります。

   size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);

最初の段階では、各スレッドはワークグループ内の他のスレッドとは独立して、誤差勾配のシェアを収集します。これをおこなうには、現在のスレッドワークグループのインデックスを持つ要素から配列の最後の要素まで、現在の層の出力にある誤差勾配バッファの要素に対して、ステップを「ワークホース」の数に等しくしてループを実行します。

ループ本体では、まずソースデータバッファ内の対応する要素へのオフセットを決定します。このオフセットは、誤差勾配を収集する重みのインデックスによって異なります。2番目の重みについては、層の誤差と入力データの勾配バッファのシフトは同じです。

   if(l < ls)
     {
      float val = 0;
      //---
      for(int i = l; i < total; i += ls)
        {
         int shift_in = i;

最初のオフセットについては、まず誤差勾配バッファ内のセグメントを定義します。次に、順列ベクトルから、元のシーケンス内の対応するセグメントを抽出します。そうすることで初めて、入力バッファ内の必要な要素へのオフセットを計算できるようになります。

         if(w == 0)
           {
            int pos = i / window;
            shift_in = positions[pos] * window + i % window;
           }

両方のデータバッファ内の対応する要素のインデックスが与えられて、その位置での重みの誤差勾配を計算し、それを累積変数に追加します。

         val += outputs_gr[i] * inputs[shift_in];
        }
      temp[l] = val;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

ループのすべての反復が完了したら、誤差勾配の累積合計をローカルメモリ配列の対応する要素に書き込み、ワークグループスレッドの同期バリアを実装します。

2番目のステップでは、ローカル配列の要素の値を合計します。

   int t = ls;
   do
     {
      t = (t + 1) / 2;
      if(l < t && (l + t) < ls)
        {
         temp[l] += temp[l + t];
         temp[l + t] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(t > 1);

カーネル操作の終了時に、ワークグループの最初のスレッドは、合計誤差勾配をグローバルバッファの対応する要素に転送します。

   if(l == 0)
      weights_gr[w] = temp[0];
  }

全体的な結果への影響に応じてすべての要素の誤差勾配を分配した後、通常はパラメータ更新アルゴリズムの作業に移ります。しかし、この記事の枠組みの中で、ネストされたニューラル層内のすべての訓練可能なパラメータを整理しました。したがって、パラメータを更新するためのアルゴリズムは、前述のオブジェクト内にすでに提供されています。したがって、ここではOpenCL側での操作を完了し、メインプログラムの操作に進みます。

2.3.CNeuronS3クラスの作成

提案されたアプローチをメインプログラム側で実装するために、新しいニューラル層クラスCNeuronS3を作成します。その構造は以下の通りです。

class CNeuronS3   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iSegments;
   //---
   CNeuronBaseOCL    cOne;
   CNeuronConvOCL    cShufle;
   CNeuronSoftMaxOCL cProbability;
   CNeuronConvOCL    cWeights;
   CBufferFloat      cPositions;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForwardS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronS3(void)   {};
                    ~CNeuronS3(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronS3;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

クラスでは、2つの変数と5つのネストされたオブジェクトを宣言します。変数には、1つのセグメントのウィンドウサイズとシーケンス内のセグメントの合計数が格納されます。ネストされたオブジェクトの目的については、クラスのメソッドを実装する際に考慮します。

クラスのすべてのオブジェクトは静的に宣言されます。これにより、クラスのコンストラクタとデストラクタを空のままにすることができます。すべてのネストされたオブジェクトの初期化はInitメソッドで実行されます。いつものように、このメソッドのパラメータでは、呼び出し元からクラスアーキテクチャの主なパラメータを受け取ります。次の2つのパラメータに注意してください。

• window：1セグメントのウィンドウサイズ
• numNeurons：層内のニューロンの数

これらのパラメータでは、時系列のステップではなく配列要素の数を示します。ただし、その値は1つの時間ステップを記述するベクトルのサイズの倍数である必要があります。つまり、実装を容易にするために、1次元の時系列を操作するためのクラスを構築します。ここで、ユーザーはセグメント内の多次元時系列の時間ステップの整合性を維持する責任があります。

bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                     uint window, uint numNeurons, 
                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

メソッド本体では、まず親クラスの同じメソッドを呼び出し、受け取ったパラメータを制御し、継承したオブジェクトを初期化します。呼び出されたメソッドの実行を制御することを忘れないでください。

継承されたオブジェクトの初期化が正常に完了すると、1セグメントのウィンドウサイズが保存され、すぐにセグメントの合計数が決定されます。

   iWindow = MathMax(window, 1);
   iSegments = (numNeurons + window - 1) / window;

次に、クラスの内部オブジェクトを初期化します。まず、セグメント順列の優先順位と重み付けされたシーケンスの合計パラメータを生成するための入力として使用される、単一の値の固定ニューラル層を初期化します。ここでは、まずニューラル層を初期化し、次に結果バッファを単一の値で強制的に入力します。

   if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buffer = cOne.getOutput();
   if(!buffer || !buffer.BufferInit(buffer.Total(),1))
      return false;
   if(!buffer.BufferWrite())
     return false;

以下の2点にご注意ください。まず、1つのニューロンの層を作成します。ご記憶のとおり、実装のアーキテクチャに取り組んでいたとき、特定の層内のニューロンの数が順列行列の次元を示すと述べました。多次元マトリックスを使用する意味がわかりません。数学的な観点から見ると、中間活性化関数を使用しない場合、複数の変数の積を定数で合計する線形関数は、使用される定数と1つの変数の積に退化します。

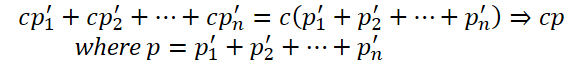
この観点から見ると、パラメータの増加は計算の複雑さの増加につながるだけで、モデルの効率に疑問のある影響を与えます。

一方、これは単なる私の意見です。したがって、これを実験的にテストすることができます。

2番目のポイントは、このネストされた層の送信接続が「0」であることを示しています。このオブジェクトを2つのニューラル層の初期データとして使用することを計画しています。後続の2つの層が存在するため、ちょっとしたトリックに頼らざるを得ませんでした。私たちの基本ニューラル層は、後続の1つの層のみの重みマトリックスを含むように設計されています。しかし、入力接続の重み係数の行列を含む畳み込みニューラル層のクラスがあります。控えめに言っても、1つの入力要素と出力での複数の順列優先順位を使用することは、畳み込み層を使用するのに適したシナリオとは言えません。でもちょっと待ってください。

1つの入力要素により、畳み込みフィルタに1つの学習可能なパラメータが確実に提供されます。また、必要な畳み込みフィルタの数を指定することにより、順列ベクトルのサイズを簡単に提供できます。この場合、畳み込み要素を1つだけ指定します。このようにして、学習可能なパラメータを後続のニューラル層に転送します。

   if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch))
      return false;
   cShufle.SetActivationFunction(None);

前述したように、SoftMax関数を使用して順列の優先順位を確率領域に変換します。

   if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch))
      return false;
   cProbability.SetActivationFunction(None);
   cProbability.SetHeads(1);

シーケンスの加重合計のパラメータを生成する目的で同じことを行います。違いは、ここでは活性化関数としてシグモイドを使用していることです。

   if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch))
      return false;
   cWeights.SetActivationFunction(SIGMOID);

初期化メソッドの最後に、セグメント順列インデックスを記録するためのバッファを作成します。

   if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

このクラスには2つの新しいメソッド(feedForwardS3とcalcInputGradientsS3)が含まれています。以前に作成したOpenCLプログラムカーネルを実行キューに配置します。ご想像のとおり、最初の方法ではフィードフォワードカーネルの実行がキューに入れられ、2番目の方法では残りの2つの誤差勾配分布カーネルがキューに入れられます。以前の記事では、カーネルを実行キューに配置するアルゴリズムについてすでに説明しました。これらの方法は同様のアルゴリズムに基づいて構築されているため、ここでは考慮しません。これらのメソッドのコードは添付ファイルにあります。添付ファイルには、記事の作成中に使用されたすべてのプログラムの完全なコードも含まれています。

私たちのクラスのフィードフォワードアルゴリズムは、feedForwardメソッドに組み込まれています。同じ名前の親クラスメソッドと同様に、このメソッドは、入力データを含む前のニューラル層のオブジェクトへのポインタをパラメーターで受け取ります。

フィードフォワードカーネルをキューに配置するメソッドを呼び出す前に、セグメント順列の優先順位と、元のシーケンスとシャッフルされたシーケンスの合計を重み付けするためのパラメーターを準備する必要があります。ここで、示されたプロセスの初期データは単位値の固定ベクトルであることに注意する必要があります。したがって、それらの値は初期データに依存せず、モデルの操作中に変化しません。指定された値は、学習プロセス中に学習パラメータが変更された場合にのみ変更できます。つまり、再計算は学習プロセス中にのみ必要になります。値を再計算するには、対応するネストされたオブジェクトのフィードフォワードメソッドを呼び出します。

bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cWeights.FeedForward(cOne.AsObject()))
         return false;
      if(!cShufle.FeedForward(cOne.AsObject()))
         return false;
      if(!cProbability.FeedForward(cShufle.AsObject()))
         return false;
     }

次に、メソッドを呼び出して、フォワードパスカーネルを実行キューに入れて、元のシーケンスをシャッフルします。

   if(!feedForwardS3(NeuronOCL))
      return false;
//---
   return true;
  }

操作の実行を制御することを忘れないでください。

勾配分布法アルゴリズムには予期しないものは何もありません。このメソッドは学習プロセス中にのみ呼び出され、モデルの現在の動作モードを確認する必要はありません。

パラメータでは、メソッドは、誤差勾配を渡す必要がある前の層のオブジェクトへのポインタを受け取り、上記で作成した誤差勾配分布カーネルをキューに入れるメソッドをすぐに呼び出します。

bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!calcInputGradientsS3(NeuronOCL))
      return false;

次に、誤差勾配をセグメントシャッフル優先順位パラメータ層に渡します。

   if(!cShufle.calcHiddenGradients(cProbability.AsObject()))
      return false;

誤差勾配を固定層レベルまでさらに伝播しても意味がありません。したがって、この手順はスキップします。可能な活性化関数に対して得られた誤差勾配を修正するだけです。

   if(cWeights.Activation() != None)
      if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation()))
         return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

対応するオブジェクトに誤差勾配が存在する場合にのみ、誤差勾配を非アクティブ化するメソッドを呼び出すことに注意してください。

全体的な結果への影響に応じてモデルのすべての要素に誤差勾配を伝播した後、全体的な誤差を減らすようにモデルパラメータを調整する必要があります。これは非常に簡単です。CNeuronS3層パラメータを調整するには、対応するネストされたオブジェクトのパラメータの更新メソッドを呼び出すだけです。

bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWeights.UpdateInputWeights(cOne.AsObject()))
      return false;
   if(!cShufle.UpdateInputWeights(cOne.AsObject()))
      return false;
//---
   return true;
  }

これで、新しいクラスのメソッドの説明は終わりです。新しいクラスのすべてのメソッドを1つの記事で説明することはできませんが、すべてのコードは添付ファイルで提供されているため、自分で学習することができます。このクラスとそのすべてのメソッドの完全なコードがそこにあります。

2.4 モデルアーキテクチャ

新しい層クラスを作成したら、それをモデルアーキテクチャに実装します。CNeuronS3クラスをEnvironment State Encoderアーキテクチャに追加することは明らかだと思います。この記事では、エンコーダーのアーキテクチャについては前回の記事から完全にコピーされているため、詳しく説明しません。ソースデータ層の直後に配置した、追加されたニューラル層についてのみ詳しく説明します。

私たちのテストモデルは、H1時間枠の履歴データを分析するために構築されていることに注意してください。分析には、それぞれ9つのパラメータで表された過去120本のバーの履歴を使用します。

#define        HistoryBars             120           //Depth of history
#define        BarDescr                9             //Elements for 1 bar description

この記事を準備している間に、エンコーダーへの入力をシャッフルする3つの連続した層を実装しました。最初の層では、12の時間ステップ（時間）のセグメントを使用しました。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 12*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

2番目の層では、セグメントサイズを4つの時間ステップに縮小しました。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 4*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

そして最後の例では、各時間ステップをシャッフルしました。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

さらに、アーキテクチャも以前の記事から変更なしで完全にコピーされています。つまり、環境と対話し、モデルを訓練およびテストするためのプログラムのアルゴリズムには変更を加えていません。ここで使用されているすべてのプログラムの完全なコードは添付ファイルにあります。

3. テスト

提案されたアプローチのアルゴリズムを構築しました。さて、おそらく最もエキサイティングな段階、つまり結果のテストと評価に移りましょう。

前述のとおり、この記事の作成中に環境相互作用プログラムに変更は加えませんでした。つまり、以前に収集した訓練データセットを使用してモデルを訓練できるということです。

モデルを訓練するために、2023年全体のEURUSD銘柄のH1時間枠の実際の履歴データを使用して、MetaTrader 5ストラテジーテスターの環境相互作用プログラムのパスの記録を使用することを思い出してください。

最初のステップでは、環境状態エンコーダーを訓練します。このモデルは、分析された時系列の次の24要素のデータを予測するように訓練されています。

#define        NForecast               24            //Number of forecast

言い換えれば、私たちのモデルは翌日の価格変動を予測しようとします。エージェントの動作方策を構築するときは、受信した予測ではなく、エンコーダーの隠し状態に依存します。したがって、モデルを訓練する際、今後の動きの正確な予測にはそれほど関心がありません。エンコーダーが今後の価格変動の主なトレンドと傾向をキャプチャして、隠し状態で暗号化する能力を評価します。

エンコーダーモデルは、口座の状態やポジションを考慮せずに市場の状態を分析するためだけに訓練されます。したがって、モデルの訓練プロセス中に訓練データセットを更新しても、追加情報は提供されません。これにより、目的の結果が得られるまで、以前に作成したデータセットでモデルを訓練できます。

最初の訓練ステップの結果に基づいて、モデルによって取得された初期データに対する新しい層の影響を評価できます。ここで、モデルはシャッフルされたシーケンスと元のシーケンスにほぼ同等の注意を払っていることに注意する必要があります。後者にもう少し注意を払ってください。

最初の層では、シャッフルされたシーケンスの係数は0.5039で、元のシーケンスの係数は0.5679でした。同時に、シーケンスはほぼ完全にシャッフルされます。インデックス7のセグメントのみがその位置に残りました。そしてシャッフルは完全にランダムです。単純に場所が入れ替わる要素のペアは1つもありません。

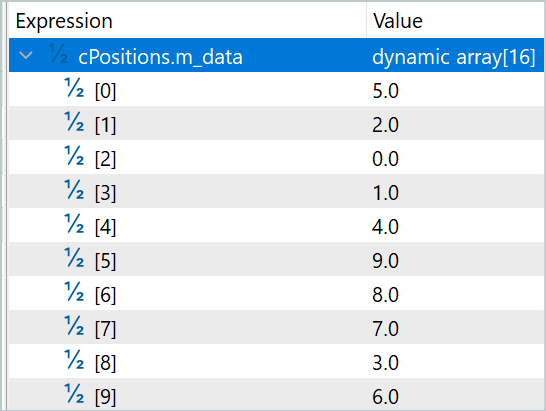
次の層では、両方の係数はそれぞれ0.6386と0.6574にわずかに増加しました。順列のリストは3倍に増えたので提供しません。シャッフルされていないセグメントは含まれなくなりました。

3番目の層では、元のシーケンスにさらに注目が集まりますが、シャッフルされたシーケンスの係数は非常に高いままです。パラメータはそれぞれ0.5064と0.7089に変更されました。

得られた結果はさまざまな方法で評価できます。私の意見では、このモデルはセグメントのペア比較において合理性を追求します。

得られた結果は非常に興味深いものですが、私たちがもっと興味を持っているのは、エージェントの最終的な方策への影響です。エンコーダーを訓練した後、モデルの訓練の第2段階に進みます。この段階では、Actor方策とCriticモデルを訓練します。これらのモデルの動作は、分析時点の口座の状態とポジションに大きく依存します。したがって、学習プロセスは反復的になり、モデルの訓練と環境との相互作用に関する追加データの収集を交互に繰り返します。これにより、エージェントの動作方策を改良し、最適化できるようになります。

訓練プロセスでは、訓練期間とテスト期間の両方で利益を生み出す方策を訓練することができました。訓練の結果を以下に示します。

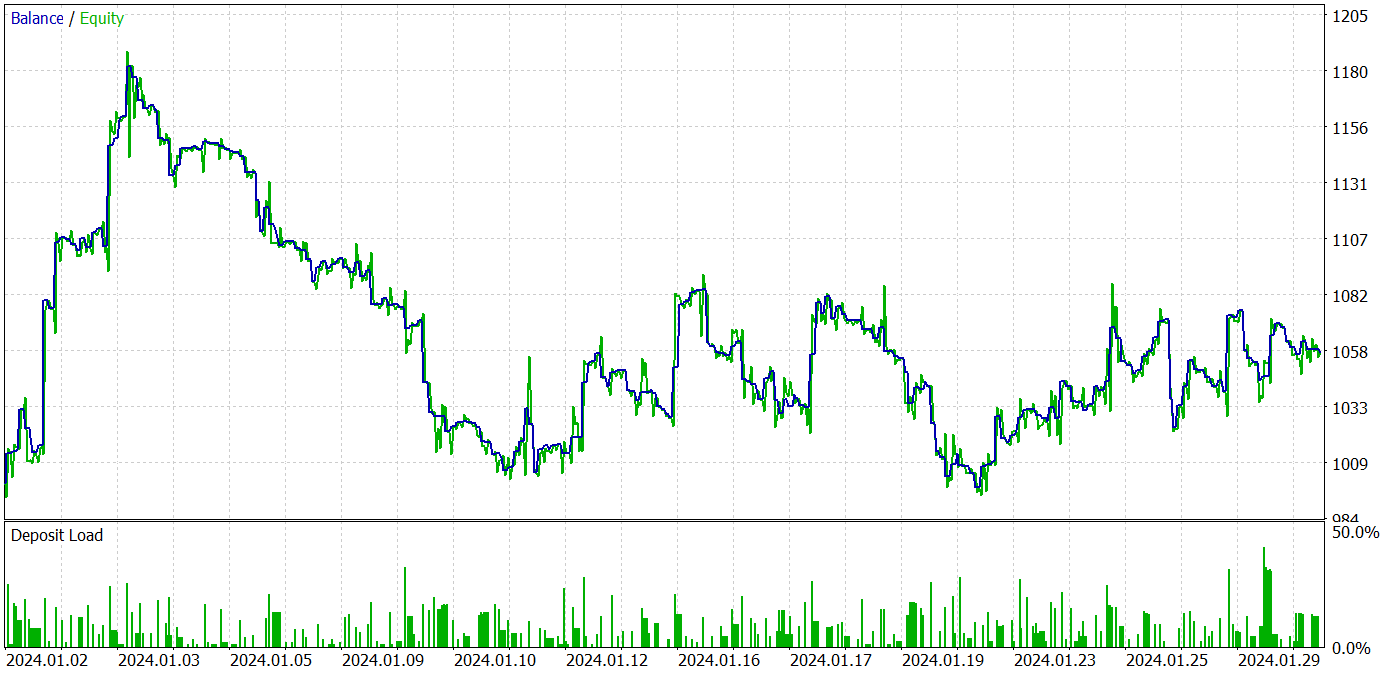
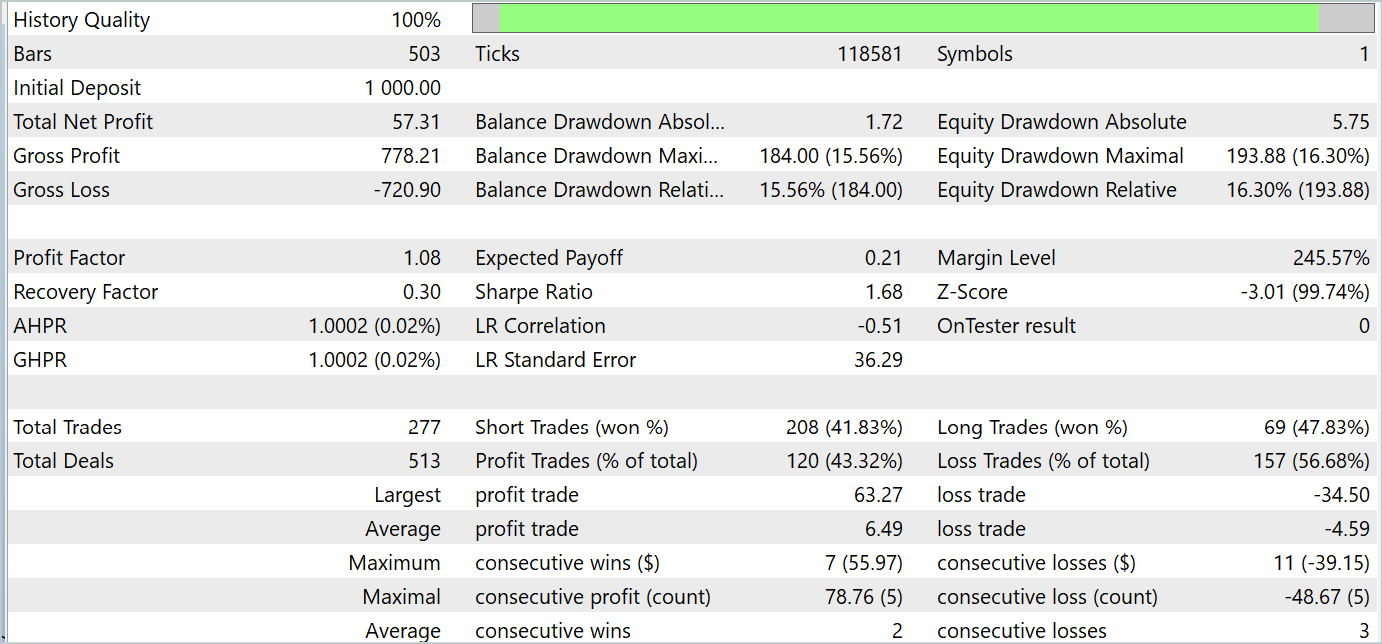
利益は得られたものの、バランスチャートは良くありません。モデルにはまだ改善の余地があります。テストレポートを詳しく見ると、最も収益性の低い月曜日と金曜日を強調表示できます。逆に、水曜日には、モデルは最大の利益を生み出します。

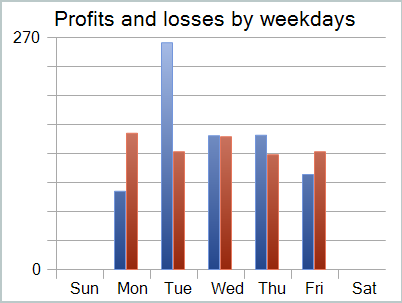
したがって、モデルの動作を特定の曜日に限定すると、モデルの全体的な収益性が向上します。しかし、この仮説には、より代表的なデータセットでのより詳細なテストが必要です。

結論

この記事では、時系列シーケンスを最適化するための興味深い手法であるS3について説明しました。この方法は論文「Segment, Shuffle, and Stitch:A Simple Mechanism for Improving Time-Series Representations」で発表されたものです。この手法の主な目的は、時系列表現の品質を向上させることにあります。S3を適用することで、分類の精度が向上し、モデルの安定性も増すことが確認されています。

この記事の実践的な部分では、MQL5を使用して提案されたアプローチを具体化しました。また、これらのアプローチを用いてモデルの訓練とテストを行いました。その結果は非常に興味深いものでした。

参照文献

• Segment, Shuffle, and Stitch:A Simple Mechanism for Improving Time-Series Representations
• この連載の他の記事記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコード訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ