
Neural Networks Made Easy (Part 94): Optimizing the Input Sequence
Introduction
A common approach when processing time series is to keep the original arrangement of the time steps intact. It is assumed that the historical order is the most optimal. However, most existing models lack explicit mechanisms to explore the relationships between distant segments within each time series, which may in fact have strong dependencies. For example, models based on convolutional networks (CNN) used for time series learning can only capture patterns within a limited time window. As a result, when analyzing time series in which important patterns span longer time windows, such models have difficulty effectively capturing this information. The use of deep networks allows to increase the size of the receptive field and partially solves the problem. But the number of convolutional layers required to cover the entire sequence may be too large, and oversizing the model leads to the vanishing gradient problem.
When used in Transformer architecture models, the effectiveness of long-term dependency detection is highly dependent on many factors. These include sequence length, various positional encoding strategies, and data tokenization.
Such thoughts led the authors of the paper "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations" to the idea of finding the optimal use of historical sequence. Could there be a better organization of time series that would allow for more efficient representation learning given the task at hand?
In the article, the authors present a simple and ready-to-use mechanism called Segment, Shuffle, Stitch (S3), designed to learn how to optimize the representation of time series. As the name suggests, S3 works by segmenting a time series into multiple non-overlapping segments, shuffling these segments into the most optimal order, and then combining the shuffled segments into a new sequence. It should be noted here that the order of segment shuffling is learned for each specific task.
In addition to this, S3 integrates the original time series via a learnable weighted sum operation with a shuffled version, which preserves key information from the original sequence.
S3 acts as a modular mechanism designed to integrate seamlessly with any time series analysis model, resulting in a smoother training procedure with reduced error. Since S3 is trained together with the backbone network, the shuffling parameters are updated purposefully, adapting to the characteristics of the source data and the underlying model to better reflect the time dynamics. Besides, S3 can be stacked to create a more detailed shuffle with a higher level of granularity.
The proposed algorithm has very few hyperparameters to tune and requires little additional computational resources.
To evaluate the effectiveness of the proposed approaches, the method authors integrate S3 into various neural architectures, including CNN and Transformer based models. Performance evaluation on various datasets of univariate and multivariate forecasting classification problems demonstrates that the addition of S3 leads to a significant improvement in the efficiency of the trained model, all other things being equal. The results show that the integration of S3 in modern methods can provide a performance improvement of up to 39.59% in classification tasks. As for the one-dimensional and multi-dimensional time series forecasting tasks, the efficiency of the model can increase by 68.71% and 51.22%, respectively.
1. S3 Algorithm
Let's consider the proposed S3 method in more detail.
For the input data the method uses a multidimensional time series X consisting of T time steps and C channels, which is divided into N non-intersecting segments.
We consider the general case of a multivariate time series, although the method works well with univariate time series as well. Actually, a one-dimensional time series can be considered as a special case of a multidimensional series, when the number of channels C equals 1.
The aim of the method is to optimally rearrange the segments to form a new sequence X', which will allow us to better capture the main temporal relationships and dependencies within a time series. This, in turn, leads to improved understanding of the target task.
S3 method authors propose a solution to the above problem in three stages: "Segmentation", "Mixing" and "Combination".
Module Segment splits the original sequence X into N non-intersecting segments, each of which contains τ time steps where τ = T/N. The set of segments can be represented as S = {s1, s2, . . . , sn}.
The segments are fed into the Shuffle module, which uses a mixing vector P = {p1, p2, . . . , pn} to rearrange the segments in the optimal order. Each shuffling parameter pj in vector P matches the segment sj in the matrix S. Basically, P is a set of learnable weights optimized by the network that controls the position and priority of a segment in a reordered sequence.
The shuffling process is quite simple and intuitive: the higher the value of pj, the higher the priority of segment sj in a shuffled sequence. A shuffled sequence Sshuffled can be represented as:
![]()
Permuting S based on the sorted order P is not differentiable by default because it involves discrete operations and introduces discontinuities. Soft sorting methods approximate the sort order by assigning probabilities that reflect how much larger each element is compared to others. While this approximation is differentiable in nature, it can introduce noise and inaccuracies, making sorting non-intuitive. To achieve differentiable sorting and shuffling that are as accurate and intuitive as traditional methods, the authors of the method introduce several intermediate steps. These steps create a path for the gradients to flow through the shuffle parameters P.
First we get the indices that sort the elements of P using σ = Argsort(P). We have a list of tensors S = {s1, s2, s3, ...sn}, which we want to reorder based on the list of indices σ = {σ1, σ2, ..., σn} in a differentiable way. Then we create a U matrix sized (τ × C) × n × n, in which we repeat each si N times.
After that we form a Ω matrix sized n x n, in which each row j has one non-zero element at position k = σj. We convert the Ω matrix to a binary matrix scaling each non-zero element to 1 using a scaling factor. This process creates a path for gradients to flow through P during backpropagation.
By performing the Hadamard product between U and Ω, we obtain a matrix V, in which each row j has one non-zero element k equal to sk. By summing over the last dimension and transposing the resulting matrix, we obtain the final shuffled matrix Sshuffled.
The use of a multidimensional matrix P' allows us to introduce additional parameters that enable the model to capture more complex representations. Therefore, the authors of the S3 method introduce a hyperparameter λ to determine the dimensionality of P'. We then performed the summation of P' over the first λ − 1 dimensions to get a one-dimensional vector P, which is then used to calculate permutation indices σ = Argsort(P).
This approach allows increasing the number of shuffling parameters, thereby capturing more complex dependencies in time series data without affecting the sorting operations.
In the final step , the Stitch module concatenates the shuffled segments Sshuffled to create one shuffled sequence X'.
In order to preserve the information present in the original order of the analyzed time series, they perform a weighted summation of the original and mixed sequences with parameters w1 and w2, which are also optimized through the training of the main model.
![]()
Considering S3 as a modular level, we can stack them into a neural architecture. Let's define ϕ as a hyperparameter that determines the number of S3 layers. For simplicity and to avoid defining a separate segment hyperparameter for each S3 layer, the authors of the method define a parameter θ as a multiplier for the number of segments in subsequent layers.
When multiple S3 layers are stacked, each ℓ level from 1 to ϕ segments and shuffles input data based on the previous layer output.
All learnable parameters of S3 are updated together with the model parameters, and no intermediate losses are introduced for the S3 layers. This ensures that the S3 levels are trained according to a specific task and basic level.
In cases where the length of the input sequence X is not divisible by the number of segments N, we resort to truncating the first T mod N time steps from the input sequence. To ensure that no data is lost and the input and output shapes are the same, we later add the truncated samples back to the beginning of output of the final S3 layer.
The original visualization of the method is shown below.
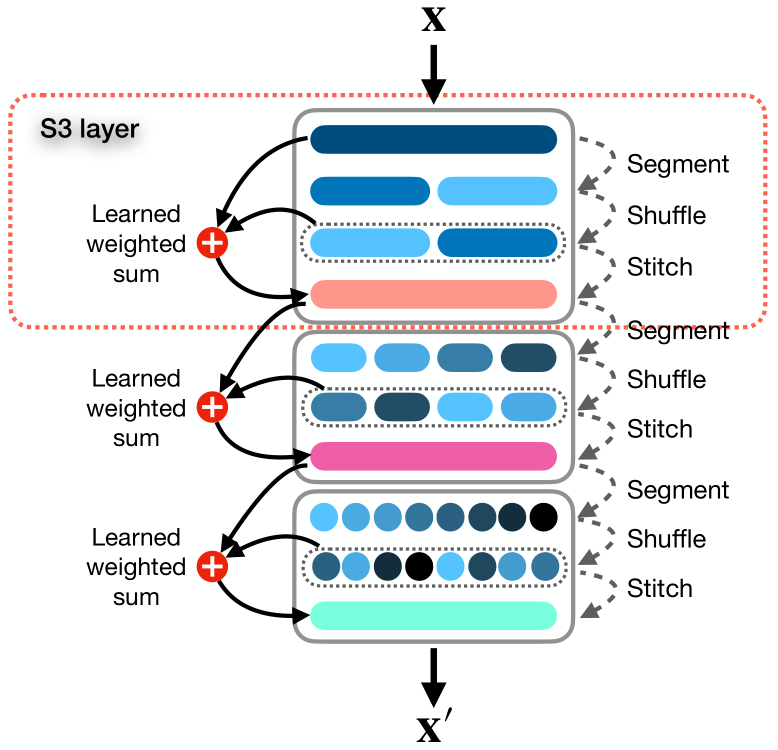
It can be added here that, based on the results of the experiments presented in the paper, the permutation parameters are adjusted at the initial stage of training. After that they are fixed and do not change later.
2. Implementing in MQL5
After considering the theoretical aspects of the S3 method, we move on to the practical part of our article in which we implement the proposed approaches in MQL5. But before we start writing code, let's think about the architecture of the proposed approaches in light of our existing developments.
2.1 Solution Architecture
To determine the data sorting order, the authors of the S3 method use a vector of learnable parameters P. In our library, learnable parameters exist only in neural layers. Well, we can use a neural layer to generate segment priorities. In this case, parameter training can be carried out using available methods within the neural layer. But there is one nuance: we need to feed the neural layer with inputs for which are not provided for the training parameters. The situation is quite simple: we input a fixed vector filled with "1" into such a neural layer.
This approach allows us to immediately solve the problem of the multidimensional matrix of permutations P'. To change the dimension of this matrix (the authors of the S3 method defined the hyperparameter λ), we just need to change the size of the original data vector. The rest of the functionality remains unchanged. The summation of individual parameters for each segment is already implemented within our neural layer. The size of the results of such a neural layer is equal to the number of segments.
To translate segment priorities into the domain of probabilistic values, we will use the SoftMax function.
We will use a similar approach for the parameters of weighting the influence of the original and shuffled sequences. This time the layer result size is 2. As the activation function of this layer, we will use the sigmoid.
These were learnable parameters. As for the algorithm for sorting segments in ascending or descending order of probabilities, we will need to implement this functionality.
Theoretically, the sorting order (ascending or descending) of the priorities of individual segments does not matter. Because we will be learning the order of permutation of segments. Accordingly, during the training process, the model will distribute priorities according to the specified sorting order. It is important here that the sorting order during training and operation of the model remains unchanged.
To enable gradient error propagation to the priority vector P, the authors of the method proposed a rather complex algorithm, in which they create multidimensional arrays and duplicate inputs. Which leads to additional computing costs and increased memory consumption. Can we offer a more efficient option?
Let's look at the process proposed by the authors of the S3 method, analyzing the actions and results.
First, a matrix U is formed, which is a multiple copying of the original data. I would like to exclude this procedure, which will reduce the memory consumption associated with storing a large matrix and the computing resources that are spent when copying data.
The second matrix Ω is a binary matrix that is mostly filled with zero values. The number of non-zero values is equal to the number of segments in the analyzed sequence (N). The number of zero elements is N - 1 times more. Here, we should use a sparse matrix, which will reduce both memory consumption and computational costs when multiplying matrices.
Next, according to the S3 algorithm, there is element-wise matrix multiplication, followed by addition along the last dimension, and transposition of the resulting matrix.
As a result of all the above operations, we simply obtain a shuffled original tensor. A simple operation of permuting tensor elements will require fewer resources and will be executed faster.
The authors developed such a complex permutation algorithm to implement the error gradient propagation to the priority vector P. This is partly a "trap" of automatic differentiation from PyTorch, which the authors of the method used when constructing their algorithm.
We are building feed-forward and backpropagation algorithms. This of course increases our costs for building algorithms, but it also gives us greater flexibility in building processes. Therefore, in the feed-forward pass, we can replace the above operations with a direct shuffling of the data. Obviously, this is a more effective approach.
Now we have to decide on the error gradient propagation question. When shuffling inputs, each segment participates in the output tensor only once. Consequently, the entire error gradient is propagated to the corresponding segment. In other words, when distributing the error gradient to the input data, we need to perform the inverse permutation of the segments. This time we will work with the error gradient tensor.
The second question: How to propagate the error gradient to the priority vector. Here the algorithm is a little more complicated. In the feed-forward pass, we use one priority for the entire segment. Therefore, in the backpropagation pass we have to collect the error gradient of the entire segment at one priority. To do this, we need to multiply the input vector of the desired segment by the corresponding segment of the error gradient tensor.
In addition, when constructing a binary matrix Ω, we used scaling factors to convert non-zero elements to 1. Obviously, to convert a non-zero number to 1, you need to divide it by the same number or multiply it by the reciprocal number. Therefore, the scaling factors are equal to the inverse of the priority numbers. This means that the error gradient value obtained above must be divided by the segment priority.
It should be noted here that the segment priority should not be equal to "0". The use of the SoftMax function allows us to exclude this option. But it does not exclude sufficiently small values, the division by which can lead to sufficiently large values of the error gradient.
In addition, the use of the SoftMax function when forming the probabilities of segment priorities guarantees that all values are in the range (0, 1). Obviously, segments with lower priority receive a larger error gradient, because division by a number less than 1 gives a result greater than the dividend.
So, these were the subtle moments in this algorithm. With these in mind, we can now move on to implementing it in code. Let's start with the implementation on the OpenCL context side.
2.2 Building OpenCL kernels
As always, we start by implementing feed-forward algorithms. On the OpenCL program side, we first create the FeedForwardS3 kernel.
I would like to remind you here that we will implement the generation of segment distribution probabilities and the weighted summation of the original and shuffled sequence in nested neural layers. This means that this kernel receives ready-made data in the form of parameters.
Therefore, our kernel receives pointers to 5 data buffers and 2 constants in parameters. The 3 buffers contain the inputs: the original sequence, segment probabilities and weights. Two more buffers are intended for recording the kernel outputs. In one of them, we will write down the output sequence, and in the second one we will write the segment shuffling indices that we will need when performing backpropagation operations.
In the constants, we will specify the window size of one segment and the total number of elements in the sequence.
Please note that in the second constant, we specify the size of the input vector and not the number of segments or time steps. In the segment window size we also specify the number of array elements, not time steps. Therefore, both constants must be divisible by the size of the vector of one time step without remainder.
__kernel void FeedForwardS3(__global float* inputs, __global float* probability, __global float* weights, __global float* outputs, __global float* positions, const int window, const int total ) { int pos = get_global_id(0); int segments = get_global_size(0);
We plan to launch the kernel in a one-dimensional task space based on the number of segments in the sequence being analyzed. In the kernel body, we immediately identify the current flow, and also determine the total number of segments based on the number of running tasks.
For the case where the total input size is not a multiple of the window size of one segment, we reduce the total number of segments by 1.
if((segments * window) > total)
segments--;
In the next step, we sort the segment priorities to determine their sequence. However, we will not organize the sorting algorithm in its pure form. Instead, we will determine the position of the analyzed segment in the sequence. To determine the position of 1 element, we only need 1 pass through the segment probability vector. However, when sorting a vector, we will need several passes through the probability vector and synchronization of computational threads.
Here we split the algorithm into 2 branches, depending on the index of the current thread. The first branch is the general case and is used if the current thread index is less than the number of segments. Considering that the index of the first thread is equal to 0, the given formulation of the condition may seem strange. Earlier, when considering cases where the input size was not a multiple of the size of the segment window, we reduced the value of the variable for the number of segments. And in this case, the last thread will follow the 2nd branch of the algorithm for determining the segment position.
In general, to determine the position of the segment corresponding to the current thread of operations, we fix its priority in a local constant. We run a loop from the first to the current segment, in which we count the number of elements with a priority less than or equal to the current one. For the case of descending sorting, we determine the number of elements with a priority greater than or equal to the current segment.
Then we organize a loop from the next segment to the last one, in which we add the number of elements with a priority strictly less (strictly more when sorting in descending order).
After completing the operations of both loops, we get the position of the current segment in the overall sequence.
int segment = 0; if(pos < segments) { const float prob = probability[pos]; for(int i = 0; i < pos; i++) { if(probability[i] <= prob) segment++; } for(int i = pos + 1; i < segments; i++) { if(probability[i] < prob) segment++; } }
Splitting of a pass through the priority vector into 2 loops is done for the special case of having 2 or more elements with the same priority. In this case, priority is given to the element that is earlier in the original sequence. Well, we could construct an algorithm with one loop, but in this case, before comparing priorities, we would have to check at each iteration whether the segment was before or after the current one in the original sequence.
In the second branch of the special case algorithm, we simply assign the segment number to its order in the sequence. In the above-mentioned special case, all complete segments will be mixed, and the last (not complete) one will remain in its place.
else
segment = pos;
Now that we have determined the position of the segment in the shuffled sequence, we can move it. To do this, we define the offsets in the input and output buffers.
const int shift_in = segment * window; const int shift_out = pos * window;
We immediately save a certain position in the corresponding buffer.
positions[pos] = (float)segment;
Let's not forget about the weighted summation of the original and mixed sequences. Naturally, to avoid unnecessary copying of data into the result buffer, we will immediately save the weighted sum of 2 segments from the original and mixed sequences. To do this, we save the weighing parameters in local constants.
const float w1 = weights[0]; const float w2 = weights[1];
We create a loop with a number of iterations equal to the window size of one segment, in which we sum the elements of 2 sequences taking into account the weights and saving the obtained values in the results buffer.
for(int i = 0; i < window; i++) { if((shift_in + i) >= total || (shift_out + i) >= total) break; outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i]; } }
After building the feed-forward pass kernel, we move on to working on the backpropagation pass. Here we start working with building the InsideGradientS3 kernel, in which we distribute the error gradient to the level of the previous layer and the priorities of the segments. In the kernel parameters, we add pointers to the buffers of the corresponding error gradients are added to the previously considered buffers.
__kernel void InsideGradientS3(__global float* inputs, __global float* inputs_gr, __global float* probability, __global float* probability_gr, __global float* weights, __global float* outputs_gr, __global float* positions, const int window, const int total ) { size_t pos = get_global_id(0);
The kernel will be launched in a one-dimensional task space according to the number of segments in the analyzed sequence. In the kernel body, we immediately identify the current operations thread. In this case, we do not need to determine the total number of segments.
Next, we load the constants determined during the feed-forward pass from the data buffers.
int segment = (int)positions[pos]; float prob = probability[pos]; const float w1 = weights[0]; const float w2 = weights[1];
After that we determine the offset in the data buffers.
const int shift_in = segment * window; const int shift_out = pos * window;
And we will declare local variables for intermediate data.
float grad = 0; float temp = 0;
In the next step, we create a loop with a number of iterations equal to the segment window size, in which we collect the error gradient for the segment priority.
for(int i = 0; i < window; i++) { if((shift_out + i) >= total) break; temp = outputs_gr[shift_out + i] * w1; grad += temp * inputs[shift_in + i];
At the same time, we transfer the error gradient to the previous layer buffer. During the feed-forward pass, we summed the original and shuffled sequence. Therefore, each input element should receive the error gradient from 2 threads with the corresponding weight.
inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2; }
Before writing the segment priority error gradient to the corresponding data buffer, we divide the output value by the probability of the current segment.
probability_gr[segment] = grad / prob; }
The above-considered gradient propagation kernel is missing one point: the propagation of the error gradient on the weights of the original and mixed sequences. To implement this functionality, we will create a separate kernel WeightGradientS3.
Here it should be said that the general approach we use, when the error gradient of 1 element is collected in each individual thread, is not very effective in this case. This is due to the small number of elements in the weight vector. As you can see, there are only 2 of them here. However, it is better to have more parallel threads to reduce the overall time spent training the model. To achieve this effect, we will create two working groups of threads, each of which will collect the error gradient for its parameter.
__kernel void WeightGradientS3(__global float *inputs, __global float *positions, __global float *outputs_gr, __global float *weights_gr, const int window, const int total ) { size_t l = get_local_id(0); size_t w = get_global_id(1);
Accordingly, the kernel will be launched in a 2-dimensional task space. The first dimension defines the number of parallel threads in one group. And the second dimension indicates the index of the parameter for which the error gradient is collected.
Then we declare a local array, into which each thread of the group will save its part of the work.
__local float temp[LOCAL_ARRAY_SIZE];
Since the number of work threads cannot be greater than the size of the declared local array, we are forced to limit the number of "workhorses".
size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);
In the first stage, each thread collects its share of error gradients independently of the other threads in the workgroup. To do this, we run a loop over the elements of the error gradient buffer at the output of the current layer, starting from the element with the index of the current thread workgroup to the last one in the array, with a step equal to the number of "workhorses".
In the loop body, we first determine the offset to the corresponding element in the source data buffer. This offset depends on the index of the weight for which we collect the error gradient. For the second weight, the shift in the gradient buffers of the layer error and the input data is the same.
if(l < ls) { float val = 0; //--- for(int i = l; i < total; i += ls) { int shift_in = i;
As for the first offset, we first define a segment in the error gradient buffer. Then, from the permutation vector, we extract the corresponding segment in the original sequence. Only then can we calculate the offset in the input buffer to the required element.
if(w == 0) { int pos = i / window; shift_in = positions[pos] * window + i % window; }
Given the indices of the corresponding elements in both data buffers, we calculate the error gradient for the weight at that position and add it to the accumulation variable.
val += outputs_gr[i] * inputs[shift_in]; } temp[l] = val; } barrier(CLK_LOCAL_MEM_FENCE);
After all iterations of the loop are completed, we write the accumulated sum of the error gradient to the corresponding element of the local memory array and implement a synchronization barrier for the workgroup threads.
In the second step, we sum the values of the elements of the local array.
int t = ls; do { t = (t + 1) / 2; if(l < t && (l + t) < ls) { temp[l] += temp[l + t]; temp[l + t] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(t > 1);
At the end of the kernel operations, the first thread of the workgroup transfers the total error gradient to the corresponding element of the global buffer.
if(l == 0) weights_gr[w] = temp[0]; }
After distributing the error gradients for all elements according to their impact on the overall result, we usually move on to working on the parameter updating algorithms. But within the framework of this article, we have organized all the trainable parameters within the nested neural layers. Consequently, the algorithms for updating parameters are already provided within the mentioned objects. Therefore, here we are completing operations on the OpenCL side and move on to working with the main program.
2.3. Creating the CNeuronS3 class
To implement the proposed approaches on the main program side, we create a new neural layer class CNeuronS3. Its structure is presented below.
class CNeuronS3 : public CNeuronBaseOCL { protected: uint iWindow; uint iSegments; //--- CNeuronBaseOCL cOne; CNeuronConvOCL cShufle; CNeuronSoftMaxOCL cProbability; CNeuronConvOCL cWeights; CBufferFloat cPositions; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool feedForwardS3(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronS3(void) {}; ~CNeuronS3(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronS3; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
In the class, we declare 2 variables and 5 nested objects. The variables will store the window size of one segment and the total number of segments in the sequence. As for the purposes of nested objects, we will consider them while implementing the methods of our class.
All objects of the class are declared statical. This allows us to leave the class constructor and destructor "empty". Initialization of all nested objects is performed in the Init method. As always, in the parameters of this method we receive the main parameters of the class architecture from the caller. Pay attention to the following 2 parameters:
- window — window size of 1 segment;
- numNeurons — the number of neurons in the layer.
In these parameters we indicate the number of array elements instead of the steps of the time series. However, their value must be a multiple of the size of the vector describing one time step. In other words, for ease of implementation we build a class for working with a one-dimensional time series. Here, the user is responsible for maintaining the integrity of the time steps of a multidimensional time series within segments.
bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false;
In the body of the method, we first call the same method of the parent class, which controls the received parameters and initializes the inherited objects. Remember to control the execution of the called methods.
After successful initialization of the inherited objects, we save the window size of 1 segment and immediately determine the total number of segments.
iWindow = MathMax(window, 1); iSegments = (numNeurons + window - 1) / window;
Next, we initialize the internal objects of the class. First we initialize a fixed neural layer of single values, which will be used as the input for generating segment permutation priorities and weighted sequence summation parameters. Here we first initialize the neural layer and then force fill the result buffer with single values.
if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *buffer = cOne.getOutput(); if(!buffer || !buffer.BufferInit(buffer.Total(),1)) return false; if(!buffer.BufferWrite()) return false;
Please pay attention to the following two points. First, we create a layer of 1 neuron. As you remember, when we were working on the architecture of our implementation, we said that the number of neurons in a given layer would indicate the dimension of the permutation matrix. I don't see the point in using a multidimensional matrix. From a mathematical point of view, without the use of intermediate activation functions, the linear function of summing the product of several variables by a constant degenerates into the product of one variable by the constant used.
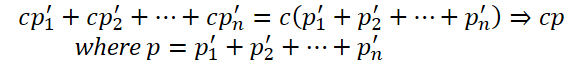
From this point of view, an increase in parameters only leads to an increase in computational complexity with a questionable impact on the efficiency of the model.
On the other hand, this is just my opinion. So, you can test this experimentally.
The second point is the indication of "0" outgoing connections for this nested layer. We plan to use this object as the initial data for 2 neural layers. It was the presence of 2 subsequent layers that forced us to resort to a little trick. Our base neural layer is designed in such a way that it contains a weight matrix only for 1 subsequent layer. But we have a class of convolutional neural layers, which contains matrices of weight coefficients for incoming connections. Using 1 input element and multiple permutation priorities at the output is, to put it mildly, not exactly a suitable scenario for using a convolutional layer. But wait.
One input element is guaranteed to give us 1 learnable parameter in the convolution filter. Also, we can easily provide the size of the permutation vector by specifying the required number of convolution filters. In this case, we will specify only 1 convolution element. In this way we will transfer the learnable parameters to the subsequent neural layers.
if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch)) return false; cShufle.SetActivationFunction(None);
As discussed earlier, we translate permutation priorities into the probability domain using the SoftMax function.
if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch)) return false; cProbability.SetActivationFunction(None); cProbability.SetHeads(1);
We do the same with the object of generating parameters of weighted summation of sequences. The difference is that here we use sigmoid as the activation function.
if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch)) return false; cWeights.SetActivationFunction(SIGMOID);
And at the end of the initialization method, we create a buffer for recording the segment permutation indices.
if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL)) return false; //--- return true; }
The class contains two new methods (feedForwardS3 and calcInputGradientsS3). They put the previously created OpenCL program kennels to the execution queue. As you can guess, the first method queues the execution of the feed-forward kernel, and the second method queues the two remaining error gradient distribution kernels. In previous articles, we have already discussed the algorithm for placing the kernel in the execution queue. These methods are built on a similar algorithm, so we will not consider them now. You can find the code of these methods in the attachment. The attachment also contains the complete code of all programs used while preparing the article.
The feed-forward algorithm of our class is built in the feedForward method. Like the parent class method with the sane name, the method receives in parameters a pointer to the object of the previous neural layer, which contains the input data.
Before calling the method of placing the feed-forward kernel in the queue, we need to prepare the priorities of the segment permutations and the parameters for weighing the sum of the original and shuffled sequences. And here it should be noted that the initial data for the indicated processes is a fixed vector of unit values. Consequently, their values do not depend on the initial data and do not change during the operation of the model. The specified values can only change when the learning parameters change during the learning process. This means that their recalculation is only necessary during the learning process. To recalculate the values, we call the feed-forward method of the corresponding nested objects.
bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL) { if(bTrain) { if(!cWeights.FeedForward(cOne.AsObject())) return false; if(!cShufle.FeedForward(cOne.AsObject())) return false; if(!cProbability.FeedForward(cShufle.AsObject())) return false; }
Next, we shuffle the original sequence by calling the method to put the forward pass kernel into the execution queue.
if(!feedForwardS3(NeuronOCL)) return false; //--- return true; }
Remember to control the execution of operations.
There is nothing unexpected in the gradient distribution method algorithm. The method is called only during the learning process and we do not need to check the current operating mode of the model.
In the parameters, the method receives a pointer to the object of the previous layer, to which the error gradient must be passed, and we immediately call the method for queuing the above-created error gradient distribution kernels.
bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!calcInputGradientsS3(NeuronOCL)) return false;
Next, we pass the error gradient to the segment shuffling priority parameter layer.
if(!cShufle.calcHiddenGradients(cProbability.AsObject())) return false;
There is no point in propagating the error gradient further to the fixed layer level. Therefore, we will skip this procedure. We just need to correct the obtained error gradient for possible activation functions.
if(cWeights.Activation() != None) if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation())) return false; if(NeuronOCL.Activation() != None) if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation())) return false; //--- return true; }
Note that we call the method for deactivating error gradients only if there is one in the corresponding object.
After propagating the error gradient to all elements of our model according to their influence on the overall result, we need to adjust the model parameters so as to reduce the overall error. This is quite straightforward. To adjust the CNeuronS3 layer parameters, we just need to call the update methods of the parameters of the corresponding nested objects.
bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cWeights.UpdateInputWeights(cOne.AsObject())) return false; if(!cShufle.UpdateInputWeights(cOne.AsObject())) return false; //--- return true; }
This concludes the description of the methods of our new class. It is not possible to describe all the methods of our new class within one article, but you can study them yourself as all codes are provided in the attachment. You will find there the complete code for this class and all its methods.
2.4 Model architecture
After creating the new layer class, we implement it into our model architecture. I think it's obvious that we'll add the CNeuronS3 class to the Environment State Encoder architecture. Within this article, I will not go into detail about the Encoder architecture, as it is completely copied from the previous article. Let's dwell only on the added neural layers, which we placed immediately after the source data layer.
Let me remind you that our test models are built to analyze historical data on the H1 timeframe. For analysis, we use the last 120 bars of history, each of which is described by 9 parameters.
#define HistoryBars 120 //Depth of history #define BarDescr 9 //Elements for 1 bar description
While preparing this article, we implemented 3 consecutive layers that shuffle the inputs into the Encoder. For the first layer, we used segments of 12 time steps (hours).
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronS3; descr.count = prev_count; descr.window = 12*BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
In the second layer, we reduced the segment size to 4 time steps.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronS3; descr.count = prev_count; descr.window = 4*BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
And in the last one, we shuffled each time step.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronS3; descr.count = prev_count; descr.window = BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Further architecture is also completely copied from the previous articles without any changes. This means we did not make any changes to the algorithm of the programs for interacting with the environment, training and testing the models. You can find the complete code of all programs used herein in the attachment.
3. Testing
We have constructed the algorithms of the proposed approaches. Now, let's move on to, perhaps, the most exciting stage - testing and evaluating the results.
As stated above, we did not make any changes to the environmental interaction programs while working on this article. This means that we can use a previously collected training data set to train models.
Let me remind you that to train the models, we use records of the passes of the environmental interaction program in the MetaTrader 5 strategy tester using real historical data of the EURUSD instrument, H1 timeframe, for the entire year 2023.
In the first step, we train the environment state Encoder. This model is trained to predict data for the next 24 elements of the analyzed time series.
#define NForecast 24 //Number of forecast
In other words, our model tries to predict the price movement for the next day. When constructing the behavior policy of our Agent, we rely not on the received forecast, but on the hidden state of the Encoder. Therefore, when training the model, we are not that interested in an accurate forecast of the upcoming movement - we evaluate the ability of the Encoder to capture and encrypt in its hidden state the main trends and tendencies of the upcoming price movement.
The Encoder model is trained only to analyze the market state without taking into account the account state and open positions. Therefore, updating the training dataset during the model training process will not provide additional information. This allows us to train the model on a previously created dataset until we get the desired result.
Based on the results of the first training step, we can evaluate the impact of our new layer on the initial data obtained by the model. Here I should note that the model pays almost equal attention to the shuffled and original sequences. Just a bit more attention to the latter one.
At the first layer, the coefficient of the shuffled sequence was 0.5039, and that of the original sequence was 0.5679. At the same time, there is almost complete shuffling of the sequence. Only the segment with index 7 remained in its position. And the shuffling is totally random. There is not a single pair of elements that would simply swap places.
At the next layer, both coefficients increased slightly to 0.6386 and 0.6574, respectively. I will not provide the list of permutations, since it has increased threefold. It no longer contains non-shuffled segments.
In the third layer, more attention is paid to the original sequence, but the coefficient for the shuffled sequence remains quite high. The parameters changed to 0.5064 and 0.7089, respectively.
The results obtained can be assessed in different ways. In my opinion, the model seeks rationality in the pairwise comparison of segments.
The result obtained is quite interesting, but we are more interested in the impact on the Agent's final policy. After training the Encoder, we move on to the second stage of training our models. At this stage, we train the Actor policy and the Critic model. The operation of these models is highly dependent on the state of the account and open positions at the analyzed moment. Therefore, our learning process will be iterative, alternating between training models and collecting additional data on interaction with the environment. This will allow us to refine and optimize the Agent's behavior policy.
During the training process, we were able to train a policy to generate profits both during the training period and during the testing period. The training results are presented below.
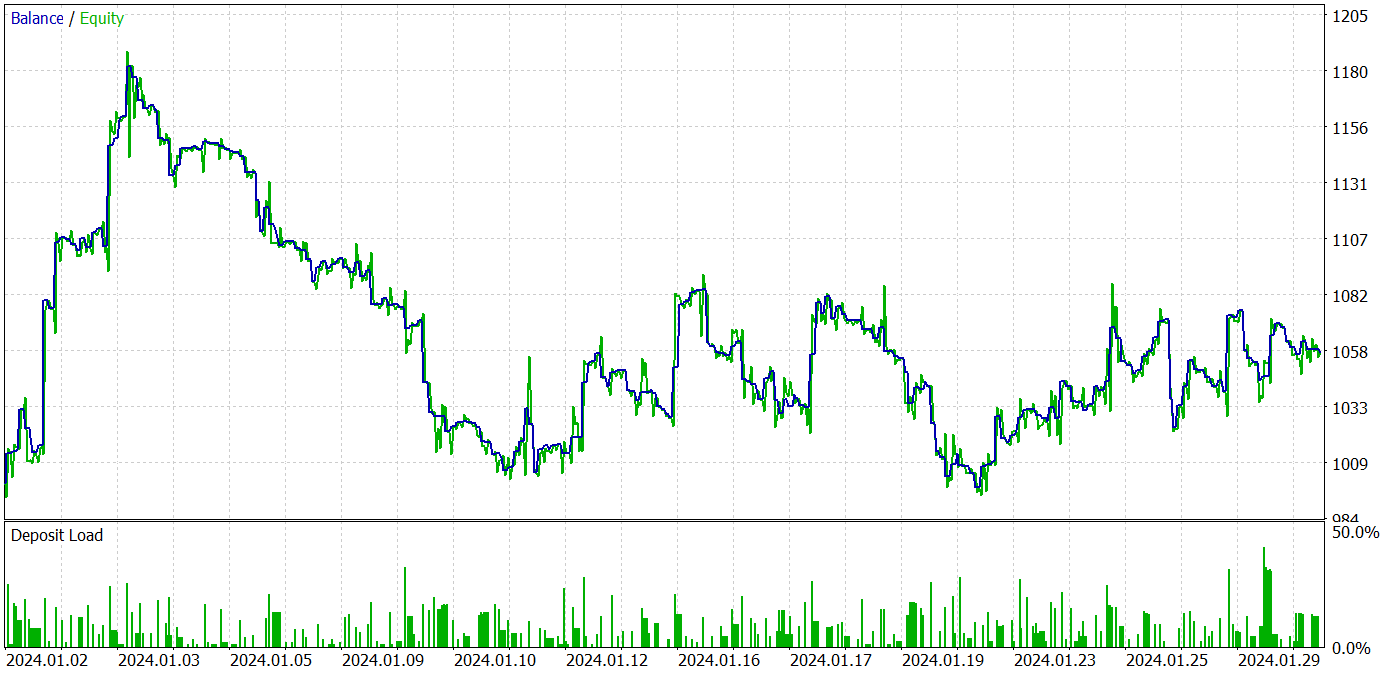
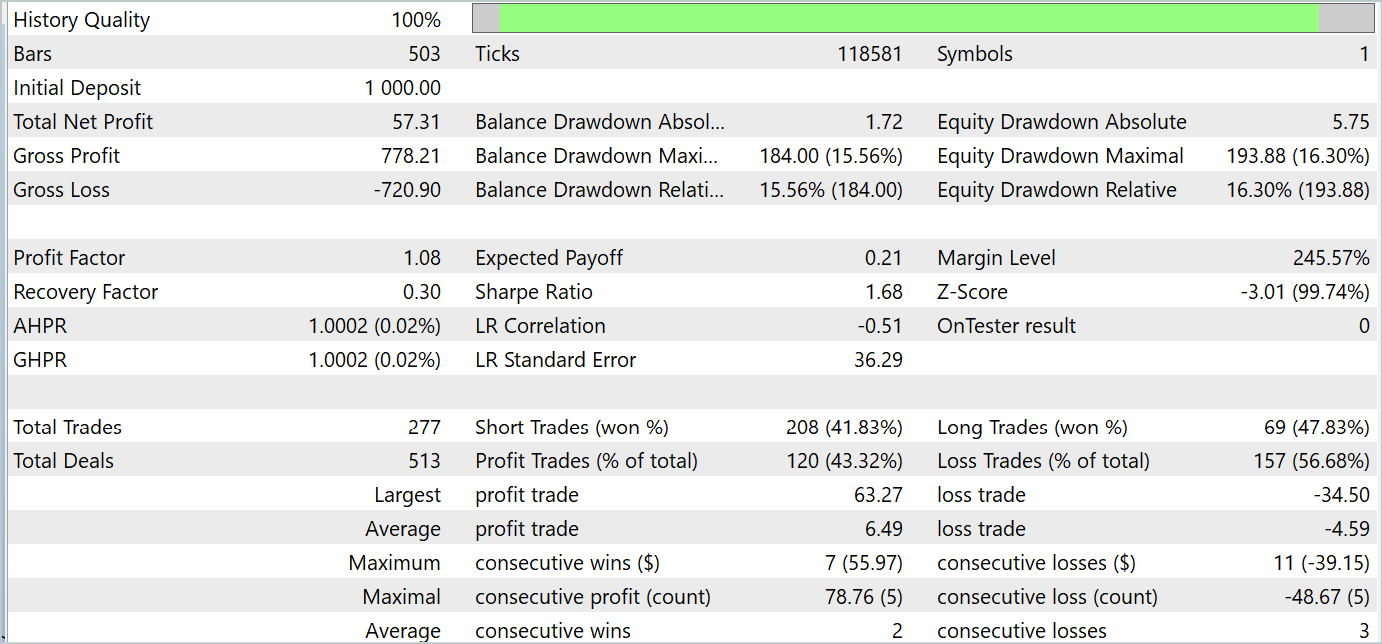
Despite the profit received, the balance chart does not look good. The model still requires some improvement. If you look more closely at the testing report, you can highlight the most unprofitable Mondays and Fridays. On Wednesday, on the contrary, the model generates maximum profit.
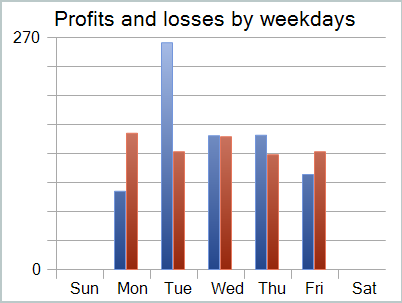
Therefore, limiting the model operation on certain days of the week will increase the overall profitability of the model. But this hypothesis requires more detailed testing on a more representative dataset.
Conclusion
In this article, we have discussed a rather interesting method of optimizing time series sequences: S3. The method was presented in the paper "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations". The main idea of the method is to improve the quality of time series representation. The application of S3 leads to increased classification accuracy and model stability.
In the practical part of our article, we have built our vision of the proposed approaches using MQL5. We have trained and tested models using the proposed approaches. The results are quite interesting.
References
- Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations
- Other articles from this series
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Example collection EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA for collecting examples using the Real-ORL method |
| 3 | Study.mq5 | Expert Advisor | Model training EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Model testing EA |
| 6 | Trajectory.mqh | Class library | System state description structure |
| 7 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 8 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/15074
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Trading with the MQL5 Economic Calendar (Part 3): Adding Currency, Importance, and Time Filters
Trading with the MQL5 Economic Calendar (Part 3): Adding Currency, Importance, and Time Filters
 Mastering Log Records (Part 1): Fundamental Concepts and First Steps in MQL5
Mastering Log Records (Part 1): Fundamental Concepts and First Steps in MQL5
 MQL5 Wizard Techniques you should know (Part 50): Awesome Oscillator
MQL5 Wizard Techniques you should know (Part 50): Awesome Oscillator
 Creating a Trading Administrator Panel in MQL5 (Part VII): Trusted User, Recovery and Cryptography
Creating a Trading Administrator Panel in MQL5 (Part VII): Trusted User, Recovery and Cryptography
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Where to find the #include "legendre.mqh" file?
The specified library was used in FEDformer. For the purposes of this article, the line can be simply deleted.
The specified library was used in FEDformer. For the purposes of this article, the string can simply be deleted.
Dmitry you could reply to my comment under the previous article of your #93