ニューラルネットワークが簡単に（第89回）：FEDformer (Frequency Enhanced Decomposition Transformer)

MetaTrader 5 — トレーディングシステム | YYYY年11月DD日, 08:35

215

Dmitriy Gizlyk

はじめに

時系列の長期予測は、さまざまな応用問題を解決する上で長年の課題となっています。Transformerベースのモデルは有望な結果を示していますが、計算の複雑さとメモリ要件が高いため、Transformerを使用して長いシーケンスをモデル化することは困難です。このため、Transformerアルゴリズムの計算コストを削減するための数多くの研究がおこなわれています。

Transformerベースの時系列予測法は進歩を遂げてきましたが、時系列分布の共通の特徴を捉えられない場合もあります。論文「FEDformer:Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting」の著者は、この問題を解決しようと試みました。著者らは、時系列の実際のデータと、バニラTransformerから取得した予測値を比較しています。以下は、その論文のスクリーンショットです。

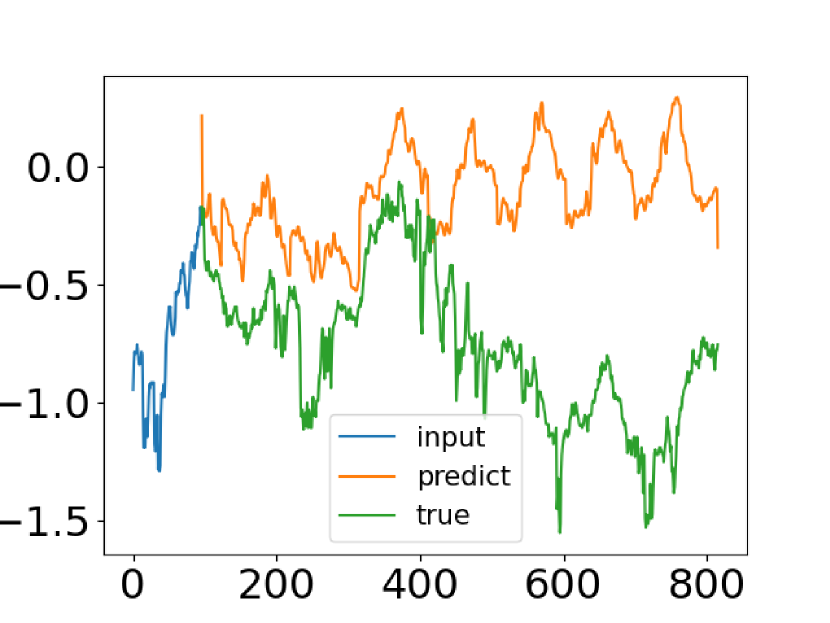
予測時系列の分布が実際の分布と大きく異なることがわかります。期待値と予測値の不一致は、Transformerのポイントアテンションによって説明できます。各時間ステップの予測は個別に独立しておこなわれるため、モデルは時系列全体のグローバルプロパティと統計を保持できない可能性があります。この問題を解決するために、著者は2つのアイデアを活用しています。

1つ目は、時系列分析で広く使用されている季節傾向分解アプローチを使用することです。論文の著者は、予測の分布を実際の分布に効果的に近似する特別なモデルアーキテクチャを提示しています。

2番目のアイデアは、Transformerアルゴリズムにフーリエ解析を実装することです。Transformerをシーケンスの時間測定に適用する代わりに、その周波数特徴を分析できます。これにより、Transformerは時系列のグローバルプロパティをより適切にキャプチャできるようになります。

提案されたアイデアの組み合わせは、FEDformer（Frequency Enhanced Decomposition Transformerモデル）に実装されています。

FEDformerに関連する最も重要な質問の 1 つは、時系列を表すためにフーリエ解析でどの周波数成分のサブセットを使用すべきかということです。このような解析では、低周波数成分が保持され、高周波成分は破棄されることが多いです。ただし、時系列の傾向の変化の一部は重要なイベントに関連付けられているため、これは時系列予測には適さない可能性があります。この部分の情報は、信号の高周波成分をすべて削除するだけで失われる可能性があります。この手法の作者は、時系列が通常、フーリエ基底に基づく未知のスパース表現を持つという事実を受け入れています。彼らの理論分析では、低周波数成分と高周波成分の両方を含むランダムに選択された周波数成分のサブセットが、時系列をより適切に表現することを示しました。この観察は、広範な実証研究によって確認されています。

長期予測の効率を改善するだけでなく、Transformerと周波数分析の組み合わせにより、計算コストを二次的な複雑さから線形の複雑さに削減することができます。

論文の著者ら、その成果を次のように要約しています。

1. 時系列の全体的な特性をより適切に捉えるために、周波数応答が改善された信号分解アーキテクチャのTransformerと季節傾向分解のエキスパートの使用を提案しています。

2. Transformerアーキテクチャにフーリエ拡張ブロックとウェーブレット拡張ブロックを導入することで、周波数特徴を調査し、時系列の重要な構造を捉えることができるようになります。これにより、自己注意ブロックや相互注意ブロックの代わりに機能することができます。

3. 固定数のフーリエ成分をランダムに選択することによって、提案されたモデルは線形の計算量とメモリコストを実現します。この選択方法の有効性は、理論的および経験的に確認されています。

4.異なるドメインの6つのベースラインデータセットで行われた実験において、提案されたモデルは多変量予測と単変量予測のそれぞれにおいて、最先端の手法に対して14.8%および22.6%の性能向上を示しました。

1. FEDformerアルゴリズム

この手法の作者は、FEDformerモデルの2つのバージョンを発表しました。1つはフーリエ基底を使用して時系列の周波数特徴を分析し、もう1つはウェーブレットを用いたもので、時間的な視点と周波数特徴の領域での分析を組み合わせることができます。

長期時系列の予測はシーケンスからシーケンスへの問題です。初期データのシーケンスのサイズをI、予測されるシーケンスをOとし、Dはシリーズの1つの状態を表すベクトルのサイズを示します。次に、サイズ I*Dのテンソルをエンコーダーに入力し、行列 (I/2+O)*D をデコーダーに入力します。

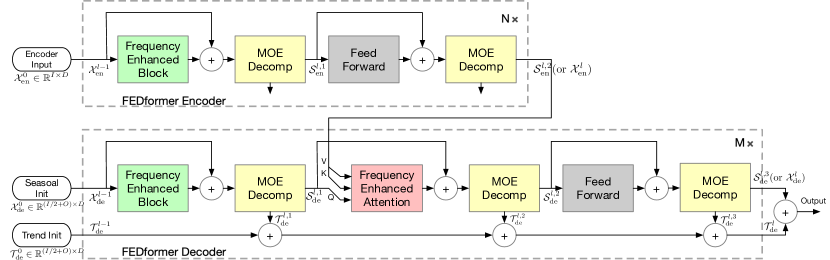
前述のように、この手法の作者は季節傾向の分解と分布の分析を導入することで、Transformer アーキテクチャを改善しました。更新されたTransformerは、深い分解アーキテクチャを特徴とし、周波数応答分析ユニット(FEB)、周波数強化アテンションブロック(FEA)、およびMixture Of Experts分解ブロック(MOEDecomp).が含まれています。

FEDformerエンコーダーは、Transformerエンコーダーに似たマルチレベル構造を使用します。その各ブロックは、次の数式で表すことができます。

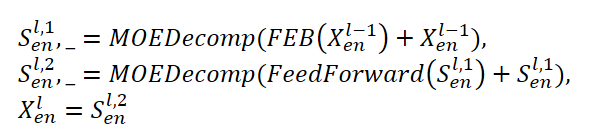
ここで、Senは、MOEDecomp分解ブロックから抽出された季節成分を表します。

FEBモジュールについては、この手法の著者は2つの異なるバージョン（FEB-fとFEB-w）を提案しています。これらはそれぞれ、離散フーリエ変換メカニズム(DFT)と離散ウェーブレット変換(DWT)を使用して実装されており、この実装では、セルフアテンションブロックが置き換えられています。

デコーダーも、エンコーダーと同様にマルチレベル構造を使用します。ただし、その構成ブロックのアーキテクチャははるかに広範囲であり、次の式で説明されます。

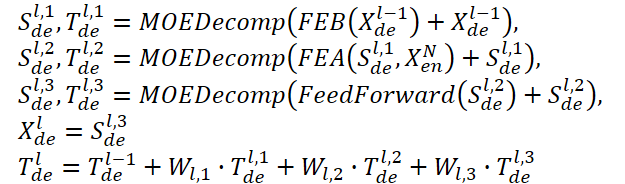
SdeとTdeは、MOEDecomp分解ブロック後の季節要素とトレンド要素を表します。Wlは抽出された傾向の投影として機能します。FEBと同様に、FEAには2つの異なるバージョン（FEA-fとFEA-w）があり、それぞれDFTおよびDWT投影を通じて実装されます。FEAFEAはアテンションデザインで実装され、バニラTransformerのクロスアテンションブロックを置き換えます。

最終的な予測は、2つの改良された分解されたコンポーネントの合計です。季節コンポーネントは、WS行列を使用してターゲット測定に投影されます。

提案されたFEDformerモデルは、離散フーリエ変換(DFT)を使用し、分析されたシーケンスをその構成高調波（正弦波成分）に分解できます。モデルの効率を向上させるために、FEDformerの作成者は高速フーリエ変換(FFT)を使用しています。

前述のように、この方法ではフーリエ基底のランダムなサブセットが使用され、サブセットのスケールはスカラーによって制限されます。DFTおよび逆DFT (IDFT)演算の前にモードインデックスを選択すると、計算の複雑さをさらに調整できます。

エンコーダーとデコーダーの両方で、フーリエ変換による拡張周波数範囲ブロック(FEB-f)が使用されます。FEB-fブロックのソースデータは、最初に線形投影され、次に時間領域から周波数応答に変換されます。取得された周波数特性からM個の高調波がランダムにサンプリングされます。その後、選択された周波数特徴がランダムパラメータで初期化され、モデル訓練プロセス中に調整されるパラメータ化されたカーネルのマトリックスで乗算されます。結果は、逆フーリエ変換を実行する前に、完全な周波数応答次元にゼロパディングされ、分析されたシーケンスが時間領域に戻されます。論文の著者によって提供されたFEB-fブロックの元の可視化を以下に示します。

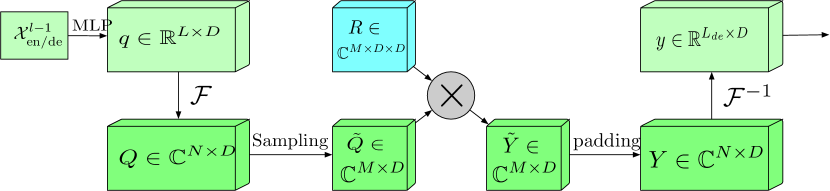
離散フーリエ変換(FEA-f)を使用した周波数応答アテンションブロックは、標準的なTransformerアプローチにわずかな追加を加えて適用されています。ソースデータはQuery、Key、Value表現に変換され、クロスアテンションではQueryがデコーダーから取得され、KeyとValueはエンコーダーから取得されます。しかし、FEA-fではQuery、Key、Valueがフーリエ変換を用いて変換され、周波数領域で標準的なアテンションメカニズムが実行されます。この際、FEB-fブロック同様、分析のためにM個の高調波がランダムにサンプリングされます。アテンション操作の結果は、元のシーケンスのサイズまでゼロパディングされ、逆フーリエ変換が実行されます。以下に、著者の可視化によるFEA-f構造を示します。

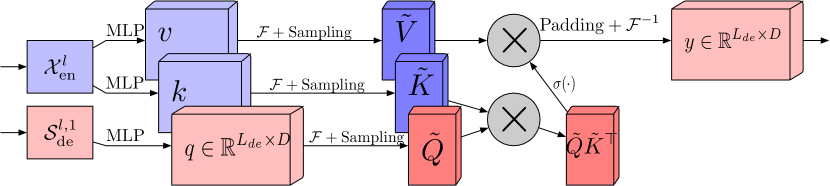
フーリエ変換は信号の周波数領域表現を作成しますが、ウェーブレット変換は信号を周波数領域と時間領域の両方で表現し、元の信号に関する局所的な情報に効率的にアクセスできます。マルチウェーブレット変換は、直交多項式とウェーブレットの利点を組み合わせた方法です。この表現は、マルチスケールとマルチウェーブレット基底のテンソル積によって取得されます。異なるスケールの基底はテンソル積によって関連付けられることに注意してください。FEDformer法の作成者は、モデルの複雑さを軽減するために非標準のウェーブレット表現を採用しています。

FEB-wアーキテクチャは、再帰メカニズムにおいてFEB-fとは異なります。元のデータは再帰的に3つの部分に分解され、それぞれが個別に処理されます。ウェーブレット分解では、この手法の作者はルジャンドルウェーブレット基底分解の固定行列を提案しています。3 つのFEB-fモジュールを使用して、それぞれ、結果として得られる高周波部分、低周波部分、ウェーブレット分解の残りの部分を処理します。各反復では、処理済みの高周波テンソル、処理済みの低周波テンソル、生の低周波テンソルが作成されます。これはトップダウンアプローチであり、分解ステップでは信号に係数1/2のギャップができます。3セットのFEB-fブロックは、異なる分解反復中に一緒に使用されます。ウェーブレット再構成に関しては、この手法の作者は出力テンソルも再帰的に作成します。

FEA-wには、FEB-wと同様に、分解ステージと再構成ステージが含まれています。ここで、FEDformerの作者は再構成ステージを変更していません。唯一の違いは分解ステージです。同じ行列を使用して、信号を Query、 Key 、Valueエンティティに分解します。上に示すように、FEB-wブロックには信号処理用の3つのFEB-fブロックが含まれています。FEB-f は、セルフアテンションメカニズムの代替として考えることができます。この方法の作者は、ウェーブレット分解を使用して周波数強化クロスアテンションを作成する簡単な方法を使用し、各FEB-f をFEA-fモジュールに置き換えます。さらに、最も粗い残基を処理するために、さらに1つのFEA-fモジュールを追加します。

トレンドコンポーネントと組み合わされた複雑な周期パターンが頻繁に観察されるため、固定ウィンドウ平均をマージするときに、実際のデータでトレンドを抽出することが困難な場合があります。この問題を克服するために、Mixture of Experts分解ブロック(MOEDecomp)が開発されました。このブロックには、元の信号から複数のトレンドコンポーネントを抽出するためのさまざまな平均サイズのフィルターセットと、それらを組み合わせて結果のトレンドを生成するためのデータ依存の重みのセットが含まれています。

FEDformer法の完全なアルゴリズムは、以下の著者のオリジナルの可視化で示されています。

2. MQL5での実装

私たちは提案されたFEDformer法の理論的側面を検討しましたが、私たちの実装は元のものとはかなり異なることを認めざるを得ません。提案されたアプローチを参考にしつつも、完全なアルゴリズムの実装には至っていません。この点については私の個人的な見解があります。

まず、どの基底を選択するかという問題があります。DFT（離散フーリエ変換）かDWT（離散ウェーブレット変換）を選ぶ必要があります。。この選択は非常に複雑で、あいまいさを伴います。しかし、ここではその背景を簡潔に説明します。元の論文で示されている方法のテスト結果を見てみましょう。

Exchange欄に注意してください。モデルが正確にどのデータでテストされたかについては詳しく述べませんが、DWT（離散ウェーブレット変換）を使用したモデルには明らかな優位性があります。これは、おそらく入力データに明確な周期性がないため、DFT（離散フーリエ変換）がトレンドの変化を適切に捉えられないからです。実際、この手法では入力データの時間的な要素が無視されています。対照的に、DWTは信号を時間と周波数の両方の次元で分析できるため、より正確な予測データを提供できます。この状況では、DWTを選択することが明らかだと思います。

2.1 DWTの実装

実装の基礎が決まったので、ライブラリにウェーブレット分解を追加してみましょう。新しいオブジェクト CNeuronLegendreWaveletsを作成します。

このオブジェクトのアーキテクチャについて考えてみましょう。前述のように、ウェーブレット分解には、ルジャンドルウェーブレット基底分解の固定行列を使用します。言い換えれば、信号を分解するためには、信号ベクトルにウェーブレット基底行列を掛けるだけで済みます。

入力データシーケンスでは、マルチモーダル時系列の複数の並列信号を分析する必要があります。各ユニタリ時系列には、同じ基底行列を使用します。

このプロセスは、複数のフィルタを使用した畳み込みに非常に似ています。ただし、ここではフィルタ行列の役割をウェーブレット基底行列が果たします。論理的には、畳み込み層の後継として新しいオブジェクトを作成することができます。適切に設計されたアプローチにより、継承されたメソッドを数個オーバーライドするだけで、最大限の効果を得ることができます。

class CNeuronLegendreWavelets :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; } 

public:
                     CNeuronLegendreWavelets(void) {};
                    ~CNeuronLegendreWavelets(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWavelets;   }
  };

新しいクラスCNeuronLegendreWaveletsの構造では、オーバーライドされたメソッドが3つあります。そのうちの1つは、クラス識別子Typeを定義済みの定数として返すものです。

2つ目のポイントは、基底ウェーブレットの固定行列を使用することです。このため、クラスにはトレーニング可能なパラメーターはなく、updateInputWeightsメソッドは「スタブ」として再定義されます。

実際には、クラスのオブジェクト初期化メソッドInitのみを使用する必要があります。このメソッドでは、ローカル変数やオブジェクトを宣言することなく、基底ウェーブレットの行列を入力するだけです。

この手法の作者は、ウェーブレットとしてルジャンドル多項式を使用することを提案しています。私は、以下に示す9つのルジャンドル多項式を選択しました。

ご覧のとおり、グラフに表示されている多項式を使用すると、かなり幅広い範囲の周波数を記述できます。

また、提示された多項式の値域が [0, 1] であることも注目すべきポイントです。これは非常に便利で、分析するシーケンスのウィンドウの長さを1と定義できます。この場合、範囲はシーケンス内の要素数で割ることにより、2つの隣接する要素間の時間ステップを固定ステップで形成することができます。ここでは、収集された初期データの時間枠は重要ではなく、元のシーケンスの可視ウィンドウ内で信号の周波数特徴を分析します。

モデル設計段階では、シーケンス内の要素数を決定するという課題に直面します。基底ウェーブレットの行列を作成する前に、その次元を指定する必要があります。この段階では、選択したフィルタの数しか決まっていません。分析するシーケンスのウィンドウサイズは、モデルを初期化する際にのみ判明します。この状況から抜け出すには、2つの選択肢があります。

基底ウェーブレットの行列の厳密な次元を決定し、その値をすぐに入力できます。また、行列の前に訓練可能な畳み込み層を使用すると、元のシーケンスの任意のサイズで作業できるようになります。
あらゆるサイズの初期データに対して、モデル初期化の段階で基底ウェーブレットの行列を埋めるための汎用アルゴリズムを作成します。

最初のオプションでは、利用可能なあらゆる方法で固定値で行列を埋めることができます。Web上で、関心のある基底ウェーブレットの係数を見つけることもできます。しかし、精度とパフォーマンスの間のこの「黄金比」をどのように決定するのでしょうか。さらに、予測精度の要件は、タスクによって大きく異なる場合があります。

私の意見では、2番目のオプションの方が目的に適しているようです。これを実装するには、選択した多項式の式をマクロ置換として作成します。以下にその一部を示します（完全なコードは添付ファイルで参照できます）。

#define Legendre4(x)    (70*pow(x,4) - 140*pow(x,3) + 90*pow(x,2) - 20*x + 1)
#define Legendre6(x)    (924*pow(x,6) - 2772*pow(x,5) + 3150*pow(x,4) - 1680*pow(x,3) + \
                         420*pow(x,2) - 42*x + 1)
#define Legendre8(x)    (12870*pow(x,8) - 51480*pow(x,7) + 84084*pow(x,6) - 72072*pow(x,5) + \
                         34650*pow(x,4) - 9240*pow(x,3) + 1260*pow(x,2) - 72*x + 1)

これらのマクロ置換を使用すると、任意の離散値に対する多項式の値を取得できます。準備作業が完了したら、新しいクラスCNeuronLegendreWavelets::Initのオブジェクトを初期化するアルゴリズムの説明に進むことができます。

メソッドのパラメータでは、オブジェクトアーキテクチャの主要なパラメータを渡します。

bool CNeuronLegendreWavelets::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                   uint window, uint step, uint units_count, 
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 9, units_count, 
                            optimization_type, batch))
      return false;

メソッドの本体では、まず親クラスの同じメソッドを呼び出します。

新しいクラスの初期化メソッドのパラメータでは、分析されるシーケンスのウィンドウサイズとシーケンス内の要素数のみを受け取ることに注意してください。親クラスの関連メソッドを呼び出すときに、ウィンドウステップとフィルタの数を追加する必要があります。フィルタの数については前に決定したので、9個になります。分析されるウィンドウのステップについては、分析されるウィンドウと同じになります。

親クラスのメソッドが正常に初期化されると、畳み込みパラメータ行列にランダムな値が設定されます。ただし、ウェーブレットの基本パラメータで設定する必要があります。そのため、最初に重み行列にゼロ値を設定します。これは、指定されたバイアスパラメータをリセットする必要があるため、非常に重要なポイントです。

   WeightsConv.BufferInit(WeightsConv.Total(), 0);

次に、ループ内で基底ウェーブレットの値で行列を埋めます。

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(i) / iWindow;
      if(!WeightsConv.Update(shift, Legendre4(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre6(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre8(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre10(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre12(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre16(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre18(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre20(k)))
         return false;
     }

埋められた行列をOpenCLコンテキストメモリに転送します。

   if(!!OpenCL)
      if(!WeightsConv.BufferWrite())
         return false;
//---
   return true;
  }

メソッドの実行を完了します。

この実装では、オブジェクトの正しい操作に必要な残りの機能をすべて親クラスから継承しました。したがって、このクラスでの作業を終了して次に進みます。

2.2 FED-wブロック

次の段階は、さらに一歩前進した段階と見なすことができます。FED-wブロックの独自のビジョンを作成します。その機能はCNeuronFEDWクラスに実装されています。このクラスの構造を以下に示します。

class CNeuronFEDW : public CNeuronBaseOCL
  {
protected:
   //---
   uint                    iWindow;
   uint                    iCount;
   //---
   CNeuronLegendreWavelets cWavlets;
   CNeuronBatchNormOCL     cNorm;
   CNeuronSoftMaxOCL       cSoftMax;
   CNeuronConvOCL          cFF[2];
   CNeuronBaseOCL          cReconstruct;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      Reconsruct(CBufferFloat* inputs, CBufferFloat *outputs);

public:
                     CNeuronFEDW(void) {};
                    ~CNeuronFEDW(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronFEDW; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

CNeuronFEDWクラスは、前のクラスと比べてより複雑なアーキテクチャを持っています。このクラスは、主要なパラメータを格納するために2つのローカル変数を宣言し、一連の内部静的オブジェクトを持っています。実装プロセス中にその目的を確認します。すべてのオブジェクトは静的に宣言されます。これにより、クラスのコンストラクタとデストラクタを空のままにすることができます。

すべてのネストされたオブジェクトの初期化は、CNeuronFEDW::Initメソッドで実行されます。オブジェクトアーキテクチャパラメータがメソッドに渡されます。これには、表示されるデータウィンドウのサイズ(window)や分析されるユニタリシーケンスの数(count)などの基本パラメータが含まれます。

bool CNeuronFEDW::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint count, 
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, 
                            optimization_type, batch))
      return false;

メソッドの本体では、まず親クラスの関連メソッドを呼び出します。その後、初期化されたオブジェクトのアーキテクチャパラメータをローカル変数に保存します。

   iWindow = window;
   iCount = count;

次に、内部オブジェクトを、使用される順序と同じ順序で初期化します。

当初は受信した生データから周波数特性を抽出する予定です。このため、上記で作成したCNeuronLegendreWaveletsクラスのインスタンスを使用します。

   if(!cWavlets.Init(0, 0, OpenCL, iWindow, iWindow, iCount, optimization, iBatch))
      return false;
   cWavlets.SetActivationFunction(None);

ここで作成しているFED-wブロックは、著者が提案した方法に比べて大幅に簡素化されています。私はDFTブロックを使用しないことにしました。時間コンポーネントから切り離した周波数分析は、私たちに不利に働き、予測の品質を低下させる可能性があるように思われます。したがって、DFTを使用することの妥当性については疑問があります。ただし、これは私の個人的な意見であり、誤りの可能性もあります。

さらに、かなり労働集約的なFFTプロセスを排除することで、モデルの訓練および操作中の計算リソースコストが大幅に削減されます。

そうは言っても、予測品質が低下するリスクを受け入れながら、モデルのパフォーマンス向上に取り組むことにしました。

まず、バッチ正規化層を使用して、ウェーブレット分解後に得られたデータを正規化します。

   if(!cNorm.Init(0, 1, OpenCL, 9 * iCount, 1000,optimization))
      return false;
   cNorm.SetActivationFunction(None);

次に、使用した各フィルタのシェアを評価します。これをおこなうには、SoftMax関数を使用して取得したデータを確率サブスペースに変換します。

   if(!cSoftMax.Init(0, 1, OpenCL, 9 * iCount, optimization, iBatch))
      return false;
   cSoftMax.SetHeads(iCount);
   cSoftMax.SetActivationFunction(None);

各ユニタリチャネルは個別に評価されます。

次に、ウェーブレット基底行列と逆畳み込みをおこなうことで、確率表現から元の時系列を再構築します。結果は、作成されたネストされた基底層に保存されます。

   if(!cReconstruct.Init(0, 2, OpenCL, iWindow, optimization, iBatch))
      return false;
   cReconstruct.SetActivationFunction(None);

上記の操作は、時系列 → ウェーブレット分解 → 正規化 → 確率表現 → 時系列という一種の循環を形成していることがわかります。ただし、出力で得られるのは、一種のデジタルフィルタを通過した入力時系列のかなり平滑化された表現です。その結果、バッチ正規化層にのみ存在する最小限の訓練可能なパラメータで、非常に効率的なデータフィルタリングが得られます。このブロックは、実装においてセルフアテンションに代わるものです。

ここで注目すべき重要な点は、モデルの訓練可能なパラメータを、定義済みのウェーブレットに置き換えるという点です。これにより、訓練可能なパラメータの「ブラックボックス」に比べてモデルが理解しやすくなりますが、柔軟性は低下します。また、これにより、特定の問題を解決するための最適なウェーブレットを見つけるという点で、モデルアーキテクトにさらなる負担がかかります。そのため、ウェーブレット多項式をマクロ置換の別のブロックに配置しました。このアプローチにより、さまざまなウェーブレットを試して最適なウェーブレットを見つけることができます。

さて、クラスの初期化メソッドに戻りましょう。デジタルフィルタブロックの次には、Transformerアーキテクチャで非常に一般的なFeedForwardブロックが続きます。ここでは、層間にLReLUを使用した変更のない2層MLPを使用します。以前と同様に、独立したチャネル処理を実装するには、畳み込み層オブジェクトを使用します。

   if(!cFF[0].Init(0, 3, OpenCL, iWindow, iWindow, 4 * iWindow, iCount, optimization, iBatch))
      return false;
   cFF[0].SetActivationFunction(LReLU);
   if(!cFF[1].Init(0, 4, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iCount, optimization, iBatch))
      return false;
   SetActivationFunction(None);

初期化メソッドの最後に、不要なデータコピー操作を最小限に抑えるために、誤差勾配バッファの置き換えを整理します。

   if(Gradient != cFF[1].getGradient())
      SetGradient(cFF[1].getGradient());
//---
   return true;
  }

オブジェクトの初期化作業が完了したら、提案されたモデルのフィードフォワードパスの実装に進みます。計画されたプロセスの説明から、得られた確率を時系列に逆畳み込みすることが重要なポイントとなります。

「逆畳み込み」は、一見新しい操作に感じられますが、実際は以前から実装してきたものです。この逆畳み込みにより、畳み込み層で誤差勾配を伝播できます。しかし今回は、この逆畳み込み処理をフィードフォワードパス内で実装する必要があります。

ここでの課題は、クラス内のすべてのメソッドが固定されたデータバッファのリストで動作する点です。固定バッファの使用により、モデル構築時に個別のデータバッファを明示的に考慮する必要がなくなります。オブジェクトへのポインタを提供すれば、必要なデータバッファはメソッド内で既に指定されているからです。しかしその「欠点」として、フィードフォワードパス内でアルゴリズムを実装する際に、通常のバックプロパゲーション手法が使えないという制約があります。そこで、新しいメソッドを作成し、以前作成したカーネルを用いて正しいバッファとパラメータを渡すという手法をとります。

これが私たちがやることです。CNeuronFEDW::Reconstructメソッドを作成し、そのパラメータで、取得した確率と再構築されたシーケンスのバッファへのポインタを渡します。

bool CNeuronFEDW::Reconsruct(CBufferFloat *sequence, CBufferFloat *probability)
  {
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = sequence.Total();

メソッド本体では、タスクスペースを定義し、必要なすべてのパラメータをカーネルに渡します。

   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_w, 
                                                                     cWavlets.GetWeightsConv().GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_g, probability.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_o, probability.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_ig, sequence.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_outputs, probability.Total()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_step, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_in, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_out, (int)9))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_activation, (int)None))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_shift_out, (int)0))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

その後、カーネルを実行キューに配置します。

   if(!OpenCL.Execute(def_k_CalcHiddenGradientConv, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

この時点で準備作業は完了し、クラスのフィードフォワードパスメソッドCNeuronFEDW::feedForwardの説明に進むことができます。いつものように、フィードフォワードメソッドのパラメータでは、必要な入力データを含むモデルの前の層のオブジェクトへのポインタを渡します。

bool CNeuronFEDW::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWavlets.FeedForward(NeuronOCL.AsObject()))
      return false;

このメソッドの本体では、まず、取得したシーケンスをその構成周波数特徴に分解します。これをおこなうには、ネストされたcWavlets オブジェクトのフィードフォワードパスメソッドを呼び出します。

次に、提案されたアルゴリズムに従って、取得したデータを正規化し、確率的サブスペースに変換します。

   if(!cNorm.FeedForward(cWavlets.AsObject()))
      return false;
   if(!cSoftMax.FeedForward(cNorm.AsObject()))
      return false;

次に、時間シーケンスを復元します。

   if(!Reconsruct(cReconstruct.getOutput(), cSoftMax.getOutput()))
      return false;

以降のアルゴリズムは、古典的なTransformerに似ています。入力と再構築された時間シーケンスを追加して正規化します。

   if(!SumAndNormilize(NeuronOCL.getOutput(), cReconstruct.getOutput(), cReconstruct.getOutput(),
                                                                        iWindow, true, 0, 0, 0, 1))
      return false;

FeedForwardブロックを通じてデータを伝播します。

   if(!cFF[0].FeedForward(cReconstruct.AsObject()))
      return false;
   if(!cFF[1].FeedForward(cFF[0].AsObject()))
      return false;

その後、2 つのデータフローからの時間シーケンスを再度合計して正規化します。

   if(!SumAndNormilize(cFF[1].getOutput(), cReconstruct.getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

フィードフォワードパスの準備ができたので、バックプロパゲーションパスメソッドの構築に進みます。まず、勾配誤差分散メソッドCNeuronFEDW::calcInputGradientsを作成します。

bool CNeuronFEDW::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

メソッド本体では、まずパラメータで受け取った前層のオブジェクトへのポインタの正しさをチェックします。正しいポインタがなければ、メソッドの操作を実行しても意味がありません。

ご存知のとおり、誤差勾配データバッファはクラス初期化メソッドで置き換えました。これで、FeedForwardブロックの操作にすぐに進むことができます。

   if(!cFF[0].calcHiddenGradients(cFF[1].AsObject()))
      return false;
   if(!cReconstruct.calcHiddenGradients(cFF[0].AsObject()))
      return false;

フィードフォワードパスのデータフローと同様に、バックプロパゲーションパスでも誤差勾配を2つの並列データフローに分散します。この段階で、両方のフローの誤差勾配を合計します。

   if(!SumAndNormilize(Gradient, cReconstruct.getGradient(), cReconstruct.getGradient(), iWindow, false))
      return false;

次に、逆畳み込み演算を通じて誤差勾配を伝播する必要があります。明らかに、これは単純な畳み込み演算です。ただし、問題が1つあります。畳み込み層のフィードフォワードメソッドは、誤差勾配バッファーでは機能しません。今回は、ちょっとしたトリックを使用します。つまり、層の結果バッファを、その勾配のバッファに一時的に置き換えます。この場合、最初に置き換えたデータバッファーへのポインタを保存します。

   CBufferFloat *temp_r = cReconstruct.getOutput();
   if(!cReconstruct.SetOutput(cReconstruct.getGradient(), false))
      return false;
   CBufferFloat *temp_w = cWavlets.getOutput();
   if(!cWavlets.SetOutput(cSoftMax.getGradient(), false))
      return false;

畳み込み層のフィードフォワードパスを実行してみましょう。

   if(!cWavlets.FeedForward(cReconstruct.AsObject()))
      return false;

データバッファを元の位置に戻します。

   if(!cWavlets.SetOutput(temp_w, false))
      return false;
   if(!cReconstruct.SetOutput(temp_r, false))
      return false;

次に、誤差勾配を前層に伝播します。

   if(!cNorm.calcHiddenGradients(cSoftMax.AsObject()))
      return false;
   if(!cWavlets.calcHiddenGradients(cNorm.AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(cWavlets.AsObject()))
      return false;

2 つのデータフローからの誤差勾配を合計します。

   if(!SumAndNormilize(NeuronOCL.getGradient(), cReconstruct.getGradient(), NeuronOCL.getGradient(),
                                                                            iWindow, false))
      return false;
//---
   return true;
  }

操作の実行を制御することを忘れないでください。そしてメソッドを完了します。

モデルのすべての要素への誤差勾配伝播の後に、モデルの訓練可能なパラメータが最適化されます。オブジェクトパラメータの最適化機能は、CNeuronFEDW::updateInputWeightsメソッドに実装されています。このメソッドのアルゴリズムは非常に単純で、ネストされたオブジェクトの同じ名前のメソッドを呼び出して、呼び出されたメソッドの論理結果によって結果を確認するだけです。

bool CNeuronFEDW::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFF[0].UpdateInputWeights(cReconstruct.AsObject()))
      return false;
   if(!cFF[1].UpdateInputWeights(cFF[0].AsObject()))
      return false;
   if(!cNorm.UpdateInputWeights(cWavlets.AsObject()))
      return false;
//---
   return true;
  }

このメソッドでは、訓練可能なパラメータを含むオブジェクトのみを処理することに注意してください。

これで、新しいクラスメソッドを構築するためのアルゴリズムの考察は終了です。説明したクラスとそのすべてのメソッドの完全なコードは添付ファイルにあります。添付ファイルには、記事で使用されているすべてのプログラムの完全なコードも含まれています。

提案された FEDformerアルゴリズムの状態エンコーダーの独自のビジョンのみを作成したことに注意してください。ただし、デコーダーは完全に省略しています。これは、利益を生み出す取引戦略を生成するというタスクに対する原則的なアプローチのために意図的におこなわれています。奇妙に思えるかもしれませんが、環境のその後の状態を可能な限り正確に予測しようとはしていません。これらの状態は、エージェントの動作に間接的にのみ影響します。その後の状態のルールを含む明確なアルゴリズムを構築する場合は、今後の価格変動を最も正確に予測する必要があります。ただし、エージェントの方策は別の方法で構築します。

最も有益なエンコーダーの隠れ状態を取得するために、エンコーダーを訓練して環境の将来の状態を予測します。次に、Actorは、本質的にActorの不可欠な部分であるエンコーダーの隠れ状態を抽出し、環境の現在の状態を分析します。次に、Actorの環境の現在の状態の分析に基づいて、独自の方策を構築します。

ここで理解する必要がある微妙な境界線があります。したがって、環境の将来の状態を最も正確に予測するために、エンコーダーの隠れた状態を分解することに過度のリソースを費やすことはありません。

2.3 モデルアーキテクチャ

モデルの構成要素となるオブジェクトを構築した後、モデル全体のアーキテクチャの説明に移ります。この作業では、一見まったく異なるアプローチを組み合わせることにしました。競合していると言ってもいいでしょう。前回の記事で検討したTiDE法を使用する前に、主な入力データ処理に時系列のウェーブレット分解を利用するという提案されたアプローチを採用しました。したがって、この変更はCreateEncoderDescriptionsメソッドにおける環境状態エンコーダーのアーキテクチャに影響を及ぼします。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

メソッドの本体では、通常どおり、まず、モデルアーキテクチャを記録するための動的配列への受信したポインタの関連性を確認し、必要に応じて新しいオブジェクトのインスタンスを作成します。

入力データを取得するには、基本的な全結合ニューラル層オブジェクトを使用します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

モデルは、いつものように「生の」入力データを受け取ります。バッチデータ正規化層でデータを前処理します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 10000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、入力データを転置して、後続の操作で使用される指標のユニタリシーケンスの独立した分析を実行します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、10個のFED-w層のブロックを使用します。

//--- layer 3-12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFEDW;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.activation = None;
   for(int i = 0; i < 10; i++)
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

その直後に、全結合の時系列エンコーダーを追加します。

//--- layer 13
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTiDEOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.window_out = NForecast;
   descr.step = 4;
     {
      int windows[] = {HistoryBars, 2 * EmbeddingSize, EmbeddingSize, 2 * EmbeddingSize, NForecast};
      if(ArrayCopy(descr.windows, windows) <= 0)
         return false;
     }
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、前と同様に、畳み込み層を使用して予測値のバイアスを修正します。

//--- layer 14
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.step = NForecast;
   descr.window_out = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

予測値を入力データの表現に転置します。

//--- layer 15
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

入力時間シーケンスの統計パラメータを返します。

//--- layer 16
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ご覧のとおり、変更はエンコーダーの内部アーキテクチャにのみ影響します。したがって、データを抽出するには、エンコーダーの潜在状態層へのポインタを変更するだけで済みます。ActorおよびCriticアーキテクチャは変更されません。

#define        LatentLayer             14

さらに、環境相互作用EAやモデル訓練EAに変更を加える必要もありません。完全なコードは添付ファイルにあります。アルゴリズムの説明については前回の記事を参照してください。

3. テスト

この記事では、時系列分析を周波数特性の領域に変換するFEDformer法について説明しました。この手法は非常に興味深く、将来性があります。MQL5 を用いて提案されたアプローチを実装するために、かなりの作業をおこなってきました。

再度申し上げますが、この記事は提案されたアプローチに関する私自身の見解を提示したものであり、元の論文で説明されている方法とはかなり異なる点があることに留意してください。したがって、モデルテスト結果から得られた結論はこの実装にのみ適用され、元の方法にそのまま当てはめることはできません。

前述のとおり、変更はエンコーダーの内部アーキテクチャにのみ影響しました。これにより、以前に収集した訓練データセットを使用してモデルを訓練できるようになりました。

オフラインモデル訓練では、環境との相互作用から事前に収集された軌跡を使用することを思い出してください。このデータセットは、2023年全体の実際の履歴データに基づいています。訓練銘柄はH1時間枠のEURUSDです。訓練済みモデルをMetaTrader 5ストラテジーテスターでテストするために、2023年1月の履歴データを使用します。

最初のステップでは、後続の環境状態を記述する実際のメトリックとその予測値の間の誤差を最小化することで、環境状態エンコーダーを訓練します。エンコーダーは、エージェントの行動に依存しない環境状態のみを分析および予測します。そのため、訓練データセットを更新せずに、エンコーダーの完全な訓練を実行します。

私の主観的な意見では、この段階において、後続の環境状態を予測する精度が向上していると感じています。これは、訓練プロセスで誤差が減少していることからも証明されています。しかし、実際の値と予測値のグラフ比較による詳細な品質分析はおこなっていません。

2番目の反復段階では、Criticのモデル訓練と並行してActorの方策を訓練します。これにより、Actorの行動の最も高い確率での評価が得られます。この段階では、Actorの行動評価の精度が非常に重要です。そのため、現在のActor方策を考慮しながら、モデル訓練と訓練データセットの更新プロセスを交互におこないます。

上記の反復を複数回繰り返した結果、訓練期間とテスト期間の両方で利益を生み出すActorの動作方策を訓練することができました。テスト結果を以下に示します。

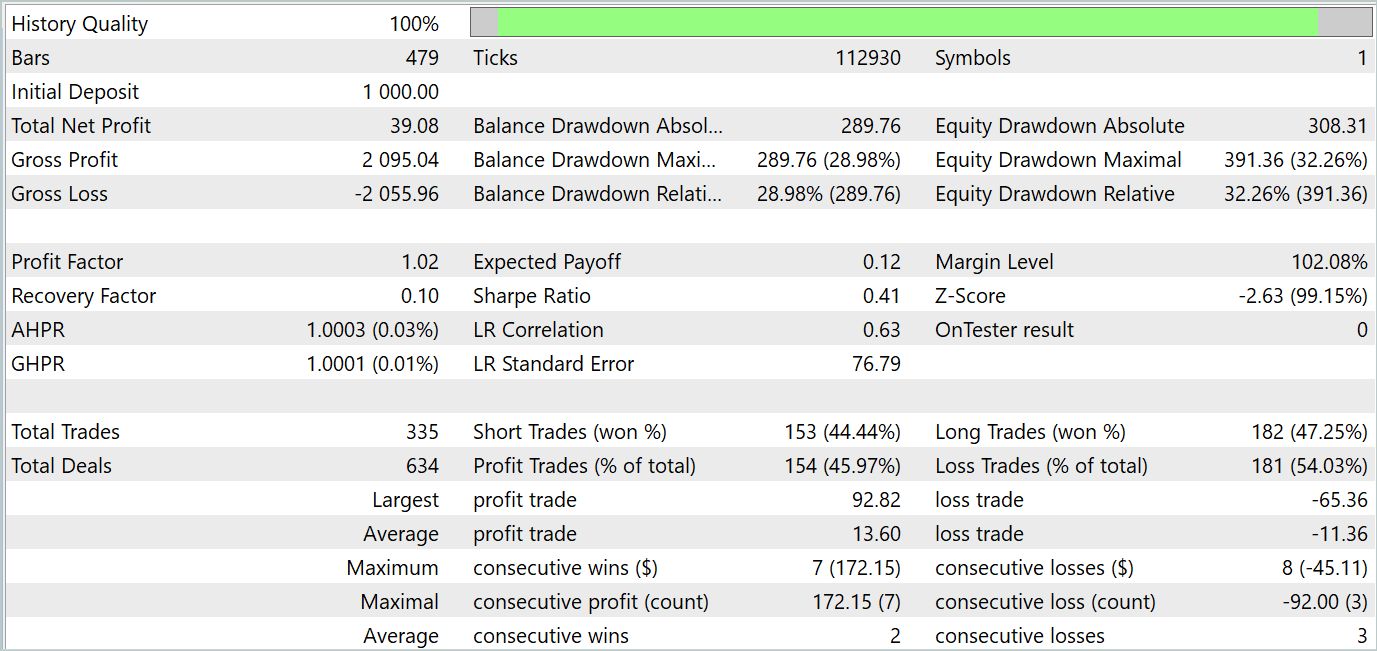
ご覧のとおり、バランスグラフは全体的に上昇傾向を維持しています。同時に、チャート上では4つのトレンドが明確に識別できます。そのうち2つは収益性が高く、残り2つは収益性が低いトレンドです。ポジティブな点としては、収益性の高いトレンドの方が可能性が高いということです。これにより、損失期間中に資金を失うことなく、十分な利益を蓄積できるようになっています。ただし、バランスの調整は非常に繊細です。テスト期間中の利益率はわずか1.02で、収益性の高い取引の割合は46％をわずかに下回りました。

全体として、このモデルは可能性を示していますが、損失期間を最小限に抑えるためにさらなる調整が必要です。

結論

この記事では、長期時系列予測を目的とした提案手法であるFEDformer法について説明しました。この方法には、分布シフトを制御するための低ランク周波数近似と混合分解を用いた注意メカニズムが含まれています。

実践部分では、MQL5を使用して提案されたアプローチのビジョンを実装し、実際の履歴データを用いてモデルの訓練とテストをおこないました。テスト結果から、このモデルには大きな可能性があることが確認できましたが、同時に、追加の注意が必要な点も見受けられました。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコード訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14858

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1188.36 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークの実践：直線関数

この記事では、データベース内のデータを表現できる関数を取得するためのいくつかの方法について簡単に説明します。統計や確率の研究を用いて結果を解釈する方法については詳細に触れません。この問題の数学的側面について深く知りたい方にお任せします。これらの問いを検討することは、ニューラルネットワークの研究において非常に重要です。ここでは、このテーマを冷静に掘り下げていきます。

リプレイシステムの開発（第50回）：物事は複雑になる(II)

チャートIDの問題を解決すると同時に、ユーザーが希望する資産の分析とシミュレーションに個人用テンプレートを使用できるようにする機能を提供し始めます。ここで提示される資料は教育目的のみであり、提示される概念の学習および習得以外の目的には決して適用されないものとします。

多通貨エキスパートアドバイザーの開発（第12回）：プロップトレーディングレベルのリスクマネージャーの育成

開発中のEAには、ドローダウンを制御するための特定のメカニズムがすでに備わっています。しかし、これは過去の価格データに対するテストの結果に基づいているため、本質的には確率的です。したがって、ドローダウンは最大予想値を超える場合があります (ただし、確率は小さいです)。指定されたドローダウンレベルへの準拠を保証するメカニズムを追加してみましょう。

リプレイシステムの開発（第49回）：物事は複雑になる(I)

この記事では、物事は少し複雑になります。前回の記事で紹介した内容を使用して、ユーザーが独自のテンプレートを使用できるようにテンプレートファイルを開きます。ただし、MetaTrader 5の負荷を軽減するために指標を改良していく予定なので、変更は徐々におこなっていく予定です。