ニューラルネットワークの実践：擬似逆行列（I）

はじめに

ニューラルネットワークに関する新しい記事へようこそ。

前回の記事「ニューラルネットワークの実践：直線関数」では、代数方程式を使用して探している情報の一部をどのように特定するかについて話しました。これは、特定のケースで方程式を定式化するために必要であり、今回は小規模なデータセットが実際に直線として表現できるため、直線の方程式を用いることになります。ニューラルネットワークの仕組みを説明する資料は多くありますが、それぞれの読者が持つ数学の知識レベルを理解しない限り、内容を適切に提示するのは容易ではありません。

インターネット上には、「独自のニューラルネットワークを開発できる」と謳うライブラリが多数存在します。それを考えれば、このプロセスが非常にシンプルで簡単だと思う人もいるかもしれません。しかし、実際はそれほど単純ではありません。

誤った期待を抱かせたくありません。知識や経験がほとんどなくても、ニューラルネットワークや人工知能を使って市場で取引をおこない、お金を稼げるような実用的なものを簡単に作れるとは言いません。もし誰かがそう主張するなら、それは間違いなく嘘です。

最も基本的なニューラルネットワークを作るだけでも、多くの場合困難を伴います。ここでは、このテーマをさらに深く探求するきっかけとなるようなプロジェクトの作り方をお伝えします。ニューラルネットワークは、少なくとも数十年にわたり研究が続けられてきた分野です。これまでの人工知能に関する3つの記事でも述べたように、このテーマは多くの人が想像する以上に複雑です。

特定の関数を使用することが、ニューラルネットワークの性能を向上または低下させることを直接意味するわけではありません。それは単に、その関数を使って計算をおこなうということに過ぎません。この点は、今日の記事の内容とも関連しています。

ニューラルネットワークに関するこの連載の最初の3つの記事と比較すると、今日の記事を読んだ後、自分には無理だと感じるかもしれません。しかし、それで諦めるべきではありません。同じ記事が、この分野をさらに深く掘り下げるきっかけになる可能性もあるからです。この記事では、純粋なMQL5を使って擬似逆計算を実装する方法について解説します。一見するとそれほど難しくないように思えるかもしれませんが、今日のコードは初心者にとって、私たちが望むよりもかなり難しいものになると思います。それでも怖がらず、落ち着いてじっくりとコードを研究してください。急ぐ必要はありません。私自身、できる限りシンプルなコードを書くよう努めました。そのため、効率的かつ迅速に動作するようには設計されていません。むしろ、教育的な価値を重視しています。ただし、行列分解を使用するため、コード自体は多くの人が普段目にするものや、書き慣れているものより少し複雑になっています。

念のため先に言っておきますが、MQL5にはこの記事で説明する内容と全く同じことをおこなう「PInv」という関数があることを知っています。また、MQL5には行列操作用の関数も用意されています。しかし、ここではMQL5で定義されている行列を使って計算をおこなうのではなく、類似しているもののメモリ内の要素へのアクセス方法がやや異なる配列を使用します。

擬似逆行列

この計算を実装することは、開発者にとって全てが明確である限り、最も難しいタスクの1つではありません。基本的には、1つの行列を使っていくつかの乗算やその他の簡単な操作をおこなうだけです。その出力は、擬似逆行列の内部因数分解すべての結果である行列となります。

ここで、ある点を明確にする必要があります。擬似逆行列は2つの方法で因数分解できます。1つ目の方法では、行列内の値をそのまま扱い、もう1つの方法では行列内の要素に最小制限値が適用されます。この最小制限値を下回る場合、その要素の値はゼロとなります。この条件は私自身が課したものではなく、擬似逆行列を計算するすべてのプログラムで採用されている計算モデルのルールによるものです。それぞれのケースには非常に特定の目的があります。したがって、ここで扱うのは擬似逆行列の最終的な計算ではありません。ここでは、MatLabやSciLabなど、擬似逆行列を実装するプログラムによって得られる結果に類似した結果を得るための計算をおこないます。

MQL5には擬似逆行列を計算する関数が組み込まれているため、ここで作成するアプリケーションを使用して得られた結果を、MQL5ライブラリの擬似逆行列関数を用いて得られた結果と比較することができます。これは、すべてが正しく動作しているか確認するために重要です。そのため、この記事の目的は単に擬似逆行列の計算を実装することではなく、その背後にある仕組みを理解することにあります。この知識は、ニューラルネットワークにおいて特定の方法をなぜ、いつ使うべきかを理解する上で重要です。

では、MQL5ライブラリの擬似逆行列関数を使用する最も簡単なコードを実装することから始めましょう。これは、後で作成する計算が正しく動作することを確認するための最初のステップです。事前にコードを確認せずに変更を加えないでください。ここで何かを変更すると、この記事で示されている結果と異なる結果になる可能性があります。まず、これからお見せするコードを試してみてください。その後で（必要があれば）、コードがどのように動作しているかをより深く理解するために修正を加えますが、必ず元のバージョンをテストしてからおこなってください。

この記事に添付されたファイルから元のコードを入手できます。それでは最初のコードを見てみましょう。以下が完全なコードです。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart()
05. {
06.     matrix M_A {{1, -100}, {1, -80}, {1, 30}, {1, 100}};
07. 
08.     Print("Moore–Penrose inverse of :");
09.     Print(M_A);
10.     Print("is :");
11.     Print(M_A.PInv());
12. }
13. //+------------------------------------------------------------------+

コード実行の結果は以下の画像に示されています。

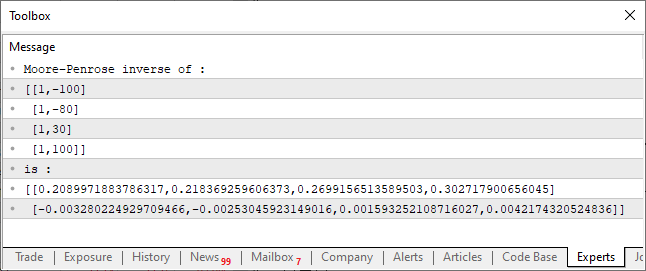
上記の非常にシンプルなコードは、行列の擬似逆行列を計算することができます。その結果は図に示されているようにコンソールに表示されます。すべてが非常に簡単です。ただし、コードの構築には注意が必要です。これは、コード作成における非常に重要なポイントの1つです。行列とベクトルを使用することで、多様で機能的な操作を実現できます。これらの操作は、標準のMQL5ライブラリに含まれており、他の言語の標準ライブラリにも組み込むことが可能です。

これは非常に便利な機能ですが、時にはコードを特定の方法で実行する必要がある場合や、そうしたい場合があります。その理由は、最適化したいからかもしれませんし、単に他の方法で実行可能なコードを生成したくないからかもしれません。結局のところ、その理由自体はそれほど重要ではありません。C/C++プログラマーが車輪の再発明を好むと言われることがありますが、私たちの場合はそうではありません。この記事では、複雑な計算の背後にある仕組みを一緒に探っていきます。結果を見ることはできますが、それがどのようにして達成されたのかまったく分からないことがあります。この結果が他の何かではなく、正確にどこから導き出されたのかを理解していない研究は、本当の研究とは言えず、ただの信仰に過ぎません。つまり、それを見て信じるしかないが、それが真実かどうか分からない、という状態です。しかし、本物のプログラマーは盲目的に信頼することはできません。自分が作ったものを本当に信じるためには、直接触れたり、見たり、味わったり、体験したりする必要があります。それでは、図に示された結果がどのようにして得られたのかを確認してみましょう。そのために、新しいトピックに移りましょう。

擬似逆行列の背後にある計算について

結果を見るだけでどのように達成されたかを知らなくても満足できるのであれば、それは素晴らしいことです。その場合、このトピックはもはやあなたにとって必要ではなく、これ以上読むことで時間を浪費するべきではありません。しかし、計算の仕組みを理解したいと考えているのであれば、しっかりと準備をしてください。プロセスをできる限り簡単に説明するよう努めますが、それでも注意深く読む必要があります。複雑な数式の使用はできるだけ避けますが、作成するコードは実際よりもずっと複雑に見える可能性があるため、慎重に進めることが重要です。まず次のことから始めましょう:。擬似逆行列は基本的に、行列の乗算と逆行列を使用して計算されます。

この乗算自体は非常に単純です。多くの人がこの目的のために何らかのリソースを利用していますが、個人的にはそれらを不要だと考えています。行列に関する以前の記事では、乗算を実行する方法について説明しましたが、その方法は非常に特定のシナリオを対象としたものでした。しかし今回は、少し汎用性の高い方法が必要です。なぜなら、ここで扱う計算は、行列に関する記事で取り上げたものとはいくつか異なる部分があるからです。

わかりやすく説明するために、コードを小さな部分に分け、それぞれ具体的な内容を解説します。まずは、以下に示す行列の乗算から始めましょう。

01. //+------------------------------------------------------------------+
02. void Generic_Matrix_A_x_B(const double &A[], const uint A_Row, const double &B[], const uint B_Line, double &R[], uint &R_Row)
03. {
04.     uint A_Line = (uint)(A.Size() / A_Row),
05.          B_Row  = (uint)(B.Size() / B_Line);
06. 
07.     if (A_Row != B_Line)
08.     {
09.         Print("Operation cannot be performed because the number of rows is different from that of columns...");
10.         B_Row = (uint)(1 / MathAbs(0));
11.     }
12.     if (!ArrayIsDynamic(R))
13.     {
14.         Print("Response array must be of the dynamic type...");
15.         B_Row = (uint)(1 / MathAbs(0));
16.     }
17.     ArrayResize(R, A_Line * (R_Row = B_Row));
18.     ZeroMemory(R);
19.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == B_Row ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
20.         for (uint c = 0; c < A_Row; c++)
21.             R[cp] += (A[Ai + c] * B[Bi + (c * B_Row)]);
22. }
23. //+------------------------------------------------------------------+

このコードを見ると、すでに混乱してしまうかもしれません。まるで世界の終わりが近づいているかのように恐怖を感じる人もいるかもしれません。神にすべての罪の赦しを願いたいと思う人もいるかもしれません。冗談はさておき、このコードは、一見変わったり非常に複雑に見えても、非常にシンプルです。

非常に圧縮されており、一度に多くのことが起こっているように見えるため、難しいと感じるかもしれません。初心者の方には申し訳ありませんが、私の記事を読んでいる方は、すでに私のコードスタイルをご存知だと思いますので、これが私の典型的なスタイルだと感じていただけると思います。さて、ここで何が起こっているのかを見ていきましょう。先ほど示したコードとは異なり、このコードは汎用的で、2つの行列を乗算できるかどうかをチェックするテストも含まれています。これには非常に便利ですが、私たちにとってはあまり便利ではないかもしれません。

2行目にはプロシージャの宣言があります。パラメータを適切な位置で宣言し、渡すように注意しなければなりません。次に、行列Aに行列Bを掛け、その結果を行列Rに配置します。行列Aの列数と行列Bの行数を指定する必要があります。最後の引数は、行列Rの列数を返します。R行列の列数を返す理由については後で説明するので、今は気にしないでください。

問題ありません。4行目と5行目では、残りの値を計算して手動で指定しなくても済むようにします。次に、7行目では、行列が乗算できるかどうかを確認するためにテストをおこないます。つまり、行列を渡す順序が重要になるということです。これがスカラー計算のコードとは異なる点です。行列計算では細心の注意を払う必要があります。

乗算が失敗した場合、9行目でMetaTrader 5コンソールにメッセージが出力されます。その直後に10行目で実行時エラーがスローされ、行列乗算を実行しようとしているアプリケーションが終了します。このエラーがコンソールに表示された場合、9行目にもメッセージが表示されているかどうかを確認する必要があります。この場合、エラーは問題のコードフラグメントにあるのではなく、このコードが呼び出されるポイントにあります。実行時エラーでアプリケーションを強制終了させるのはエレガントとは言えませんが、この方法で誤った結果が表示されるのを防ぐことができます。

ここからは、多くの人が怖くなる部分です。17行目で、出力全体を保存するためのメモリを割り当てます。したがって、行列Rは呼び出し元で動的に作成される必要があります。静的配列を使用すると、12行目で検出され、コードは実行時エラーで終了し、14行目にその理由を示すメッセージが表示されます。

エラー生成方法の一つとして、実行時にゼロ除算を試みることで、プロセッサが内部割り込みをトリガーし、オペレーティングシステムが割り込みの原因となったアプリケーションに対してアクションを実行し、強制的に終了させることになります。オペレーティングシステムが何もしなくても、プロセッサが割り込みモードに入り、組み込みシステムであってもアプリケーションが終了します。

注目すべき点は、コンパイラが実行時エラーを検出しないようにするトリックを使用していることです。これが異なる方法でおこなわれた場合、通常はコンパイルエラーが発生しますが、この方法ならコンパイルを成功させることができます。強制終了が必要な場合は、この方法を使用することができますが、エレガントではないため、ユーザーがあなたのアプリケーションやプログラムに不満を持つかもしれません。そのため、この方法は慎重に使用するべきです。

18行目では、動的に割り当てたメモリ内のすべてを完全にクリアします。通常、コンパイラが自動的にクリーンアップを行いますが、MQL5でのプログラミングを長時間行った結果、動的に割り当てられたメモリが自動的にクリーンアップされないことに気づきました。MetaTrader 5では、動的メモリがインジケーターバッファとして使用されることを意図しており、これらのバッファはデータの受信や計算時に更新されるため、メモリをクリーンアップしても意味がないと考えられます。さらに、クリーンアップに時間がかかるため、他の作業に充てた方が効率的です。そのため、メモリのクリーンアップは手動でおこない、不要な値を計算で使用していないことを確認する必要があります。動的メモリを使用し、インジケーターバッファとして使わない場合は、この点に注意してください。

次に、最も興味深い部分に進みます。行列Aと行列Bを掛け、その結果を行列Rに格納します。この操作は2行で行われます。19行目は一見複雑に見えますが、細かく分解してみると理解しやすくなります。目的は、2つの行列の乗算を完全に動的で普遍的にすることです。つまり、行や列の数が異なっていても、手順がこの時点に達すれば、行列の乗算は成功します。

行列の順番が結果に影響するように、19行目での演算順序も結果に影響を与えます。長くなりすぎないように説明を簡略化します。コードをそのまま、つまり左から右へ読んでいくと、何がおこなわれているのかが分かります。コンパイラが実行可能ファイルを作成する際に、こうした処理が行われるため、コードが混乱して見えるかもしれませんが、実際には簡潔で、通常使われる方法とは少し異なります。行列Aの列ごとに読み取り、行列Bの行ごとに読み取って掛け算をおこなう仕組みです。このように、係数の順番が結果に影響を与えることになります。行列Bがどのように構成されているか（行や列）は気にする必要はありません。行列Aと同じ構成にしておけば、この乗算手順はうまくいきます。

擬似逆行列を計算するために必要な最初のステップが完了しました。次に、どのような計算を行うべきかを確認して、擬似逆行列の値を求めるために必要な処理を見ていきます。乗算の場合のような一般解は必要ないかもしれませんが、擬似逆数の値を決定するのに役立つ、より具体的なものが必要になる場合があります。

擬似逆行列を計算する式を以下に示します。

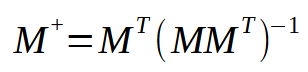
この式では、Mは使用される行列を表します。常に同じものであることに注意してください。しかし、この式を見ると、元の行列と転置行列との間で乗算を行う必要があることがわかります。次に、その結果を使って逆行列を計算します。そして最後に、転置行列に逆行列の結果を掛けます。簡単そうに聞こえませんか。ここでいくつかのショートカットを作成することができます。もちろん、完璧なショートカットを作成するためには、疑似逆行列を計算する専用の手順を作成する必要があります。しかし、そのような手順を作るのは難しくないものの、それがどのように機能するのかを説明するのはかなり難しくなります。私が言いたいことをよりよく理解するために、次のように進めましょう。転置行列と元の行列の乗算をひとつの手順にまとめます。大学でこの問題を学ぶ際には、通常、2つのブロックに分けて計算するよう求められます。すなわち、まず転置行列を作成し、その後に乗算手順を使って最終的な結果を得る方法です。しかし、これらの2つのステップを省略して、ひとつのステップで実行する方法を作成することも可能です。これは非常に簡単に実装できますが、そのコードを理解するのは難しいかもしれません。

さて、上記の画像にある括弧内の操作を、以下のコードでどのように実行するか見てみましょう。

01. //+------------------------------------------------------------------+
02. void Matrix_A_x_Transposed(const double &A[], const uint A_Row, double &R[], uint &R_Row)
03. {
04.     uint BL = (uint)(A.Size() / A_Row);
05.     if (!ArrayIsDynamic(R))
06.     {
07.         Print("Response array must be of the dynamic type...");
08.         BL = (uint)(1 / MathAbs(0));
09.     }
10.     ArrayResize(R, (uint) MathPow(R_Row = (uint)(A.Size() / A_Row), 2));
11.     ZeroMemory(R);
12.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == BL ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
13.         for (uint c = 0; c < A_Row; c++)
14.             R[cp] += (A[c + Ai] * A[c + (Bi * A_Row)]);
15. }
16. //+------------------------------------------------------------------+

このコードは前のコードと非常によく似ていますが、結果を生成する行が2つのコードでわずかに異なる点に注意してください。しかし、このスニペットは、元の行列に転置行列を乗算するために必要な計算を実行できるため、転置行列を作成する手間が省けます。このような最適化を実装することができます。もちろん、この同じ手順でさらに多くの機能を組み込むこともできます。たとえば、逆行列を生成したり、逆行列と入力行列の転置を掛け算したりすることも可能です。しかし、すでに想像がつくかもしれませんが、これらの各ステップは、手順全体ではなく局所的に複雑化します。だからこそ、何が起こっているのかを理解できるように、少しずつ紹介することを好みます。実際に概念を試してみることもできます。

ただし、車輪の再発明は避けたいので、すべてを1つの関数にまとめることはしません。この部分を示したのは、学校で学んだことが必ずしも実際の応用に役立つわけではないことを理解してもらいたいためです。多くの場合、プロセスは特定の問題を解決するために最適化されており、その最適化により、より一般的なプロセスを使う場合よりも、はるかに速く問題を解決できます。

次に、次のことをおこないます。すでに掛け算の計算はおこなっていますが、次に必要なのは、結果の行列の逆行列を生成する計算です。逆行列をプログラムする方法はいくつかあります。数学的な表現方法は限られていますが、プログラミング方法によっては、あるアルゴリズムが他のものより速く動作することがあります。しかし、私たちが本当に重要視しているのは正しい結果を得ることであり、それをどのように生成するかはそれほど重要ではありません。

行列の逆行列を計算するには、行列の行列式を使用する特別な方法を好んで使います。別の方法で行列式を求めることも可能ですが、私は習慣的にSARRUS法を使うことを好みます。これがプログラミング的に簡単だからです。Sarrus法についてよく知らない方のために説明します。Sarrus法は、対角線の値に基づいて行列式を計算する方法です。これをプログラミングするのは非常に興味深い作業です。以下のスニペットに、これを実行するための方法の1つを示します。正方行列であれば、どんな行列（配列）でも機能します。

01. //+------------------------------------------------------------------+
02. double Determinant(const double &A[])
03. {
04. #define def_Diagonal(a, b)  {                                                                                                                       \
05.                 Tmp = 1;                                                                                                                            \
06.                 for (uint cp = a, cc = (a == 0 ? 0 : cp - 1), ct = 0; (a ? cp > 0 : cp < A_Row); cc = (a ? (--cp) - 1 : ++cp), ct = 0, Tmp = 1)     \
07.                 {                                                                                                                                   \
08.                     do {                                                                                                                            \
09.                         for (; (ct < A_Row); cc += b, ct++)                                                                                         \
10.                             if ((cc / A_Row) != ct) break; else Tmp *= A[cc];                                                                       \
11.                         cc = (a ? cc + A_Row : cc - A_Row);                                                                                         \
12.                     }while (ct < A_Row);                                                                                                            \
13.                     Result +=  (Tmp * (a ? -1 : 1));                                                                                                \
14.                 }                                                                                                                                   \
15.                             }
16. 
17.     uint A_Row, A_Size = A.Size();
18.     double Result, Tmp;
19. 
20.     if (A_Size == 1)
21.         return A[0];
22.     Tmp = MathSqrt(A_Size);
23.     A_Row = (uint)MathFloor(Tmp);
24.     if ((A_Row != (uint)MathCeil(Tmp)) || (!A_Size))
25.     {
26.         Print("The matrix needs to be square");
27.         A_Row = (uint)(1 / MathAbs(0));
28.     }
29.     if (A_Row == 2)
30.         return (A[0] * A[3]) - (A[1] * A[2]);
31.     Result = 0;
32. 
33.     def_Diagonal(0, A_Row + 1);
34.     def_Diagonal(A_Row, A_Row - 1);
35. 
36.     return Result;
37. 
38. #undef def_Diagonal
39. }
40. //+------------------------------------------------------------------+

ここで見られるこの美しい断片は、行列の行列式の値を求めることに成功しています。ここでは、コードの説明がまったく必要ないほど素晴らしいことがおこなわれています。

4行目にはマクロが定義されています。このマクロは、配列、またはこの場合配列内の配列を斜めに走査することができます。まさにその通りです。このコードの背後にある数学により、主対角線の方向と副対角線の方向の両方で、対角線の値を1つずつ計算し、すべてをエレガントかつ効率的におこなうことができます。コードで指定する必要があるのは、行列を含む配列だけであることに注意してください。返される値はその行列の行列式です。ただし、このコードで実装されているSarrus法にはいくつかの制限があります。もし行列の次元が1x1であれば、行列式はその行列自体となり、21行目に示すようにすぐに返されます。もし配列が空であるか、正方行列でない場合、27行目でRUN-TIMEエラーがスローされ、その後コードは実行されません。行列のサイズが2x2の場合、対角線の計算はマクロを通さず、30行目で直接計算されます。それ以外のサイズの場合、行列式の計算はマクロを使って行われます。まず、33行目で主対角線が計算され、次に34行目で副対角線が計算されます。何が起こっているのか分からない場合は、以下の図を参照してください。これはSARRUS法に詳しくない方のために、すべてをわかりやすく示したものです。

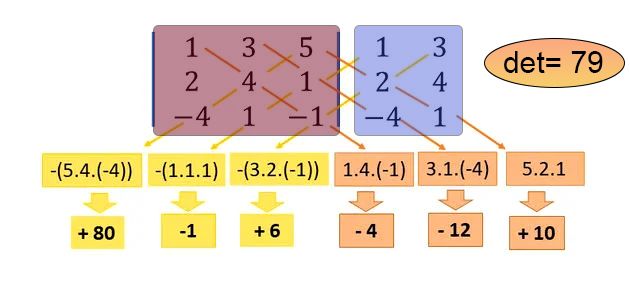
この画像では、赤い領域は行列式を計算する行列を表し、青い領域は行列の一部の要素の仮想コピーです。マクロコードは、図に示されている計算を正確に実行し、行列式を返します。この例では、行列式は79です。

最終的な考察

さて、読者の皆様、また1つの記事が終了しました。しかし、擬似逆行列の値を計算するために必要な手順はまだすべて実装されていません。この点については次の記事で詳しく解説し、その中でこのタスクを実行するアプリケーションを紹介します。この記事の付録に記載されたコードを使用することは可能ですが、問題は、あらゆる種類の構造を自由に使用できるわけではないということです。擬似逆行列(PInv)を使用するためには、実際には行列型を操作する必要があります。計算の説明で示しているものでは、任意のデータモデリングを使用できますが、何でも使えるようにするためには必要な変更を加えるだけで済みます。では、次の記事でお会いしましょう。