Neuronale Netze leicht gemacht (Teil 94): Optimierung der Eingabereihenfolge

Einführung

Ein gängiger Ansatz bei der Verarbeitung von Zeitreihen besteht darin, die ursprüngliche Anordnung der Zeitschritte beizubehalten. Es wird davon ausgegangen, dass die historische Reihenfolge die optimalste ist. Den meisten bestehenden Modellen fehlen jedoch explizite Mechanismen zur Erforschung der Beziehungen zwischen entfernten Segmenten innerhalb der einzelnen Zeitreihen, die in der Tat starke Abhängigkeiten aufweisen können. So können beispielsweise Modelle auf der Grundlage von Faltungsnetzen (CNN), die für das Lernen von Zeitreihen verwendet werden, können nur Muster innerhalb eines begrenzten Zeitfensters erfassen. Bei der Analyse von Zeitreihen, in denen sich wichtige Muster über längere Zeitfenster erstrecken, haben solche Modelle daher Schwierigkeiten, diese Informationen effektiv zu erfassen. Die Verwendung von tiefen Netzen ermöglicht eine Vergrößerung des rezeptiven Feldes und löst das Problem teilweise. Die Anzahl der Faltungsschichten, die erforderlich sind, um die gesamte Sequenz abzudecken, kann jedoch zu groß sein, und eine Überdimensionierung des Modells führt zu dem Problem des verschwindenden Gradienten.

Bei Verwendung in Transformer-Architekturmodellen ist die Wirksamkeit der Erkennung langfristiger Abhängigkeiten in hohem Maße von vielen Faktoren abhängig. Dazu gehören die Sequenzlänge, verschiedene Strategien der Positionskodierung und die Tokenisierung der Daten.

Diese Überlegungen veranlassten die Autoren des Dokuments „Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations“ zu der Idee, die optimale Nutzung historischer Sequenzen zu finden. Könnte es eine bessere Organisation von Zeitreihen geben, die angesichts der gestellten Aufgabe ein effizienteres Repräsentationslernen ermöglichen würde?

In diesem Artikel stellen die Autoren einen einfachen und sofort einsetzbaren Mechanismus namens Segment, Shuffle, Stitch (S3, segmentieren, mischen, zusammennähen), vor, mit dem man lernen kann, wie man die Darstellung von Zeitreihen optimiert. Wie der Name schon sagt, unterteilt S3 eine Zeitreihe in mehrere sich nicht überschneidende Segmente, mischt diese Segmente in der optimalen Reihenfolge und kombiniert die gemischten Segmente zu einer neuen Sequenz. Dabei ist zu beachten, dass die Reihenfolge der Segmentverschiebung für jede einzelne Aufgabe gelernt wird.

Darüber hinaus integriert S3 die ursprüngliche Zeitreihe über eine lernfähige gewichtete Summenoperation mit einer gemischten Version, bei der die Schlüsselinformationen der ursprünglichen Sequenz erhalten bleiben.

S3 fungiert als modularer Mechanismus, der so konzipiert ist, dass er sich nahtlos in jedes beliebige Zeitreihenanalysemodell integrieren lässt, was zu einem reibungsloseren Trainingsverfahren mit geringerem Fehler führt. Da S3 zusammen mit dem Backbone-Netz trainiert wird, werden die Shuffling-Parameter gezielt aktualisiert und an die Merkmale der Quelldaten und des zugrunde liegenden Modells angepasst, um die zeitliche Dynamik besser widerzuspiegeln. Außerdem kann S3 gestapelt werden, um einen detaillierteren Shuffle mit höherer Granularität zu erstellen.

Bei dem vorgeschlagenen Algorithmus müssen nur wenige Hyperparameter eingestellt werden, und es werden nur wenige zusätzliche Rechenressourcen benötigt.

Um die Effektivität der vorgeschlagenen Ansätze zu bewerten, integrieren die Autoren der Methode S3 in verschiedene neuronale Architekturen, einschließlich CNN- und Transformer-basierte Modelle. Die Leistungsbewertung an verschiedenen Datensätzen von univariaten und multivariaten Vorhersageklassifizierungsproblemen zeigt, dass die Hinzufügung von S3 zu einer erheblichen Verbesserung der Effizienz des trainierten Modells führt, wenn alle anderen Faktoren gleich bleiben. Die Ergebnisse zeigen, dass die Integration von S3 in moderne Methoden eine Leistungsverbesserung von bis zu 39,59 % bei Klassifizierungsaufgaben bringen kann. Bei den ein- und mehrdimensionalen Zeitreihenprognosen kann die Effizienz des Modells um 68,71 % bzw. 51,22 % gesteigert werden.

1. S3-Algorithmus

Betrachten wir die vorgeschlagene S3-Methode im Detail.

Als Eingangsdaten verwendet das Verfahren die mehrdimensionale Zeitreihe X, die aus T Zeitschritten und C Kanälen besteht und in N sich nicht überschneidende Segmente unterteilt ist.

Wir betrachten den allgemeinen Fall einer multivariaten Zeitreihe, obwohl die Methode auch mit univariaten Zeitreihen gut funktioniert. Eine eindimensionale Zeitreihe kann als Spezialfall einer mehrdimensionalen Reihe betrachtet werden, wenn die Anzahl der Kanäle C gleich 1 ist.

Ziel der Methode ist es, die Segmente optimal zu einer neuen Sequenz X' anzuordnen, die es uns ermöglicht, die wichtigsten zeitlichen Beziehungen und Abhängigkeiten innerhalb einer Zeitreihe besser zu erfassen. Dies wiederum führt zu einem besseren Verständnis der Zielaufgabe.

Die Autoren der Methode S3 schlagen eine dreistufige Lösung für das oben genannte Problem vor: „Segmentieren“, „Mischen“ und „Kombinieren“.

Das Modul Segment unterteilt die ursprüngliche Sequenz X in N sich nicht überschneidende Segmente, von denen jedes τ Zeitschritte enthält, wobei τ = T/N ist. Die Menge der Segmente kann dargestellt werden als S = {s1, s2, . . . , sn}.

Die Segmente werden dem Modul Shuffle zugeführt, das einen Mischvektor P = {p1, p2, . . . , pn} verwendet, um die Segmente in der optimalen Reihenfolge neu anzuordnen. Jeder Parameter pj von Shuffle im Vektor P entspricht dem Segment sj in der Matrix S. Grundsätzlich ist P ein Satz lernfähiger Gewichte, die vom Netz optimiert werden und die Position und Priorität eines Segments in einer neu geordneten Folge steuern.

Das Mischverfahren ist recht einfach und intuitiv: je höher der Wert von pj, desto höher die Priorität des Segments sj in einer gemischten Folge. Eine gemischte Folge Sshuffled kann wie folgt dargestellt werden:

Die Permutation von S auf der Grundlage der sortierten Reihenfolge P ist standardmäßig nicht differenzierbar, da sie diskrete Operationen beinhaltet und Unstetigkeiten einführt. Weiche Sortiermethoden nähern sich der Sortierreihenfolge an, indem sie Wahrscheinlichkeiten zuweisen, die widerspiegeln, wie viel größer jedes Element im Vergleich zu anderen ist. Diese Annäherung ist zwar von Natur aus differenzierbar, kann aber Rauschen und Ungenauigkeiten mit sich bringen, wodurch die Sortierung nicht intuitiv ist. Um ein differenzierbares Sortieren und Mischen zu erreichen, das genauso genau und intuitiv ist wie traditionelle Methoden, führen die Autoren der Methode mehrere Zwischenschritte ein. Diese Schritte schaffen einen Pfad für die Gradienten, der durch die Shuffle-Parameter P fließt.

Zunächst erhalten wir die Indizes, die die Elemente von P sortieren, mit σ = Argsort(P). Wir haben eine Liste von Tensoren S = {s1, s2, s3, ...sn}, die wir auf der Grundlage der Liste von Indizes σ σ = {σ1, σ2, ..., σn} auf differenzierbare Weise umordnen wollen. Dann erstellen wir eine Matrix U der Größe (τ × C) × n × n, in der wir jedes si N-mal wiederholen.

Danach bilden wir eine n x n große Ω-Matrix, in der jede Zeile j ein Element ungleich Null an der Position k = σj hat. Wir wandeln die Matrix Ω in eine binäre Matrix um und skalieren jedes Element, das nicht Null ist, mit einem Skalierungsfaktor auf 1. Dieser Prozess schafft einen Pfad für Gradienten, die während der Backpropagation durch P fließen.

Mit dem Hadamard-Produkt zwischen U und Ω erhält man eine Matrix V, in der jede Zeile j ein von Null verschiedenes Element k hat, das gleich sk ist. Summiert man über die letzte Dimension und transponiert die resultierende Matrix, erhält man die endgültige gemischte Matrix Sshuffled.

Die Verwendung einer mehrdimensionalen Matrix P' ermöglicht es uns, zusätzliche Parameter einzuführen, mit denen das Modell komplexere Darstellungen erfassen kann. Daher führen die Autoren der Methode S3 einen Hyperparameter λ ein, um die Dimensionalität von P' zu bestimmen. Wir haben dann die Summierung von P' über die ersten λ - 1 Dimensionen durchgeführt, um einen eindimensionalen Vektor P zu erhalten, der dann zur Berechnung der Permutationsindizes σ = Argsort(P) verwendet wird.

Dieser Ansatz ermöglicht es, die Anzahl der Shuffling-Parameter zu erhöhen und so komplexere Abhängigkeiten in Zeitreihendaten zu erfassen, ohne die Sortiervorgänge zu beeinträchtigen.

Im letzten Schritt verkettet das Modul Stitch die gemischten Segmente Sshuffled, um eine gemischte Sequenz X' zu erstellen.

Um die in der ursprünglichen Reihenfolge der analysierten Zeitreihen enthaltenen Informationen zu erhalten, führen sie eine gewichtete Summierung der ursprünglichen und gemischten Sequenzen mit den Parametern w1 und w2 durch, die ebenfalls durch das Training des Hauptmodells optimiert werden.

Wenn wir S3 als eine modulare Ebene betrachten, können wir sie zu einer neuronalen Architektur zusammenfügen. Definieren wir ϕ als einen Hyperparameter, der die Anzahl der S3-Schichten bestimmt. Der Einfachheit halber und um zu vermeiden, dass für jede S3-Schicht ein eigener Segment-Hyperparameter festgelegt wird, definieren die Autoren der Methode einen Parameter θ als Multiplikator für die Anzahl der Segmente in den nachfolgenden Schichten.

Wenn mehrere S3-Schichten gestapelt werden, segmentiert und mischt jede Ebene ℓ von 1 bis ϕ die Eingabedaten auf der Grundlage der Ausgabe der vorherigen Schicht.

Alle lernbaren Parameter von S3 werden zusammen mit den Modellparametern aktualisiert, und es werden keine Zwischenverluste für die S3-Schichten eingeführt. Damit wird sichergestellt, dass die S3-Stufen aufgaben- und stufengerecht ausgebildet werden.

In Fällen, in denen die Länge der Eingangssequenz X nicht durch die Anzahl der Segmente N teilbar ist, werden die ersten T mod N Zeitschritte der Eingangssequenz abgeschnitten. Um sicherzustellen, dass keine Daten verloren gehen und die Eingabe- und Ausgabeformen gleich sind, fügen wir die abgeschnittenen Samples später wieder an den Anfang der Ausgabe der letzten S3-Schicht.

Die originale Visualisierung der Methode ist unten dargestellt.

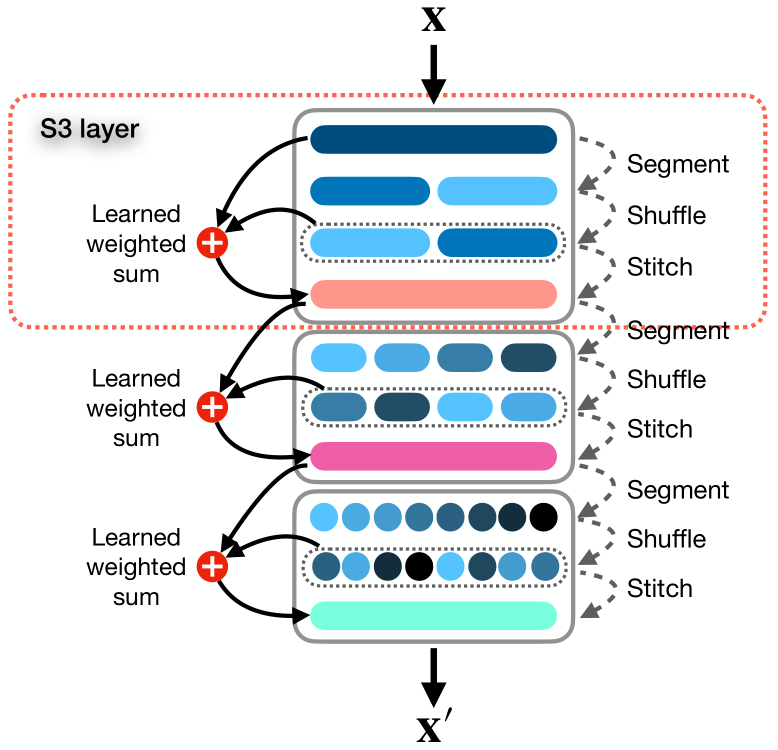
An dieser Stelle kann hinzugefügt werden, dass die Permutationsparameter auf der Grundlage der Ergebnisse der in dieser Arbeit vorgestellten Experimente in der Anfangsphase des Trainings angepasst werden. Danach sind sie festgelegt und ändern sich später nicht mehr.

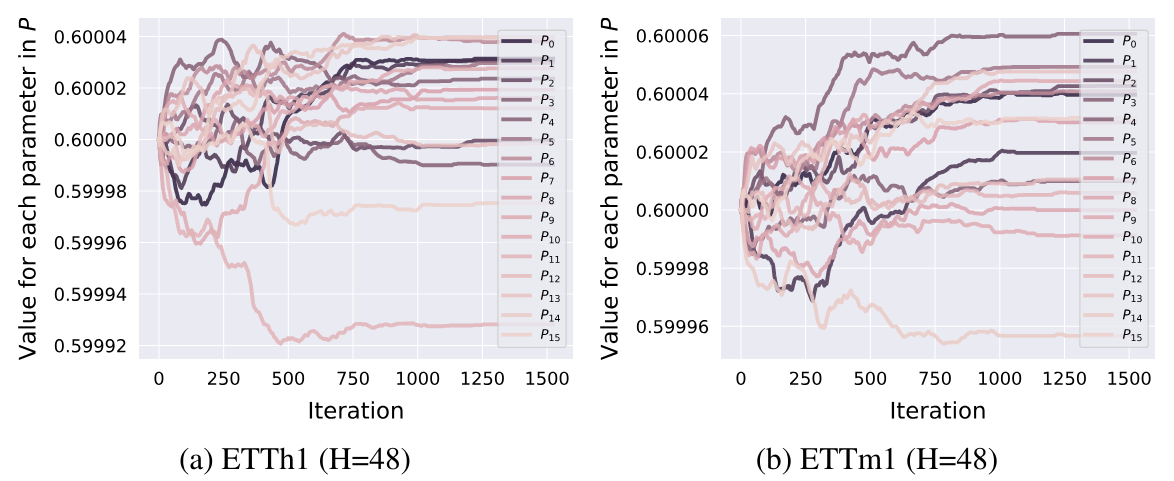
2. Implementierung in MQL5

Nach der Betrachtung der theoretischen Aspekte der S3-Methode gehen wir zum praktischen Teil unseres Artikels über, in dem wir die vorgeschlagenen Ansätze in MQL5 implementieren. Doch bevor wir mit dem Schreiben von Code beginnen, sollten wir die Architektur der vorgeschlagenen Ansätze im Lichte unserer bestehenden Entwicklungen betrachten.

2.1 Lösungsarchitektur

Um die Sortierreihenfolge der Daten zu bestimmen, verwenden die Autoren der Methode S3 einen Vektor lernbarer Parameter P. In unserer Bibliothek gibt es lernfähige Parameter nur in neuronalen Schichten. Nun, wir können eine neuronale Schicht verwenden, um Segmentprioritäten zu erzeugen. In diesem Fall kann das Parametertraining mit den verfügbaren Methoden innerhalb der neuronalen Schicht durchgeführt werden. Aber es gibt eine Nuance: Wir müssen die neuronale Schicht mit Eingaben füttern, die nicht für die Trainingsparameter vorgesehen sind. Die Situation ist ganz einfach: Wir geben einen festen Vektor, der mit „1“ gefüllt ist, in eine solche neuronale Schicht ein.

Mit diesem Ansatz können wir das Problem der mehrdimensionalen Matrix der Permutationen P' sofort lösen. Um die Dimension dieser Matrix zu ändern (die Autoren der S3-Methode haben den Hyperparameter λ definiert), müssen wir nur die Größe des ursprünglichen Datenvektors ändern. Der Rest der Funktionalität bleibt unverändert. Die Summierung der einzelnen Parameter für jedes Segment ist bereits in unserer neuronalen Schicht implementiert. Die Größe der Ergebnisse einer solchen neuronalen Schicht ist gleich der Anzahl der Segmente.

Um die Segmentprioritäten in den Bereich der Wahrscheinlichkeitswerte zu übertragen, wird die SoftMax-Funktion verwendet.

Wir werden einen ähnlichen Ansatz für die Parameter zur Gewichtung des Einflusses der ursprünglichen und der gemischten Sequenzen verwenden. Diesmal ist die Ergebnisgröße der Ebene 2. Als Aktivierungsfunktion dieser Schicht wird das Sigmoid verwendet.

Diese Parameter waren erlernbar. Was den Algorithmus für die Sortierung der Segmente in aufsteigender oder absteigender Reihenfolge der Wahrscheinlichkeiten betrifft, so müssen wir diese Funktionalität implementieren.

Theoretisch spielt die Sortierreihenfolge (auf- oder absteigend) der Prioritäten der einzelnen Segmente keine Rolle. Denn wir werden die Reihenfolge der Permutation von Segmenten lernen. Dementsprechend wird das Modell während des Trainingsprozesses die Prioritäten entsprechend der festgelegten Sortierreihenfolge verteilen. Wichtig ist dabei, dass die Sortierreihenfolge beim Training und im Betrieb des Modells unverändert bleibt.

Um eine Gradientenfehlerfortpflanzung auf den Prioritätsvektor P zu ermöglichen, schlugen die Autoren der Methode einen recht komplexen Algorithmus vor, bei dem sie mehrdimensionale Arrays und doppelte Eingaben erstellen. Dies führt zu einem zusätzlichen Rechenaufwand und erhöhtem Speicherbedarf. Können wir eine effizientere Option anbieten?

Schauen wir uns den von den Autoren der S3-Methode vorgeschlagenen Prozess an und analysieren wir die Maßnahmen und Ergebnisse.

Zunächst wird eine Matrix U gebildet, die eine mehrfache Kopie der ursprünglichen Daten ist. Ich möchte dieses Verfahren ausschließen, um den mit der Speicherung einer großen Matrix verbundenen Speicherbedarf und die beim Kopieren von Daten verbrauchten Rechenressourcen zu verringern.

Die zweite Matrix Ω ist eine binäre Matrix, die überwiegend mit Nullwerten gefüllt ist. Die Anzahl der Nicht-Null-Werte ist gleich der Anzahl der Segmente in der analysierten Sequenz (N). Die Anzahl der Nullelemente ist N - 1 mal größer. Hier sollten wir eine dünnbesetzte Matrix verwenden, die sowohl den Speicherverbrauch als auch die Rechenaufwand bei der Multiplikation von Matrizen reduziert.

Nach dem S3-Algorithmus erfolgt als Nächstes eine elementweise Matrixmultiplikation, gefolgt von einer Addition entlang der letzten Dimension und einer Transposition der resultierenden Matrix.

Als Ergebnis aller oben genannten Operationen erhalten wir einfach einen gemischten ursprünglichen Tensor. Eine einfache Operation, bei der Tensorelemente permutiert werden, erfordert weniger Ressourcen und wird schneller ausgeführt.

Die Autoren entwickelten einen solchen komplexen Permutationsalgorithmus, um die Fehlergradientenfortpflanzung auf den Prioritätsvektor P zu implementieren. Dies ist teilweise eine „Falle“ der automatischen Differenzierung von PyTorch, die die Autoren der Methode bei der Konstruktion ihres Algorithmus verwendet haben.

Wir entwickeln Feedforward- und Backpropagation-Algorithmen. Das erhöht natürlich unsere Kosten für die Erstellung von Algorithmen, gibt uns aber auch mehr Flexibilität bei der Erstellung von Prozessen. Daher können wir im Feed-Forward-Durchgang die oben genannten Operationen durch ein direktes Mischen der Daten ersetzen. Dies ist offensichtlich ein effektiverer Ansatz.

Nun müssen wir über die Frage der Ausbreitung des Fehlergradienten entscheiden. Beim Mischen der Eingänge nimmt jedes Segment nur einmal am Ausgangstensor teil. Folglich wird der gesamte Fehlergradient auf das entsprechende Segment übertragen. Mit anderen Worten: Bei der Verteilung des Fehlergradienten auf die Eingabedaten müssen wir eine umgekehrte Permutation der Segmente durchführen. Dieses Mal werden wir mit dem Fehlergradiententensor arbeiten.

Die zweite Frage: Wie wird der Fehlergradient auf den Prioritätsvektor übertragen? Hier ist der Algorithmus ein wenig komplizierter. Beim Vorwärtsdurchgang wird eine Priorität für das gesamte Segment verwendet. Daher müssen wir im Rückwärtsdurchgang den Fehlergradienten des gesamten Segments mit einer Priorität erfassen. Zu diesem Zweck müssen wir den Eingangsvektor des gewünschten Segments mit dem entsprechenden Segment des Fehlergradiententensors multiplizieren.

Darüber hinaus haben wir bei der Konstruktion einer binären Matrix Ω Skalierungsfaktoren verwendet, um Elemente, die nicht Null sind, in 1 umzuwandeln. Um eine Zahl, die nicht Null ist, in 1 umzuwandeln, muss man sie natürlich durch dieselbe Zahl dividieren oder mit dem Kehrwert multiplizieren. Daher sind die Skalierungsfaktoren gleich dem Kehrwert der Prioritätsnummern. Das bedeutet, dass der oben ermittelte Wert des Fehlergradienten durch die Segmentpriorität geteilt werden muss.

Dabei ist zu beachten, dass die Segmentpriorität nicht gleich „0“ sein sollte. Durch die Verwendung der SoftMax-Funktion kann diese Option ausgeschlossen werden. Sie schließt jedoch hinreichend kleine Werte nicht aus, deren Division zu hinreichend großen Werten des Fehlergradienten führen kann.

Außerdem wird durch die Verwendung der SoftMax-Funktion bei der Bildung der Wahrscheinlichkeiten der Segmentprioritäten gewährleistet, dass alle Werte im Bereich (0, 1) liegen. Es liegt auf der Hand, dass Segmente mit niedrigerer Priorität einen größeren Fehlergradienten erhalten, da die Division durch eine Zahl kleiner als 1 ein Ergebnis ergibt, das größer ist als die Dividende.

Das waren also die subtilen Momente in diesem Algorithmus. Mit diesen Überlegungen können wir uns nun an die Umsetzung in Code machen. Beginnen wir mit der Implementierung auf der Kontextseite von OpenCL.

2.2 Erstellung der Kernel von OpenCL

Wie immer beginnen wir mit der Implementierung der Algorithmen der Vorwärtsdurchgänge. Auf der Programmseite von OpenCL erstellen wir zunächst den FeedForwardS3-Kernel.

Ich möchte an dieser Stelle daran erinnern, dass wir die Generierung von Segmentverteilungswahrscheinlichkeiten und die gewichtete Summierung der ursprünglichen und der gemischten Sequenz in verschachtelten neuronalen Schichten implementieren werden. Das bedeutet, dass dieser Kernel fertige Daten in Form von Parametern erhält.

Daher erhält unser Kernel Zeiger auf 5 Datenpuffer und 2 Konstanten als Parameter. Die 3 Puffer enthalten die Eingaben: die ursprüngliche Sequenz, die Segmentwahrscheinlichkeiten und die Gewichte. Zwei weitere Puffer sind für die Aufzeichnung der Kernel-Ausgaben vorgesehen. In eine davon schreiben wir die Ausgabesequenz und in die zweite die Segment-Shuffle-Indizes, die wir bei der Durchführung von Backpropagation-Operationen benötigen.

In den Konstanten geben wir die Fenstergröße eines Segments und die Gesamtzahl der Elemente in der Sequenz an.

Bitte beachten Sie, dass wir in der zweiten Konstante die Größe des Eingabevektors angeben und nicht die Anzahl der Segmente oder Zeitschritte. Bei der Größe des Segmentfensters geben wir ebenfalls die Anzahl der Array-Elemente und nicht die Zeitschritte an. Daher müssen beide Konstanten ohne Rest durch die Größe des Vektors eines Zeitschritts teilbar sein.

__kernel void FeedForwardS3(__global float* inputs,
                            __global float* probability,
                            __global float* weights,
                            __global float* outputs,
                            __global float* positions,
                            const int window,
                            const int total
                           )
  {
   int pos = get_global_id(0);
   int segments = get_global_size(0);

Wir planen, den Kernel in einem eindimensionalen Aufgabenraum zu starten, der auf der Anzahl der Segmente der zu analysierenden Sequenz basiert. Im Kernelkörper identifizieren wir sofort den aktuellen Fluss und bestimmen auch die Gesamtzahl der Segmente auf der Grundlage der Anzahl der laufenden Aufgaben.

Für den Fall, dass die gesamte Eingabegröße kein Vielfaches der Fenstergröße eines Segments ist, wird die Gesamtzahl der Segmente um 1 reduziert.

   if((segments * window) > total)
      segments--;

Im nächsten Schritt sortieren wir die Segmentprioritäten, um ihre Reihenfolge zu bestimmen. Wir werden den Sortieralgorithmus jedoch nicht in seiner reinen Form organisieren. Stattdessen bestimmen wir die Position des analysierten Segments in der Sequenz. Um die Position eines Elements zu bestimmen, brauchen wir nur einen Durchlauf durch den Segmentwahrscheinlichkeitsvektor. Bei der Sortierung eines Vektors sind jedoch mehrere Durchläufe durch den Wahrscheinlichkeitsvektor und die Synchronisierung von Rechenthreads erforderlich.

Hier teilen wir den Algorithmus in 2 Zweige auf, abhängig vom Index des aktuellen Threads. Der erste Zweig ist der allgemeine Fall und wird verwendet, wenn der aktuelle Thread-Index kleiner ist als die Anzahl der Segmente. Wenn man bedenkt, dass der Index des ersten Threads gleich 0 ist, mag die gegebene Formulierung der Bedingung seltsam erscheinen. Früher haben wir in Fällen, in denen die Eingabegröße kein Vielfaches der Größe des Segmentfensters war, den Wert der Variable für die Anzahl der Segmente reduziert. Und in diesem Fall folgt der letzte Thread dem 2. Zweig des Algorithmus zur Bestimmung der Segmentposition.

Um die Position des Segments zu bestimmen, das dem aktuellen Arbeitsgang entspricht, legen wir im Allgemeinen seine Priorität in einer lokalen Konstante fest. Wir führen eine Schleife vom ersten bis zum aktuellen Segment durch, in der wir die Anzahl der Elemente zählen, deren Priorität kleiner oder gleich der des aktuellen Segments ist. Bei der absteigenden Sortierung wird die Anzahl der Elemente ermittelt, deren Priorität größer oder gleich dem aktuellen Segment ist.

Dann organisieren wir eine Schleife vom nächsten bis zum letzten Segment, in der wir die Anzahl der Elemente mit einer strikt geringeren Priorität addieren (strikt mehr, wenn wir in absteigender Reihenfolge sortieren).

Nach Abschluss der Operationen beider Schleifen erhalten wir die Position des aktuellen Segments in der Gesamtsequenz.

   int segment = 0;
   if(pos < segments)
     {
      const float prob = probability[pos];
      for(int i = 0; i < pos; i++)
        {
         if(probability[i] <= prob)
            segment++;
        }
      for(int i = pos + 1; i < segments; i++)
        {
         if(probability[i] < prob)
            segment++;
        }
     }

Die Aufteilung eines Durchlaufs durch den Prioritätsvektor in 2 Schleifen erfolgt für den speziellen Fall, dass 2 oder mehr Elemente mit der gleichen Priorität vorhanden sind. In diesem Fall hat das Element Vorrang, das in der ursprünglichen Reihenfolge weiter vorne steht. Nun, wir könnten einen Algorithmus mit einer Schleife konstruieren, aber in diesem Fall müssten wir vor dem Vergleich der Prioritäten bei jeder Iteration prüfen, ob das Segment vor oder nach dem aktuellen in der ursprünglichen Sequenz liegt.

Im zweiten Zweig des Spezialfall-Algorithmus ordnen wir einfach die Segmentnummer ihrer Reihenfolge in der Sequenz zu. In dem oben erwähnten Sonderfall werden alle vollständigen Segmente gemischt, und das letzte (nicht vollständige) Segment bleibt an seinem Platz.

   else
      segment = pos;

Nachdem wir nun die Position des Segments in der gemischten Sequenz bestimmt haben, können wir es verschieben. Dazu legen wir die Offsets in den Eingangs- und Ausgangspuffern fest.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Wir speichern sofort eine bestimmte Position in dem entsprechenden Puffer.

   positions[pos] = (float)segment;

Nicht zu vergessen ist die gewichtete Summierung der ursprünglichen und der gemischten Sequenzen. Um unnötiges Kopieren von Daten in den Ergebnispuffer zu vermeiden, speichern wir natürlich sofort die gewichtete Summe von 2 Segmenten aus der ursprünglichen und der gemischten Sequenz. Zu diesem Zweck speichern wir die Gewichtungs-Parameter in lokalen Konstanten.

   const float w1 = weights[0];
   const float w2 = weights[1];

Wir erstellen eine Schleife mit einer Anzahl von Iterationen, die der Fenstergröße eines Segments entspricht, in der wir die Elemente von 2 Sequenzen unter Berücksichtigung der Gewichte summieren und die erhaltenen Werte im Ergebnispuffer speichern.

   for(int i = 0; i < window; i++)
     {
      if((shift_in + i) >= total || (shift_out + i) >= total)
         break;
      outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i];
     }
  }

Nach der Erstellung des Kernels für den Vorwärtsdurchgang wird mit der Arbeit am Rückwärtsdurchgang fortgefahren. Hier beginnen wir mit dem Aufbau des Kernels von InsideGradientS3, in dem wir den Fehlergradienten auf die Ebene der vorherigen Schicht und die Prioritäten der Segmente verteilen. In den Kernelparametern fügen wir Zeiger auf die Puffer der entsprechenden Fehlergradienten zu den zuvor betrachteten Puffern hinzu.

__kernel void InsideGradientS3(__global float* inputs,
                               __global float* inputs_gr,
                               __global float* probability,
                               __global float* probability_gr,
                               __global float* weights,
                               __global float* outputs_gr,
                               __global float* positions,
                               const int window,
                               const int total
                              )
  {
   size_t pos = get_global_id(0);

Der Kernel wird in einem eindimensionalen Aufgabenraum entsprechend der Anzahl der Segmente in der analysierten Sequenz gestartet. Im Kernelkörper identifizieren wir sofort den aktuellen Operations-Thread. In diesem Fall ist es nicht erforderlich, die Gesamtzahl der Segmente zu bestimmen.

Als Nächstes laden wir die während des Vorwärtsdurchgangs ermittelten Konstanten aus den Datenpuffern.

   int segment = (int)positions[pos];
   float prob = probability[pos];
   const float w1 = weights[0];
   const float w2 = weights[1];

Danach bestimmen wir den Offset in den Datenpuffern.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Und wir werden lokale Variablen für Zwischendaten deklarieren.

   float grad = 0;
   float temp = 0;

Im nächsten Schritt erstellen wir eine Schleife mit einer der Fenstergröße der Segmente entsprechenden Anzahl von Iterationen, in der wir den Fehlergradienten für die Segmentpriorität sammeln.

   for(int i = 0; i < window; i++)
     {
      if((shift_out + i) >= total)
         break;
      temp = outputs_gr[shift_out + i] * w1;
      grad += temp * inputs[shift_in + i];

Gleichzeitig wird der Fehlergradient in den Puffer der vorherigen Schicht übertragen. Während des Vorwärtsdurchgangs wurden die ursprüngliche und die gemischte Sequenz summiert. Daher sollte jedes Eingabeelement den Fehlergradienten von 2 Threads mit dem entsprechenden Gewicht erhalten.

      inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2;
     }

Bevor der Fehlergradient der Segmentpriorität in den entsprechenden Datenpuffer geschrieben wird, wird der Ausgabewert durch die Wahrscheinlichkeit des aktuellen Segments dividiert.

   probability_gr[segment] = grad / prob;
  }

Dem oben betrachteten Gradientenausbreitungskern fehlt ein Punkt: die Ausbreitung des Fehlergradienten auf die Gewichte der ursprünglichen und gemischten Sequenzen. Um diese Funktionalität zu implementieren, werden wir einen separaten Kernel WeightGradientS3 erstellen.

An dieser Stelle sollte gesagt werden, dass der von uns verwendete allgemeine Ansatz, bei dem der Fehlergradient eines Elements in jedem einzelnen Thread gesammelt wird, in diesem Fall nicht sehr effektiv ist. Dies ist auf die geringe Anzahl von Elementen im Gewichtsvektor zurückzuführen. Wie Sie sehen können, gibt es hier nur 2 davon. Es ist jedoch besser, mehr parallele Threads zu haben, um die Gesamtzeit für das Training des Modells zu reduzieren. Um diesen Effekt zu erzielen, werden wir zwei Arbeitsgruppen von Threads erstellen, von denen jede den Fehlergradienten für ihren Parameter erfasst.

__kernel void WeightGradientS3(__global float *inputs,
                               __global float *positions,
                               __global float *outputs_gr,
                               __global float *weights_gr,
                               const int window,
                               const int total
                              )
  {
   size_t l = get_local_id(0);
   size_t w = get_global_id(1);

Dementsprechend wird der Kernel in einem 2-dimensionalen Aufgabenraum gestartet. Die erste Dimension definiert die Anzahl der parallelen Threads in einer Gruppe. Und die zweite Dimension gibt den Index des Parameters an, für den der Fehlergradient erfasst wird.

Dann deklarieren wir ein lokales Array, in dem jeder Thread der Gruppe seinen Teil der Arbeit speichert.

   __local float temp[LOCAL_ARRAY_SIZE];

Da die Anzahl der Arbeits-Threads nicht größer sein kann als die Größe des deklarierten lokalen Arrays, sind wir gezwungen, die Anzahl der „Arbeitstiere“ zu begrenzen.

   size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);

In der ersten Stufe sammelt jeder Thread seinen Anteil an Fehlergradienten unabhängig von den anderen Threads in der Arbeitsgruppe. Dazu führen wir eine Schleife über die Elemente des Fehlergradientenpuffers am Ausgang der aktuellen Schicht durch, beginnend mit dem Element mit dem Index der aktuellen Thread-Arbeitsgruppe bis zum letzten Element im Array, mit einem Schritt, der der Anzahl der „Arbeitspferde“ entspricht.

Im Schleifenkörper ermitteln wir zunächst den Offset zum entsprechenden Element im Quelldatenpuffer. Dieser Offset hängt vom Index des Gewichts ab, für das wir den Fehlergradienten erfassen. Bei der zweiten Gewichtung ist die Verschiebung in den Gradientenpuffern des Schichtfehlers und der Eingabedaten identisch.

   if(l < ls)
     {
      float val = 0;
      //---
      for(int i = l; i < total; i += ls)
        {
         int shift_in = i;

Wie beim ersten Offset definieren wir zunächst ein Segment im Fehlergradientenpuffer. Dann extrahieren wir aus dem Permutationsvektor das entsprechende Segment in der ursprünglichen Sequenz. Erst dann können wir den Versatz im Eingangspuffer zum gewünschten Element berechnen.

         if(w == 0)
           {
            int pos = i / window;
            shift_in = positions[pos] * window + i % window;
           }

Anhand der Indizes der entsprechenden Elemente in den beiden Datenpuffern berechnen wir den Fehlergradienten für das Gewicht an dieser Position und fügen ihn der Akkumulationsvariablen hinzu.

         val += outputs_gr[i] * inputs[shift_in];
        }
      temp[l] = val;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Nachdem alle Iterationen der Schleife abgeschlossen sind, schreiben wir die akkumulierte Summe des Fehlergradienten in das entsprechende Element des lokalen Speicherarrays und implementieren eine Synchronisationsbarriere für die Arbeitsgruppen-Threads.

Im zweiten Schritt summieren wir die Werte der Elemente des lokalen Arrays.

   int t = ls;
   do
     {
      t = (t + 1) / 2;
      if(l < t && (l + t) < ls)
        {
         temp[l] += temp[l + t];
         temp[l + t] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(t > 1);

Am Ende der Kerneloperationen überträgt der erste Thread der Arbeitsgruppe den Gesamtfehlergradienten an das entsprechende Element des globalen Puffers.

   if(l == 0)
      weights_gr[w] = temp[0];
  }

Nach der Verteilung der Fehlergradienten für alle Elemente entsprechend ihrer Auswirkung auf das Gesamtergebnis wird in der Regel mit der Arbeit an den Algorithmen zur Aktualisierung der Parameter fortgefahren. Im Rahmen dieses Artikels haben wir jedoch alle trainierbaren Parameter innerhalb der verschachtelten neuronalen Schichten organisiert. Folglich sind die Algorithmen zur Aktualisierung der Parameter bereits in den genannten Objekten enthalten. Daher schließen wir hier die Operationen auf der Seite von OpenCL ab und gehen zur Arbeit mit dem Hauptprogramm über.

2.3. Erstellen der Klasse CNeuronS3

Um die vorgeschlagenen Ansätze auf der Seite des Hauptprogramms zu implementieren, erstellen wir eine neue neuronale Schichtklasse CNeuronS3. Seine Struktur wird im Folgenden dargestellt.

class CNeuronS3   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iSegments;
   //---
   CNeuronBaseOCL    cOne;
   CNeuronConvOCL    cShufle;
   CNeuronSoftMaxOCL cProbability;
   CNeuronConvOCL    cWeights;
   CBufferFloat      cPositions;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForwardS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronS3(void)   {};
                    ~CNeuronS3(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronS3;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

In der Klasse deklarieren wir 2 Variablen und 5 verschachtelte Objekte. In den Variablen wird die Fenstergröße eines Segments und die Gesamtzahl der Segmente in der Sequenz gespeichert. Was die verschachtelten Objekte betrifft, so werden wir sie bei der Implementierung der Methoden unserer Klasse berücksichtigen.

Alle Objekte der Klasse werden als statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse „leer“ lassen. Die Initialisierung aller verschachtelten Objekte wird in der Methode Init durchgeführt. Wie immer erhalten wir in den Parametern dieser Methode die Hauptparameter der Klassenarchitektur vom Aufrufer. Achten Sie auf die folgenden 2 Parameter:

• window — Fenstergröße von 1 Segment;
• numNeurons — die Anzahl der Neuronen in der Schicht.

In diesen Parametern geben wir die Anzahl der Array-Elemente anstelle der Schritte der Zeitreihe an. Ihr Wert muss jedoch ein Vielfaches der Größe des Vektors sein, der einen Zeitschritt beschreibt. Mit anderen Worten: Um die Implementierung zu erleichtern, erstellen wir eine Klasse für die Arbeit mit eindimensionalen Zeitreihen. Hier ist der Nutzer für die Wahrung der Integrität der Zeitschritte einer mehrdimensionalen Zeitreihe innerhalb von Segmenten verantwortlich.

bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                     uint window, uint numNeurons, 
                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

Im Hauptteil der Methode rufen wir zunächst dieselbe Methode der Elternklasse auf, die die empfangenen Parameter kontrolliert und die geerbten Objekte initialisiert. Denken Sie daran, die Ausführung der aufgerufenen Methoden zu kontrollieren.

Nach erfolgreicher Initialisierung der abgeleiteten Objekte speichern wir die Fenstergröße von 1 Segment und ermitteln sofort die Gesamtzahl der Segmente.

   iWindow = MathMax(window, 1);
   iSegments = (numNeurons + window - 1) / window;

Als Nächstes initialisieren wir die internen Objekte der Klasse. Zunächst wird eine feste neuronale Schicht mit Einzelwerten initialisiert, die als Eingabe für die Generierung von Segment-Permutationsprioritäten und gewichteten Sequenzsummationsparametern verwendet wird. Hier wird zunächst die neuronale Schicht initialisiert und dann der Ergebnispuffer mit Einzelwerten gefüllt.

   if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buffer = cOne.getOutput();
   if(!buffer || !buffer.BufferInit(buffer.Total(),1))
      return false;
   if(!buffer.BufferWrite())
     return false;

Bitte beachten Sie die folgenden beiden Punkte. Zunächst erstellen wir eine Schicht mit 1 Neuron. Sie erinnern sich, dass wir, als wir an der Architektur unserer Implementierung arbeiteten, sagten, dass die Anzahl der Neuronen in einer bestimmten Schicht die Dimension der Permutationsmatrix angeben würde. Ich sehe keinen Sinn darin, eine mehrdimensionale Matrix zu verwenden. Aus mathematischer Sicht entartet die lineare Funktion der Summierung des Produkts mehrerer Variablen durch eine Konstante ohne die Verwendung von Zwischenaktivierungsfunktionen in das Produkt einer Variablen durch die verwendete Konstante.

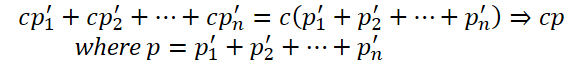
Unter diesem Gesichtspunkt führt eine Erhöhung der Parameter nur zu einem Anstieg der Rechenkomplexität mit fragwürdigen Auswirkungen auf die Effizienz des Modells.

Andererseits ist dies nur meine Meinung. Sie können dies also experimentell testen.

Der zweite Punkt ist die Angabe von „0“ ausgehenden Verbindungen für diese verschachtelte Schicht. Wir planen, dieses Objekt als Ausgangsdaten für 2 neuronale Schichten zu verwenden. Das Vorhandensein von 2 aufeinanderfolgenden Schichten zwang uns, zu einem kleinen Trick zu greifen. Unsere neuronale Basisschicht ist so konzipiert, dass sie nur für eine nachfolgende Schicht eine Gewichtsmatrix enthält. Es gibt jedoch eine Klasse von neuronalen Faltungsschichten, die Matrizen von Gewichtskoeffizienten für eingehende Verbindungen enthalten. Die Verwendung von 1 Eingangselement und mehreren Permutationsprioritäten am Ausgang ist, gelinde ausgedrückt, nicht gerade ein geeignetes Szenario für die Verwendung einer Faltungsschicht. Doch halt.

Ein Eingangselement liefert garantiert 1 lernbaren Parameter im Faltungsfilter. Außerdem können wir die Größe des Permutationsvektors leicht angeben, indem wir die erforderliche Anzahl von Faltungsfiltern spezifizieren. In diesem Fall wird nur 1 Faltungselement angegeben. Auf diese Weise übertragen wir die lernbaren Parameter auf die nachfolgenden neuronalen Schichten.

   if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch))
      return false;
   cShufle.SetActivationFunction(None);

Wie bereits erwähnt, übersetzen wir die Permutationsprioritäten mit Hilfe der SoftMax-Funktion in den Wahrscheinlichkeitsbereich.

   if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch))
      return false;
   cProbability.SetActivationFunction(None);
   cProbability.SetHeads(1);

Wir tun dasselbe mit dem Ziel, Parameter für die gewichtete Summierung von Sequenzen zu erzeugen. Der Unterschied ist, dass wir hier Sigmoid als Aktivierungsfunktion verwenden.

   if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch))
      return false;
   cWeights.SetActivationFunction(SIGMOID);

Und am Ende der Initialisierungsmethode erstellen wir einen Puffer für die Aufzeichnung der Segment-Permutationsindizes.

   if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Die Klasse enthält zwei neue Methoden (feedForwardS3 und calcInputGradientsS3). Sie stellen die zuvor erstellten OpenCL-Programme in die Ausführungswarteschlange. Wie Sie sich denken können, stellt die erste Methode die Ausführung des Feed-Forward-Kerns in die Warteschlange, und die zweite Methode stellt die beiden verbleibenden Fehlergradientenverteilungs-Kerne in die Warteschlange. In früheren Artikeln haben wir bereits den Algorithmus zur Platzierung des Kernels in der Ausführungswarteschlange erörtert. Diese Methoden beruhen auf einem ähnlichen Algorithmus, sodass wir sie hier nicht weiter betrachten werden. Den Code für diese Methoden finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code aller bei der Erstellung des Artikels verwendeten Programme.

Der Vorwärtsdurchgangsalgorithmus unserer Klasse ist in der Methode feedForward enthalten. Wie die Methode der Elternklasse mit dem gleichen Namen erhält die Methode als Parameter einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, das die Eingabedaten enthält.

Vor dem Aufruf der Methode zur Platzierung des Feed-Forward-Kerns in der Warteschlange müssen wir die Prioritäten der Segment-Permutationen und die Parameter für die Gewichtung der Summe der ursprünglichen und der gemischten Sequenzen vorbereiten. Dabei ist zu beachten, dass die Ausgangsdaten für die angegebenen Prozesse ein fester Vektor von Einheitswerten sind. Ihre Werte hängen also nicht von den Ausgangsdaten ab und ändern sich während des Betriebs des Modells nicht. Die angegebenen Werte können sich nur ändern, wenn sich die Lernparameter während des Lernvorgangs ändern. Das bedeutet, dass ihre Neuberechnung nur während des Lernprozesses erforderlich ist. Um die Werte neu zu berechnen, rufen wir die Vorwärtsdurchgangs-Methode der entsprechenden verschachtelten Objekte auf.

bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cWeights.FeedForward(cOne.AsObject()))
         return false;
      if(!cShufle.FeedForward(cOne.AsObject()))
         return false;
      if(!cProbability.FeedForward(cShufle.AsObject()))
         return false;
     }

Als Nächstes mischen wir die ursprüngliche Sequenz, indem wir die Methode aufrufen, um den Forward-Pass-Kernel in die Ausführungswarteschlange zu stellen.

   if(!feedForwardS3(NeuronOCL))
      return false;
//---
   return true;
  }

Vergessen wir nicht, die Ausführung von Vorgängen zu kontrollieren.

Der Algorithmus der Gradientenverteilungsmethode birgt nichts Unerwartetes in sich. Die Methode wird nur während des Lernprozesses aufgerufen, und wir müssen den aktuellen Betriebsmodus des Modells nicht überprüfen.

In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorangegangenen Schicht, dem der Fehlergradient übergeben werden muss, und wir rufen sofort die Methode zum Einreihen die oben erstellten Kernel zur Verteilung der Fehlergradienten auf.

bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!calcInputGradientsS3(NeuronOCL))
      return false;

Als Nächstes wird der Fehlergradient an die Schicht der Prioritätsparameter für das Mischen der Segmente weitergegeben.

   if(!cShufle.calcHiddenGradients(cProbability.AsObject()))
      return false;

Es hat keinen Sinn, den Fehlergradienten weiter auf die Ebene der festen Schicht zu propagieren. Daher überspringen wir dieses Verfahren. Wir müssen lediglich den erhaltenen Fehlergradienten für mögliche Aktivierungsfunktionen korrigieren.

   if(cWeights.Activation() != None)
      if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation()))
         return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Beachten Sie, dass wir die Methode zur Deaktivierung von Fehlergradienten nur dann aufrufen, wenn ein solcher im entsprechenden Objekt vorhanden ist.

Nachdem wir den Fehlergradienten auf alle Elemente unseres Modells entsprechend ihrem Einfluss auf das Gesamtergebnis übertragen haben, müssen wir die Modellparameter anpassen, um den Gesamtfehler zu verringern. Das ist ganz einfach. Um die Parameter der CNeuronS3-Schicht anzupassen, müssen wir nur die Aktualisierungsmethoden der Parameter der entsprechenden verschachtelten Objekte aufrufen.

bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWeights.UpdateInputWeights(cOne.AsObject()))
      return false;
   if(!cShufle.UpdateInputWeights(cOne.AsObject()))
      return false;
//---
   return true;
  }

Damit ist die Beschreibung der Methoden unserer neuen Klasse abgeschlossen. Es ist nicht möglich, alle Methoden unserer neuen Klasse in einem Artikel zu beschreiben, aber Sie können sie selbst studieren, da alle Codes im Anhang enthalten sind. Dort finden Sie den vollständigen Code für diese Klasse und alle ihre Methoden.

2.4 Modellarchitektur

Nachdem wir die neue Ebenenklasse erstellt haben, implementieren wir sie in unsere Modellarchitektur. Ich denke, es ist offensichtlich, dass wir die CNeuronS3-Klasse zur Environment State Encoder-Architektur hinzufügen werden. In diesem Artikel werde ich nicht im Detail auf die Encoder-Architektur eingehen, da sie vollständig aus dem vorherigen Artikel übernommen wurde. Sehen wir uns nur die hinzugefügten neuronalen Schichten an, die wir unmittelbar nach der Quelldatenschicht platziert haben.

Ich möchte Sie daran erinnern, dass unsere Testmodelle für die Analyse historischer Daten im H1-Zeitrahmen konzipiert sind. Für die Analyse werden die letzten 120 Balken der Historie verwendet, die jeweils durch 9 Parameter beschrieben werden.

#define        HistoryBars             120           //Depth of history
#define        BarDescr                9             //Elements for 1 bar description

Während der Vorbereitung dieses Artikels haben wir 3 aufeinanderfolgende Schichten implementiert, die die Eingaben in den Encoder mischen. Für die erste Schicht haben wir Segmente von 12 Zeitschritten (Stunden) verwendet.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 12*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

In der zweiten Schicht haben wir die Segmentgröße auf 4 Zeitschritte reduziert.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 4*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Und im letzten Fall haben wir jeden Zeitschritt gemischt.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Auch die weitere Architektur ist vollständig und unverändert aus den früheren Artikeln übernommen worden. Das bedeutet, dass wir keine Änderungen am Algorithmus der Programme für die Interaktion mit der Umgebung, das Training und den Test der Modelle vorgenommen haben. Den vollständigen Code aller hier verwendeten Programme finden Sie im Anhang.

3. Tests

Wir haben die Algorithmen der vorgeschlagenen Ansätze entwickelt. Kommen wir nun zur vielleicht spannendsten Phase - dem Testen und Auswerten der Ergebnisse.

Wie bereits erwähnt, haben wir während der Arbeit an diesem Artikel keine Änderungen an den Umweltinteraktionsprogrammen vorgenommen. Das bedeutet, dass wir einen zuvor gesammelten Trainingsdatensatz verwenden können, um Modelle zu trainieren.

Ich möchte Sie daran erinnern, dass wir zum Trainieren der Modelle die Aufzeichnungen der Durchläufe des Umgebungsinteraktionsprogramms im MetaTrader 5-Strategietester mit realen historischen Daten des Instruments EURUSD, Zeitrahmen H1, für das gesamte Jahr 2023 verwenden.

Im ersten Schritt trainieren wir den Environment State Encoder. Dieses Modell wird trainiert, um Daten für die nächsten 24 Elemente der analysierten Zeitreihe vorherzusagen.

#define        NForecast               24            //Number of forecast

Mit anderen Worten: Unser Modell versucht, die Kursentwicklung für den nächsten Tag vorherzusagen. Bei der Konstruktion der Verhaltenspolitik unseres Agenten verlassen wir uns nicht auf die empfangene Prognose, sondern auf den verborgenen Zustand des Encoders. Daher sind wir beim Training des Modells nicht so sehr an einer genauen Vorhersage der bevorstehenden Bewegung interessiert - wir bewerten die Fähigkeit des Encoders, die wichtigsten Trends und Tendenzen der bevorstehenden Preisbewegung zu erfassen und in seinem verborgenen Zustand zu verschlüsseln.

Das Encoder-Modell wird nur für die Analyse des Marktzustands trainiert, ohne den Kontostand und die offenen Positionen zu berücksichtigen. Eine Aktualisierung des Trainingsdatensatzes während des Modelltrainings liefert daher keine zusätzlichen Informationen. So können wir das Modell auf einem zuvor erstellten Datensatz trainieren, bis wir das gewünschte Ergebnis erhalten.

Anhand der Ergebnisse des ersten Trainingsschritts können wir die Auswirkungen unserer neuen Schicht auf die vom Modell erhaltenen Ausgangsdaten bewerten. An dieser Stelle sollte ich anmerken, dass das Modell den gemischten und den ursprünglichen Sequenzen fast die gleiche Aufmerksamkeit schenkt. Nur ein bisschen mehr Aufmerksamkeit für das Letztere.

Auf der ersten Ebene lag der Koeffizient der gemischten Sequenz bei 0,5039 und der der ursprünglichen Sequenz bei 0,5679. Gleichzeitig kommt es zu einer fast vollständigen Umstellung der Reihenfolge. Nur das Segment mit dem Index 7 blieb an seinem Platz. Und das Mischen ist völlig zufällig. Es gibt kein einziges Paar von Elementen, das einfach die Plätze tauschen würde.

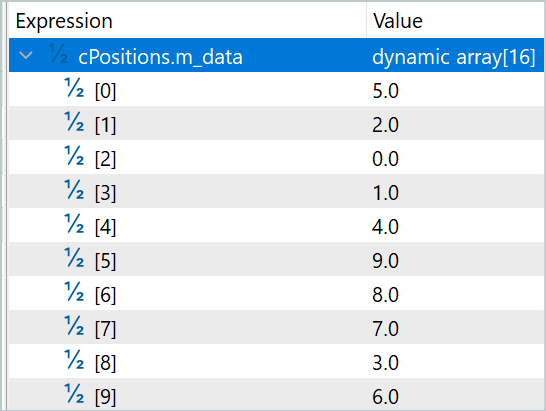
In der nächsten Schicht stiegen beide Koeffizienten leicht auf 0,6386 bzw. 0,6574 an. Ich werde die Liste der Permutationen nicht aufführen, da sie sich verdreifacht hat. Sie enthält keine nicht gemischten Segmente mehr.

In der dritten Ebene wird der ursprünglichen Sequenz mehr Aufmerksamkeit gewidmet, aber der Koeffizient für die gemischte Sequenz bleibt recht hoch. Die Parameter wurden auf 0,5064 bzw. 0,7089 geändert.

Die erzielten Ergebnisse können auf unterschiedliche Weise bewertet werden. Meiner Meinung nach sucht das Modell die Rationalität im paarweisen Vergleich der Segmente.

Das erhaltene Ergebnis ist recht interessant, aber wir sind mehr an den Auswirkungen auf die endgültige Politik des Agenten interessiert. Nachdem wir den Encoder trainiert haben, gehen wir zur zweiten Stufe des Trainings unserer Modelle über. In diesem Stadium trainieren wir die Politik des Akteurs und das Modell des Modell des Kritikers. Die Funktionsweise dieser Modelle hängt in hohem Maße vom Stand des Kontos und der offenen Positionen zum analysierten Zeitpunkt ab. Daher wird unser Lernprozess iterativ sein, indem wir abwechselnd Modelle trainieren und zusätzliche Daten über die Interaktion mit der Umwelt sammeln. So können wir die Verhaltensregeln des Agenten verfeinern und optimieren.

Während des Trainingsprozesses konnten wir eine Strategie so trainieren, dass sie sowohl in der Trainings- als auch in der Testphase Gewinne erzielt. Die Ergebnisse der Ausbildung werden im Folgenden dargestellt.

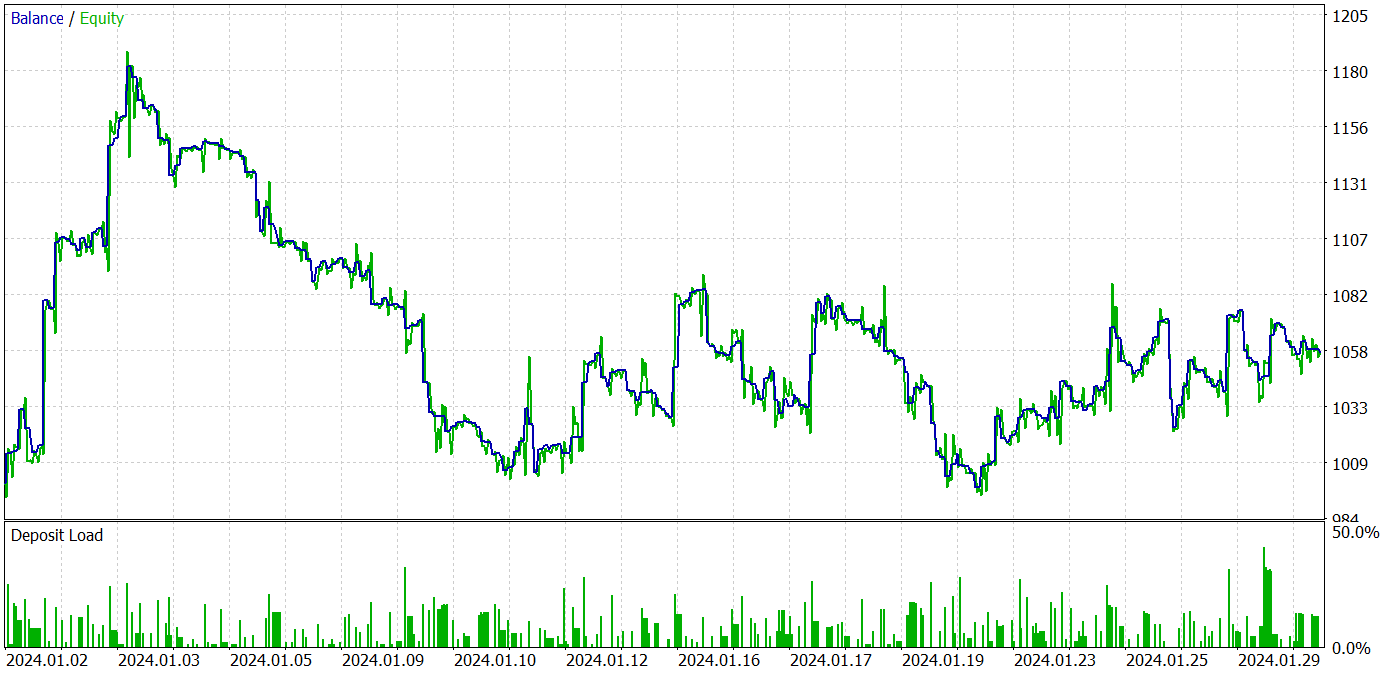
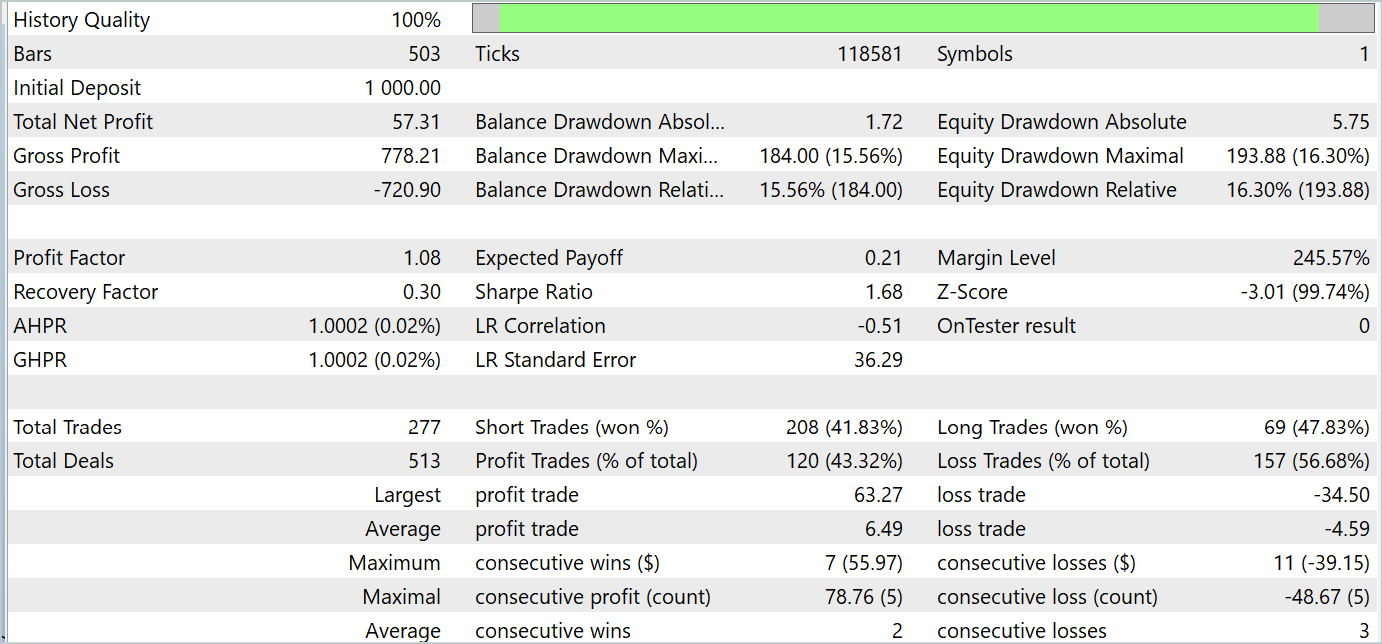
Trotz des erzielten Gewinns sieht die Bilanz nicht gut aus. Das Modell bedarf noch einiger Verbesserungen. Wenn Sie sich den Testbericht genauer ansehen, können Sie die unrentabelsten Montage und Freitage hervorheben. Am Mittwoch hingegen erzielt das Modell einen maximalen Gewinn.

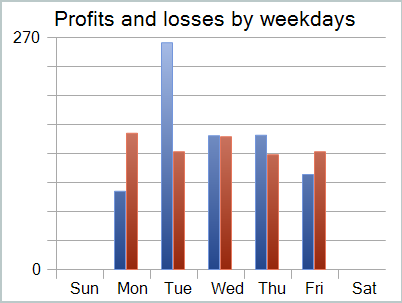
Die Beschränkung des Modellbetriebs auf bestimmte Wochentage wird daher die Gesamtrentabilität des Modells erhöhen. Diese Hypothese muss jedoch anhand eines repräsentativeren Datensatzes genauer geprüft werden.

Schlussfolgerung

In diesem Artikel haben wir eine recht interessante Methode zur Optimierung von Zeitreihenfolgen erörtert: S3. Die Methode wurde in der Veröffentlichung „Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations“ vorgestellt. Die Hauptidee der Methode besteht darin, die Qualität der Darstellung von Zeitreihen zu verbessern. Die Anwendung von S3 führt zu einer höheren Klassifizierungsgenauigkeit und Modellstabilität.

Im praktischen Teil unseres Artikels haben wir unsere Vision der vorgeschlagenen Ansätze unter Verwendung von MQL5 entwickelt. Wir haben mit den vorgeschlagenen Ansätzen Modelle trainiert und getestet. Die Ergebnisse sind recht interessant.

Referenzen

• Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Beispielsammlung EA
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	StudyEncoder.mq5	Expert Advisor	Encode Training EA
5	Test.mq5	Expert Advisor	Trainings-EA für das Model
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL